1 Introduction
The dynamic relationship between predators and prey has long been, and will continue to be, one of the dominant themes in both ecology and mathematical ecology due to its universal existence and importance (Berryman, [1]). In most of ecosystems, the population of one species does not respond instantaneously to interactions with other species. To incorporate this idea in a modeling approach, time delay models have been developed. In most cases, time delays have a destabilizing effect towards dynamical behavior and often time delays are responsible for oscillations of various species. The question of global stability and uniform persistence of individual species involved with the model under consideration is important in a delay differential equation model. There are several publications which explain from mathematical and ecological points of view the necessity of delay differential equation models (Gopalsamy, [2]; Kuang, [3]).
Time delays of one type or another have been incorporated into biological models by many researchers. Freedman and Rao [4] obtained criteria for local stability of predator–prey model with delays. Freedman and Waltman [5] consider a general model of two predators competing for a single prey. They derived criteria for strong persistence in terms of conditions on system parameters. Kuang [6] studied global stability results obtained from comparison analysis, Bendixson–Dulac criterion or limit cycle stability analysis for the general, Gauss-type, predator–prey system without delay. The obtained criteria involve restrictions on the functions (such as prey species growth rate in the absence of predation and predator functional response). Delay models have also been investigated by Hale and Waltman, [7]; Waltman, [8] and Wang and Ma, [9]; for Lotka–Volterra systems. Lu and Takeuchi [10] have proved that a two species Lotka–Volterra delayed competition system is permanent under any delay effect provided that the corresponding undelayed system has a globally stable positive equilibrium. They have also obtained conditions for global stability of positive equilibrium.
Modeling of population ecological interactions involving time delay is being dealt by Kuang [3]. Aziz-Alaoui and Daher Okiye [11], Cao and Freedman [12], Upadhyay and Rai [13], and Upadhyay and Iyenger [14] consider prey predator models and find some significant results. Xiao and Chen [15] consider a system of retarded functional differential equations as a predator prey model with disease in the prey. Permanence and global stability are analyzed. They show that positive equilibrium is locally asymptotically stable when the time delay is suitably small, while a loss of stability by Hopf-bifurcation can occur as the delay increases. Mukherjee and Roy [16] proposed a generalized prey–predator system with time delay and find the conditions for uniform persistence and global stability. Recently, Kar [17] studied a Gaussian-type prey–predator model with selective harvesting and introduced a time delay in the harvesting term. In general, delay differential equations exhibit much more complicated dynamics than ordinary differential equations since the time delay could cause a stable equilibrium to become unstable and cause the population to fluctuate.
In this article, we have considered a two predator-one prey system with time delay due to gestation. The response function is of the Holling type II.
Before we introduce the model and its analysis we would like to present a brief sketch of the construction of the model which may indicate the biological relevance of it:
(i) There are three populations namely, two predators whose population densities are y and z, and one prey whose population density is denoted by x;
(ii) In absence of predation, the prey population grows according to a logistic law of growth with intrinsic growth rate r and carrying capacity K;
(iii) One predator species consumes the prey with the functional response
(iv) Mortality rates of predators are assumed to be proportional to their populations. We have also considered density dependent mortality rate of both the consumer species as
Several researchers at the present time claimed that the effect of time delay must be taken into account to form a biologically meaningful mathematical model (MacDonald, [19]). Form this view point we have introduced the delay in our model and this delay is referred to as the gestation period.
So our proposed model is as follows:
| (1) |
| (2) |
| (3) |
In our system, all the parameters are positive constants. There is a time delay of time τ in the prey species; γ and δ denote the intraspecific competition coefficients of the predators;
2 Equilibria, stability and Hopf bifurcation
System (1)–(3) has five possible non-negative equilibria, namely
| (4) |
| (5) |
| (6) |
| (7) |
Case I
Lemma 1
All the solutions of the system
(1)–(3)
with
Proof
We define the function
Now we shall discuss the stability of the equilibrium points.
For
For
So,
For,
For
So,
For
| (8) |
Obviously A, B, D and E are all positive. So, by the Routh–Hurwitz criterion equation (8) has all negative roots if
| (9) |
Theorem 2.1
- (i)
- (ii)
- (iii)
and it is asymptotically stable if - (iv)
and it is asymptotically stable if - (v)
The interior equilibrium
Now in order to investigate the global stability of the interior equilibrium point let us consider a positive definite function about
| (10) |
Therefore,
| (11) |
| (12) |
So, we arrive at Theorem 2.2:
Theorem 2.2
Assume that the positive equilibrium
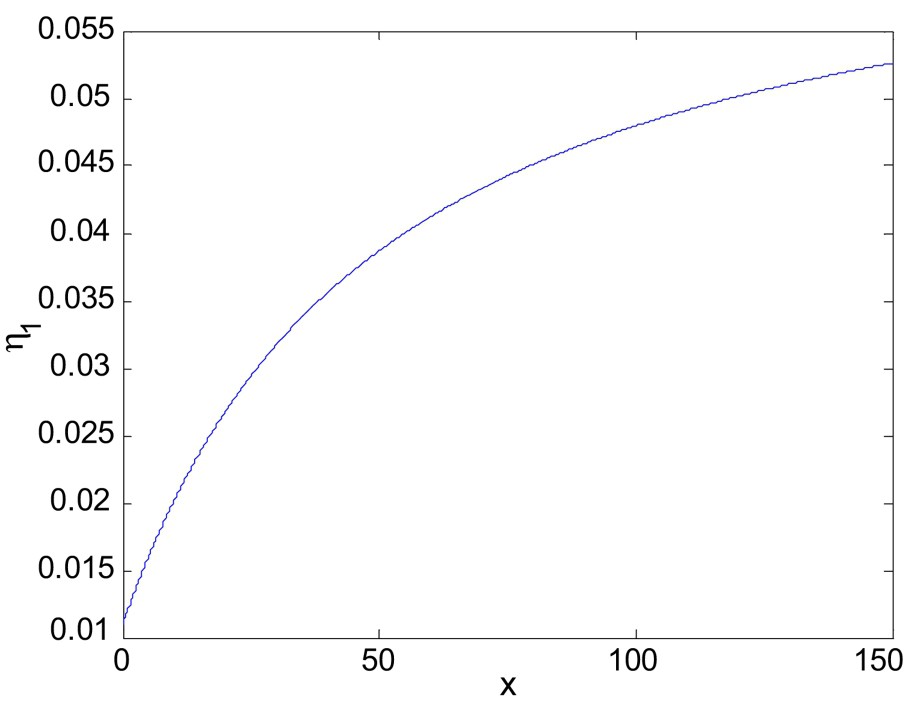
The plot of the function
The plot of
Case II
For
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
Now, from (14) and (15) we get,
| (18) |
| (19) |
Theorem 2.3
If
Remark 2.1
If the interior equilibrium depends smoothly on a parameter θ in an open interval I of R and if there exists a
Liu's criterion
If the characteristic equation of the interior equilibrium point is given by
- (I)
- (II)
Now in order to investigate the global stability of
Theorem 2.4
Let
3 Simulation and discussion
In this article we have studied the dynamical behaviors of a two predator one prey system. The interaction between prey and predators are assumed to be governed by a Holling type II functional response. Here two predators are competing for a single prey.
Often we come across several biological systems in nature exhibiting cyclical behavior. Due to this cyclic nature some populations exhibit periodic fluctuation in abundance, with periodic crashes. One could avoid such crashes and stabilize the population by controlling one of the interacting species (Hudson et al. [22]). Thus it is relevant to find conditions under which a multispecies system exhibits cyclic behavior, and it is equally important to find conditions under which cycles can be prevented in a multispecies system.
First we consider the case with
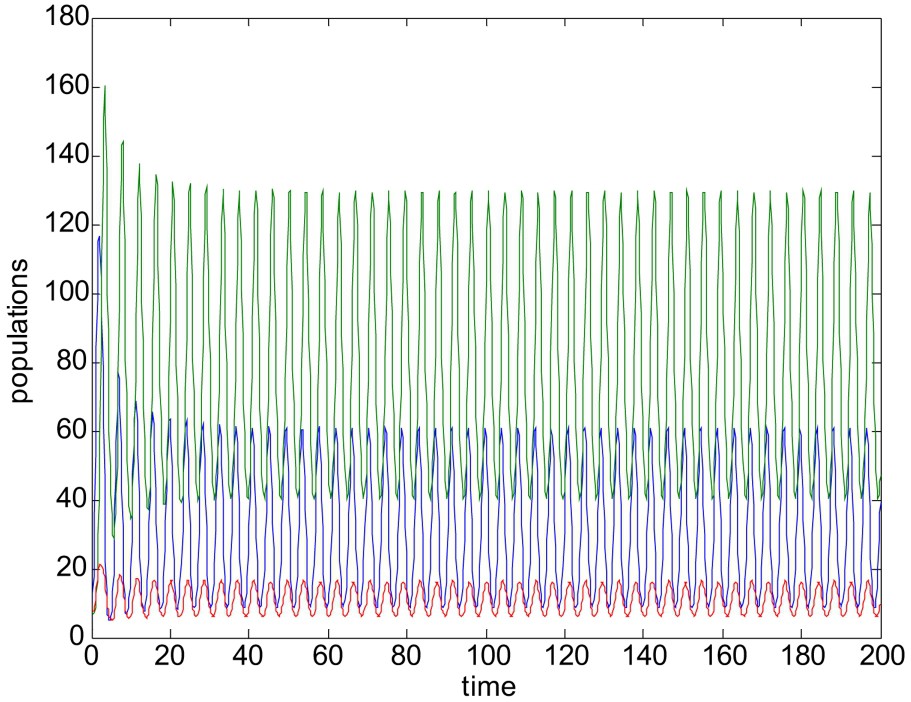
Unstable solution of system (1)–(3). Here parameter values are r = 3.5, K = 150,

When
When
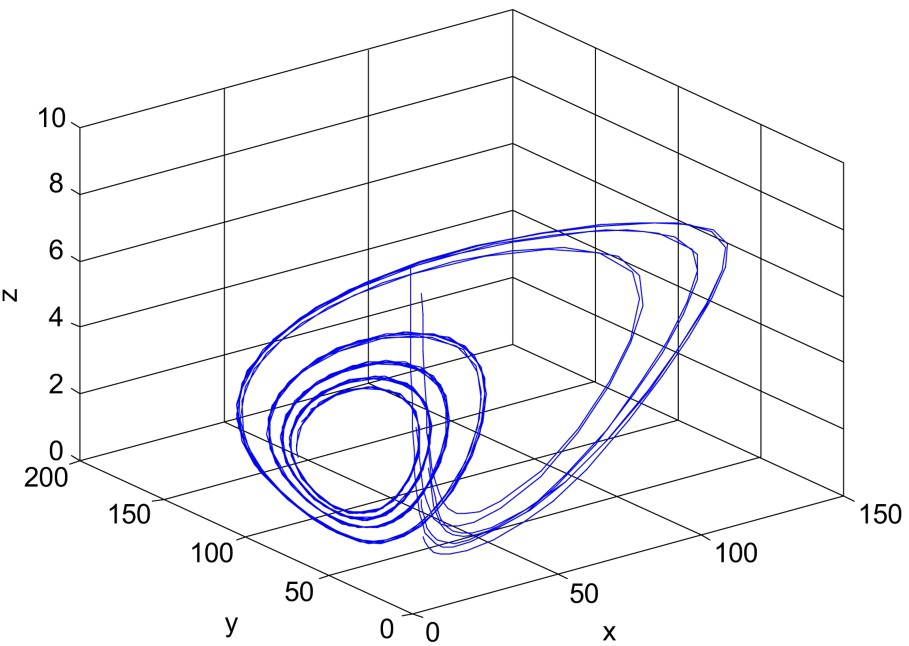
For
Next consider

When
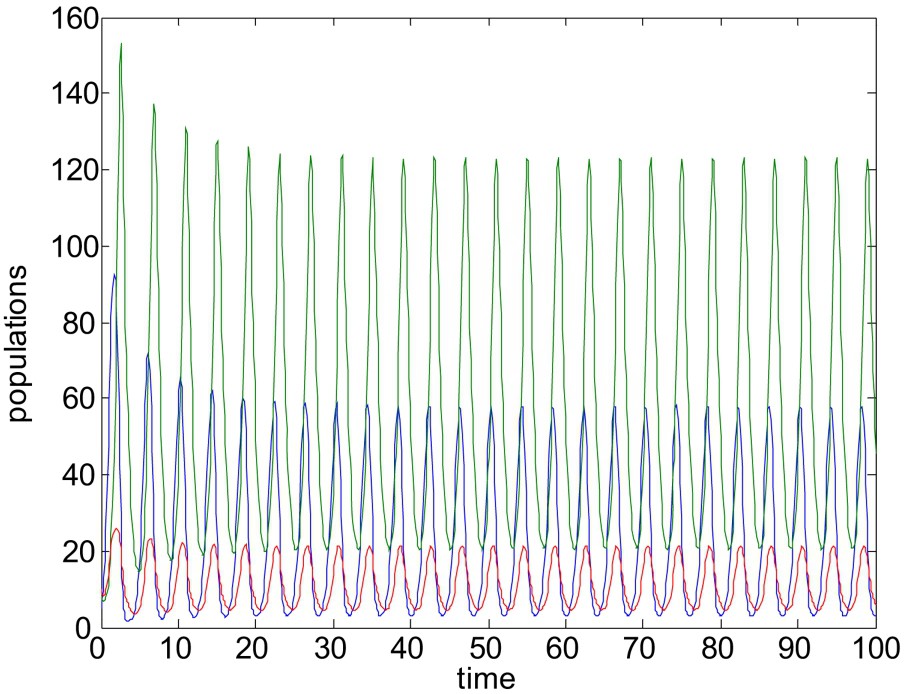
Unstable solution of system (1)–(3). Here all the parameters are same as in Fig. 5, except
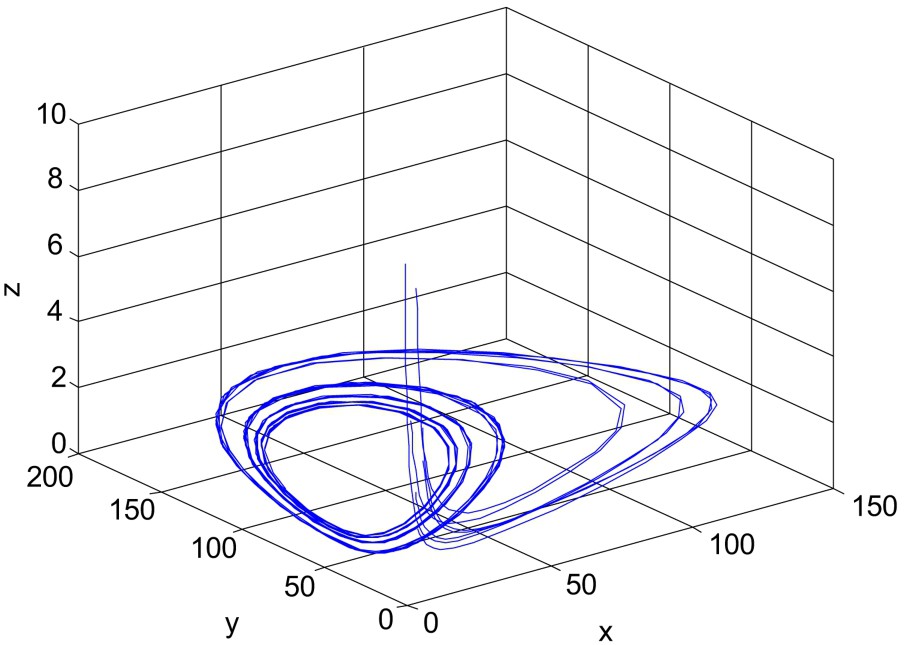
For
The numerical study presented here shows that, using parameter γ or
Now we would like to mention that the stability criteria of the system without delay do not necessarily guarantee the stability of the system with delay. It has been shown that the positive equilibrium which is stable without delay, remains stable under certain conditions when the time delay is less than the threshold value, otherwise the stable equilibrium become unstable. To illustrate the results numerically, choose
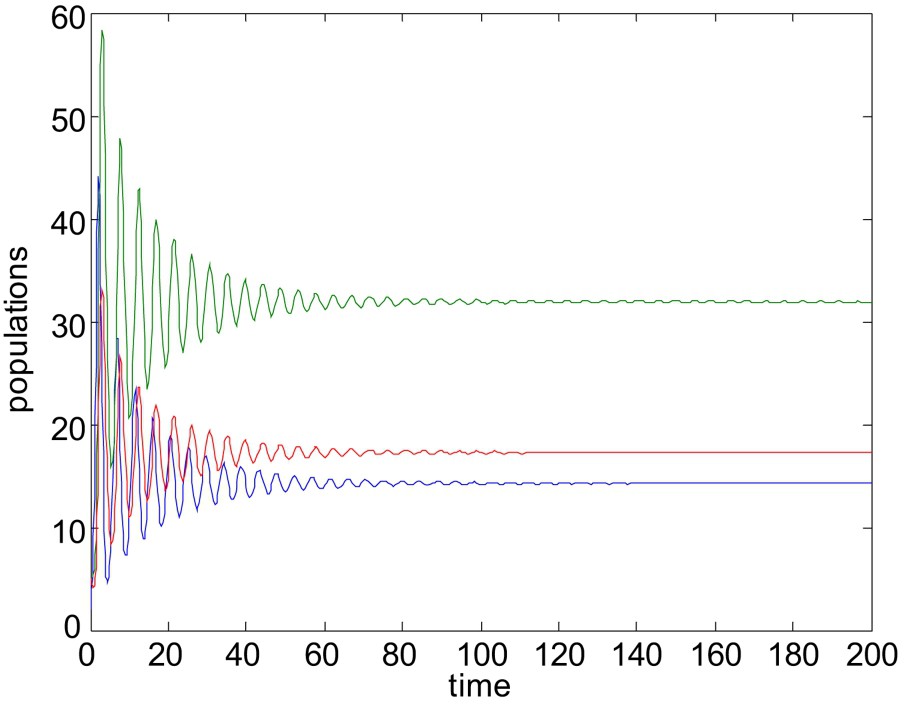
When
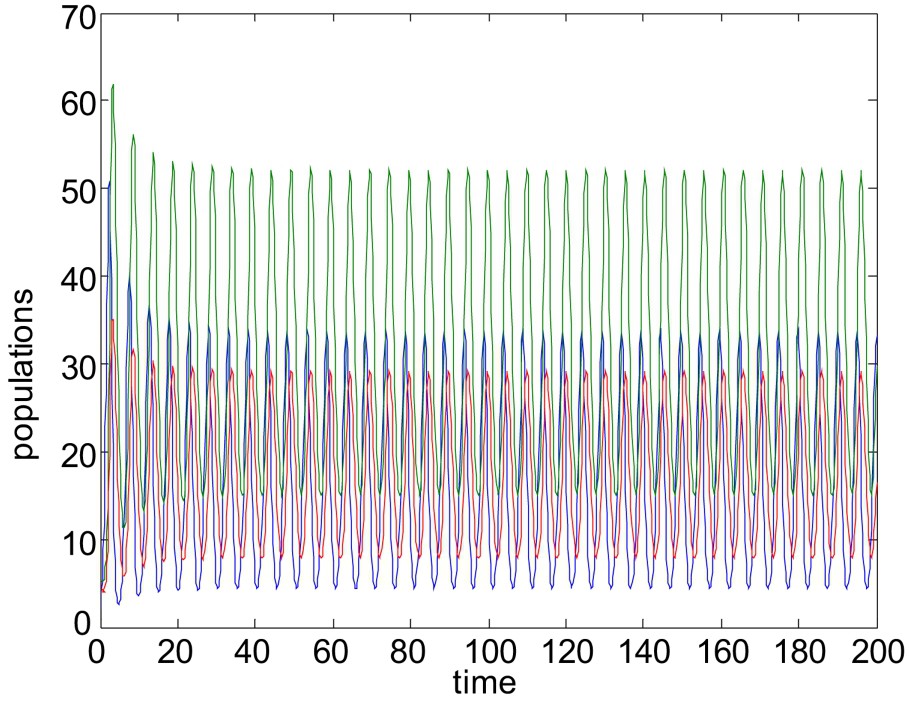
Unstable solution of system (1)–(3). Here all the parameters are same as in Fig. 8, except
For the above choices of parameters
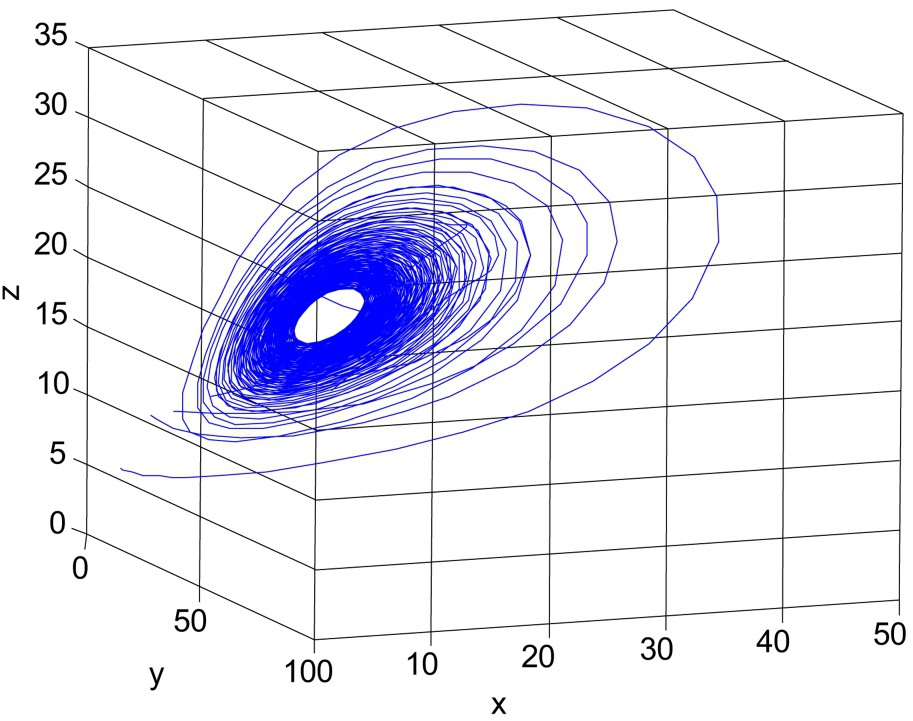
For
We have also given some graphical support in favor of our numerical results.



Vous devez vous connecter pour continuer.
S'authentifier