1 Introduction
In the last century, considerable progress has been made in separating, identifying and purifying the molecules that constitute living cells. In particular, purification of information-bearing molecules such as nucleic acids, proteins and polysaccharides has elucidated the relationship between structure and function under rigorously defined, controlled in vitro conditions. Despite the continuing importance of this reductionist approach to both fundamental biology and biotechnology, it is clear that macromolecules are in completely different conditions in vitro from in vivo. In the latter, they are located in compartments or at compartment boundaries and are surrounded by a variety of small mobile solutes that may be ionised; this heterogeneity means that the important parameters are not only concentrations of reactants and products but also electric fields, gradients of solute activities (including pH gradients), and transport and reaction rates.
In the present paper, we approach the problem of biological complexity by studying the behaviour of two different types of systems: (i) simple, in vitro enzymatic systems in which the media is either of a controllable structural complexity or of an aqueous-hydrophobic nature and (ii) a complex, in vivo system subjected to an extra constraint that in the case presented here is the frog skin after a specific alteration of its ionic environment.
2 Simple, in vitro enzymatic systems
This section concerns simple, in vitro enzymatic systems in which the media is either of a controllable structural complexity or of an aqueous-hydrophobic nature.
A number of studies have dealt with the in vitro behaviour of immobilised enzymes [1–3]. Studies in our group, as explained in the examples given below, illustrate the emergence of a complex behaviour in cases in which simple, ‘monosteric’ (as opposed to ‘allosteric’) enzymes were inserted in various types of artificial structures.
2.1 The problem
The simplest possible behaviour for a monosteric enzyme, E, catalysing the reaction between substrate, S, and product, P, according to:
| (1) |
| (2) |
| (3) |
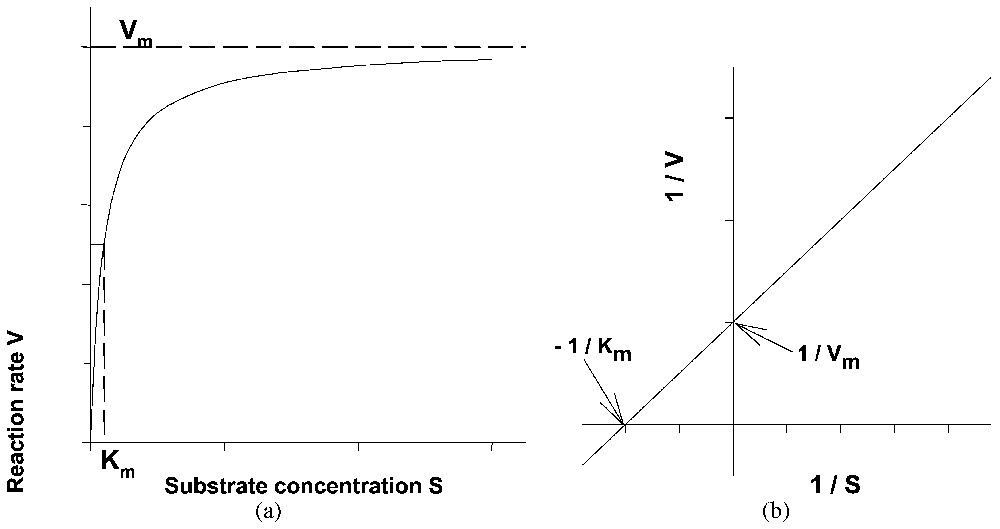
Representative curve of the kinetics of a Michaelis and Menten enzyme reaction using either (a) the direct or (b) the reciprocal system of coordinates.
Now, let us consider model systems in which monosteric enzymes, Ej, are inserted at random in a gel slice, with thickness l, separating two aqueous solutions, and (Fig. 2) [6]. Locally, the rate, Vj, of the catalysed reaction(s) of substrate(s) Sj and product(s) Pj (4):
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
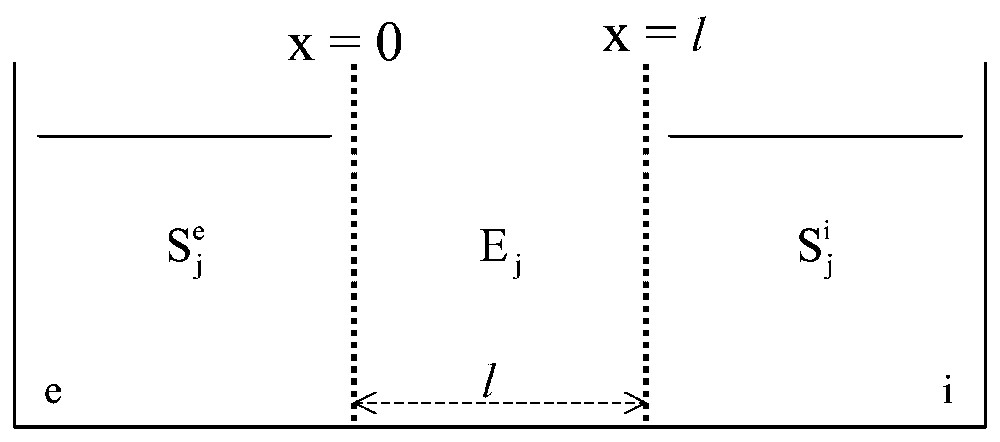
General scheme of the in vitro systems studied. A gel slice, l in thickness and containing one or several enzymes, Ej, distributed at random, is used to separate two aqueous media, and , containing one or several solutes Sj.
2.2 Kinetic behaviour of a monosteric enzyme inserted in a gel slice separating aqueous compartments
In the simplest possible case, i.e. when the system is monoenzymatic (index j thus may be deleted), the concentration of S is the same in and (Se=Si), the system is without any pH effect (γ=constant) and the stationary state has been established everywhere in the gel slice (∂S/∂t=0), one may consider the dimensionless, diffusion–reaction parameter:
| (10) |
| (11) |
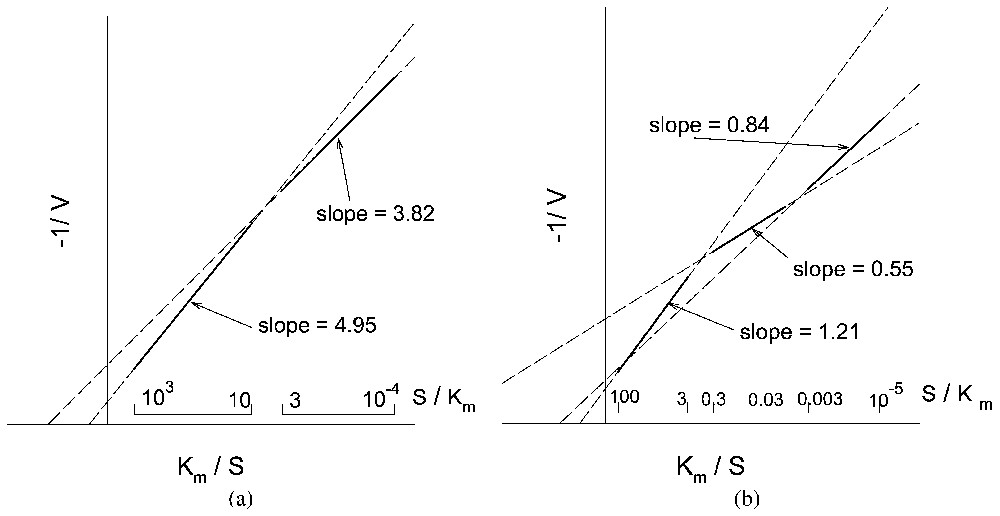
Kinetic behaviour (reciprocal system of coordinates) of a monosteric enzyme system, similar to that described in Fig. 2, for increasing values of αl: (a) dual-phasic behaviour and (b) sigmoidal behaviour.
2.3 Two-enzyme artificial first-order transport systems
Let us consider again [6] a model system made of a gel slice separating two aqueous compartments, and , but now let us insert two monosteric enzymes, E1 and E2, differing in their optimum pH value and catalysing the associated reactions
| (12) |
| (13) |
| (14) |
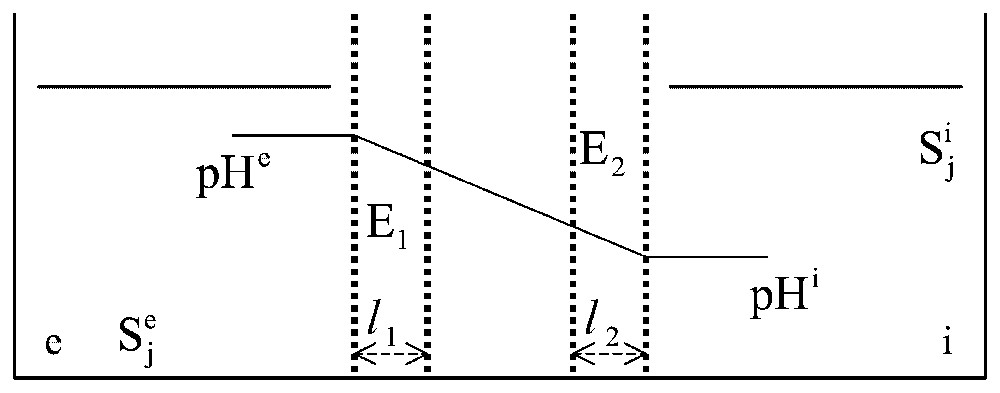
Two-enzyme systems. In a system structurally similar to that described in Fig. 2, two enzymes, E1 and E2, are distributed at random in the gel slice. Two different pH values, pHe and pHi, are imposed on compartments and , in order that only enzyme E1 is active in layer l1 facing and only E2 is active in layer l2 facing .
As an example, let us consider the simple case when the two enzymes have the same Vm and the same Km in solution (Vm1=Vm2=Vm and Km1=Km2=Km) and the two layers, l1 and l2, have the same thickness (. Within each layer, the enzyme activity is treated as constant with x, while the intermediate layer (thickness is considered as purely diffusive, without any significant enzyme activity. The experiment starts with identical concentrations of S in compartments and (i.e. at time 0, Se=Si=S). Under these conditions, a dimensionless, diffusion–reaction parameter:
| (15) |
- • When , whether or not there is a pH feedback, the plot is linear; the transport process thus behaves as a single Michaelis–Menten type process; moreover, in this case, the apparent Km of the transport process is found to be equal to the actual Km of the enzymes in solution.
- • When , again whether or not there is a pH feedback, the plot in reciprocal co-ordinates appears to be made of two asymptotic straight lines, corresponding to S⪡Km and S⪢Km (dual-phasic plot), connected by a monotonous curve. Although there are only two types of enzymes with identical values for Km and for Vm, it might seem that there are two transport processes, one with low apparent Km and Vm and the other with high apparent Km and Vm playing the major role at low and high substrate concentrations, respectively. Moreover the apparent Km and Vm of transport no longer bear a simple relationship to the actual Km and Vm of the enzymes in solution.
- • When and when a pH feedback exists (e.g., consumption or production of protons in reactions (12) and (13)), the curve connecting the two asymptotic straight lines may become sigmoidal.
2.4 Monoenzymatic artificial second-order transport systems
In the preceding sections 2.2 and 2.3, we discussed purely theoretical systems. Let us now consider from both the theoretical and experimental points of view a soluble enzyme constrained to work as a transporter by particular conditions of structure and concentrations [8,9].
Yeast alcohol deshydrogenase (ADH) catalyses the reversible reaction:
| (16) |
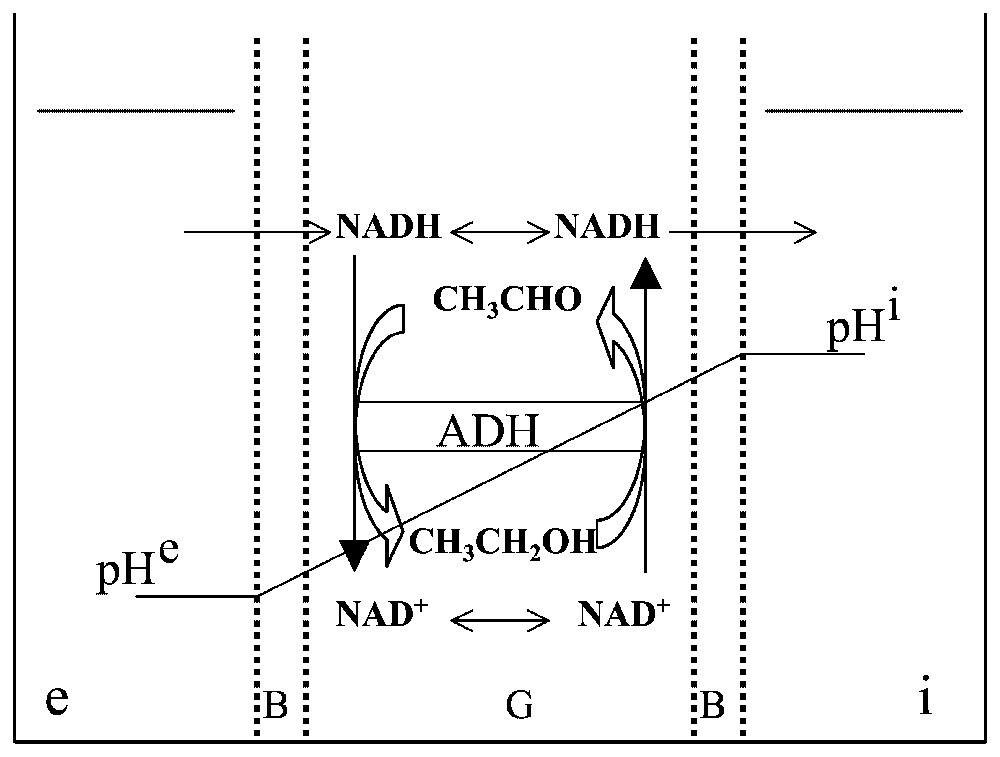
A gel slice, G, with both sides covered with a barrier, B, is used to separate two aqueous compartments, and . The gel slice contains a random distribution of the enzyme ADH which catalyses the oxido-reduction reaction CH3CHO/CH3CH2OH with the cofactor NAD. Two different pH values, pHe and pHi, are imposed on and in order that the reaction is in favour of the alcohol on the side of the gel and in favour of the aldehyde on the side. NADH, but not NAD+, can diffuse freely through barrier B.
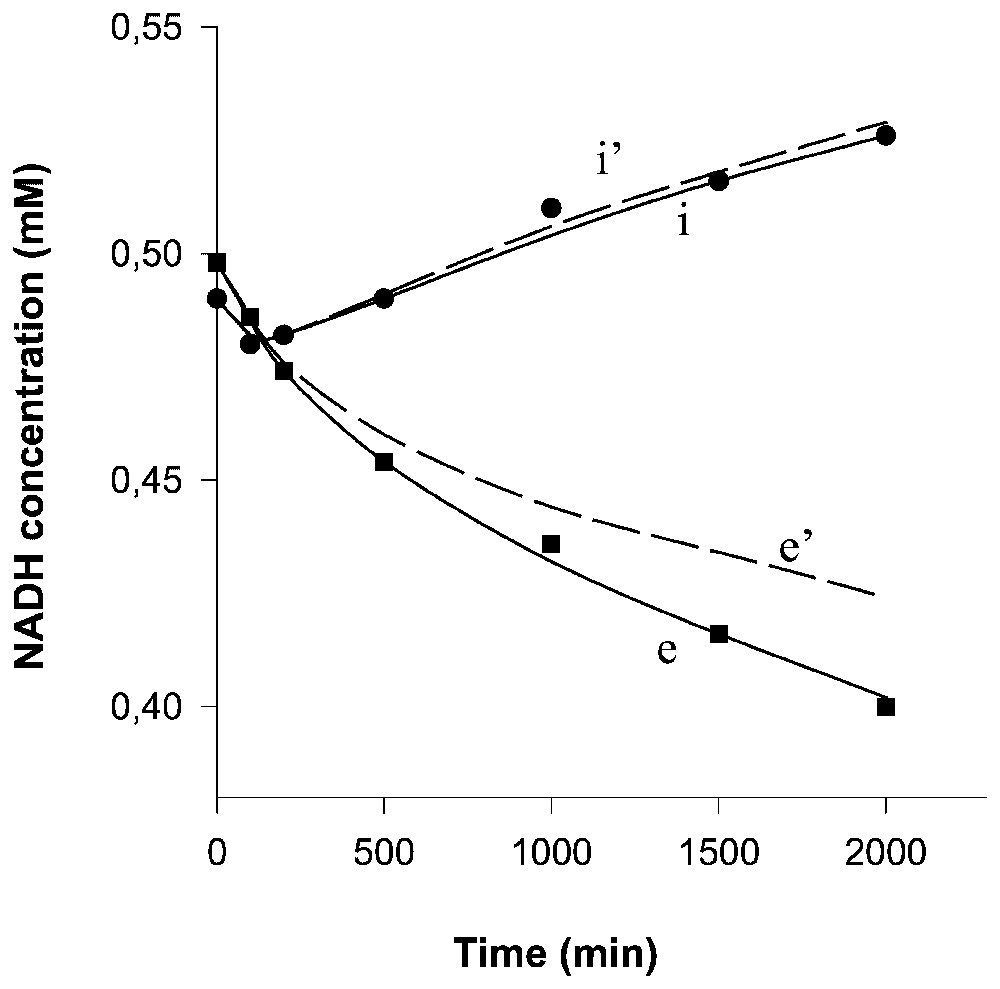
Computed time-courses of the NADH concentrations in compartments (curve e) and (curve i). Curves e' and i' correspond to the concentration changes due only to the transport (i.e. after subtracting the spontaneous, non-enzymatic NADH degradation). Experimental points in compartments (■) and (●).
The analysis and the numerical calculations [9] were performed essentially as above (sections 2.1 and 2.2) using diffusion–reaction equations of the type:
| (17) |
2.5 Enzyme-catalysed reactions in an aqueous/hydrophobic reaction medium
The kinetics of the hydrolysis and synthesis reactions of the peptide bond of the dipeptide, N-Cbz-l-tryptophanyl-glycineamide, catalysed by α-chymotrypsin, have been studied in mixtures of water and 1,4-butanediol [10]. Although the polarity of 1,4-butanediol is not very high, it is miscible with water in all proportions. The initial reaction rates decreased exponentially with decreasing water content in the solvent mixture. The study of the substrate dependencies have revealed that both the apparent and the actual kinetic parameters were dependent on the water content, and thus on the polarity, of the solvent mixture. However, the exponential decrease in the initial rate of hydrolysis was due mainly to the Km increase and only slightly to the modification of the Vm.
A reduction of the water content from 100 to 20% (v/v) did not alter Vm by more than a factor of 4. Such variation in Vm is due to changes in the conformation of the enzyme. One of the main causes of such changes in mixtures of water and organic solvent is the substitution of essential water molecules in the vicinity of the protein surface by organic solvent molecules. However, with organic solvents like 1,4-butanediol, the interactions between organic solvent molecules and the enzyme are similar to those between water molecules and enzyme; these organic solvents thus do not alter the enzyme conformation very much. Another cause is the possible modification of the ionisation/neutralisation constant of ionisable groups of the protein, in particular in the active site, as a consequence of the variation of the polarity of the reaction medium.
Decreasing the polarity of the reaction medium by decreasing its water content led to an exponential increase in the apparent Km for the hydrolysis of the dipeptide (see above) and in the solubility of this dipeptide (Fig. 7). Since the interactions between substrate and the active site of α-chymotrypsine are mainly hydrophobic, this means that decreasing the water content of the reaction medium tends to favour the interactions of the dipeptide with the solvent mixture and thus to weaken the interactions of the dipeptide with the active site of the enzyme. Moreover, it has been established that the ratio of the actual rate constants for the formation/dissociation of the enzyme–substrate complex in the solvent mixture is given by the corresponding ratio in aqueous medium divided by the equilibrium constant for the transfer of the dipeptide from water to the solvent mixture (which is equal to the ratio of the dipeptide solubility in the solvent mixture to that in water).
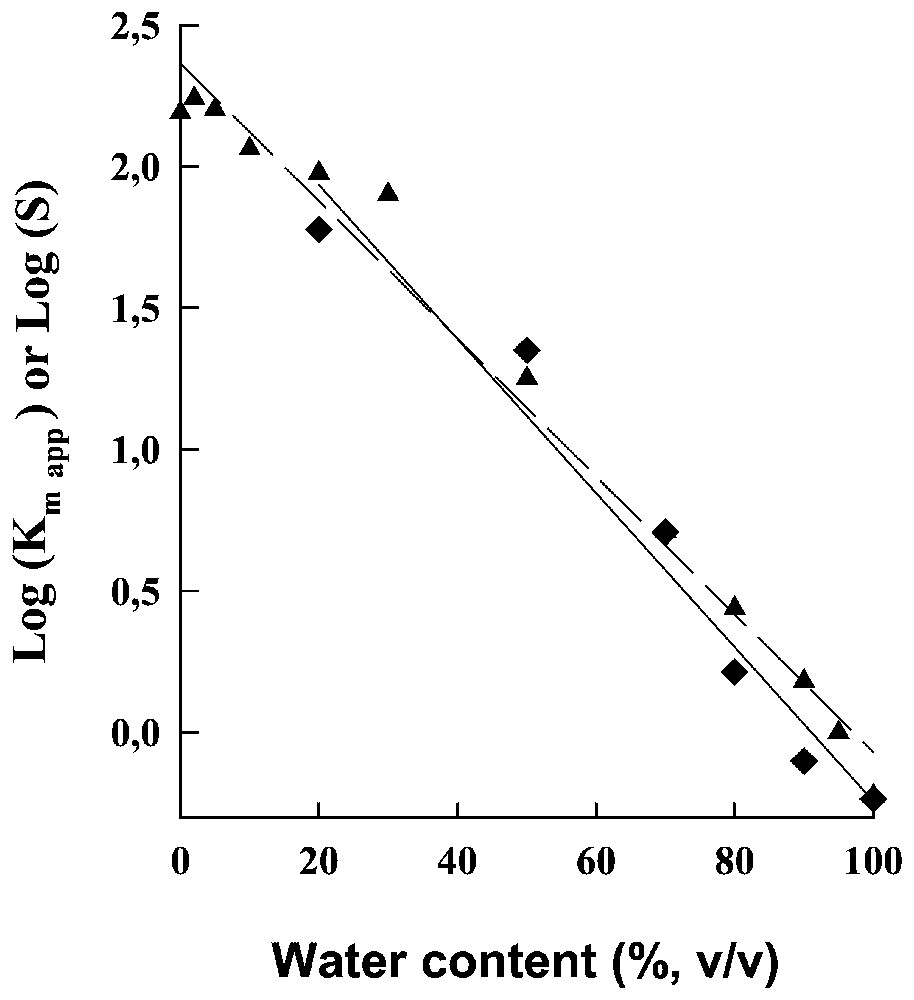
Logarithms of the apparent Km, , for the hydrolysis of the dipeptide ( ) and for the solubility limit, S, of this dipeptide (▴) as a function of the water content of the solvent mixture.
3 Effect of lithium on the electrical potential of frog skin
Frogs maintain the saline concentration of their internal medium, even when immersed in freshwater ponds, due to the activity of a Mg-dependent Na-K-ATPase that creates a steady transepithelial potential difference in the range of a few tens to more than a hundred millivolts (positive inside). This active ion-pumping system has been studied in great detail, especially by Ussing's group [11,12], using the ventral skin of frogs mounted between two aqueous compartments filled with appropriate saline solutions. Maintaining the electrical potential of frog skin in these conditions requires sodium in the external medium. Lithium is the only ion that can be used instead [13]. However, when all or part of the external sodium is replaced by lithium, the electric potential frequently oscillates [14–16], which it never does in the absence of lithium (Fig. 8).
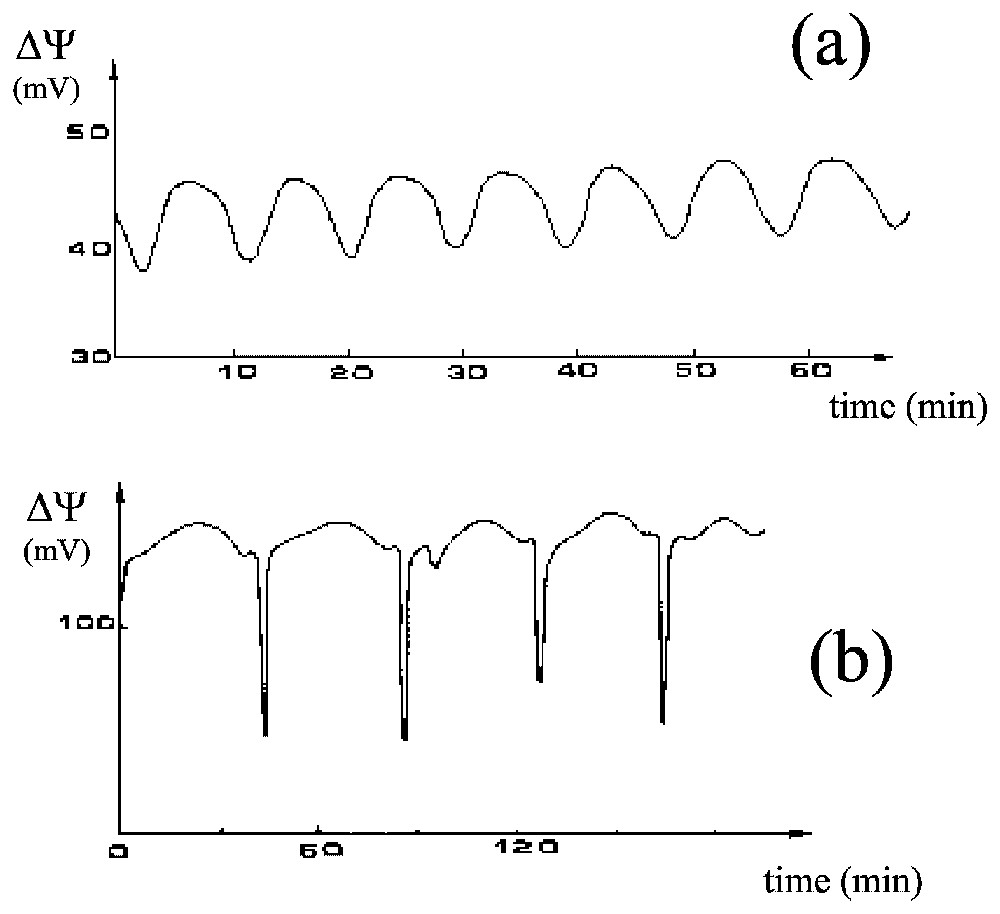
Two cases of oscillations of the electric potential difference, ΔΨ (mV), of the frog skin, (a) almost sinusoidal and (b) much more complex.
A body of evidence obtained by others, cited in Lassalles et al. [17], demonstrates that all the ionic processes are controlled at the level of the skin epithelium, which comprises a few layers of cells separating the external medium from the internal medium . The epithelium may be modelled as follows (Fig. 9): it is made of two main compartments, C1 and C2; the membrane, , at the external face of the epithelium is relatively permeable to Na+ and Li+ whilst it is almost impermeable to K+; the membrane, , between compartments C1 and C2 is permeable to K+ but not to Na+ and contains the Na-K-ATPase pumping sodium and lithium from C1 to C2 and potassium from C2 to C1; the face, c, between epithelium and internal medium is not an actual membrane, but may be considered rather as a non-selective diffusive barrier.
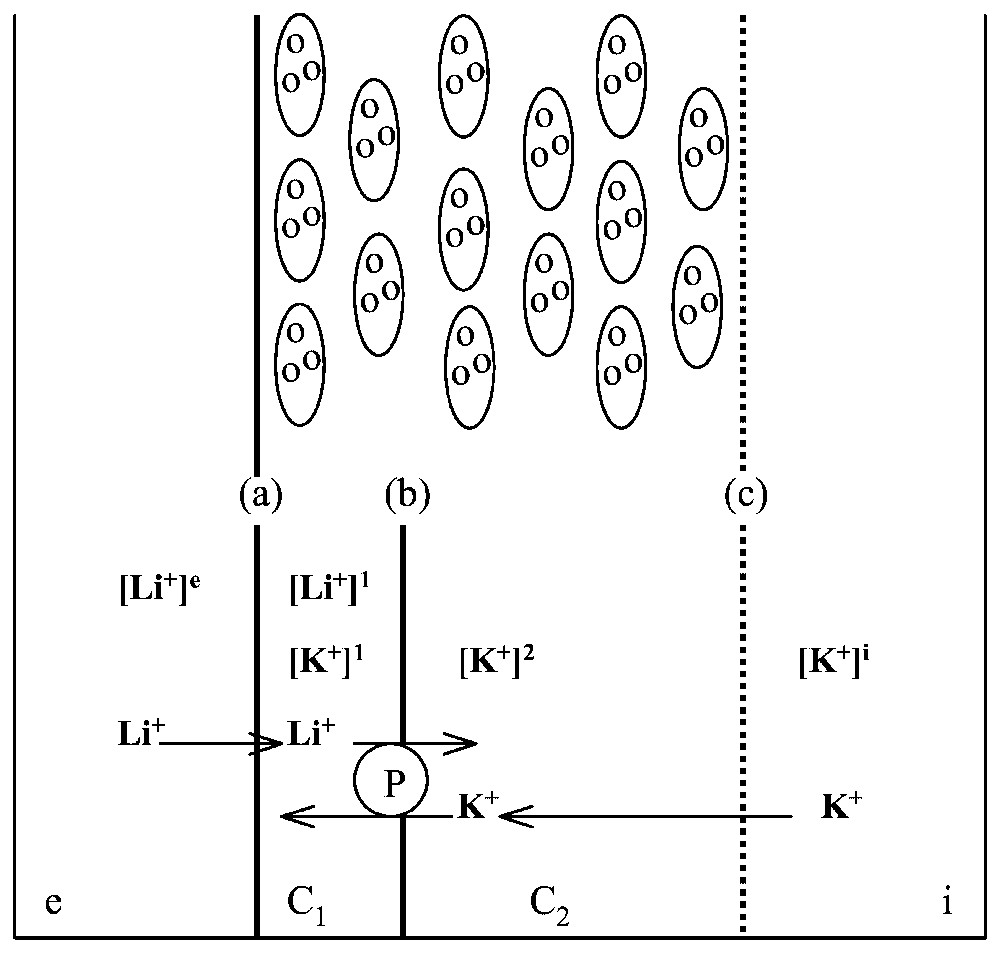
Modelling frog skin epithelium. Top: schematic representation of the cellular structure of frog skin epithelium, mounted between two aqueous, saline solutions, and . Bottom: the epithelium model for ionic exchange. The frog epithelium is modelled as corresponding to two compartments C1 and C2 with three barriers, between and C1, between C1 and C2 and between C2 and . Symbol [x]j stands for concentration of cation x in compartment j. The Na-K-ATPase, P, pumps actively Li+ from C1 to C2 and K+ from C2 to C1.
In studies of the oscillatory process, our group [17–20] has shown experimentally that (i) when no transepithelial potential is imposed, sustained oscillations with a period of about 10 min are maintained for several hours, (ii) an oscillation of the Na+ influx accompanies the electric oscillation (the two oscillations have approximately the same period but are not in phase), (iii) under conditions of imposed potential the transepithelial electric current has damped oscillations, (iv) the shape of the oscillations in potential is quite variable (from almost sinusoidal to very complex), (v) theophyllin (which induces an accumulation of cyclic AMP within the cells) promotes a significant decrease in the mean electric potential of the skin but does not affect the characteristics of the oscillation very much, (vi) important factors influencing the oscillations include temperature, the permeability of the external membrane to lithium and the potassium concentration in the internal medium, (vii) no evident correlation exists between skin area and the characteristics of the oscillations, which may therefore have a local origin (possibly in local oscillators at the level of the cell) and the coupling of these oscillators would generate the macroscopic oscillations and (viii) synchronisation of local oscillators can be controlled by varying the coupling resistance in the absence of diffusion, which is consistent with electrical coupling rather than diffusion being responsible for the synchronisation.
After extensive numerical simulation of the oscillatory process, it proved impossible to obtain all the above characteristics unless the model had a few well-defined properties, the following ones in particular.
- • If £1 and £2 represent the volumes of compartments C1 and C2 per unit surface of epithelium, they obey the relation £1/£2⪡1, i.e. compartment C2 has to be much larger than compartment C1. This makes it possible to choose one of the various possible modes of transport of Na+ through the epithelium proposed in the literature and cited in Lassalles et al. [17]. Indeed, £2⪢£1 does not support the idea that compartment C1 merely corresponds to most of the cytoplasmic volume and C2 is restricted to a few endoplasmic cisternae, whereas it strongly supports the idea that compartment C1 corresponds to a few cytoplasmic vacuoles transporting Na+ (and Li+) and compartment C2 is part or all of the intercellular spaces and possibly some endoplasmic cisternae (in this case, most of the cell cytoplasm would remain inactive in Na+ (or Li+) transport).
- • The main variables are the concentration of Li+ in compartment C1 and that of K+ in compartment C2. When the characteristic times τ1 and τ2 are defined as corresponding to Li+ modifications in C1 and K+ modifications in C2, respectively, the ratio of the characteristic times obeys the relation 0<τ1/τ2<1 with 1 min⩽τ1⩽5 min.
- • Two parameters, ρ and u, represent the relative importance of the active to the passive fluxes of Li+ and K+, respectively, such that ρ⪢1 and u⪢1, with ρ⩽u⩽2ρ (i.e., ρ and u are of the same order of magnitude).
- • P represents the permeability coefficients of interfaces , and for ions K+ and Li+, such that PKb/PKc⪡1 and PLia/PKc⪡1.
4 Discussion and conclusions
Embedding simple Michaelis–Menten enzymes in a gel slice allows them to catalyse not only scalar processes but also vectorial ones, including the uphill transport of a substrate between two compartments. Moreover, a system containing a single species of a simple enzyme can be made to behave as if it contained two different enzymes (or transporters) or an allosterically controlled enzyme (or transporter). These effects are more pronounced the larger the term characteristic of the reaction (Vmγ/Km) compared with that of substrate diffusion (D/l2). The existence of a pH feedback also tends to increase these effects. In the presence of a partially hydrophobic environment (which is likely to be the case with membrane-bound enzymes or transport systems in vivo), the measured kinetic parameters are usually different, sometimes very different from those characteristic of the protein behaviour in homogeneous, aqueous solutions. Another group [21,22] has also shown that it is possible to induce oscillatory phenomena in immobilised enzyme systems or spatio-temporal pattern formation in immobilised bienzymatic systems.
These results are of general relevance to the interpretation of kinetic data on membrane-bound enzymes or transport systems. In reciprocal co-ordinates, such experimental data are often better fitted by two straight lines (one for the high and the other for the low concentrations) than by a single line. In line with the original proposal of Epstein and co-workers [23–25], most authors interpret such data as revealing the presence of two different membrane mechanisms of reaction or transport, with the apparent Km and Vm of the membrane processes being equated to the actual Km and Vm of the catalytic proteins involved. Similarly, sigmoidal experimental curves have been taken as indicative of an allosteric character of the membrane-bound active proteins [26]. Our results clearly show that such interpretations can be wrong, since the complexity of the kinetic behaviour may as well correspond to the partially hydrophobic nature and other features of the cellular structures in which the enzyme or transport systems are inserted (for a more detailed discussion, see Thellier et al. [27]). Indeed, an alternative interpretation to allosteric interaction has been given for sigmoidal kinetic behaviour in an actual biological system in vivo [28].
A real cell membrane is obviously not the same as a thick homogenous gel slice or a water/hydrophobic mixture. Nevertheless, the values of the parameters used in the experiments reviewed here cover the range of biological possibilities [6,8,9]. Moreover, since real membranes are far more complex than our gel slices or aqueous/hydrophobic mixtures, it is likely that the effects of membrane structure and/or hydrophobicity in vivo are even more numerous and diverse than they are in vitro.
In the artificial transport systems discussed here (sections 2.3 and 2.4), a functional asymmetry such as a proton gradient sufficed to induce an active uphill transport even under symmetrical structural conditions. Therefore, although all the active-transport systems isolated until now correspond to proteins asymmetrically anchored in a membrane, one cannot exclude the possibility that structurally symmetrical systems of transport do exist in as yet unstudied organisms or did once exist earlier in evolution.
Situations exist in biology (see Vincent et al. [9]) where the same enzymatic activity is present on each side of a membrane and where the ionic conditions are different in the media on each side. Such a situation, which closely resembles the artificial ones studied here, is important in the homeostasis of inorganic ions in cellular compartments or in the operation of relay and amplification mechanisms (in which the direction of transfer depends on differences in ion concentrations in the compartments). Moreover, the frog epithelium in vivo resembles some of the in vitro set-ups described here (sections 2.3 and 2.4), since it can be modelled as a thick two-compartment slice with both passive ion diffusion and active ion transport by an enzyme.
It is remarkable that increasing the complexity of the behaviour of the living frog-skin system by inducing electric oscillations via lithium addition to the external solution provided information on this system (such as the relative size of compartments and the values of other parameters) that could not have been provided by a conventional, reductionist approach. This may be the basis for the introduction of ‘complexification’, as opposed to reductionism, as a method for studying those properties of a complex system that are destroyed when adopting the conventional, reductive, biochemical approaches.
Further study of the model systems discussed above would benefit from knowledge of the distribution of ions. This may be provided by secondary ion mass spectrometry (SIMS), a method largely used by physicists for materials studies (see, e.g., [29,30]), now available for application to biological specimens [31–33] after appropriate preparation of dehydrated tissue sections [34,35] or using frozen hydrated samples [36].


