1 Introduction
It is no doubt difficult, or even impossible, to offer a scenario of the origins of life that is not, in part, hypothetical, for we do not know the precise conditions that have led to the appearance of the first living organisms. Most of the present studies devoted to the problem of the origins of life are based on the proposal that the first living systems have emerged, in a primordial RNA world, from the unexpected properties of some RNA molecules, more precisely from the fact that some RNA fragments, called ribozymes, are able to catalyse chemical reactions in addition to their ability to replicate [1–4]. As outlined by Kauffman [5,6], there is, however, a problem if we accept this view of an RNA world. This difficulty is related to the fact it has been so far difficult, or even impossible, to obtain the spontaneous replication of RNA molecules in the absence of a replicase. Indeed, the lack of evidence for a spontaneous replication of RNA molecules in the absence of a replicase does not completely invalidate the idea of a primordial RNA world for the spontaneously replicating RNA fragments may still have to be discovered. This situation makes it difficult, however, to accept as such the classical view of a primordial RNA world without reservation.
On the other hand one cannot imagine a living, or a prebiotic, system, whatever its simplicity, as not being made up of connected catalysed chemical reactions. This idea has led a number of biologists, in particular Fox [7,8] and Kauffman [5,6], to propose the view that the first prebiotic systems could have been encapsulated networks of chemical reactions. Such networks of catalysed biochemical reactions having global collective properties, one is led to the view that the problem of the origins of life could be discussed in the frame of the “new science” of systems biology [9,10] as applied to catalysed chemical, or biochemical, networks. This approach necessitates the use of both physical concepts and mathematical developments. In order to make the paper understandable to those who are not familiar with these mathematical developments, the paper has been organized as to remain understandable, even if Sections 5 and 6 are omitted.
2 Basic properties of biochemical networks
Sets of connected catalysed chemical reactions constitute biochemical networks. Any node of these networks is a catalysed chemical reaction or, more precisely, the probability that this catalyst has bound its substrates. Any link between two nodes is identified to the transport of a metabolite from catalyst to catalyst. We shall discuss later, in this article, the mathematical expressions of both the nodes and the links. If, as stated before, a catalysed reaction is identified to a node, this means that the overall network is in fact a network of networks, or a meta-network, for every catalysed reaction is itself a network. From a mathematical viewpoint such biochemical meta-networks are described by directed graphs for the links between the nodes are, in most cases, unidirectional. Moreover these meta-networks should be considered open-systems with, at least, one input and one output of matter. They should be viewed as dissipative structures [11–13].
It then appears obvious that the way we are going to represent biochemical networks by mathematical models is both different and incompatible with that found in current recent literature [14,15]. Networks, as described in many scientific papers, and whatever the physical nature of their nodes, are in fact represented by the same type of graph. This reasoning is incorrect for at least three reasons:
- • it is erroneous to think that networks of social relationships and chemical reactions, for instance, could be described by the same model. As a matter of fact, social relationships in a city are not submitted to thermodynamic laws whereas chemical reactions are under the control of – Networks of social relationships, for instance, should be described by non-directed graphs. This does not apply to biochemical networks that should, to a large extent, be represented by directed graphs;
- • networks of social relationships can be viewed as closed systems. Networks of chemical reactions should be considered open systems with input and output of matter.
Hence, it is an illusion, to claim there should exist a general science of networks as found in scientific literature [15].
3 Main features of living systems
Living systems possess features that are either essential or accessory. Essential features present in all living organisms can be used to define the concept of living system. These features are defined now:
- • living systems are able to reproduce thus giving birth to systems identical, or similar, to themselves;
- • a living system is an entity that should be considered a coherent whole possessing an identity specific for both its organization and functional properties. Today, this identity is defined from the structure of some macromolecules namely DNA and RNA;
- • living systems are associated with a history. This means they can distinguish in a sequence of events the one that is occurring first. Put in other words, they can realise whether the intensity of a signal increase, or decrease. Hence they are sensitive to some kind of a time-arrow;
- • living systems can evolve by selection of random alterations of their structure.
In the following, I would like to demonstrate that simple systems, viz. encapsulated networks of catalysed chemical reactions, may possess these properties and can therefore be considered models of prebiotic systems.
4 Prebiotic systems should be able to reproduce
It is well known that DNA and RNA are able to replicate in the presence of a suitable replicase. The problem of anteriority of RNAs over proteins displays a logical circularity as we need RNAs to make proteins but also proteins to make RNAs. A possibility to avoid circularity between proteins and RNAs at the origins of life is to assume that some kind of an encapsulated network of catalysed chemical reactions can display some kind of spontaneous “duplication” and self-organization. Let us assume an encapsulated network of catalysed chemical reactions. Even though the protein catalysts are neither very efficient nor very specific for a given chemical process, the overall network may possess surprising properties if some of the individual reactions display autocatalysis [3,16].
Autocatalysis is the process where a chemical reaction becomes activated when a reaction product appears. For instance, in a process S1 → S2, S2 stimulates its own production by activating the proteinoid E1 that catalyses the conversion of S1 into S2. The idea that autocatalysis may have played an important role in the emergence of life on Earth [5] is not a gratuitous assumption for we know numerous autocatalytic processes that take place in living systems today. Thus, in vertebrates, the protein pepsin is formed by specific cleavage of another protein pepsinogen. This process is activated by pepsin itself.
If inserted in a catalysed chemical network, an autocatalytic process may give rise to some special kind of self-organization, namely the duplication of the network. This situation is linked to the fact that for a certain period of time, the system cannot be in steady state. This lack of steady state is due to a large difference of velocities of two successive steps of which one is autocatalytic and the other is not. Let us assume we have two successive steps S1 → S2 → S3 in a reaction network, the first step being catalysed by proteinoid E1 and the second step by proteinoid E2. If one postulates that the first process is autocatalytic whereas the second is not, this means that the rate of the first process increases as S2 accumulates. In this model, E1 is a poor catalyst in the absence of its reaction product S2. Hence the catalytic reaction is very slow during the induction phase (Step 1 of Fig. 1). After a while, however, a reaction sequence is initiated (Step 2 of Fig. 1). Owing to the fact that one of the two reaction processes is autocatalytic S2 accumulates (Step 3 of Fig. 1) and this situation has three effects: S2 activates by autocatalysis its own production; as the local concentration of S2 increases, it tends to diffuse away and activates another E1 molecule; the consumption of S1, which is being converted into S2, results in the pumping of S1 from the outside. It then appears that the activation by S2 of two molecules of E1 results in the duplication of the metabolic network. A new metabolic pathway is thus formed. One can then imagine that, in a next step, the protocell increases its volume and divides into two halves each containing a reaction network (Step 3 of Fig. 1). This purely speculative event is plausible for it is based on the physical process of autocatalysis.

Tentative mechanism for the duplication of a biochemical network. Protenoids E1 and E2 are represented by E(1) and E(2), S1, S2 and S3 by S(1), S(2) and S(3), respectively (see main text).
5 Prebiotic systems should possess an identity
This Section can be omitted on a first reading.
An essential feature of living systems is the fact they possess an identity. Today the concept of identity is defined by a specific sequence of base pairs in DNA, or a sequence of bases in RNA molecules. In the case of networks of catalysed chemical reactions that do not possess any DNA, or RNA, one may wonder whether they can possess an identity. As a matter of fact, the concept of identity has been defined and discussed in ancient Greek civilization. Thus Aristotle [17] coined the terms of form and essence (oussia) to express this concept of identity. Information, in its Aristotelian meaning, is the ontological principle that represents the very basis of identity. From a practical viewpoint information is both what makes a material entity different from its neighbours and the ability we have to identify this entity. If, for instance, we face material entities that display slight differences, the ability we have to identify one of these entities, viz. its information, will depend upon its probability of occurrence. The smaller the probability and the larger is the information of this entity. More precisely, the amount of information of an entity will be an increasing function of the reciprocal of its probability of occurrence.
If we consider a network of proteinoid-catalysed chemical reactions and if a node is bearing ligand xi, or ligand yj, or both ligands xi and yj, one has
| (1a) |
| (1b) |
| (1c) |
where the functions h express the information associated with the binding of xi, yj or both xi and yj to a proteinoid of the network (1a)–(1c). In order to do so, the point is now to define the expression of f. To answer this point, one can consider the situation where the two ligands xi and yj do not interact upon binding to the same proteinoid. Then one should have
| (2) |
It is then obvious that the simplest function f that meets this requirement is a logarithmic one, for one should have
| (3) |
If now there exists an interaction between xi and yj during their binding to a node of the network, Bayes theorem requires that
| (4) |
In this expression, and are conditional probabilities that the proteinoid binds yj given it has already bound xi and that it binds xi given it has already bound yj. Making use of the h functions, expression (4) allows one to write
| (5) |
In order to determine whether the interaction between xi and yj increases or decreases the amount of information of the node bearing both xi and yj one can define the function
| (6) |
and taking advantage of expressions (5) one finds
| (7) |
It then appears that if information is taken up upon the interaction between xi and yj. If, alternatively, then information is generated by the interaction of the two ligands. In the first case the process is integrated and in the second case it is emergent. It then appears that the function i(xi : yj) is a measure of the information taken up, or generated, by the interaction between xi and yj.
This reasoning can be extended to a set of proteinoids. Let us consider for instance a proteinoid edifice that can bind n molecules of ligand x and n molecules of ligand y. The network can be depicted by a square lattice ΩN defined as [18]
| (8) |
Here, p(Nκ,λ) is the probability that a proteinoid of the lattice has bound κ molecules of x and λ molecules of y. One can distinguish three subsets in the ΩN set: ΩO, ΩNx and ΩNy. ΩO collects the probabilities of occurrence of the proteinoids that have bound neither x nor y. ΩNx assembles the probabilities that the proteinoids of the lattice have bound x and possibly y. ΩNy gathers the probabilities of the proteins that have bound y and possibly x. One can define these subsets as
| (9a) |
| (9b) |
One can define the probability that the proteinoid lattice has bound i molecules of x whether or not it has bound molecules of y as
| (10) |
Similarly the probability that the proteinoid lattice has bound j molecules of y whether or not it has also bound molecules of x is
| (11) |
From the values of p(xi) and p(yj) generated by expressions (10) and (11) one can define two sets ΩX and ΩY as
| (12a) |
| (12b) |
The states xi and yj allow one o define two sets X and Y whose Cartesian product is XY. Its corresponding probability space is then
| (13) |
One can define from relations (10) and (11) the corresponding h functions as
| (14a) |
| (14b) |
| (14c) |
Also from the h values one can define two sets
| (15a) |
| (15b) |
that allow one to define in turn two functions, H(X)N and H(Y)N, as
| (16a) |
| (16b) |
These functions are generalisations of h functions for lattices of xi and yj states. By convention these relationships are expressed per node having bound both x and y. Even though these relationships are reminiscent of Shannon entropies [19–21] they are usually different from classical entropies. In the case of a communication channel one should have
| (17a) |
| (17b) |
whereas for a proteinoid lattice some proteinoid molecules may have bound either x or y but not both of them, this is impossible for a communication channel where x is always associated to y. As we shall see, the consequence of this difference is of major importance.
We can define conditional H functions for a protein lattice and we have
| (18a) |
| (18b) |
As outlined above, these functions possess values conventionally expressed per node bearing both ligands x and y. We can now generalize Eq. (7), obtained for a node, to a proteinoid lattice by defining, for the whole system, the so-called mutual information of integration as
| (19) |
The function I(X : Y)N may take, for a proteinoid lattice, positive or negative values. In the first case, the whole system is integrated, whereas in the second it is emergent. In the case of a communication channel, however, I(X : Y)N is of necessity positive. This is the well known subadditivity principle of classical communication theory [19–21]. The reason for this difference relies upon the lack of identity between Eqs. (10) and (11) on one hand, (17a) and (17b) on the other hand. In the perspective of the problem of the origins of life the interesting idea is the possibility of the spontaneous emergence or consumption of information in a system that could be considered a quantitative expression of its identity.
6 Prebiotic systems should be able to sense chemical signals
This Section can be omitted on a first reading.
A fundamental property of living systems is their ability to sense whether the intensity of a signal is increasing, or decreasing. They are sensitive to some kind of a time-arrow. This is remarkable for most “simple” physical systems do not possess this property. Thus, for instance, the fundamental relation of dynamics F = m ∂ 2x/∂ t2 remains unchanged whether t increases, or decreases. We shall see in the following that the ability to be sensitive to time- arrow is also a property of networks of catalysed chemical reactions. Let us consider an ideal and simple chemical transformation, S → S'. If this process is catalysed by a proteinoid, which can be considered as a primitive enzyme E, one has
In this ideally simple scheme K is the ratio of two rate constants and k the rate constant for catalysis and product desorption from the enzyme surface. Now let us consider the same process inserted in a sequence of enzyme-catalysed reactions
Of particular interest in this scheme is the fact that reactant Si−1 is being converted into a reaction product, , that diffuses, with a diffusion constant up to the point it binds to the enzyme Ei. and Si are thus two different concentrations of the same substance. If the concentrations of the two enzymes are Xi−1 and Xi one has
| (20a) |
| (20b) |
From a formal point of view, Xi−1 and Xi are the total (free plus substrate-bound) concentrations of enzymes. The segment of reaction network above can thus be described in compact form as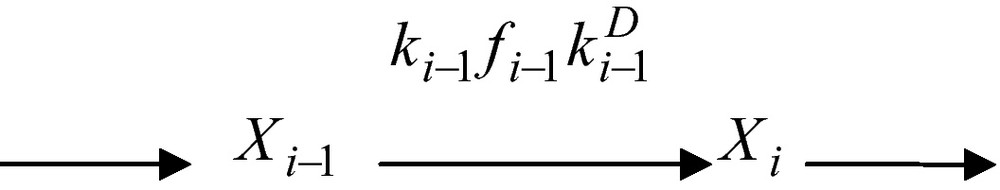
Here fi−1 is the so-called fractionation factor viz.
| (21) |
One realizes at once that the fractionation factor, fi−1, is equivalent to the probability, p(Si−1), that substrate Si−1 has bound to enzyme Ei−1. As previously mentioned, is the diffusion constant of the chemical reactant, from the immediate vicinity of enzyme Ei−1 to the enzyme Ei. The time constant, τi−1, of the transition from enzyme Ei−1 to enzyme Ei is then
| (22) |
The interesting idea that emerges from this reasoning is that the transition from an enzyme reaction to another one involves both the release of a reactant from an enzyme (Ei−1) and its diffusion to another enzyme (Ei). Under steady state conditions, these two processes should possess the same reaction rate . One has thus for the diffusion process
| (23) |
It must be pointed out again that, in expression (23), and Si represent different concentrations of the same substance.
Let assume now that the enzyme reaction, which uses this substance as a substrate be inhibited by an excess substrate. The corresponding reaction scheme will be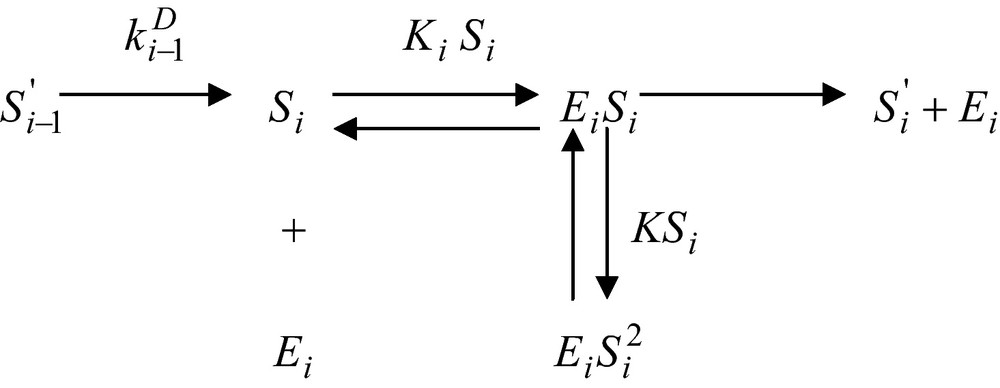
and the corresponding enzyme reaction rate assumes the form
| (24) |
In order to simplify the expression of Eqs. (23) and (24) one can define dimensionless variables and parameters as
| (25a) |
| (25b) |
and the equation of diffusion becomes
| (26) |
Similarly, the enzyme reaction assumes the form
| (27) |
Hence under steady state one has
| (28) |
which can be rearranged to
| (29) |
The resulting equation is third-degree in si. According to the Descartes rule of signs, this equation can, possibly, display three changes of signs of its coefficients. Hence it can possibly display three positive real roots. In order to demonstrate this situation to be effective one has to demonstrate that expression (29) can be expressed as
| (30) |
where the roots λ1, λ2 and λ3 should be positive real numbers. If we compare Eqs. (29) and (30) it appears that the coefficients of Eq. (30) are based upon physical parameters and substrate concentrations () of Eq. (29) that cannot adopt negative values. Hence there might exist some constraints between the coefficients of Eq. (29) that would lead to the conclusion that it possesses one real and two imaginary roots. Alternatively, if Eqs. (29) and (30) are compatible one can conclude that polynomial (29) possesses, for a definite domain of concentrations , three positive real roots. In that case it should be possible to express and in terms of mathematical expressions involving the three positive roots λ1, λ2 and λ3. Moreover these mathematical expressions should always be positive.
If we intend to express and in terms of the positive roots λ1, λ2 and λ3 of Eq. (30) this can be done only in the interval . Under these conditions, the coefficient of the term of Eq. (29) can be expressed as
| (31) |
Moreover, one has
| (32) |
It then follows that
| (33) |
and
| (34) |
Combining expressions (32) and (34) one finds
| (35) |
In the same way, the coefficient of the term in si in Eq. (29), assumes the form
| (36) |
that can be rearranged to
| (37) |
and to
| (38) |
Hence it is clear that positive values of the roots can generate positive values of and .
It appears from the above reasoning that Eqs. (29) and (30) have three positive real roots. Such a situation takes place in the interval . Below the limit and above , Eq. (29) has one positive and two imaginary roots. The existence of three real positive roots in the interval is depicted in Fig. 2. Owing to the existence of these three real roots the system displays some kind of chemical hysteresis. This means that within a limited range of concentration defined by the limits 1/λK and 1, the system follows two different routes depending on the concentration increases or decreases (Fig. 2). This situation is due to the coupling between diffusion and non-linear catalytic reaction. The magnitude of this non-linearity is expressed by the magnitude of the constant λK. If this constant is very small one cannot expect Eq. (29) to display three real positive roots and no hysteresis is to be expected.
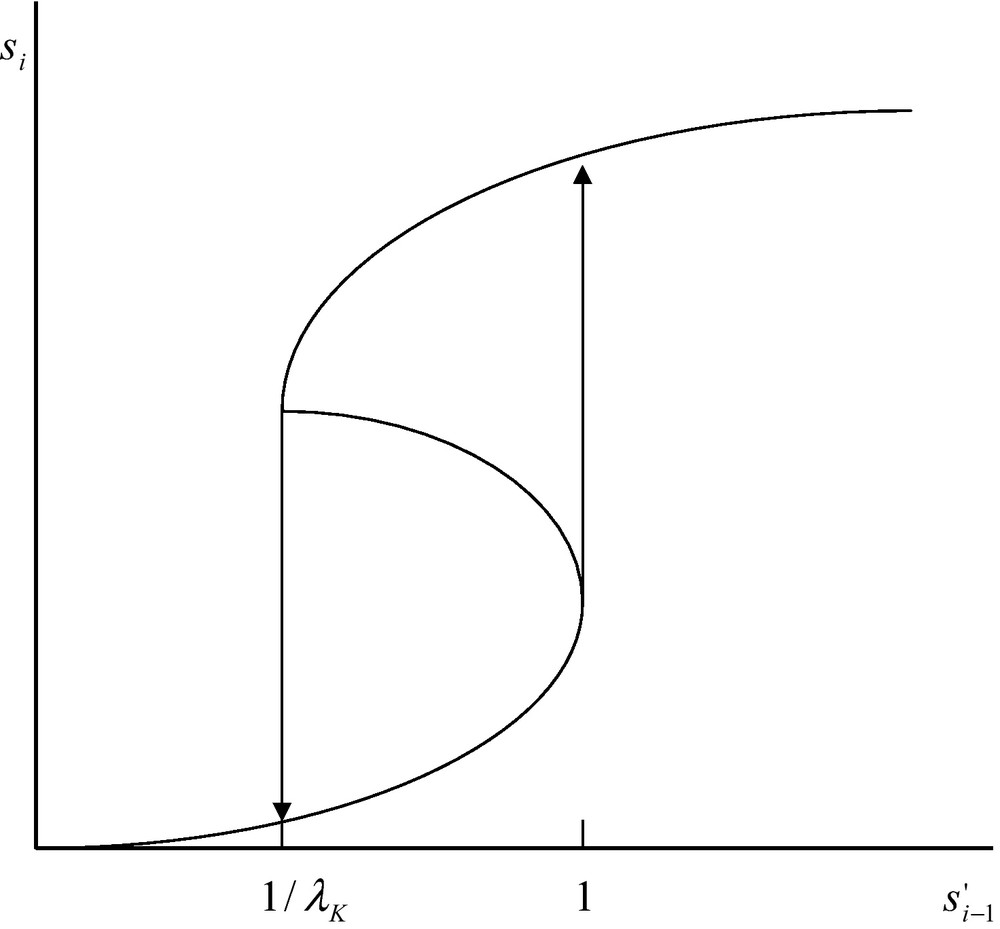
Multiple steady states and hysteresis for the coupling of diffusion and catalysed chemical reaction (see main text). In the interval the system has three steady states of which two are stable and one is unstable. The lower stable steady state is occupied only when increases. The upper stable steady state is occupied only when decreases. The unstable steady state is never occupied.
The situation, depicted in Fig. 2, mimics, in a way, the fact that living systems are perfectly able to sense whether the intensity of a signal increases, or decreases, and are able to react accordingly. What this theoretical study shows is that a network of catalysed reactions possess a typical property of the living systems viz. the property of sensing, not only the intensity of a signal, but also whether this intensity increases or decreases. This property is directly related to the perception of a time-arrow which is a property considered typical of living systems. Last but not least, the property of chemical hysteresis, which has been discussed above, has been experimentally found to occur with artificially bound enzyme systems [22].
7 Discussion
In this Note, we have outlined three well-known general properties of living systems, namely their ability to self-reproduce, their identity, and their ability to perceive signals or, put in other words, their ability to be sensitive to a time-arrow. We have tackled the problem of the origins of life by raising the question to know whether some physico-chemical systems could precisely possess these properties. These physico-chemical systems are encapsulated networks of chemical reactions. Such an idea has been proposed some time ago by Kauffman [5,6]. The main difference between the present model and that of Kauffman is that it is assumed in the latter that chemical reactions are uncatalysed and that the whole system is closed, viz. it has no input and output of matter. Alternatively, we are assuming that the system is open with both an input and output of matter and that the chemical reactions are catalysed by poorly specific membrane-bound protein catalysts. These electrostatically-bound proteins are randomly distributed over the membrane surface. When a substrate S1 enters the protocell and diffuses within the available space it undergoes chemical transformation when it comes into contact with the nearest catalyst molecule. If this reaction is autocatalytic whereas the next one is not, the system should derive from a steady state and reaction intermediates such as S2 (Fig. 1) accumulates then diffuses within the protocell thus generating another reaction pathway. In such a system, there is no increase of the number of proteinoids but, progressively, all of them become involved in network activity. As a consequence there is an increase of the number of encapsulated networks, which is not associated with a parallel increase of the number of proteinoids involved in these networks. In such a process one implicitly postulates that synthesis of new proteinoids takes place through simple polymerization of aminoacids, as suggested by some authors [5–7]. One cannot expect that catalysts synthesized under these conditions to be highly specific of one chemical process only.
Perhaps the most difficult question to solve is that of the identity of such a system. In the case of present day living organisms, their identity is defined from the sequence of bases, or of base pairs, in RNAs, or DNAs. This criterion of identity is related to two others, namely that of an internal organization of the system and that of the communication of a message. In the case of present day living organisms, their identity, organization and ability to communicate are partly defined from the sequence of bases, or of base pairs, in RNAs, or DNAs. It is evident that today identity of a living system is defined from the sequence of base pairs in DNA. Moreover this identity is reflected in the internal organization of the system. Gene expression is in fact a communication process between DNA and proteins. It is striking that these functions, identity, organization and communication are related and can be expressed in the same mathematical language based on the concept of information, viz. a function of the reciprocal of the probability of occurrence of a given feature. The physical nature of this feature does not matter, it is only its low probability of occurrence that is important. As already outlined, the identity of a material entity relies upon some features specifically borne by this entity. For present day living organisms, it is the sequence of DNA base pairs that is important for the definition of their identity. We propose that for encapsulated biochemical networks it is the nature, the sequence and the probability of occurrence of the connected nodes that allow to define the identity of the network. Last but not least, from the interaction that may possibly occur between two ligands that bind to the same node emerges a new specific function, or property, out of the interaction between two events, viz. the binding of two different ligands to the same protein state. The emergence of this novel property is important for it gives the system a global behaviour that cannot be reduced to that of its constitutive elements. This property is characteristic of systems and in particular of biological systems. This matter will be discussed more thoroughly in the accompanying article [23].
If, as it has been already suggested [6], it is true that the first living systems did not possess any nucleic acids, the appearance of these types of molecules in living organisms may have represented a major step in the evolutionary process. It is therefore of interest to discuss briefly what could have given rise to the appearance of nucleic acids in prebiotic systems. Even though it is probably impossible to formulate a definitive answer to this question, it is sensible to assume that the appearance of different enzymes that, after a mutation for instance, could possess, respectively, a polymerase and a replicase activity, would give the system an advantage in the “struggle for life”.
Physicists have often discussed the question of the reality of time-arrow for simple physical systems [24]. With the notable exception of Prigogine, most of them are convinced that simple physical systems remain unchanged when the variable t is replaced by –t. It is obvious, on the other hand, that biological systems are sensitive to a time-arrow. For instance they are perfectly able to “distinguish” whether the intensity of a signal has been reached after an increase, or a decrease, of intensity. Such a property, however, is not specific for biological systems as physical systems can also display this property. The mathematical requirement for obtaining a different response of a system to the same signal intensity reached after either an increase, or a decrease, of intensity is that the system displays multiple steady states. This requires that the curve describing the response of the system as a function of the signal intensity to be, at least, of the third degree. As we have seen, this condition is necessary but, by no means, sufficient. The sufficient condition is that, within a given range of signal intensity, the system displays three real roots, viz. three different steady states. Two of them should be stable and one should be unstable. This means that if a signal intensity decreases, the upper branch of the curve is populated and if a critical value is reached the system falls from the upper branch to the lower one. Alternatively, if the signal intensity is increased the system jumps from the lower branch to the upper branch of the curve. This is illustrated in Fig. 2. If the concentration increases in the interval , the corresponding value, si, will vary along the lower steady state. Upon reaching the critical point, the value of si will jump from the lower to the upper branch of the curve. Alternatively, if the concentration decreases in the same interval as above, viz. , the value of the concentration si will decrease along the upper branch of the curve and then falls from the upper to the lower steady state. It then appears that depending on whether the same concentration, , is reached after an increase, or a decrease, the corresponding si concentration will be low, or high, exactly as our eye, connected to our brain, is able to sense whether a given light intensity is reached after an increase, or a decrease, of intensity. Such a physical system can be considered biomimetic. The properties that generate this behaviour are neither the properties of the enzyme reaction nor the properties of diffusion but the collective properties of the global system. The conditions required for obtaining such a behaviour is that the system be away from thermodynamic equilibrium and that the resulting equation be non-linear. Hence non- linearity of the system is essential for obtaining the remarkable properties that have been described.
The reader may be struck by the fact that the results presented in this article are speculative. However, one has to remember that knowledge about the origins of life can only, by essence, be speculative. The main question is to know whether these speculations are physically sound.
Conflict of interest statement
Nothing declared.


