1 Introduction
Les odeurs que nous percevons sont le plus souvent celles de mélanges contenant des centaines de composants, qui peuvent être perçus différemment selon qu’on les sent isolément ou dans le mélange.
La modélisation correcte de l’odeur de ces mélanges complexes semble actuellement hors de portée et la plupart des études portent sur des mélanges binaires. De plus, ces travaux portent plutôt sur l’intensité que sur la qualité de l’odeur 〚1–3〛.
Parmi les modèles les plus simples 〚3〛, certains (modèle de la somme arithmétique et modèle de la plus forte composante) ne tiennent pas compte des interactions entre composants, alors que d’autres (modèle de l’additivité euclidienne) prennent en considération une interaction non spécifique.
L’équipe de Berglund 〚4〛 a proposé de prendre en compte les interactions, en considérant que l’intensité du mélange est la somme vectorielle des intensités des composants purs. Cette approche a permis de développer un modèle, dit vectoriel, dans lequel l’angle α entre les deux vecteurs est caractéristique d’un couple donné 〚4〛.
À la suite de ces travaux, Patte et Laffort 〚5〛 ont proposé les modèles dits en V et en U, qui reprennent le principe du modèle vectoriel, en introduisant un terme d’interaction spécifique à chaque paire d’odorants.
Il a été observé par Laffort et Dravnieks 〚6〛 et Laffort et al. 〚7〛 qu’une partie des effets observés dans les mélanges est due à l’exposant de la loi de Stevens de chacun des composants, qui traduit l’influence différente des concentrations sur l’intensité perçue pour les composés purs. Pour tenir compte de ce phénomène, Laffort et Dravnieks 〚6〛 proposent le modèle UPL et définissent un indice d’interaction vrai Γ, dont la valeur est 1 lorsqu’une substance est ajoutée à elle-même. Laffort 〚7–8〛 a proposé ensuite un modèle dit Γ, nécessitant le calcul d’un indice UPL2 et qui tient compte de l’influence des exposants (pentes) de la loi de Stevens. Ce modèle est capable de rendre compte avec succès 〚3〛 de la dissymétrie des effets observés dans certains mélanges (pyridine et essence de lavandin 〚9〛 ou pyridine et disulfure de méthyle 〚10〛).
1.1 Critique des modèles existants
Les modèles courants 〚3〛 supposent que l’intensité de l’odeur d’un mélange est la somme des intensités des composés purs, modulée par un terme correctif permettant de tenir compte de l’interaction entre les deux composés. Certains mélanges de composés odorants présentent une certaine dissymétrie dans les effets observés sur l’intensité perçue. Parmi les modèles proposés dans la littérature, seul le modèle Γ permet de prendre en compte la dissymétrie des effets de mélange.
Les mesures d’intensité étant souvent longues et délicates, il paraît important de pouvoir disposer d’un outil de modélisation basé sur les concentrations des composés purs. Ces dernières sont, en effet, plus facilement accessibles par analyse physico-chimique que les intensités odorantes.
Par ailleurs, il n’existe pas, à notre connaissance, d’évaluation comparative des performances respectives des différents modèles sur un ensemble commun de données.
1.2 Présentation du modèle MBO
Dans le cadre d’une étude sur le masquage d’odeurs désagréables 〚11〛, nous avons été amenés à proposer 〚12〛 un modèle dérivé de l’équation de Hill et reliant l’intensité odorante des produits purs à leur concentration (équation (1)) :
Ce modèle présente un certain nombre d’avantages, dans la mesure où il s’appuie sur la totalité de la courbe théorique reliant l’intensité odorante et la concentration et permet d’en rendre compte de manière plus efficace que les modèles existants 〚12〛.
Sur la base du modèle précédent, un modèle pour les mélanges, inspiré de celui de Beidler pour les mélanges de saveurs 〚13〛 et appelé MBO (mélange binaire d’odorants), a été développé 〚11〛.
Dans le modèle MBO, l’intensité de l’odeur du mélange correspond à la somme des intensités Ia et Ib des composés purs, calculées en admettant que la présence du composant B entraîne une modification de la sensibilité au composant A et vice versa (équation (2)). Cette modification, qui affecte uniquement la constante Cip de l’équation (1), peut résulter d’une compétition pour les sites récepteurs ou de la différence entre les temps de latence des deux composés ou encore de phénomènes plus centraux. Les autres paramètres de l’équation (1) ne sont pas modifiés.
Cette altération de la perception est prise en compte en multipliant Cip pour le composé A par un terme de la forme (1 + αb CB), si l’on suppose une dépendance linéaire de la concentration du composé B ou un terme de la forme (1 + αb CB + βb CB1/2), dépendant non linéairement de la concentration du composé B. Pour un composé A pur, la concentration en composé B est nulle et l’on retrouve bien l’équation (1). Il est à noter que les paramètres αa, αb, βa et βb sont caractéristiques d’un couple donné de composés odorants.
On a :
L’introduction de ces paramètres d’interaction (α et β) permet de prendre en compte la dissymétrie éventuelle des interactions.
1.3 But de l’article
Chacun des modèles classiques présentés plus haut présente des avantages reconnus. Aucune comparaison systématique n’ayant été publiée, il nous a paru intéressant de tester, sur un même ensemble important de données fiables, les efficacités relatives des modèles existants et du nouveau modèle MBO.
2 Matériels et méthodes
2.1 Mélange acétate d’heptyle/salicylate d’éthyle
Moskowitz et Barbe 〚14〛 ont publié des données fiables sur plusieurs couples d’odorants, dont le couple acétate d’heptyle (fruité, poire)/salicylate d’éthyle (menthe, wintergreen), où l’on observe des effets fortement dissymétriques sur l’intensité globale du mélange. Il est à noter que ce mélange est un des rares exemples publiés présentant des effets aussi marqués et différents. Il serait très intéressant de dupliquer et d’étendre cette expérimentation pour confirmer l’importance de la dissymétrie des effets de mélange.
Pour chacun des composés, quatre concentrations (10%, 2,5%, 0,625% et 0,153% de la vapeur saturante) ont été utilisées. Les intensités de 24 stimuli (dont huit contenant un composé pur et 16 des mélanges) ont été évaluées par un panel composé de huit femmes entraînées.
2.2 Autres mélanges
Moskowitz 〚15〛 a publié des données sur l’intensité pour quatre autres couples de composés odorants présentant des effets de mélange moins dissymétriques (acétate d’amyle/salicylate d’éthyle, acétate d’heptyle/acétate d’amyle, acétate d’isoamyle/acétate d’amyle, salicylate de méthyle/salicylate d’éthyle). Pour chacun, Moskowitz a utilisé quatre concentrations, dont on ne connaît que les valeurs relatives (1, 4, 16 et 64). Il a donc étudié au total 16 mélanges et quatre concentrations pour chacun des composés purs.
2.3 Représentation des intensités des mélanges
Les résultats des modélisations sont représentés graphiquement dans le système σ = f(τ) proposé par Patte et Laffort 〚5〛. Si RA et RB sont les réponses obtenues pour les composés A et B purs et RAB la réponse obtenue pour le mélange, on définit le rapport τ = RB/(RA + RB), qui reflète une proportion de l’intensité perçue, et le rapport σ = RAB/(RA + RB), qui mesure l’écart à l’additivité.
2.4 Principes d’utilisation du modèle MBO
On détermine tout d’abord, sur les données relatives aux composés purs, les paramètres Im, I0, Cip et n selon l’équation (1). Puis, à l’aide des données d’intensité concernant les mélanges, on calcule les paramètres d’interaction α et β. Tous les paramètres sont optimisés par régression non linéaire, à l’aide du logiciel UNISTAT® Statistical Package.
2.5 Comparaison des modèles
La comparaison entre les intensités perçues (pour les cinq couples de composés odorants retenus) et les intensités calculées selon les différents modèles étudiés est basée sur le coefficient de détermination R2 et sur la statistique ψ2 de Exner 〚16, 17〛. Ce dernier indice statistique permet de prendre en compte le nombre de paramètres impliqués dans les modèles.
3 Résultats et discussion
3.1 Cas d’un mélange présentant des effets fortement dissymétriques
Nous avons testé les principaux modèles sur les données relatives à l’intensité de mélanges d’acétate d’heptyle et de salicylate d’éthyle.
Les modèles dits simples (somme arithmétique, additivité euclidienne et plus forte composante), dont les valeurs de R2 sont comprises entre 0,58 et 0,65, ne rendent pas correctement compte de l’évolution de l’intensité perçue pour les mélanges.
Pour le modèle en V, R2 ne dépasse pas 0,59, même après optimisation de l’angle α (111,3 ± 8,4°) par un processus itératif. Le modèle en U, avec un angle α de 112,8°, est un peu meilleur (R2 = 0,64), mais l’optimisation de l’angle n’améliore pas la qualité de la modélisation. Quant au modèle UPL, son application aux mélanges ne fournit pas des résultats plus satisfaisants (R2 = 0,61).
Ainsi, comme attendu, les modèles symétriques ne peuvent pas prendre en compte la forte dissymétrie du mélange considéré.
Pour appliquer le modèle Γ, on calcule, selon Laffort 〚3〛, le coefficient d’interaction Γ pour chacun des mélanges, puis la moyenne des valeurs obtenues. On en déduit l’intensité prédite par le modèle pour chacun des points expérimentaux. Le résultat, assez moyen (R2 = 0,59), est sans doute lié à la forte variabilité de Γ (entre 0,09 et 1,94, pour une valeur moyenne de 0,81), qui empêche de le considérer comme constant pour ce mélange.
3.2 Application du modèle MBO
Nous avons d’abord déterminé les paramètres (Im, I0, Cip et n) des composés odorants purs, puis nous avons effectué deux calculs pour déterminer les paramètres d’interaction, le premier avec le paramètre α seulement et le second avec les deux paramètres α et β (Tableau 1 et Fig. 1). Les paramètres I0 trouvés non significativement différents de zéro ont été fixés à zéro. La modélisation est acceptable avec α seul (R2 = 0,85 et ψ2 = 0,157) et excellente avec α et β (R2 = 0,96 et ψ2 = 0,054), comme le montre aussi la Fig. 1.
Valeurs des différents paramètres obtenus avec le modèle MBO, pour l’intensité des mélanges de salicylate d’éthyle et d’acétate d’heptyle. Les chiffres entre parenthèses indiquent l’erreur standard sur les paramètres.
| Salicylate pur | Acétate pur | Salicylate en mélange | Acétate en mélange | Salicylate en mélange | Acétate en mélange | ||
| n | 0,81 (0,01) | 1,00 (0,1) | α | –0,06 (0,01) | 7,6 (3,2) | 3,5 (0,7) | –0,7 (0,1) |
| C ip | 3,1 (0,1) | 3,5 (1,1) | β | — | — | –2,9 (0,4) | 2,5 (0,3) |
| I m | 69 (1) | 43 (5) | R2 (ψ2) | 0,853 (0,157) | 0,957 (0,054) |
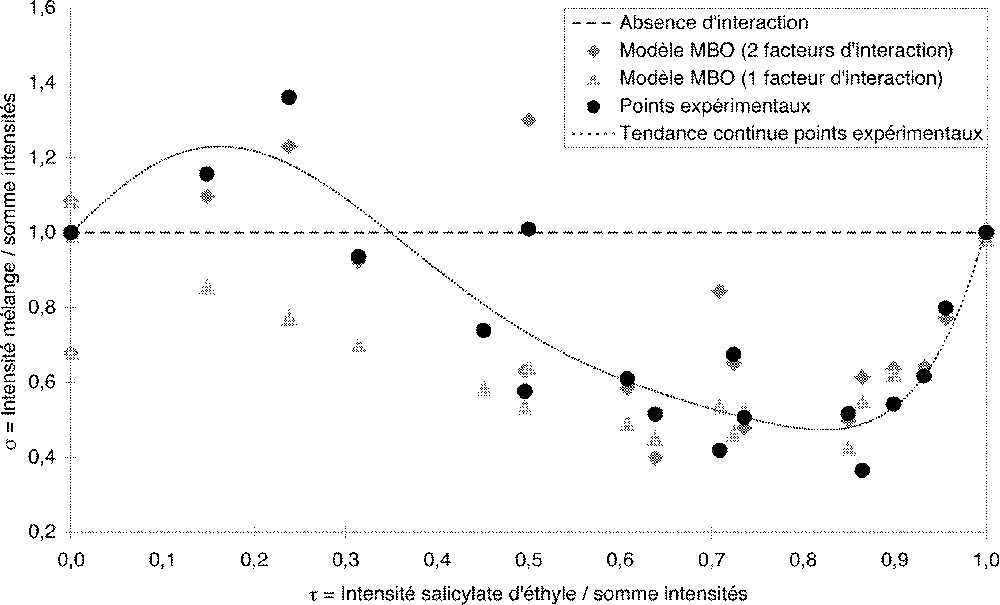
Modélisation par le modèle MBO des données d’intensité concernant les mélanges de salicylate d’éthyle et d’acétate d’heptyle.
Avec le seul facteur α, le modèle MBO permet de rendre compte de l’hypo-addition observée lorsqu’on ajoute de l’acétate d’heptyle dans le salicylate d’éthyle, mais pas de l’effet synergisant du salicylate d’éthyle sur l’acétate d’heptyle. Le modèle à deux facteurs rend compte de l’hypo-addition et de la synergie (Fig. 1).
Le calcul des paramètres des composés purs repose ici sur un nombre réduit de points. Cependant, on peut utiliser l’ensemble des 24 points expérimentaux, y compris ceux concernant les mélanges, pour déterminer simultanément les paramètres du modèle MBO. Les résultats de ces calculs confirment les conclusions précédentes.
3.3 Interprétation des paramètres du modèle MBO
Les paramètres α et β sont caractéristiques du comportement de chacun des composés odorants dans les mélanges. La valeur négative du coefficient d’un composé indique qu’il a un effet synergisant sur l’autre composé du mélange. Inversement, un coefficient d’interaction positif traduit un effet d’hypo-addition (inhibition). Le coefficient α permet de tenir compte de toute la plage des concentrations, alors que β permet de tenir compte des effets aux faibles concentrations. Or, la majorité des effets les plus marqués se produisent lorsque l’un des composants est présent en faible concentration 〚18〛.
Dans les mélanges de salicylate d’éthyle et d’acétate d’heptyle, le coefficient β du salicylate, négatif et assez élevé (–2,9), traduit l’effet synergisant de ce composé lorsqu’il est ajouté en faible quantité dans le mélange (Fig. 1). En revanche, le coefficient β positif (+2,5) de l’acétate d’heptyle indique que ce composé diminue l’intensité perçue lorsqu’il est ajouté en faible quantité dans le mélange.
La faible valeur du coefficient α de l’acétate d’heptyle indique qu’il n’a pas beaucoup d’influence lorsqu’il est ajouté en forte quantité. En revanche, le coefficient α positif et assez élevé du salicylate traduit bien l’effet d’inhibition observé lorsqu’il est ajouté à forte concentration dans l’acétate d’heptyle.
3.4 Modélisation de quatre autres mélanges binaires
Pour les quatre couples de composés odorants étudiés (acétate d’amyle/salicylate d’éthyle, acétate d’heptyle/acétate d’amyle, acétate d’isoamyle/acétate d’amyle et salicylate de méthyle/salicylate d’éthyle), le modèle MBO à un seul facteur permet de représenter assez fidèlement les résultats expérimentaux et se situe toujours parmi les meilleurs modèles.
Il est à noter que certains modèles simples donnent parfois de bons résultats. Ces conclusions pourraient être reliées au fait que les interactions dues au mélange sont simples ou peu marquées et/ou que le domaine de concentrations couvert reste assez faible, ce qui ne permet pas d’appréhender la totalité de la courbe stimulus–réponse.
4 Conclusion
L’application de différents modèles d’intensité aux données de Moskowitz et al. 〚14–15〛 sur cinq mélanges binaires de composés odorants a montré leurs limites dans le cas d’effets marqués et très dissymétriques. Le modèle MBO, qui comporte un ou deux paramètres spécifiques de l’action de chaque composé dans le mélange, est en général le meilleur. De plus, c’est le seul modèle qui soit fidèle aux données expérimentales pour certains mélanges présentant des effets intensitifs inverses selon les proportions des constituants. Les perspectives d’application de ce modèle paraissent donc intéressantes, tant pour le masquage des odeurs que pour la recherche de synergies. De plus, les études doivent être poursuivies de manière à tenter de relier les paramètres d’interaction à des caractéristiques intrinsèques des odorants, ou encore à leurs propriétés olfactives comparées (similitude, caractère hédonique...). Il serait également intéressant de relier ces paramètres d’interaction, semble-t-il assez explicatifs, à des facteurs plus physiologiques et liés au fonctionnement du système olfactif. À ce titre, le modèle MBO pourrait être appliqué de manière prometteuse à des données résultant de l’expérimentation animale ou in vitro, où la totalité de la courbe sigmoïde est facilement obtenue.
Remerciements
Les auteurs remercient le GDR CNRS–TOTAL « Environnement industriel et olfaction » pour le soutien financier apporté à ces études.
Abridged version
At the moment, it does not appear to be possible to model the perceived odour of complex mixtures correctly. Most of the publications in this field deal with intensity, and especially the intensity of binary mixtures.
Several mathematical equations have been proposed to model the odour intensity of binary mixtures. Some are simple (arithmetic sum, strongest component, Euclidean additivity), and others take account of specific interaction between the two components (vectorial model, V and U models and UPL model). Very often, an asymmetry is observed in the evolution of perceived intensity with changing ratios of the two components. In order to illustrate this observation, a Γ model, derived from the UPL model, has been proposed.
All these published models are based on mixture intensity, which is the sum of the component intensities, corrected for interaction. However, it would be of interest to use concentrations instead of intensities, as they are more easily available from physicochemical analysis.
In this context, we developed a new model for binary mixtures intensity, based on components’ concentrations. This model, called MBO, derives from an equation previously reported by our team for modelling the whole stimulus–response intensity curve of pure odorous compounds.
In the MBO model, the odour intensity of a mixture is calculated from the sum of the odour intensities of the two components in the mixture. The intensity of each component is calculated using an equation that allows the impact of the presence of one component on the sensitivity of the response to the other to be taken into account. This modification of response sensitivity induced by the mixture could be the result of either a competition for receptor sites or a difference in latency between the two odorants. It could also result from more central phenomena.
We applied the MBO model to a set of published data and compared its modelling efficiency to each of the above-mentioned models.
We first used all the models to represent data for a mixture of heptyl acetate and ethyl salicylate. For this mixture, there is great asymmetry of perceived intensity illustrated by a synergy for small and inhibition for large proportions of ethyl salicylate. With all the models, except MBO, the determination coefficient did not exceed 0.65, including even the Γ model, specifically designed to model asymmetry (R2 = 0.59). The MBO model gave better modelling (R2 = 0.85) using only one interaction parameter (α) for each compound, and very good modelling (R2 = 0.96) with two interaction parameters (α and β) per compound.
We tried to interpret the interaction parameters in the MBO model. The α and β interaction parameters are related to the behaviour of one of the two compounds in the mixture. That is to say that, when a parameter is negative, the related compound has a synergetic effect in the mixture. On the contrary, if the parameter is positive, the related compound has an inhibitory effect in the mixture. The difference between the two parameters, α and β, is that β is more strongly related to small proportions of a compound in the mixture. On the contrary, α is more relevant to the whole range of proportions. For the mixture examined, we obtained α = 3.5 and β = –2.9 for ethyl salicylate and α = –0.7 and β = 2.5 for heptyl acetate. These figures are fully representative of experimental observations and show that small proportions of ethyl salicylate in the mixture lead to synergy (β is negative). On the contrary, large proportions of ethyl salicylate and small proportions of heptyl acetate lead to intensity inhibition (α for ethyl salicylate and β for heptyl acetate are positive).
We also applied all the above-mentioned models to four couples of odorous compounds that do not lead to great asymmetry of intensity. In these cases, the MBO model with only one parameter was always among the best ones.
In conclusion, we investigated the modelling efficiency of a new model (MBO) for intensity of binary mixtures. This model, which incorporates one or two interaction parameters related to the effect of each compound on mixture intensity, was generally the one that best modelled the experimental data. Moreover, the MBO model was the only model able to account correctly for the intensity of a mixture with very asymmetric effects (synergy and inhibition for inverse proportions of each component). Thus this MBO model appears to be a very useful tool for masking and synergy research studies. It would now be interesting to try to relate the interaction parameters, α and β, to intrinsic characteristics of odorous compounds or to physiological parameters related to the functioning of the olfactory system.



