1 Introduction
Ferroelectric materials may be divided into two classes: classical or relaxor ferroelectrics 〚1〛. Typically, relaxors have at least one crystallographic site that is occupied by two or more ions. In addition to the usual applications for classical ferroelectrics, relaxors are of great interest for dielectrics in capacitors and actuators. Most used relaxors are lead-based perovskite ceramics such as PbMg1/3Nb2/3O3 (PMN) and derived compounds 〚2〛. However, these compositions have the obvious disadvantages associated with the volatility and toxicity of PbO. Therefore, much current research is directed towards more environmentally friendly Pb-free relaxor materials. In this way, a large number of relaxor lead-free BaTiO3 derived ceramics with perovskite structure was recently prepared and characterised 〚3〛.
Likewise lead-free relaxor compositions belonging to tetragonal tungsten bronze (TTB) could be also of interest. Fig. 1 shows a schematic representation of the TTB structure projection along a 001 direction. For a general formulation A2BC2M5X15 (X = O, F), large cations (e.g. Na+, K+, Sr2+, Ba2+, Pb2+, La3+, Bi3+...) occupy the 15 CN (A) and the 12 CN (B) sites, small cations like Li+ are in the 9 CN (C) sites and small and highly charged cations (e.g. Nb5+, Ta5+...) are in the octahedral (M) site.
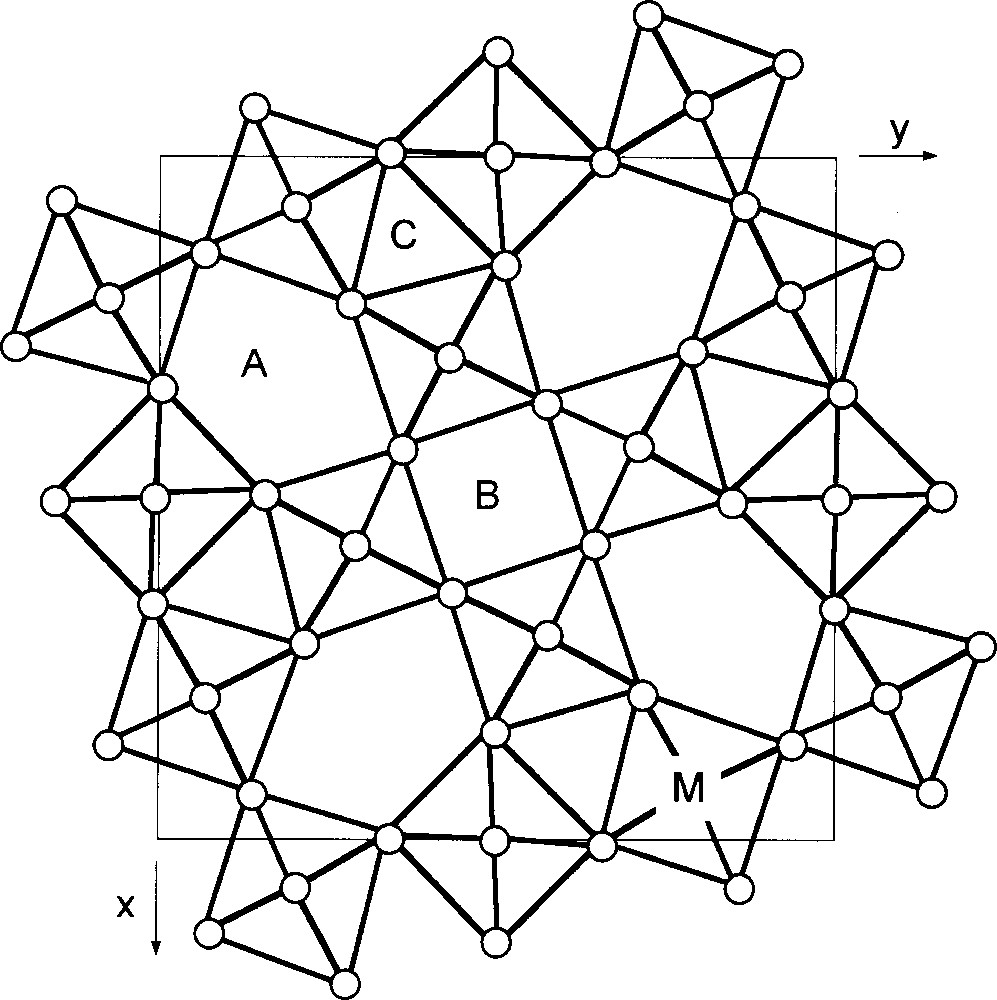
Schematic projection of the anionic TTB structure along the 4-fold c axis (A, B and C correspond to cationic sites with 15, 12 and 9 coordination number).
Previous authors had announced the solid-state solution Sr2.5(1–x)Ba2.5xNb5O15 to be relaxor 〚4–9〛. The present work is devoted to other lead-free relaxor compositions selected among a great number of TTB-type compositions.
2 Experimental
The oxides and the oxyfluorides were prepared by solid state reaction at temperatures between 900 and 1100 °C for 15 h from intimate and ground mixings of starting oxides, fluorides and carbonates in stoichiometric amounts. After new intimate and ground mixings, powders obtained were pressed under 100 MPa into disks of 8 mm diameter and about 1 mm thickness. Depending on the compositions, heat treatments were then performed at temperatures between 1150 and 1450 °C in air for the oxides and in platinum sealed tube under dry oxygen for the oxyfluorides, in order to avoid hydrolysis at high temperature.
Room temperature powder X-ray diffraction patterns were recorded on a Philips diffractometer, using CuKα radiation (λ = 1.5406 Å), in the angular range 5 ≤ 2θ ≤ 60°. This made it possible to verify that the samples were single phase. The diameter shrinkages ΔΦ/Φ were systematically determined as (Φinit – Φfin)/Φinit.. Their values were in the range 0.13–0.17.
Dielectric measurements were performed on the ceramic disks after deposition of gold or platinum electrodes on the circular faces. The real ε′r and imaginary ε′′r relative permittivities were determined under helium as a function of both temperature (77–900 K) and frequency (102–2 × 105 Hz) using a Wayne–Kerr 6425 component analyser.
3 Results
In addition to barium–strontium niobates, a relaxor behaviour was recently demonstrated in various other TTB compositions including niobates, tantalates, niobo-tantalates and niobo-titanates (Table 1). As an example, Fig. 2 shows the typical temperature dependence of ε′r for a relaxor ceramic with composition Sr2K(Nb0.775Ta0.225)O15: the temperature Tm of ε′r maximum is shifted towards higher values for increasing frequencies.
Lead-free TTB relaxor compositions.
| Relaxor compositions | Tm (± 10 K) at 103 Hz | ΔTm (K) |
| K2LaNb5O15 | 165 | 22 |
| K2BiNb5O15 | 220 | 80 |
| BaLa□Nb5O15 | 203 | 55 |
| BaBi□Nb5O15 | 319 | 73 |
| BaLa2/3□1/3NaNb5O15 | 210 | 34 |
| BaLaNa(Nb4Ti)O15 | 171 | 41 |
| BaLaK(Nb4Ti)O15 | 146 | 13 |
| Ba2Bi(Nb3Ti2)O15 | 270 | 25 |
| Sr2NaTa5O15 | 120 | 25 |
| Sr2KTa5O15 | < 80 | * |
| Ba2NaTa5O15 | < 80 | * |
| Ba2KTa5O15 | < 80 | * |
| K3LiNb5O14F | 210 | 40 |
| Ba2.25□0.75Nb5O14.5F0.5 | 175 | 30 |
| SrK2Nb5O14F | 112 | 16 |
| BaNa2Nb5O14F | 140 | 17 |
| Sr2Na(Nb1–xTax)5O15 (0.40 ≤ x ≤ 1) | 222 ≥ Tm ≥ 120 | 20 (0.40) to 25 (1) |
| Sr2K(Nb1–xTax)5O15 (0.16 ≤ x ≤ 1) | 263 ≥ Tm ≥ 80 | 21 (0.16) to * (1) |
| Ba2Na(Nb1–xTax)5O15 (0.65 ≤ x ≤ 1) | 260 ≥ Tm ≥ 80 | 6 (0.65) to * (1) |
| Ba2–xNa1+xNb5O15–xFx (0.31 ≤ x ≤ 1) | 250 ≥ Tm ≥ 140 | 40 (0.31) to 17 (1) |
| Ba2Na(Nb5–xTix)O15–xFx (0.31 ≤ x ≤ 0.50) | 265 ≥ Tm ≥ 168 | 15 (0.31) to 30 (0.50) |
| Sr2–xK1+xNb5O15–xFx (0.20 ≤ x ≤ 1) | 290 ≥ Tm ≥ 112 | 15 (0.20) to 16 (1) |
| Sr2.5(1–x)Ba2.5x□0.5Nb5O15 ** | ** | ** |
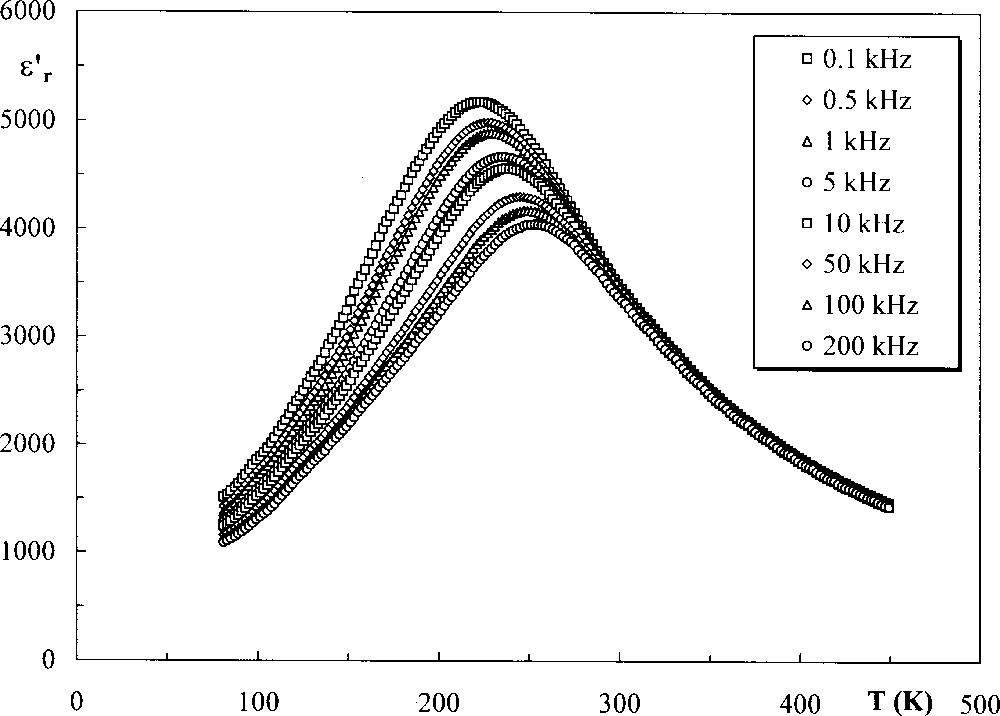
Temperature dependence of ε′r, the real part of the permittivity, for a ceramic with composition Sr2K(Nb0.775Ta0.225)O15.
Of all the lead-free compounds studied, it is with one of the compositions containing Bi3+, another 6(sp)2 lone pair cation, that the highest value of Tm was obtained: Tm (BaBiNb5O15) = 319 K at 103 Hz. In addition, independently of the value of Tm, the bismuth compositions allow the highest values of ΔTm: ΔTm = 80 and 73 K for the potassium and barium niobates respectively. Such a result is in good agreement with that obtained for lead-free compositions derived from BaTiO3 〚10〛.
Some solid solutions situated between classical ferroelectric and relaxor ones have also been studied. Such is the case with A2B(Nb1–xTax)5O15. The relaxor behaviour occurs for the highest values of x. Fig. 3 shows, as an example, the variations of TC (0 ≤ x < 0.16) and Tm (0.16 ≤ x ≤ 1) for ceramics with composition Sr2K(Nb1–xTax)5O15. Both values decrease when the tantalum rate increases.
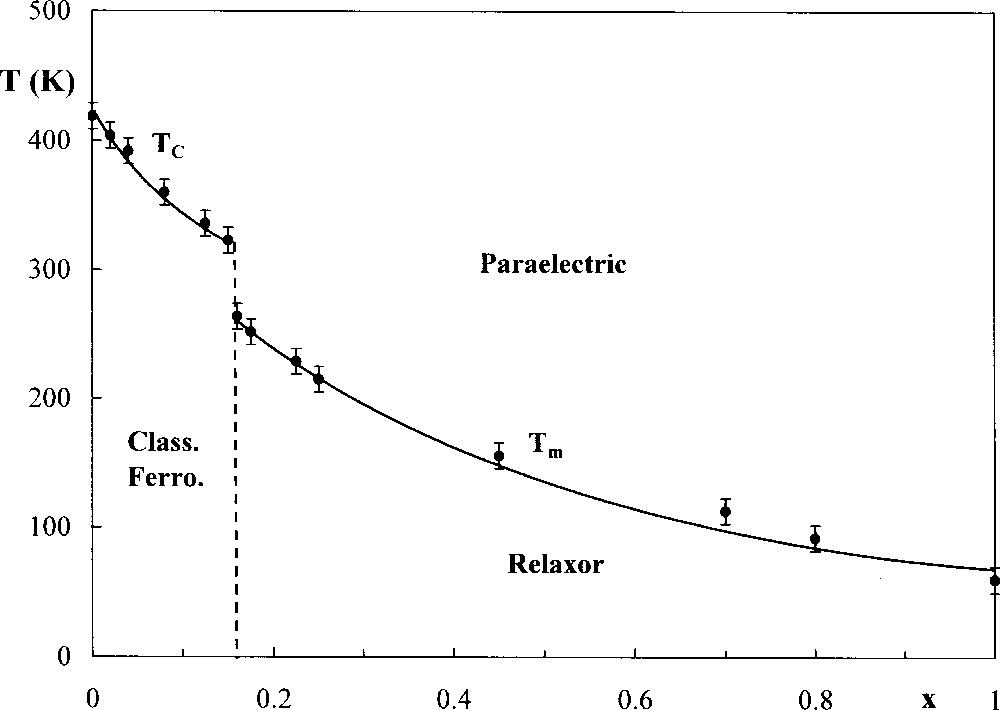
Variation of transition temperatures with x for ceramics with composition Sr2K(Nb1–xTax)5O15.
This is also the case with the Sr2KNb5O15/SrK2Nb5O14F and Ba2NaNb5O15/BaNa2Nb5O14F systems; for the compositions close to the oxide, the behaviour is ferroelectric, while it becomes relaxor when the fluorine rate and thus the sodium or potassium rate are sufficiently high. Fig. 4 shows as an example the variations of TC (0 ≤ x ≤ 0.25) and Tm (0.20 ≤ x ≤ 1) for the barium/sodium system. It is interesting to notice that both relaxor and classical ferroelectric phases coexist for compositions (0.20 ≤ x ≤ 0.25) giving thus the transition sequence: relaxor–classical ferroelectric–paraelectric, on heating. Here also both values of TC and Tm decrease when x increases. The frequency dependence of the permittivities of a ceramic with a composition BaNa2Nb5O14F clearly displays a frequency relaxation at 77 K, while it disappears at 300 K, i.e. for T > Tm (Tm = 140 K at 103 Hz) (Fig. 5).
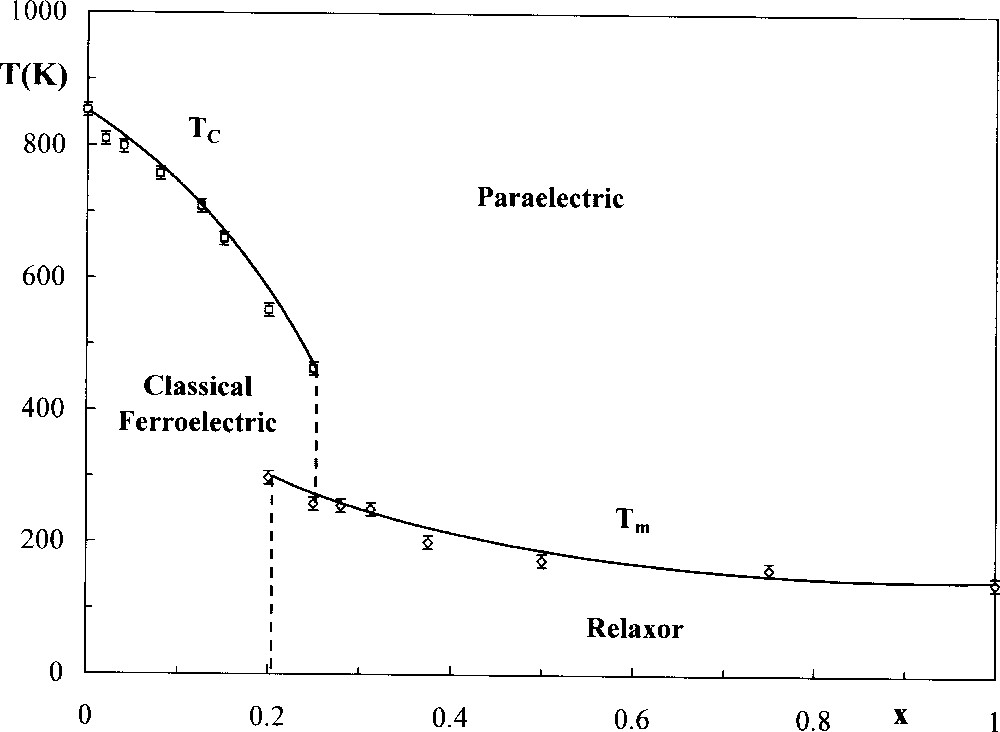
Variation of transition temperatures with x for ceramics with composition Ba2–xNa1+xNb5O15–xFx.
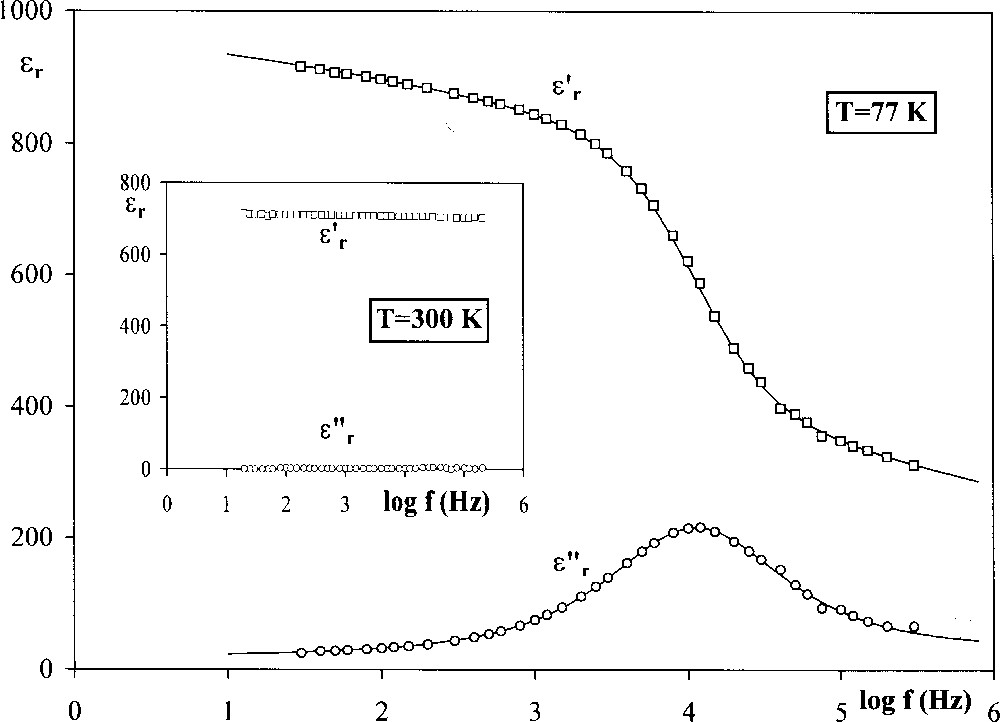
Frequency dependencies of the permittivities ε′r and ε′′r for a ceramic with composition BaNa2Nb5O14F.
4 Discussion
Some compositions had been previously prepared and characterised. They had been announced to be ferroelectric, measurements having been realised only at one frequency (103 Hz) and not at various frequencies as it has to be the case for relaxor property studies. It is the automation of dielectric measurements performed with an impedance analyser that allows us to obtain such actual results.
As for the perovskites, the relaxor effect appears in many TTB-type compounds when at least two ions occupy the same crystallographic site. The co-existence of cations seems as favourable in the A site as in the M site. In addition, at least one cation ferroelectrically active (Ti4+, Nb5+, Ta5+) must be present in the octahedral site.
The relaxor effect can be due to a cationic disorder in the A site, whatever the coupled substitution ensuring the electrical neutrality; this is the case with BaLaNb5O15, when Ba2+ and La3+ occupy only the A site. Ba2NaNb5O15, in which the same two Ba2+ cations occupy the A site, is a classical ferroelectric; on the contrary, BaNa2Nb5O14F is a relaxor one. The crystal structure determination of this last compound is in good agreement with the dielectric properties, i.e. the A-site is statistically occupied by equal quantities of Ba2+ and Na+, thereby giving a cationic disorder in this A-site while the B-site is filled by Na+ cations 〚11〛. In addition, there is here coexistence of F– and O2– in the anionic sites.
Concerning the Ta–Nb substitution, the replacement of Nb5+, highly polarisable, by Ta5+ transforms the macroscopic polarisation into a local one. This results in a relaxor state as the long-range order is not induced by a local dipolar order. The higher the associated cationic order in the A and B sites, the higher the Ta–Nb substitution rate leading to relaxor behaviour (Table 1); e.g. x = 0.16 for Sr2K(Nb1–xTax)5O15 and x = 0.65 for Ba2Na(Nb1–xTax)5O15. In fact, there is no ambiguity regarding the disordered distribution of the two small Sr2+ cations and the single large K+ one, nor regarding the ordered distribution of the two large Ba2+ cations and the single small Na+ ones, since both occur in two large A sites and in one smaller B one.
For oxyfluorides, F––O2– substitution is coupled with a cationic one in order to ensure the electric neutrality. The origin of the relaxor effect comes from cationic or/and anionic substitutions when there are two different cations in the same crystallographic site, e.g. Ba2–xNa1+xNb5O15–xFx, the A site being filled by both Ba2+ and Na+ for x > 0. However, it seems that it can be attributed to the only anionic F––O2– substitution in the lack of different cations in the same site, e.g. K3LiNb5O14F: due to their very different sizes, the K+ and the Li+ cations occupy only the (A + B) sites and C site respectively. It is also the case of Ba2.25□0.75Nb5O14.5F0.5, where A and B sites are occupied by only Ba2+. In these two compositions, the relaxor effect is induced by a dilution of the oxygen network, leading to a local polarisation that breaks the long-range order usually at the origin of classical ferroelectric properties.
5 Conclusion
In TTB-type compositions, the relaxor behaviour appears when at least two ions occupy the same crystallographic site. The Mn+ cations in the octahedral site have to be ferroelectrically active (e.g. Ti4+, Nb5+ or Ta5+). In any case, local polarisation leads to a relaxor effect; on the contrary a macroscopic one gives a classical ferroelectric behaviour. The relaxor effect is due to either a cationic or an anionic disorder in the A or B sites, or to a dilution of the ferroelectric character by cationic or anionic substitutions. Some of these materials could prove valuable (dielectrics for capacitors and actuators), because they are environment-friendly.



