1 Introduction
Electrochemical properties of tin-oxide-based glasses have been intensively studied since 1997, when Idota et al. 〚1〛 have reported that the glasses work as anode materials for lithium secondary batteries. The electrical capacity of the glasses is over 600 mA h g–1, which is almost twice as large as the capacity of graphitic carbon materials used as anodes for commercial lithium-ion secondary batteries. Although a large number of studies have been made on anode properties of tin oxide based glasses 〚2–7〛, little is known about fundamental properties such as thermal and viscous properties of the glasses. Recently, we have prepared several glasses based on SnO and indicated that the glasses exhibit not only excellent performance as anode materials but relatively low glass-transition temperatures 〚8〛. Glasses including large amounts of PbO have been commercially used as a sealing glass because of their low softening temperature. Tin-oxide-based glasses are the most promising candidates of Pb-free low melting glasses, which are desirable from an environmental point of view 〚9, 10〛. Glass properties are well known to closely relate to glass structure. It is thus important to investigate local structure of glasses in order to understand and improve their properties. We have analyzed glass structure of the SnO–B2O3 binary system by several spectroscopic techniques 〚11〛.
In the present study, glasses in the system Li2O–SnO–B2O3 have been prepared by a conventional melt-quenching method and the glass-forming region of the system has been determined. Glass-transition temperature (Tg) and viscosity in the vicinity of Tg are systematically investigated. Local structure of the glasses is also analyzed by using solid-state NMR and X-ray photoelectron spectroscopy, and a structural model of the glasses is proposed. The correlation between glass properties and structure in the SnO–B2O3 binary system is discussed.
2 Experimental
The mixture of Li2O (Kishida Chem., 99.9%), SnO (Furuuchi Chem., 99.9%), and B2O3 (Koujundo Chem., 99.9%) was heated in a carbon crucible at 850–1200 °C for 0.5–1 h in a dry N2-filled glove box. The molten samples were cooled by a conventional press quenching method (the cooling rate is in the range 102–103 K s–1) to yield thin disks less than 1-mm thick.
Glass-transition temperatures were determined for the samples sealed into Al pan in a dry N2-filled glove box by a differential scanning calorimetry (DSC) (PerkinElmer, DSC 7). The heating rate was 10 °C min–1 in the temperature range 25–500 °C under N2 atmosphere in all the measurements. Viscosity in the vicinity of Tg was determined using the beam-bending technique developed by Hagy et al. 〚12〛. The measurement was performed using a thermomechanical analyzer (Mac Science, TMA-4000) to obtain activation energies Eη for viscous flow around Tg 〚13–15〛.
11B MAS-NMR measurements were carried out at 96.23 MHz on a NMR spectrometer (Varian, Unity Inova 300). A pulse sequence with a single π/8 pulse was used in order to perform quantitative analysis on the spectra of quadrupolar nuclei such as 11B 〚16, 17〛. The width of a π/8 pulse length was found to be 0.7 μs for the SnO–B2O3 glasses. A recycle pulse delay, a spinning speed, and number of scans were respectively 2.0 s, 5 kHz, and 64–320 scans. O1s photoelectron spectroscopy was performed with an S-probe ESCA (Fions Instrument, SSX100S) using a monochromatic AlKα radiation (hν = 1486.6 eV). Rod-shaped glass samples were fractured in an ultra-high vacuum chamber (7 × 10–8 Pa) and the generated fresh surfaces of the glasses were analyzed. In order to remove the influence of the charging effect on spectra, neutralization of the glass surface was performed during the measurement by the combined use of a low-energy flood gun and an electrically grounded nickel mesh screen placed 1 mm above the glass surface 〚18–20〛. Calibration of the spectra was done by setting the measured binding energy of the C1s peak to 284.4 eV due to adventitious carbon accumulated in the analysis chamber of the spectrometer.
3 Results and discussion
3.1 Glass-forming region and glass-transition temperature (Tg)
Fig. 1 shows the glass-forming region and the Tg isotherms (°C) in the system Li2O–SnO–B2O3. Open circles and triangles respectively denote glassy samples and glassy samples with trace amounts of metallic Sn. The other marks denote that crystalline components were precipitated with small amounts of glasses; detailed crystalline phases are described in the caption. In the binary Li2O–B2O3 system, glasses are obtained in the composition range 0 ≤ Li2O (mol%) ≤ 40, which has been reported in a previous report 〚21〛. Glasses are obtained in the composition range 0 ≤ SnO (mol%) ≤ 75 in the binary SnO–B2O3 system. The glass-forming region in the binary system with SnO is considerably wider than that in the system with Li2O, which suggests that SnO plays the role of a network former as well as that of a network modifier. A change in the Tg isotherms in the Li2O–SnO–B2O3 system is notably complicated with Li2O and SnO contents; Tg ranges from 320 to 490 °C, which depends on a glass composition.

Glass-forming region and glass-transition temperature isotherms (°C) in the system Li2O–SnO–B2O3; ○: glass only, ▵: glass + traces of Sn, ▾: Sn crystals precipitated in small amounts of glass, ■: SnO crystals precipitated in small amounts of glass, and : Li2B4O7 crystals precipitated in small amounts of glass.
Fig. 2 shows the composition dependence of Tg in the SnO–B2O3 system. The values of Tg increase up to 40 mol% SnO and then decrease with an increase in the SnO content. The 40 SnO·60 B2O3 (mol%) glass exhibits a maximum Tg of 384 °C. A similar composition dependence of Tg was also reported in other borate glasses such as Na2O–B2O3 〚22〛 and PbO–B2O3 glasses 〚23〛. The maximum Tg was 475 °C at the composition with 30 mol% Na2O and 455 °C at the composition with 27 mol% PbO. It is revealed that Tg in the SnO–B2O3 glasses is much lower than that in the other borate glasses with Na2O or PbO.

Composition dependence of glass-transition temperature for the SnO–B2O3 glasses.
In the SnO–B2O3 binary system, no exothermic peaks due to crystallization were observed on DSC curves in the temperature range up to 500 °C, which suggests that the binary system with SnO has an excellent thermal stability against crystallization. In the case of an addition of Li2O to the SnO–B2O3 system, however, an exothermic peak due to crystallization was observed in the temperature range up to 500 °C, which suggests that the addition of Li2O lowers the thermal stability of the glasses.
3.2 Viscous properties in the vicinity of Tg
Fig. 3 shows viscosity data in the vicinity of Tg for the SnO–B2O3 glasses versus reciprocal temperatures normalized by Tg. In such a narrow temperature region, viscosity data obey the Arrhenius equation in the viscosity range 1010–1013 Pa s. The values of Eη and Eη/Tg, where Eη is an activation energy for viscous flow in the glass-transition range, are calculated from a slope of the viscosity data.
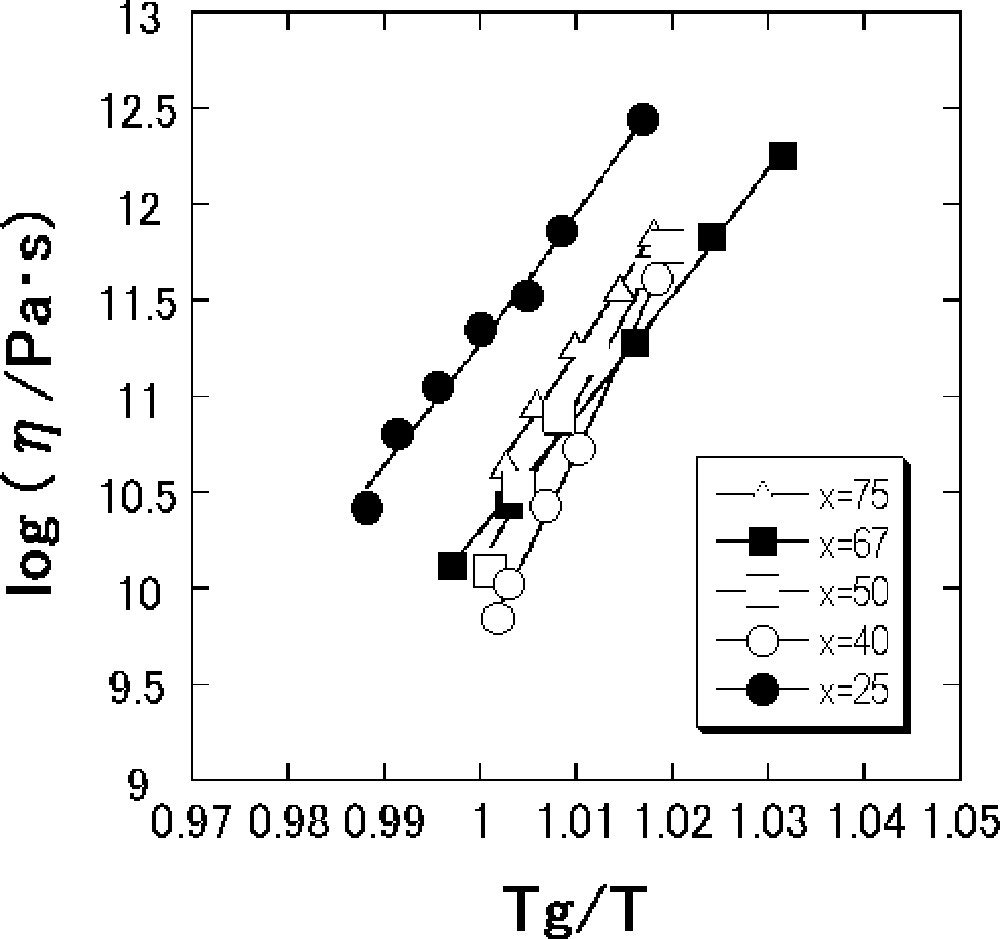
Temperature dependence of viscosity in the vicinity of Tg for the x SnO·(100 – x) B2O3 (mol%) glasses.
Fig. 4 shows the composition dependence of Eη and Eη/Tg of the SnO–B2O3 glasses. The composition dependence of Eη/Tg is very similar to that of Eη. Both values of Eη and Eη/Tg g increase up to the composition with 40 mol% SnO, then decrease up to 67 mol% SnO, and increase again up to 75 mol% SnO. The maximum Eη and Eη/Tg values are respectively 1266 kJ mol–1 and 1.93 kJ mol–1 K–1 for the composition with 40 mol% SnO.
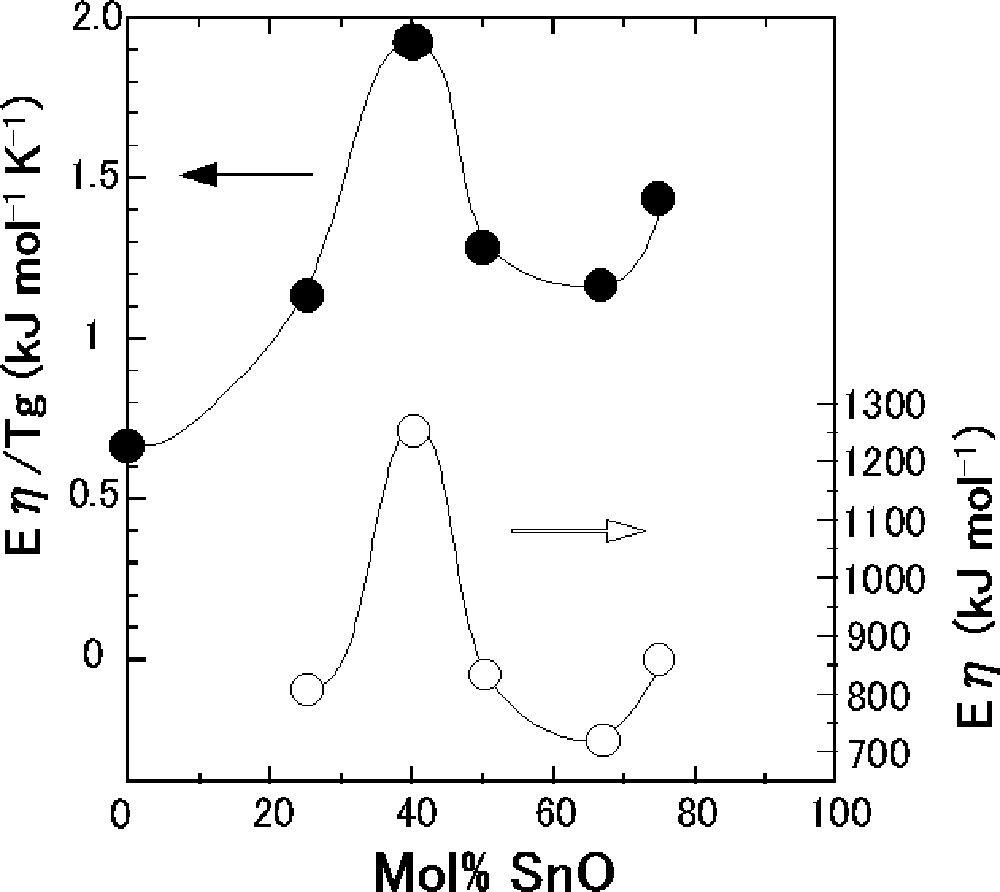
Composition dependence of Eη and Eη/Tg for the SnO–B2O3 glasses.
Eη/Tg is one of the measures of fragility of liquids; the concept of fragility has been proposed by Angell 〚24〛. The 40 SnO·60 B2O3 (mol%) liquid is the most fragile in the SnO–B2O3 system. A similar composition dependence of Eη/Tg was reported in the conventional alkali borate systems such as Na2O–B2O3 〚25〛. In this system, the maximum Eη/Tg value of 1.53 kJ mol–1 K–1 was obtained at the composition with 30 mol% Na2O. The maximum value of Eη/Tg in the SnO–B2O3 system is larger than that of the Na2O–B2O3 system, suggesting that borate glasses with SnO are more fragile than alkali borate glasses.
3.3 Glass structure
11B MAS-NMR measurements were performed to determine the fraction of four-coordinated boron (N4, which means the ratio of 〚BO4〛/(〚BO3〛+〚BO4〛)) present in the SnO–B2O3 glasses. Fig. 5 shows the composition dependence of N4 obtained from 11B NMR spectra. It is well known that there are only BO3 units in the pure B2O3 glass 〚17〛. The BO4 units are present at the composition with 25 mol% SnO, where N4 is 0.16. The N4 values increase up to 50 mol% SnO and then decrease with increasing SnO. The maximum value of N4 is 0.28 at the composition with 50 mol% SnO.
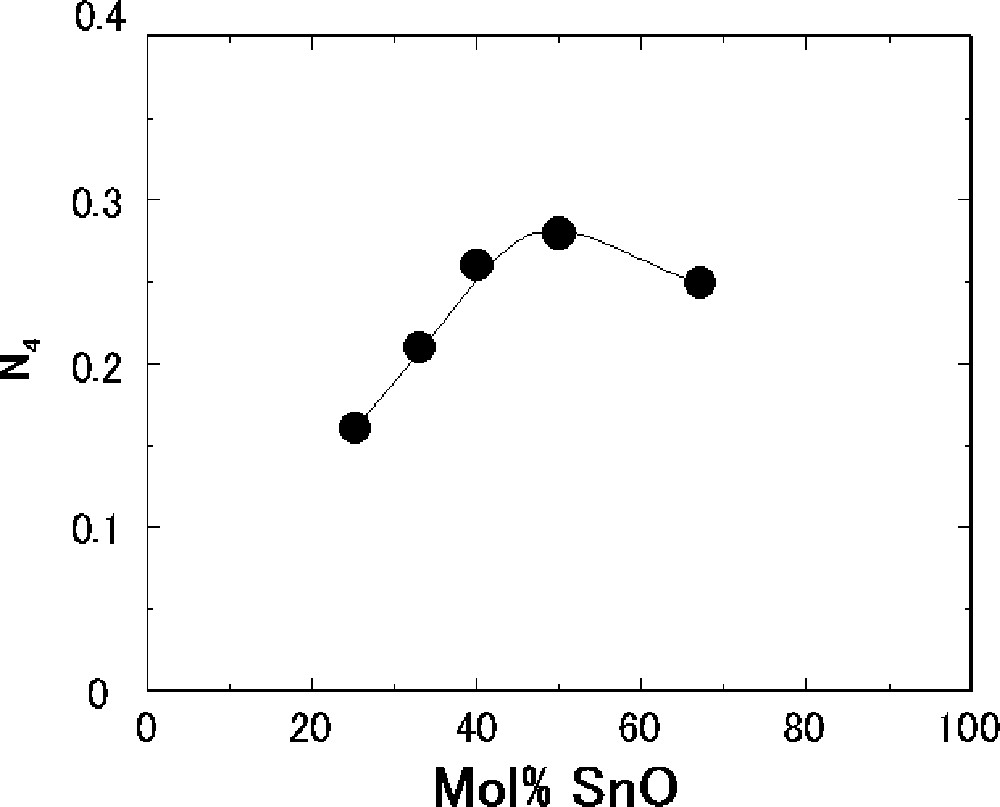
Composition dependence of fraction of four-coordinated boron (N4) for the SnO–B2O3 glasses.
O1s photoelectron spectroscopy was measured to investigate electronic states of oxygen in the SnO–B2O3 glasses. Fig. 6 shows O1s photoelectron spectrum of the 25 SnO·75 B2O3 (mol%) glass. The peak shape of the glass is asymmetrical; we confirmed that the peak of the glass was broadened at the lower energy side as compared with the symmetrical peak of the pure B2O3 glass. This broadening of the O1s peak suggests that at least two peaks are partially overlapped. A peak separation was carried out by the best-fitting program using Gaussian (70%) and Lorentzian (30%) 〚19, 20〛; the separated peaks are also shown in Fig. 6.
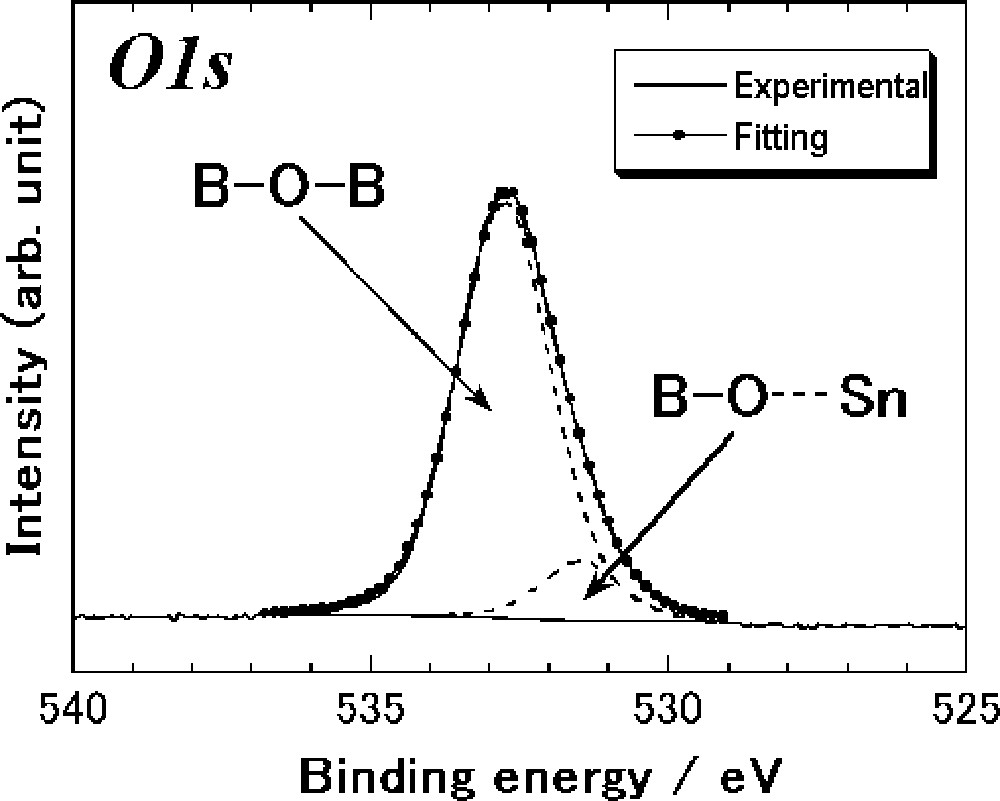
O1s photoelectron spectrum of the 25 SnO·75 B2O3 (mol%) glass. The peak separation is also shown in this figure.
In the O1s spectra of the alkali borate glasses such as the Na2O–B2O3 system, two distinct peaks obviously appear; a peak at a higher energy side is assigned to bridging oxygens and the other one at a lower energy side to nonbridging oxygens 〚26〛. We have already mentioned that the SnO–B2O3 system has a wide glass-forming region and four-coordinated boron is still present at compositions with high SnO content. These results suggest that SnO acts not only as a network modifier, but also as a network former. Hence, typical ionic nonbridging oxygen observed in the alkali borate glasses is not present but rather more covalent nonbridging oxygen is mainly present in the SnO–B2O3 glasses. Since the binding energy of the nonbridging oxygen with partial covalency is close to that of bridging oxygens, the spectrum of the SnO–B2O3 glass could not be clearly divided into two distinct peaks. The peak at the higher energy side in Fig. 6 is thus assigned to bridging oxygen (B–O–B) and the peak at the lower energy side to nonbridging oxygen (B–O···Sn). The component of oxygens in SnO (Sn···O···Sn) is also included probably in the peak at the lower energy side.
The relative amounts of those two kinds of oxygens were obtained from the relative areas under the two separated peaks. Fig. 7 shows the composition dependence of the relative amounts of bridging oxygen and nonbridging oxygen of the SnO–B2O3 glasses. Only bridging oxygens are present in the B2O3 glass. Addition of SnO to B2O3 forms nonbridging oxygens and the amounts of bridging and nonbridging oxygens are estimated to be respectively 89% and 11% at the composition with 25 mol% SnO. The amounts of nonbridging oxygens slowly increase up to the composition with 40 mol% SnO and then drastically increase with an augmentation of the SnO contents. The amounts of bridging and nonbridging oxygens are respectively 32% and 68% at the composition with 67 mol% SnO.
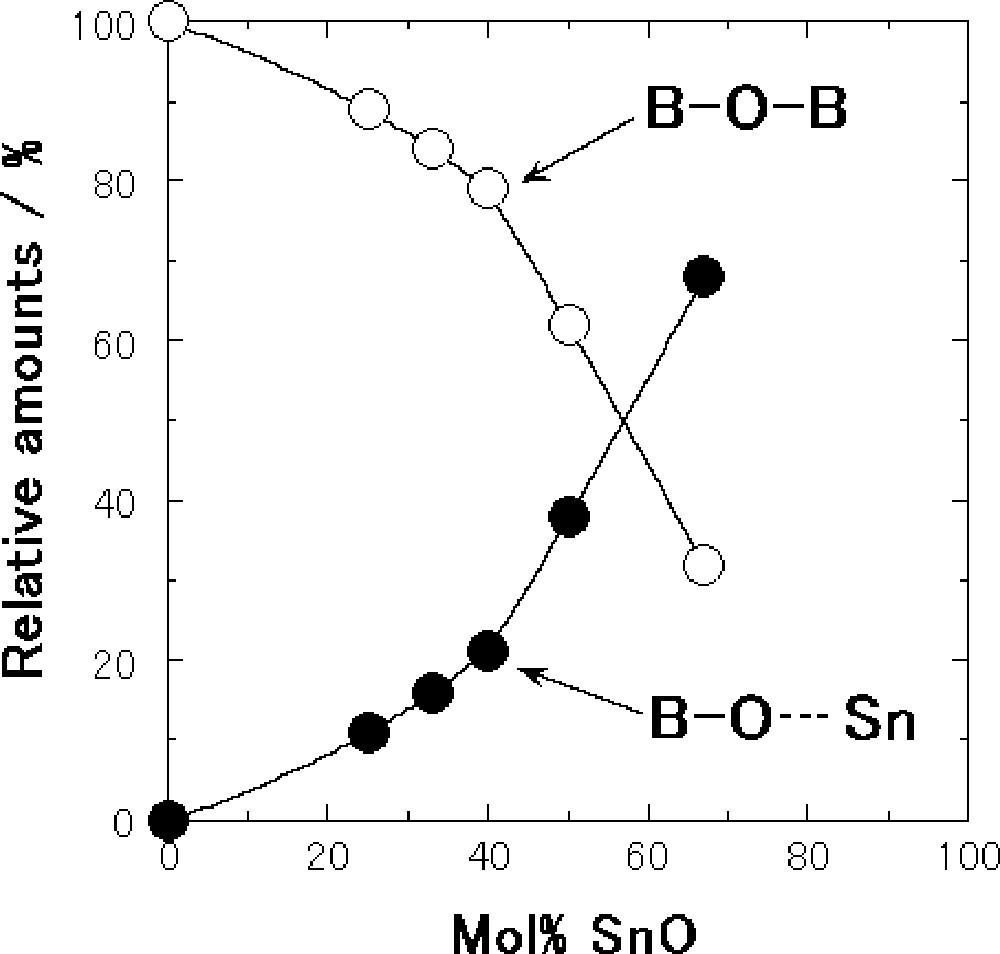
Composition dependence of relative amounts of bridging oxygen (B–O–B) and nonbridging oxygen (B-O···Sn) for the SnO–B2O3 glasses.
The structural model of the SnO–B2O3 glasses is proposed on the basis of the spectroscopic data mentioned above. The 11B NMR measurement of the 50 SnO·50 B2O3 (mol%) glass revealed that the fraction of four-coordinated boron was 0.28, whereas that of three-coordinated boron was 0.72. The O1s photoelectron spectroscopy of the glass indicated that the relative amount of bridging oxygens (B–O–B) was 62%, whereas that of nonbridging oxygens (B–O···Sn) was 38%. The estimated structural model of the 50 SnO·50 B2O3 (mol%) glass is shown in Fig 8. The glass network consists of BO3 (72%) and BO4 (28%) units, and Sn(II) compensates for negative charges of BO4 units and nonbridging oxygens.
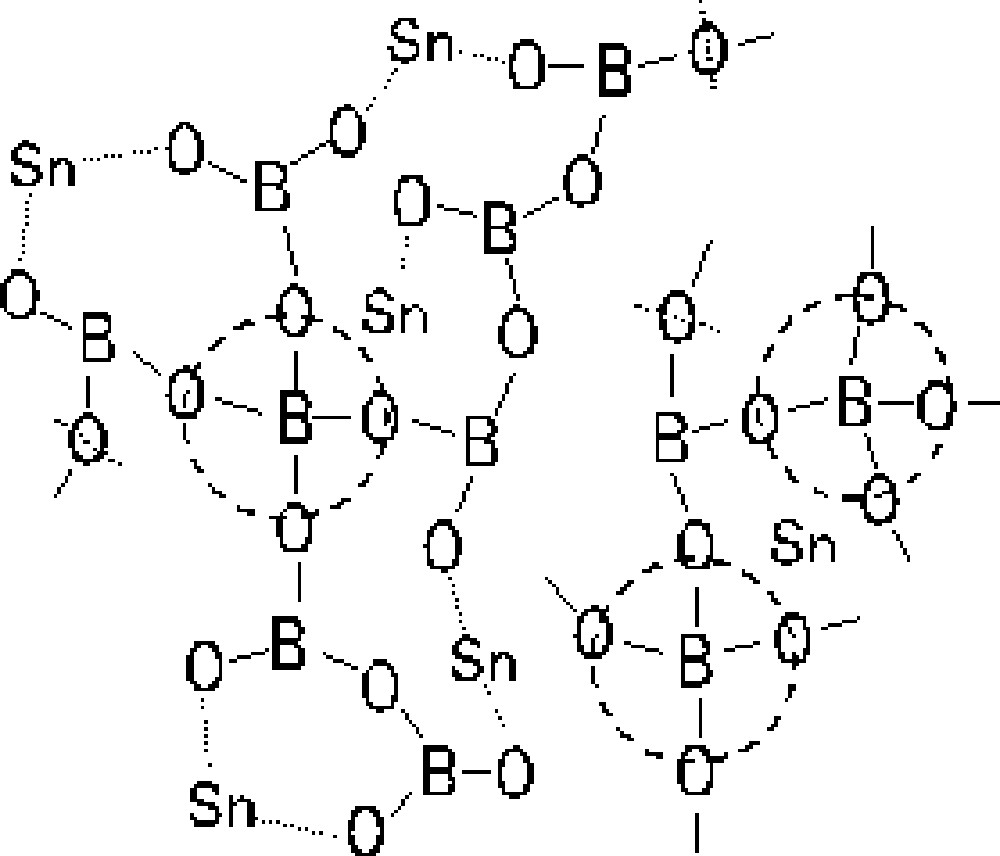
Structural model of the 50 SnO·50 B2O3 (mol%) glass.
3.4 Correlation between glass structure and properties
The thermal and viscous properties of the SnO–B2O3 glasses are discussed from the point of view of the glass structure.
As shown in Fig. 2, the Tg values have increased up to 40 mol% SnO and then decreased with an increase in the SnO content. The composition dependence of N4 (Fig 5) is similar to that of Tg. However, the maximum composition of Tg is different from that of N4; the values of Tg maximize at the composition with 40 mol% SnO, whereas N4 does with 50 mol% SnO. This difference in composition between the maximum Tg and N4 has also been observed in the alkali borate glasses 〚27〛 and PbO–B2O3 glasses 〚23, 28〛. The BO4 tetrahedral units make three-dimensional network and, therefore, Tg increases with an increase in N4. In the SnO–B2O3 glasses, the amounts of nonbridging oxygens have drastically increased for the compositions with more than 40 mol% SnO, as shown in Fig. 7. An increase in nonbridging oxygen generally lowers Tg. The maximum composition of Tg must depend on both amounts of four-coordinated boron and nonbridging oxygen in the glass structure. In this balance, Tg has maximized for the composition with 40 mol% SnO in the SnO–B2O3 glasses.
The values of Eη/Tg have maximized for the composition with 40 mol% SnO (Fig. 4) whereas N4 maximized for the composition with 50 mol% SnO (Fig. 5). As mentioned in section 3.2, Eη/Tg is used as a measure of fragility of liquids. Lee et al. 〚15, 25〛 have reported in several borate glasses that Eη/Tg is closely linked to an average coordination number <r> of elements, which was introduced by Phillips 〚29〛 in order to explain strong glass-forming ability in chalcogenide systems. The <r> value in the Na2O–B2O3 glasses was maximized for the composition with 30 mol% Na2O, for which the value of Eη/Tg was also maximized 〚25〛. The correlation between <r> and Eη/Tg was explained as follows. The <r> value of the B2O3 glass was calculated to be 2.40, which suggests that this glass is the most stable from the Phillips’ topological point of view 〚29〛. Since the Na2O–B2O3 glasses, whose <r> value was larger than the 2.40 value of the B2O3 glass, was in the over-constrained coordination state, the glasses exhibited larger fragility 〚25〛.
We try to calculate the <r> value of the SnO–B2O3 glasses on the basis of the structural data mentioned above and discuss the correlation between <r> and Eη/Tg. In the Na2O–B2O3 glasses 〚25〛, bonds with strong covalent character such as B–O were only taken into account and ionic bonds such as O–···Na+ were neglected in the calculation of <r>. On the other hand, the bond of O···Sn present in the SnO–B2O3 glasses is more covalent than the typical ionic bond O–···Na+ (see section 3.3). We have thus calculated <r> in extreme two manners: in a case (a), the O···Sn bond is assumed to be perfectly ionic, and, in the other case (b), the O···Sn bond is assumed to be perfectly covalent. In other words, only the B–O covalent bond is taken into account in the case (a) and both B–O and O···Sn bonds are considered in the case (b). In the case (a), the <r> values of the borate structural units BO3/2, (BO4/2)–, BO2/2O–, BO1/2O22–, and BO33– were respectively calculated to be 2.40, 2.67, 2.00 1.71, and 1.50. In the case (b), the <r> values of the units BO3/2, BO4/2Sn, BO2/2OSn, BO1/2O2Sn2, and BO3Sn3 were respectively 2.40, 3.14, 2.22, 2.15, and 2.12; the coordination number of Sn was assumed to be 6 in the BO4/2Sn unit and 2 in the other units.
The composition dependence of <r> calculated for the SnO–B2O3 glasses is shown in Fig. 9. Open and closed circles denote the <r> values in the cases (a) and (b), respectively. The <r> value of pure B2O3 glass is 2.40. The <r> value calculated in the case (a) slowly decreases up to the composition with 40 mol% SnO and then drastically decreases with an increase in the SnO content. On the other hand, the <r> value calculated in the case (b) increases up to the composition with 40 mol% SnO and then decreases. The proper <r> value of the SnO–B2O3 glasses must be an intermediate value between the extreme two cases of (a) and (b), and hence <r> is presumed to be maximized at the composition with 40 mol% SnO. This suggests that the composition dependence of <r> is closely related with that of fragility with Eη/Tg in the SnO–B2O3 system.
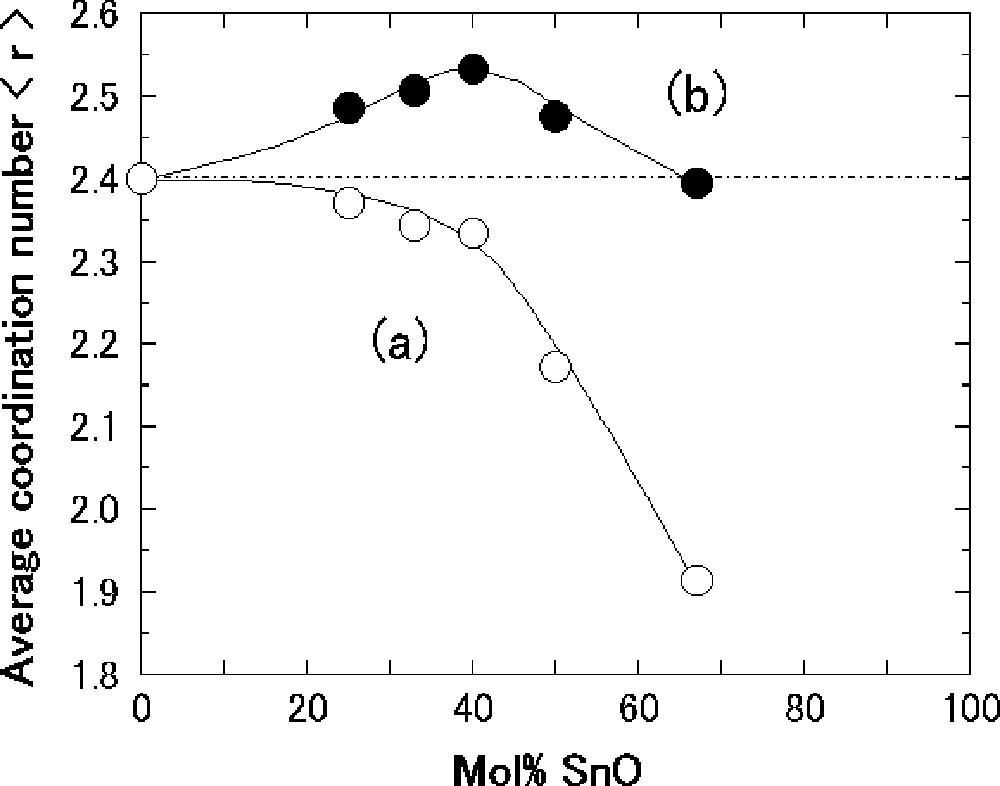
Composition dependence of average coordination number <r> for the SnO–B2O3 glasses. The calculation of <r> was carried out in two manners: in the first case (a), the O···Sn bond was assumed to be perfectly ionic, and in the other case (b), the O···Sn bond was assumed to be perfectly covalent. See text for details.
4 Conclusions
Glasses in the system Li2O–SnO–B2O3 were prepared by a conventional melt-quenching method. The glass-forming region of the SnO–B2O3 system was 0 ≤ SnO (mol%) ≤ 75, which region was considerably wider than that of the Li2O–B2O3 system (0 ≤ Li2O (mol%) ≤ 40). The SnO–B2O3 glasses showed relatively low glass-transition temperature (Tg) around 350 °C and excellent thermal stability against crystallization, which suggests that these glasses are one of the most promising Pb-free low melting glasses. On the other hand, an addition of Li2O to the glasses lowered thermal stability. Both values of Tg and Eη/ Tg were maximized at the composition with 40 mol% SnO in the SnO–B2O3 system. In particular, it is noteworthy that the 40 SnO·60 B2O3 (mol%) glass with a large Eη/Tg of 1.93 kJ mol–1 K–1 is considerably fragile compared to other oxide glasses.
11B MAS NMR measurements indicated that the fraction of four-coordinated boron was maximized at the composition with 50 mol% SnO. It was revealed from O1s photoelectron spectra that an addition of small amounts of SnO formed nonbridging oxygen, which is not purely ionic in alkali borate systems but partially covalent in the SnO–B2O3 system. The amounts of nonbridging oxygen gradually increased in the range SnO ≤ 40 mol% and then drastically increased in the range SnO > 40 mol%, with an increase in the SnO content.
The correlation between glass properties and structure in the SnO–B2O3 system was discussed. The composition dependence of Tg was expected to be influenced by the fraction of not only four-coordinated boron but also nonbridging oxygen. We also explained the composition dependence of Eη/Tg in terms of the calculated average coordination number <r>.
Acknowledgements
This work was supported by the Grand-in-Aid for Scientific Research on Priority Areas (B) and Section (B) from the Ministry of Education, Culture, Sports, Science and technology of Japan, and by Research Fellowships of the Japan Society for the Promotion of Science for Young Scientists.



