1 Introduction
The modelling of physical and chemical properties of silicate glasses and melts and the evolution of these properties as a function of temperature or chemical composition relies on a correct understanding of the structural properties of these materials. The amorphous nature and the complex chemical composition do not allow the construction of a unique structural model, as in crystalline compounds. If glasses lack the periodicity and long-range order, which characterise crystalline compounds, they still retain a characteristic short-range order, which obeys the same crystal-chemical rules as in crystals. The structural models of complex multicomponent glasses rely on the combination of experimental data, such as diffraction of X-rays and neutrons together with various spectroscopic methods and of numerical modelling. However, even in simple glasses, such as silica and amorphous Si, this determination remains a difficult task. Actually, deriving a unique structural model for a glass or melt from any experimental method or computer simulation is impossible because of their disordered nature. Nonetheless, these methods are important for relating the localised character of several physical properties of glasses to local atomic arrangements, and in certain cases, more extended topologies.
The modelling of the glass structure relies on the determination of interatomic distances and bond angles, an information which is smeared out as interatomic distances increase, due to disorder effects. Various scales of order can be defined at short-range (1.5–2.9 Å), medium-range (2.9–5.5 Å) and more extended scale (5.5→10 Å) 〚1〛. Short-range order concerns cation-oxygen polyhedral units. It is mostly accessible by a wide range of spectroscopic methods. Medium-range order involves the ordering of silicate tetrahedra (i.e., Qn units) and cationic sites, together with the relationships between these two kinds of glass components. X-ray and neutron wide-angle diffraction methods are generally used to get insight in this range 〚2〛. More extended medium-range order in glasses and melts, including the network topology, is generally derived from numerical modelling 〚3〛. A noticeable exception is the evidence for an extended cationic ordering, which has been evidenced by neutron diffraction on isotopically substituted glasses 〚4〛.
Due to the lack of periodicity, radiation diffraction results in a one-dimensional information. Important structural information has been gained from the radial distribution functions (rdf) calculated from the neutron and wide angle X-ray diffraction. The total rdf that can the be obtained is generally used to determine the network structure at short and medium range scales, including the average first- and further-neighbour distances, bond angles, and cation coordination numbers. The structural methods used to determine the surrounding of cations in silicate glasses include two kinds of techniques. Spectroscopic methods, such as optical absorption spectroscopy, X-ray absorption spectroscopy or Mössbauer effect, are sensitive to the local geometry, site symmetry and to the nature of the chemical bond. They have the advantage of the chemical selectivity, which is important in the study of multicomponent glasses such as nuclear waste glasses 〚5〛. These methods help in determining the immediate surrounding of cations in glasses, with some insight into the relationships between the cationic sites and the polymeric network of the glass. Scattering methods give access to the medium-range structure 〚1, 2, 6, 7〛. A chemical selectivity is achieved by using difference methods: anomalous wide-angle X-ray scattering (AWAXS) and neutron diffraction with isotopic substitutions (NDIS). As the interaction of photons with matter samples a short time-domain in the UV-visible and X-ray range, most spectroscopic and diffraction methods provide isotropically averaged information on the local structure of glasses, with some insight into medium-range structural correlations. Due to the multicomponent nature of silicate and, more generally, of oxide glasses, only one kind of experiment cannot give information on the whole structure. For a compound with n components, n (n + 1)/2 different pair functions are needed to solve its structure, which is in practice impossible to satisfy. However, some structural information may be obtained by combining various methods, such as X-ray and neutron diffraction. A major limitation of the combination of various experimental approaches is their contrasted sensitivity to disorder effects, which may give distinct apparent structural evidences: average geometry, continuous distribution between discrete surroundings or apparent predominance of a specific site. By contrast to other glasses such as halide glasses, oxide glasses are based on a polymeric network of edge-sharing tetrahedra chemically associated to cations. Cations are usually classified as network formers (including some transition elements), network modifiers, which interact with the bridging oxygens to depolymerise the network, or cations that ensure charge compensation for non-tetravalent network-forming elements (Si, Al, B and some transition elements: see below).
Many glass properties, such as coloration, chemical resistance, mechanical properties, crystalline nucleation and phase separation or ionic and electrical conductivity, may depend on glass structure, defined in turn by the glass composition. In some cases, it has been possible to establish relations with the structural role of some key elements. We will present in this review some structural characteristics that appear to control physicochemical properties of multicomponent glasses, with a special attention to cations, which control the polymeric structure. New data have been recently obtained on the peculiar geometry of cationic sites, the relationships between these sites and the glassy framework and the general evidence of cationic domains in complex oxide glasses. We will restrict this review to the oxide glasses, such as silicate, alumino-silicate, borate, borosilicate, etc.
2 The structural organisation around cations in oxide glasses
2.1 A peculiar site geometry
Cations often occupy unusual sites in oxides glasses, and crystalline models need to be used with caution. A general observation is a trend towards lower coordination numbers in glasses than in crystals. Another property is the contrast between cations that are encountered in a strong association with the polymeric framework, such as network forming cations Zn and Fe3+ (see below), and the modifier cations, which do not show fixed relationships with this polymeric framework. The former are generally in a tetrahedral site, interconnected in the framework, while the latter correspond to higher coordination numbers, with the frequent occurrence of the 5-fold coordination for transition metal ions, which imparts glasses specific properties such as their coloration (see below). Obviously, the two kinds of surroundings will not affect glass properties at the same extent. The influence of the presence of network-forming cations on glass properties will be described below in the case of divalent Zn and Ni, as well as Fe3+ in nuclear waste glasses.
Five-fold coordination is frequently encountered in silicate and alumino-silicate glasses around Mg and divalent transition elements, such as divalent Ni or Fe, and imparts them specific spectroscopic properties (see below). These modifier ions are reactive intermediate species that indicate associative/dissociative reactions 〚8〛. For instance, 〚5〛Si 〚9〛 and 〚5〛Al 〚10〛 are associated with the viscous flow and the chemical diffusion that characterise silicate melts. 〚5〛Ni has been extensively studied in glasses by a combination of spectroscopic techniques 〚11, 12〛. By contrast to 〚4〛Ni, it does not show a well-defined geometrical relationship with the silicate framework and neutron diffraction indicates the presence of other cations (Ca, Ni) as second neighbours 〚4〛. 〚5〛Ni may be formed either from 〚4〛Ni by an associative reaction involving the bonding of a 〚4〛Ni species to a fifth oxygen, e.g., a bridging oxygen, or from unstable 〚6〛Ni species by a dissociative reaction implying the loss of a sixth ligand because of the oxygen motion accompanying the viscous flow. Indeed, the frustration of ligand spatial correlation is likely to be at the origin of the small coordination numbers of most cations in glasses and melts, one of the major finding of EXAFS and neutron diffraction studies of glasses 〚13, 14〛. A dissociative reaction, together with an easier cation–oxygen bond-breaking ability, may explain why, by contrast to 〚5〛Si species that only affect a minority of the Si atoms, 〚5〛Ni is the predominant species for Ni in most silicate glasses.
Highly charged cations, such as tetravalent Zr and Ti, present an intermediate case between tetrahedral cations in a network-forming position and modifier ions, which present higher coordination numbers. Zr usually occurs in silicate glasses in a regular octahedral coordination, with a clear connection to the silicate network (Fig. 1), shown in the EXAFS spectra by the presence of corner-sharing SiO4 tetrahedra 〚5〛. However, by contrast to network forming cations, the mean Zr–Si distance suffers important variations as a function of glass composition, with values ranging from 3.37 Å to 3.71 Å (e.g. 3.40 Å in Na–borosilicate glasses used as analogues for nuclear waste glasses 〚5〛). The variations indicate that Zr is a good structural probe, sensitive to local modifications of the glass structure. As for divalent network-forming cations, a charge compensation brought by alkalis or alkaline earths is needed to stabilise this unusual coordination state. This Zr surrounding is only encountered in natural uncommon crystalline alkali zirconosilicates.
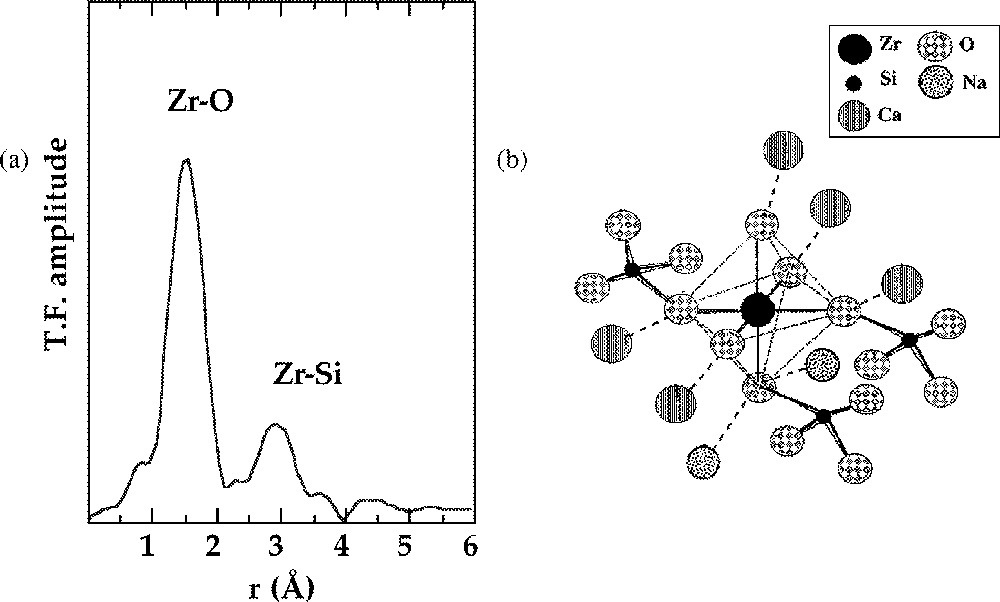
a. k3-weighted Fourier transform of the Zr K-edge EXAFS spectra for a technological glass. b. Schematic representation of the connectivity of the ZrO6 octahedra with the silicate network based on the EXAFS results (from 〚5〛).
2.2 Medium-range organisation around cations: percolation domains and modified random network in silicate glasses
A modification of the Zachariasen–Warren random network model has been proposed by Greaves et al. 〚15, 16〛 for Na2O–SiO2 glasses, which involves two interlacing ‘sublattices’, i.e., network regions made up of network formers and inter-network regions made up of network modifiers. The modified random network (MRN) proposes that network-modifier regions would extend to percolation channels, when their volume fraction exceeds 16%, making it easier for network modifier cations to diffuse in the glass. The diffusion properties of many binary alkali silicate glasses are predicted using the MRN, with the evidence of a percolation threshold 〚17, 18〛. The MRN model has received a structural basis, with the structural methods such as EXAFS spectroscopy, wide-angle X-ray scattering and neutron diffraction coupled with isotopic substitution 〚2, 19, 20〛, which found extended M–M correlations between network-modifying cations, M, in oxide glasses. Earlier studies by X-ray diffraction have shown that in oxide glasses containing a heavy metal ion as a major component, the scattering responsible for the M–M pair correlation is stronger than other pair correlations 〚21〛. In Cs–silicate glasses, a strong pair-correlation is observed in the rdf at 4.1 Å, due to Cs–Cs pairs, with additional features at 6.9 and 8.0 Å, due to an extensive heterogeneous distribution of Cs in the glass 〚22〛.
The use of isotopes with different neutron scattering lengths gives access to a chemical selectivity, which has given fascinating results about cation distribution in glasses 〚2, 20〛. In K2O–TiO2–SiO2 glass, Ti–Ti correlations are found at 3.4 Å (Fig. 2), while a random distribution of Ti atoms would give a correlation length of 6.1 Å 〚23〛. This short distance was interpreted as indicating preferential clustering of Ti in this glass. Gaskell et al. 〚20, 24, 25〛 performed similar experiments on CaO–SiO2 and NiO–2 CaO–3 SiO2 glasses. In both studies, evidence for cation clustering was found. For example, in CaO–SiO2 glass, Ca–Ca correlations at 3.8 Å and 6.4 Å were detected. The shortest distance indicates edge-sharing CaO6 octahedra, whereas the longer Ca–Ca distance was interpreted as evidence for bi-dimensional arrangements of edge-sharing CaO6 octahedra. Anomalous X-ray scattering can also provide useful information on longer-range M–M pair correlations and takes advantage of the anomalous variations of the absorption coefficient in the vicinity of an X-ray absorption edge for a specific element. This method has shown a clustering of Y cations in Y2O3–Al2O3–SiO2 glass 〚26〛 and of Sr cations in SrO–SiO2 glasses 〚27〛.
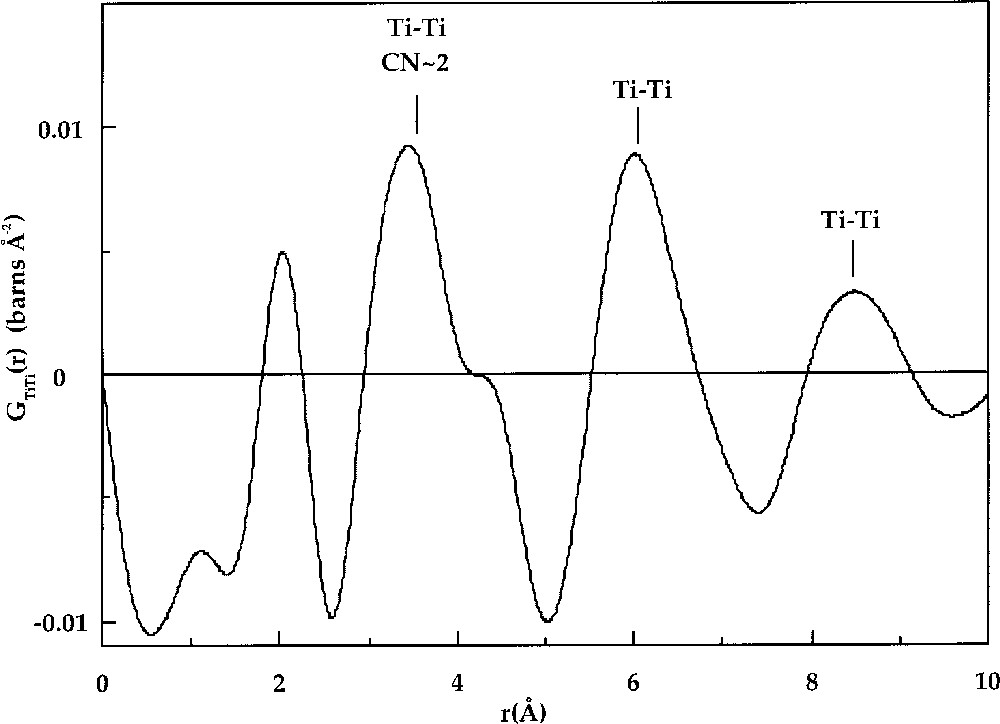
Ti–Ti distribution, GTi–Ti(r), obtained for the K2O·TiO2·2 SiO2 glass 〚14〛. The first Ti–Ti distance corresponds to corner sharing of square-based TiO5 pyramids with a mean Ti–Ti coordination number of 2.
2.3 The competition between network formers and network modifiers in multicomponent glasses
Hess 〚28〛 proposed the use of bond valence to help in understanding the structural role of cations in glasses and melts. Pauling bond valence, ν (= Zc/N, in valence units, v.u.), helps in describing the charge equilibria of the chemical bonds in solids. Network modifiers may be defined as having a bond valence smaller than 0.75 valence units (v.u.). Some exceptions may however be observed. Four-coordinated divalent cations, with bond valences of ∼0.5 v.u., have been described to be part of the polymeric network, as proposed for Fe(II) 〚29〛 and for Ni(II) 〚12〛. Consideration of bond valence also indicates that oxygens bonded to highly charged cations like Mo(VI), which occur as tetrahedral MoO4 units (Mo–O bond valence = 1.4), cannot form bonds with Si, and thus act as network modifiers 〚30〛.
The structure of multicomponent silicate glasses is based on a polymeric network with coexisting cations, which may act as modifiers or as charge compensating cations needed for balancing the charge deficit of oxygen neighbours. This situation occurs when trivalent cations are substituted to silicon in the polymeric network. Glass properties may be strongly affected, depending whether cations are network modifiers or charge compensators. This has been shown in alkali-bearing glasses in which transport properties are strongly affected by the substitution of silicon by aluminium, in correlation with important structural modifications 〚18〛. Borosilicate glasses are a good example of materials in which cations may occur in these two situations. These glasses are of great interest in a wide range of applications, such as electronics, materials science, waste management, etc. One of their peculiar structural properties comes from the ability of boron to occur in three- or four-coordination, depending on its possibility to get charge compensation from the coexisting cations. However, the complex chemical composition makes the radial distribution functions difficult to interpret beyond the first coordination shell, in the absence of a structural model. We have investigated the competition for charge compensation between different highly charged cations, boron, aluminium and zirconium in multicomponent borosilicate glasses 〚31, 32〛, for which molecular dynamics (MD) models have been proposed 〚33〛. The direct determination of the glass structure by wide-angle X-ray scattering (WAXS) has been combined with molecular dynamics calculations, allowing us to decipher the various pair contributions to the rdf. This investigation allows a better understanding of the competition of cations (Na and Ca) for charge compensation of B and Al polyhedra within the glass structure. In presence of alumina, we observe a bimodal distribution of the Na–O distances, with contributions at 2.20 and 2.55 Å. The larger one can be assigned to Na atoms charge-compensating network forming aluminium or boron atoms. Furthermore, when alumina is present, less Si and B neighbours are detected around Na. These results are consistent with sodium atoms charge-balancing preferentially the (AlO4)– tetrahedra at the expense of boron. As a consequence, we observe a conversion of some (BO4)– units into BO3 units. These results have shown that aluminium has thus a higher ability to be present in tetrahedral sites than boron. With the addition of CaO, (AlO4)– groups are preferentially charge-compensated by Ca2+ ions rather than by Na+ ions, which remain charge-compensators of (BO4)– groups. Space limitations may account for the preference of Ca2+ ions in the vicinity of Al atoms, since the (AlO4)– groups are larger than the (BO4)– groups. On the other hand, Ca2+ ions were observed to be closer to the nonbridging oxygens than Na+ ions and can be charge-compensators as well as modifiers. The higher charge of Ca2+ ions probably prevents them from being incorporated in large quantities in the polymerised network as charge compensators – i.e. distant from any nonbridging oxygen atoms. Another highly charged cation, zirconium, occurs in six-fold coordination, with Zr–O distances of 2.08 Å, as determined by EXAFS studies (see above) 〚5〛. The zirconium surrounding is not affected by the presence of aluminium or calcium, and this element retains its charge-compensating cations at the expense of boron, which partly remains in triangular sites.
3 Glass stabilisation and cation coordination: the example of zinc
In alkali silicate glasses, low contents (<5 wt%) of ZnO usually improve mechanical properties, as well as the chemical durability 〚34〛. By contrast, Zn has a nucleating role in alkaline-earth silicate and aluminosilicate glasses 〚35〛. In alkali silicate glasses, Zn is found in tetrahedral and octahedral coordination (referred to as 〚4〛Zn and 〚6〛Zn, respectively), with a marked preference for tetrahedral coordination. The 〚4〛Zn/〚6〛Zn ratio increases as the Zn/Na or alkali ratio decreases, the sodium ions or alkalis compensating the charge deficit of the ZnO4 tetrahedra. The EXAFS data obtained on glasses, reporting average Zn–O distances of ∼1.96 Å and Zn coordination numbers of 3.8 to 4.7, are consistent and indicate a four-fold coordination for Zn 〚36〛. Beyond the first coordination shell, a Zn–Si distance of 3.20 ± 0.03 Å is consistent with corner-sharing ZnO4 and SiO4 tetrahedra (Fig. 3a). Similar Zn–Si distances were found in cordierite glasses and in mixed alkali borosilicate glasses, by EXAFS 〚35〛 and WAXS 〚37〛, respectively. Two distinct local structures correspond to this local configuration and satisfy Pauling rules: a network-forming position of Zn and the presence of oxygen triclusters. In the former, ZnO4 tetrahedra are copolymerised with the silicate network, as in the latter, three-coordinated oxygens are linked to three tetrahedral units (one SiO4 and two ZnO4). The EXAFS data do not indicate any contribution of Zn atoms in the second atomic shell. In addition, the presence of triclusters would give a significant radial disorder around Zn, higher than the value found for the Debye–Waller factor of this second shell of neighbours in the inactive nuclear glasses (σ = 0.11 ± 0.03 Å). Zn is then in a network-forming position. Mean Zn–O–Si angles of 127° indicate corner-sharing tetrahedra and are smaller than the 147° Si–O–Si angle in vitreous silica, due to lower cation–cation repulsion. Zn environment in glasses may be rationalised using a bond-valence model (Fig. 3b), which shows that the Zn–O distances derived from EXAFS are close to the equilibrium value when considering for instance two Na+ ions charge compensating each oxygen bound to both Zn and Si.
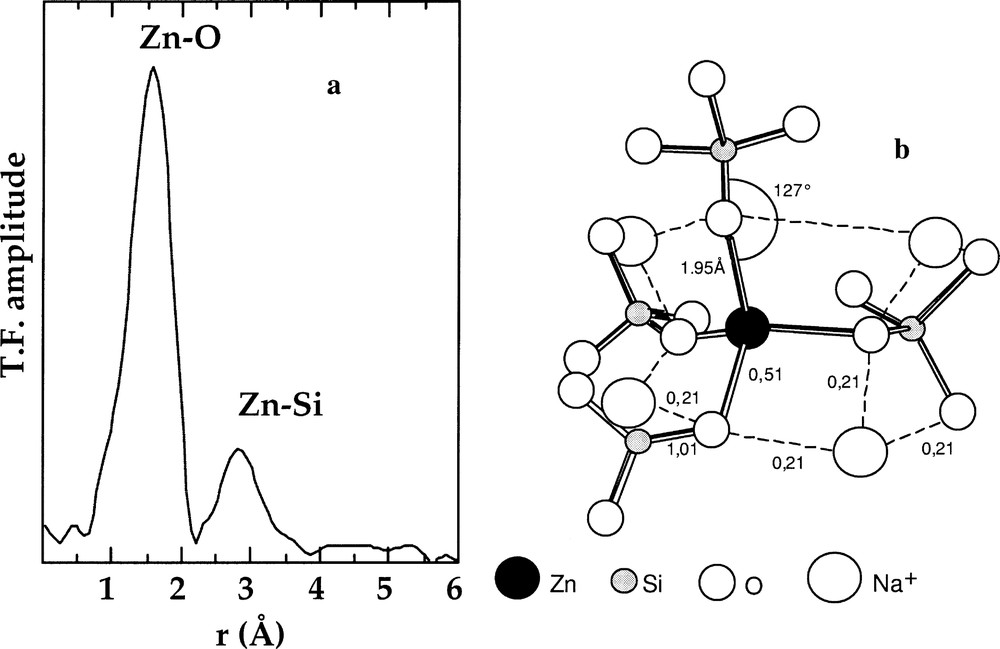
a. k3-weighted Fourier transform of the Zn K-edge EXAFS spectra for a technological glass. b. Schematic representation of the connectivity of the ZnO4 tetrahedra with the silicate network based on the EXAFS results (from 〚36〛).
The network forming position of Zn can explain the improvement of the mechanical properties, glass thermal stability and durability induced by the presence of low Zn contents in borosilicate glasses containing low-field strength cations (Na, K, Cs, Rb...). Indeed, the presence of Zn decreases the effective modifier concentration, as more alkalis are involved in charge compensation. The structure-reinforcing effect of Zn may also arise from the specific location of the ZnO4 tetrahedra within the glassy network, belonging to small size rings, such as four-membered rigid rings. Pauling rules hinder the possibility of Zn–O–Zn linkages, due to the underbonding of oxygen atoms. This local topology explains the absence of Zn-rich clusters. Owing to the low variability of the Zn–O distances, the values of 1.99 Å, found in low Zn-bearing Mg aluminosilicate glasses 〚35〛, can be interpreted as indicating the presence of some 〚6〛Zn. In these glasses, the nucleating properties of Zn may come from a significant proportion of 〚6〛Zn at room temperature 〚36〛.
4 Glass coloration by transition metal ions: the nickel-bearing silicate glasses
Transition metal ions are the most widely used colouring agents in oxide glasses. In some cases, e.g., chromate groups, trivalent Cr and Mn or divalent Co and Cu, the coloration observed is similar to that observed in crystals. In other cases, transition metal ions impart oxide glasses peculiar colours, as in nickel- and iron-bearing glasses, in which cations are found in unusual geometries, such as five-coordination. Nickel is probably one of the elements that impart oxide glasses the widest range of coloration: green, yellow, brown, purple, and blue. These modifications of the glass colour have been interpreted in the past as arising from two kinds of sites, octahedral and tetrahedral, the proportion of which varies as a function of glass composition 〚38〛. The correlation of optical absorption spectra with XANES and EXAFS spectra has shown a more complex picture, with nickel ions located in three distinct kinds of sites in oxide glasses, tetrahedral, trigonal bi-pyramid and less frequent octahedral 〚11, 38〛. The distribution of nickel among these well-defined sites will define the colour of the glass.
4.1 The purple-blue coloration and the presence of tetrahedral nickel
A blue to purple coloration is observed as nickel coexists with potassium or large alkalis in oxide glasses encompassing a large range of compositions, silicates and alumino-silicates, borates and borosilicates, germanates... This coloration is due to the presence of tetrahedral nickel (〚4〛Ni), the structural role of which has been clarified by EXAFS spectroscopy. Ni–K edge XANES and EXAFS data on a potassium silicate glass are consistent with the presence of 〚4〛Ni 〚39〛. The two characteristic XANES features that are diagnostic for a tetrahedral symmetry are an intense pre-edge and a weak shape resonance, as in 〚4〛Ni-bearing crystalline references. EXAFS-derived 〚4〛Ni-O distances are 1.95 Å, a typical value for tetrahedral Ni. These spectroscopic data are close to those obtained on Ni-bearing potassic borate glasses 〚40〛, an indication that the sites occupied by 〚4〛Ni are independent of the type of glass, as far as site symmetry and Ni–O distances are concerned.
Purple potassic silicate glasses show an optical spectrum that is typical of 〚4〛Ni (Fig. 4). The most intense bands near 15 500 cm–1 and 18 000 cm–1 correspond to the 3T1(F)→3T1(P) transition of 〚4〛Ni 〚39, 41〛. The distortion of the 〚4〛Ni site does not affect the orbital singlet 3A2(F). The spin-forbidden, weakly field-dependent transitions 3T1(F)→1T2(D) and 3T1(F)→1E(D) at 13 000 and 13900 cm–1, respectively, have a small linewidth (300 cm–1), as in crystalline references. This indicates that the Ni–O bond covalency and hence the charge of oxygen neighbours are not distributed, which is consistent with the presence of 〚4〛Ni in a well-defined site, as a framework cation (see section 2). The low-energy transition near 4500 cm–1 is also found at the same position as in 〚4〛Ni compounds. Crystal field parameters of 〚4〛Ni in silicate glasses, Δt = 4700 cm–1 and B = 850 cm–1, are similar to those encountered in most 〚4〛Ni-bearing crystalline compounds. The B-parameter value is decreased by about 20% as compared to the free-ion value B = 1030 cm–1 〚42〛. A contribution of 〚4〛Ni transitions is observed in all Ni-bearing glasses, the most apparent being the 15 500-cm–1 transition, which may be used to determine the 〚4〛Ni/〚5〛Ni ratio in glasses.
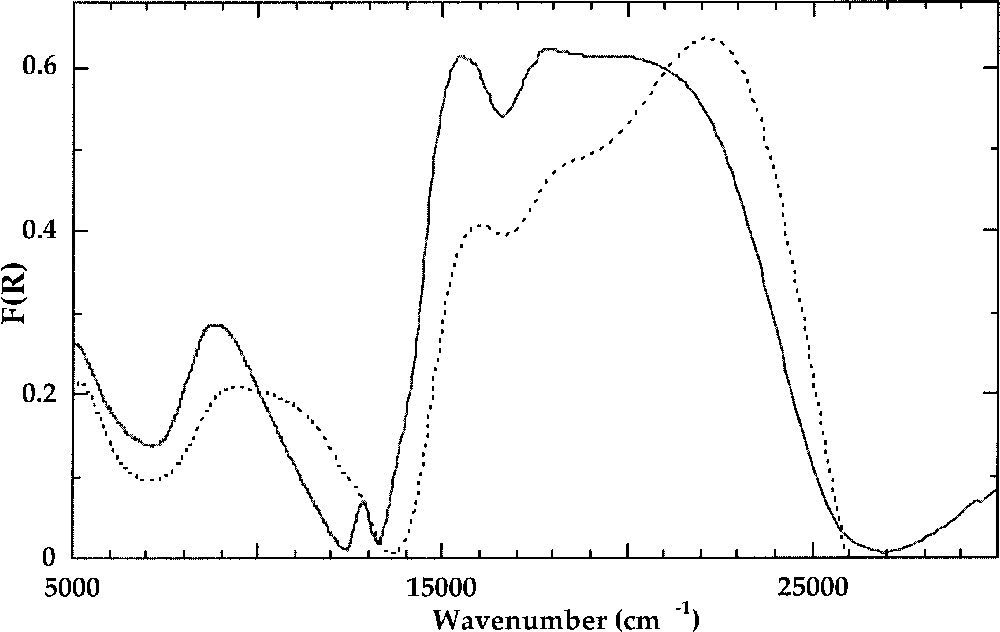
Crystal field spectra of K2NiSi3O8 glass (solid line) containing 〚4〛Ni and Na2NiSi3O8 glass (dashed line) containing 〚5〛Ni.
The presence of Ni–Si correlations in the EXAFS spectra of the 〚4〛Ni-bearing glasses indicates that tetrahedral Ni is closely linked to the silicate tetrahedral network (Fig. 5a). The obtained EXAFS-derived Ni–Si distances are consistent with NiO4 tetrahedra sharing corners with SiO4 tetrahedra and thus with 〚4〛Ni being in a position of network-forming element (Fig. 5b), similar to Mg in magnesiosilicates (i.e. 〚4〛Mg-bearing silicates) 〚43〛. Large alkalis bring a charge compensation of the oxygen atoms belonging to the NiO4 tetrahedra, in a fashion similar to that described above for 〚4〛Zn. The 〚4〛Ni–O–Si inter-tetrahedral angle (α) is about 130°, an unusually low value as compared to the T–O–T bond angles (where T is the tetrahedral cation) in silica and alumino-silicate glasses. α is close to the minimum energy angle in the H6SiMgO7 molecule, derived from molecular orbital calculations 〚44〛. This small α value indicates a smaller repulsion between tetrahedral cations T and Si as the valence of T cation decreases 〚11〛 and implies that corner-sharing NiO4 and SiO4 tetrahedra belong to four- or five-membered or strongly distorted six-membered rings, whatever the field strength of the charge-compensating cation. The bond valence model 〚45〛 indicates that Ni–O–Ni linkages are forbidden, as they would result in strongly underbonded O oxygens and that Ni–O–Si–O–Ni-O linkages are also forbidden, as they would result in a strong overbonding of the Si atoms located between the NiO4 tetrahedra. These two limitations hinder any 〚4〛Ni-segregation inside the glassy framework, on the contrary to 〚5〛Ni (see below), and limit the solubility of nickel in these glasses. Similar conclusions have been drawn using NMR in Mg-leucite 〚43〛.
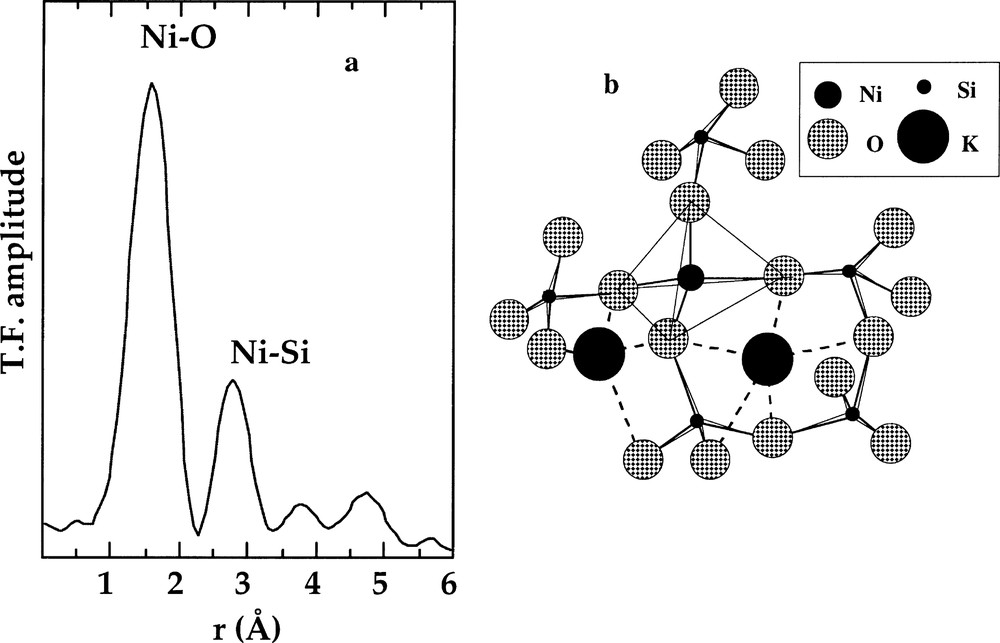
a. k3-weighted Fourier transform of the Ni K-edge EXAFS spectra for a of K2NiSi3O8 glass containing 〚4〛Ni. b. Schematic representation of the NiO4 tetrahedra sharing corner with the SiO4 tetrahedra based on the EXAFS results (from 〚12〛).
4.2 The brown coloration and the presence of five-coordinated nickel
Brown glasses are observed in presence of alkalis such as Na or Li and of alkaline earths, such as the soda-lime glass. The origin of this peculiar coloration has only been explained by comparing data from X-ray absorption spectroscopy and from optical absorption spectroscopy 〚12, 46〛. It arises from the presence of nickel in five-coordination, in trigonal bipyramids. The EXAFS-derived Ni–O distances are comprised between 〚5〛Ni–O and 〚4〛Ni–O distances, observed at about 1.95 Å and 2.00 Å, respectively. Similar short mean Ni–O distances have been also determined by neutron diffraction in Ca2NiSi3O9 glass 〚25〛. XANES features such as pre-edge and shape resonance intensity are also intermediate between those measured in 〚4〛- and 〚5〛Ni-bearing compounds. EXAFS and XANES data are consistent with the absence of a significant proportion of 〚6〛Ni in silicate and alumino-silicate glasses.
Crystal field spectra of Ni in brown glasses share some characteristics (Fig. 4): (i) a transition near 15500 cm–1, the intensity of which varies among the glasses; (ii) an unsplit, narrow absorption band near 5500 cm–1; (iii) a broad, asymmetric absorption band near 10000 cm–1 corresponding to several overlapping transitions; (iv) a major absorption band near 22000 cm–1 split into two components. (i) corresponds to the major transition of 〚4〛Ni (see above). The number, position and relative width of the other absorption bands (ii–iv) are only compatible with the presence of 〚5〛Ni. The positions of these absorption bands are almost independent of glass composition. Using electron energy level diagrams for 〚5〛Ni 〚47〛, the bands observed in Ni-bearing silicate glasses show a good agreement with the transitions of 〚5〛Ni in a trigonal bipyramid. The 3Eˈ(F)→3E”(F) transition near 5500 cm–1 inherits its small line width from the non-bonding and weakly anti-bonding character of ground and excited states of 5-coordinated Ni, respectively. The broad, asymmetric band near 10 000 cm–1 corresponds to unresolved 3Eˈ(F) →3A”1,3A”2(F) and 3Eˈ(F) →3Aˈ2(F) transitions. The intense absorption band near 22 000 cm–1 corresponds to the two-electron 3Eˈ(F) →3Aˈ2(P) transition (symmetry-allowed). Crystal field splitting parameters 〚48〛 are: Dq = 1000 cm–1 (assuming equal apical and basal crystal field splitting), B2/B4 = 2.5, and α = 90° (α = Obas–Ni–Oap). As expected, Dq is higher for 〚5〛Ni than for 〚6〛Ni (800–900 cm–1), owing to shorter 〚5〛Ni–O distances relative to 〚6〛Ni–O distances, three ligands remaining at the same position relative to 3d-orbitals. B is equal to 830 cm–1, as for 〚4〛Ni. There is no broadening of the absorption bands relative to crystalline references, indicating a good local order around 〚5〛Ni in glasses, as revealed by neutron diffraction 〚25〛. This moderate site distortion explains the absence of splitting of XANES shape resonance.
The interatomic distances and medium-range ordering observed in silicate glasses have been rationalised by Gaskell 〚25〛 as indicating a close packing of oxygens. Indeed, a trigonal bipyramid may be considered as arising from two face-sharing tetrahedra, and may thus be explained by subcompact hexagonal close packing. The stability of the 〚5〛NiO5 site is consistent with the observation of Ni–Ni distances corresponding to edge-linked NiO5 polyhedra 〚25〛 (Fig. 6), because edge-sharing limits radial disorder in the second shell, in contrast to corner-sharing.
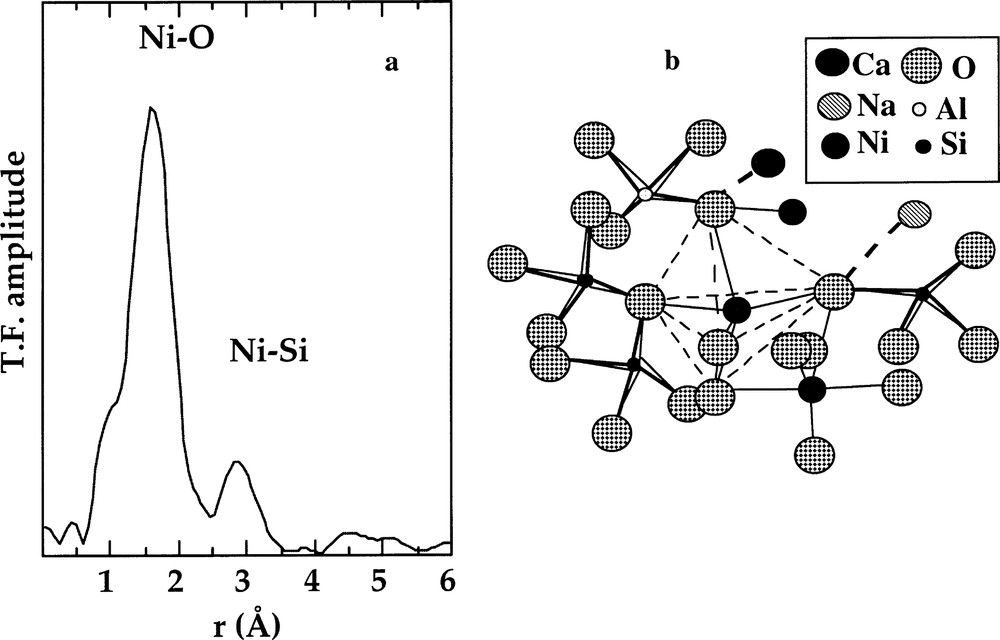
a. k3-weighted Fourier transform of the Ni K-edge EXAFS spectra for a Na2NiSi3O8 glass containing 〚5〛Ni. b. Schematic representation of NiO5 trigonal bipyramid sharing corner with the SiO4 tetrahedra and sharing edges with NiO5 bipyramids, based on the EXAFS results (from 〚12, 25〛).
4.3 The peculiar green colour of low alkali borate glasses and the presence of octahedral nickel
Oxide glasses never exhibit a green colour, with the noticeable exception of low alkali borate glasses. In these glasses, this unusual property arises from the presence of octahedral nickel. The observation of Ni–Ni correlations up to 6 Å in EXAFS spectra has shown a noteworthy inhomogeneous distribution of Ni 〚49, 50〛. The Ni-enriched domains consist of corner- and edge-sharing NiO6 octahedra, with three-dimensional connections extending up to 6 Å, and this medium-range organisation is independent of the nature of the alkali and of nickel concentration. Multiple scattering features in the EXAFS spectra characterise the presence of collinear NiO6 octahedra, an indication of an extended intermediate-range order around Ni. This observation is confirmed by the fact that the Ni–Ni distances found in the glass correspond to 3 of the 4 shortest Ni–Ni distances observed in NiO. XANES spectroscopy confirms the octahedral coordination of nickel in low-alkali borate glasses. Despite their diluted character, nickel ions are then inhomogeneously distributed within the glass structure. This peculiar structure may be a direct consequence of the presence of rigid borate units in low-alkali borate glasses. The disappearance of these units with the coordination change of boron as a function of alkali concentration explains the limited compositional range of the glasses that exhibit this green colour.
4.4 Compositional control of the coloration of Ni-bearing glasses
Nickel coordination depends on glass composition, the nature of the cations associated with nickel being the major parameter. Silicate and alumino-silicate glasses present all the intermediate stages between almost pure 〚4〛Ni and 70% of Ni as 〚5〛Ni, as estimated from XANES and optical spectroscopy 〚11, 12〛. However, in the absence of other transition elements, optical spectroscopy is more accurate than XANES, owing to a wider range of variation of the 〚4〛Ni absorption band.
The influence of cations on the nickel surrounding in silicate glasses shows an interaction between the silicate network and the other cations, due to the competition for oxygen between these cations and tetrahedral network formers such as Si or Al. The predominant parameter is the cation field strength, which increases from large alkalis such as K, Rb and Cs to smaller cations as Na and divalent cations, Ca, Mg and Ni. The probability that three-dimensional silicate networks can accommodate divalent network-forming cations is higher when charge compensation arises from large, low field strength cations. Indeed the 〚4〛Ni–O–Si angle has a small value (125–130°) and cannot be much reduced. Due to an increasing competition for oxygen as the field strength of the charge compensating cation increases, the relative 〚4〛Ni concentration will decrease when going from K- to Na- and Ca/Mg-bearing glasses. The small chemical dependence of α derived from EXAFS confirms the impossibility of a stronger closure of α with increasing cation field strength. This lower limit of α might correspond to direct cation–cation repulsions (i.e. non-bonded interactions 〚51〛).
5 The physical dissolution of gases in silicate glasses: the relation with the hole structure of the polymeric network
Physical dissolution in silicate melts and glasses of neutral molecular species such as noble gases has been interpreted as indicating the presence of voids within the silicate polymer network (e.g., Carroll and Stolper 〚52〛, and references therein), and provides fundamental information to understand more complex dissolution processes of reactive gaseous species (e.g., CO2, H2O). The size distribution of these voids may control the transport properties of gas molecules. The free volume concept 〚53〛 relates the size distribution of the interstitial holes in the frozen melt to the solubility of noble gases. Simple models 〚52, 54〛 give estimates of hole dimensions ranging from 0.5 to 4 Å.
By contrast to gaseous noble gases, which do not exhibit any EXAFS features, the EXAFS spectrum of a Kr-bearing silica glass shows a single rapidly damped frequency, without any structure beyond the coordination shell: Kr occurs in a well-defined environment of oxygen atoms, without evidence of ordered Kr clusters 〚55〛. The mean Kr–O distance is refined to 3.45 ± 0.1 Å, with an associated Debye–Waller term σ2 of 0.06 Å2. An anharmonic distribution of the Kr–O distances does not significantly improve the fit quality of the EXAFS data. The experimental d(Kr–O) EXAFS value is close to that derived from MD simulations (3.37 Å) 〚56〛.
MD simulations 〚57〛 as well as a simple random network model 〚54〛 predict a lognormal hole size distribution from 0.4 up to 5 Å, with few voids having diameters larger than 4 Å. The existence of a well-defined site with EXAFS-derived Kr–O distances beyond the upper limit of the accessible voids in silica is incompatible with a simple physical dissolution process of krypton in the broadly distributed voids existing in glassy silica. The existence of specific sites may result from a forced close-packed environment resulting in a clathrasil local structure, as predicted from MD simulations 〚56〛. This finding contrasts with the generally accepted assumption that noble gases are chemically inert species and do not modify the glassy network. Kr–O distances are around 3.8 Å and 3.93 Å, in water and ethanol, respectively 〚58〛. These compositional effects may indeed affect the energy of formation of the clathrasil surroundings around heavy noble gases. Recent MD simulations of the environment of noble gases in silica melt 〚56〛 indicate a cristobalite-like environment for helium and neon, while a clathrasil local structure is found around heavier noble gases.
6 The structural study of the atomic-scale mechanisms governing the alteration of inactive nuclear waste glasses
Vitrification of liquid high-level radioactive waste in borosilicate glasses has received great attention in several countries. The fundamental properties of the waste forms are their chemical and mechanical durability. It is then necessary to understand the reaction of glass with water and to understand the nuclear glass leaching and gel long-term stability. Three stages have been distinguished during the alteration of nuclear glasses 〚59〛. During the initial stage of leaching, there is a water diffusion followed by an early ion/proton exchange and diffusion in the parent glass, resulting in a congruent release of elements into the solution, as ion concentration in solution is lower than the solubility limit of most secondary phases. The second stage corresponds to an increasing silica concentration as a result of the glass dissolution, with a subsequent decrease of the dissolution rate. During these two first stages, the reactivity of the glass–water interface will be modified by (i) the extensive exchange of alkali ions in the glass with hydronium ions from water, which results in the formation of a hydration layer, (ii) the dissolution of the outer part of the bulk glass and (iii) the subsequent formation of an alteration surface layer on the glass, with specific adsorption properties and a role as a diffusion barrier. The progressive development of this alteration layer, together with the precipitation of crystalline phases, results from the solution reaching the solubility limits of the secondary phases. These various steps are responsible for the zoning observed at the surface of the altered glasses. There are major implications for the modification of the glass–water interface with time. The modification of the reactivity at the glass–solution interface may explain the retardation processes in the migration of actinides within the alteration layer 〚60〛 and the main consequence of the development of a gel layer is the modification of the source term.
Previous studies have demonstrated the importance of the characteristics of the leaching solution on the alteration mechanisms and on the dissolution rate. The composition and local structure of the inactive analogue of the French nuclear glass have been investigated in previous studies, indicating a complex interplay between the glass components to ensure charge compensation of the various polyanions in an alumino-borosilicate polymeric structure 〚5, 31, 61〛. The chemical and mineralogical compositions of the altered layer have been investigated at 90 °C 〚62〛 and under hydrothermal conditions 〚63〛. The formation of the altered layer may arise from a hydrolysis/condensation process, without significant release of silica into the leaching solution 〚64〛. A dissolution/precipitation process may also occur at the contact with a saturated solution 〚63〛. The main gel layer contains two intimately associated components, an amorphous silica-alumina gel enriched in transition elements, actinides and lanthanides and crystalline precipitates, mainly clay minerals. A recent study has determined the leaching mechanisms at the atomic scale, in relation with the structural behaviour of some glass components concentrated within the gel layer during glass alteration, such as zirconium, zinc or iron.
The evolution of the local atomic structure during the alteration of a nuclear glass and the subsequent gel formation has been investigated at 90 °C, using EXAFS and XANES measurements of glasses altered in open or closed systems chosen to model various repository conditions 〚65〛. The modification of the glass surface during the first stages of glass alteration under static conditions has been followed using electron detection of Fe and Zr L-edge and Si and Al K-edge XAS, a surface sensitive structural method. The surface chemistry of the glass monoliths is modified during short-term experiments and is characterised by an accumulation of several elements, such as Zr or Fe, until one day of leaching. The composition of the glass surface suffers a stronger modification when in contact with deionised water than under silicon near-saturation conditions. An early modification of the Zr and Fe surrounding occurs during the first hours of leaching, despite the absence of gel formation at the glass surface, evidencing the formation of a modified glass layer. Both elements are connected to the borosilicate polymeric framework in the starting glass: iron occurs mostly as tetrahedral Fe3+ ions in a network-forming position, as Zr4+ ions are in octahedral sites, which share corners with silicate tetrahedra, with a local charge compensation brought by Ca2+ ions. In contact with deionised water, Zr and Fe show a dramatic coordination change, which is easily detected using a surface-sensitive detection of XANES 〚5〛. These structural modifications indicate that poorly ordered Zr hydrous oxides form at the glass surface after 3 h of glass leaching with undersaturated solutions. Under the same scheme, Fe changes coordination from a tetrahedral network-forming position to the distorted octahedral sites characteristic of hydrous ferric oxides. By contrast, under silicon near-saturation conditions, Zr remains connected with the silicate groups, as in the pristine glass structure. This local organisation implies that Zr retains Ca as a charge compensator, in order to satisfy the Pauling rules, and thus participates to the preservation of the silicate network connectivity. This may be related with a less efficient dissolution process and a protective role of the forming alteration layer.
Over the long term, a gel forms progressively at the expense of the glass, an important parameter for the assessment of the long-term stability of nuclear glasses. Several glass components, such as zirconium, iron, zinc and lanthanides accumulate in the alteration layer and then contribute to the formation and long-term stability of the gel. The local structure around these elements in the alteration products produced by long term leaching experiments (6 to 17 months) at 90 °C have been investigated using XANES and EXAFS spectroscopy 〚65〛. The gel structure is modified as a function of time, with a faster rate in under-saturated than in silicon near-saturated conditions. However, as for the dissolution processes, zirconium exhibits a contrasted behaviour, depending on the leaching conditions. In under-saturated conditions, there is a coordination change corresponding to the formation of an amorphous hydrated zirconium oxide, which is not structurally connected to the silica gel formed simultaneously at the expense of the starting glass. In near-saturated conditions, zirconium occurs in octahedral coordination, as in the glass, preserving the connectivity between zirconium and the silicate network. By contrast, under all leaching conditions, iron participates to the formation of an amorphous ferric oxide gel, a two-line ferrihydrite, not connected structurally to the silica gel network. This different behaviour shows that there is not a unique mechanism for the formation of the gel layer. The preservation of octahedral zirconium connected to the silicate network of the gel is typical of a hydrolysis/condensation process. The coordination changes observed during the formation of hydrous zirconium oxide and ferrihydrite characterise a dissolution/precipitation process. An evolution of the gel surface in under-saturated conditions is observed, with the formation of a hematite-like surface, corresponding to the normal aging of ferrihydrite at 90 °C, which may influence the trapping of elements at the gel–solution interface. By contrast, in near-saturated conditions, the poorly ordered structure of ferrihydrite is preserved in the gel, showing that the presence of silica hinders the structural reconstruction of the gel and preserving element trapping at the gel–solution interface. Some elements such as Zn mostly contribute to the formation of crystalline phyllosilicates, observed by EXAFS at the gel surface since the first stages of glass leaching. At the gel surface, Si is partitioned between Q3 and Q4 surroundings, corresponding to crystalline and amorphous silicate networks, respectively. Al remains in tetrahedral coordination in the gel, which explains the preservation of cations such as Ca or Sr in the gel. The presence of octahedral Zr when leaching under near-saturated conditions participates to the additional stabilisation of these cations in the gel.
7 Conclusion
The direct determination of the local surrounding around specific glass components remains a unique tool to predict some important physical and chemical properties of glasses. The evolution of spectroscopic and scattering methods, for instance with the use of the new generation of synchrotron sources, will allow in the future the investigation of the time-resolved evolution of smaller samples, under controlled conditions. The combination with computational approaches on multicomponent glasses will give ways for incorporating glass properties in a structural description of the long-range ordering and mesoscopic description of these glasses.
Acknowledgements
We are grateful to V. Briois, S. Belin, A.M. Flank (LURE synchrotron facility, France) for experimental assistance. Special thanks are due to P.H. Gaskell and G.E. Brown Jr for fruitful discussions. This is IPGP contribution No. 1888.


