The relaxation time towards thermal equilibrium in glass-forming liquids grows increasingly upon cooling, till it becomes larger than the experimental timescale. Although they remain microscopically disordered like a liquid 〚1〛, glasses have a very high viscosity, which gives them the mechanical properties of a solid. By convention, the glass-transition temperature Tg is where the viscosity reaches the value of 1012 Pa s. In glass science, it has been known for several millennia that this temperature can be considerably changed by alloying two or several components. Window glass and domestic glasses are the most well known examples in history, for which craft or industrial furnaces determined the accessible Tg and hence the possible glass compositions. Various proposals have been made in the past in order to relate this quantity with some easily measurable factor. Here, we show that in the case of low modified network glasses such as metallic chalcogenides, the variation of Tg is mostly controlled by the entropy of the glass network, being related to its connectedness. Furthermore, we show that the magnitude of the glass-transition temperature in certain systems can be quantitatively understood in terms of combinatorial arrangements of metal–chalcogen bondings, which are again related to the network entropy.
During the past decade, there has been a resurgence of the interest in non-oxide covalent glasses 〚2–4〛, especially in chalcogenides based on sulphides, selenides and tellurides, because they represent promising glass systems for testing experimentally recent advances in mechanical rigidity transitions of amorphous networks and structure related properties. From a technological viewpoint, metal chalcogenide based glasses are interesting low-phonon host materials for luminescent rare-earth dopants with potential applications in the fibre optic laser industry 〚5〛. Their use as solid electrolytes has been stressed, with potential applications for batteries and displays 〚6〛.
The glass-transition temperature, Tg, is one of the most important parameters for the characterisation of the glassy state of these materials. Although its does not seem to play an essential role in the description of the kinetics of glass formation 〚7〛, this quantity remains of huge interest in applied glass science, as well as for the glass manufacturing. Undoubtedly, kinetic and sample thermal history effects 〚1〛 change the absolute value of Tg, but there are also much larger structure-related effects that apparently control the magnitude of Tg in glass-forming alloys. Recently, substantial efforts have been realised to improve the usual technique of Tg measurement (differential scanning calorimetric, DSC) by superposing a sinusoidal variation of temperature on the ordinary DSC linear ramp (renamed modulated DSC). This has led to a more precise measure of the glass-transition temperature, unpolluted by kinetic effects 〚8〛.
Empirical relationships have been proposed in the past, in order to relate the value of Tg with some macro- or microscopic properties of the glass-forming melt, involving either the melting temperature (the so-called ‘two-third rule’ 〚7〛), or the Debye temperature of the phonon spectrum 〚9〛. In chalcogenide glasses, one has the luxury to change in a continuous fashion the concentration xi of modifier atoms with coordination number ri. This produces a change in the network connectivity or in the mean coordination number and a continuous variation of structure-related physical properties 〚2, 4〛. Different authors have examined reported data in the literature by considering <r> as the central quantity in order to understand compositional trends of Tg. For instance, Tanaka 〚10〛 has derived from viscoelastic considerations the relation:
Varshneya and co-workers 〚4〛 have observed that Tg follows a modified Gibbs–DiMarzio equation in multicomponent chalcogenide glasses, expressed as:
The purpose of this article is to show that some underlying factors determine the absolute variation of Tg in multicomponent glasses. These factors are related to the network entropy (or network connectivity). We have examined about 240 different reported temperatures from binary and ternary chalcogenides of the form A1–xBx and A1–x–yBxCy with coordination numbers rA, rB, and rC. The symbol A refers to the chalcogen base glass (S, Se, Te) with coordination number rA = 2.
Fig. 1 upper panel gives the glass-transition temperature ratio Tg/T0 as a function of the mean coordination number <r> in binary chalcogenides involving an element of Group IV (rB = 4), and <r> = 2 + 2 x. T0 has the same definition as in equation (1), i.e. it is the glass-transition temperature of the base chalcogen glass. On can easily remark that almost all systems behave very similarly up to <r> ∼ 2.35. For a higher mean coordination number, the slope changes and increases dramatically for sulphide and selenide systems, whereas the telluride systems keep their variation almost constant. On the other hand, we have plotted in the lower panel of Fig. 1 the same quantity, Tg/T0, as a function of the overall mean bond energy <E> of the network, following the covalent bond approach (CBA, see below) 〚16〛. From this analysis, it appears that Tg is here also a linear function of <E> for the selected systems, as already determined for some of them by Tichy and Ticha 〚16〛. It is also convenient to plot the glass-transition temperature as a function of <E> – EA–A (see the insert in the lower panel of Fig. 1), EA–A being the Pauling chalcogen–chalcogen bond energy (Table 1). In CBA, the linear relationship between Tg and <E> is obtained from a least-squares fit.
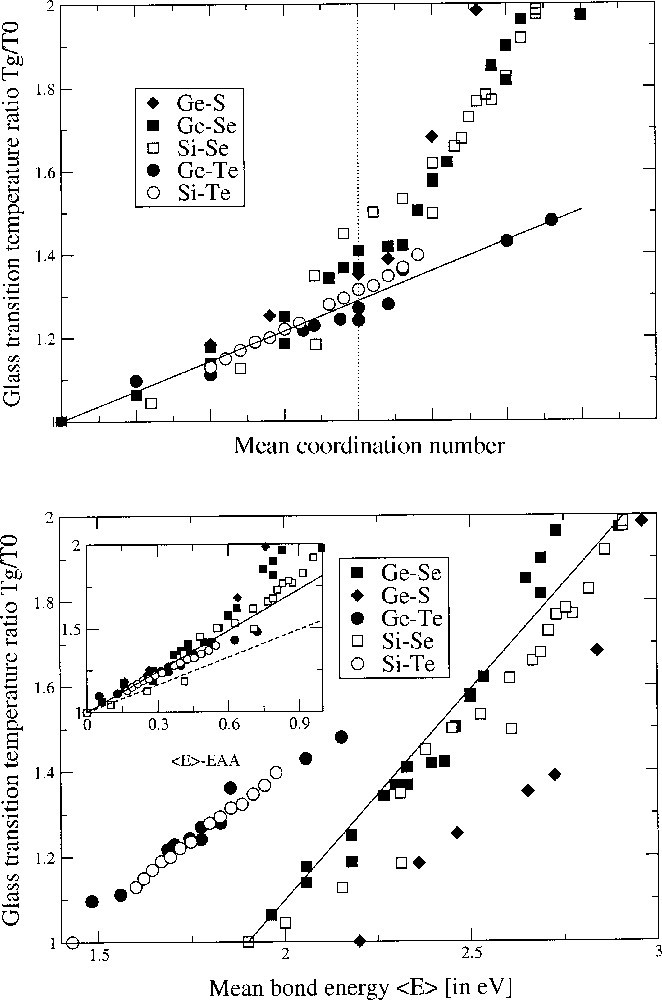
Upper panel. Glass-transition temperature ratio Tg/T0 as a function of the mean coordination number <r> in binary chalcogenides: Ge–Se 〚2〛, Si–Se 〚12〛, Ge–S 〚13〛, Ge–Te 〚14〛, Si–Te 〚15〛. The straight line is a parameter-free prediction from SAT with slope 1/(2 ln 2). The vertical dotted line corresponds to the composition of the mean-field rigidity transition. Note the deviation around the magic average coordination number of 2.4 and the maxima attained by Tg in the Ge–Se system around <r> = 2.67. Lower panel. Glass-transition temperature ratio Tg/T0 as a function of the overall mean bond energy <E> from a CBA analysis in the same systems with the same data sources. The insert shows the same quantity as a function of <E> – EAA with the solid and dashed line corresponding to equation (7) for Ge–Se and Si–Se systems.
Stochastic agglomeration theory (SAT) has proved to be helpful 〚18, 19〛 in understanding the role of local structure in Tg variation and provides a quantitative framework to analyse compositional trends of the glass-transition temperature in a stochastic regime. The Tg(x) variation in binary chalcogenides (e.g., GexSe1–x) or fast ionic conducting glasses (such as (1 – x) SiO2–x Na2O systems) can for instance be predicted when the concentration of modifier x goes to zero 〚19〛. This theory provides a good measure of the stochastic nature of the network, which is obviously the situation in the chalcogen rich region, where metallic atoms randomly cross-link the chalcogen chains. In network glass formers (also called strong glass formers), the Arrhenius-like increase of the viscosity in the supercooled state is directly related to the creation of covalent bonds between atomic or molecular species, which enhances progressively the possibility of molecular motion. SAT assumes that the most relevant process during glass transition is an agglomeration process in which typical local structural configurations with coordination numbers ri stick together, creating new covalent bonds. At the glass-transition temperature, structural arrest manifests, so that these configurations cease to move and are trapped. This condition serves to define Tg. In the case of binary chalcogenide glasses AxB1–x, the prediction yields a parameter-free slope equation when the presence of metal homopolar B–B bonds is neglected 〚19〛:
It appears from this analysis that the glass-transition temperature variation with respect to an initial glass-transition temperature T0 is entirely controlled by connectivity (the coordination numbers rB and rA of the involved atoms A and B). No kinetic or thermal contributions arise. Bond energies are absent, although they appear in the mathematical construction of the theory. The denominator of equation (3) is related to the entropy ΔSAB = ln(WAB/2 WAA) of the network, which depends on the number of equivalent ways WAB = 2 rA rB and WAA = rA2. A and B atoms can join to each other to produce all possible bonds A–B and A–A. Then, ΔSAB = ln(rB/rA). Thus, an increase in connectivity of a network can also result from an increase in the number of equivalent accessible structural states W (such as double bonding) and an increase of ΔS, accounting for a decrease in the slope. For ternary glasses, the prediction of Tg with the average coordination number <r> remains parameter-free (Fig. 2).
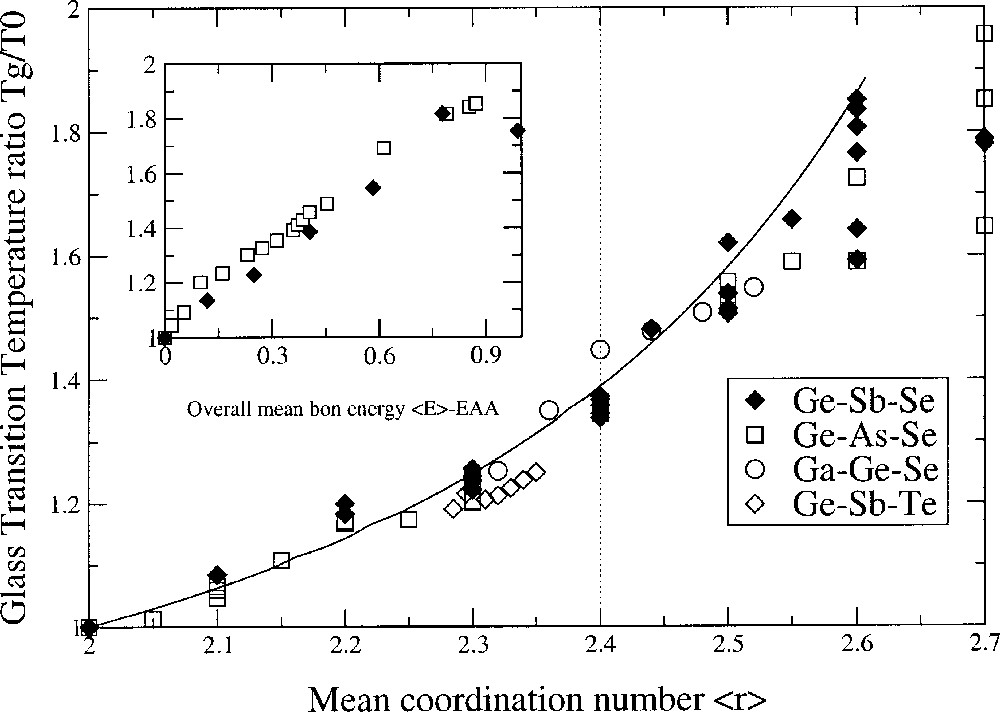
Glass-transition temperature variation Tg/T0 as a function of the mean coordination number <r> in ternary chalcogenides: Ge–As–Se 〚20〛, Ge–Sb–Te 〚21〛, Ga–Ge–Se 〚22〛 and Ge–Sb–Se 〚4〛. The curve is a parameter-free prediction from SAT. The insert shows the same quantity Tg/T0 as a function of the overall mean bond energy <E> – EAA following a CBA analysis.
Consequently, for all the systems displayed in Fig. 1, the slope computed from SAT is 1/(2 ln2). We can observe that this value is in a very accurate agreement with the experimental data. However, close to <r> = 2.35, the deviation becomes significant for the sulphide and selenide systems, as suggested independently by Mössbauer spectroscopy, showing the loss of stochastic character of the network around this composition 〚23〛. The Tgs of the telluride glasses remain linear and can be predicted over the concentration range of interest. Also, the Si–Se system has its glass-transition temperature systematically lower than the other data systems displayed, although the Si–Se bond strength is higher (Table 1) than the other energies EAB.
Chemical bonds and bond energies (in eV) calculated from Pauling 〚17〛.
| Bond | Bond energy (eV) | EA–B – EA–A (eV) | |
| Chalcogen–chalcogen | S–S | 2.2 | |
| Se–Se | 1.9 | ||
| Te–Te | 1.43 | ||
| Heteropolar bonds | As–S | 2.0 | –0.20 |
| As–Se | 1.8 | –0.10 | |
| Sb–Se | 1.86 | –0.04 | |
| Ge–Se | 2.12 | 0.22 | |
| Ge–S | 2.4 | 0.20 | |
| Si–Se | 2.23 | 0.33 | |
| Si–Te | 1.72 | 0.29 | |
| Ge–Te | 1.62 | 0.19 |
The difference between telluride, and sulphide and selenide systems can be interpreted as follows. Vitreous selenium or sulphur consists of polymeric chains, beside which some eight-member rings can exist, especially in v-S. The addition of an atom of Group IV creates cross-linking between these chains in a random fashion and globally the whole network can be considered random. This structural modification goes up to the mean coordination number <r> = 2.4, which corresponds to the optimal glass composition where mechanical stability reaches its maximum. The latter behaviour is very well understood in terms of the constraint theory developed by Phillips and Thorpe 〚24, 25〛, which predicts a rigidity transition when the average coordination number of the network reaches <r> = <r>c = 2.4. For larger concentrations, chemical stability (which is maximum at the stoichiometric mean coordination number <r> = 2.67) is preferred to mechanical stability, and chemical stability breaks the random character of the network. At <r> = 2.67 (x = 0.33), the structure will be stoichiometrically balanced and stable crystalline compounds GeSe2, GeS2 or SiSe2 can be formed 〚26〛. Thus, the local structure of these glass systems in the mean coordination number range (2.4–2.67) will be very close to the crystalline counterpart and each chalcogen will tend to be surrounded by two atoms of Group IV, and vice-versa. In any case, the description in terms of random A–A and A–B bondings, such as the one proposed by SAT, will become inappropriate, and the glass-transition temperature will show a systematic deviation with the predicted slope (3). In the telluride systems, there is no chemical stability composition at x = 0.33. The reason is that there are neither crystalline SiTe2 nor GeTe2 compounds, but Si2Te3 and GeTe instead 〚26〛. But there is still an optimal glass composition (mechanical stability) at <r> = 2.4, which can be detected either by observing the coalescence of the crystallisation temperatures of the floppy and rigid parts of the network (for SixTe1–x) 〚15〛 or the reversing heat flow window (for GexTe1–x) 〚27〛. As a consequence, the chemical ordering provoked by the larger amount of Group-IV atoms does not appear immediately as it does for the selenide and the sulphide glasses, and therefore the network can remain random over a larger concentration range, consistently with the data’s agreement of equation (3).
In the covalent-bond approach, the mean bond energy of the average cross-linking/atom <Ec> in a glass A1–x–yBxCy at high chalcogen content is defined by:
Since Tg is linear in <r> (SAT, parameter-free) and <E> (CBA, one parameter), we can compare both, calculating from equations (4) and (5) the overall linearised bond energy <E> in the chalcogen-rich region, we obtain from (4) and (5):
More generally, for higher-chalcogen-content glasses (when x is close to zero, or <r> close to 2), the network is supposed to be composed of species of the base glass (e.g., Se) and by cross-linking species (such as germanium). In this case, the molecular character of the glass network (i.e. the connectivity) and its influence on Tg should not be neglected, thus the covalent bond approach might not be correct in this region. Moreover, a certain number of exceptions to CBA have emerged in the recent years, suggesting that some underlying physical or chemical quantities are still to be found in this approach. For example, maxima in Tg are observed in many stoichiometric glasses such as GeSe2 〚28〛 and As2Se3 〚29〛. According to CBA, one should expect a maximum in the related As–Ge–Se ternary, as it does in the As–Se and the Ge–Se, but this does not happen 〚20〛.
These ideas on Tg variation and network connectivity are again reinforced in a rather striking fashion in the binary chalcogenides involving an atom of Group V. For instance, in the P–Se system 〚30〛, the glass-transition temperature shows a maximum near <r> = 2.5. It is associated with onset of phase separation of P4Se3 monomers from the backbone as the P content first exceeds <r> = 2.45 (Fig. 3). At <r> > 1/2, the global connectivity is diminished so much that there is little backbone left and the Tg approaches room temperature or below. According to SAT, it is possible to extract from the Tg data the local structures of the glass in the chalcogen-rich region. Based on simple single bonding arguments, one would expect that since rB = 3 for these systems, the slope should be 1/ln(3/2). This is obviously not the case, as represented in Fig. 3 (solid line). For all the displayed glass systems, the slope is lower, suggesting that the number of equivalent ways WAB to connect a chalcogen A to a Group-V atom B is substantially higher, thus yielding a higher network entropy ΔSAB. From a least-square fit of the data represented in Fig. 3, we obtain WPSe = 24, WPS = 16.6 and WAsSe = 17.1. In single bonding of a Group-V chalcogenide, one has WA–B = 2 × 2 × 3 = 12. In double bonding, WA=B = 40 〚19〛. This analysis has been confirmed by 31P NMR and MDSC measurements, which have shown that some double bondings A=B should exist in these systems, leading to a non-negligible fraction of pseudo four-fold coordinated species of the type Se=(AsSe)3/2 〚29, 30〛.
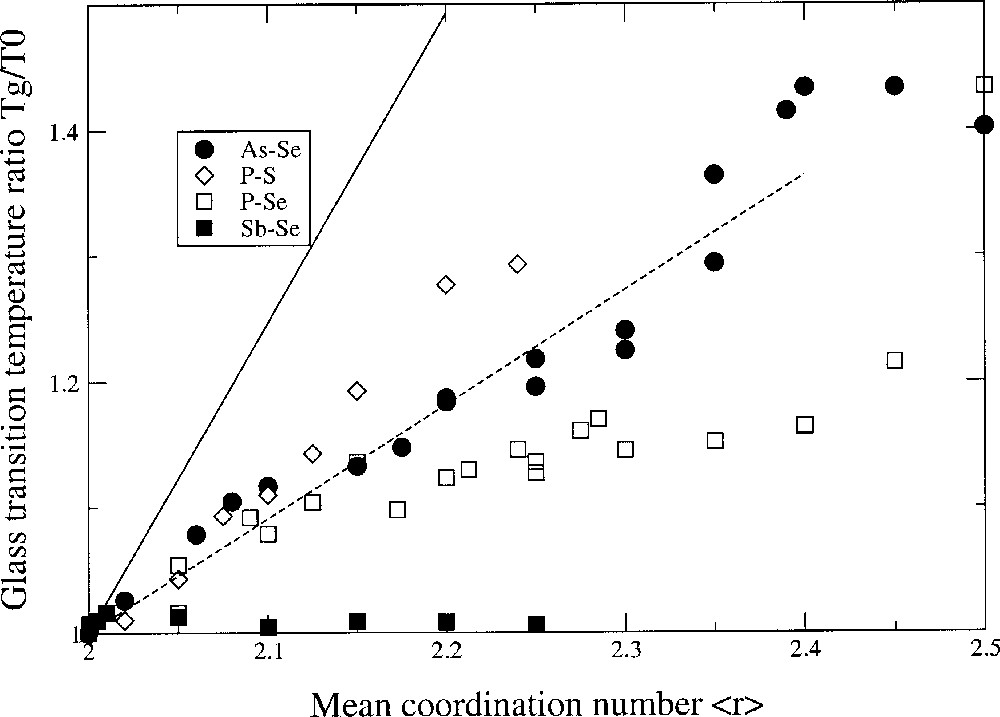
Glass-transition temperature variation Tg/T0 as a function of the mean coordination number <r> in chalcogenides involving en element of Group V: As–Se 〚29〛, P–Se 〚30〛, P–S 〚31〛 and Sb–Se 〚32〛. The solid line is a prediction of SAT in the case of single metal–chalcogen bonding. The dashed line is a prediction of SAT when a finite fraction (50%) of four-fold phosphorus atoms is allowed. Note the flatness of the data in the case of Sb–Se, due to strong chemical ordering 〚32〛 (formation of Sb2Se3 clusters) hence deviation from stochastic character.
Determining the relationship between structure, energy and glass-transition temperature continues to be challenging. Here we have shown that at in low-modified chalcogenides, one could relate the entropic and energetic contributions to the Tg variation, in order to understand global trends, but also the details. In this respect, this kind of relationship will be helpful to investigate the entire concentration range, especially close to the so-called ‘Tanaka transition’ at <r> = 2.67 and the glass-transition maximum 〚16〛. Here, the maximum in Tg in glasses parallels the maximum in the liquidus of the corresponding melts, showing a signature of two separate phases nucleating. This supports the idea that the transition near 2.67 is a transition initiated by nanoscale phase separation of the backbone into two separate clusters 〚28〛. The study of this phenomenon by means of global connectivity and stochastic agglomeration should shed some light on this debated issue.


