1 Introduction
In the last two decades, large metal clusters have become the focus of great attention because of their fascinating structural aesthetics, physical properties, and implication in the active sites of metalloproteins [1–3]. In particular, the discovery that transition-metal clusters can behave as single-molecule magnets has fuelled impressive synthetic efforts aimed at obtaining new spin topologies [1,2]. Many different approaches have thereby been developed, which range from serendipitous assembly [4,5] to rational design [6–13]. Undoubtedly, the former strategy has provided an amazing variety of unpredicted structural types leading at the same time to the observation of new physical phenomena like quantum tunnelling of the magnetization and quantum phase interference [1,14]. Nevertheless, the rational design and realization of complicated structural motifs remains a very attractive, though extremely elusive goal.
The controlled assembly of transition-metal based building blocks can be realized exploiting the coordination bond as a supramolecular tool. Specific architectures can be rapidly assembled in a single step under thermodynamic equilibrium conditions, based on the information content of the reaction system. This includes the preferred coordination geometry of the metal, the favoured coordination mode of the ligand, and the composition of the reaction mixture as given by the ligand-to-metal ratio, the solvent, the presence of counterions or ‘helper’ species (templates), etc. [10,15,16]. The molecular information stored in the building blocks is read at the supramolecular level to yield one or more possible structures. For instance, the metal-ion directed formation of ring structures can be explained on the basis of non-covalent intramolecular interactions [17], template effects [18], or the interplay between metal- and ligand-centred contributions to the turning angle [3,10,19]. Indeed, it is informational complexity that determines the predictability of the final structure(s), thus marking the difference between serendipitous assembly and rational design.
Grids [11,12] and linear arrays [13] are among the most fascinating recent examples of molecular magnetic clusters assembled by fully rational design. Verdaguer, Marvaud and Mallah also synthesized heptanuclear clusters by connecting a first generation of paramagnetic centres to a central hexacyanometallate unit (Fig. 1a) [6–9]. Following a similar strategy, we attempted a controlled expansion of polynuclear rather than mononuclear units. As central cores, we used robust metallasiloxane cages, whose structure comprises two hexaphenylcyclohexasiloxanolate ligands, (PhSiO2)66– (Fig. 2), coordinated to six divalent metal ions in a sandwich-like fashion, affording an inert and thermodynamically stable torus-like complex [20–23]. The cage often encapsulates a chloride ion exhibiting an unusual μ6 coordination mode [20–22]. A key feature is the presence of labile solvent molecules that usually occupy six coordination sites available on the external ‘surface’ of the torus. Upon ligand exchange, the cage can thus function as a hexatopic receptor [15] for monodentate units (Fig. 1b), including paramagnetic complex ligands.
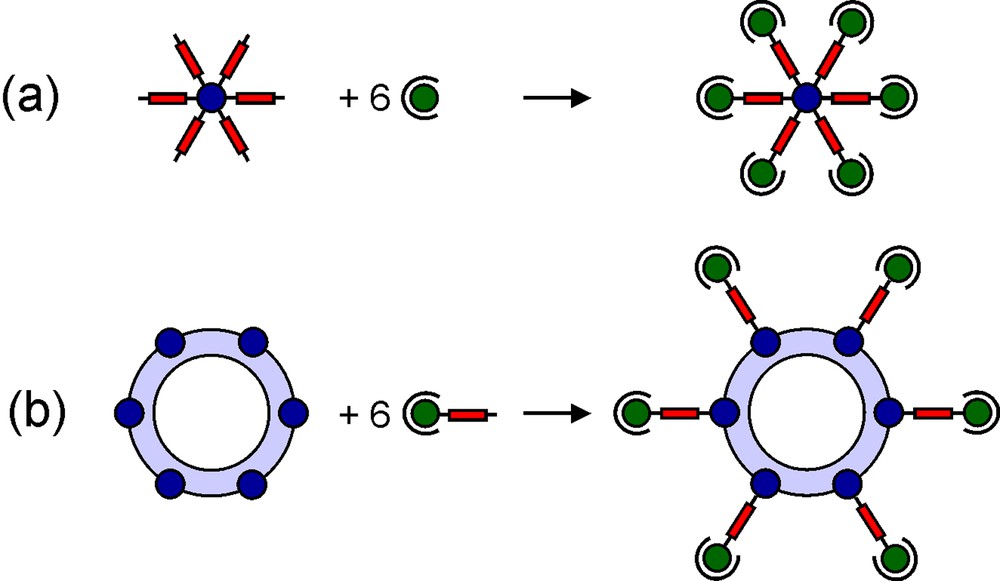
Controlled expansion of mono- (a) and polynuclear (b) magnetic units.
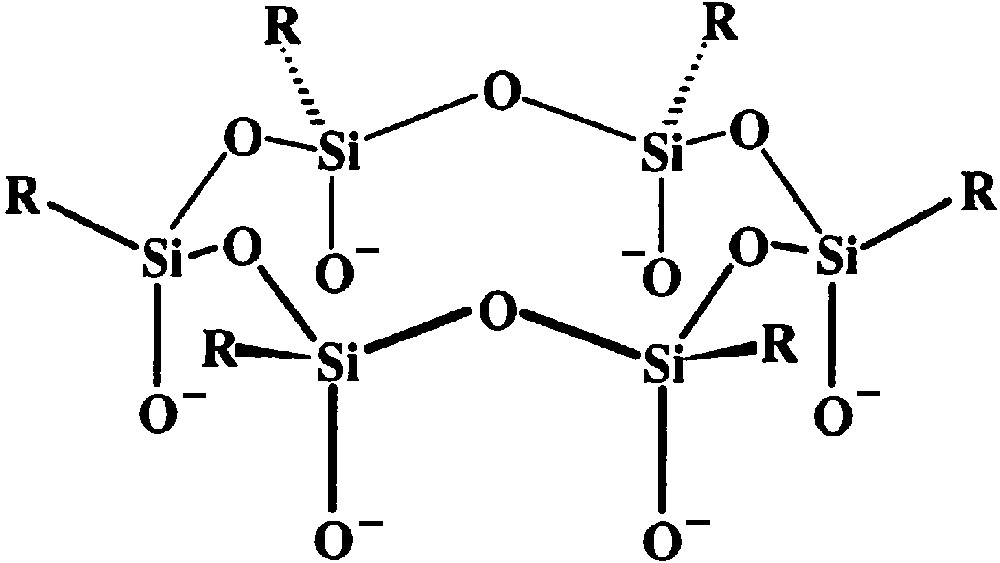
The hexaphenylcyclohexasiloxanolate ligand, (RSiO2)66– (R = Ph).
In this paper, we report the synthesis, X-ray structure and magnetism of a high-spin hexacopper(II) complex [Cu6{(PhSiO2)6}2(BuOH)5]·3 nBuOH (1·3 nBuOH) that can function as a central preformed unit for controlled cluster expansion. A self-assembly reaction with the trigonal-bipyramidal copper(II) mononuclear [Cu(tmpa)CN]PF6 (2) [24], which contains terminal-cyanide and capping polyamine ligands (tmpa = tris(2-pyridylmethyl)amine), affords a decacopper(II) cluster [Cu6{(PhSiO2)6}2{NCCu(tmpa)}4](PF6)4 (3), with an unprecedented spin topology (see [25] for a preliminary report).
2 Experimental
2.1 Synthesis
n-Butanol was distilled over CaO shortly before use, while all the other solvents were used as received. The tmpa ligand was synthesized as described elsewhere [26,27].
2.1.1 [Cu6{(PhSiO2)6}2 (BuOH)5]·3 nBuOH (1·3 nBuOH)
Poly-(phenylsilsequioxane) [PhSiO1.5]n [22] (3.226 g, 0.0250 mol) and KOH 85% (1.710 g, 0.0259 mol) were heated in 60.0 ml of n-butanol with vigorous stirring until complete dissolution and then refluxed for ca. 60 min. To the solution of potassium phenylsiloxanolate thus obtained was then added dropwise with continuous stirring and heating CuCl2 (1.683 g, 0.0125 mol) dissolved in 30.0 ml of n-butanol. The colour of the mixture quite immediately turned to green-bluish, and then to dark green. At about two thirds of the addition, a greenish precipitate started to appear. After the addition was complete, the suspension was refluxed for further 10 min then left undisturbed and allowed to cool for 15 min. The greenish solid was removed by filtration and the blue solution kept at room temperature in a closed vessel. Green–blue crystals separated in a few days (yield: ~23%). Elemental analysis found on a vacuum dried sample (0.2 mmHg for ca. 1 h): C 45.73, H 4.81%. Calculated for [Cu6{(PhSiO2)6}2(nBuOH)5] (Cu6C92H110O29Si12): C 46.08, H 4.62%.
2.1.2 [Cu(tmpa)CN]PF6 (2)
The compound was synthesized by a literature procedure [24]. Purity was checked by elemental analysis.
2.1.3 [Cu6{(PhSiO2)6}2{NCCu(tmpa)}4](PF6)4·2 CHCl3·2.75 MeOH·0.25 H2O (3·2 CHCl3·2.75 MeOH·0.25 H2O)
Compound 2 (0.0314 g, 0.0592 mmol) was dissolved in 10 ml of chloroform and slowly added dropwise with vigorous stirring to a solution of 1·3 nBuOH (0.0251 g, 0.0103 mmol) in 1.0 ml of chloroform. During the addition a few drops of methanol were quickly added whenever precipitation started to appear. Rapid diffusion of methanol vapours into the filtered blue solution afforded small blue blocks in two days (yield ca. 25%). Elemental analysis found on a vacuum dried sample (0.1–0.2 mm Hg, 90 min): C 41.09, H 3.44, N 6.37%. Calculated for 3·2 CHCl3·2.75 MeOH·0.25 H2O (C152.75H145.5Cl6Cu10F24N20O27P4Si12): C 41.15, H 3.39, N 6.28%. IR (NaBr): ν = 2172 cm–1 (w, CN–).
2.2 X-ray crystallography
Detailed crystal data and experimental parameters are reported in Table 1, while selected interatomic distances and angles are shown in Tables 2 and 3 for compounds 1·3 nBuOH and 3·2 CHCl3·2.75 MeOH·0.25 H2O, respectively. The structures were solved by direct methods (SIR-92) [28] and refined on FO2 using the SHELXL-97 program [29] implemented in the WINGX suite [30]. The hydrogen atoms were treated as fixed contributors in calculated positions and refined isotropically with B(H) = 1.5 Beq(C) and 1.2 Beq(C) for aliphatic and aromatic carbon atoms, respectively.
Crystal data and experimental parameters for 1·3 nBuOH and 3·2 CHCl3·2.75 MeOH·0.25 H2O
| 1 ·3 n BuOH | 3 2 CHCl3 ·2.75 MeOH·0.25 H2O | |
| Formula | Cu6C102H135O31.5S 12 a | Cu10C152.75H145.5Cl6F24N20O27P4Si12 |
| Formula weight | 2583.42 a | 4458.51 |
| Crystal habit | blue–green blocks | blue prisms |
| Crystal system | monoclinic | orthorhombic |
| Space group (No.) [31] | P21/c (14) | Pc21n (33) |
| a (Å) | 19.963(3) | 21.0176(2) |
| b (Å) | 24.368(3) | 25.2589(2) |
| c (Å) | 26.148(3) | 33.5011(3) |
| β (°) | 99.570(10) | |
| V (Å 3 ) | 12543(3) | 17785.1(3) |
| Z | 4 | 4 |
| ρcalc (g cm –3 ) | 1.368 a | 1.660 |
| ρexp (g cm –3 ) | 1.39(1) | 1.64(1) |
| T (K) | 293(2) | 223(2) |
| Radiation | Mo-Kα | Mo-Kα |
| λ (Å) | 0.71069 | 0.71069 |
| μ (mm –1 ) | 1.183 a | 1.475 |
| F (000) | 5364 | 8962 |
| Data collection range (°) | 1.79 ≤ θ ≤ 18.75 | 1.14 ≤ θ ≤ 28.69 |
| Data index range | –1 ≤ h ≤ 18 | 27 ≤ h ≤ 27 |
| –22 ≤ k ≤ 1 | –34 ≤ k ≤ 34 | |
| –23 ≤ l ≤ 23 | –44 ≤ l ≤ 44 | |
| Collected reflections | 11 441 | 208 363 |
| Unique reflections | 9521 b | 44176 c |
| Restraints – parameters | 70–893 | 22–2280 |
| GOF [29] | 1.031 | 1.113 |
| Absorption correction | ψ-scans [32] | multiscan [33] |
| R indices [ I > 2 σ ( I )] [29] | R 1 = 0.0793, wR2 = 0.1951 | R 1 = 0.0648, wR2 = 0.1415 |
| R indices (all data) [29] | R 1 = 0.1671, wR2 = 0.2588 | R 1 = 0.1213, wR2 = 0.1814 |
| Largest Δ F map peak | ||
| and hole (e Å 3) | 0.561 and –0.422 | 1.147 and –1.321 |
Selected interatomic distances (Å) and angles (°) for 1·3 nBuOH a
| Molecule a | Molecule b | |
| Cu1–O1 | 1.951(13) | 1.942(11) |
| Cu1–O2 | 1.962(11) | 1.937(11) |
| Cu1–O3 | 1.943(11) | 1.962(11) |
| Cu1–O4 | 1.986(12) | 1.958(11) |
| Cu1–O13 | 2.214(15) | 2.292(14) |
| Cu2–O1 | 1.971(12) | 1.975(11) |
| Cu2–O2 | 1.961(11) | 1.936(11) |
| Cu2–O5 | 1.985(11) | 1.978(11) |
| Cu2–O6 | 1.988(11) | 1.962(11) |
| Cu2–O14 | 2.186(15) | 2.234(13) |
| Cu3–O3 | 1.911(11) | 1.952(11) |
| Cu3–O4 | 1.929(12) | 1.949(11) |
| Cu3–O5′ | 1.921(11) | 1.963(11) |
| Cu3–O6′ | 1.936(11) | 1.959(11) |
| Cu3–O15 | 2.283(16) | |
| Cu1 ... Cu2 | 2.846(4) | 2.847(3) |
| Cu1 ... Cu3 | 2.830(4) | 2.852(3) |
| Cu2 ... Cu3′ | 2.819(3) | 2.818(3) |
| Cu1 ... Cu1′ | 5.807(5) | 5.603(4) |
| Cu2 ... Cu2′ | 5.857(5) | 5.801(4) |
| Cu3 ... Cu3′ | 5.296(5) | 5.625(4) |
| Cu1–O1–Cu2 | 93.0(5) | 93.2(5) |
| Cu2–O2–Cu1 | 93.0(5) | 94.6(5) |
| Cu3–O3–Cu1 | 94.5(5) | 93.5(5) |
| Cu3–O4–Cu1 | 92.6(5) | 93.7(5) |
| Cu3′–O5–Cu2 | 92.4(5) | 91.3(5) |
| Cu3′–O6–Cu2 | 91.9(4) | 91.9(5) |
| Cu3 ... Cu1 ... Cu2 | 116.23(10) | 121.45(10) |
| Cu3′ ... Cu2 ... Cu1 | 115.17(11) | 117.25(9) |
| Cu2′ ... Cu3 ... Cu1 | 128.60(11) | 121.30(10) |
Selected interatomic distances (Å) and angles (°) for 3·2CHCl3·2.75 MeOH·0.25 H2O
| Cu1–O1 | 1.907(4) | Cu1–O2 | 1.900(5) |
| Cu1–O11 | 1.889(4) | Cu1–O12 | 1.901(5) |
| Cu2–O1 | 1.977(5) | Cu2–O2 | 1.974(5) |
| Cu2–O3 | 1.921(5) | Cu2–O4 | 1.949(5) |
| Cu2–N1A | 2.124(7) | ||
| Cu3–O3 | 1.951(5) | Cu3–O4 | 1.909(5) |
| Cu3–O5 | 1.943(5) | Cu3–O6 | 2.002(4) |
| Cu3–N1B | 2.135(7) | ||
| Cu4–O5 | 1.922(5) | Cu4–O6 | 1.880(4) |
| Cu4–O7 | 1.876(5) | Cu4–O8 | 1.913(4) |
| Cu5–O7 | 2.005(5) | Cu5–O8 | 1.953(4) |
| Cu5–O9 | 1.937(5) | Cu5–O10 | 1.968(5) |
| Cu5–N1C | 2.149(7) | ||
| Cu6–O9 | 1.943(5) | Cu6–O10 | 1.938(5) |
| Cu6–O11 | 1.991(5) | Cu6–O12 | 1.986(5) |
| Cu6–N1D | 2.122(7) | ||
| Cu1 ... Cu2 | 2.7614(12) | Cu2 ... Cu3 | 2.9083(12) |
| Cu3 ... Cu4 | 2.7598(12) | Cu4 ... Cu5 | 2.7769(12) |
| Cu5 ... Cu6 | 2.9129(11) | Cu6 ... Cu1 | 2.7742(11) |
| Cu1 ... Cu4 | 5.4164(11) | Cu2 ... Cu5 | 5.7408(11) |
| Cu3 ... Cu6 | 5.7205(11) | ||
| Cu1–O1–Cu2 | 90.63(19) | Cu1–O2–Cu2 | 90.91(19) |
| Cu2–O3–Cu3 | 97.4(2) | Cu2–O4–Cu3 | 97.9(2) |
| Cu3–O5–Cu4 | 91.13(19) | Cu3–O6–Cu4 | 90.57(18) |
| Cu4–O7–Cu5 | 91.31(19) | Cu4–O8–Cu5 | 91.84(18) |
| Cu5–O9–Cu6 | 97.3(2) | Cu5–O10–Cu6 | 96.5(2) |
| Cu6–O11–Cu1 | 91.25(18) | Cu6–O12–Cu1 | 91.04(19) |
| Cu2–N1A–C1A | 153.0(7) | Cu3–N1B–Cu1B | 153.2(7) |
| Cu5–N1C–C1C | 159.9(7) | Cu6–N1D–C1D | 156.3(7) |
| Cu7–C1A–N1A | 173.5(8) | Cu8–C1B–N1B | 171.9(8) |
| Cu9–C1C–N1C | 170.1(7) | Cu10–C1D–N1D | 168.8(7) |
| Cu2 ... Cu1 ... Cu6 | 126.19(4) | Cu1 ... Cu2 ... Cu3 | 116.77(4) |
| Cu4 ... Cu3 ... Cu2 | 117.26(4) | Cu3 ... Cu4 ... Cu5 | 126.15(4) |
| Cu4 ... Cu5 ... Cu6 | 116.57(4) | Cu1 ... Cu6 ... Cu5 | 117.05(4) |
2.2.1 1·3 nBuOH
The crystal employed for data collection was obtained directly as reported above. Dry crystals of 1·3 nBuOH loose solvent quickly at room temperature and immediately crack when cooled down to –70 °C. As a consequence, the selected individual (0.50 × 0.50 × 0.25 mm) was sealed in a glass capillary containing a small amount of mother liquid and transferred to a Siemens P4–RA diffractometer for a room temperature data collection. Due to the low value of θmax reached, only non-carbon atoms of the cluster were refined anisotropically, while restraints were applied to the thermal parameters and to the geometry of some n-butanol molecules. Disordered non-coordinated n-butanol molecules were located and refined with fractional occupancy factors to give a total of 2.5 solvent molecules per cluster. Residual peaks (< 0.56 e Å–3) probably arise from additional highly disordered solvent molecules, as suggested by a comparison between measured and calculated density values (1.368 and 1.39(1) g cm–3, respectively). The latter is in good agreement with the value predicted for eight n-butanol molecules per cluster (1.388 g cm–3).
2.2.2 3·2 CHCl3·2.75 MeOH·0.25 H2O
Prismatic crystals suitable for a X-ray diffraction study were obtained by slow diffusion of methanol vapours into the reaction mixture. The selected individual (0.60 × 0.40 × 0.40 mm) was mounted on a glass fibre with vacuum grease and transferred to a SMART-CCD device for a low-temperature data collection. All non-hydrogen atoms were refined anisotropically, except for those belonging to methanol and water molecules and for some fluorine atoms of a disordered hexafluorophosphate ion. Hydrogen atoms of the solvent molecules were not included in the model.
2.3 Magnetic measurements and HF–EPR spectra
Magnetic measurements on 1·3 nBuOH and 3·2 CHCl3·2.75 MeOH·0.25 H2O were performed with a Cryogenics SQUID Magnetometer in the temperature range 2.0–300 K. Raw data were reduced assuming molecular weights corresponding to the given formulas (2620.54 and 4458.51, respectively) and diamagnetic corrections estimated from Pascal’s constants (–1420.2 × 10–6 and –2216.12 × 10–6 emu mol–1, respectively). A microcrystalline sample of 1·3 nBuOH (15.63 mg) was rapidly dried in vacuum and measured with applied fields of 1 T (T > 50 κ) and 0.1 T (T < 50 κ). Magnetization-vs-field data were recorded at 4.6 and 1.9 K in fields up to 6 T. A microcrystalline sample of 3·2 CHCl3·2.75 MeOH·0.25 H2O (8.63 mg) was dried in vacuo and measured with an applied field of 1 T. Magnetization-vs-field data were recorded at 4.5 and 2.0 K in fields up to 6 T.
The HF-EPR measurements on 1·3 nBuOH have been performed on a polycrystalline sample pressed into a pellet. Spectra were recorded at 230 GHz at temperatures ranging from 5 to 100 K. The spectrometer used is of single-pass type. The exciting light, supplied by a Gunn oscillator (115 GHz) coupled to a frequency doubler, is propagated with oversized brass tubes. The intensity transmitted through the sample is measured with an InSb hot-electron bolometer. The main magnetic field is supplied by a superconducting magnet with 12 T maximum field. A small oscillating field is superimposed to the main one so that the derivative of the signal is recorded.
3 Synthesis and X-ray structure
The synthesis of cage-like metallaorganosiloxanes containing transition metals is commonly based on the exchange reaction of alkali-metal organosiloxanolates [34] with transition metal chlorides in alcohol-containing media [20–23,35,36].
The resulting cage complexes often display a ‘sandwich-like’ structure supported by two organocyclohexasiloxanolate, (RSiO2)66–, ligands and encapsulating a μ6-chloride ion [20–22]. Copper(II)-containing metallasiloxanes are peculiar in that they exhibit two structural types: sandwich-like (with no Cl– guest) [20,23] and globular-like [37,38], the latter featuring an organocyclododecasiloxanolate, (RSiO2)1212–, ligand. The formation of either structural motif can be controlled by carefully tuning the reaction conditions, such as the particular solvent and alkali metal used. For instance, the use of potassium phenylsiloxanolate is known to favour the formation of the sandwich-like cages [37,38]. Although n-butanol as a reaction media generally favours globular-like structure, thus decreasing the yield of sandwich-like one, the resulting cage complex presents a good solubility in organic solvents, which greatly facilitates the subsequent ligand-exchange reaction.
Reaction between CuCl2 and potassium phenylsiloxanolate, previously synthesized in situ from poly-(phenylsilsequioxane) [22] and potassium hydroxide, in n-butanol affords 1·3 nBuOH as large green–blue crystals. The crystal packing of 1 is shown in Fig. 3. The unit cell contains two [Cu6{(PhSiO2)6}2(nBuOH)x] molecules [x = 4 (molecule a) and 6 (molecule b)] packed in an almost orthogonal fashion, the dihedral angle between the mean Cu6 planes being 87.69(5)°. The overall metal ion topology is analogous to that of the hexacopper(II) siloxanolates [Cu6{(PhSiO2)6}2(EtOH)6] (4) [20] and [Cu6{(PhSiO2)6}2(DMF)6]·4 DMF [23]. The metal ions are located at the vertices of almost planar hexagons (deviations from the average Cu6 planes ± 0.0017(13) Å) and are coordinated by four oxygen atoms from two (PhSiO2)66– ligands (Fig. 4). The most remarkable structural feature of the cage is the presence of 12 six-membered CuO3Si2 chelate rings, which exhibit a distorted pseudo-chair conformation. The nBuOH-bound copper(II) ions show a distorted square-pyramidal (SP) coordination, with 0.37- and 0.31-Å mean shifts (for molecule a and b, respectively) from their basal planes toward the apical oxygen donors. By contrast, Cu3 displays a square-planar (S) coordination and a 0.145(6)-Å basal shift. As a consequence the copper–oxygen core of molecule a is compressed along the Cu3...Cu3′ axis as compared with molecule b and shows a much more pronounced deviation from idealized 6/mmm symmetry. Interestingly, the Cu-O-Cu angles are very similar in both molecular units (mean value 92.8(7) and 93.0(12)° for molecules a and b, respectively) in spite of the presence of copper(II) ions with different coordination geometries.
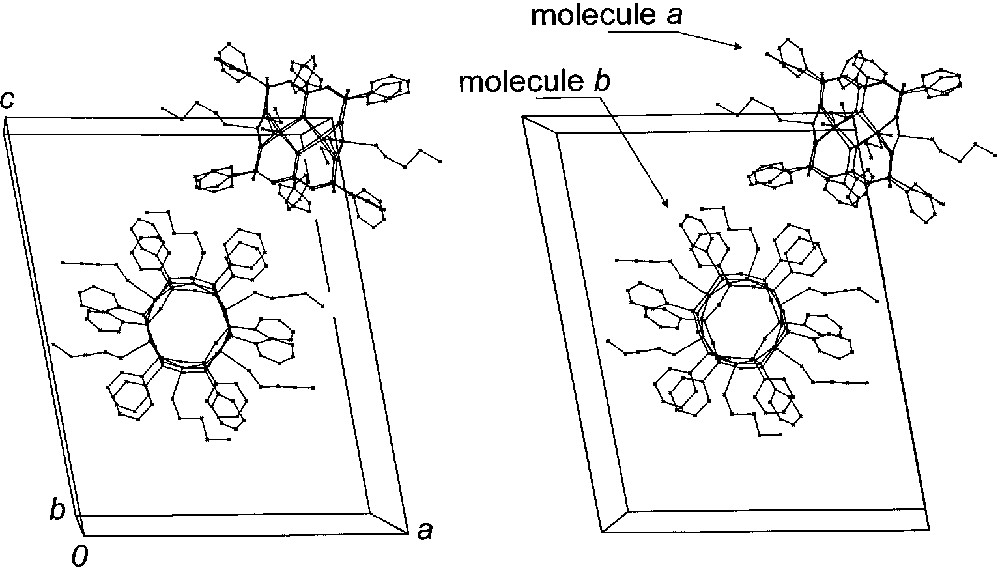
Stereoview of crystal packing in 1·3 nBuOH. Non-coordinated solvent molecules and hydrogen atoms have been omitted for clarity.
Structure of 1 (molecule a) with 30%-probability thermal ellipsoids for Cu, O and Si atoms and the atom labelling scheme. Carbon atoms are represented as spheres with arbitrary radius. Hydrogen atoms have been omitted for clarity.
While the previously reported cluster 4 [20] is only sparingly soluble in organic solvents, complex 1·3 nBuOH can be easily dissolved in chloroform. Reaction with complex ligand 2 gives a decacopper(II) cluster 3 in low yield:
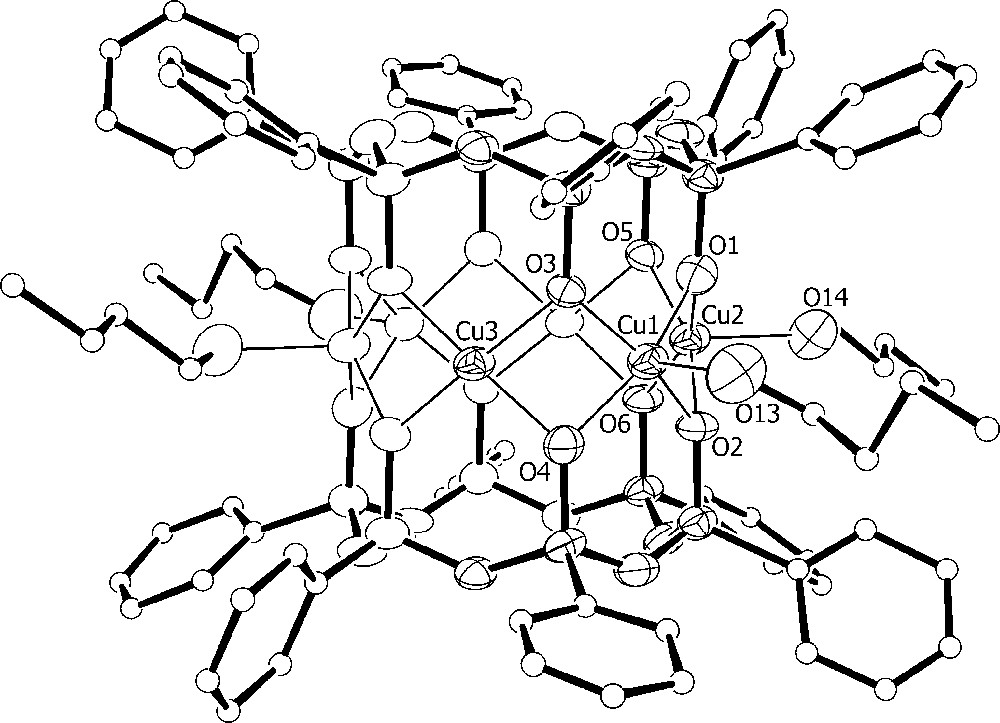
The asymmetric unit of 3·2CHCl3·2.75MeOH·0.25H2O comprises one cluster and four hexafluorophosphate ions along with two chloroform and disordered lattice methanol and water molecules. The [Cu6{(PhSiO2)6}2{NCCu(tmpa)}4]4+ cation shown in Figs. 5 and 6 approaches D2 point-group symmetry. The inner hexagonal Cu6 array, featuring four SP and two S metal centres, is surrounded by four trigonal-bipyramidal (TB) Cu(tmpa) units linked to the central core through cyanide bridges. The bulky tmpa ligands limit the number Cu(tmpa) units that can be arranged around the Cu6 core and lead to a cisoid conformation of the Cu–N–C–Cu(tmpa) moieties. Selected structural parameters of the copper–oxygen cores of 1 (molecule a) and 3 are compared in Table 4. Upon substitution of the nBuOH molecules with [Cu(tmpa)CN]+ units, the Cu6 ring becomes slightly less planar (deviation from the mean plane ± 0.0108(6) Å), but it approaches 6/mmm symmetry more closely. The CuS...CuS′ distance, in-fact, increases from 5.296(5) in 1 to 5.4164(11) Å in 3, while the CuSP...CuSP′ mean distances decrease [5.83(11) vs. 5.731(14) Å in 1 and 3, respectively). CuSP-type ions display an increased shift from their oxygen basal plane (av. 0.41 Å) as compared with 1, while the basal shift of four-coordinated CuS ions is somewhat reduced (< 0.13 Å). A marked effect can be observed also on the angles at the bridging siloxanolate oxygen atoms where CuS–O–CuSP and CuSP–O–CuSP values become very different (av. 91.1(4)° and 97.3(5)°, respectively). The formation of the cyanide bridges has only minor effects on the structure of the [Cu(tmpa)CN]+ moieties, affecting mainly the observed departures from trigonal bipyramidal geometry [25].
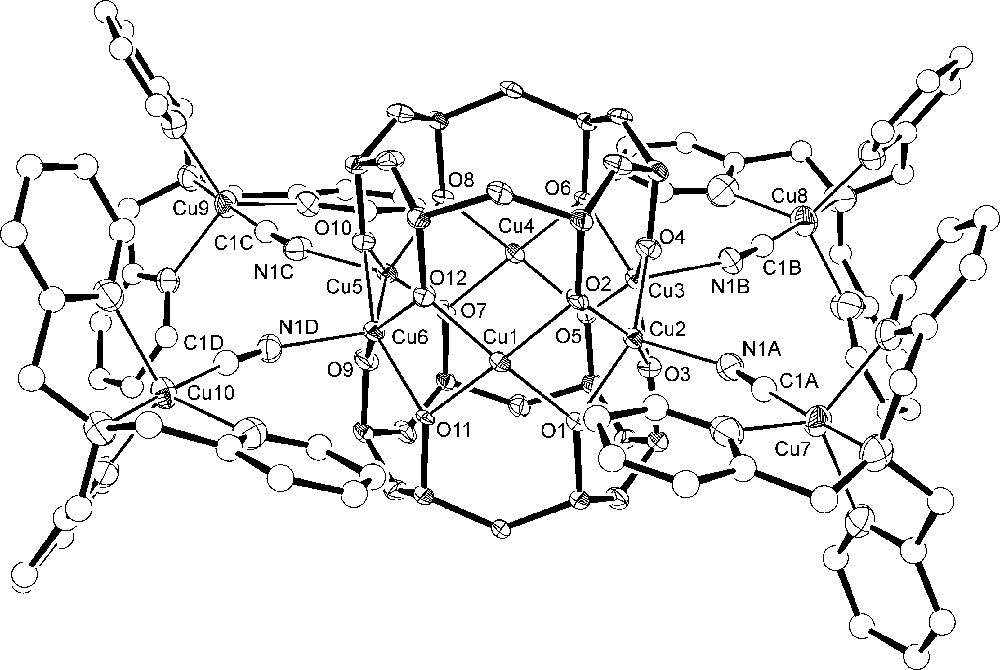
Structure of the [Cu6{(PhSiO2)6}2{NCCu(tmpa)}4]4+ cation in 3 with the atom-labelling scheme and 50%-probability thermal ellipsoids for Cu, Si, O and N atoms. C atoms are represented as spheres with arbitrary radius. The phenyl rings of the siloxanolate ligand, as well as hydrogen atoms, have been omitted for clarity.

Perspective view of the [Cu6(PhSiO2)12{NCCu(tmpa)}4]4+ cation. Colour code: light blue = Cu; yellow = Si; dark blue = N; red = O; grey = C. Hydrogen atoms have been omitted for clarity.
Selected structural data [interatomic distances (Å) and angles(°)] for 1·3 nBuOH (molecule a) and 3·2 CHCl3·2.75 MeOH·0.25 H2O.
| 1 ·3 n BuOH | 3 ·2 CHCl 3 ·2.75 MeOH·0.25 H2O | |
| CuS...CuS a | 5.296(5) | 5.4164(11) |
| CuSP...CuSP a | 5.807(5)–5.857(5) | 5.7205(11)–5.7408(11) |
| CuS...CuSP b | 2.819(3)–2.830(4) | 2.7598(12)–2.7769(12) |
| CuSP...CuSP b | 2.846(4) | 2.9129(11)–2.9083(12) |
| CuS–O c | 1.911(11)–1.936(11) | 1.876(5)–1.922(5) |
| CuSP–O c | 1.943(11)–1.988(11) | 1.909(5)–2.005(4) |
| Cu...Cu...Cu | 115.17(11)–128.60(11) | 116.57(4)–126.19(4) |
| CuS –O–CuSP | 91.9(4)–94.5(5) | 90.57(18)–91.84(18) |
| CuSP–O–CuSP | 93.0(5) d | 96.5(2)–97.9(2) |
4 Magnetic properties and HF–EPR spectra
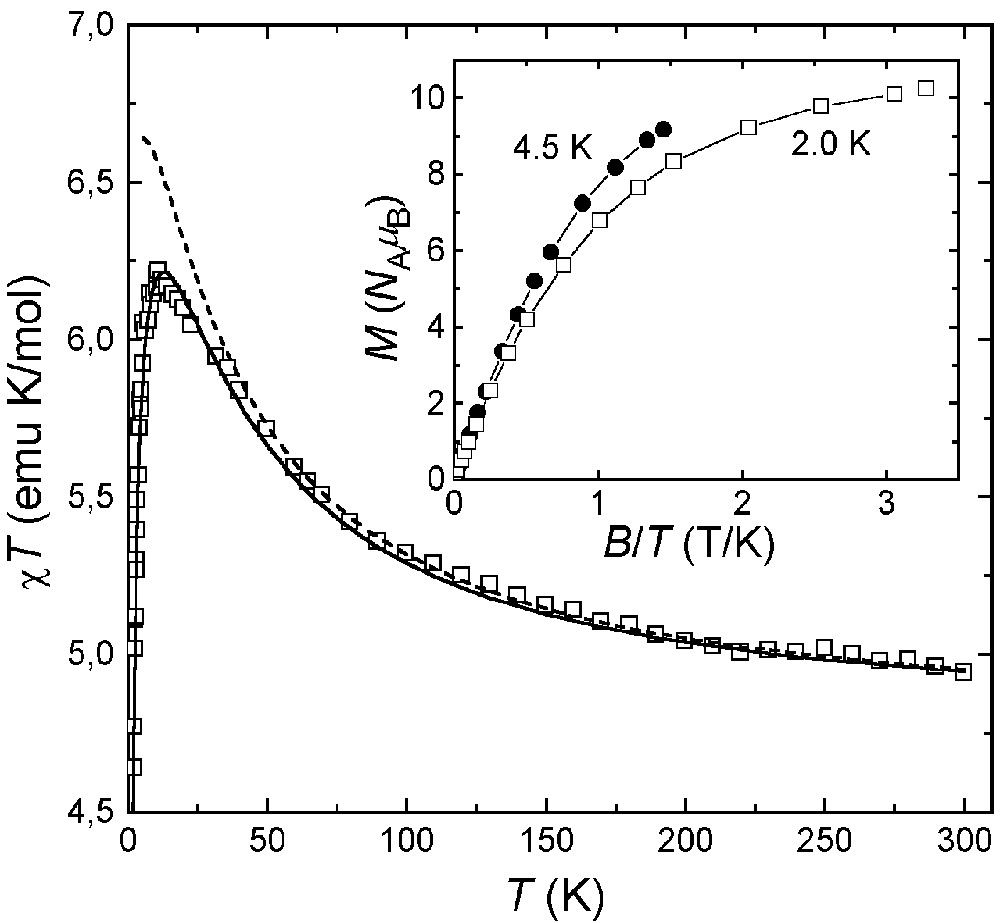
The magnetic properties of 1·3nBuOH are reported in Fig. 7 as a χ T-vs-T plot. The χ T product at 300 K (2.8 emu K mol–1) is higher than expected for six uncoupled S = 1/2 spins (2.25 emu K mol–1 with g = 2.00) and increases upon lowering temperature, reaching 6.2 emu K mol–1 at 3.0 K and decreasing slightly at the lowest temperatures. This behaviour is indicative of moderate ferromagnetic interactions between copper(II) ions, as found in 4 [39]. This conclusion is confirmed by the low temperature χT value, which is expected to approach 6 emu K mol–1 for an S = 3 ground spin state with g = 2.00. A Heisenberg Hamiltonian with six identical nearest-neighbour coupling constants gave no satisfactory agreement with experimental data (dashed line). We thus attempted to refine the model by using two independent J values, J1 and J2 [see Eq. (1) and Fig. 8].
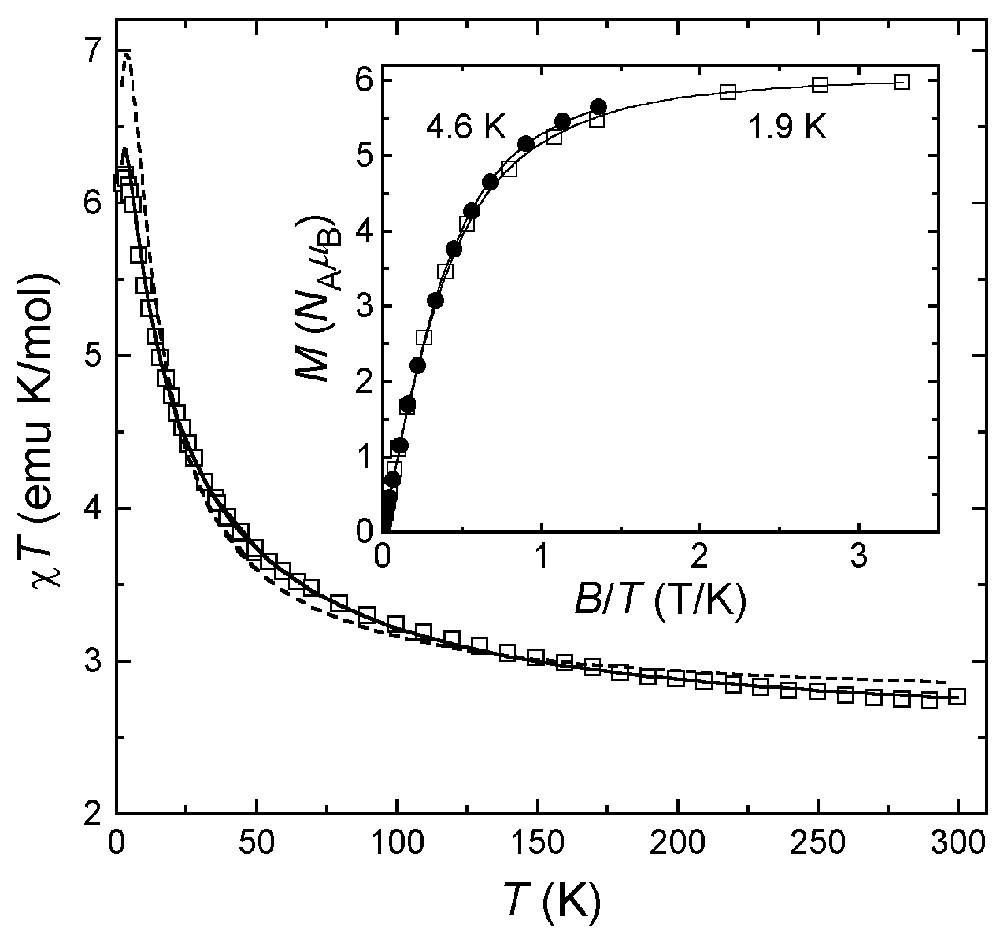
Experimental χT-vs-T data for 1·3 nBuOH, with best-fit calculated data as solid (g = 2.107, J1 = –62 cm–1, J2 = –10.6 cm–1) and dashed (g = 2.193, J1 = J2 = –23.6 cm–1) curves. The inset shows M-vs-B/T data at two different temperatures. Solid lines represent best-fit calculated data based on Hamiltonian (2) with S = 3, g = 2.009 and D = 0.30(3) cm–1.
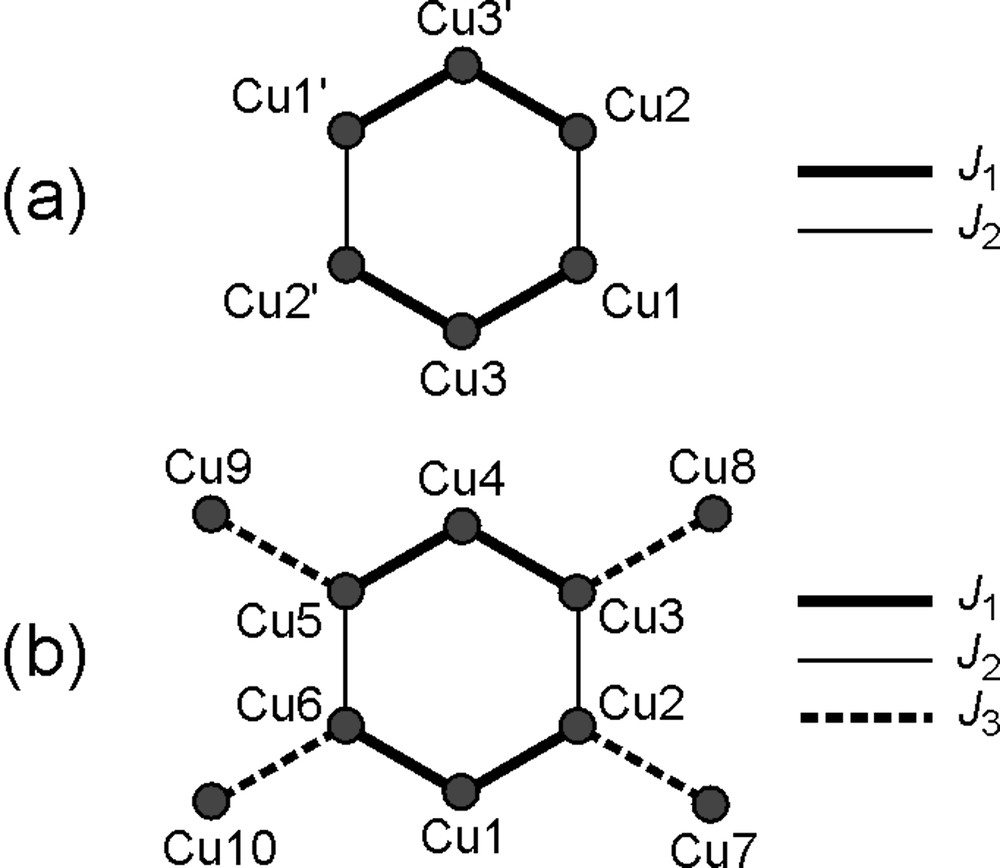
Exchange-coupling scheme used to analyse the magnetic properties of 1·3 nBuOH (a) and 3·2CHCl3·2.75MeOH·0.25H2O (b).
An excellent fit was obtained for T > 10 K with J1 = –62(1) cm–1, J2 = –10.6(2) cm–1 and g = 2.107(4) (solid line). However, due to (i) the presence of two independent molecules containing a different number of S and SP copper(II) centers, and (ii) the complicated pattern of Cu–O–Cu angles around the ring(s) (Table 2), these best-fit parameters must be taken with great care. The g values are significantly lower than the average Lande’s factor resulting from the analysis of HF-EPR spectra (<g> = 2.172, vide infra), possibly reflecting systematic errors in bulk magnetic measurements. The field dependence of the magnetization at low temperature is shown in the inset in Fig. 7. At the highest fields explored, the magnetization approaches the saturation value 6 NA μB expected for a S = 3 state with g = 2.00. Also, the non-coincidence of the curves recorded at 4.6 and 1.9 K points to the presence of sizeable magnetic anisotropy effects. The experimental magnetization data have been modelled using a second-order spin Hamiltonian with axial symmetry (Eq. (2)):
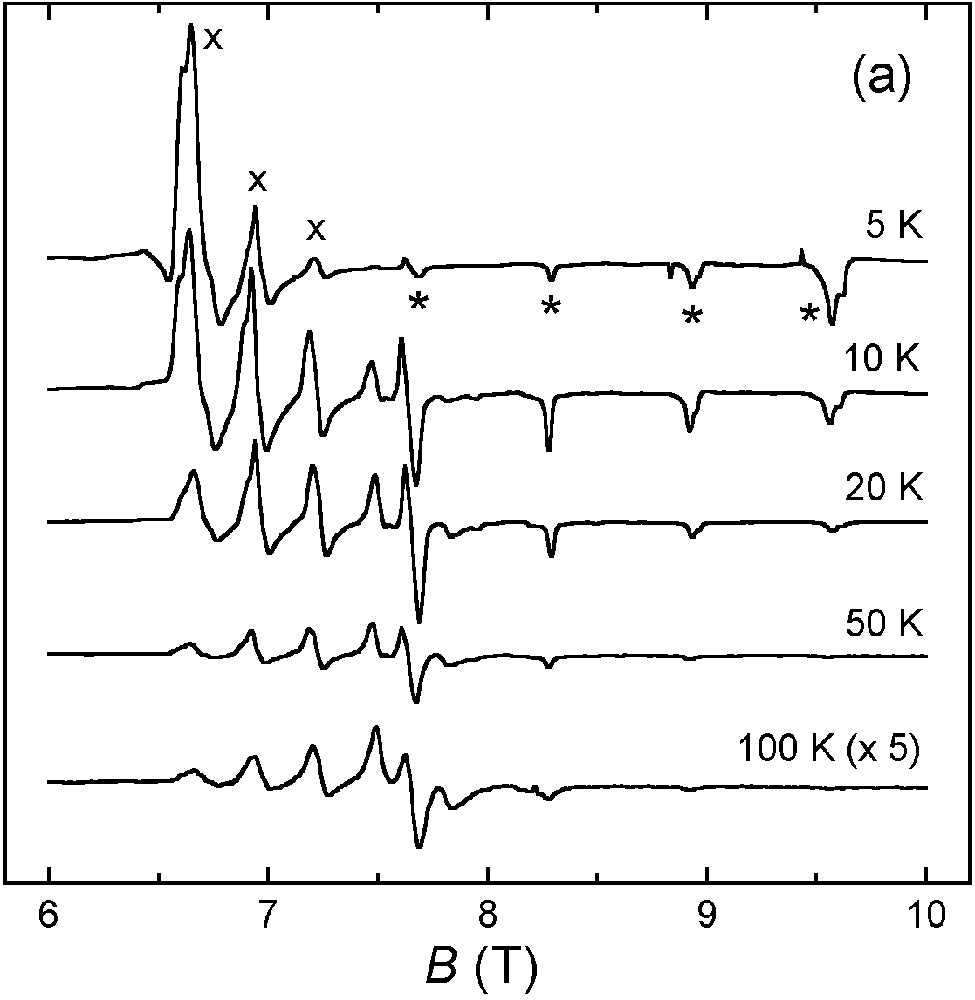
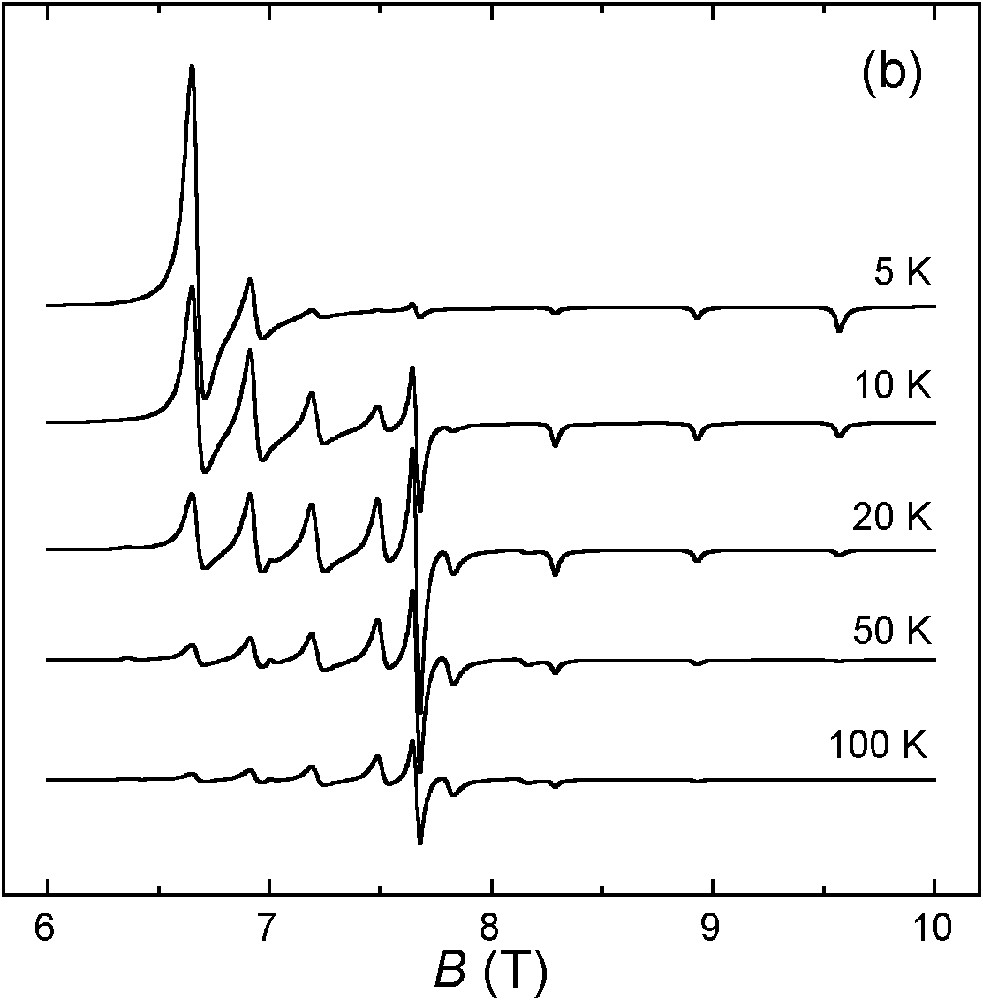
(a) Variable-temperature HF–EPR spectra of 1·3 nBuOH at 230 GHz. The parallel and perpendicular transitions are marked with * and ×, respectively. (b) Spectra calculated with g|| = 2.063, g⊥ = 2.225 and D = 0.308 cm–1 (linewidths: Δw|| = 150 G, Δw⊥ = 350 G).
We now turn to the magnetic properties of 3·2CHCl3·2.75 MeOH·0.25 H2O, which are reported in Fig. 10. The χ T product is 4.9 emu K mol–1 at 300 K, hence larger than expected for ten uncoupled S = 1/2 spins (3.75 emu K mol–1 with g = 2.00). It increases smoothly upon lowering temperature down to ca. 10 K (6.2 emu K mol–1) and then decreases rapidly to 4.6 emu K mol–1 at 2.0 K. A quantitative analysis of χT-vs-T data was based on the Heisenberg Hamiltonian in Eq. (3):
Experimental χT-vs-T data for 3·2CHCl3·2.75 MeOH·0.25 H2O, with best-fit calculated data as solid (g = 2.25, J1 = –47 cm–1, J2 = 0, J3 = 1.7 cm–1) and dashed (g = 2.25, J1 = –47 cm–1, J2 = 0, J3 = 0) curves. The inset shows a M-vs-B/T plot at two different temperatures (solid lines provide a guide to the eye).
5 Conclusions and outlook
The hexacopper(II) siloxanolate cage 1·3 nBuOH featuring labile nBuOH ligands has been synthesized and characterized by single-crystal X-ray diffraction, magnetic measurements and HF–EPR spectra. The complex has a high-spin S = 3 ground state arising from ferromagnetic exchange interactions among the six S = 1/2 copper(II) centres, as found for the EtOH analogue [39]. However, 1·3 nBuOH is much more soluble in organic solvents and can be used as a robust, preformed unit for the controlled assembly of larger spin clusters via ligand exchange. This approach has led to the isolation of a decacopper(II) complex, [Cu6{(PhSiO2)6}2{NCCu(tmpa)}4](PF6)4 (3) [25], containing four paramagnetic complex ligands [Cu(tmpa)CN]+. Though prevalent ferromagnetic coupling within the Cu6 core is maintained, the distortions introduced by the new ligands weaken exchange interactions in the ring. In addition, due to unfavourable overlap between magnetic orbitals, magnetic coupling with the peripheral copper(II) ions is weak. Further synthetic studies on similar structures containing transition-metal ions other than copper(II) are in progress.
6 Supplementary material
Crystallographic data (excluding structure factors) for 1·3 nBuOH and 3·2 CHCl3·2.75 MeOH·0.25 H2O have been deposited with the Cambridge Crystallographic Data Centre as supplementary publications Nos. CCDC-191357 and CCDC-186933, respectively. These data can be obtained free of charge via www.ccdc.cam.ac.uk/conts/retrieving.html(or from the CCDC, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033; e–mail: deposit@ccdc.cam.ac.uk).
Acknowledgements
We thank M. Monari and V. Albano (Department of Chemistry ‘G. Ciamician’, University of Bologna, Bologna, Italy) for assistance in X-ray data collection on 3·2 CHCl3·2.75 MeOH·0.25 H2O, and H. Weihe (Institute of Chemistry, University of Copenhagen, Copenhagen, Denmark) for providing the programs SIM and SIMSPC used to simulate EPR spectra. This work was financially supported by the University of Modena and Reggio Emilia, by Italian MIUR and CNR, by MOLNANOMAG network and by the ESF Programme ‘Molecular Magnets’.


