1 Introduction
Dendritic polymers are a class of synthetic macromolecules with a highly branched, three-dimensional architecture [1,2,3,4,5]. This molecular architecture can be used to advantage creating a core-shell molecular architecture of end groups surrounding the internal core composed of the branching units and focal point (see Fig. 1). Further, this type of molecular design can be used to host guest molecules that are released on a molecular scale in novel drug delivery schemes [6] or to change a linear polymer’s conformation in a dendrimer – linear hybrid block copolymer [7,8]. Rather than present an exhaustive review of the synthesis and utility of dendrimers (see e.g. [9,10]) an account of the author’s research will be given.
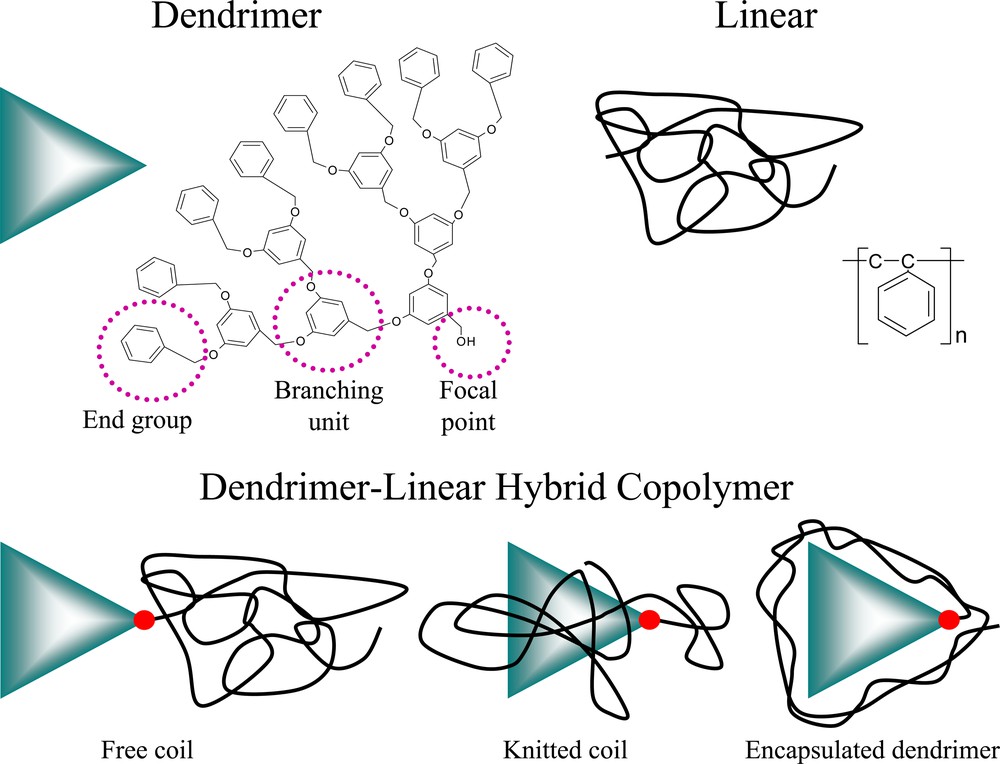
The cartoon and chemical structure of a poly(benzyl ether) dendron containing a focal point, branching units and end groups is shown in the top left. A linear polymer, such as polystyrene, is represented as a coil in the top right. The bottom part of the figure shows a dendrimer–linear hybrid block copolymer with three possible linear polymer states: the free coil, the knitted coil and an encapsulated dendrimer. The red dot represents the dendrimer–linear covalent bond at the dendron focal point.
This account is organized to first reveal how much free volume is in a dendrimer and to elucidate it distribution. This is an important quantity since application of dendrimers depends in many cases on whether they can contain guest molecules. Next it has been hypothesized that dendrimer – linear hybrid block copolymers have unique conformations in solution. Specifically, the linear block can achieve various molecular morphologies depending on its mass and relative interaction with the solvent; this will be discussed to determine if this type of block copolymer can be used as a molecular machine. Finally, self-assembly of dendrimer – linear hybrid block copolymers will be mentioned. It has been found that regular arrays of dendrimer spheres or cylinders can be fabricated that defy theoretical and experimental predictions. This builds on the work of Leclère et al. [11] who considered assembly of rod-coil type hybrid block copolymers, to cite only one key reference in the vast block-copolymer literature. In our work, we consider assembly of sphere-coil hybrid block copolymers, see also Tande et al. in this volume [12].
2 Free volume and its distribution
De Gennes and Hervet [13] suggested that dendrimers or starburst polymers have a crowding of monomer units towards the molecular periphery as suggested by their chemical structure given in Fig. 1. The monomer density rapidly increases from essentially zero at the focal point to large values with increasing distance from the molecular center. Recent simulations show that thermal fluctuations cause, in some cases, an essentially constant monomer density [14,15,16,17]. Thus, end groups must back-fold and perhaps saturate the entire molecule. Yet, the experimental results of Topp et al. [18] suggest the end groups are localized near the periphery and so agreement of simulation and experiment is not easily realized.
However, experiments in our laboratory [8] show that dendrimers, at least poly(benzyl ether) dendrons (PBE dendrons), are quite flexible and change volume depending on the generation and solvent used. In fact, the dendrons collapsed to such an extent in one solvent (chloroform) that the intrinsic viscosity ([η]) was constant with generation. This certainly affects end group distribution.
To further this discussion, one can relate the intrinsic viscosity to the viscosimetric volume (Vη) and molecular mass (M) via
where NA is Avogadro’s number and ρm, the molecular density. A spherical architecture is implicitly assumed through use of this expression. Measuring the volume with a technique such as dynamic light scattering yields the hydrodynamic volume. This volume is usually quite close to Vη and is different only if the two flow fields, uniform versus shear, distort the molecule and hydrodynamic flow properties. Regardless of architecture, if [η] is constant, then so is ρm and the monomer density or free volume is uniform throughout the dendron and the end groups must move from the molecular periphery. When making this statement it is assumed that the molecular morphology or architecture does not change with molecular mass.
Further results, in collaboration with others [19], reveals that neutron scattering from a dendrimer is also quite complicated and dependent on the solvent. A powerful technique, which relies on scattering data as well as Vη, is to grade the segment distribution by using Burchard’s P–ratio [20],
where Rg is the radius of gyration and Rη, the viscosimetric radius (Vη = 4/3 π Rη3). To understand the utility of this ratio, one must first realize that the radius of gyration is intimately related to the density profile through a molecule (ρ(r), r is the radial distance from the center of mass):
where R is the sphere radius. One can assume a generalized density distribution such as:
to arrive at:
If the dendron has zero density at the center and a maximum at the edge (say, a = 0, n = 1) then P equals 0.816 while in the opposite case with a density maximum at the center and zero at the molecular periphery (say, a = 1, b = –1, n = 1) has P equal to 0.632, a 30% change. These calculations, of course, must be carried out assuming R is represented by Rη, however, the power of this technique is that one can estimate the density distribution within a spherical architecture without complicated modeling.
Comparison of experimental to theoretical P–ratios for PBE dendrons is given in Fig. 2 [19] and it is clear that the solvent makes a large difference in the monomer distribution. Further, the results in d–benzene suggest that the distribution approaches that of a Gaussian which linear macromolecules adopt [21]. It may be argued that the dendrons adopts a non-spherical shape that could affect conclusive inferences about the density distribution. For example, an extended rod-like conformation significantly increases P.
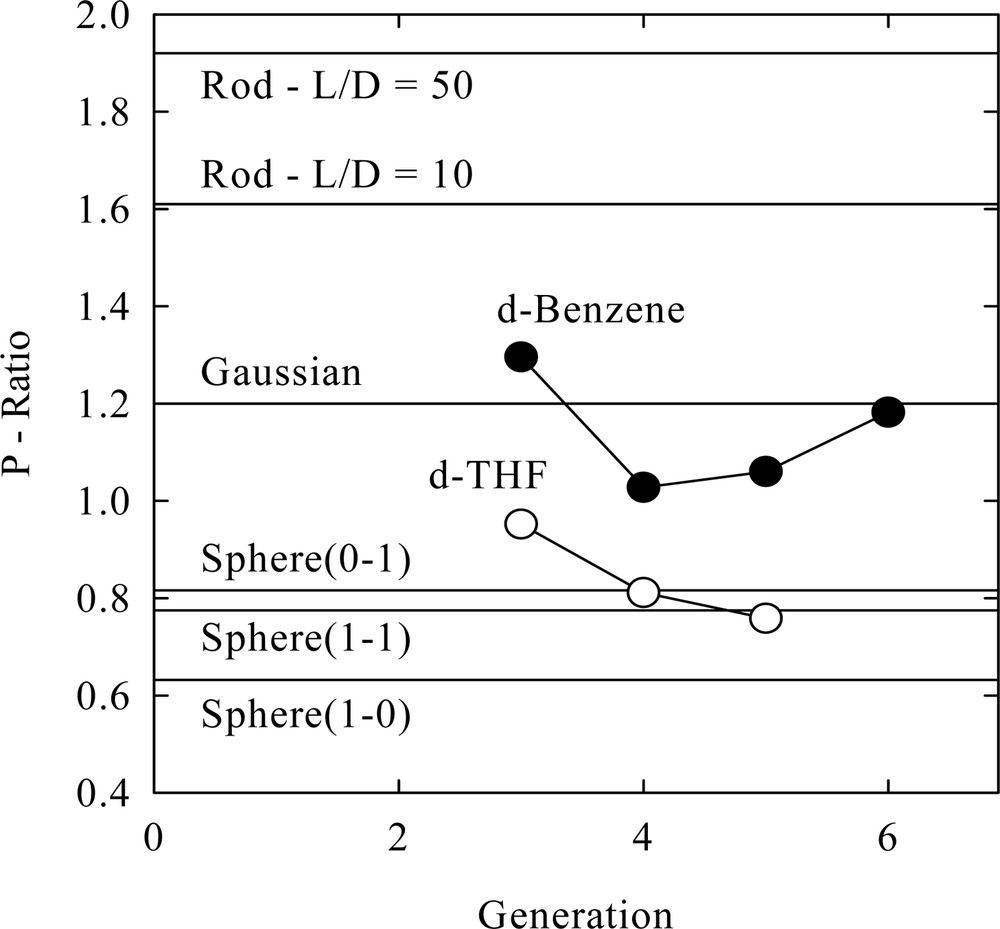
Ratio of the radius of gyration to viscosimetric ratio (P–ratio) as a function of dendrimer generation number. The poly(benzyl ether) dendrimers were dispersed in d–benzene and d–THF at low concentration [19]. The horizontal lines are for a sphere that has a maximum density at the center which linearly decays to zero at the sphere radius (Sphere[1-0]), a homogeneous density sphere (Sphere[1-1]), a sphere where the density increases linear from zero at the center to a maximum at the sphere radius (Sphere[0-1]), a Gaussian coil (Gaussian), a rod with a length on diameter ratio of 10 (Rod – L/D = 10) and a rod with length on diameter ratio of 50 (Rod – L/D = 50).
The radius of gyration is measured from a Guinier-type analysis and is not model dependent, yet, the viscosimetric radius changes by a factor like,
assuming a rod-like prolate spheroid or a disk-like oblate spheroid [8] thereby increasing P. However, very large or small aspect ratios, rp, need be assumed to increase P from the value determined in d–THF to that in d–benzene. It is believed that adoption of these extreme elongated shapes (rp > 5, or rp < 0.2) is not possible and so the dendron is nearly spherical in shape and solvent change creates a significant re-distribution of the segment and free volume distribution.
A further and unique observation can also be drawn from the data. The P–ratio in Fig. 2 shows the PBE dendron in d–THF approaches that of a constant density sphere at large generation in agreement with the calculations by Mansfield [14]. Yet, the intrinsic viscosity for the PBE dendrons in chloroform is constant with generation [8] also implying the molecular density is constant. The intrinsic viscosity is also twice as large in THF and so the dendron is in a much lower density state, see eq. (1), than in chloroform. Thus, these two solvents have created, to first approximation, two constant density states, one that is twice as dense as the other.
The magnitude of the free volume within the entire molecule can be determined by comparing it to the van der Waals occupied volume [22]. An example of this is given in Fig. 3 where the viscosimetric volume is compared to the van der Waals volume as a function of dendron generation (see Appendix 3 of Jeong et al. [8] for detailed calculations of the van der Waals and free volumes). It is clear that the free volume can achieve very large values, however, its calculation must be carefully performed. When the molecular density is low, as in gas-like states, then the free volume (Vf) is merely the difference between the molecular (V ≈ Vη) and van der Waals volumes (V*),
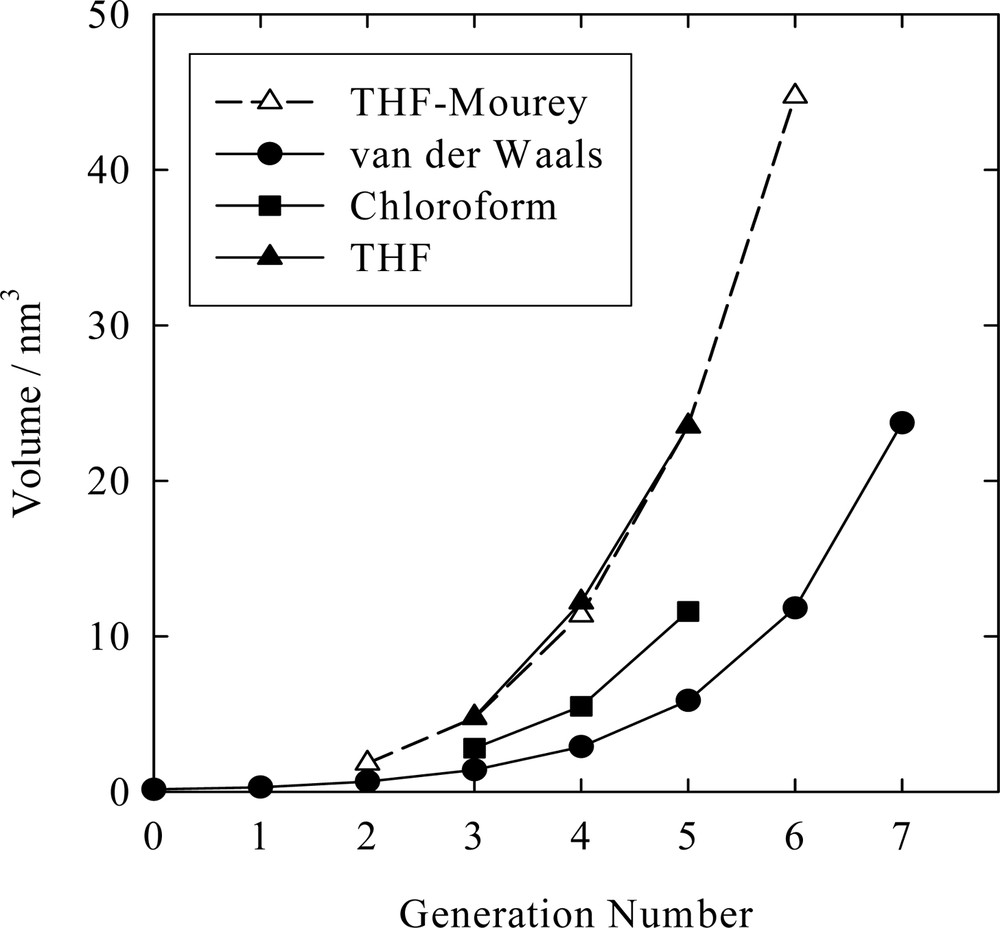
Viscosimetric volume, determined from the intrinsic viscosity, as a function of generation number for poly(benzyl ether) dendrons in tetrahydrofuran (THF) or chloroform solvent at 30 °C. Data are from Mourey et al. [5] (THF-Mourey) or Jeong et al. [8] (THF, chloroform). Note the good agreement of the data for the dendrons in THF from the two laboratories. The curve labeled van der Waals was calculated by knowing the van der Waals volumes of atoms with the distance between this curve and others representative of the molecular free volume.
However, at higher, liquid-like, densities the free volume should be calculated by [23],
In general, the lower of these values should be used. Correct interpretation of the available free volume may be crucial in rational molecular design and interpretation of results. For example, the available free volume in fourth generation PBE dendron in THF is 5.4 nm3 (instead of 9.3 nm3 as calculated by Eq. (5a)) while in chloroform the identical dendron has only 0.30 nm3 of available free volume.
Many of the above results may be peculiar to the system studied, PBE dendrons. Changing the monomer flexibility as well as the chemical composition of the end groups will surely affect the monomer and free volume distribution. For example, great chemical dissimilarity of the branching units and end groups may create a core – shell molecular morphology, interpretation of the viscosimetric volume for a hyperbranched polymer showed that this type of morphology was possible [24]. The core for this highly branched dendritic macromolecule was a polyester surrounded by C20/22 alkane end groups [25]. It was found that the molecular radius did not significantly change in different solvents despite the fact that the core, with terminal hydroxyl groups rather than the alkanes, was quite flexible and the volume varied by a factor of two in similar solvents. Thus, chemical dissimilarity within this class of highly branched macromolecules created a size invariant molecule with a dense core (V ≈ 3.3 nm3, Vf ≈ 0.8 nm3) surrounded by a less dense alkane shell (V ≈ 14.9 nm3, Vf ≈ 5.5 nm3), which may be useful in some applications such as dye retention [26].
Finally, to demonstrate the collapsed globular structure of dendrons compared to linear polymers, the hydrodynamic radius was measured for a fifth generation PBE dendron and compared to that for an exact linear analogue synthesized by Hawker et al. [27]. Using dynamic light scattering in THF at 30 °C the radius was determined to be 2.0 ± 0.3 nm for the dendron while the linear analogue had a radius of 2.4 ± 0.2 nm. This represents a decrease in the hydrodynamic volume of ~ 40%, in agreement with the GPC trace interpretation given by Hawker et al., clearly showing that dendrimers are more dense than an exact linear polymer and so contain less free volume.
3 Molecular machine
The PBE dendrons are flexible macromolecules and although more dense that a linear analogue still have significant free volume. So, a guest can certainly be sequestered within the dendron. However, if the guest were a polymer, would its conformation be affected? Furthermore, a hybrid block copolymer can be synthesized with a dendron as one block and a linear polymer as the other (see Fig. 1), will this affect the polymer or dendron conformation? Here we use fourth generation PBE dendron–linear polystyrene hybrid block copolymers in dilute solution to answer this question.
A polymer has significant degrees of freedom, that can be interpreted as entropy, some of which may be lost if it were to enter the dendrimer block due to excluded volume interactions. However, complete avoidance of the dendrimer would also provide an entropy penalty via reflection from the dendrimer ‘surface’. Solvent–polymer, solvent–dendron and dendron–polymer enthalpic interactions must also be taken into account to ascertain the block copolymer conformation. Note the solubility parameter of PBE dendrons and linear polystyrene are almost equivalent [8] and so enthalpic interactions may be minimized in this system.
The intrinsic viscosity results of Jeong et al. [8] showed an unusual phenomenon where the hybrid had a lower viscosimetric volume (Vη) than the linear polymer alone in benzene (see Fig. 4). This was interpreted by Jeong et al. as a phase transition. At intermediate molecular masses, the linear polymer wanders through the dendrimer (Knitted Coil in Fig. 1), which reduces the overall viscosimetric volume (the details of this decrease is not yet explained). As the linear chain’s mass is increased this knitting and the concomitant entropy loss is not (free) energy acceptable and the chain no longer wanders through the dendron (Free Coil). The fourth generation dendron has a very large free volume (6.2 nm3 or a fractional free volume of ~ 50%) and this is a key variable in allowing this hypothesized phase transition to occur. A similar transition is not seen in chloroform, where the dendron has a very small free volume (0.3 nm3), and so the linear polymer cannot wander through the dendron as freely.

Viscosimetric volume of the fourth-generation poly(benzyl ether) dendrimer–linear polystyrene hybrid block copolymer relative to the volume of linear polystyrene with the same mass as a function of hybrid molecular mass in chloroform and benzene at 30 °C. Note the dendrimer mass (generation) is kept constant (3288 Da), while the linear polymer mass is changed.
This hypothesis draws heavily on the work of Skvortsov et al. [28], who predicted similar phase transitions with one end of a linear coil pinned in a high (entropic or enthalpic) energy half-space which is next to a zero energy half-space. As the linear chain is made longer and longer it can sample more of the low energy region until it is energetically favorable for it to linearly extend through the high-energy region into the low-energy region (coil–flower transition).
The details of this Knitted–Free coil transition is currently an area of active research in our group and it is hoped that neutron scattering will reveal the details. Regardless it is proposed that manipulation of the dendron volume will allow this transition to occur thereby activating the molecular machine. This is an entropic-based machine and different to those which can be crudely designated as operating via enthalpic based interactions (see, e.g. [29]), although it is admitted that this classification is imprecise at best.
Previous work with hybrid block copolymers, where the solubility of the two components is vastly different in the given solvent, showed that an Encapsulated Dendrimer (see Fig. 1) might be the more appropriate molecular morphology [30]. Thus, it should be possible to achieve a variety of morphologies and hence machines with this unique molecular architecture. Further work is warranted and the architectural differences between dendrons and linear chains is certain to provide interesting results.
4 Self-assembly
Here the assembly of dendron – linear hybrid block copolymers in the bulk is considered. The block copolymer literature is immense and the work of Bates [31] as well as Gido and Wang [32] is mentioned. Basically, linear–linear block copolymers phase separate into spherical, cylindrical, ordered bicontinuous double diamond (OBDD) and lamellar morphologies (see Fig. 5). With the exception of research such as that by Leclère et al. [11], Meijer and co-workers [33,34], Lee et al. [35] and work by us [36] and others [37], little research has focused on using molecular architecture instead of enthalpic differences in linear blocks to achieve microphase separation. A detailed analysis of architectural effects on microphase separation is given in another article in this volume by Tande et al. [12], here generalities are considered.
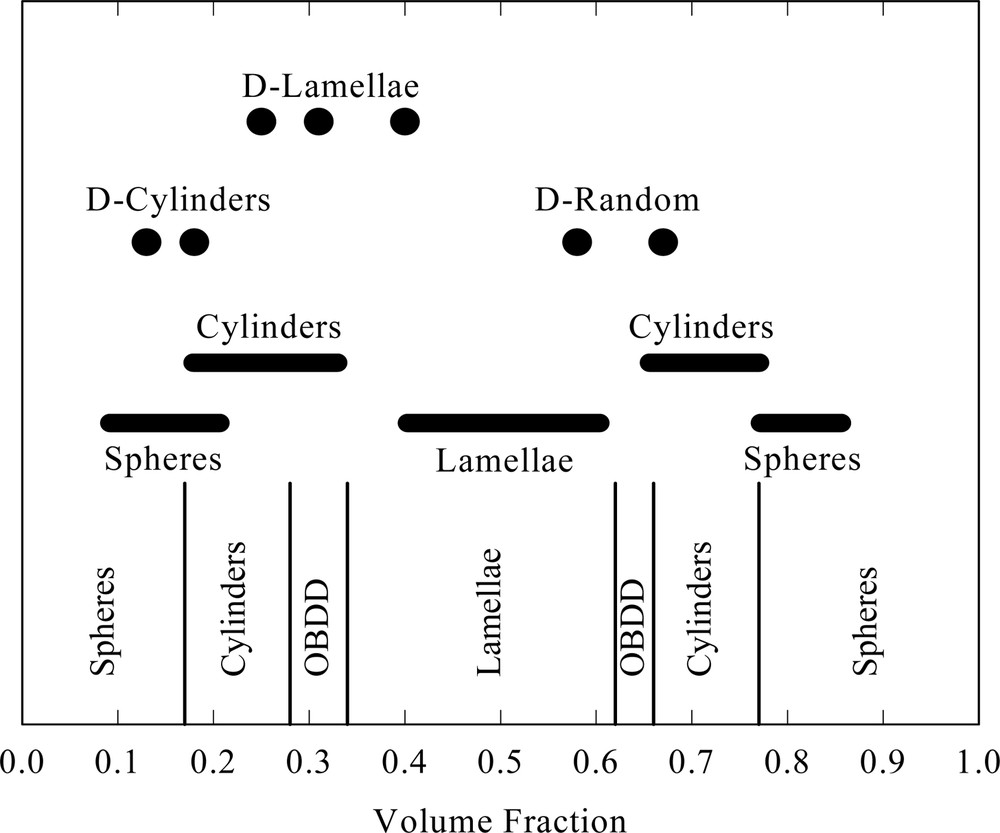
Morphology as a function of volume fraction for block copolymers. The vertical lines separate the various morphologies developed in the linear polystyrene–linear polyisoprene system [31]. The thick horizontal lines show the range for morphologies developed by a variety of linear–linear block copolymer systems (average volume fraction ± standard deviation) [32]. Circles are the morphologies for two dendrimer–linear hybrid block copolymer systems [33, 34, 36]. For this system, the volume fraction is that for the dendrimer.
The phase separation of linear–linear block copolymers is forced by chemical differences between the two or more blocks. This provides an enthalpic driving force to create unique morphologies that have been observed for many years and put on firm theoretical grounds by Leibler [38] over twenty years ago. Due to the interest in using these morphologies to create nanoscopic semiconducting devices, sensors and the like we were interested in whether one can affect the phase diagram developed by block copolymers through molecular architecture changes.
The results shown in Fig. 5 clearly show that dendrimer cylinders and lamellae can be assembled at dendron volume fractions (φD) outside the regimes typically predicted and observed for linear–linear block copolymer systems. This may be critical in some applications.
Characterization of phase-separated structures is frequently performed by small angle neutron scattering (SANS). The hexagonally close packed (HCP) cylinder morphology geometry is shown in Fig. 6a together with typical scattering patterns shown in Figs. 6b and c. A primary scattering intensity maximum occurs at the smallest wave vector (q), which is denoted as q*, followed by other maxima with correlation peaks at √3 q*, 2 q*, … The correlation peaks are the rings in Figs. 6b and through angular averaging one arrives at an intensity–scattering vector graph such as that in Fig. 6c. The interplanar distance, d, is related to q* through d = 2 π/q* and so for the example in Fig. 6c, one finds d = 29 nm.
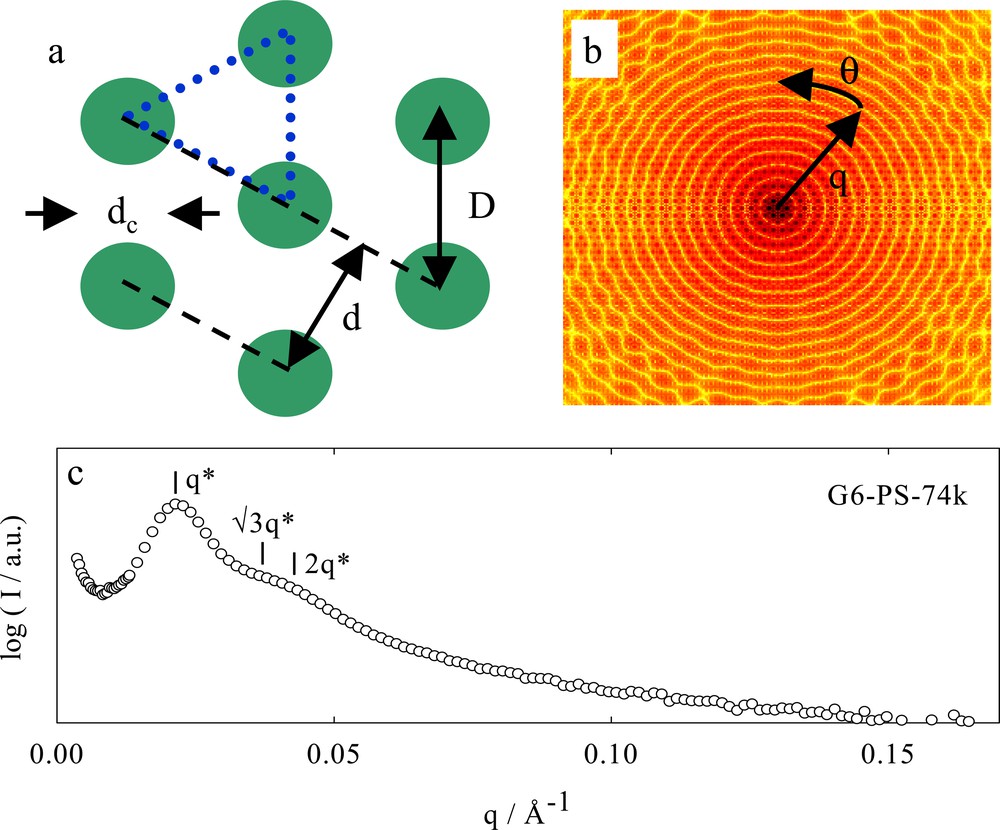
Scattering from a hexagonally close packed (HCP) cylinder morphology. (a) The geometry associated with HCP cylinders; dc is the cylinder diameter, d, the interplanar spacing and D, the cylinder-to-cylinder distance. The area enclosed by the blue triangle can be used to calculate the cylinder phase volume fraction. There is one-half of a cylinder enclosed in an area equal to d D/2. (b) Fourier transform (intensity scattering pattern) of the HCP cylinder morphology. The q vector is related to the distance from the center of the figure. Typically the intensity scattering pattern is averaged around the angle θ. (c) Angular averaged intensity (I) of SANS scattering from a bulk sample of sixth generation poly(benzyl ether) dendron–linear d8–polystyrene hybrid block copolymer with a total molecular mass of 74 kDa as a function of scattering vector. The correlation peaks at √3 q* and 2 q* shows that the HCP cylinder morphology is present. This data is from reference [36].
The dendron cylinder volume fraction is related to geometric variables defined in Fig. 6a through:
and by realizing d = √3 D/2, one can write:
The cylinder-to-cylinder distance, D, or separation distance, D–dc, may be critical parameters in making a device from self-assembled block copolymers. Taking a typical linear–linear block copolymer, such as polystyrene–polyisoprene, one can determine that the maximum separation distance is 2.3 × dc, whereas a dendrimer–linear hybrid block copolymer will have 3.0 × dc. The cylinder separation as well as the cylinder diameter itself can both be manipulated by using a dendron as one block, this may be crucial in the design and fabrication of devices assembled from nanoscopic materials.
5 Conclusion
A brief discussion of dendrimer utility has been given from the author’s perspective. It has been found that dendrimers, at least certain kinds, are flexible and readily change volume. This has an influence on their interaction with guests such as small molecules or a covalently bonded linear polymer. The free volume distribution may be critical in allowing the guest the ability to penetrate within the dendrimer. Due to a large free volume it is possible to create a molecular machine albeit more work must be performed to understand the mechanism of this machine. Dendrimers also allow self-assembly of various microstructures such as lamellae and hexagonally close packed cylinders. Since the molecular architecture of dendrimers is vastly different to linear polymers this allows another degree of freedom and so one can influence the phase diagram to create and fine tune nanostructures.
Acknowledgements
Collaborations with Dr. Craig Hawker, IBM Almaden Research Center, Dr. Eva Malmström, KTH Stockholm, and Prof. Jean Fréchet, University of California, Berkeley, have allowed the author the ability to explore the world of dendrimers and hyperbranched polymers, these collaborations are gratefully acknowledged. Drs. Norman Wagner and Brian Tande, University of Delaware, also aided the author in determining the physical structures developed by dendrimers. My students and postdoctoral fellows who actively participated in this pursuit of understanding the unique properties of dendrimers significantly contributed to this work. Finally, I would like to acknowledge funding sources over the years such as NSF-CTS/Nano 0296166, ACS-PRF 36388–AC7, NSF-NIRT 0210247 and Michigan State University.


