1 Introduction
An understanding of the thermodynamic properties of dendrimers and hyperbranched polymers is crucial to their successful technological application. This is especially true for use in such applications as crosslinking agents or rheology modifiers. Work in our groups and other studies [1–8] have shown that dendritic polymers show promise for these uses, but importantly, their efficacy depends on the miscibility of dendritic polymers with melts of linear chains. In addition, some of the more unique dendrimer properties, such as their intrinsic viscosity maximum in solution and their ability to encapsulate other molecules, are known to be dependent on the quality of the solvent [9].
On a fundamental level, it is of scientific interest how the highly branched architecture of dendritic polymers distinguishes these materials thermodynamically from linear polymers. First consider the prevalence of branch points within the molecule. This property generally results in a globular structure and higher molecular densities in solution, which suggests that penetration of other molecules into the interior of the dendrimer may be more difficult than for a corresponding linear polymer. Next consider the prevalence of end groups in dendritic polymers. It is reasonable to assume that the dendritic end groups will have a different contribution to the overall thermodynamic behavior than the interior segments of the molecule by virtue of their location in the molecule and greater accessibility to solvents. This also provides a possible means of varying the degree of interaction between the dendrimer and other molecules and polymers through endgroup modification without affecting the interior of the dendrimer, i.e. core-shell morphologies. Finally, there is an entropic difference between dendritic and linear polymers as dendrimers are chemically constrained from adopting the more probable conformations found in linear polymers. Of particular importance here, if this branched architecture also excludes linear polymers from interpenetrating dendrimers there may be a strong entropic penalty against miscibility when blended with linear polymers.
In this article we build on our previous work [10] and related work of others [11] investigating the interesting microphase separation of a series of hybrid diblock copolymers comprised of chemically similar dendritic and linear blocks. Theoretical predictions of the phase behavior of diblock copolymers with one linear and one branched diblock [12, 13] show that the branched block segregates more strongly than a corresponding linear analog, in qualitative agreement with these experimental results. These materials are novel in that the phase separation is primarily entropic in origin, a consequence of the globular, compact nature of the dendritic block. TEM and SANS are used to probe the miscibility and microphase morphology of these copolymers in the bulk as well as in blends with varying molecular weights of the linear homologue (polystyrene). The results demonstrate that the architecture of dendrimers creates an unfavorable entropic penalty to mixing with linear chains, which has profound consequences on the phase behavior of these hybrid copolymers.
2 Background
Diblock copolymers consisting of dendritic and linear blocks have been the subject of several recent studies [14–18]. These hybrid diblock copolymers have been shown to exhibit amphiphilic behavior in both solutions and in their pure phase. As in surfactants and linear block copolymers, these molecules can self-assemble into various morphologies, ranging from micelles to lamella, depending on the relative block sizes.
Most notably, Van Hest, et al. studied a block copolymer system consisting of a linear polystyrene ‘tail’ grafted to a poly(propylene imine) dendrimer ‘head’ in aqueous solution [16]. They observed the aggregation behavior of these molecules was dependent on the generation of the dendrimer and appeared to be qualitatively consistent with Israelachvilli’s theory for amphiphiles [19]. As the generation of the head group was increased from 2 to 4, the morphology of the microphase-separated domains changed from bilayers to rods to spheres. Later work by the same group [15] studied the morphology of these hybrid molecules in their solid state and found a similar dependence of the morphology on the size of the dendritic block.
Another class of dendritic-linear hybrid molecules, consisting of a poly(benzylether) head grafted to a linear chain of polystyrene, has been the focus of recent studies by Mackay et al. [9, 10]. The solution behavior of these molecules, in particular their intrinsic viscosity as a function of solvent quality, displayed evidence of novel interactions between the dendritic and linear portions of the molecule. In recent work [10], the phase behavior of these materials in the pure melt state was studied using small-angle neutron scattering (SANS), small-angle X-ray scattering (SAXS), and transmission electron microscopy (TEM). These investigations have revealed that dendritic-linear block copolymer morphologies are distinct from those found in completely linear systems. A quantitative analysis of these results suggests that substantial deformation of the dendrimer block is necessary to achieve the observed morphologies. A major conclusion from this work is that the novel block copolymers have a substantial entropic driving force favoring phase separation.
The study reported here extends this work to investigate blends of these hybrid diblock copolymers diluted with polystyrene homopolymers. Using SANS, with contrast afforded by selective deuteration, we study the dependence of the morphology of these microphase-separated systems on the head group generation, tail length, concentration, and homopolymer molecular weight. The goal is to provide additional insight into the effect of molecular architecture on the thermodynamic properties of dendrimers.
3 Experimental methods
3.1 Preparation of samples
Diblock copolymers of dendritic poly(benzyl ether) and linear polystyrene were obtained from C. Hawker & R. Vestberg of IBM-Alamden and the synthesis has been described in detail elsewhere [9]. Nine different molecules were synthesized for this study in which both the generation number of the dendritic head group and the molecular weight of the linear tail group were varied (see Table 1). The polystyrene tails were fully deuterated to provide a contrast in scattering length density. The codes for each sample indicate first the generation of the dendritic portion and second the molecular weight of the linear polystyrene portion. For example G6–61k refers to a copolymer that is comprised of a sixth generation dendron grafted to a polystyrene chain with a molecular weight of 61 000 g mol–1.
List of block copolymers included in this study
| Sample | PBE Dendron Gen.# (Mw) | Deuterated polystyrene block Mw (kg mol–1 ) | Blend Concentrations (wt. %) |
| G4–97k | 4 (3,288) | 96.7 | 10,5,1 |
| G4–42k | 4 (3,288) | 41.7 | 10,5,1 |
| G4–17k | 4 (3,288) | 16.7 | 10,5,1 |
| G5–62k | 5 (6,687) | 62.3 | 10,5,1 |
| G5–23k | 5 (6,687) | 23.3 | 10,5,1 |
| G5–12k | 5 (6,687) | 12.3 | 10,5,1 |
| G6–61k | 6 (13,464) | 60.5 | 100,10,5,1 |
| G6–30k | 6 (13,464) | 29.5 | 100,10,5,1 |
| G6–7k | 6 (13,464) | 6.5 | 100,10,5,1 |
Blends of each of these molecules with linear polystyrene (h–PS) of two molecular weights, 190 and 28.9 kg mol–1 (Scientific Polymer Products), at the concentrations listed in Table 1 were prepared by first dissolving both components in benzene, mixing, and then evaporating the solvent under vacuum. Samples for neutron scattering were prepared by pressing the blend into thin disks (8 mm in diameter by 1 mm thick) at temperatures above the glass transition temperature of polystyrene.
3.2 SANS measurements
The SANS measurements were made on the 30–m NG3 SANS instrument at the National Institute for Standards and Technology (NIST) Center for Neutron Research (NCNR) in Gaithersburg, MD. Two instrument configurations were used. The first had five guides, a sample-to-detector distance of 3.9 m, and a 20-cm detector offset. The second configuration had one guide, a sample-to-detector distance of 13.0 m, and no detector offset. Both configurations used a neutron wavelength of 6 Å with a 15% spread. The total q range covered was 0.0039 to 0.1667 Å–1. All measurements were taken either at 170 °C or at room temperature after annealing at 170 °C and quenching to room temperature.
The raw scattering data were subjected to the standard reduction procedures employed by NIST to generate one-dimensional data on an absolute scale. The scattering intensity is proportional to the square difference of the scattering length density (SLD) between the deuterated polystyrene (dPS) of the block copolymer tails and the hydrogenated polystyrene (PS) homopolymer. The values of SLD, calculated knowing the chemical formula and the bulk density of the molecule, are 0.14 × 10–5 Å–2 and 0.642 × 10–5 Å–2 for PS and dPS, respectively [20]. There is also contrast between the PBE head groups and PS, but the value of the PBE SLD (~0.20 × 10–5 Å–2) is close enough to that of PS such that this contribution to the scattering is negligible.
4 Results and discussion
4.1 Fourth-generation copolymers
Fig. 1 shows the SANS curves from the polymers consisting of fourth generation head groups blended with hydrogenated polystyrene of 190 kg mol–1 at 10 wt.%. In this series, the molecular weight of the deuterated polystyrene tail is varied from 17 to 97 kg mol–1. The SANS results show scattering that is typical of Gaussian polymers chains, with a q–2 dependence of scattered intensity in the large q regime. The solid lines in Fig. 1 are the fits of the data to the Debye equation, which is the form factor for Gaussian chains. The results of these fits (see Table 2) show that the radius of gyration, Rg, of these molecules increases with the molecular weight of the tails. The scattering from blends with polystyrene of 28.9 kg mol–1 (Fig. 2) is similar, although the measured radii are generally lower, as expected (Table 2).
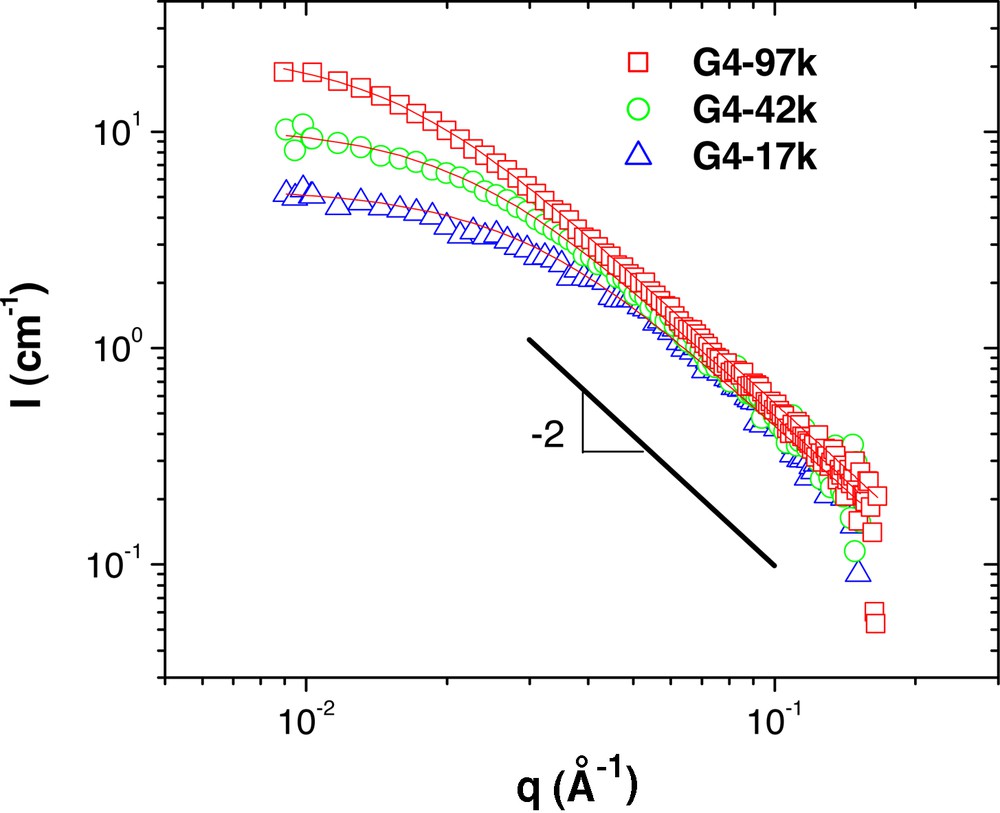
SANS measurements from G4 series of dendritic-linear block copolymers in hydrogenated polystyrene (190 kg mol–1). The linear polystyrene segments of the copolymers are deuterated to provide the necessary scattering contrast. The solid lines are the fits of the data to the Debye equation, the results of which are given in Table 2.
Results of fitting scattering data from G4 and G5 copolymers to the Debye form factor. The calculated Rg uses the relation developed by Cotton et al., Rg(nm) = 0.87 M (k Da)1/2 [23]
| Sample | Calculated | From SANS Measurements | |
| Rg (nm) (θ-solvent) | Rg (nm) (in 190k PS) | Rg (nm) (in 28.9k PS) | |
| G4–97k | 8.55 | 9.28 ± 04 | 9.19 ± 07 |
| G4–42k | 5.62 | 6.59 ± 08 | 5.96 ± 15 |
| G4–17k | 3.55 | 4.81 ± 05 | 4.51 ± 03 |
| G5–62k | 6.87 | 8.88 ± 05 | 8.29 ± 13 |
| G5–23k | 4.20 | — | 6.87 ± 04 |
| G5–12k | 3.05 | — | — |
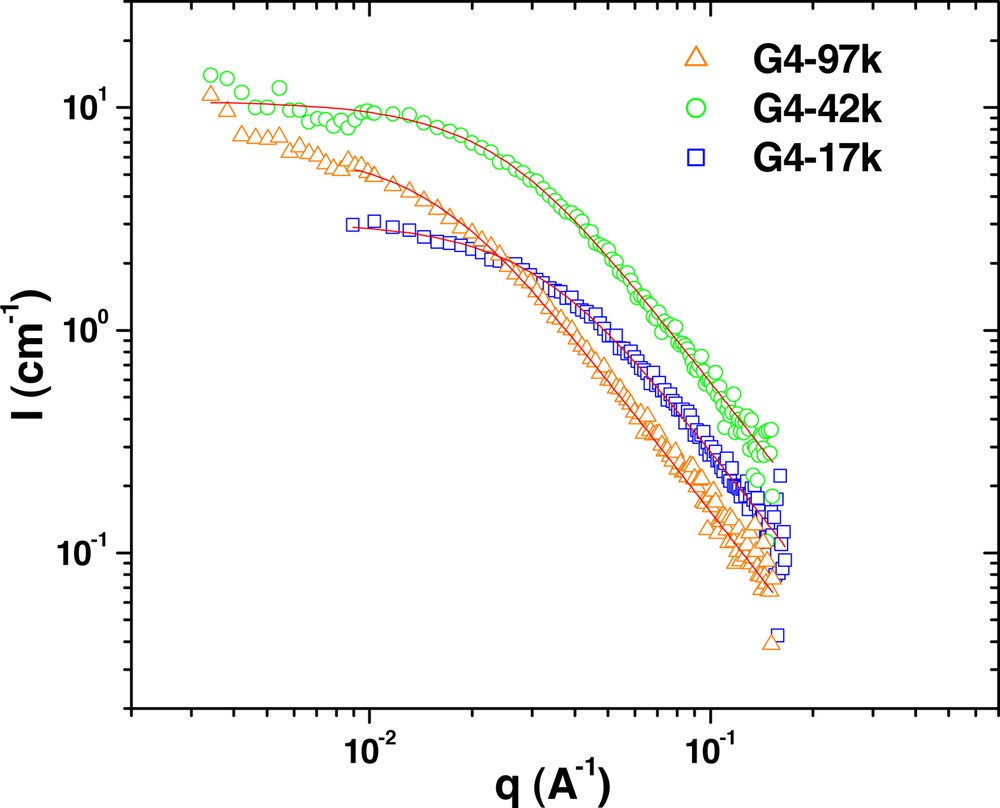
SANS measurements from G4 series of dendritic-linear block copolymers in hydrogenated polystyrene (28.9 kg mol–1). The linear polystyrene segments of the copolymers are deuterated to provide the necessary scattering contrast. The solid lines are the fits of the data to the Debye equation, the results of which are given in Table 2.
For this series of copolymers, the data indicate that these samples are completely homogeneous with no observed phase separation. The fourth generation PBE head group is quite small, with a molecular weight of 3288 g mol–1 and an Rg of 1.5 nm. Therefore, it is not entirely surprising that the dendrimer does not have much of an effect, as the PS block is significantly larger.
4.2 Fifth-generation copolymers
Fig. 3 shows the SANS spectra from the G5 copolymer series in polystyrene of 190 kg mol–1 at 10 wt.%. For the molecule with the longest tail, 62 kg mol–1, the scattering is again typical of a Gaussian chain. The Debye equation fits the data well; the fit results are given in Table 1. However, as the length of the tail is decreased to 23 kg mol–1 and then further to 12 kg mol–1, it can be seen that microphase separation begins to occur in the sample, as evidenced by the increase in scattered intensity at low q. From the curve for the G5–12k hybrid, a correlation peak begins to emerge around q = 0.05 Å–1, suggesting a phase separated system in which the average distance between domains of microphase separated diblock copolymer is on the order of 126 Å (12.6 nm). Note that bulk visual inspection revealed no noticeable differences between samples, suggesting that any phase separation is into domains smaller than that required to significantly scatter visible light.
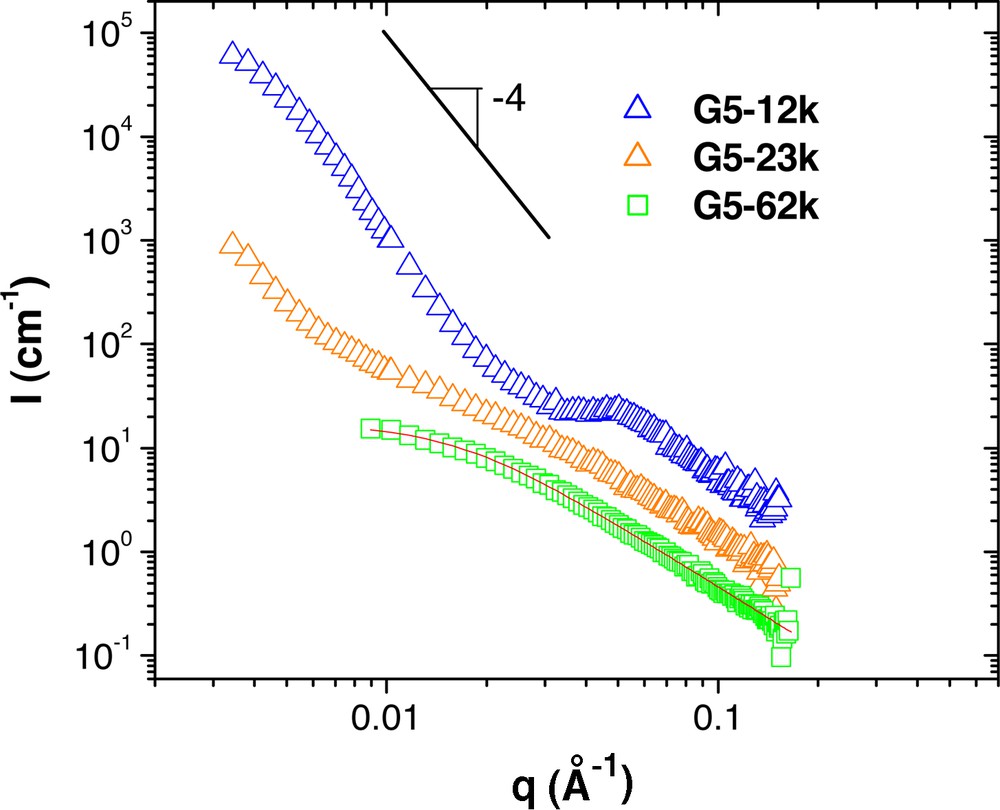
SANS measurements from the G5 series dendritic-linear block copolymers in hydrogenated polystyrene of 190 kg mol–1. The linear polystyrene segments of the copolymers are deuterated to provide the necessary scattering contrast. The curves have been shifted vertically for clarity. The solid line is a fit of the G5–62k data to the Debye equation, the result of which is given in Table 2.
In the lower molecular weight polystyrene blends (Fig. 4), the copolymer is slightly more miscible. Both the G5–62k and G5–23k samples appear to be generally homogeneous, and are fit by the Debye equation (Table 2). However, phase separation becomes evident for the G5–12k sample, where strong forward scattering is again seen.
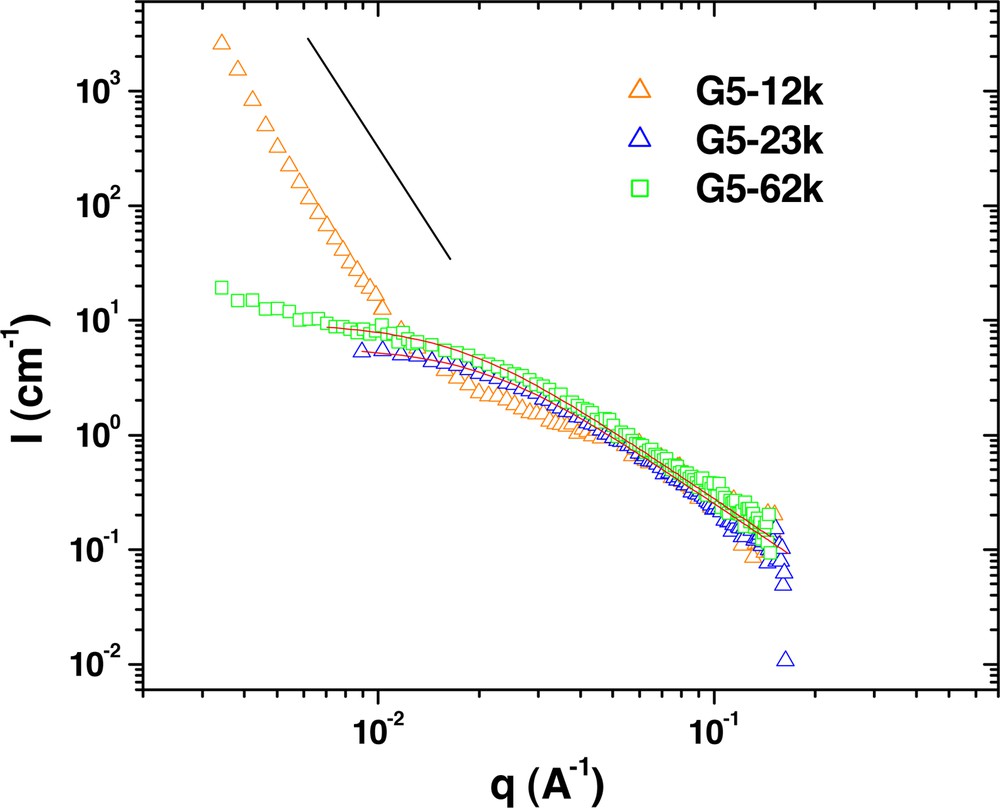
SANS measurements from the G5 series dendritic-linear block copolymers in hydrogenated polystyrene of 28.9 kg mol–1. The linear polystyrene segments of the copolymers are deuterated to provide the necessary scattering contrast. The solid lines are fits to the Debye equation, the results of which are given in Table 2.The lone black line illustrates the slope of –4 expected for mesoscale domains.
Compared to the previous series, the PBE block is one generation larger (Mw = 6687 g mol–1 and Rg ~ 1.9 nm) and its influence on the overall phase behavior of the system is now becoming evident. For the sample with the longest tail, the PS block still dominates. But when the tail molecular weight becomes more comparable with the PBE head, there is a tendency for phase separation. The results also show that phase separation occurs more easily in the blends with a larger homopolymer molecular weight. Note, however that this phase separation is neither a bulk phase separation (i.e. the samples do not bulk demix over the timescale of the measurements) nor a microphase separation, but rather, some level of mesophase separation with unstructured domains much larger than the molecular dimensions of either component. The thermal stability of this mesophase separation may suggest an entropic component to this phase behavior, an idea that will be further explored in later sections.
4.3 Sixth-generation copolymers in bulk
The phase behavior of the copolymers containing sixth generation head groups has been studied using SANS, SAXS, and TEM. These results have been the subject of a recent publication [10]. The TEM images from this paper are reproduced in Fig. 5 and the resulting domain dimensions are given in Table 3. In the TEM measurements, the dendrimers have been stained and show up as the darker regions in the micrographs. Scattering measurements (given in Figs. 6–8) were also used to determine the domain sizes formed in these systems.

Transmission electron micrographs of sixth generation poly(benzyl ether) dendrimer – linear polystyrene block copolymers: (a) G6–7k sample showing random morphology, (b) G6–30k with lamellar morphology, and G6–61k with the cylinder morphology viewed parallel to the cylinder axis (c) and perpendicular to the cylinder axis (d) [10].
Morphology observed in the G6 series of copolymers in the pure state [10]
| Sample | Morphology | q* (nm–1 ) | d (nm) † | r (nm) ‡ |
| G6–7k | Micellar | 0.433 | 14.5 | 2.6 |
| G6–30k | Lamellar | 0.306 | 20.5 | 6.8 |
| G6–61k | Cylindrical | 0.214 | 34.2 | 7.8 |

SANS measurements from G6–7k dendritic-linear block copolymer concentration series in polystyrene of 190 kg mol–1. The pure phase small-angle X-ray scattering (SAXS) curve is included for comparison and is from [10].

SANS measurements from G6–30k dendritic-linear block copolymer concentration series in polystyrene of 190 kg mol–1. The pure phase small-angle X-ray scattering (SAXS) curve is included for comparison and is from [10].
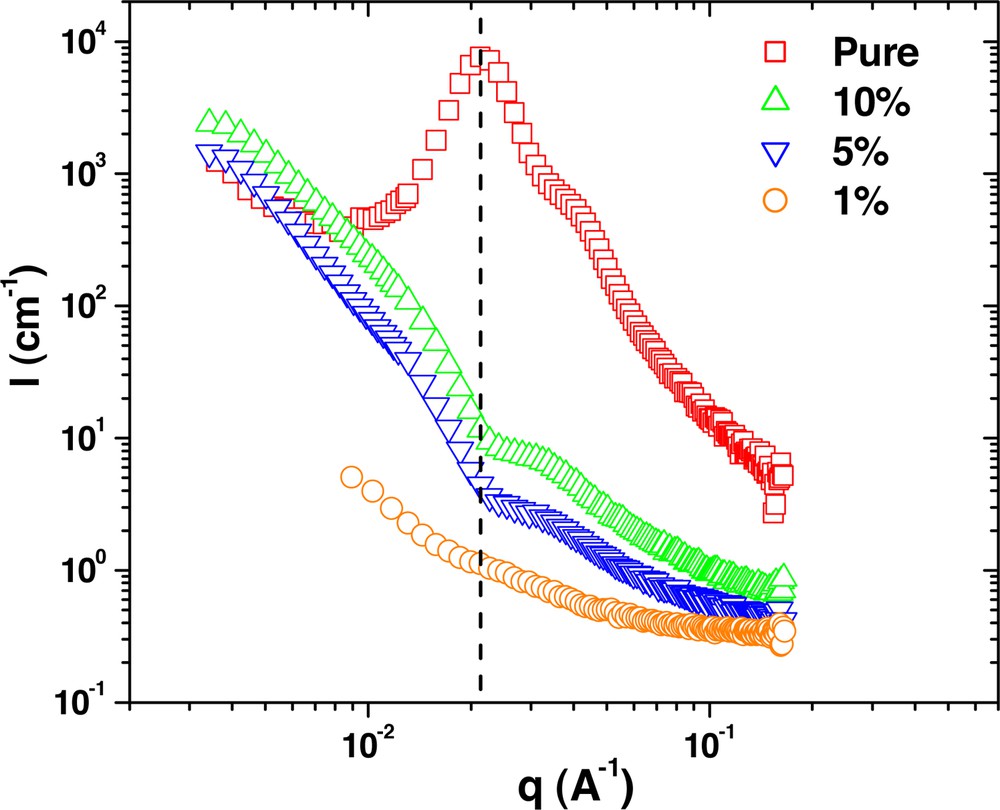
SANS measurements from G6–61k dendritic-linear block copolymer concentration series in polystyrene of 190 kg mol–1.
Fig. 5a is the TEM image from the G6–7k sample and shows that they form a random micelle phase. The dendritic portion of the micelles has a radius of around 2.6 nm, as determined from scattering. The average spacing between the micelles is 14.5 nm.
The G6–30k copolymers, shown in Fig. 5b, form a lamellar phase, as indicated by the fingerprint-like pattern of the micrograph. The dendrimer layer has a thickness of 6.9 nm with an overall repeat distance of 20.5 nm.
The G6–61k samples, shown in Fig. 5c and d, form a well-aligned cylindrical phase. Fig. 5c is an image oriented perpendicular to the cylinder axis, while figure d is oriented parallel. The radius of the cylinders, which are formed by the dendrimer blocks, is 7.8 nm. The distance between the centers of the cylinders is 34.2 nm.
This progression of morphologies, from micelles to lamellae to cylinders, as the molecular weight of the PS tail increases is consistent with what is typically observed for linear diblock copolymers [21]. However, the absolute location of these phases on the phase diagram do differ somewhat from the linear case, with the phase envelope characteristic of a linear polymer with a higher molecular weight block than that of the dendritic block. In other words, the dendritic block has a larger influence on the phase behavior than a linear block of equal weight. This was attributed to the lack of intermolecular penetration of the dendritic block. It was also suggested that an entropic driving force for phase separation is important for these systems, as the enthalpic difference between blocks was minor.
4.4 Sixth-generation copolymers in homopolymer blends
To further study their phase behavior, the sixth generation copolymers were diluted in homopolymer blends at 1, 5, and 10%. Figs. 6–8 are plots of the SANS data from this series of copolymers in hydrogenated polystyrene of 190 kg mol–1 at 170 oC. Included in these plots for comparison are the scattering curves (small-angle X-ray scattering in some cases) from the pure diblocks reproduced from Mackay et al. [10]. The scattering from these systems shows two important features. First, correlation peaks are seen in each curve, which are a result of microphase separation (i.e. micelles, lamellae, and cylinders). Also increased forward scattering is also observed, indicating mesoscale phase separation (i.e., aggregation of microphase domains on a larger length scale), as was seen in the G5 series.
The scattering from the pure phase G6–7k copolymer (Fig. 6) shows a distinct correlation peak at q = 0.433 nm–1, the result of the micelle morphology with an average spacing of 14.5 nm. Since this copolymer contains mostly PBE, the micelles consist of polystyrene core surrounded by a PBE shell, as confirmed by the TEM images [10]. As the concentration is reduced from the pure phase down to 1 wt.%, it is observed that the position of the correlation peak does not change significantly. This is unusual, as one would expect that diluting the micelles would increase the distance between them, which in q–space would correspond to a shifting of the peak to lower q values.
Another observation in the diluted blends is the emergence of large forward scattering at low q with a q–4 power-law dependence, suggesting that the sample contains larger objects with sharp boundaries.
These results can be interpreted as follows: upon dilution with homopolymer, the micelles do not disperse in the polystyrene, but rather form compact aggregates within which the homopolymer does not substantially penetrate. As a result, the average distance between the individual micelles in the micelle rich domain remains the same as in the bulk. These larger aggregates of micelles are then responsible for the large forward scattering, typical of mesoscale phase separation. This can perhaps be attributed by a lack of solubility between the PS of the tail and that of the homopolymer matrix.
The SANS results from the G6–30k hybrids are given in Fig. 7, which shows scattering typical of lamellae with correlation peaks found at q* = 0.3 nm–1 and 2 q* = 0.6 nm–1. Here, the lamellae consist of alternating layers of dendrimer and PS. As in the G6–7k sample, it is seen that the location of the primary correlation peak does not change significantly as the copolymers are diluted with PS. This again can be explained by a lack of penetration of the matrix PS into the PS regions of the lamellar domains. Thus, the lamellar domains contain the same morphology as the bulk sample, although the coherence is clearly diminished with dilution. The forward scattering is the result of interference from these larger domains.
Finally, the scattering from the G6–61k sample is shown in Fig. 8. From the TEM measurements, it is known that in the pure phase this sample forms well-ordered cylinders with an average spacing between domains of about 34 nm [10]. Here, the cylinders are comprised of the dendrimer blocks and are surrounded by a shell of dPS. The scattering of Fig. 8 is typical of cylinders, with one peak at q = q* = 0.214 nm–1 and higher order peaks at 31/2 q* and 2 q*. However, for the diluted blends, it is clear that there is significant structure change upon dilution. For the 5 and 10 wt.% samples, the observed scattering closely resembles that of spheres, with some possible aggregation that shows up as forward scattering. Thus, increasing the tail block length leads to limited solubility of the homopolymer into the dendrimer.
4.5 Effect of matrix molecular weight
Blends of the dendrimer diblocks with polystyrene of 190 kg mol–1 results in either dissolution, for the lowest generation number or the formation of mesoscale domains, some with microphase separation, depending on the generation number of the dendritic block and the tail molecular weight. For the 6th-generation hybrids, only the copolymers with the longest linear portion (61 kg mol–1) show evidence of homopolymer penetration into the microphase-separated domains when diluted. As the G6 copolymers with lower molecular weight tails do not show evidence of swelling by the homopolymers, the effect is most likely due to the large molecular weight difference between the homopolymer and the tails of the copolymer. Large molecular weight differences are well known to cause phase separation in homopolymer blends. To further explore this, blends were also prepared using a PS of lower molecular weight (28 900 g mol–1), which is much closer in molecular weight to tails of our samples. This was found to have a significant effect on both the microphase morphology and the domain aggregation, as seen in Figs. 9–11, which provides for a comparison between each of the 10% samples in both PS homopolymers.
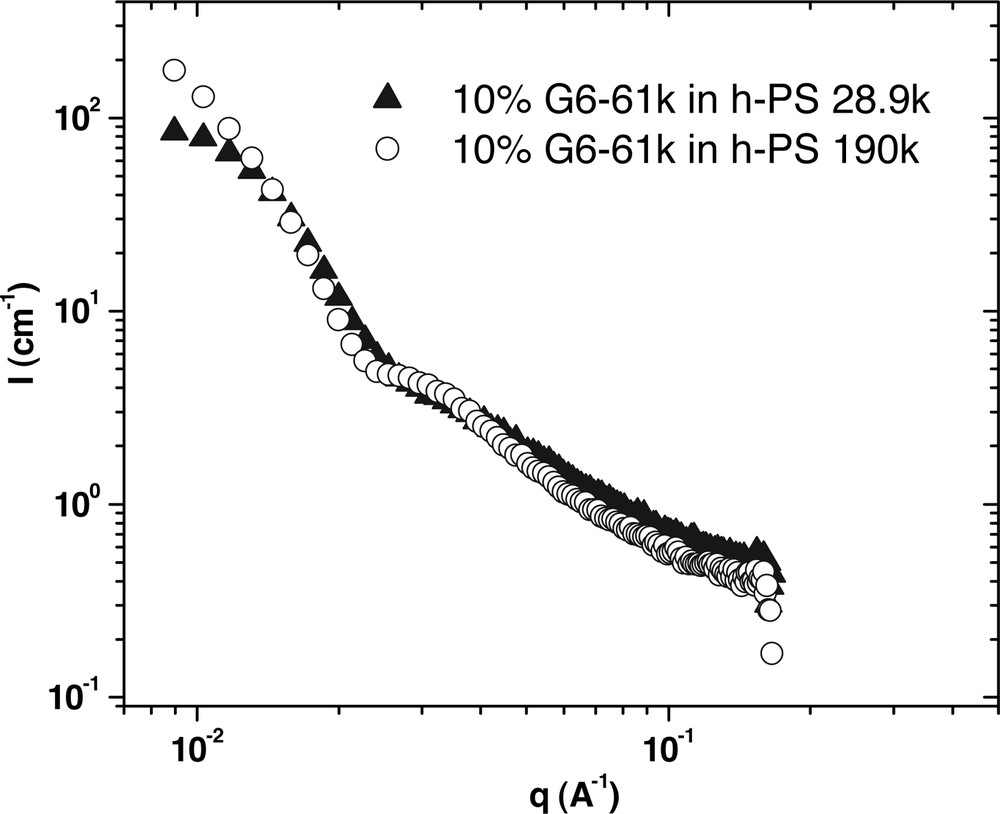
The effect of matrix molecular weight on the morphology of G6–61k at 170 °C. This data shows that in the lower molecular weight PS, there appears to be less forward scattering, which suggests less aggregation of individual micelles.
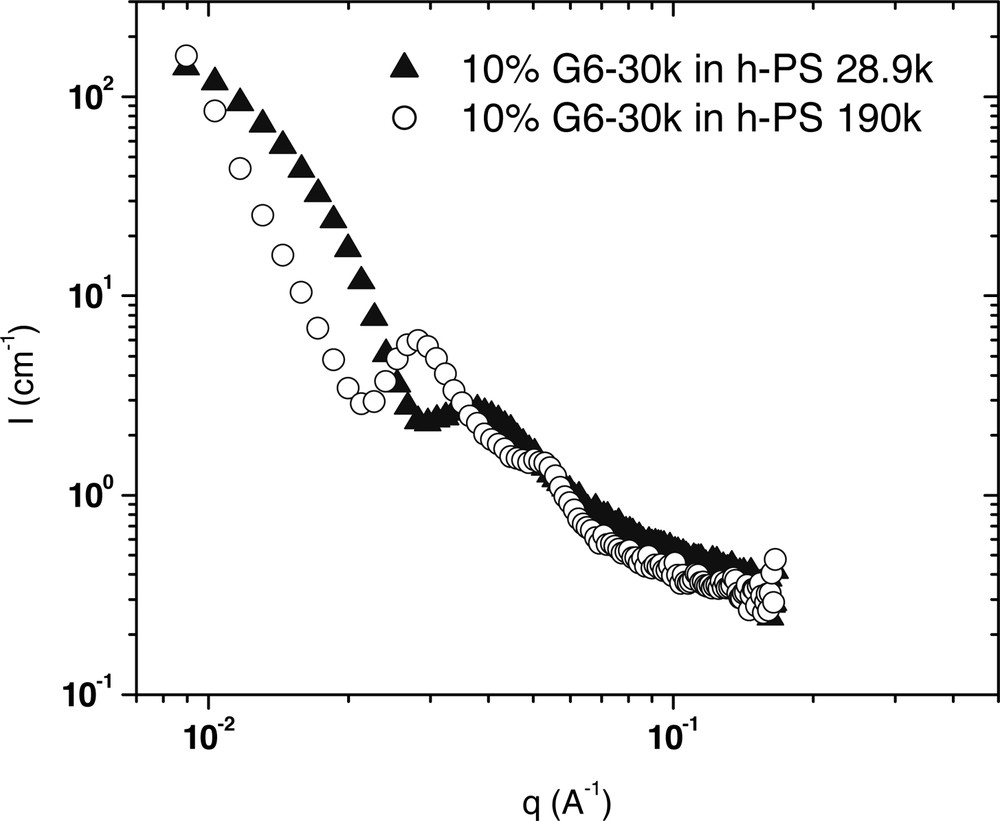
The effect of matrix molecular weight on the morphology of G6–30k at 170 °C. This data shows that when the PS molecular weight is lowered, there appears to be a transition from a lamellar to a micellar morphology.
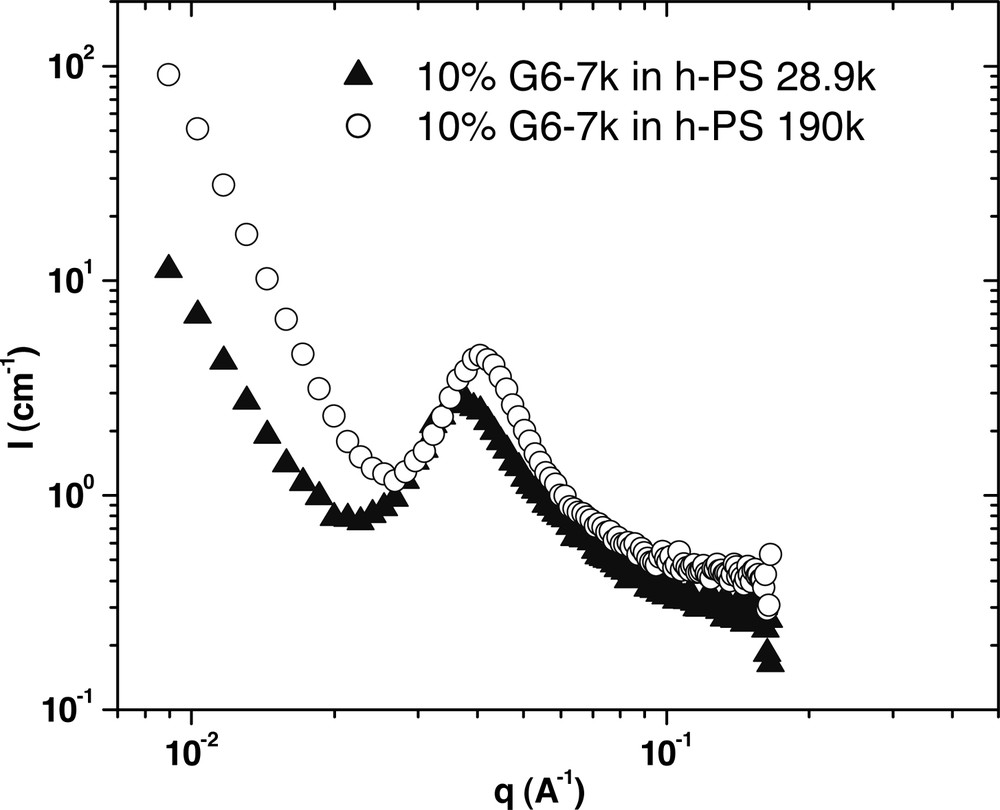
The effect of matrix molecular weight on the morphology of G6–7k at 170 °C. This data shows that when the PS molecular weight is lowered, there is no change in morphology, but the aggregated micelles are further apart on average, suggesting the matrix PS has swollen the region between micelles.
For the G6–61k sample (Fig. 9), in 190k PS the sample shows typical spherical micelle scattering. However in the lower molecular weight matrix, the amount of forward scattering is significantly less. This suggests that the micelles are not aggregating in the 28.9k PS as they are in the 190k PS. For G6–30k (Fig. 10), the lamellar scattering that is evident in 190k PS gives way to spherical scattering in 28.9k PS, with a much smaller slope at low q values. Further the q–4–dependence is no longer observed, but a low q plateau emerges. This suggests complete dispersion of micelles in the sample. For G6–7k (Fig. 11), both curves have a similar shape, meaning that no change in morphology occurs upon lowering the matrix molecular weight. However, there is a slight shift in the location of the correlation peak. In 28.9k PS, the peak occurs at a slightly lower q value, which corresponds to an increase in the average distance between micelles.
These results can all be explained by considering the solubility of the tail groups into the matrix polymer. The compatibility of polymers is known to depend on molecular weight, and polymers that are chemically identical but of very different molecular weight have been found to phase separate. By lowering the PS molecular weight to a value that is closer to that of the tail groups, the compatibility of the tails with the matrix is increased and thus, homopolymer penetration into the microphase separated block copolymer is enhanced. For G6–43k, this compatibility increase was significant enough to change the morphology from lamellar to micellar. In the case of G6–7k, there is only a limited amount of miscibility between the 7k tails and the 28.9k matrix, resulting in a slight swelling of the intermicellar distance.
4.6 Effect of temperature
All of the previous scattering results have been from the melt state at 170 °C. However, temperature is an important variable when studying phase behavior, and so measurements were taken under other conditions. Figs. 12–14 are comparisons of the scattering from 10% and 5% blends at both 170 °C and at 25 °C. The 25–°C samples are in the glassy state, but were annealed by being heating to 170 °C and allowed to cool slowly. Consequently, these samples represent the state of the blend when it was ‘frozen’ at 100 °C, the Tg of PS.
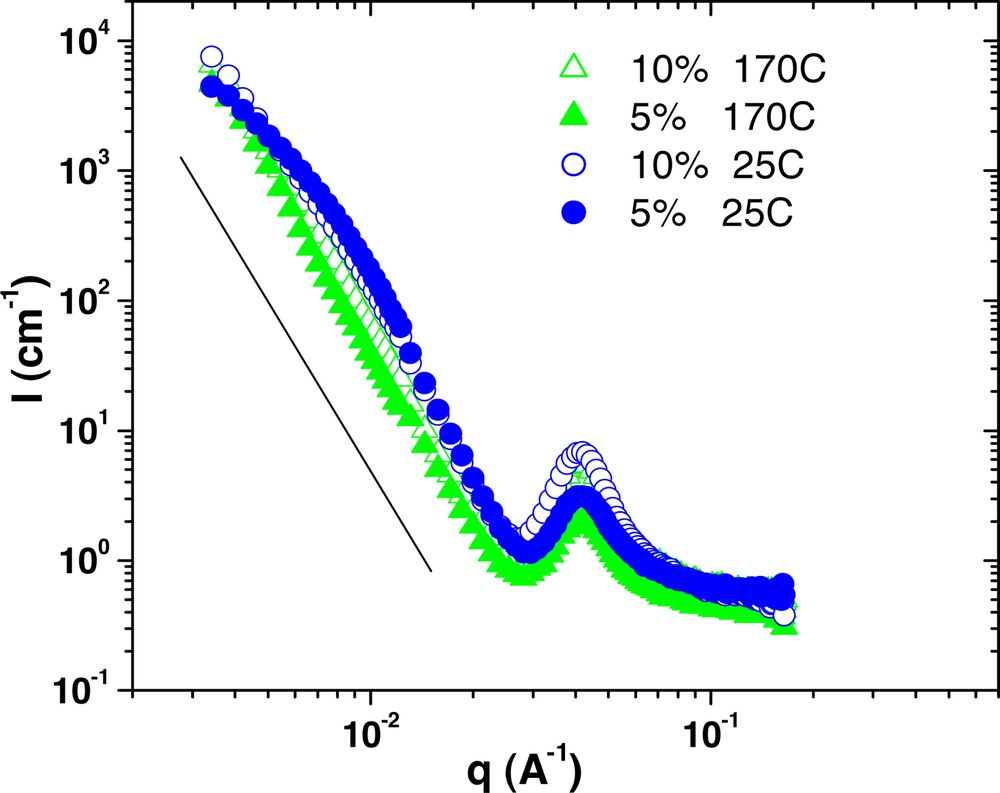
Scattering from 5% and 10% G6–7k samples in PS 190k at both 170 °C and 25 °C after annealing.
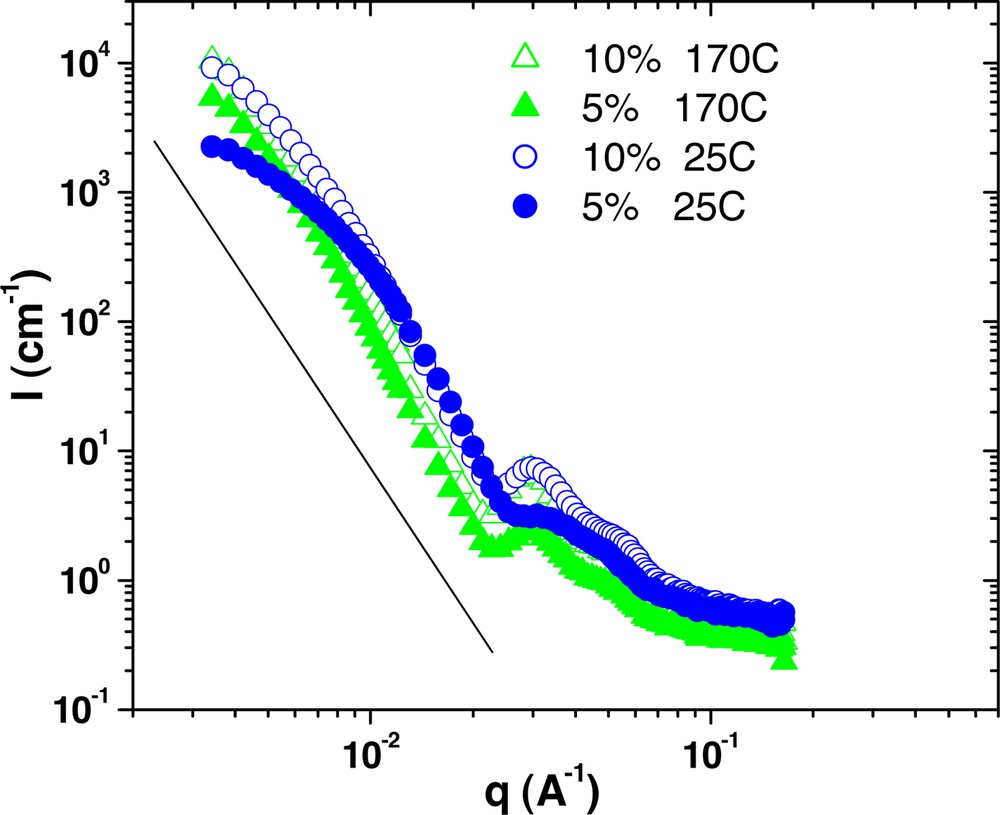
Scattering from 5% and 10% G6–30k samples in PS 190k at both 170 °C and 25 °C after annealing.
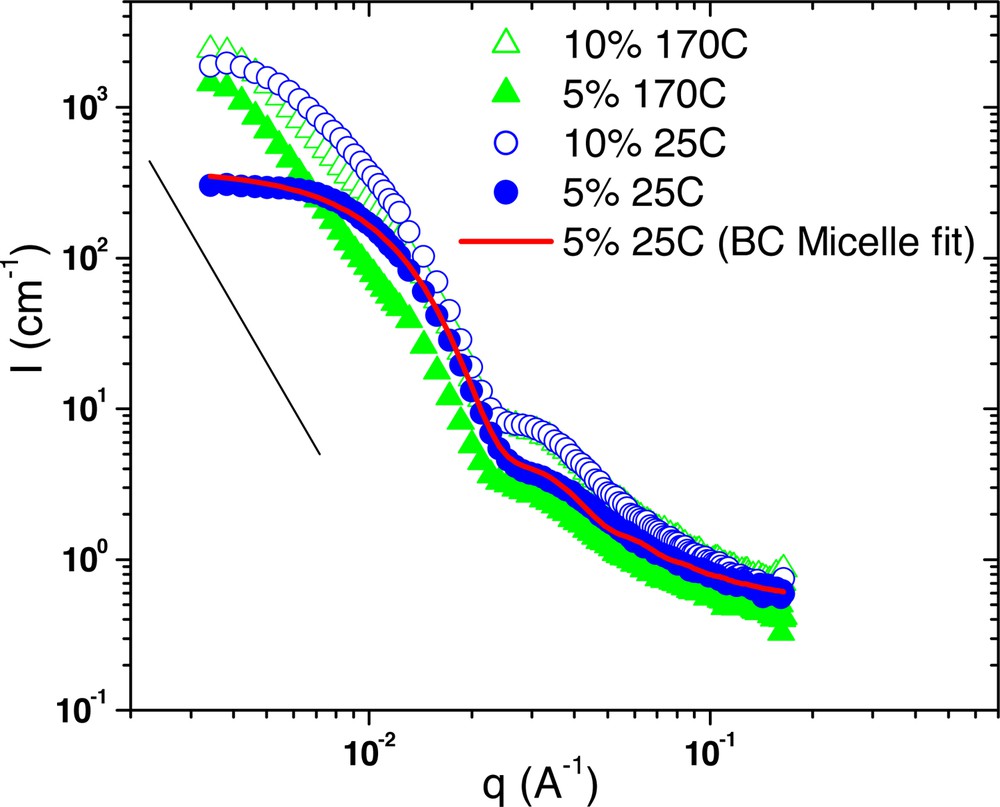
Scattering from 5% and 10% G6–61k samples in PS 190k at both 170 °C and 25 °C after annealing.
Comparing the two different temperatures reveals that the microphase-separated architecture does not change over this temperature range. The correlation peak location and the overall shape of the scattering curves are constant. However, a common feature of these plots is that the amount of forward scattering is dramatically reduced at 25 °C relative to 170 °C. So, while temperature does not change the microphase separation, it does affect the dispersion of these domains into the homopolymer matrix. This result is unusual, as morphology in typical linear block copolymer is strongly dependent on temperature, such that molecular mixing is predicted at higher temperatures.
Phase diagrams are usually put in terms of the product of the Flory χ parameter and the degree of polymerization, χ N. The χ parameter has an inverse temperature dependence and is given by:
Here, Vr is the molar volume (~100 cm3 mol–1 for many polymers), R is the gas constant (1.987 cal mol–1 K–1), and Δδ is the difference in solubility parameter between the two polymers. Systems with lower values of χ N tend to be more miscible, and consequently, increasing temperature leads to increased solubility.
According to Jeong et al. [9], the solubility parameter difference between PS and PBE is at most 0.1 (cal cm–3)1/2. The temperature range over which this system can be studied is limited by the Tg of the polymer, 100 °C, and the point at which they begin to thermally degrade, ~200 °C. Over this range, the χ parameter is approximately 1 × 10–3 to 2 × 10–3 for our system. Therefore, χ N ~ 0.7 to 1.0, which is well below the critical value for weak phase separation (~10 as given by Hamley [21]). Thus, the evidence is that the microphase separation observed in these samples is much stronger than predicted on purely enthalpic grounds. Recent theoretical calculations for structurally similar hybrid diblocks by Pickett [13] and Frischknecht and Fredrickson [12] demonstrate that branching of one block strongly shifts the phase diagram to lower concentrations in the branched block in the strong segregation limit and that the effect increases with generation number. Because of this, the complex phase behavior we observe in these hybrid diblock-linear polymer blends is suspected to be the result of an unfavorable entropic interaction between the highly branched dendritic block and the linear block. Solution viscosity measurements on these systems suggest that at the higher generation numbers, the linear PS block cannot penetrate into the dendritic block [9]. Consequently, there would be an entropic penalty to mixing, as the molecular configurations of the PS tail will be greatly restricted in the presence of the dendron block. More evidence for an entropic component to phase separation can be found in the literature for blends of comb-branched and linear polyethylenes, where a microphase separation is observed [22]. There, it was suggested that the non-Gaussian structure of the branched polymer would lead to entropically unfavorable chain distortions in the linear polymer. Therefore, these blends had a tendency to phase separate, even though the two components were chemically identical.
5 Conclusions
In these novel, dendritic-linear block copolymer homopolymer blends there exists two levels of phase separation. The first is microphase separation and occurs due to unfavorable entropic interactions between the dendritic block and the polystyrene. For molecules with linear blocks that are much larger than the dendrimer there is no phase separation. However, as the linear tail is shortened, the architecture driven entropic penalty for mixing overcomes the usual entropy of mixing. This is most evident in the case of the G5 systems: G5–62k is homogeneous, but G5–12k shows phase separation. There is also a dependence on the molecular weight of the homopolymer, as phase segregation occurs at lower concentration in the 190k PS than in the 28.9k PS. The G6 systems are all phase separated and in the bulk state show several morphologies, from cylinders to lamellae to micelles as the tail length is decreased (see summary in Fig. 15).
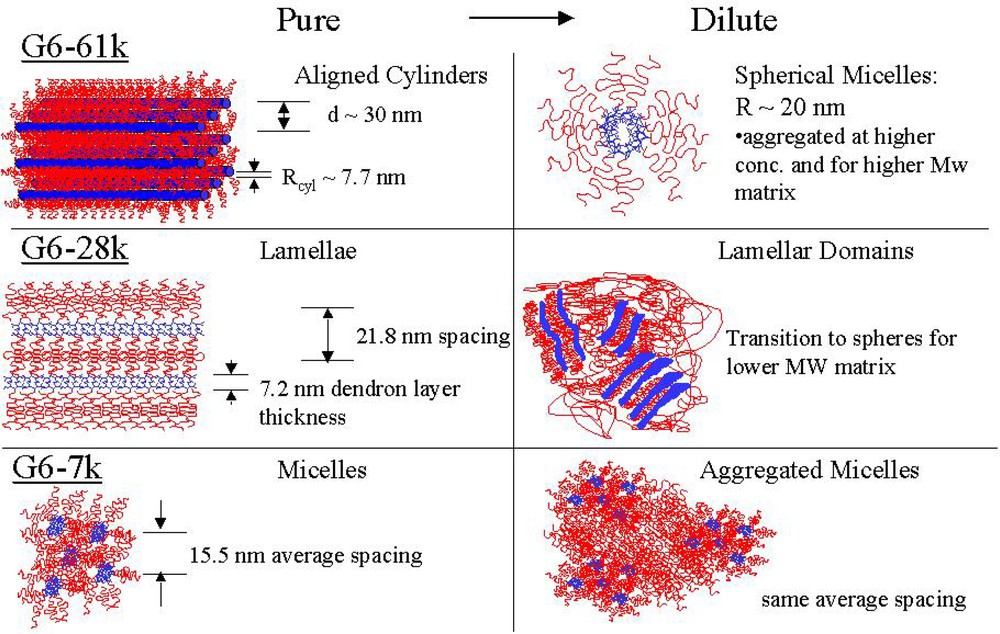
Summary of G6 series morphology.
In studying the dilution of the G6 copolymers with homopolymer, it becomes apparent that there is also a second level of mesoscale phase separation, as domains of microphase separated block copolymer. Dilution of the G6–7k micelles results in large clusters of micelles. Dilution of the G6–30k lamellae leads to a phase consisting of large lamellar domains surrounded by polystyrene. Dilution of the G6–61k cylinders leads to a phase consisting of clustered micelles.
Two parameters were found to influence this secondary phase behavior. Raising the temperature lead to increased aggregation, although the microphase microstructure was not affected. Also, lowering the matrix molecular weight was found to increase the dispersion of the domains, most likely due to increased compatibility between the matrix and tail chains.
From these results we can draw several important conclusions regarding the phase behavior and morphology of dendritic-linear block copolymers. The phase segregation seen in these systems is consistent with an entropic driving potential. This is supported by the lack of temperature dependence on the primary phase behavior as well as by the dependence on the matrix molecular weight. The enthalpic driving force for phase separation is minimal, as the PBE head groups are chemically very similar to the PS.
Acknowledgements
Robert Vestberg and Craig J. Hawker (IBM-Almaden) are gratefully acknowledged for providing the hybrid dendron-linear diblock copolymers used in this research. SANS measurements were performed at the National Institute of Standards and Technology. This material is based on activities supported by the NSF under DMR-9423101. Funding from DuPont is gratefully acknowledged by NJW and BMT, as well as insightful discussions with Dr. Young Kim of DuPont.


