1 Introduction
The reaction of olefins with aldehydes under acidic conditions has been known for years to produce the condensation of both molecules with formation of a carbon–carbon bond, in a process known as the Prins reaction [1–3]. The practical application of the classical description of this process has been nevertheless quite limited because of the requirement of strong acidic media (i.e., sulphuric acid) and high reaction temperatures, a set of conditions that seriously limits the potential selectivity of the reaction. Things have been changing in recent years due to the development of new experimental techniques using milder acid groups [4,5]. In this sense, the introduction of indium trichloride as acid catalyst [6,7] for this reaction has been a very successful contribution [8,9].
A particularly interesting example of Prins reaction induced by indium trichloride is the synthesis of derivatives of tetrahydropyran [10–13]. This process, shown schematically in Fig. 1 for unsubstituted reactants, leads to the formation of the six-membered ring of tetrahydropyran from two separate fragments. When reactants are substituted, the reaction can be highly regioselective and stereoselective. Tetrahydropyrans are relevant molecules, being present as structural features of biologically active products like polyether antibiotics and pheromones [14].
The Prins cyclisation of formaldehyde and 3-buten-1-ol assisted by indium trichloride.
Despite the growing experimental body of data on the application of the Prins reaction to the synthesis of tetrahydropyrans, little is known on the reaction mechanism. Such a knowledge would nevertheless help a better understanding of the reaction features, which could in turn lead to the eventual design of more efficient catalytic systems. It is particularly intriguing, for instance, why indium trichloride introduces such a high efficiency in this process. Computational chemistry is a well-proven tool for the calculation of reaction mechanisms [15], and it has been previously used for systems containing indium [16,17].
In this paper, we characterize computationally with a DFT-based B3LYP method the reaction mechanism of the Prins reaction induced by indium trichloride on the model system depicted in Fig. 1.
2 Computational method
All calculations were carried out using the B3LYP density functional [18–20] as implemented in the Gaussian98 package [21]. An effective core potential was used to replace the 36 innermost electrons of indium [22]. The valence double-ζ basis set associated with the pseudopotential in the program [21], with the contraction labelled as LANL2DZ, was used for this element, supplemented with a d shell [23]. The valence double-ζ 6-31G basis set was used for all other elements: hydrogen, carbon, oxygen and chlorine [24,25]. All geometry optimisations were full, with no constraints.
3 Reactants and products
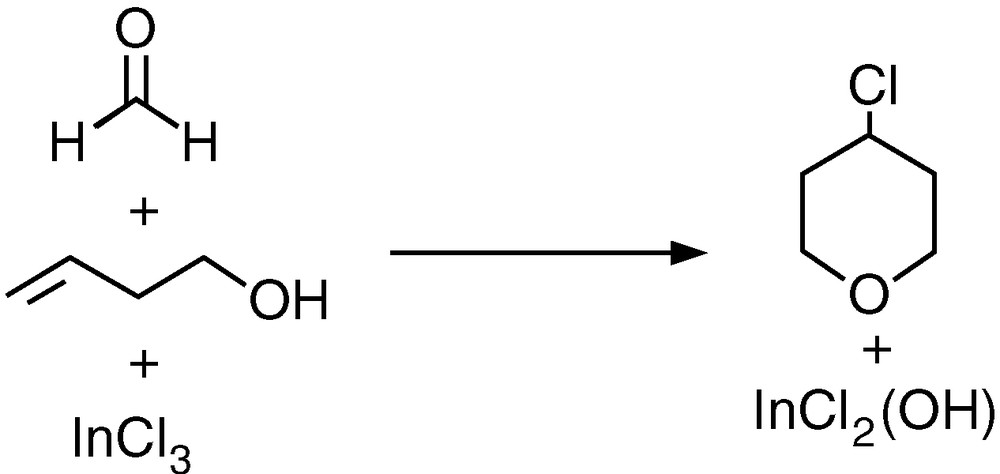
The structures of the species involved in the reaction depicted in Fig. 1 were computed with the B3LYP method. The reactants are 3-buten-1-ol (1), formaldehyde (2), and indium trichloride (3). The products are the chlorinated tetrahydropyran ring (4) and the hydroxylated indium salt (5).
The calculated geometries of the five compounds are collected in Fig. 2. They correspond to what could be expected. For the linear alcohol 1, we were able to optimise up to three different conformational minima with energies within a span of 1 kcal mol–1, separated by barriers below 3 kcal mol–1. The one presented here is the most stable, and, furthermore, it is directly connected to the efficient reaction mechanism 1. Formaldehyde 2 is planar. The two indium salts, 3 and 5, present a trigonal planar arrangement around the indium centre, the system having a high D3h symmetry in the case of indium trichloride. The computed indium–chloride distance of 2.319 Å in the trichloride species is not far from the value of 2.284 Å previously computed with a different method [26]. The six-membered ring of the tetrahydropyran product 4 is in a chair conformation, with the bulkier chlorine substituent in an equatorial position.
B3LYP-optimised structures of the reactants (1–3) and products (4–5) of the overall reaction.
The overall reaction is found to be clearly exothermic with an associated energy change of –27.6 kcal mol–1. The favourable thermodynamics are in agreement with the experimental observation of the process taking place at room temperature. Nevertheless, in order for a reaction to occur the kinetics must also be favourable. This is analysed in the next sections through the evaluation of the energy barriers of two different possible mechanisms.
4 Mechanism 1
Two possible mechanisms have been considered. This section presents the results on the first of them. This mechanism goes through three intermediates and two transition states, which are presented in Figs. 3 and 4, respectively. The section is divided in different subsections related to each of the steps of the mechanism.
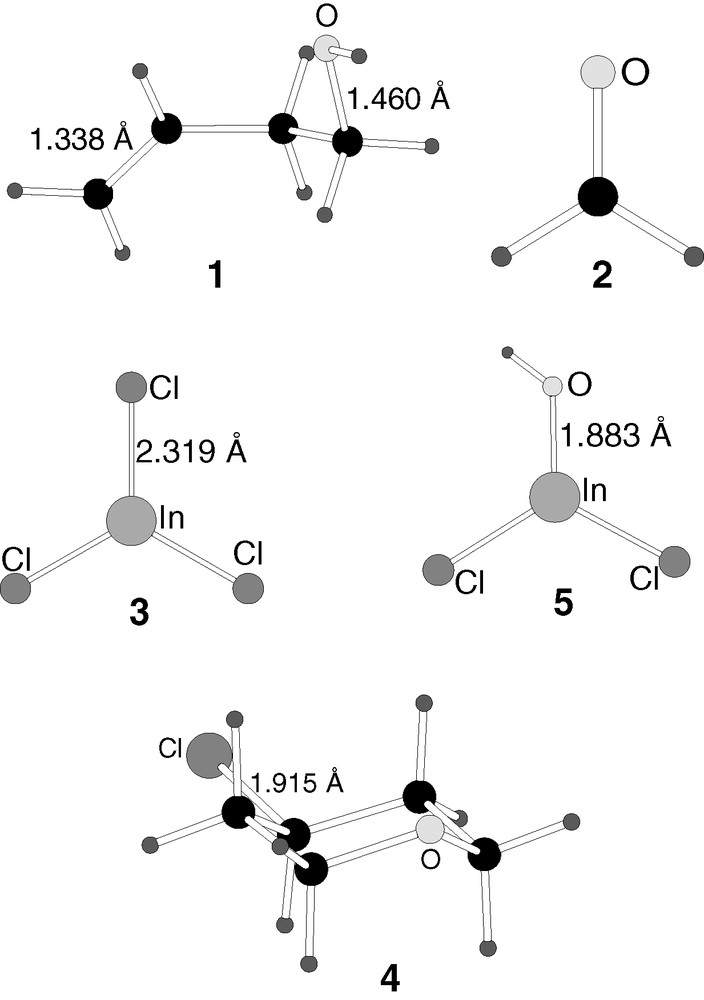
B3LYP-optimised structures of the intermediates (6–8) in reaction mechanism 1.
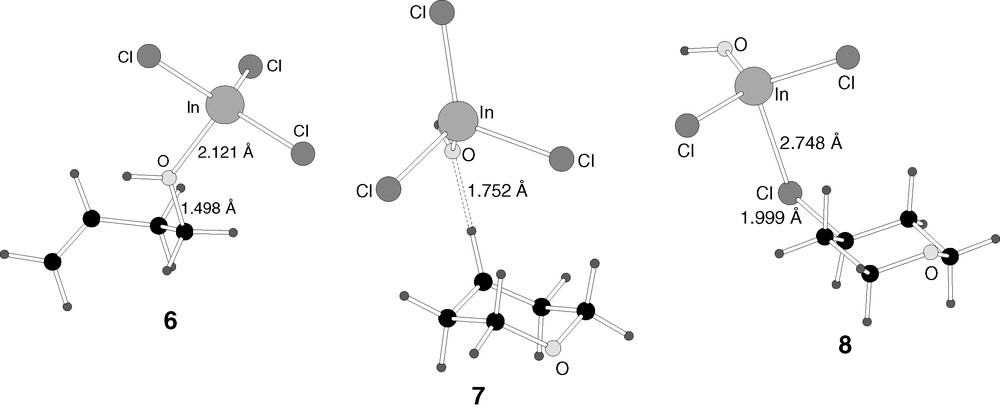
B3LYP-optimised structures of the transition states (9, 10) in reaction mechanism 1.
4.1 Coordination of indium trichloride to 3-buten-1-ol
Indium trichloride, 3, is a strong Lewis acid. The organic reactants 1 and 2 possess a number of basic centres where an acid can in principle coordinate. The most evident ones are the hydroxylic oxygen and the double bond in 1 and the oxygen atom in 2. Among all possible complexes formed by acid–base interactions, here we present only the one involved as intermediate in the reactive path of mechanism 1.
This intermediate, 6, is the result of the coordination of indium trichloride to the oxygen in the hydroxyl group of olefin 1. The distance between indium and oxygen in 6 is 2.121 Å, still significantly longer than the In–O bond distance of product 5 (1.883 Å), but clearly indicative of a strong chemical interaction. Other geometrical parameters are consistent with this interaction. The C–O distance is lengthened from that in 1 (1.498 vs 1.460 Å), and the indium trichloride fragment is pyramidalized (average Cl–In–Cl angle of 115.7°, compared to 120.0° in 3).
The energy of 6 is 37.2 kcal mol–1 below that of the reactants 1 and 3, consistent with a strong acid–base interaction. There is probably a small barrier connecting the reactants to 6, which must account for the change in the conformation of the olefin fragment from 1 to 6, but it cannot be expected to be very high, and it has not been computed.
4.2 Attack of formaldehyde and cyclisation
The approach of formaldehyde 2 to the intermediate 6 induces a number of changes which take place in a single step, and which are characterized by transition state 9, connecting 6 to a new intermediate 7.
In the reaction step represented by transition state 9, two processes are taking place simultaneously. The first of them is obvious from the inspection of its geometry in Fig. 4. An SN2 reaction takes place on the hydroxylic carbon. The oxygen atom of formaldehyde acts as entering group, and the hydroxyl is the leaving group, being transferred to indium trichloride. The O–C distance corresponding to the entering group is 1.867 Å, while that corresponding to the leaving group is 2.239 Å. The leaving hydroxyl is already practically transferred to indium, with a bond distance of 1.995 Å. A second process that is taking place in transition state 9 is the approach of the carbon of formaldehyde 2 to the terminal carbon of the olefin 1.
The second process is not so apparent from the geometry of the transition state 9, but it appears clearly when its structure is relaxed towards products. It corresponds to the formation of the chemical bond between the carbon atom of formaldehyde and the terminal carbon of the olefin. These atoms are still 3.170 Å away in transition state 9, but they are bound when this geometry is relaxed away from the reactants. It is worth noticing that both processes, departure of the hydroxyl and formation of a carbon–carbon bond, take place in a single step. This process is thus not stepwise.
Intermediate 7 is obtained from the relaxation of transition state 9. The form of the final product can be already easily recognized in it. The six-membered ring of tetrahydropyran is already present, the two new bonds being formed having distances of 1.423 Å (C–O) and 1.659 Å (C–C), although quite strained, as proved for instance by the long C–C distance. The reason for this strain is the presence of one significant difference between this fragment of the intermediate and the product, namely, the presence of a carbocationic centre in 7. The olefinic carbon in 6 that is not attacked by reactant 2 ends up connected only to three single bonds. This is the carbon that will receive the chlorine atom in the final product 4. In this intermediate 7, the three chlorine atoms are still bound to indium. Since indium has abstracted the hydroxyl group from the alcohol, now it has four ligands, with the associated tetrahedral geometry and anionic character. Intermediate 7 can be thus seen as an ionic pair, formed by a cationic organic fragment C5OH9+ and an anion centred at indium InCl3OH–. The shortest distance between both fragments is the 1.752 Å between the oxygen bound to indium and the hydrogen bound to the carbocationic centre.
The reaction step that goes from intermediate 6 to intermediate 7 through transition state 9 is slightly endothermic (8.6 kcal mol–1), and has a moderate energy barrier of 25.6 kcal mol–1. It is remarkable that intermediate 7 has an energy only 8.6 kcal mol–1 above 6, despite the presence of a carbocationic centre in the former. The role of the bulky anionic fragment centred at indium seems to be key in this stabilization. This anion is bulky enough to abstract the hydroxyl from one end of the cationic fragment while keeping a strong interaction with the other end. This is likely a key factor on the efficiency of indium trichloride in accelerating this reaction. This reaction step includes most of the bond-breaking and bond-forming processes involved in the overall reaction. The fact that its barrier is a relatively low 25.6 kcal mol–1 is very promising for the viability of this mechanism. Furthermore, this energy barrier would be likely further lowered if solvation effects were taken into account, because this step involves the formation of an ionic pair, a process disfavoured by the gas-phase conditions of the current calculations.
4.3 Transfer of the chlorine atom
The ionic pair formed in intermediate 7 reverts to a system composed by two neutral fragments, 8, through transfer of a chloride group from the anion to the cation. The transition state for this process corresponds to structure 10.
The geometry of 10 (Fig. 4) is very similar to that of 7 (Fig. 3). The only difference between them is a slight tilt of the indium trichloride that approaches one of its chlorine atoms to the carbocationic centre. The two shorter C–Cl distances in 7 are quite symmetric, 3.923 and 4.117 Å, while this symmetry is broken in transition state 8, with distances of 3.511 and 4.217 Å.
Intermediate 8 is the result of the transfer of the chloride between the two ions. Intermediate 8 can be viewed as an acid/base pair between products 4 and 5. The chlorine has already been essentially transferred to the carbocation, with the C–Cl distance being 1.999 Å and the In–Cl distance 2.748 Å. The respective distances in 4 and 5 are 1.915 and 2.319–2.337 Å, respectively. The interaction between both fragments is therefore still quite strong, but the product is already practically formed.
As for the energetics of this step, 8 is 10.4 kcal mol–1 below 7, and the energy barrier associated with 10 is only 0.1 kcal mol–1. The small barrier is fully consistent with the similarity between intermediate 7 and transition state 10, and indicates that 7 lies in a very shallow valley within the potential hypersurface.
4.4 Separation of the products
The products of the reaction 4 and 5 can be obtained directly by lengthening the distance between indium and chloride in intermediate 8. This process, which has a very low barrier at most, is endothermic in gas phase, with an energy cost of 11.4 kcal mol–1. Things may be different in this concern if solvent or entropic effects were to be introduced, but the effect on the overall validity of the mechanism would be minimal.
4.5 Energy profile for mechanism 1
Fig. 5 presents the energy profile for mechanism 1. The mechanism is quite smooth, with the higher barrier around 25 kcal mol–1, and is therefore very likely valid for this reaction taking place in mild conditions. The highest barrier corresponds to transition state 9, where most of the bond breaking/forming processes involved in the overall reaction take place. The structure of this transition state gives also a clue on why indium chloride is more efficient in this reaction than other acid catalysts. It is obvious from the structure of 9 that the bulky indium trichloride fragment is able to abstract the hydroxyl group from a carbon in one side of the organic fragment, while at the same time stabilizing through ionic interactions the carbocationic being formed at the other side of the organic fragment.
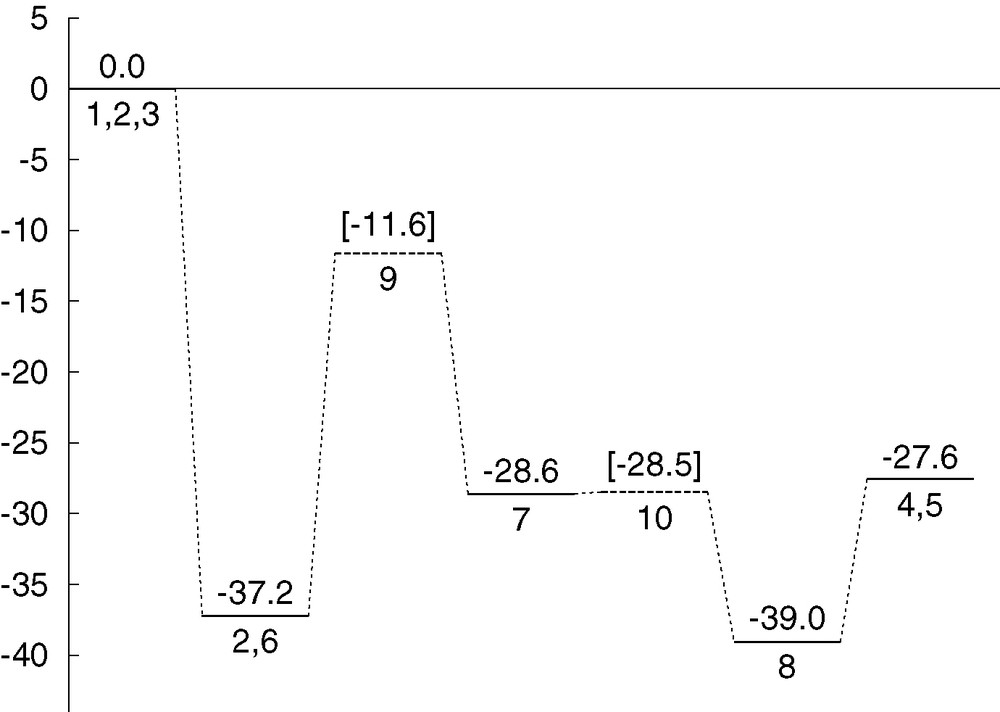
Energy profile (kcal mol–1) for reaction mechanism 1.
5 Mechanism 2
Mechanism 1, presented in the previous section, has a quite low energy barrier and is therefore a good candidate to be the correct one. Nevertheless, others mechanisms can be imagined, and in this section we present one of them. This new mechanism goes through four intermediates and four transition states, which are presented in Figs. 6 and 7, respectively. Mechanism 2, albeit reasonable in principle, has a prohibitively high energy barrier, and because of this, it will be discussed in less detail than mechanism 1. In particular, most steps will be discussed together in one single subsection, while another subsection will be essentially devoted to the high barrier step.
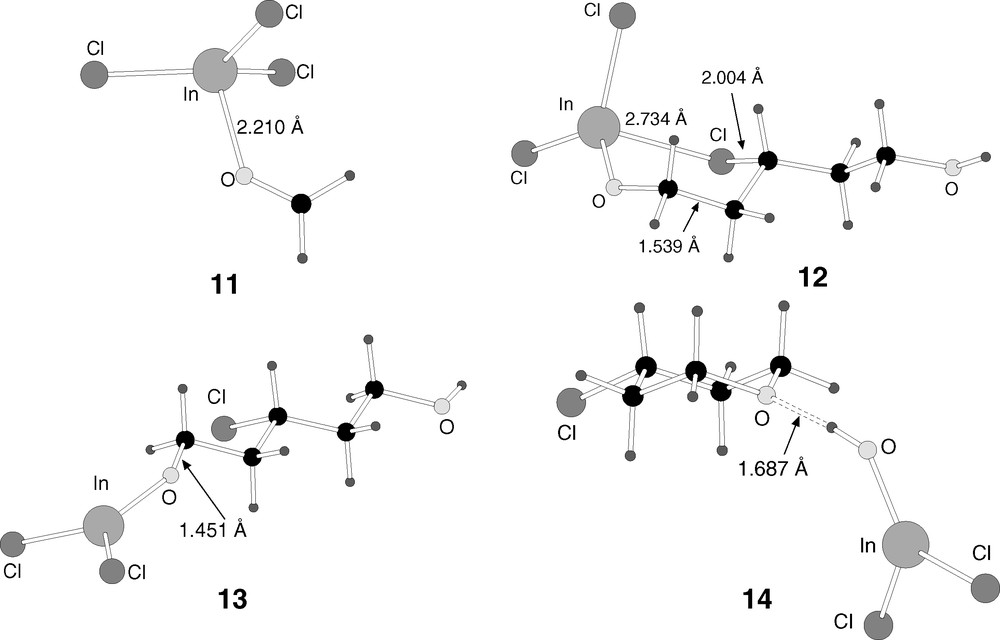
B3LYP-optimised structures of the intermediates 11–14 in reaction mechanism 2.
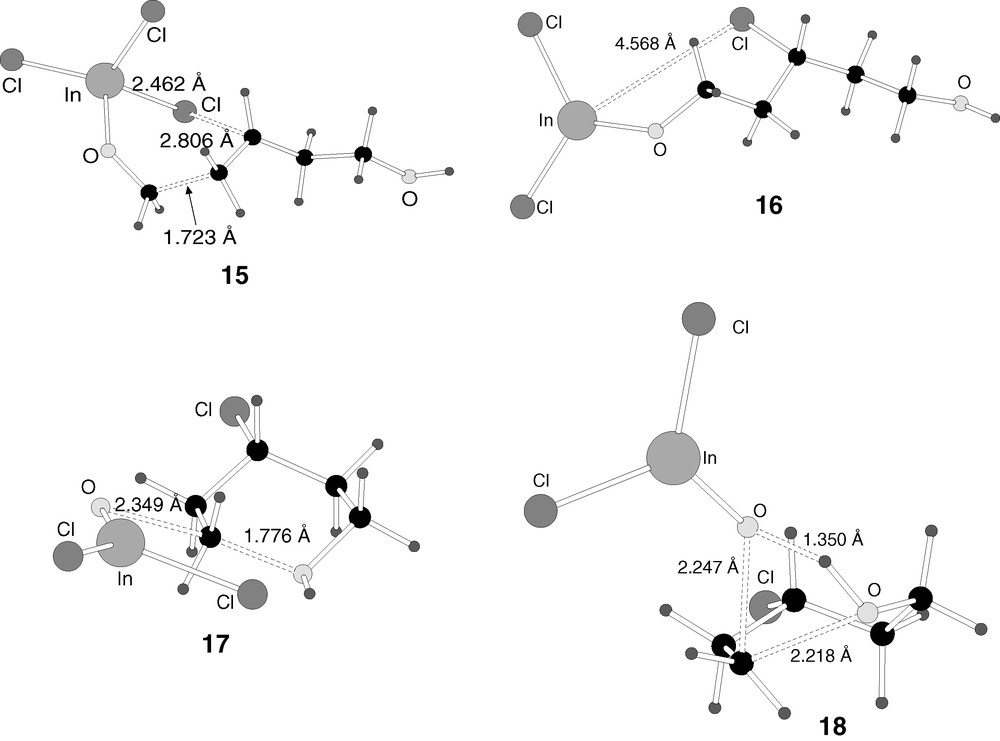
B3LYP-optimised structures of the transition states 15–18 in reaction mechanism 2.
Other mechanisms could be imagined. For instance indium trichloride could attack the third basic centre in the system, namely the double bond of 3-buten-1-ol 1. However, this possibility has not been further explored because it is not obvious how a reactive path leading to the overall Prins reaction could be started from this point.
5.1 Formation of linear intermediate 13
Reaction mechanism 2 starts with the coordination of the oxygen atom of formaldehyde 2 to indium trichloride 3. This produces intermediate 11, which is 25.3 kcal mol–1 below the reactants. This is different from mechanism 1, where the Lewis acid was initially coordinated to olefin 1, though the energetics of this initial step are similar.
Adduct 11 then attacks the double bond of olefin 1. The reaction is formally an addition, with the carbon of formaldehyde attacking the terminal carbon of the olefin, and one of the chloride ligands of indium attacking the other carbon of the olefin. This produces intermediate 12. This intermediate can be seen as containing a six-membered ring, although the chlorine atom is closer to carbon (2.004 Å) than to indium (2.734 Å). The new carbon–carbon bond is completely formed (1.539 Å). The reaction from 11 to 12 is slightly exothermic (–5.2 kcal mol–1), and the barrier through transition state 15 (Fig. 7) is quite low (5.2 kcal mol–1).
The reaction advances by breaking the six-membered ring in intermediate 12, leading to the formation of intermediate 13. In this intermediate, the indium–chlorine distance is 5.959 Å, and the strong interaction between both atoms in the previous intermediate (12) is thus completely broken. The reaction from 12 to 13 is slightly endothermic (5.9 kcal mol–1), and the energy barrier, through transition state 16 (Fig. 7) is only 9.7 kcal mol–1.
Intermediate 13 is thus reached quite easily from the reactants, with the highest barrier to its formation being the 9.7 kcal mol–1 of the last step. Its geometry, shown in Fig. 6, is linear, with (InCl2)O and OH in the terminal positions of a disubstituted chloropentane. It contains already some of the features of the product, namely the new carbon–carbon and chlorine–carbon bonds. In fact, the only main feature missing is the closure of the six-membered ring through formation of a carbon–oxygen bond, and the subsequent release of InCl2OH. This step will be analysed in the next subsection.
5.2 From linear intermediate 13 to the products
The logical evolution of intermediate 13 towards products is the formation of intermediate 14 (Fig. 6). In 14, the six-membered ring of tetrahydropyran is closed, and the structure of reaction products 4 and 5 is clearly recognizable. 4 and 5 are simply connected through a hydrogen bond in structure 14 with an oxygen–hydrogen distance of 1.687 Å.
The energy of intermediate 14 is fully consistent with a smooth profile. It is 13.7 kcal mol–1 below intermediate 13, and 10.8 kcal mol–1 below reaction products 4 + 5. The step from 14 to products is furthermore straightforward, consisting of the simple separation between the two products, with an expected very low energy barrier, if any. Things are however very different for the conversion of 13 into 14. We were able to characterize two different transition states connecting these two intermediates. They are 17 and 18. Both of them are presented in Fig. 7, and both of them have very high energies of 53.0 and 54.3 kcal mol–1 over 13, respectively.
Structure 17 can be seen as the transition state corresponding to an SN2 reaction taking place at the carbon making a bond to oxygen. The terminal alcohol group acts as entering group, and InOCl2– acts as leaving group. The O–C–O angle around the centre is 150.6º, smaller than the 180º expected from an ideal SN2 transition state. This distortion is probably associated with the attractive interaction between one of the chloride ligands of indium and the hydroxylic oxygen. However, the chlorine–hydrogen distance is still large, 2.416 Å. This is probably another of the reasons why this structure has such a high energy, the indium fragment is not large enough to stabilize simultaneously the partial positive charges located at both sides of the SN2 carbon.
In view of the high energy of 17, 53.0 kcal mol–1 above 13, an alternative mechanism was sought for this particular step. This produced the optimisation of a second transition state, 18, also presented in Fig. 7. The idea was to solve the problem of the Lewis acid not being able to stabilize the charges at carbon and oxygen centres by changing its relative position. In transition state 18, the oxygen bound to indium has relatively short distances to both the cationic carbon and the hydroxylic hydrogen, with values of 2.247 Å and 1.350 Å. The resulting structure has however an even higher energy of 54.3 kcal mol–1 above intermediate 13. This is because, with this arrangement, the reaction taking place at the carbon making the bond is a very uncommon type of SN2 process, with both the entering and the leaving group on the same side. The cost of this unusual arrangement overtakes whatever energy gains are obtained through stabilization of the hydroxyl group. Therefore, the barrier for the conversion from 13 to 14 remains prohibitively high, with a value above 50 kcal mol–1.
5.3 Energy profile for mechanism 2
Fig. 8 collects the energetics presented throughout this section for mechanism 2. The reaction proceeds smoothly until intermediate 13, but then it finds a high barrier above 50 kcal mol–1 that precludes the process from moving further towards products. This mechanism cannot explain the facility of the experimental reaction. Furthermore, it cannot in any way compete with mechanism 1, and because of this, mechanism 2 has to be discarded.
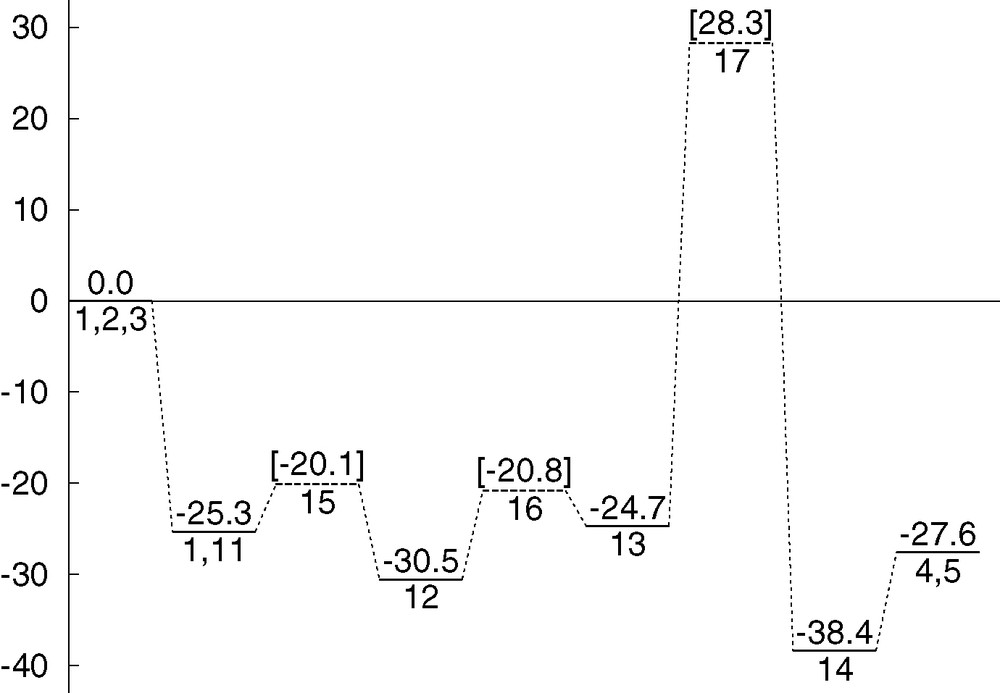
Energy profile (kcal mol–1) for reaction mechanism 2.
The lack of efficiency of mechanism 2 can in fact be related with the need for strong acidic media and high reaction temperatures for the Prins reaction to take place in the absence of indium trichloride or similar Lewis acids [1–3]. In mechanism 2, the role of indium trichloride is quite simple, and there is no apparent reason why it could not be replaced by a more conventional acid group, like hydronium H3O+ or a simple proton H+. Because of this, the high barrier associated with this mechanism can be viewed as further confirmation of the good reproduction of experimental data by the current calculations.
6 Free energies vs potential energies
The energies presented above are in all cases potential energies, corresponding to the internal energy that the systems would have in gas phase at a temperature of zero degrees Kelvin, and without zero-point energy contributions. This is the energy parameter used in geometry optimisations, and, for the mechanistic comparison presented in this article, it is sufficiently accurate. In any case, within the field of computational chemistry, there are other energy values that can be computed. One of them is the Gibbs free energy, related to the corresponding thermodynamical magnitude. Its calculation is based on a series of assumptions on ideal gas behaviour of the molecules, but it has the quality of introducing the effect of temperature and entropy, being thus closer to experimental measurements.
The free energies corresponding to the different systems involved in the profile for mechanism 1, with potential energies shown in Fig. 5, are 0.0, –26.3, 12.0, –0.7, 0.1, –11.2 and –10.0 kcal mol–1, respectively. The corresponding values for mechanism 2 (potential energies in Fig. 8) are 0.0, –13.8, 7.2, –1.6, 7.7, 2.6, 58.5, –9.1 and –10.0 kcal mol–1. The main differences between the values of free energies and potential energies are in all cases associated with the number of fragments involved in the calculation. Free energies, including entropic effects, systematically stabilize the systems with more fragments because of the increase in the number of degrees of freedom. This stabilization can be quite important, in the range of 10 kcal mol–1l, but it is likely to be rather artificial, because these effects would be much reduced if the presence of a solvent was taken into account. More importantly to the topic of the paper, the overall comparison of the two energy profiles remains unchanged. Mechanism 1 has an affordable free energy barrier, while this value is much higher in the case of mechanism 2.
7 Concluding remarks
The computational study with the B3LYP method of the Prins reaction in the model system constituted by 3-buten-1-ol, formaldehyde and indium trichloride leads to the proposal of a reaction mechanism for this process. This mechanism starts with the coordination of indium trichloride to the hydroxyl group of the olefin, which is followed by the attack of formaldehyde on this adduct. This attack leads to the formation of a ionic pair where one of the fragments contains already the six-membered ring characteristic of tetrahydropyran. The formation of this ring is the limiting step of the overall mechanism, with a barrier of 25.6 kcal mol–1. Afterwards, a chloride group is transferred between the two members of the ionic pair, and the products are obtained. All relevant intermediates and transition states in this mechanism have been computed, resulting in a smooth energy profile consistent with the feasibility of the reaction under mild conditions.
The specific efficiency of indium trichloride for this reaction seems related to the fact that, due to its relatively large size, in the critical transition state, indium forms an anion able to stabilize simultaneously partial positive charges existing in different regions of the organic molecule. This particular effect cannot be achieved by mineral acids, which require much more demanding reaction conditions, both in terms of concentration and of temperature, as pointed out by experimental data.
An alternative mechanism was computed, where indium trichloride played a more conventional role as acid, and the barrier was found to be higher than 50 kcal mol–1, indicative of a forbidden reaction under mild conditions. This further confirms the validity of the mechanism indicated above and of the qualitative explanation of the specific role of indium trichloride in this reaction.


