1 Introduction
Group-IV metallocenes can be considered as the quintessential single-site early transition metal olefin polymerization catalysts. This type of catalysts was developed more than 20 years ago when Andersen et al. [1b] Ewen [1c] and Brintzinger et al. [1a–d] demonstrated that derivatives of the generic zirconocene compound Cp2ZrMe2 could be activated by Lewis acids (A) to polymerize olefins. In the activation process A will abstract a methide group from Cp2ZrMe2 to produce the ion-pair [Cp2ZrMe]+[AMe]–. Jordan [1e] and others [1c] have further established that the cation Cp2ZrMe+ is the active species in the polymerization process and that the propagation proceeds [1c] according to the Cossée [1f] and Arlman [1e] mechanism, see Fig. 1. Following the pioneering work by Marks [1h], attempts have also been made to establish the possible influence of the anion AMe– on the polymerization process. However, the role of the anion is still the subject of intense scrutiny.

Mechanism for olefin polymerization by the bare cation [Cp2ZrMe+].
Theoretical studies on the insertion process catalyzed by coordinatively unsaturated bare cations such as Cp2ZrMe+ (Fig. 1) have been pioneered by Jolly and Marynick [2b], Morokuma [2b], Rappé [2c] and others [2d–f], with the result that there by now is a good understanding of this process for different central d0-metals and ancillary ligands [2d–e]. On the other hand, studies of the insertion process with the anion included [2–4] are just beginning to emerge with the work of Lanza et al. [4a], Fusco et al. [4b], Nifant'ev et al. [4f], Chan et al. [4d] and others [4]. We shall in the current account follow previous investigations by Nifant'ev et al. [4f] and Chan [4d] in a study of the insertion by ethylene into the zirconium–alkyl bond of [Cp2ZrR+][B(C6F5)3Me–] with R = CH3, C3H7, Fig. 2. The Lewis acid A = B(C6F5)3 was chosen here since it often is used as an activator in olefin polymerization, catalyzed by group-IV metallocenes.
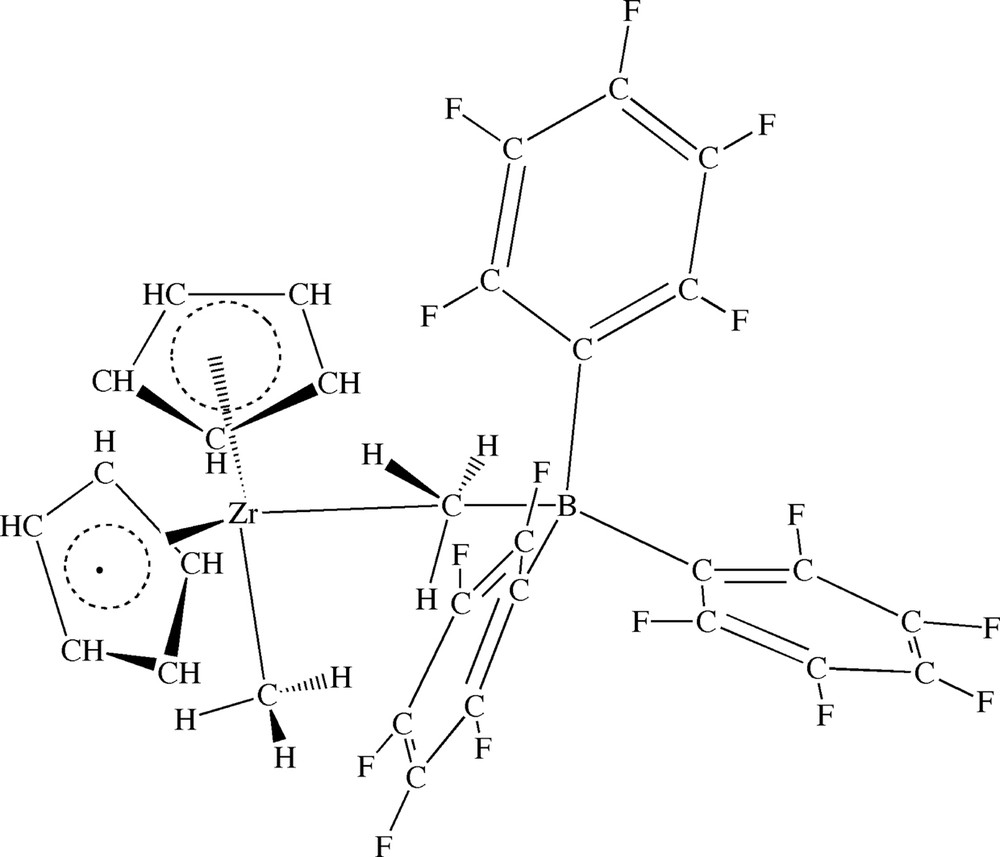
Molecular structure of ion-pair [ZrCp2Me+][Me–B(C6F5)3–].
The current investigation will begin with a study of ethylene insertion into the zirconium–methyl bond with and without the [B(C6F5)3Me]– counterion present. This part models the first initial step in the polymerization of ethylene. In the presence of the anion, olefin will have to enter cis to the methyl group for insertion to occur and a CMe–Colefin bond to be formed, Fig. 3. This can be accomplished in an approach where ethylene enters[4f] either opposite (trans) or cis to [B(C6F5)3Me–], Fig. 3. We shall in the following discuss both pathways. The next part will be concerned with the insertion of ethylene into a zirconium–propyl bond as a model for the second and subsequent insertion steps. This insertion process is more complex than the initiation path since the growing chain can adopt different orientations with or without one or more hydrogens forming agostic bonds to the metal center. The final part deals with termination of polymer growths. This process can take place by a number of different pathways [5]. We have found in previous studies [5] that the transfer of a hydride from the β-carbon of the growing chain to one of the carbons of the incoming ethylene is the most facile termination mechanism for the bare cation in which the influence of the B(C6F5)3Me– is neglected. We shall here study how this process is influenced by the presence of B(C6F5)3Me–. Nifant'ev et al. [4f] has previously carried out a pioneering and extensive study on [Cp2ZrR+][B(C6F5)3Me–] in which they represented the growing chain R by an ethyl group and neglected solvent effects. However, it will be shown in this study that solvation effects are important. Also, studies have shown [2g] that ethyl is a poor model for the polymer chain, especially in the description of the agostic interaction between chain and metal center. Nevertheless, as we shall see, a number of key findings obtained by Nifant'ev et al. [4f] are confirmed by the current study. The current study is part of a larger attempt [6] in our group to understand the role of the anion in polymerization carried out by cationic group-IV catalysts.
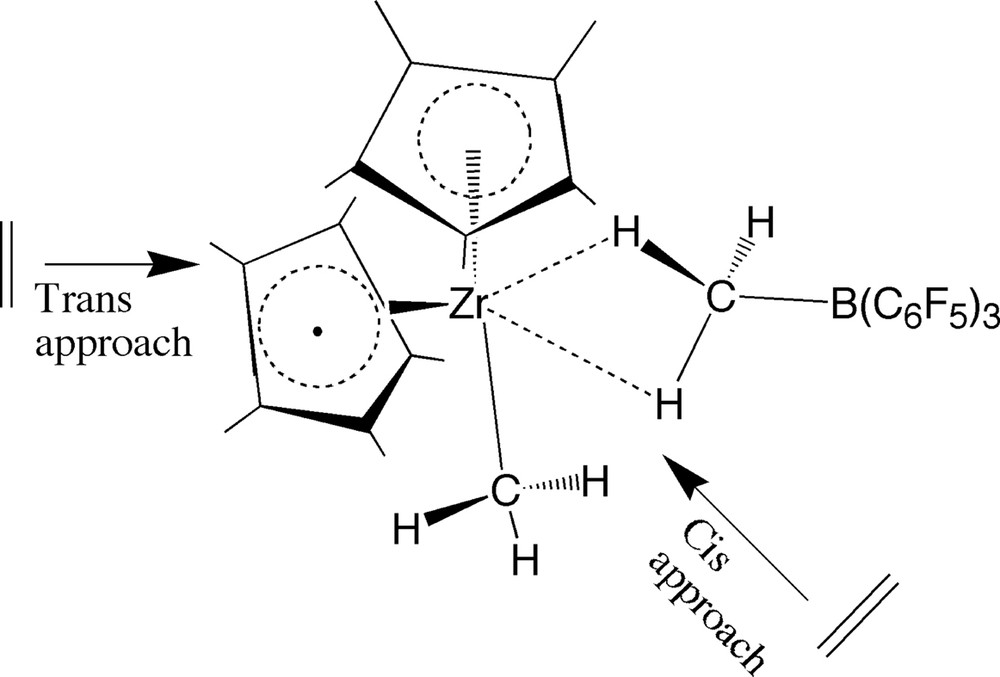
Cis- and trans-approach of ethylene to ion-pair [ZrCp2Me+][Me–B(C6F5)3–].
2 Computational details
The density functional theory calculations were carried out using the Amsterdam density functional (ADF) program version 2000.01, developed by Baerends et al. [7] and vectorized by Ravenek [7c]. The numerical integration scheme applied was developed by te Velde and Baerends [8] and the geometry optimization procedure was based on the method of Verslius and Ziegler [9]. Geometry optimizations were carried out using the local exchange-correlation potential of Vosko et al. [10] without any symmetry constraints. The electronic configurations of the atoms were described by a triple-ζ basis set on zirconium for 4s, 4p, 4d and 5s, augmented with a single 5p polarization function. Double-ζ STO basis sets were used for carbon (2s, 2p), hydrogen (1s) and boron (2s, 2p) and chlorine(3s, 3p), augmented with a single 3d polarization function except for hydrogen where a 2p polarization function was used. Shells of lower energy were treated by the frozen core approximation. A set of auxiliary s, p, d, f and g STO functions centered on all nuclei was used to fit the molecular density and represent Coulomb and exchange potentials accurately in each SCF cycle [11]. The gas-phase energy difference was calculated by augmenting the local density approximation energy with Perdew and Wang's non-local correlation and exchange corrections (PWB91) [12]. The solvation energies based on gas-phase geometries were calculated by the conductor-like screening model (COSMO) [13] with a dielectric constant of 2.023 to represent cyclohexane as the solvent. The radii used for the atoms in Å were as follows: 2.0 (C), 1.16 (H), B 1.15 (B), 1.2 (F), 2.4 (Zr), 2.1 (Cl). Only the electrostatic contribution [13] to the solvation energy was calculated in order to evaluate the enthalpy of the reactions considered in this work. The enthalpies (ΔH) reported in the following sections are potential energy differences without zero point corrections or vibrational finite temperature corrections. Such corrections are still too expensive to calculate for the size of molecules considered here. We expect these corrections to be of the order of ± 2–3 kcal/mol [4f]. The insertion barriers were obtained from linear transit calculations with the distance between one olefin carbon and the alpha-carbon of the growing chain as the reaction coordinate. The barriers for the termination by hydride transfer were obtained from linear transit calculations where the difference between the Colefin–H distance and the Cβ–H distance involving the migrating hydride was taken as the reaction coordinate. The B(C6F5)3CH3– anion was represented by a well tested QM/MM model [14,6] where the quantum mechanical (QM) part was represented by BCl3CH3–, whereas the C6F5 groups were modeled by molecular mechanics (MM) using the SYBYL/TRIPOS 5.2 force field constants [15a]. The remaining parts of the systems discussed here were all treated by quantum mechanical DFT calculations. The code for QM/MM in ADF has been implemented by Woo et al. [15b]. The electrostatic part of the solvation energy for the species discussed here was determined from full QM calculations based on QM/MM geometries.
3 Results and discussion
3.1 The first insertion
We shall first consider the insertion into the zirconium–methyl bond as a model for the initial propagation step. The energy profiles presented in the following are all with respect to changes in the (electronic) enthalpy. However one can obtain a rough estimate of the corresponding free energy profiles by adding 8–10 kcal/mol to all the enthalpies given relative to free ethylene and the ion-pair (bare cation) [4f]. This correction corresponds to the entropic contribution to the free energy change due to ethylene complexation [4f].
3.1.1 The first insertion in the presence of B(C6F5)3CH3–
The cis-approach. In the cis-approach of Fig. 3 ethylene enters the crowded space between the counterion B(C6F5)3CH3– and the methyl group. The energy profile for the cis-attack is displayed in Fig. 4. The profile gives energies in solution (cyclohexane) as well as in the gas-phase (numbers in parentheses). We shall only discuss the solution data in details.
Energy profile for insertion of ethylene into the Zr–Me bond of [ZrCp2Me+][Me–B(C6F5)3–] by cis-approach of ethylene. Energy in kcal/mol.
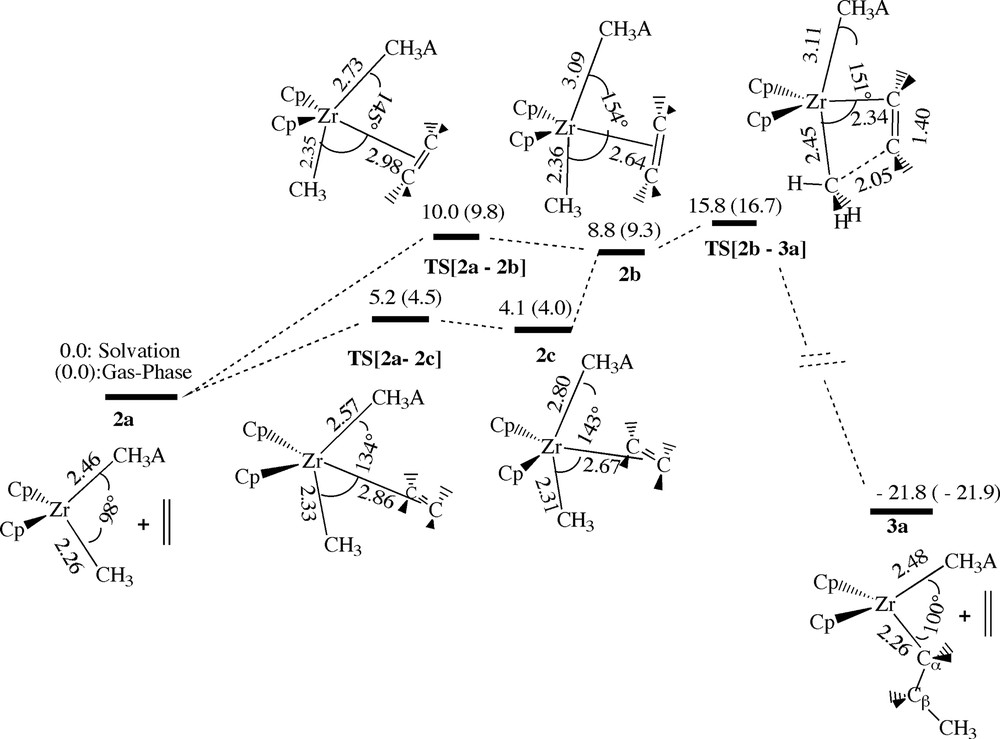
One cis-path (2a → 2b of Fig. 4) has the ethylene C=C double bond in the CH3–Zr–CH3A– coordination plane. This approach leads to the π-complex 2b with an endothermic complexation energy of 8.8 kcal/mol and an uptake barrier associated with the transition state TS[2a–2b] of 10 kcal/mol. As ethylene proceeds towards the zirconium center in the cis-path 2a → 2b, the CH3–Zr–CH3A– angle opens up from 98° in 2a to 145° in TS[2a–2b] and 154° in 2b. The opening of the CH3–Zr–CH3A– angle towards 180° forces the CH3 and CH3A– ligands to compete for the same acceptor orbitals with the consequence that their bonds to zirconium are weakened. Thus, the Zr–CH3A– bond is elongated from 2.46 Å in 2a to 2.73 Å in TS[2a–2b] and 3.09 Å in 2b, whereas the Zr–CH3 distance increases from 2.26 Å in 2a to 2.36 Å in 2b. The geometrical changes mention above in conjunction with the steric interaction between ethylene and the ion-pair [Cp2ZrMe]+ [B(C6F5)3Me]–, 2a, all contributes to the endothermic ethylene uptake energy. The only stabilizing factor is the bonding interaction between zirconium and ethylene.
The ethylene monomer of the ‘in-plane’ π-complex 2b can readily insert into the Zr–CH3 bond. The internal barrier for this process (2b → 3a) is 7.0 kcal/mol corresponding to an energy of 15.8 kcal/mol for the transition state TS[2b–3a]. In TS[2b–3a] the Zr–CH3 bond is weakened further to a distance of R(Zr–CH3) = 2.45 Å as the local methyl C3-axis is rotated from pointing towards zirconium to pointing in the direction of one of the ethylene carbons. At the same time the ethylene unit slides so as to form one short (2.34 Å) Zr–C bond and one emerging C–C bond (2.05 Å). The kinetic product from the insertion process is the ion-pair [Cp2ZrPr]+ [B(C6F5)3Me]–, 3a, with an energy of –21.8 kcal/mol. It is interesting to note that the ion-pair has completely recombined in 3a with a R(Zr-μ-Me)) distance of 2.48 Å that is similar to the value of 2.46 Å for 2a. Thus, in the second insertion ethylene will again have to displace the anion. It is worth to mention that the propyl chain in 3a is oriented in such a way that the dihedral angle Cμ–Zr–Cα–Cβ is nearly 180°.
An alternative cis-approach has the ethylene C=C double bond perpendicular to the CH3–Zr–CH3A– coordination plane, so as to minimize the steric interaction between ethylene and the CH3A– anion. This approach leads to the ‘perpendicular’ ethylene π-complex 2c of Fig. 4 with an endothermic complexation energy of 4.1 kcal/mol. The complexation or uptake process (2a → 2c) is associated with a barrier of 5.2 kcal/mol, TS[2a–2c] of Fig. 4. The perpendicular approach distorts the [Cp2ZrMe]+ [B(C6F5)3Me]– ion-pair in the same way as the ‘in-plane’ ethylene attack, but to a lesser extend due to the smaller steric interaction between ethylene and the ion-pair. The complexation energy and uptake barrier is as a consequence less endothermic in this approach. Insertion is not possible from 2c without rotation of the ‘perpendicular’ ethylene monomer into the CH3–Zr–CH3A– coordination plane. Such a rotation has a barrier of 0.3 kcal/mol and leads to the ‘in-plane’ ethylene π-complex 2b from which insertion can proceed readily as discussed above.
We shall finally note that gas-phase and solution energies are quite similar. The largest differences are for species with a substantial charge separation such as TS[2b–3a] where the gas-phase energies as expected are higher. However the difference is not more than 1 kcal/mol for a non-polar solvent such as cyclohexane.
3.1.2 The trans-approach for the first insertion in the presence of B(C6F5)3CH3–
For the trans mechanism (Fig. 3) ethylene can approach the metal center with the C=C bond in the CH3–Zr–CH3A– coordination plane, Fig. 5. This path leads directly to the insertion transition state TS[2a–3b] without any uptake barrier or π-complex formation, Fig. 5. In the course of the approach CH3A– is displaced to a R(Zr-μ-Me) distance of 3.08 Å and the total insertion barrier is 13.0 kcal/mol in solution compared to 14.3 kcal/mol in gas-phase. The geometry of the transition state TS[2a–3b] resembles to some degree that of a typical SN2 type reaction with the incoming (C2H4) and leaving (CH3A–) nucleophiles in the axial positions and the two Cp-centroids and the methyl–carbon in the equatorial positions. One notice in addition as for TS[2b–3a] the four center pattern for the insertion transition state TS[2a–3b]. However, the emerging C–C and Zr–C bonds are seen to be longer in the trans attack. One might also imagine an approach in which the ethylene C=C double bond is perpendicular to the CH3–Zr–CH3A– coordination plane. However, as the ethylene approach the zirconium center the C=C double bond invariably rotates down into the CH3–Zr–CH3A– coordination plane. Thus, we were unable to locate a ‘perpendicular’ π-complex for the trans case.

Energy profile for insertion of ethylene into the Zr–Me bond of [ZrCp2Me+][Me–B(C6F5)3–] by trans-approach of ethylene. Energy in kcal/mol.
The kinetic insertion product for the trans-approach is a new ion-pair [Cp2ZrPr]+ [B(C6F5)3Me]–, 3b, with an anion that has reattached itself to the metal center at a R(Zr-μ-Me) distance of 2.46 Å. The ion-pair 3b differ slightly from the cis product 3a in that the dihedral angle Cμ–Zr–Cα–Cβ is nearly 60° rather then 180°. Further on, 3b has an energy of –21.9 kcal/mol which is lower than 3a by 0.1 kcal/mol. We shall discuss the structures of 3a and 3b in more details in a later section.
3.1.3 A comparison of the insertion pathways with and without the anion B(C6F5)3CH3–
Insertion of ethylene into the zirconium methyl bond of the bare cationic species Cp2ZrMe+ (2A) has already been studied extensively [2]. The uptake (2A → 2B) of ethylene to produce the π-complex 2B is exothermic by –17.4 kcal/mol and proceeds without any barrier, Fig. 6. From 2B ethylene can insert with a modest internal barrier of 0.8 kcal/mol via the transition state TS[2B–3A] (–16.6 kcal/mol) to produce the propyl species Cp2ZrPr+ , 3A, at an energy of –28.1 kcal/mol.

Energy profile for the insertion of ethylene into the Zr–Me bond of [ZrCp2Me+]. Energy in kcal/mol.
The energy profile for the insertion process of the bare cation 2A (Fig. 6) differ considerably from that of the ion-pair 2a (Figs. 4 and 5). In the latter case the uptake is endothermic since ethylene has to compete with the anion for coordination space. As a consequence, compared to 2B ethylene is not as tightly bound and closely spaced to the metal in 2b (Fig. 7). Also due to the higher coordination, the Zr–CH3 bond in 2b is elongated compared to 2B (Fig. 7). A decomposition analysis revealed that roughly 25% of the difference in uptake energy between 2b and 2B is due to the stretch of the Zr–Me and Zr–ethylene bond distances in 2b compared to 2B, 25% comes from increasing the R(Zr-μ-Me) distance (compared to 2A) whereas the rest is due to increased steric interaction.
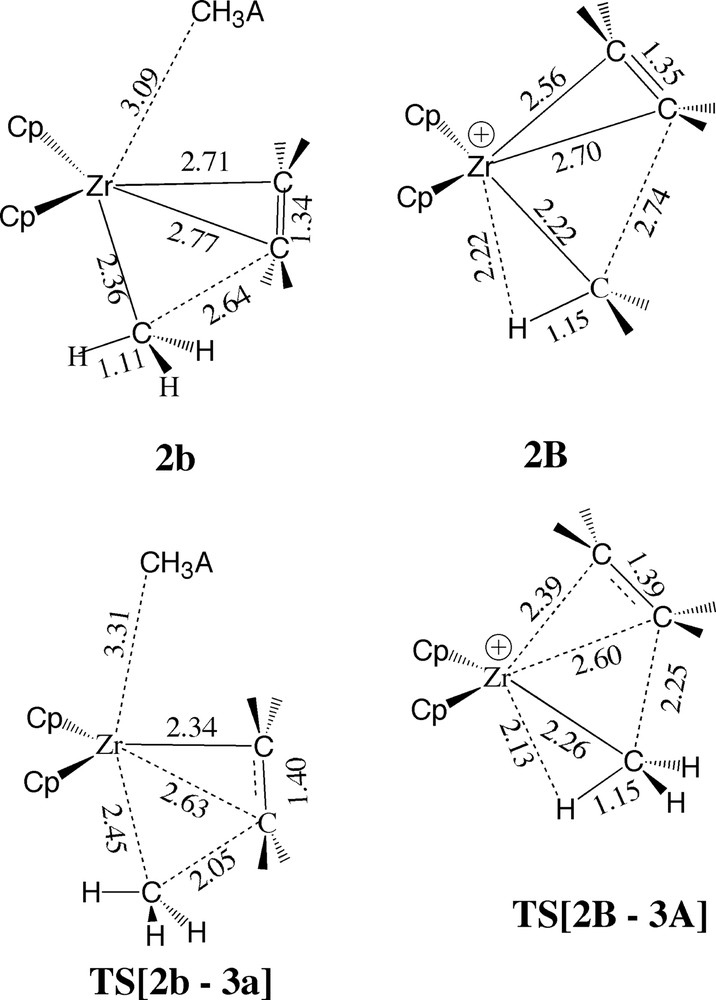
Comparison of the structures of the ethylene π-complexes and insertion transition states without (2B; TS[2B–3A]) and with (2b; TS[2b–3a]) the counterion [Me–B(C6F5)3–].
3.2 The second insertion
We shall now turn to a discussion of the second propagation step in which ethylene is inserted into the Zr–Cα bond of the [Cp2ZrPr]+[AMe]– ion-pair. This process should also serve as a good model for subsequent propagation steps to the extent that different substituents on the γ-carbon have a minor influence on the rate of insertion.
3.2.1 Conformation of the propyl chain in the ion-pair [Cp2ZrPropyl+][AMe–]
The possible orientation of the propyl group around the Cα–Cβ bond is shown in the Newman diagram of Fig. 8. The chain has three minimum structures of similar energy (± 0.2 kcal/mol) corresponding to the staggered conformations with ϕ of Fig. 8 at 54° (3b), 163° (3a) and –50° (3c), respectively. On the other hand, the eclipsed conformations at 0°, 110° and –100° represent rotational transition states with barriers of 2.2 kcal/mol (–110°), 2.6 kcal/mol (110°) and 3.8 kcal/mol (0°) (3d), respectively. Thus, under polymerization conditions at 100–200 °C the chain can rotate around the Cα–Cβ bond between the staggered equilibrium structures. The chain does not form agostic bonds between the metal and hydrogens on the α-, β- or γ-carbons of the chain. Presumably, the metal center is already coordinately saturated from the interaction with the anion ACH3– and the ancillary ligands. It is important to note that the three minima (3b–3d) are distinct due to the unsymmetrical structure of ACH3– Fig. 2. However, 3b and 3c are closely related.
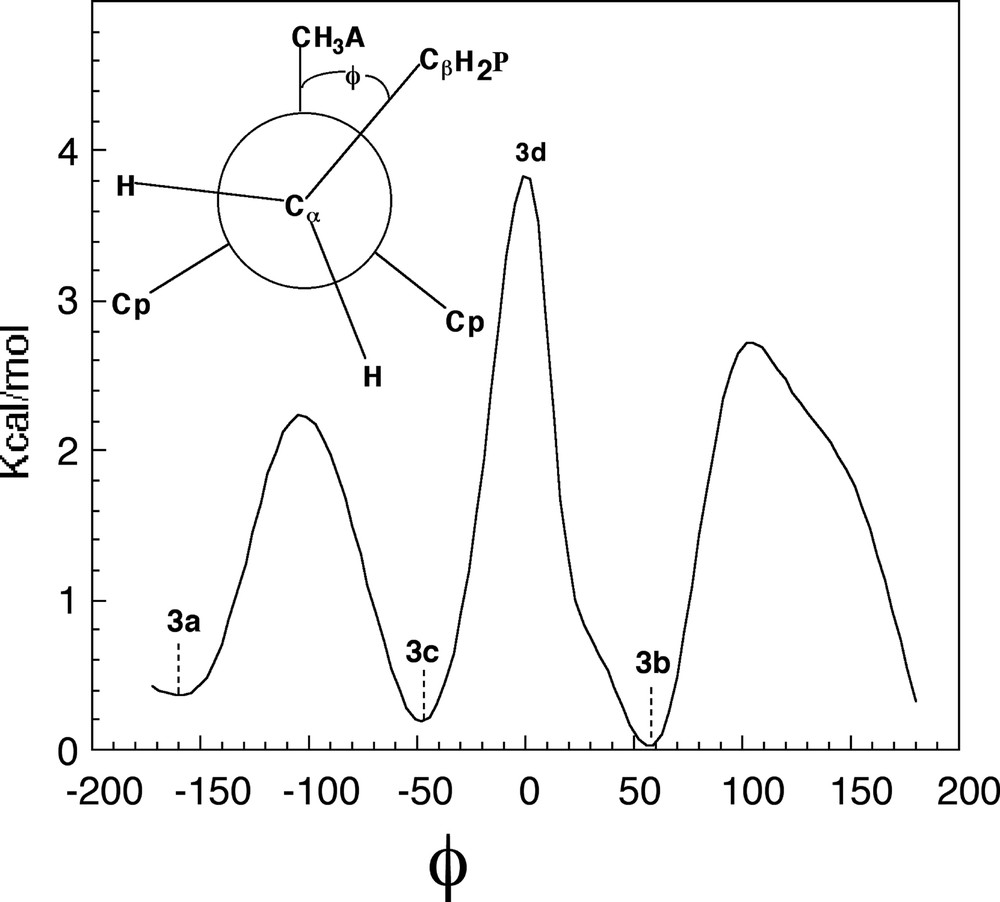
The energy of [ZrCp2Pr+][Me–B(C6F5)3–] as a function of the rotation of the propyl chain (Pr) around the dihedral angle Ame–Zr–Cα–Cβ. Energy in kcal/mol.
In the following discussion we will encounter insertion processes in which the interaction between a hydrogen on the β-carbon of the propyl (growing) chain is of crucial importance, as well as cases in which such an interaction is absent. We shall begin with the latter case which involves the cis and trans-approach (Fig. 3) to the ion-pair conformations 3b and 3c.
3.2.2 Cis and trans-approach to the ion-pair conformations 3b and 3c
The two conformations 3b (ϕ = 54°) and 3c (ϕ = –50°) with the chain out of the CH3–Zr–CH3A– coordination plane are very similar. Thus we shall restrict our investigation to the cis and trans-approach of ethylene towards 3b. In the trans-case ethylene can attack while situated either in the CH3–Zr–CH3A– coordination plane or oriented perpendicular to the same plane. The in-plane ethylene approach has no uptake barrier or π-complex. It leads instead directly to the insertion transition state TS[3b–10a] with a barrier of 12.8 kcal/mol, Fig. 9. On the other hand, any initial approach of ethylene in the perpendicular position invariably results in a rotation of the C=C bond down into the CH3–Zr–CH3A– coordination plane without the formation of a “perpendicular” π-complex. After insertion, the counterions recombine to form the pentyl ion-pair 10a. Thus, in the next insertion ethylene will again have to displace the anion. It is worth noting how similar the trans-reaction profile is for the first (Fig. 5) and second insertion, Fig. 9. Even comparable geometrical parameters are quite similar in magnitude. Thus replacing the methyl group by a propyl chain does not change the essential features of the trans attack.
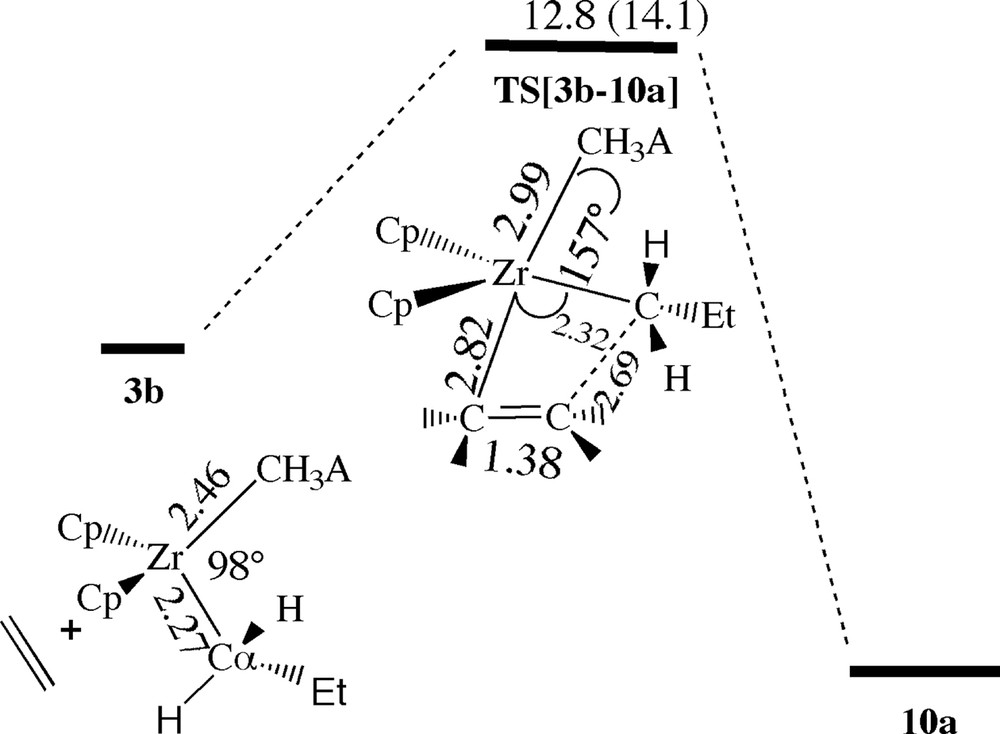
Energy profile for insertion of ethylene into the Zr–Pr bond of [ZrCp2Pr+][Me–B(C6F5)3–] by trans-approach of ethylene without formation of a β-agostic interaction. Energy in kcal/mol.
In the cis-case ethylene can attack while either situated in the CH3–Zr–CH3A– coordination plane or oriented perpendicular to the same plane, Fig. 10. In the first case the path leads to a considerable uptake barrier of 15.4 kcal/mol (TS[3b–4b]), followed by the π-complex 4b (5.8 kcal/mol) in which the anion is displaced to a R(Zr-μ-Me) distance of 4.23 Å, Fig. 10. On the other hand, the path with ethylene in the perpendicular orientation leads to less steric congestion thus resulting in a smaller uptake barrier of 9.5 kcal/mol (TS[3b–4c]) and a more stable π-complex 4c (4.5 kcal/mol) with a shorter R(Zr-μ-Me) distance of 3.29 Å. Finally, insertion from either of the two π-complexes 4b or 4c takes place via the same transition state TS[4b–10a] with a barrier of 6.8 kcal/mol, Fig. 10. Our calculations indicate that the most facile cis-approach initially proceeds along the perpendicular path 3b → TS[3b–4c] → 4c followed by a rotation of ethylene into the CH3–Zr–CH3A– coordination plane to reach the insertion transition state TS[4b–10a], just as in the cis-approach for the first insertion. We note as well that the distortions of the ion-pair due to the approaching ethylene are similar for the first and second cis insertion. The most important geometrical changes are the opening of the CH3–Zr–CH3A– angle and the elongation of the Zr-alkyl and Zr–CH3A– bonds.
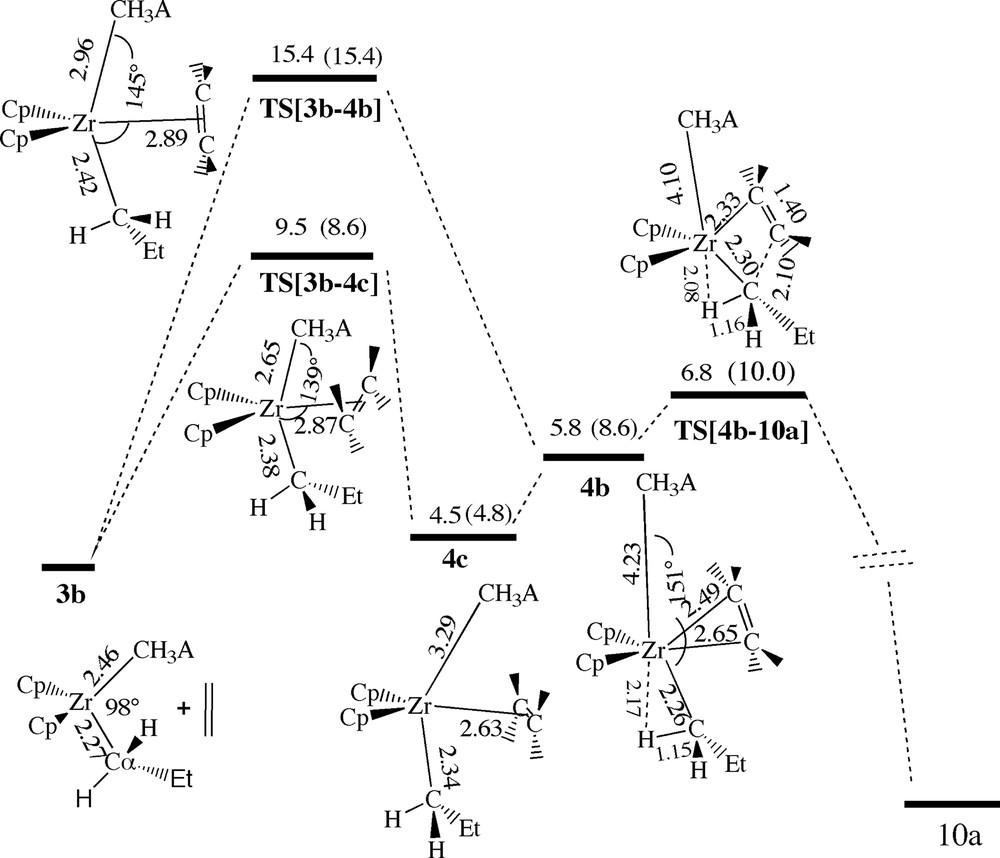
Energy profile for insertion of ethylene into the Zr–Pr bond of [ZrCp2Pr+][Me–B(C6F5)3–] by cis-approach of ethylene without formation of a β-agostic interaction. Energy in kcal/mol.
It is interesting to point out that after solvent effects have been taken into account, the rate determining step along the path 3b → TS[3b–4c] → 4c → TS[4b–10a] is the olefin uptake since the insertion transition state TS[4b–10a] has a substantial charge separation that is stabilized by solvation. Of the two cis-insertion processes the second is seen to have a lower barrier than the first even in the gas-phase. This is due to the fact that the Zr–Pr bond is weaker than the Zr–methyl linkage. Also, in the second insertion the transition state TS[4b–10a] is stabilized by the interaction of one of the hydrogens on the α-carbon of the growing (propyl) chain. Such an α-agostic interaction was not found in the case of TS[2b–3a]. On the other hand the uptake barriers associated with the second insertion are seen to be larger than the corresponding barriers of the first insertion due to the added steric bulk on the growing chain. However, we do not expect the uptake barriers to grown further for longer chains.
We shall now turn to insertion processes in which the interaction between a hydrogen on the β-carbon of the propyl (growing) chain and the metal center is of crucial importance. Such β-agostic species can form during the approach of the ethylene monomer, and they have been discussed extensively [2] in studies on ethylene polymerization catalyzed by the bare cation Cp2ZrPr+. In the case of [Cp2ZrPr]+[CH3A]– one can envision four conformers for the corresponding β-agostic π-complex, Fig. 11. Thus, ethylene can enter cis or trans to the anion CH3A– with the β-agostic hydrogen on the opposite side of the Zr–Cα bond to form the two back-side [5a] π-complexes with the cis-back (5b) and trans-back (6b) conformations, Fig. 11. Alternatively, ethylene can enter cis or trans to the anion CH3A– with the β-agostic hydrogen on the same side of the Zr–Cα bond to form the two front-side [5a] π-complexes with the cis-front (7b) and trans-front (8b) conformations. We shall first discuss the role of the cis-back and trans-back conformations.

Possible conformations of the β-agostic ethylene complexes.
3.2.2.1 The role of the cis-back (5b) and trans-back (6b) conformations
The β-agostic ethylene complex 5b with the cis-back conformation is formed with an endothermic complexation energy of 4.9 kcal/mol, Fig. 12, from a cis-attack of ethylene towards 3a. It follows that 5b is slightly more stable than the α-agostic ethylene complex 4b (5.8 kcal/mol) formed from the cis-approach discussed above and involving 3b, Fig. 9. The uptake barrier for the formation of 5b is as high as 18.2 kcal/mol with a transition state TS[3a–5b] where the β-agostic bond already is formed. The high barrier is due to the steric congestion around the zirconium center which makes it impossible for ethylene to coordinate properly to zirconium. Thus ethylene is situated completely in the CH3–Zr–CH3A– coordination plane in a way that minimize the steric interaction without gaining any stabilizing bonding to zirconium. After TS[3a–5b] the anion dissociate to provide ethylene with an axial coordination in 5b. In the final insertion step, the β-agostic bond is maintained in the transition state TS[5b–10a] with a barrier of 10.8 kcal/mol. The cis-attack discussed here in Fig. 12 is less favorable than the cis-attack in Fig. 9 because of the higher uptake barrier. Thus the formation of a β-agostic bond is not necessary going to make the insertion more facile in the presence of the anion CH3A–.
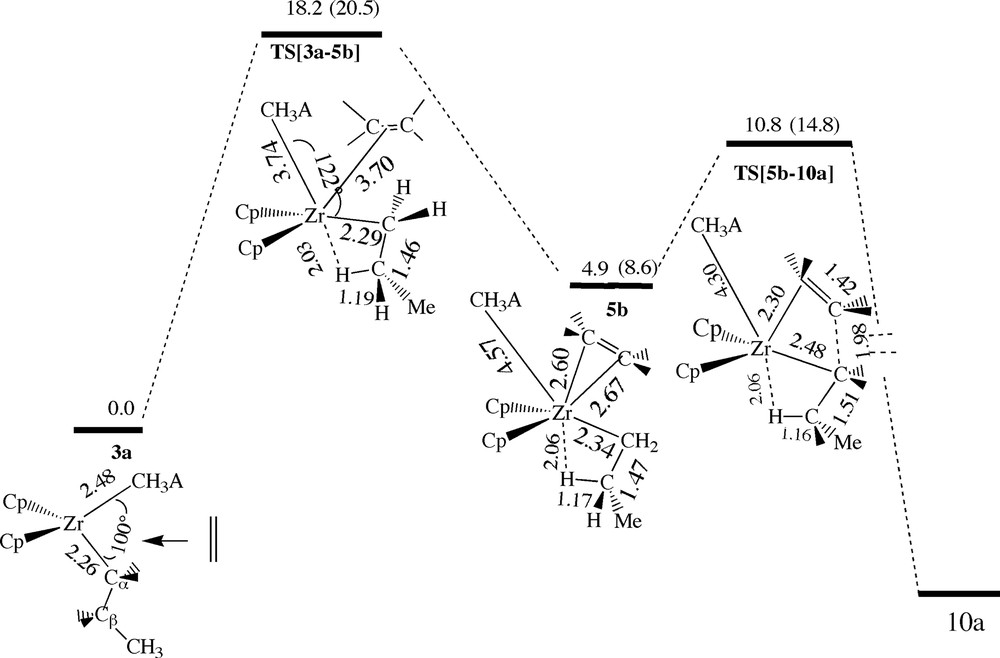
Energy profile for insertion of ethylene into the Zr–Pr bond via the β-agostic cis-back ethylene complex 5b, see Fig. 11. Energy in kcal/mol.
The β-agostic ethylene complex 6b, Fig. 13, can formally be considered formed in a trans-approach of ethylene towards the ion-pair where the latter adopts the high energy geometry 3d (ϕ = 0°). The complexation process is endothermic (6.4 kcal/mol) with an uptake barrier of 14.1 kcal/mol, Fig. 13. The uptake transition state TS[3d–6b] already reveals a β-agostic bond. It has further a bipyramidal structure with the entering (ethylene) and leaving (CH3A–) nucleophiles situated in the axial positions as it is typical for SN2 type reactions. The insertion transition state TS[6b–10a] in which the β-agostic bond is maintained has a barrier of 9.4 kcal/mol, which is somewhat lower (12.8 kcal/mol) than the barrier obtained in the previously discussed trans approach, Fig. 9, where an agostic bond was absent in the transition state structure TS[3b–10a]. In total, the trans-approach involving β-agostic bonds is seen to be marginally less facile due to the uptake barrier.
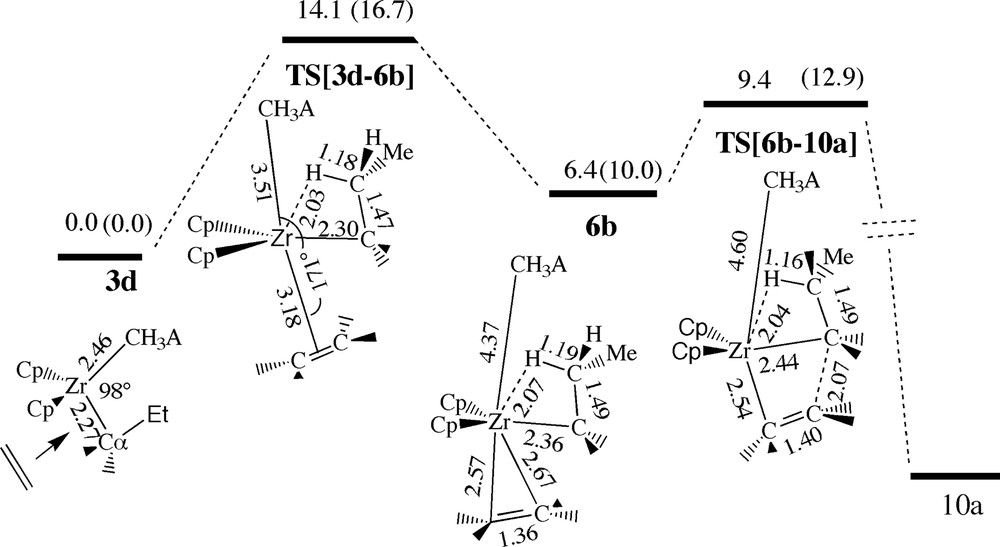
Energy profile for insertion of ethylene into the Zr–Pr bond via the β-agostic trans-back ethylene complex 6b, see Fig. 11. Energy in kcal/mol.
We have also studied ethylene polymerization by the bare cation Cp2ZrPr+ IIIA which has a β-agostic hydrogen–zirconium bond in its most stable conformation, Fig. 14. The formation of a back-side ethylene complex VB is exothermic by 19.0 kcal/mol and proceeds without any uptake barrier. The final insertion takes place with an internal barrier of 7.2 kcal/mol via the transition state TS[VB–XA] which is 11.8 kcal/mol below IIIA and free ethylene. We note that the π-complex VB and transition state TS[VB–XA] have many features in common with, respectively, the π-complexes 5b, 6b and transition states TS[5b–10a], TS[6b–10a], if one disregard the counterion in the latter species. Further, the internal insertion barrier for TS[VB–XA] of 7.2 kcal/mol is somewhat larger than the corresponding barrier for TS[5b–10a] of 5.9 kcal/mol and more than double as large as the barrier for TS[6b–10a] of 3.0 kcal/mol.
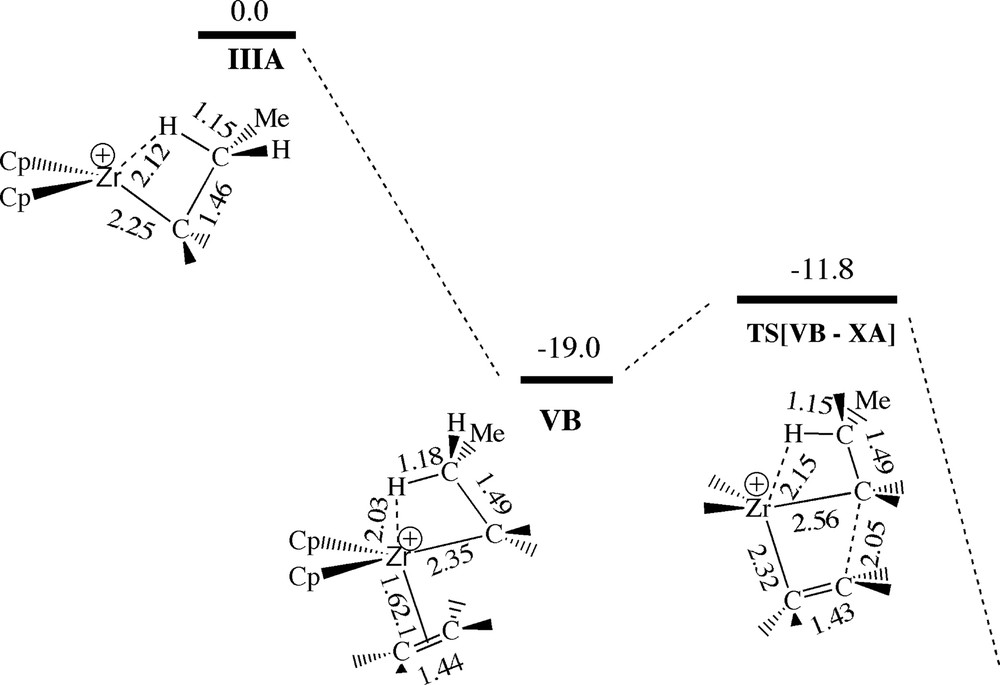
Energy profile for insertion of ethylene into the Zr–Pr bond of the bare cation [ZrCp2Pr]+. Energy in kcal/mol.
3.2.2.2 Chain termination and the role of the cis-front (7b) and trans-front (8b) conformations
We shall finally discuss the role of the β-agostic π-complexes 7b and 8b. The first can be considered as a product from a cis-attack of ethylene on the ion-pair 3d, Fig. 15, whereas the second is produced by a trans-approach of ethylene towards 3a, Fig. 16.
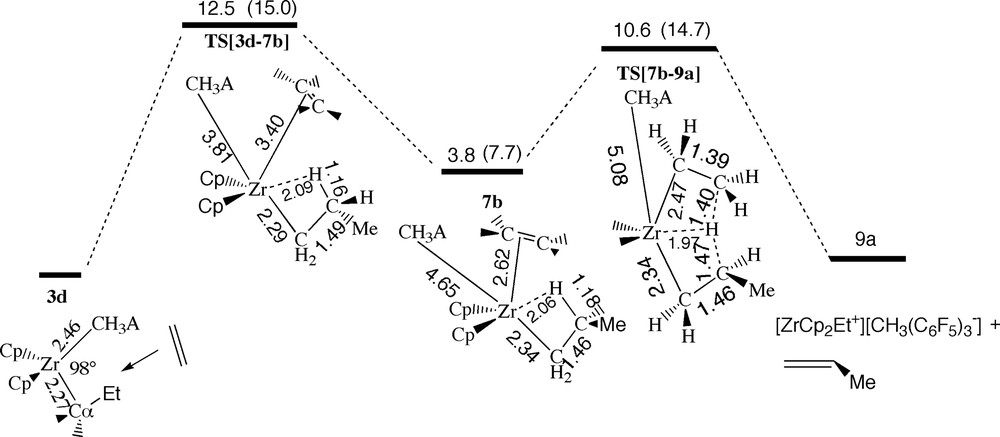
Energy profile for hydrogen transfer via the β-agostic cis-front ethylene complex 7b, see Fig. 11. Energy in kcal/mol.
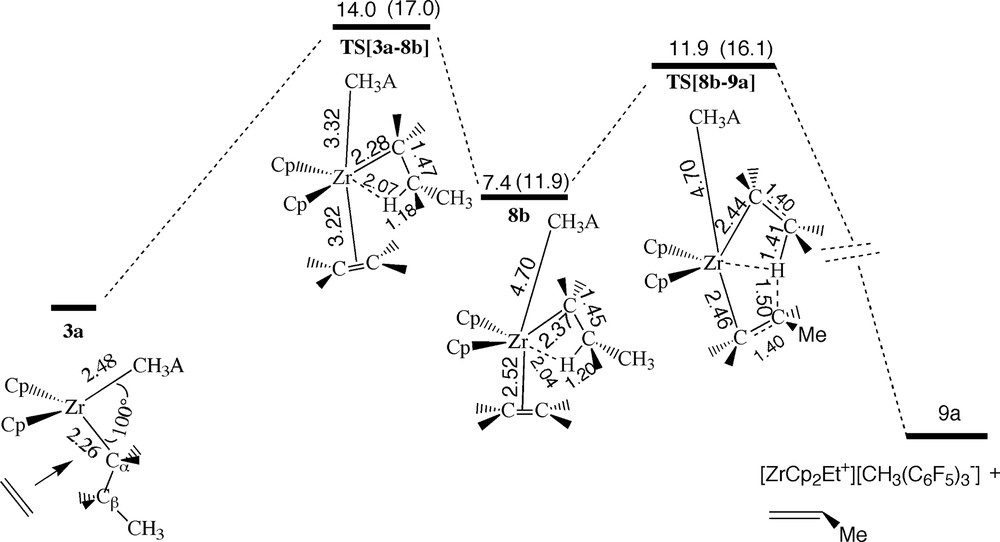
Energy profile for hydrogen transfer via the β-agostic trans-front ethylene complex 8b, see Fig. 11. Energy in kcal/mol.
The β-agostic π-complex 7b has a relatively low energy of 3.8 kcal/mol, Fig. 15. However, the formation of 7b is associated with a substantial uptake barrier of 12.5 kcal/mol corresponding to the transition state TS[3d–7b] in which a β-agostic bond already is formed in order to compensate for the partial dissociation of the anion CH3A– with R[Zr-μ-CH3] = 3.81 Å. Unfortunately, the steric requirement of the β-agostic bond makes it difficult for ethylene to participate in the stabilization of TS[3d–7b] and it remains weakly coordinating with R[Zr–X] = 3.40 Å. The position of the β-hydrogen between the α-carbon and the approaching monomer prevents a direct insertion to take place unless the β-hydrogen is removed from the Zr–Cα–Cβ plane by a rotation around the Cα–Cβ bond. However such a rotation has a barrier of more than 15 kcal/mol and will not be considered further. Instead 7b can undergo a termination process in which the β-hydrogen is transferred from the propyl chain to the ethylene monomer, Fig. 15. The result is a new ion-pair 9b with an ethyl chain and a propene monomer originating from the former propyl group. The total barrier for the elimination process is 10.6 kcal/mol corresponding to the transition state TS[7b–9a].
The corresponding trans-front π-complex 8b is also stabilized by a β-agostic interaction and requires again a high uptake barrier (14.0 kcal/mol) to be formed, Fig. 16. The uptake transition state TS[3a–8b] is typical of an SN2 reaction with the two nucleophiles CH3A– and ethylene in the axial positions. As in the case of 7b, the trans-front π-complex 8b can not readily undergo insertion as the β-agostic hydrogen blocks the approach of the monomer towards the α-carbon of the propyl chain. Instead, the β-hydrogen is transferred to the monomer resulting in the elimination of the propyl chain as propene and the formation of a new ion-pair 9a with an ethyl chain. The barrier TS[8b–9a] for this process is 11.9 kcal/mol. It is interesting to note that the rate for the two hydride transfer processes discussed here is determined by the barriers of the olefin uptake rather than the hydride transfer, Fig. 17. This is in contrast to studies of hydride transfer based on the bare cation where the uptake proceeds without any activation energy and the only (internal) barrier is the energy required to move from the cis-front and trans-front π-complexes to the hydride transfer transition state [2e,5].
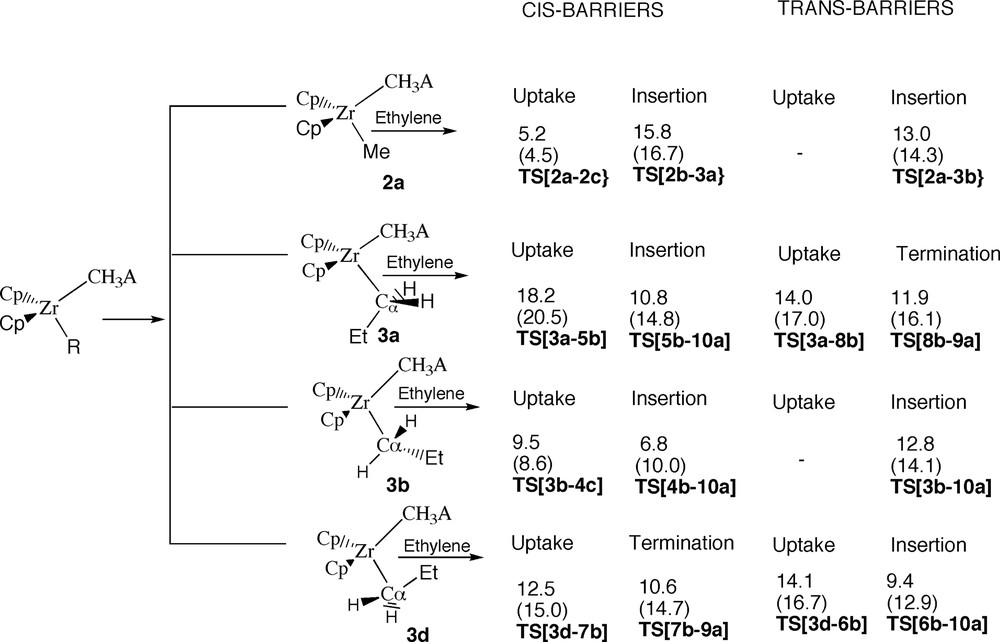
Summary for the calculated energy barriers. Energy in kcal/mol.
4 Concluding remarks
We have studied the reaction of ethylene with the ion-pair [ZrCp2R]+[Me–B(C6F5)3]– as well as the bare cation [ZrCp2R+] for R = Me, Pr in order to probe the influence of the anion [Me–B(C6F5)3]– on the insertion of ethylene into the Zr–R bond.
The reaction between ethylene and the bare cation [ZrCp2R]+ leads in the first place to a π-complex in a strongly exothermic and exogonic reaction without any (uptake) barrier [2,3], Figs. 6 and 13. Even the subsequent insertion process has a transition state that is lower in energy than ethylene and the cation at full separation. The only (intrinsic) barrier is the energy required (1.2 kcal/mol R = Me; 7.2 kcal/mol R = Pr) to proceed from the π-complex to the insertion transition state.
For the ion-pair [ZrCp2R]+[Me–B(C6F5)3]– ethylene can approach cis and trans to the Zr-μ-CH3 bridge that binds the ion-pair together, Fig. 3. For the second (and subsequent) approaches of the ethylene monomer (R = Pr) the insertion process is further complicated by the fact that the chain in the ion-pair have three equilibrium (staggered) conformations with respect to rotation around the Cα–Cβ bond at ϕ = 163° (3a), ϕ = 54° (3b) and ϕ = –50° (3c), Fig. 8. The barrier for a complete rotation of the chain is 3.8 kcal/mol. It is thus reasonable to assume that the chain can rotate freely around the Cα–Cβ bond under normal polymerization conditions (140–200 °C). We have studied both the cis and the trans-approach for three orientations of the chain corresponding to 3a (ϕ = 163°); 3b (ϕ = 54°) and 3d (ϕ = 0°), Figs. 8 and 17.
The cis-approach leads in general to an endogonic and endothermic π-complexation that is associated with a substantial (uptake) barrier. The uptake transition state is approximately bipyramidal with the anion and R in the axial positions and ethylene in the equatorial plane, Figs. 4 and 10. The uptake barrier is caused by increased steric congestion and the partial dissociation of the anion as well as trans-destabilization between R and the anion. The anion dissociation is larger for R = Pr (ΔR(Zr-μ-CH3) = 0.19 Å) than for R = Me (ΔR(Zr-μ-CH3) = 0.11 Å). The subsequent insertion process leads to a new barrier and associated transition state in which the anion is displaced further with ΔR(Zr-μ-CH3) = 0.65 Å for R = Me (Fig. 4) and ΔR(Zr-μ-CH3) = 1.64 Å for R = Pr (Fig. 10). Solvent effects tend to stabilize the insertion transition state with the larger (charge) separation more (3.2 kcal/mol R = Pr; 0.9 kcal/mol R = Me) than the uptake barrier with the modest anion displacement. Solvent effects are for the same reason more important for R = Pr than for R = Me.
The trans-approach leads for R = Me directly to insertion without the formation of a π-complex, Fig. 5, and this is also the case for the trans-approach towards 3b, Figs. 9 and 16. All other cases give rise to the formation of an endogonic π-complex. Both uptake barriers and insertion barriers are SN2-like with the nucleophiles (the anion and ethylene) in the axial positions of a bipyramide. The anion displacement is again more pronounced for R = Pr than for P = Me and more substantial in the insertion transition state than in the uptake transition state, Figs. 5,9,11 and 14. Solvent stabilization is likewise most important (~4 kcal/mol) for the insertion transition state, Fig. 17.
We find the first insertion (R = Me) to favor a trans-attack without the formation of an intermediate, Fig. 5. The corresponding (insertion) barrier was calculated to be 13.0 kcal/mol. For the second insertion (and likely also all subsequent insertions) we find that a cis-approach is preferred with a barrier of 9.5 kcal/mol, Fig. 10. This trend is in agreement with the work of Liu et al. [16] where it was found that the activation energy for the first insertion of 1-hexene into the Z–Me bond of [rac(C2H4(1-indenyl)2ZrMe]+ [MeB(C6F5)3]– was 11.2 kcal/mol whereas the subsequent insertion has a barrier of 6.4 kcal/mol.
It is important to note that the barrier for the second propagation step is associated with olefin uptake rather than with olefin insertion into the Zr–Pr bond, Fig. 10. This observation indicates in the first place that barriers of activation for propagation might be strongly related to the ion-pair separation energy [4f, 6a–e, 14] so that more tightly bound ion-pairs give rise to higher propagation barriers and reduced polymerization activity. Further, the uptake transition state has the incoming monomer much further away from the metal center than the insertion transition state. This might have implications for the way in which one rationalize stereoregular polymerization of higher α-olefins, a point we will return to in a later investigation. Finally, even the rate of termination might be determined by olefin uptake, Figs. 14 and 15, with the results that one will need new consideration to determine molecular weights.
Acknowledgements
This investigation was supported by the Natural Science and Engineering Research council of Canada (NSERC) and by Nova Research and Technology Corporation (NRTC). T.Z. would like to thank the Canadian government for a Canada Research Chair in theoretical inorganic chemistry.


