1 Introduction
Dehydrogenation of alkanes is an important reaction as it constitutes the starting point in the conversion of cheap and abundant chemical compounds into valuable products. Olefins that are obtained from dehydrogenation of alkanes are precursors in fine organic chemistry, or polymers synthesis [1]. Among other catalysts, zeolites have been shown to catalyze this reactions. Zeolites are microporous aluminosilicates built up by linking SiO4 tetahedra together by sharing oxygen atoms [2]. They exist as such naturally or can be obtained synthetically. The presence of aluminum is a prerequisite for zeolite showing catalytic activity [3]. When aluminum substitution occurs, the resulting negative charge in excess is balanced by the introduction of cations in the micropores. These cations can be of different nature and will govern the catalytic activity. Normally, sodium is present as charge compensating cation but it can virtually be exchanged with any other cation [2,4]. A well-known example is the exchange with ammonium ion which will leave proton as charge-compensating cation after desorption of ammonia and renders a solid acid catalyst. Alternatively, also gallium can be employed as charge-compensating cation [5].
Although sodium or proton-exchanged zeolites also shows some catalytic activity in dehydrogenation reactions [6], the activity is rather low due to the high barriers associated with the generation of carbonium ions. Gallium-exchanged zeolites allow higher dehydrogenation activities [5,7]. Nevertheless, high reaction temperatures are still needed because of the endothermic nature of dehydrogenation reactions [8]. Moreover, conversion of alkanes leads to the formation of aromatic when the reaction is catalyzed by gallium-exchanged zeolite [7,9]. The commercial Cyclar process uses this class of catalyst [10].
The details of the reaction mechanisms and the nature of the gallium active sites in these reactions are not precisely known [11,12]. However, the structure of gallium in the zeolitic precursors is understood to a better extent. Gallium is present as Ga(III). The gallium cation in tetrahedral position is connected to two hydrogen and interacts with two oxygen atoms of an AlO4 tetrahedron (Scheme 1). During alkanes dehydrogenation, the structure of the catalytic site becomes more complex. The first reason for this is that high temperature is required to achieve the reaction, which blurred significantly a clear identification of reaction intermediates and lead to reconstructions of the catalytic active site [13].
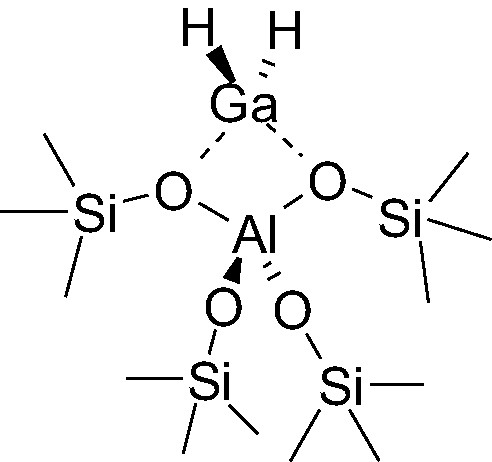
Structure of [Ga(III)H2]-zeolitic site.
Frash and Van Santen have performed a quantum chemical study of the dehydrogenation of ethane by gallium-exchanged zeolite [11]. For this purpose, they used as model of the gallium-exchanged zeolite catalyst a small molecular fragment within the framework of the cluster approach [14,15]. Various structural alternatives of the active site were compared and the complete catalytic cycle for dehydrogenation was completed. The most likely reaction sequence is depicted in Scheme 2. The limiting step in dehydrogenation of ethane catalyzed by a gallium-exchanged zeolite cluster model corresponds to a transition state structure that leads to the formation of ethene from ethyl chemisorbed to GaH-Z, where Z is the zeolite cluster (see TS3 in Scheme 2). One notices that the energy barrier of the rate-limiting step in this reaction pathway is particularly high. A possible reason for this is probably inherent to the cluster approach method. It is now well understood that the zeolite framework can have a significant stabilizing effect of transition state structures [15,16]. In the cluster approach method, activation energy barriers are generally overestimated as the zeolite framework is not described. However, if on the one hand the zeolite framework stabilizes charge separation in transition states of carbocationic nature [17], on the other hand, absence of stabilization or even destabilization can occur for transition states of different nature [18]. A closer look at this reaction pathway reveals other interesting facts. The Int2 intermediate has been considered to be an intimately associated complex, whereas, considering the bond order in this structure it might equally be considered to be a zeolite Brønsted site on which is physisorbed a GaH3 molecule (Scheme 2). The gas phase cluster approach method has a tendency to overemphasize interactions between the different fragments as they cannot behave differently due to the limited size of the system. In a zeolite micropore, there is room for more favorable arrangements.
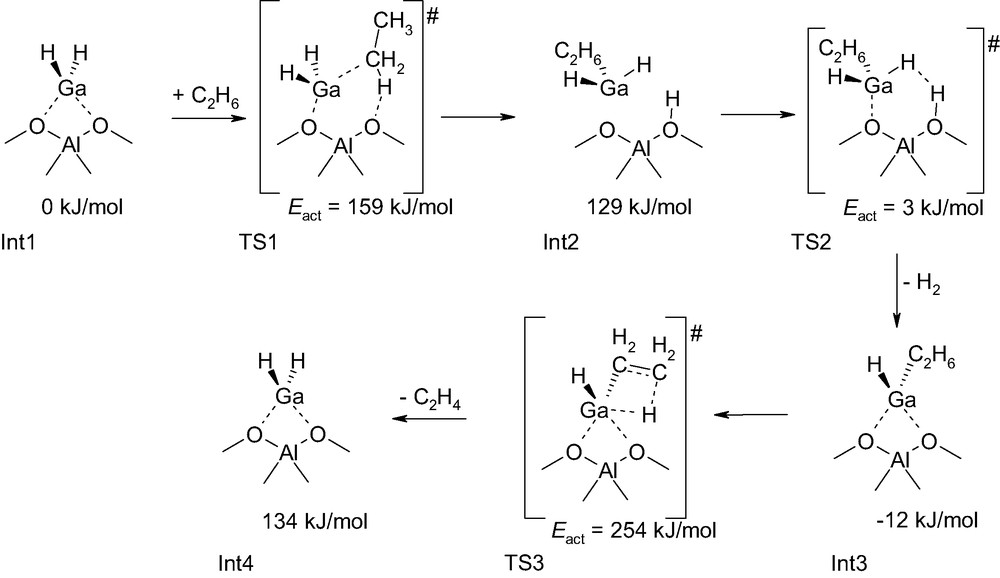
Intermediates and transition state structures in the ethane dehydrogenation catalyzed by gallium-exchanged zeolite [11].
In this study, we will use periodic density functional theory to describe the zeolite framework as realistically as possible. We will check different alternatives of the reconstruction of gallium-exchanged zeolite. We select mordenite as zeolite framework because it has a small unit cell [19,20]. Experimentally, mordenite and ZSM-5 are employed in the conversion of alkanes into aromatics [9,21].
In addition to the periodic density functional theory calculations, we will perform few gas-phase cluster calculations to check the viability of some structures as potential active sites in dehydrogenation. We will use a similar model and similar methods as those used by Frash and Van Santen [11] to ease comparison.
2 Methods
The periodic density functional theory calculations are performed employing the Vienna ab initio simulation package (VASP) [22–24]. The total energy is calculated solving the Kohn–Sham equations using the local exchange-correlation functional proposed by Perdew and Zunger [25]. The results are corrected for non-locality in the generalized gradient approximation with the Perdew-Wang functional (PW91) [26]. VASP uses plane waves, and ultrasoft pseudopotentials [27]. A 300 eV energy-cutoff and a Brillouin-zone sampling restricted to the Γ-point were selected in our calculations.
Relaxation of the adsorbed compounds and intermediates was performed employing a quasi-Newton algorithm based on analytical forces minimization. Convergence was assumed to be reached when all forces were below 0.05 eV/Å.
As previously mentioned, we selected mordenite as host structure for the gallium-cations. The unit cell of the periodically repeated image of the system is defined as a = 13.648 Å, b = 13.672 Å, c = 15.105 Å, α = 96.792°, β = 90.003°, and γ = 90.022°. The details of the optimization of the mordenite unit cell can be found elsewhere [20]. In the unit cell, two aluminum substitute tetrahedrally coordinated silicon atoms. They are located at the junction of the 12-membered ring side pocket. When an aluminum substitution takes place on one side of the 12-membered ring channel, the next one takes place on the opposite side (Fig. 1), therefore respecting the Loewenstein [28] rule.

Geometries and energies of [Ga(III)H2]-MOR (A), [Ga(II)H2Ga(II)H]-MOR and H-MOR (B), and [Ga(III)H3·Ga(I)]-MOR and H-MOR (C) as obtained in the periodic density functional theory calculations.
A main reason why periodic density functional theory method has been chosen is that we are going to investigate different possible reconstructions of the gallium-exchanged zeolite catalyst. It is known that density functional theory is poorly suited to account for Van der Waals contribution. This has some consequences on the results that is, however, balanced by the uniform shift that is generally obtained when Van der Waals contribution is correctly described [29]. An alternative to pure density functional theory would be to use QM/MM or QM/QM method. [29,30] However, in the present case, this is actually not really suitable as we cannot a priori define what will be the sufficient and self-consistent size of the part of the system that needs high accuracy QM description.
In the present study, we will first consider a mordenite unit cell in which the compensating cation at the aluminum substituted tetrahedral is GaH2+. Then, we will add a GaH3 molecule to the systems. Lastly, incorporation of propene and H2 within the micropore will be considered. For each of the three systems, reconstruction of the catalytic active sites in gallium-exchanged mordenite will be investigated.
To support the relevance of the reconstructed catalytic sites in the dehydrogenation of alkane, we have also performed gas-phase calculations. For these calculations, we have employed similar method and a similar model as those in the study of Frash and Van Santen [11]. This allows a comparison with their values. We used the Gaussian98 [31] package with the B3LYP method [32] and 6-31g basis set [33]. With these calculations we are not interested in quantitative values but qualitative ones. Therefore, this limited approach is self-sufficient. It is known that zeolite framework can seriously shift the energies of transition state structures or sterically hindered intermediates [15,16]. However, our objective in the present study is not to investigate these effects but to propose and analyze reconstructions of gallium-exchanged zeolite and to check whether or not they are relevant in the catalytic cycle of alkane dehydrogenation.
3 Results and discussion
3.1 Reconstructions in gallium-exchanged mordenite
In its most stable configuration in zeolite, Ga3+ adopts a tetrahedral coordination [5,11]. Within the zeolite micropores after reductive treatment, GaH2+ interacts with two oxygen atoms of an aluminum tetrahedral unit (Fig. 1a and Scheme 1). Two GaH2+ adopting this conformation are set in our mordenite unit cell, which contains two aluminum atoms at the locations as described before. This system is shown in Fig. 1a and the most important geometrical parameters are reported in Table 1a. The oxygen-gallium bond length distances range from 2.02 to 2.04 Å. This is slightly larger than that was found by Frash and Van Santen in their quantum chemical study using a Al(OHSiH3)2H2– zeolite model [11].
Main geometrical parameters of the two [Ga(III)H2]-MOR as obtained in the calculations (Fig. 1a). Distances in Å, angles in °
| Al1O1 | 1.80 | Al2O3 | 1.78 |
| Al1O2 | 1.81 | Al2O4 | 1.80 |
| O1Ga1 | 2.04 | O3Ga2 | 2.04 |
| O2Ga1 | 2.02 | O4Ga2 | 2.03 |
| Ga1H1 | 1.53 | Ga2H3 | 1.53 |
| Ga1H2 | 1.53 | Ga2H4 | 1.53 |
| Al1O1Ga1 | 95.0 | Al2O3Ga2 | 96.3 |
| Al1O2Ga1 | 95.5 | Al2O4Ga2 | 96.1 |
| O1Al1O2 | 91.0 | O3Al2O4 | 89.6 |
| O1Ga1O2 | 78.5 | O3Ga2O4 | 76.6 |
| O1Ga1H1 | 109.1 | O3Ga2H3 | 112.0 |
| O1Ga1H2 | 104.7 | O3Ga2H4 | 103.5 |
| O2Ga1H1 | 105.1 | O4Ga2H3 | 104.8 |
| O2Ga1H2 | 107.6 | O4Ga2H4 | 108.4 |
| Al1O1Ga1O2 | 2.9 | Al2O3Ga2O4 | 8.6 |
| Al1O1Ga1H1 | –91.0 | Al2O3Ga2H3 | –109.5 |
| Al1O1Ga1H2 | 89.8 | Al2O3Ga2H4 | 97.4 |
It is possible to generate a Brønsted acidic site starting from a [GaH2]-zeolite structure [34]. We have checked the reconstruction in which [Ga(III)H2]-MOR evolves toward H-MOR (Figs. 1 and 2). It is known that gallium-exchanged zeolite at high temperature can evolve toward the formation of metallic gallium, i.e. reduction of Ga(III) to Ga(0) [35]. García-Sánchez et al. [36] have suggested that Ga(III)Hx species can evolve toward Ga(II), Ga(I) and eventually to Ga(0) under reducing conditions. As we will show, this reconstruction to H-MOR and Ga(I)H is not very stable. Therefore, we have considered conditions under which the reconstruction of [GaH2]-MOR to reduced Ga could be stabilized.
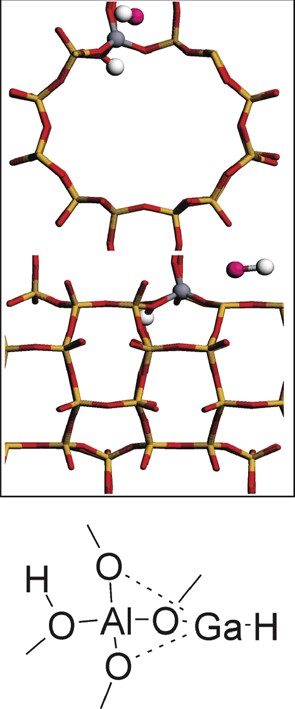
Geometry of Ga(I)H and H-MOR.
Potential reconstructions have been checked employing periodic density functional theory calculations and are displayed in Fig. 1. Initially, the unreconstructed species in mordenite is a system where two [Ga(III)H2]-MOR are present (Fig. 1a). This site can decompose to H-MOR and Ga(I)H. To stabilize GaH, we have considered its association with [Ga(III)H2]-MOR, leading to a system in which Ga(I) is reoxidized (Fig. 1b and Table 1b). The [GaH2GaH]-MOR species is in essence similar to the intermediate [i-C2H6-GaH]-MOR in the ethane dehydrogenation reaction pathway (Int3 in Scheme 2) [11]. The energy of this system is +136 kJ/mol with respect to the unreconstructed system. [Ga(II)H2Ga(II)H]-MOR can evolve through hydrogen transfer to a system having both Ga(I) and Ga(III): a GaH3 molecule can be formed leaving [Ga(I)] coordinated to the zeolite wall (Fig. 1c). The main geometrical parameters of this structure can be seen in Table 1c. The energy for this structure is +128 kJ/mol with respect to the initial unreconstructed system.
Main geometrical parameters of the [Ga(II)H2Ga(II)H]-MOR and H-MOR as obtained in the calculations (Fig. 1b). Distances in Å, angles in °
| Al1O1 | 1.91 | Al2O3 | 1.77 |
| Al1O2 | 1.70 | Al2O4 | 1.79 |
| O1Ha | 0.97 | O3Ga1 | 2.09 |
| O4Ga1 | 2.06 | ||
| Al1O1Ha | 108.1 | Ga1Ga2 | 2.46 |
| O1Al1O2 | 94.6 | Ga1H1 | 1.55 |
| Ga2H2 | 1.56 | ||
| Ga2H3 | 1.56 | ||
| Al2O3Ga1 | 96.1 | ||
| Al2O4Ga1 | 96.6 | ||
| O3Al1O4 | 90.2 | ||
| O3Ga1O4 | 75.1 | ||
| O3Ga1H1 | 107.3 | ||
| O3Ga1Ga2 | 104.3 | ||
| Ga1Ga2H2 | 120.2 | ||
| Ga1Ga2H3 | 119.9 | ||
| Al2O3Ga1Ga2 | –9.6 | ||
| Al2O3Ga1H1 | –107.2 | ||
| O3Ga1Ga2H2 | 142.3 | ||
| O3Ga1Ga2H3 | –36.4 |
Main geometrical parameters of the [Ga(III)H3Ga(I)]-MOR and H-MOR as obtained in the calculations (Fig. 1c). Distances in Å, angles in °
| Al1O1 | 1.91 | Al2O3 | 1.78 |
| Al1O2 | 1.70 | Al2O4 | 1.81 |
| O1Ha | 0.97 | O3Ga1 | 2.08 |
| O4Ga1 | 2.06 | ||
| Al1O1Ha | 109.6 | Ga1Ga2 | 2.65 |
| O1Al1O2 | 97.2 | Ga2H1 | 1.55 |
| Ga2H2 | 1.56 | ||
| Ga2H3 | 1.56 | ||
| Al2O3Ga1 | 97.1 | ||
| Al2O4Ga1 | 96.8 | ||
| O3Al1O4 | 89.2 | ||
| O3Ga1O4 | 75.1 | ||
| Ga1Ga2H1 | 96.1 | ||
| Ga1Ga2H2 | 93.6 | ||
| Ga1Ga2H3 | 92.8 | ||
| Al2O3Ga1Ga2 | 163.4 | ||
| O3Ga1Ga2H1 | –124.9 | ||
| O3Ga1Ga2H2 | –75.7 | ||
| O3Ga1Ga2H3 | 164.5 |
The calculations show that the non-assisted reduction of Ga(III) is quite highly energetic. However, one notices that comparable energy reaction intermediates are present in the catalytic cycle of ethane dehydrogenation (Scheme 2) [11]. Hence, it remains possible that these reconstructions occur under reaction conditions.
However, before such reconstructions as seen in Fig. 1b, c can occur, H-MOR and GaH must be formed. Using a mordenite unit cell with a single aluminum atom and a [Ga(III)H2]-MOR as starting point, we have evaluated the reaction energy to reach H-MOR and GaH (Fig. 2). The geometry details are not reported here as they are rather straightforward: the systems can be described as H-MOR and GaH present in the micropore. The free GaH molecule has no significant effect on the zeolite framework. The GaH bond length is 1.67 Å. More important is the energy of this structure: it is +215 kJ/mol with respect to [Ga(III)H2]-MOR. Considering this energy, spontaneous reduction of [Ga(III)H2]-MOR to Ga(I)H and H-MOR is unlikely. This is in line with the experimentally observations that show that such transformation only occurs under reducing conditions and at high temperature [35].
3.2 Reconstructions in gallium-exchange mordenite in presence of GaH3
Next, we analyze different alternatives that allow the reconstruction of the Ga(III) dihydrate species with assistance of external molecules. The ancillary molecules include GaH3 and H2 and propene.
As a first ancillary molecule for reconstruction of [Ga(III)H2]-MOR, GaH3 is considered (Fig. 3). In the initial system, two [Ga(III)H2]-MOR and GaH3 are present (Fig. 3a). The [Ga(III)H2]-MOR are similar to those reported before (Fig. 1a and Table 1a). The energy of [Ga(III)H2]-MOR and GaH3 is used as energy reference. We observe that the formation of H-MOR and Ga(I)H is probably prevented because of the high energy that is required to reach this structure. Here, GaH can associate with GaH3, leading to the formation of [GaH3·GaH] and H-MOR (Fig. 3b and Table 2). The energy of this system is +164 kJ/mol. This corresponds to an energy stabilization energy of around 50 kJ/mol with respect to the energy of formation of H-MOR and GaH. A proton jump can transform Ga(III)H3·Ga(I)H in Ga(II)H2–Ga(II)H2 (Fig. 3c). Then, the energy of the system becomes +144 kJ/mol, corresponding to a 20-kJ/mol stabilization of the energy with respect to its previous state. The reaction energies for these reconstructions of [Ga(III)H2]-MOR are now on the same order of magnitude as the reaction energies in alkane dehydrogenation [11].
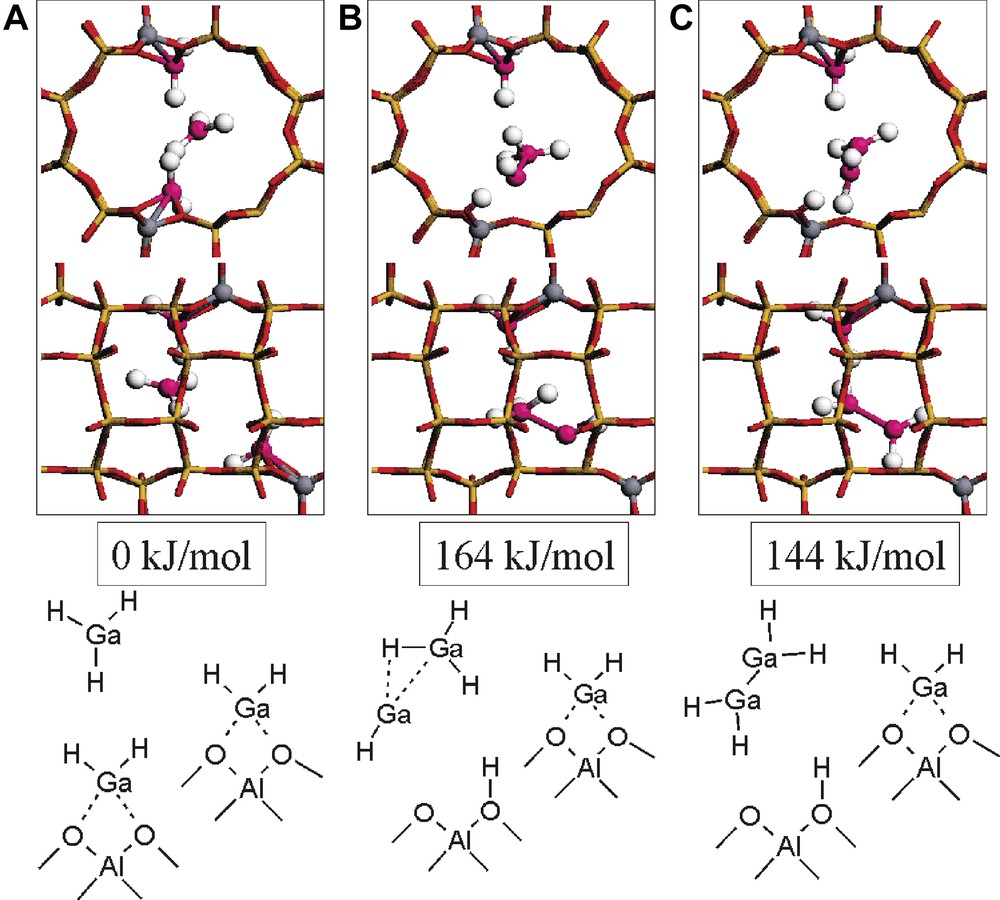
Geometries and energies of [Ga(III)H2]-MOR, [Ga(III)H2]-MOR, and GaH3 (A), [Ga(III)H2]-MOR, H-MOR, and Ga(I)H·Ga(III)H3 (B), and [Ga(III)H2]-MOR, H-MOR, and Ga(II)H2Ga(II)H2 (C) as obtained in the periodic density functional theory calculations.
Main geometrical parameters of the Ga(III)H3·Ga(I)H, H-MOR and [Ga(III)H2]-MOR as obtained in the calculations (Fig. 1c). Distances in Å, angles in °
| Al1O1 | 1.79 | Al2O3 | 1.68 |
| Al1O2 | 1.81 | Al2O4 | 1.67 |
| O1Ga1 | 2.04 | Al2O5 | 1.90 |
| O2Ga1 | 2.02 | O3Ga2 | 3.53 |
| Ga1H1 | 1.53 | O4Ga2 | 3.79 |
| Ga1H2 | 1.53 | Ga2H3 | 1.60 |
| Ga2H4 | 2.13 | ||
| Al1O1Ga1 | 96.3 | Ga2Ga3 | 2.43 |
| Al1O2Ga1 | 96.5 | Ga3H4 | 1.66 |
| O1Al1O2 | 89.7 | Ga3H5 | 1.54 |
| O1Ga1O2 | 77.5 | Ga3H6 | 1.55 |
| O1Ga1H1 | 107.8 | O5Ha | 0.98 |
| O1Ga1H2 | 106.8 | ||
| O2Ga1H1 | 106.1 | Al2O3Ga2 | 52.6 |
| O2Ga1H2 | 107.2 | Al2O4Ga2 | 61.4 |
| Al2O5Ha | 110.6 | ||
| Al1O1Ga1O2 | –1.2 | O3Al2O4 | 114.0 |
| Al1O1Ga1H1 | –102.0 | O4Al2O5 | 97.4 |
| Al1O1Ga1H2 | 105.1 | O3Ga2O4 | 72.3 |
| O3Ga2H3 | 61.5 | ||
| O4Ga2H3 | 52.8 | ||
| O3Ga2Ga3 | 21.7 | ||
| O4Ga2Ga3 | 7.8 | ||
| Ga2Ga3H4 | 59.3 | ||
| Ga2H4Ga3 | 78.8 | ||
| Ga2Ga3H5 | 117.8 | ||
| Ga2Ga3H6 | 108.6 | ||
| Al2O3Ga2Ga3 | 139.5 | ||
| Al2O4Ga2Ga3 | –32.4 | ||
| H3O4Ga2Ga3 | –11.4 | ||
| H3Ga2Ga3H5 | –116.4 | ||
| H3Ga2Ga3H6 | 92.5 | ||
| O4Al2O5Ha | 12.7 |
3.3 Reconstructions in gallium-exchanged mordenite in presence of propene and hydrogen
The last series of periodic density functional theory calculations were performed on the reconstruction of two [Ga(III)H2]-MOR, propene, and H2 (Fig. 4). It is important to mention that alkanes dehydrogenation produces H2 [37], which probably keeps the catalyst under reductive conditions. From the starting system, generation of a zeolite Brønsted acidic site was considered. The energy of the initial structure was used as energy reference (Fig. 4a).

Geometries and energies of [Ga(III)H2]-MOR, [Ga(III)H2]-MOR, propene, and H2 (A), [Ga(III)H2]-MOR, H-MOR, GaH3, and propene (B), [Ga(III)H2]-MOR, [i-C3H7]-MOR, and GaH3 (C), and [Ga(II)H2Ga(II)H]-MOR, [i-C3H7]-MOR, and H2 (D) as obtained in the periodic density functional theory calculations.
Previously, GaH3 was used as hydrogen source to assist in the generation of the Brønsted acidic site. Here, H2 is directly used for this purpose. [Ga(III)H2]-MOR and H2 dissociate leading to the formation of GaH3 and H-MOR (Fig. 4b). The energy of this system is +108 kJ/mol. It is known that propene is readily protonated in protonic zeolite [38]. Moreover, the propyl carbocation is not stable in zeolite and eventually chemisorbs to Z– where Z– is the deprotonated Brønsted acidic site [39]. This GaH3 [Ga(III)H2]-MOR, and [i-C3H7]-MOR system was checked (Fig. 4c). It leads to an even more stable intermediate as expected because of the exothermic propene chemisorption to H-zeolite corresponding to an energy is +65 kJ/mol.
The GaH3 molecule that is generated here may be involved in the [Ga(III)H2]-MOR reconstruction as shown in Fig. 3. Also, a reconstruction of [Ga(III)H2]-MOR as shown in Fig. 1 may be relevant. We have only considered the situation where GaH3 associates to [Ga(III)H2]-MOR to lead to the formation of [Ga(II)H2Ga(II)H]-MOR (Fig. 4d). The energy of this system is +114 kJ/mol with respect to the energy reference structure. This means that the reaction of formation of [Ga(II)H2Ga(II)H]-MOR from GaH3 and [Ga(III)H2]-MOR is only around 50 kJ/mol. This decrease in energy is partly obtained because of the exothermic nature of the formation of the alkoxy species.
Moreover, it can be seen that the reconstruction of [Ga(III)H2]-MOR to other structures in the presence of propene and H2, both products of alkane dehydrogenation, have energies that are equivalent or lower than that of reaction intermediates in alkane dehydrogenation (Scheme 2) [11]. However, the generation of alkoxy and eventually of aromatics compounds results in a favorable thermodynamic driving force when propene is present.
3.4 Dehydrogenation activity of the reconstructed sites
At the moment it is not know whether these intermediates are kinetically relevant if the activation energies in alkane dehydrogenation are considered. To give some insight in the answer we performed small gas-phase and cluster approach calculations using similar method as employed by Frash and Van Santen [11].
The results of these calculations are summarized in Schemes 3 and 4. In Scheme 3, reaction (1) is the dehydrogenation step from the study of Frash and Van Santen [11]. From the transition state in reaction (1), we derive the transition states for reactions (2) to (5). Ga(III)H2–C2H5 dissociates to Ga(III)H3 and C2H4 in reaction (2). The activation energy corrected from zero point energy, the activation enthalpy and free energy at 298 K are reported in Scheme 3. One observes that the activation energy barrier for this step is around 110 kJ/mol lower than that of [Ga(III)HC2H5]-Z to [GaH2]-Z and ethylene. Interestingly, this decrease in activation energy matches roughly the reaction energy associated with the generation of ‘free’ Ga(III) from Ga(III)-MOR as obtained in the periodic density functional theory calculations (Fig. 3c). However, a reaction following the reaction pathway as suggested in reaction (2) might be kinetically preferred over reaction (1). Reaction (2) can also be used as a reference to check how the reconstruction and association of gallium atoms in mordenite as shown in Fig. 1b, c, and Fig. 3c will affect the reaction energy barrier in the rate determining step of the dehydrogenation catalytic cycle (Scheme 2) [11]. In reaction (3), the same reaction is considered when the activation occurs by a –Ga(II)HGa(II)H2 instead of –Ga(III)H2 (Scheme 3). The activation energy decreases by around 20 kJ/mol with respect to the activation energy in reaction (2). When the reaction is activated by –Ga(II)HGa(0), the decrease of the activation energy is even more important (reaction (4) in Scheme 3) and becomes around 60 kJ/mol compared to the activation energy barrier in reaction (2).

Reaction intermediates and transition states and their energies as obtained in the calculations when different gallium-based molecules are tested in the rate limiting step of the ethane dehydrogenation reaction. Eact is the activation energy barrier corrected from zero point energy. ΔHact and ΔGact are enthalpy and free energy of activation at 298 K, respectively. All values are in kJ/mol.
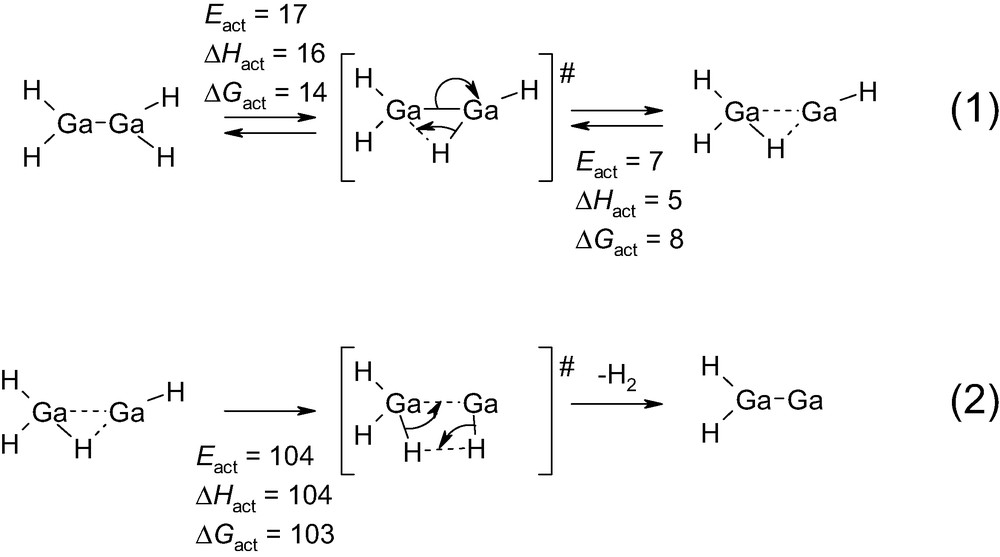
Reaction intermediates and transition states and their energies for the isomerization of Ga(II)H2–Ga(II)H2 to Ga(III)H3·Ga(I)H, and consecutive dehydrogenation to Ga(II)H2–Ga(0) as obtained in the calculations. Eact is the activation energy barrier corrected from zero point energy. ΔHact and ΔGact are enthalpy and free energy of activation at 298 K, respectively. All values are in kJ/mol.
Finally, we checked the same step in the case of activation by –Ga(I) (reaction (5) in Scheme 3). For this situation no decrease in activation energy is observed but a higher energy barrier is obtained.
A further point to be discussed is the ease of formation of the Ga(I) cation. The conversion of Ga(II)H2–Ga(II)H2 to Ga(III)H3·Ga(I)H is indeed relatively easy (reaction (1) in Scheme 4). Considering the order of magnitude of the activation energies that are required in alkane dehydrogenation (Scheme 2), this suggests that an equilibrium between Ga(II)H2–Ga(II)H2 and Ga(III)H3·Ga(I)H is obtained under reaction conditions.
Starting from Ga(III)H3·Ga(I)H, further dehydrogenation can be achieved (reaction (2) in Scheme 4). This step is energetically more demanding with an activation energy around 104 kJ/mol. However, this remains well below the activation energies that are identified in alkane dehydrogenation (Scheme 2 and Scheme 3).
Therefore, it appears that the reconstructions of gallium sites as proposed in the periodic density functional theory calculations can catalyze alkane dehydrogenation. Considering the limited models that were employed here, more studies must be achieved to truly clarify the role of the reconstructions in catalysis. However, the reaction energy of the gallium reconstructions, i.e. 101–128 kJ/mol for the most stable reconstructions, is well below the reaction energy of ethane dehydrogenation, i.e. 134 kJ/mol. The reconstructions are thermodynamically more favorable than alkane dehydrogenation.
Another interesting result is that the activation energy for the reaction of [Ga(III)HC2H5]-Z to C2H4 and [Ga(III)H2]-Z is higher than that of systems in which Ga(III) is not chemisorbed to the zeolite. This suggests that an alternative reaction route from Int2 in Scheme 2 is possible. This reaction route might follow the sequence Int1–TS1–Int2 as in Scheme 2. Then, the route would fold toward a transition state structure as in reaction (2) (Scheme 3). Using the same energy reference as in Scheme 2, there is no energy gain in this reaction route. However, when one considers that a previously formed olefin can chemisorb to the zeolite Brønsted acidic site that is hence made available, this leads to a stabilization of the system by around 25–40 kJ/mol [15,16]. This alternative reaction route becomes kinetically dominant. It would result in the formation of GaH3, C2H4, and H-Z. The last step in this reaction route is then the restoration of the initial catalytic site, namely [GaH2]-Z, from GaH3 and H-Z. We performed the calculation for this transition state which is in essence similar to TS2 in Scheme 2. We did not put GaH3 in contact with H-Z because the optimization of GaH3 physisorbed to H-Z, where Z is AlH2(SiH3)2–, resulted in an unrealistic deformation and interactions of the cluster due to its limited size. We found an activation energy for this reaction of 128 kJ/mol (ΔHact = 131 kJ/mol and ΔGact = 84 kJ/mol at 298 K). This last step again does not constitute a rate determining step as demanding as Int3 to TS3 in Scheme 2.
4 Conclusions
We have performed a quantum chemical analysis of various structural changes of gallium-exchanged mordenite using periodic density functional theory method. It appears that these reconstructions exhibit relatively high reaction energies. However, those high energy intermediates are reachable when they are set in the perspective of the alkane dehydrogenation catalytic cycle. A succession of Ga(III)Hx, Ga(II)Hx, and Ga(I)Hx intermediates have almost equivalent energies. Some of these intermediates can lead to enhanced rates of dehydrogenation. Especially, it appears that condensation of gallium to dimeric species can reduce the activation energy of the rate determining step in alkane dehydrogenation. Moreover, non-coordinated to the zeolite gallium species are observed to be more active than when they are chemisorbed to a zeolite aluminum oxide tetrahedron. The generation of alkoxy results in a favorable thermodynamic driving force in the system. Based on these results, an alternative reaction route in alkane dehydrogenation that goes through direct decomposition of GaH2CyHz (see Int2 in Scheme 2) to olefin and GaH3 is proposed. The gallium species is then restored to the chemisorbed state with assistance of a zeolitic Brønsted acidic site. When dimeric gallium species are involved, the reaction goes through decomposition of Ga2HxCyHz to olefin and Ga2Hx+1. The restoration of the catalytically active gallium-exchanged by a zeolitic Brønsted acidic site follows the same sequence as with monomeric species.


