1 Introduction
Microporous materials presenting the faujasite (FAU) structure type [1] are widely involved in many industrial molecular sieving, distillation, detergent-builder or catalytic processes [2,3]. The framework structure of Y-type faujasites usually crystallizes in the cubic Fd3m space group. It is built up by sodalite cages (also called β-cages, centered on 8a positions) linked together by double hexagonal rings (D6R, hexagonal prism, 16c positions). The large cavity (also called super-cage or α-cage, centered on 8b positions) is created by the arrangement of eight sodalite units. Each super-cage communicates with four adjacent super-cages through single twelve-ring windows (S12R, centered on 16d positions) and with four sodalite cages through single six-ring (S6R) windows. Neutron powder diffraction [4] and computational methods [5] show that the ideal cation distribution in anhydrous NaY (Si/Al = 2.43) is 8NaI (in the D6R hexagonal prisms, half- populated 16c positions) +16 NaI′ (in the beta-cages, half-populated 32e positions) +32 Na (in the alpha-cages close to S6R, fully populated 32e positions). Concerning NaY [4,6–13] and other cation-exchanged FAU [14–19], or deluminated Y (DAY or US-Y) [20–22], many experimental and theoretical work [23-27 and many references therein] describing the state of benzene molecules sorbed in these materials are reported in the literature. Nevertheless, there are still some conflicting results concerning the benzene and/or cation distributions, the adsorption heats and the sorption capacities of benzene in NaY and DAY faujasites. Computer simulations by molecular mechanics and molecular dynamics using several force-fields have been widely used for the prediction of preferential adsorption sites of many aromatic and aliphatic species in zeolitic host/guest systems [23–27]. Hereafter it is shown that the van der Waals type Buckingham exp-6-1 atom-atom interaction model combined with crystal structure results have been successfully used for simulating the experimental NaY/benzene and DAY/benzene calorimetric curves. Structural results concerning prehydrated pHyNaY/benzene complexes show that the benzene distributions and cation populations are heavily perturbated by polar water molecules.
2 Experimental
The computer simulation methodology (simplex type variable step method) concerning the charge distributions on the zeolite T(Si,Al) and O framework atoms and the potential energy parameters of the Si,O,C,Na atoms used in this work (Table 1) for the exp-6-1 van der Waals-type Buckingham intermolecular atom–atom potential interaction model (equation 1) are detailed in [28–30].(1)
The Buckingham model: atomic potential parameters a,b and c used for the simulations of sorbent/sorbate interactions in the FAU structure type
| Atom | a (kJ/mol)1/2Å3 | b (kJ/mol)1/2Å3 | c (Å–1) | Ref. |
| H | 11.662 | 108.06 | 1.87 | [30] |
| C | 49.132 | 606.01 | 1.80 | [30] |
| O | 33.211 | 536.21 | 1.98 | [30] |
| Si (Al) | 66.000 | 493.00 | 1.41 | [30] |
| Na | 66.000 | 680.00 | 1.86 | [30] |
3 Results and discussion
3.1 Structure refinements
The starting crystal parameters for the FAU framework are those given in [4] (Fd3m space group). In all cases the planar geometry of the benzene species has been constrained to that described in [31,34] for crystals at 270 K (C–C = 1.397, C–H = 1.027 Å, all angles = 120°). In the case of prehydrated NaY/benzene phases (pHyNaY) the starting crystal parameters of the water molecules obtained by computer simulations (see Fig. 3 and section 3.3) are comparable to those reported in [15]. The benzene species close to the NaII cations and those in the S12R windows are labelled BZ(C) and BZ(W) respectively. The water species coordinated to NaI′ and NaII cations are labelled WI′ and WII respectively. The BZ(C)/BZ(W) ratio obtained for the three NaY/benzene, DAY/benzene and pHyNaY/benzene systems are represented in Fig. 1. The unit-cell parameter variations versus benzene loadings for these three systems are given in Fig. 2.

Structural detail of a prehydrated NaY+24benzene+24water complex (only one eighth of the unit-cell is represented).
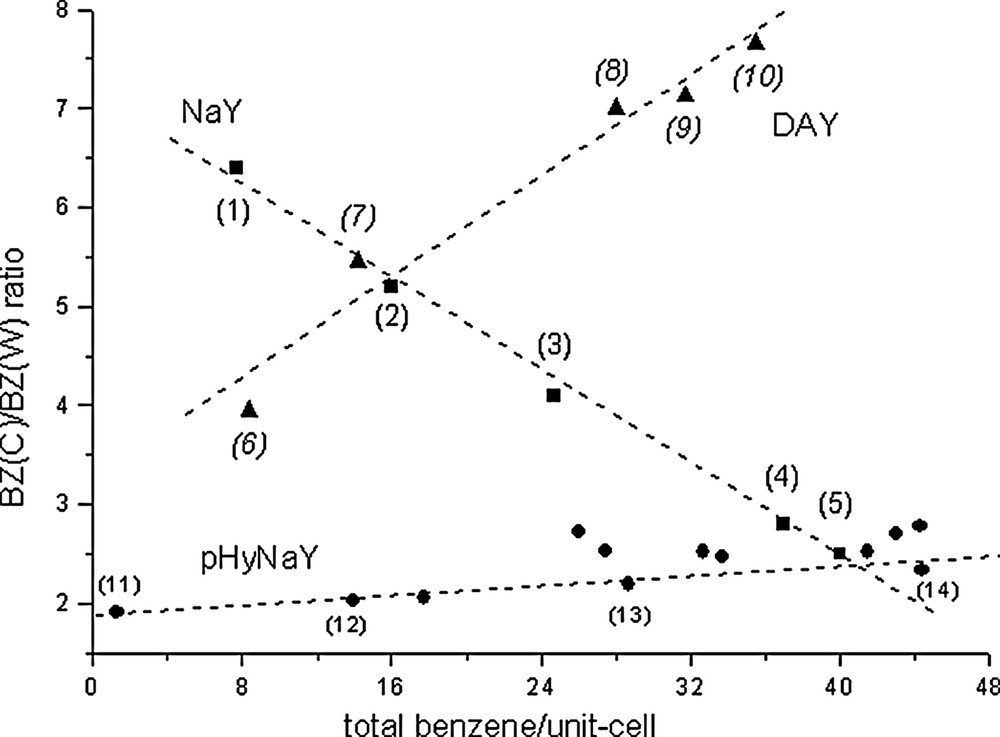
BZ(C)/BZ(W) ratio versus benzene loadings observed for the three NaY/benzene, prehydrated NaY/benzene and DAY/benzene systems.
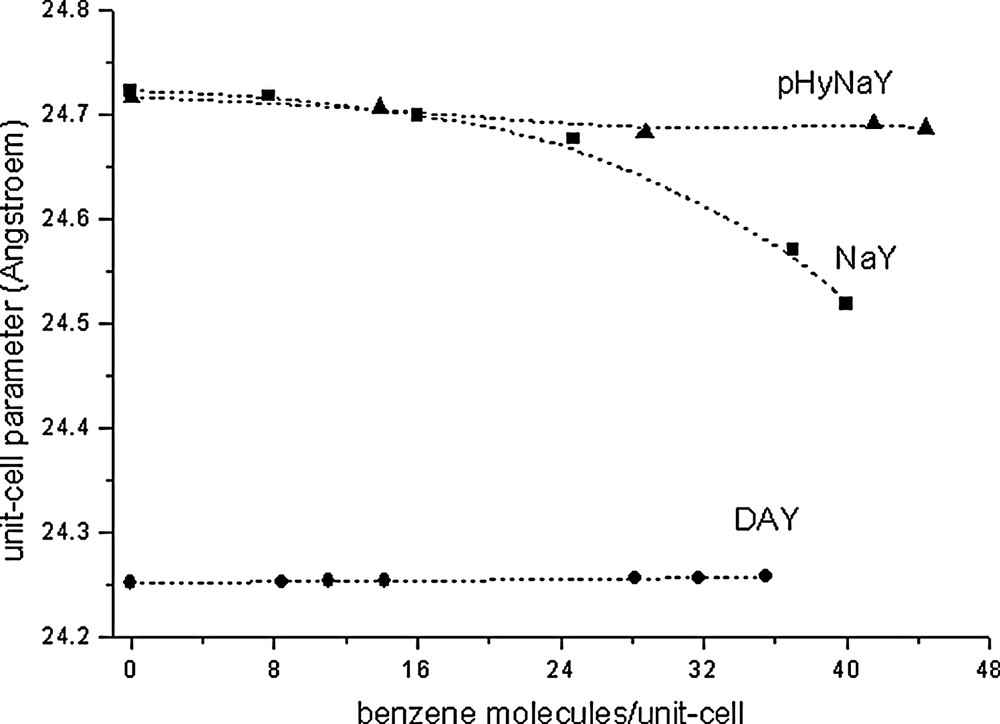
Unit-cell parameter (Å) versus benzene loadings observed for the three NaY/benzene, prehydrated NaY/benzene and DAY/benzene systems.
3.1.1 The NaY/benzene system
In this system the variation of the r = BZ(C)/BZ(W) ratio versus benzene loadings is almost linear. Points 1 and 3 are from reference [4], points 2 and 4 correspond to NaY/C6H6 (D1B) complexes and point 5 to a sample in a glass capillary (X-rays). The BZ(C)/BZ(W) distributions might be calculated for all loadings by the r = 7.235 – 0.122 × (total benzene/uc) (R = 0.995). Accordingly, the r ratio decreases with sorbate fillings. At zero filling this ratio is 7.24 (close to 8) and extrapolated to 48 benzene/uc (theoretical maximum) its value is about 1.4. The experimentally observed sorption capacity of benzene in NaY (Si/Al = 2.43) is close to 42–43 molecules/uc (42.5 [10], 43.2 [8]), which roughly corresponds to point 5 with r ≈ 2. Fig. 2 shows that for this system the unit-cell parameter of the FAU framework decreases rather rapidly with higher benzene loadings. For all benzene loadings the cation site populations remain almost constant [4, this work]. The Rietveld plots and some structural results corresponding to points 2, 4 and 5 are reported in Appendix 1 and Figs. A.I.1 to A.I.3.
3.1.2 The DAY/benzene system
For this system, the r versus fillings ratio increases rapidly with increasing benzene loadings. At saturation (39.5 molecules/uc [20]) the BZ(W) species have almost disappeared. This particularity will be discussed in the sections concerning the calorimetric curve and the computer simulations. The crystal structure corresponding to a DAY/32benzene phase (r = 7.1) close to the saturation capacity has been reported in [21]. The corresponding atomic coordinates are reported in Appendix 2 as additional data and the Rietveld plot is given in Fig. A.II.6. Fig. 2 shows that for this system the unit-cell parameter of the FAU framework increases slowly and linearly with increasing benzene loadings. The Rietveld plots, refined benzene molecules and some structural results corresponding to points 6–10 are reported in Appendix 2 and Figs. A.II.1 to A.II.5. Unfortunalety no intermediate benzene loading between points 7 and 8 is presently available.
3.1.3 The pHyNaY/benzene system
For this system, the r versus benzene/uc variation is also linear. For all compositions, r is slightly increasing, its mean value being close to 2. Fig. 2 shows that the unit-cell parameter of the FAU framework decreases slowly and linearly with increasing benzene loadings. The WI′ and WII water molecules have been localized near the NaI′ and NaII cations respectively. Table 2 reports some structural results concerning three pHyNaY/benzene complexes and compares them to the sorbate free NaY. In the present case several details must be emphasized.
Distribution of the NaI, NaI′ and NaII cationic species, the BZ(C) and BZ(W) benzene species, and the WI′ and WII water species in three prehydrated pHyNaY/benzene complexes (per unit cell)
| Sample | a(Å) | NaI | NaI′ | NaII | BZ(C) | BZ(W) | WI′ | WII |
| empty NaY | 24.715(1) | 8a | 16 | 32 | 0 | 0 | 0 | 0 |
| PL_1.3BZ | 24.716 | 8 | 17 | 31 | 0.85 | 0.45 | 0 | 18 |
| PL_15BZ | 24.705(1) | 5 | 25 | 26 | 8 | 7 | 1 | 17 |
| PL_29BZ | 24.693(1) | 3 | 26 | 27 | 19 | 10 | 3 | 15 |
| PL_43BZ | 24.690(1) | 1 | 25 | 30 | 30 | 13 | 8 | 10 |
a Site population e.s.ds are typically 2–4% of the refined value.
At constant water loading (18 molecules/uc):
- – (1) the Na cation distribution is heavily disturbed; this is a direct result of water/framework and/or water/Na interactions as in prehydrated BaX/xylene phases where cation migrations have also been observed [15];
- – (2) with increasing benzene concentrations the population of site NaI decreases almost to nil, whereas the population of site NaI′ remains almost constant and that of site NaII increases as a consequence of a compensating effect of the decreasing NaI population;
- – (3) at the same time, the WII site population decreases at the advantage of WI′ coordinated to NaI′ and with increasing benzene loadings some water molecules are forced into the sodalite cage.
3.2 Calorimetric results
The differential molar adsorption heats at 300 K for the NaY/benzene and US-Y/benzene systems are represented in Fig. 4. For the first system, the adsorption heat increases linearly from zero-filling (extrapolated value ≈ –78 kJ/mol) up to 32 benzene/uc (–86 kJ/mol). This corresponds to a mean heat increase of 0.27 kJ/mol per adsorbed benzene molecule and corresponds to Coulombic intermolecular benzene/benzene interactions. After 32 benzene/uc (4 molecules per super cage), the adsorption heat decreases abruptly down to –58 kJ/mol at saturation (42.5 benzene/uc), which corresponds to 5.31 benzene molecules per super cage. The heat decrease corresponds to increasing repulsive interactions between the adsorbed species: even if the theoretical crystal chemical sorption capacity is 48 benzene/uc ([4 BZ(C) + 2BZ(W)] per super cage), at this concentration there is not enough place for so much sorbate. For the US-Y/benzene system the situation is much more complicated. The US-Y sample corresponds to Si/Al = 95 [10] and contains still 2 Na cations per unit-cell. These residual cations and unavoidable structural defects provoked by the dealumination process itself may play a specific role in the starting adsorption process and therefore the initial heats are rather high: the initial curve might be extrapolated at zero filling and compared to the NaY/benzene initial heat (–78 kJ/mol). Accordingly, the first data points of the US-Y/benzene curve should be discarded and the true initial adsorption heat be extrapolated to about –42 kJ/mol. Up to 12 benzene/uc the mean heat increment is about 0.29 kJ/mol and from 12 up to 20 benzene/uc it is 0.75 kJ/mol, the maximum heat being –52.5 kJ/mol. After 20 benzene/uc the heat decreases down to –41 kJ/mol, the mean decrement being 0.96 kJ/mol. Finally, up to saturation (39.5 benzene/uc or 4.94 benzene per super cage) the heat decrement is about 0.36 kJ/mol, the minimum adsorption heat being –37.5 kJ/mol. For this system the benzene condensation heat is almost attained (–33.5 kJ/mol at 300 K).
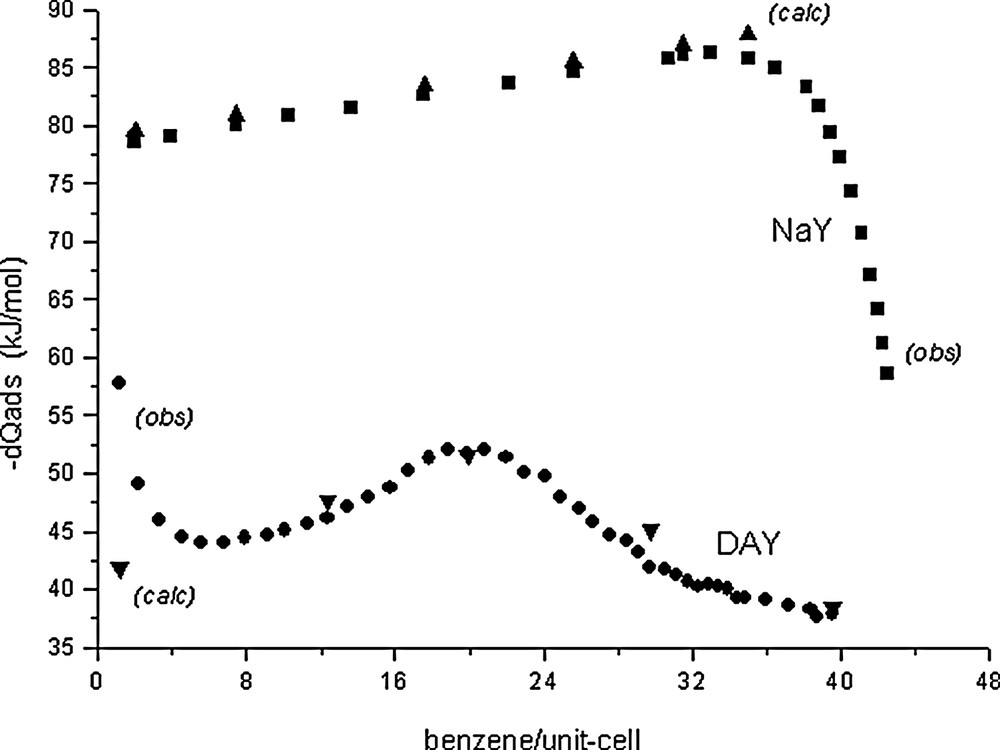
Experimental differential molar adsorption heat curves at 300K for the NaY/benzene [20] and US–Y/benzene systems [10].
3.3 Computer simulations
3.3.1 The NaY/benzene system
Energy-minimization calculations using the exp-6-1 Buckingham model yield –79.0 and –46.7 kJ/mol for the adsorption heats of isolated BZ(C) and BZ(W) species at infinite dilution respectively [30]. The relatively large difference between these energies explains why at lower loadings the cationic site is favoured. This is in agreement with the r ratio line and the crystal structure refinements [4, this work]. It has been verified that at all loadings the benzene locations and orientations remain the same [4, this work]. This is a direct consequence of the specific BZ(C)/cation and BZ(W)/framework interactions. Knowing the distributions of the two types of benzene species for all loadings, the estimated adsorption heats for points 1 to 4 in Fig. 1 have been estimated. The benzene/benzene interactions between BZ(C)/BZ(C), BZ(C)/BZ(W) and BZ(W)/BZ(W) have been calculated for increasing benzene species in a spherical faujasite structural moeity centered on the super cage (x,x,x = 3/8) with 20Å radius. The mean BZ/BZ interaction increment for increasing loadings amounts to 0.252 kJ/mol, which is in correct agreement with the experimentally observed 0.27 kJ/mol value. The calculated values (triangular ▲ and ▼symbols) are compared to the experimental adsorption heats in Table 3 and reported in Fig. 4. After 32 benzene/uc the unit-cell parameter decreases (Fig. 2) and at the same time the adsorption heat drops. This rapid decrease of the adsorption heats might be the consequence of simultaneaous effects due (a) to increasing unfavourable benzene/ benzene interactions as a consequence of unit-cell volume decrease, (b) to increasing concentrations of the BZ(W) species which present much lower adsorption heat contributions and (c) to the end of the pore-filling effect.
Observed and calculated adsorption heats for four NaY/benzene fillings
| Point | BZ(C)/BZ(W) ratio | Benzene/uc | –Eobs (kJ/mol) | –Ecal (kJ/mol) |
| 1 | 6.4 | 7.7 | 80 | 80.9 |
| 2 | 5.2 | 16.0 | 82 | 83.0 |
| 3 | 4.1 | 24.7 | 84 | 85.2 |
| 4 | 3.3 | 37.0 | 86 | 87.1 |
3.3.2 The US-Y/benzene system
There are no adsorption heats available for the DAY/benzene system (Si/Al ≈ 200). The only comparable data are those reported in [10] and represented in Fig. 4 (Si/Al = 95). Fig. 5a,b compare the locations of the two independent benzene species in NaY and DAY. These locations correspond to isolated species at zero filling. For DAY the calculated adsorption heats for BZ(C) and BZ(W) are –41.2 and –35.9 kJ/mol respectively. The extrapolated experimental value at zero filling is about –42 kJ/mol. The calculated heats for both benzene species are very close. Accordingly, we might expect that both sites are equally probable. The r line for this system shows that at increasing benzene fillings the BZ(W) species is less and less favoured: in other terms, everything happens as if the BZ(W) species progressively vanish at higher loadings. In fact, the structure refinements and the simulations show that when the two benzene species coexist, BZ(W) quits the S12R window and gets closer to BZ(C): the non-interacting molecules in Fig. 5b yield those represented in Fig. 6a when both benzene species interact. The starting structural models for the BZ(C) and BZ(W) benzene species in DAY which have been simulated by molecular mechanics are given in Table 4. These positions are very close to those reported for DAY/benzene complexes analyzed by neutron powder diffraction (see Appendix 2 and the results corresponding to Figs. A.II.1 and A.II.6). It might be preferable to label the two independent sorbate species BZ1 and BZ2, but for homogeinity with the NaY/benzene and pHyNaY/benzene systems we still label them BZ(C) and BZ(W). The energy-minimization calculations show that the benzene/benzene interactions are much higher than in the NaY/benzene system, where the benzene species could not quit their sorption sites. Fig. 6 shows some benzene distributions for 2,3,4 and 5 benzene/super cage respectively. The calculated benzene/benzene mean interaction increment up to 20 benzene/uc amounts to 0.59 kJ/mol and at higher loadings up to saturation there is a decrement of about 0.67 kJ/mol. For comparison, the experimentally observed mean increment and decrement are 0.52 and 0.66 respectively. The benzene sorption capacity of US-Y is 39.5 molecules/uc. Since there are no Na cations in US-Y, the BZ(C) are closer to the framework and in greater confinement. As a consequence the centre of the alpha cage is able to accept a benzene molecule, the result being the formation a (C6H6)5 cluster (Fig. 6d) at 40 benzene/uc, which is comparable to the saturation capacity of US-Y. Compared to NaY/benzene, where the sorbate species are fully ordered, in DAY/benzene they are completely disordered at room temperature. Accordingly, the distributions represented in Fig. 6a,b,c,d are some among an infinity of possible solutions.

The two independent benzene molecules in (a) NaY and (b) DAY at infinite dilution.
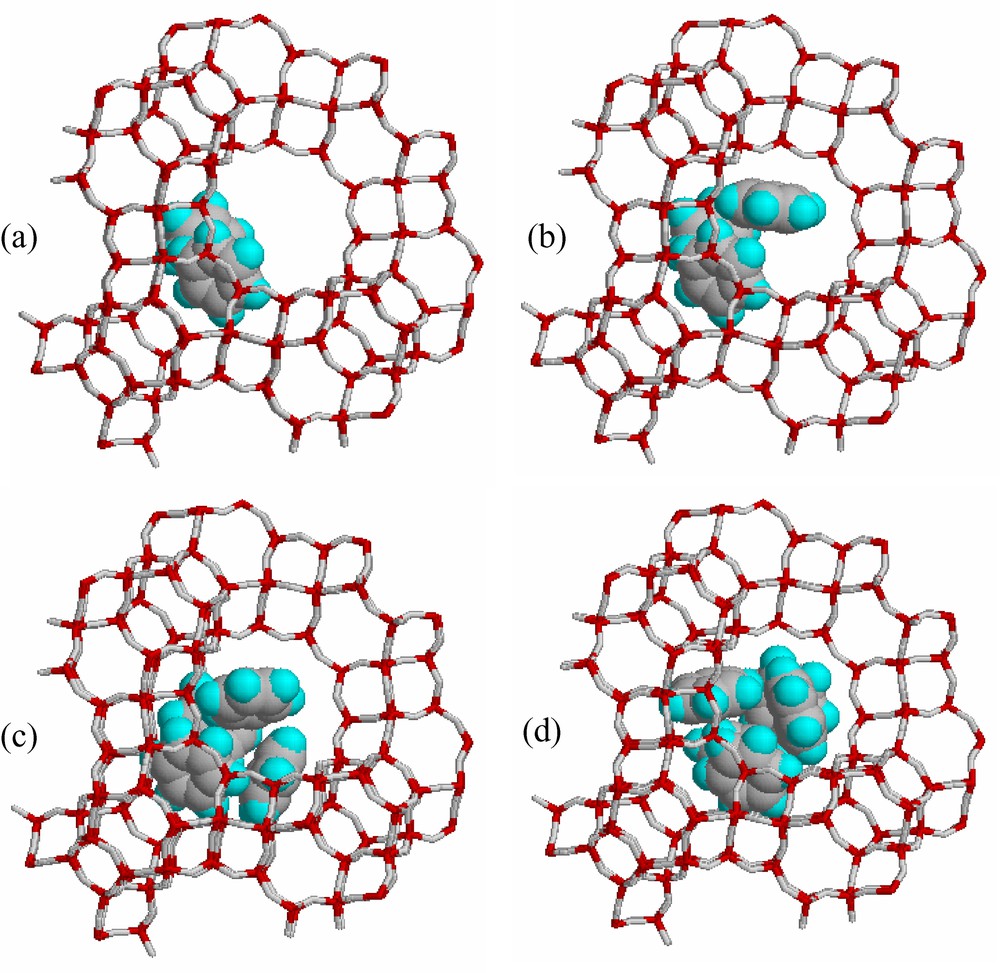
Computer simulation of the DAY/benzene system: possible benzene distributions at (a) 2, (b) 3, (c) 4 and (d) 5 benzene/super cage.
Modelisation of isolated BZ(C) and BZ(W) in DAY by molecular mechanics
| BZ(C) | BZ(W) | ||||||
| C11 | .3187 | .4076 | .2226 | C21 | .5348 | .4641 | .4745 |
| C12 | .3245 | .3014 | .2668 | C22 | .4671 | .5378 | .5316 |
| C13 | .2767 | .3884 | .2571 | C23 | .4983 | .4980 | .4456 |
| C14 | .3665 | .3206 | .2323 | C24 | .5036 | .5039 | .5605 |
| C15 | .2796 | .3353 | .2792 | C25 | .4644 | .5348 | .4741 |
| C16 | .3636 | .3737 | .2103 | C26 | .5375 | .4671 | .5319 |
| H11 | .3166 | .4467 | .2061 | H21 | .5597 | .4370 | .4535 |
| H12 | .3266 | .2623 | .2830 | H22 | .4423 | .5649 | .5526 |
| H13 | .2437 | .4133 | .2662 | H23 | .4963 | .4968 | .4033 |
| H14 | .3995 | .2956 | .2232 | H24 | .5056 | .5061 | .6027 |
| H15 | .2488 | .3212 | .3044 | H25 | .4376 | .5598 | .4529 |
| H16 | .3944 | .3878 | .1849 | H26 | .5643 | .4421 | .5532 |
3.3.3 The pHyNaY/benzene system
The atomic coordinates of the adsorbed WI′ and WII water species simulated by molecular mechanics are gien in Table 5. In order to avoid undesired parameter correlations, these coordinates together with the known benzene coordinates have been fixed during the refinement process and only their populations have been relaxed.
Modelisation of isolated WI′ and WII in pHyNaY by molecular mechanics
| WI′ | WII | ||||||
| Ow1 | .1668 | .1672 | .1708 | Ow2 | .2111 | .3246 | .3286 |
| Hw11 | .1807 | .1345 | .1914 | Hw21 | .1710 | .3307 | .3227 |
| Hw12 | .1340 | .1825 | .1901 | Hw22 | .2214 | .3375 | .3662 |
4 Conclusion
It appears that the benzene adsorption process in faujasite type zeolites drastically depends on the starting material. The preference of the benzene molecules for a cationic or a window site is very different in NaY and DAY. The comparison of structural results, experimental calorimetric curves and van der Waals type computer simulations yields a better knowledge on the intimate mechanism of benzene adsorption in faujasite. Some details of this mechanism could only be attained by the interpretation of the calorimetric curve. Therefore, whenever possible, structural and calorimetric investigations should be performed on the same sample, since small variations in the chemical composition or the presence of residual cations, which are not easely detected by diffraction techniques, might be revealed by the differential molar adsorption heat curve. In order to illustrate the specific role of a polar molecule on the benzene adsorption process in NaY, a prehydrated NaY/benzene system has also been investigated. It appears that in this system the benzene distribution over the cationic and window sites is almost constant at all fillings. With increasing sorbate amounts the water molecules coordinated to the NaII cation are progressivley forced into the sodalite cage where the benzene molecules do not penetrate, the sorption capacities of the pure NaY and the prehydrated NaY being almost the same. The most important result of water/benzene coadsorption is the dramatic cationic migration effect: at constant water content (about 18 molecules/uc) the NaI cations migrate completely into the sodalite cage.
Appendix 1 – Points 1 to 5 in Fig. 1 for the NaY/benzene system. Points 1 and 3 are given in ref. [4]
In all cases: upper/medium/lower traces correspond to calculated/experimental/difference plots
Point 2
Sample label: NA56YBZ
Sample formula: Na56Al56Si136O384·16 C6H6
Sample origin: Linde sodium-Y zeolite (see ref. [4]) in Al-tube
Diffractometer: D1B – ILL
Wavelength (Å): 2.5224
Angular range (°2θ): 7.0 – 83.6 (limited data-collection)
Angular step (°2θ): 0.2
Unit-cell parameter (Å): 24.699(4)
Number of observables: 384 + 37 = 421
Number of hkl triplets: 73
Rp/Rwp/Rex/RI (%): 9.9/16.0/1.9/8.2
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0544(5) | .0351(6) | .1244(5) | 0.8 | 192 |
| O1 | –.1090(5) | 0 | .1090(5) | 2.5 | 96 |
| O2 | –.0028(5) | –.0028(5) | .1418(7) | 2.5 | 96 |
| O3 | –.0343(8) | .0714(5) | .0714(5) | 2.5 | 96 |
| O4 | –.0684(8) | .0758(5) | .1742(5) | 2.5 | 96 |
| NaI | 0 | 0 | 0 | 3.3 | 8(1) |
| NaI' | .055(3) | 16(1) | |||
| NaII | .236(2) | 32(1) | |||
| C1 | .257 | .337 | .297 | 9.0 | 13.4(6) |
| H1 | .226 | .368 | .297 | ||
| C2 | .477 | .477 | .546 | 9.0 | 2.6(5) |
| H2 | .459 | .459 | .582 | 9.0 | |
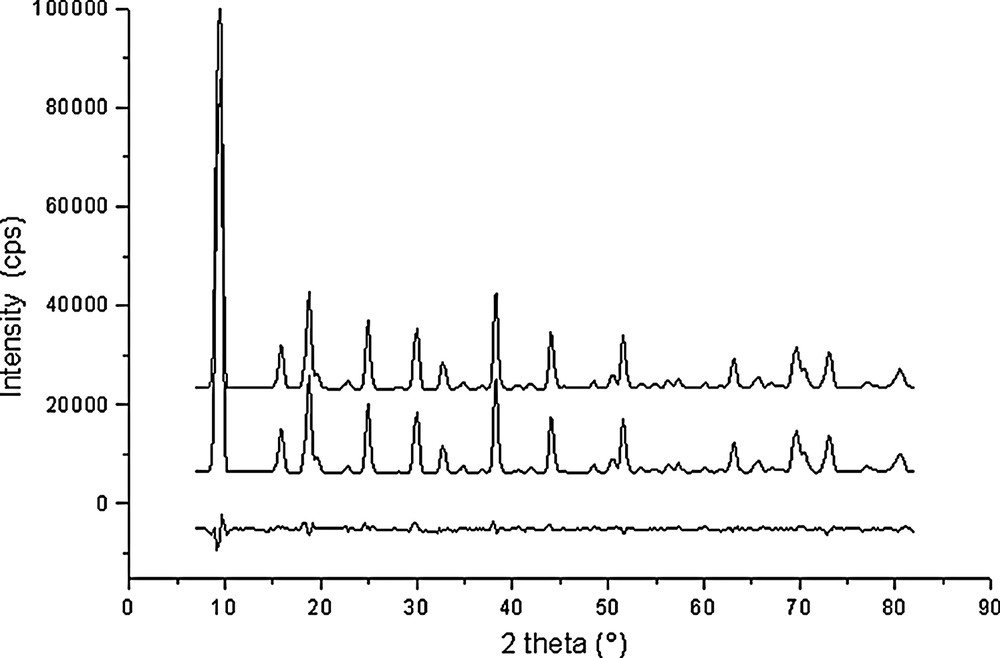
Rietveld plots for Na56Al56Si136O384·16 C6H6 (point 2 in Fig. 1).
Point 4
Sample label: L52ALBZ
Sample formula: Na56Al56Si136O384·37 C6H6
Sample origin: LZY-52 (sigma Aldrich) in Al tube
Diffractometer: D1B – ILL
Wavelength (Å): 2.5224
Angular range (°2θ): 7.0–82.0 (limited data-collection)
Angular step (°2θ): 0.2
Unit-cell parameter (Å): 24.570(4)
Number of observables: 376 + 37 = 413
Number of hkl triplets: 73
Rp/Rwp/Rex/RI (%): 10.2/16.4/2.0/7.9
| Atom | x/a | y/b | z/c | B(iso) | population/uc |
| Si | –.0541(4) | .0355(4) | .1242(4) | 0.8 | 192 |
| O1 | –.1086(3) | 0 | .1086(3) | 2.5 | 96 |
| O2 | –.0024(4) | –.0024(5) | .1435(7) | 2.5 | 96 |
| O3 | –.0354(7) | .0708(4) | .0708(4) | 2.5 | 96 |
| O4 | –.0719(7) | .0759(4) | .1741(4) | 2.5 | 96 |
| NaI | 0 | 0 | 0 | 3.3 | 8(1) |
| NaI' | .059(4) | 16(1) | |||
| NaII | .238(2) | 32(1) | |||
| C1 | .257 | .337 | .297 | 9.0 | 27.0(7) |
| H1 | .226 | .368 | .297 | ||
| C2 | .477 | .477 | .546 | 9.0 | 9.8(5) |
| H2 | .459 | .459 | .582 | 9.0 |
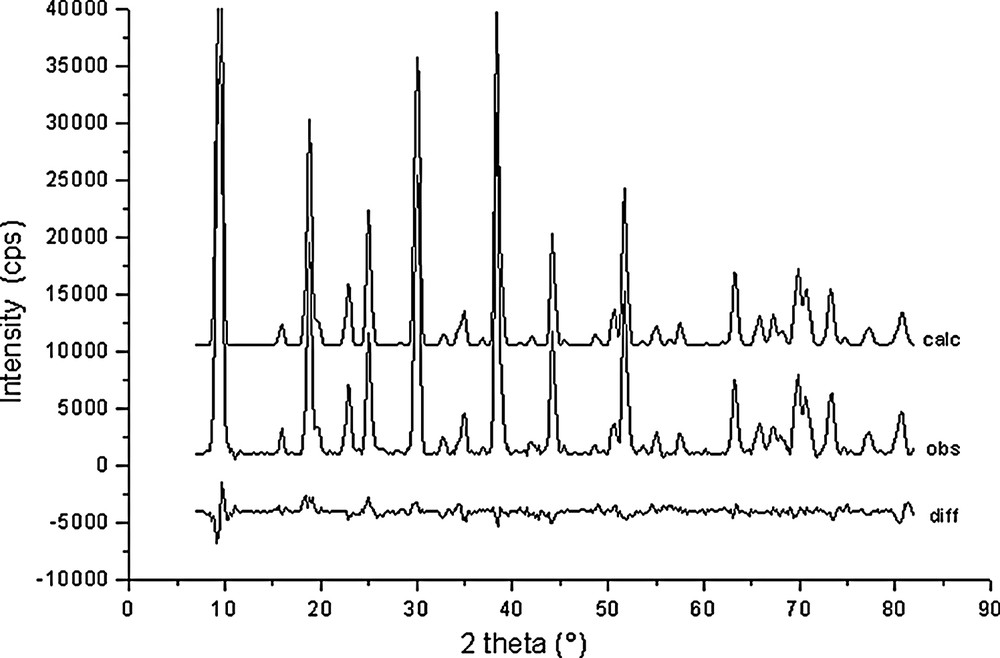
Rietveld plots for Na56Al56Si136O384·37C6H6 (point 4 in Fig. 1).
Point 5
Sample label: cpY56BZ2
Sample formula: Na56Al56Si136O384·40 C6H6
Sample origin: LZY-52 (Sigma Aldrich) in glass capillary
Diffractometer: Philips – X′Pert
Wavelength (Å): Cu Kα
Angular range (°2θ): 4.0 – 84.0
Angular step (°2θ): 0.025
Unit-cell parameter (Å): 24.518(4)
Number of observables: 3201 + 37 = 3238
Number of hkl triplets: 282
Rp/Rwp/Rex/RI (%): 5.8/7.6/7.7/13.1
| Atom | x/a | y/b | z/c | B(iso) | population/uc |
| Si | –.0532(2) | .0357(2) | .1261(2) | 0.8 | 192 |
| O1 | –.1066(2) | 0 | .1066(2) | 2.5 | 96 |
| O2 | –.0017(2) | –.0017(2) | .1443(4) | 2.5 | 96 |
| O3 | –.0344(4) | .0746(2) | .0746(2) | 2.5 | 96 |
| O4 | –.0729(4) | .0727(2) | .1773(2) | 2.5 | 96 |
| NaI | 0 | 0 | 0 | 3.3 | 8(1) |
| NaI' | .0625(9) | 16(1) | |||
| NaII | .2359(6) | 32(1) | |||
| C1 | .257 | .337 | .297 | 9.0 | 28.5(5)2) |
| H1 | .226 | .368 | .297 | ||
| C2 | .477 | .477 | .546 | 9.0 | 11.4(2) |
| H2 | .459 | .459 | .582 | 9.0 |
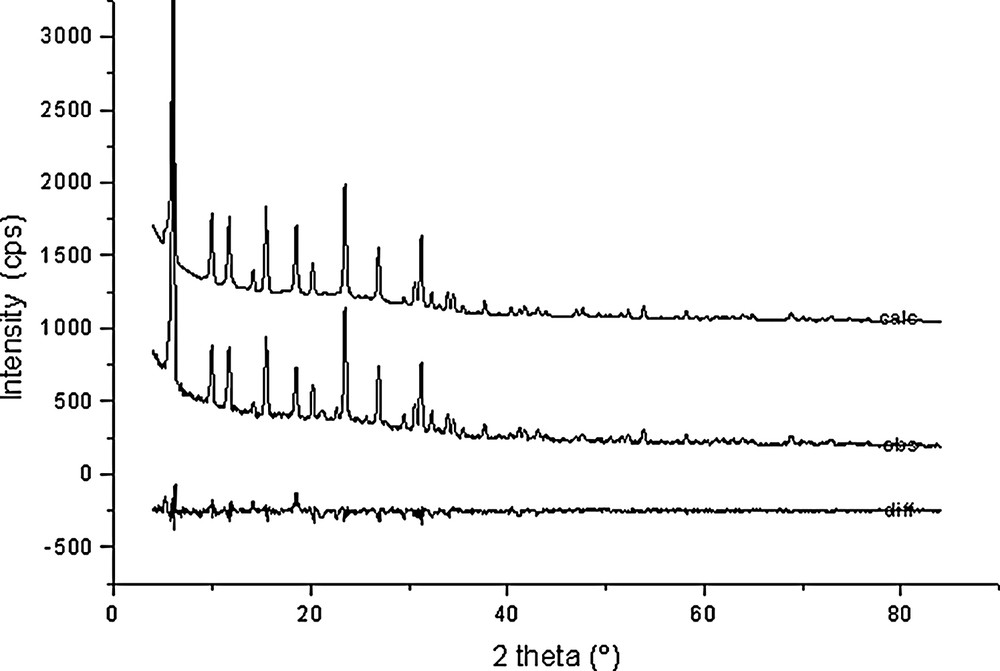
Rietveld plots for Na56Al56Si136O384·40 C6H6 (point 5 in Fig. 1).
Appendix 2 – Points 6 to 10 in Fig. 1 for the DAY/benzene system
DAY/benzene complex at lower loading
Point 6
Sample label: Y20a_bz1
Sample formula: Si192O384·8.4 C6D6
Sample origin: see text
Diffractometer: D2B – ILL quartz tube
Wavelength (Å): 1.59263
Angular range (°2θ): 4.55–106.55
Angular step (°2θ): 0.05
Unit-cell parameter (Å): 24.252
Number of observables: 2201 + 94 = 2295
Number of hkl triplets: 407
Rp/Rwp/Rex/RI (%): 5.5/7.0/8.5/10.4
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0541(1) | .0359(2) | .1251(1) | 0.61(9) | 192 |
| O1 | –.1065(1) | 0 | .1065(1) | 1.0(2) | 96 |
| O2 | –.0038(1) | –.0038(1) | .1403(2) | 0.8(2) | 96 |
| O3 | –.0358(2) | .0762(1) | .0762(1) | 2.3(2) | 96 |
| O4 | –.0705(3) | .0712(2) | .1722(2) | 1.9(2) | 96 |
| C11 | .3274(9) | .4114(4) | .2345(9) | 10(2) | 6.7(2) |
| C12 | .328(2) | .3032(7) | .233(3) | ||
| C13 | .293(2) | .3964(6) | .278(3) | ||
| C14 | .367(2) | .3200(8) | .235(2) | ||
| C15 | .292(1) | .3419(5) | .296(1) | ||
| C16 | .368(1) | .3750(6) | .217(2) | ||
| D11 | .326(2) | .4518(6) | .222(2) | ||
| D12 | .329(3) | .263(1) | .285(4) | ||
| D13 | .266(2) | .4232(7) | .297(3) | ||
| D14 | .396(4) | .294(2) | .219(5) | ||
| D15 | .263(3) | .327(1) | .324(3) | ||
| D16 | .397(3) | .389(1) | .189(3) | ||
| C21 | .549(1) | .476(2) | .471(1) | 15(3) | 1.7(1) |
| C22 | .487(1) | .557(1) | .526(1) | ||
| C23 | .501(1) | .498(1) | .446(1) | ||
| C24 | .535(1) | .536(1) | .550(1) | ||
| C25 | .469(1) | .537(1) | .474(1) | ||
| C26 | .566(1) | .496(1) | .522(1) | ||
| D21 | .572(2) | .449(3) | .449(1) | ||
| D22 | .467(2) | .589(2) | .544(2) | ||
| D23 | .591(1) | .489(2) | .406(1) | ||
| D24 | .551(1) | .553(2) | .585(1) | ||
| D25 | .431(1) | .548(2) | .460(1) | ||
| D26 | .598(2) | .476(2) | .541(1) |
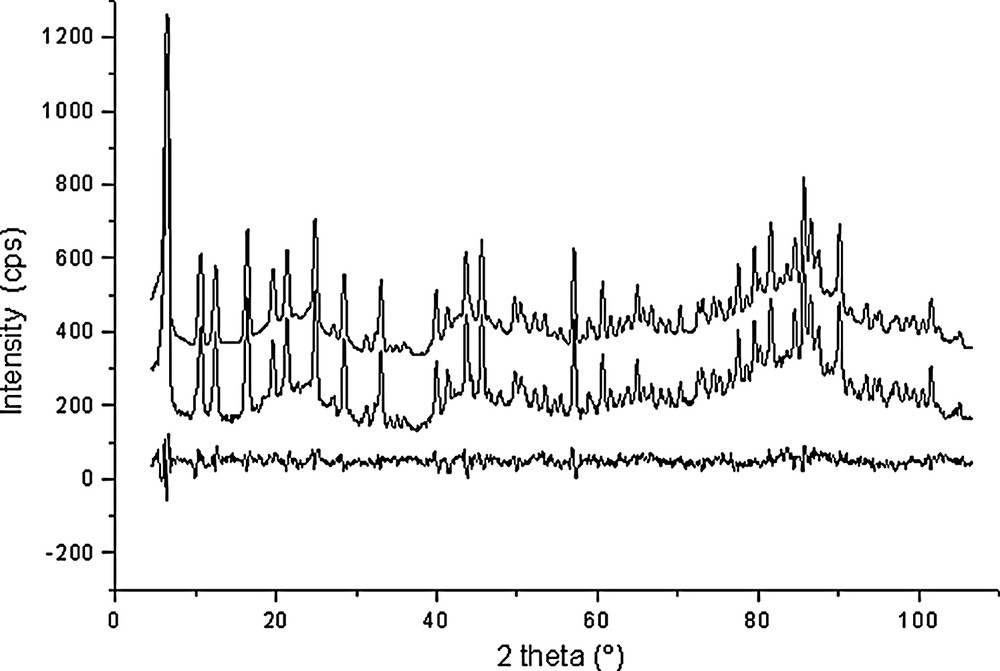
Rietveld plots for Si192O384·8.4 C6D6 (point 6 in Fig. 1).
Point 7
Sample label: Y20a_bz10
Sample formula: Si192O384·14.2 C6H6
Sample origin: see text
Diffractometer: Philips – X′Pert – in air-tight brass sample-holder
Wavelength (Å): Cu Kα
Angular range (°2θ): 4–80
Angular step (°2θ): 0.025
Unit-cell parameter (Å): 24.253(1)
Number of observables: 3041 + 94 = 3135
Number of hkl triplets: 221
Rp/Rwp/Rex/RI (%): 9.3/12.2/2.6/9.8
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0544(2) | .0354(3) | .1256(3) | 0.8 | 192 |
| O1 | –.1076(3) | 0 | .1076(3) | 2.5 | 96 |
| O2 | –.0038(4) | –.0038(4) | .1397(6) | 2.5 | 96 |
| O3 | –.0385(6) | .0753(4) | .0753(4) | 2.5 | 96 |
| O4 | –.0709(6) | .0711(4) | .1789(4) | 2.5 | 96 |
| BZ(C) | see neutron results | 9.0 | 12.0(3) | ||
| BZ(W) | 9.0 | 2.2(3) |
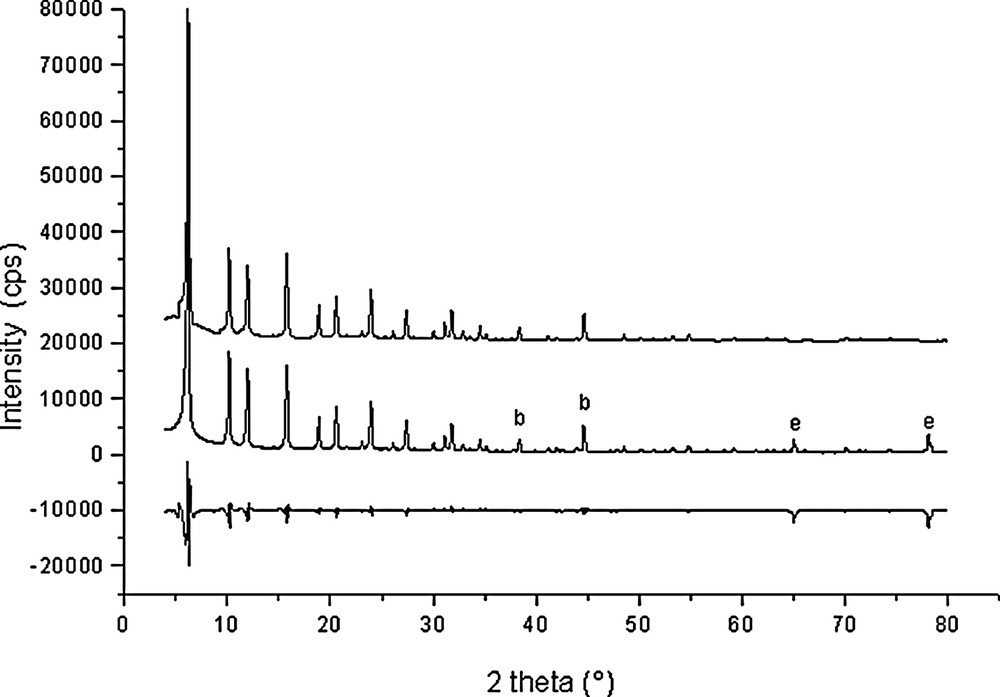
Rietveld plots for Si192O384·14 C6H6 (point 7 in Fig. 1).
Point 8
Sample label: Y20a_bz100
Sample formula: Si192O384·28 C6H6
Sample origin: see text
Diffractometer: Philips – X′Pert – in air-tight brass sample-holder
Wavelength (Å): Cu Kα
Angular range (°2θ): 4–77.4
Angular step (°2θ): 0.025
Unit-cell parameter (Å): 24.254(1)
Number of observables: 2937 + 94 = 3031
Number of hkl triplets: 225
Rp/Rwp/Rex/RI (%): 7.5/9.6/3.0/8.5
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0530(2) | .0361(2) | .1243(2) | 0.8 | 192 |
| O1 | –.1048(3) | 0 | .1048(3) | 2.5 | 96 |
| O2 | –.0012(3) | –.0012(3) | .1421(5) | 2.5 | 96 |
| O3 | –.0317(5) | .0777(3) | .0777(3) | 2.5 | 96 |
| O4 | –.0706(4) | .0718(3) | .1782(3) | 2.5 | 96 |
| BZ(C) | see neutron results | 9.0 | 24.5(5) | ||
| BZ(W) | 9.0 | 3.5(2) |
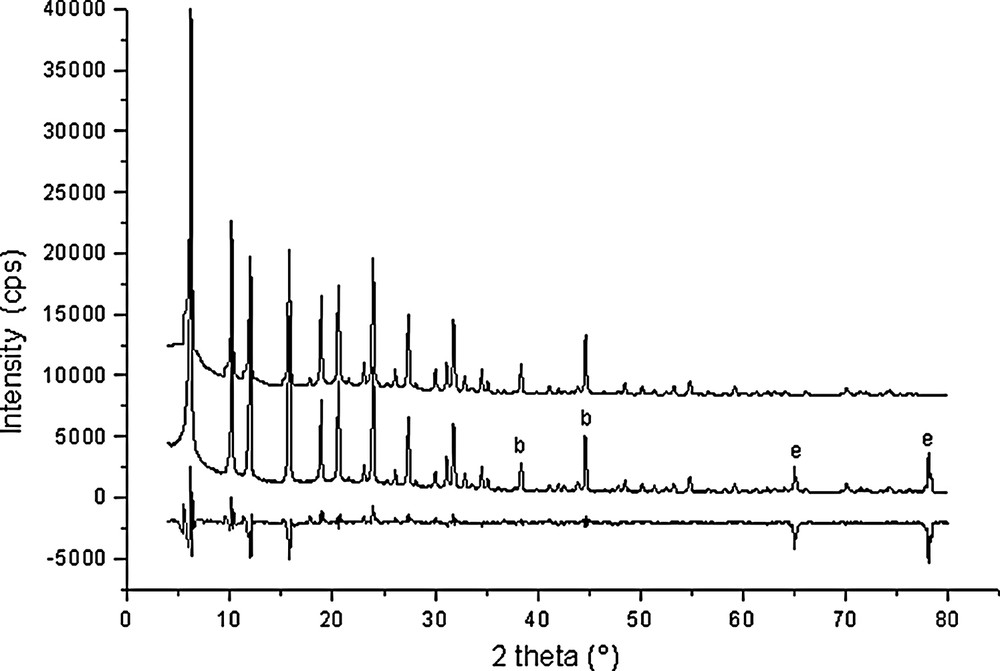
Rietveld plots for Si192O384·28 C6H6 (point 8 in Fig. 1).
Point 9
Sample label: Y20a_bz20
Sample formula: Si192O384·31.7 C6H6
Sample origin: see text
Diffractometer: Philips – X′Pert – in air-tight brass sample-holder
Wavelength (Å): Cu Kα
Angular range (°2θ): 4–80
Angular step (°2θ): 0.025
Unit-cell parameter (Å): 24.256(1)
Number of observables: 3041 + 94 = 3135
Number of hkl triplets: 244
Rp/Rwp/Rex/RI (%): 8.4/11.1/2.7/8.5
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0538(3) | .0359(3) | .1260(3) | 0.8 | 192 |
| O1 | –.1060(4) | 0 | .1060(4) | 2.5 | 96 |
| O2 | –.0030(4) | –.0030(4) | .1429(6) | 2.5 | 96 |
| O3 | –.0385(6) | .0764(4) | .0764(4) | 2.5 | 96 |
| O4 | –.0699(6) | .0707(4) | .1793(4) | 2.5 | 96 |
| BZ(C) | see neutron results | 9.0 | 27.8(3) | ||
| BZ(W) | 9.0 | 3.9(3) |
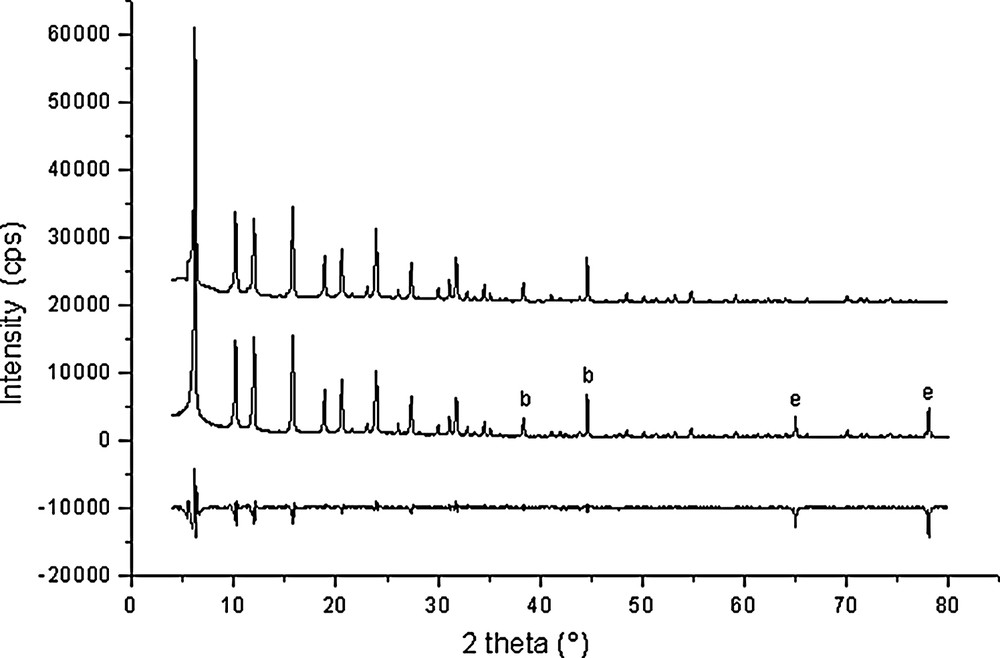
Rietveld plots for Si192O384·31.7 C6H6 (point 9 in Fig. 1).
Point 10
Sample label: Y20a_bz30
Sample formula: Si192O384·35.5 C6H6
Sample origin: see text
Diffractometer: Philips – X′Pert – in air-tight brass sample-holder
Wavelength (Å): Cu Kα
Angular range (°2θ): 4–80
Angular step (°2θ): 0.025
Unit-cell parameter (Å): 24.257(1)
Number of observables: 3041 + 94 = 3135
Number of hkl triplets: 222
Rp/Rwp/Rex/RI (%): 8.1/10.6/2.7/9.5
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0536(2) | .0356(2) | .1257(2) | 0.8 | 192 |
| O1 | –.1055(4) | 0 | .1055(4) | 2.5 | 96 |
| O2 | –.0030(4) | –.0030(4) | .1440(6) | 2.5 | 96 |
| O3 | –.0398(6) | .0774(4) | .0774(4) | 2.5 | 96 |
| O4 | –.0702(6) | .0701(4) | .1799(4) | 2.5 | 96 |
| BZ(C) | see neutron results | 9.0 | 31.4(3) | ||
| BZ(W) | 9.0 | 4.1(2) |
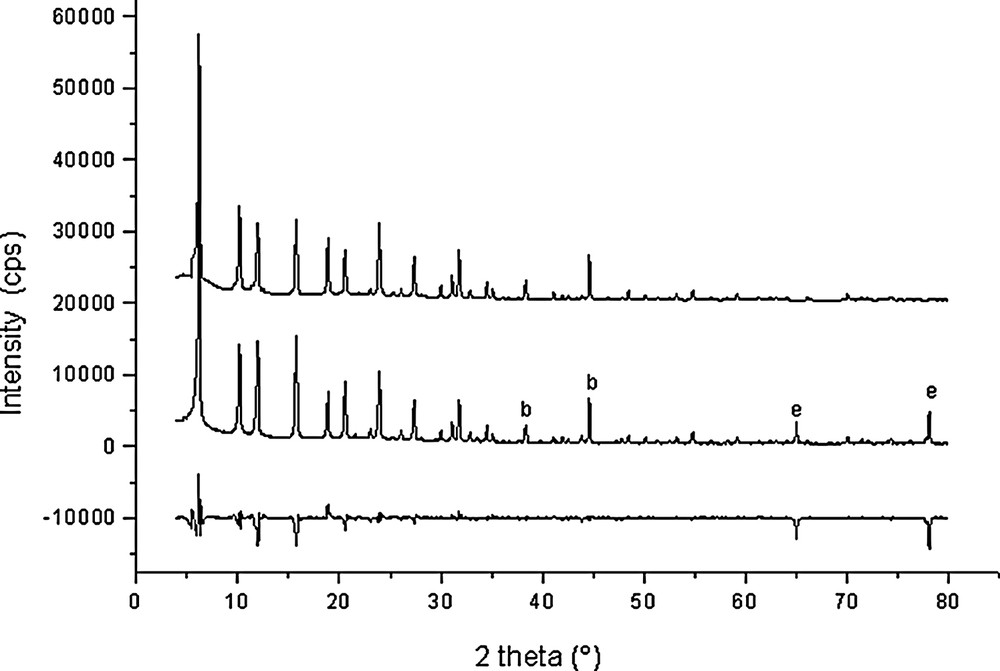
Rietveld plots for Si192O384·35.5 C6H6 (point 10 in Fig. 1).
DAY/benzene complex at higher loading
Additional data (compare with sample of point 6)
Sample label: Y20a_BZ600
Sample formula: Si192O384·32 C6D6
Sample origin: see text
Diffractometer: D2B
Wavelength (Å): 1.59263
Angular range (°2θ): 4.55–154.35
Angular step (°2θ): 0.05
Unit-cell parameter (Å): 24.253(1)
Number of observables: 2997 + 94 = 3091
Number of hkl triplets: 702
Rp/Rwp/Rex/RI (%): 7.9/10.2/7.3/11.2
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0539(2) | .0355(2) | .1254(2) | 0.98(9) | 192 |
| O1 | –.1063(2) | 0 | .1063(2) | 1.4(2) | 96 |
| O2 | –.0032(2) | –.0032(2) | .1409(3) | 1.5(2) | 96 |
| O3 | –.0365(3) | .0758(2) | .0758(2) | 1.4(2) | 96 |
| O4 | –.0706(3) | .0709(2) | .1791(2) | 1.3(2) | 96 |
| C11 | .3227(8) | .4084(6) | .229(1) | 20(2) | 27.8(5) |
| C12 | .337(1) | .3078(8) | .283(1) | ||
| C13 | .283(2) | .390(2) | .266(3) | ||
| C14 | .373(1) | .3232(9) | .241(1) | ||
| C15 | .2908(7) | .3406(7) | .295(1) | ||
| C16 | .3698(5) | .3768(5) | .219(1) | ||
| D11 | .321(1) | .448(1) | .216(2) | ||
| D12 | .340(2) | .269(1) | .299(3) | ||
| D13 | .248(2) | .413(2) | .273(4) | ||
| D14 | .406(2) | .299(1) | .231(3) | ||
| D15 | .259(1) | .324(1) | .317(2) | ||
| D16 | .4040(8) | .3948(7) | .202(2) | ||
| C21 | .549(2) | .477(2) | .470(1) | 15(4) | 3.9(3) |
| C22 | .487(1) | .558(2) | .525(1) | ||
| C23 | .507(1) | .506(1) | .443(1) | ||
| C24 | .535(1) | .536(1) | .549(1) | ||
| C25 | .473(1) | .542(2) | .472(1) | ||
| C26 | .563(2) | .493(3) | .523(2) | ||
| D21 | .567(3) | .444(3) | .452(2) | ||
| D22 | .468(3) | .589(3) | .544(2) | ||
| D23 | .594(2) | .493(2) | .404(1) | ||
| D24 | .552(2) | .554(2) | .583(2) | ||
| D25 | .437(2) | .556(3) | .455(2) | ||
| D26 | .596(4) | .475(4) | .542(3) |
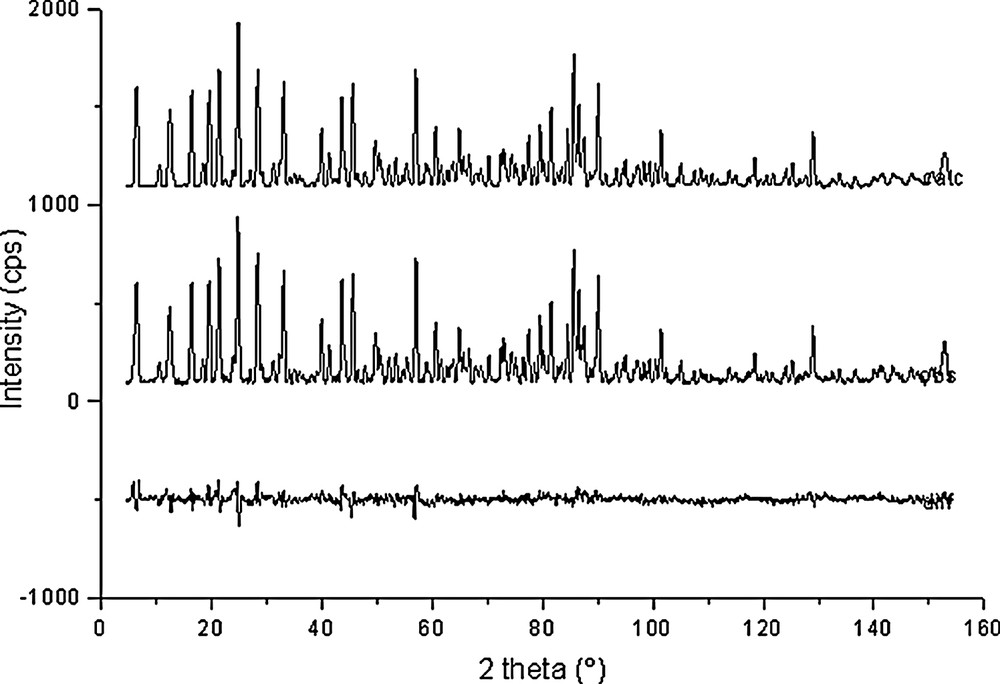
Rietveld plots for Si192O384·32 C6D6
Appendix 3 – Points 11 to 14 in Fig. 1 for the prehydrated pHyNaY/benzene system
Point 11
Sample label: PL52_A10
Sample formula: Na56Al56Si136O384·1.3 C6H6 + 18 H2O
Sample origin: LZY-52 (Sigma–Aldrich)
Diffractometer: Philips – X′Pert – in air-tight brass sample-holder
Wavelength (Å): Cu Kα
Angular range (°2θ): 4–66
Angular step (°2θ): 0.025
Unit-cell parameter (Å): 24.716(1)
Number of observables: 2481 + 16 = 2497
Number of hkl triplets: 165
Rp/Rwp/Rex/RI (%): 6.5/9.0/3.5/7.5
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0540(3) | .0353(3) | .1247(3) | 0.8 | 192 |
| O1 | –.1073(4) | 0 | .1073(4) | 2.5 | 96 |
| O2 | –.0023(4) | 0023(4) | .1438(6) | 2.5 | 96 |
| O3 | –.0330(7) | .0755(4) | .0755(4) | 2.5 | 96 |
| O4 | –.0713(6) | .0715(4) | .1785(4) | 2.5 | 96 |
| NaI | 0 | 0 | 0 | 3.3 | 8(1) |
| NaI' | .0614(7) | 17(1) | |||
| NaII | .2342(5) | 31(1) | |||
| C1 | .258 | .338 | .298 | 9.0 | 0.85(8) |
| H1 | .227 | .369 | .298 | 9.0 | |
| C2 | .477 | .477 | .546 | 9.0 | 0.45(5) |
| H2 | .459 | .459 | .582 | 9.0 | |
| OW1 | .167 | .167 | .171 | 9.0 | 0(1) |
| H11 | .181 | .134 | .191 | 9.0 | |
| H21 | .134 | .181 | .191 | 9.0 | |
| OW2 | .211 | .326 | .326 | 9.0 | 18(1) |
| H21 | .171 | .331 | .323 | 9.0 | |
| H22 | .221 | .337 | .366 | 9.0 |
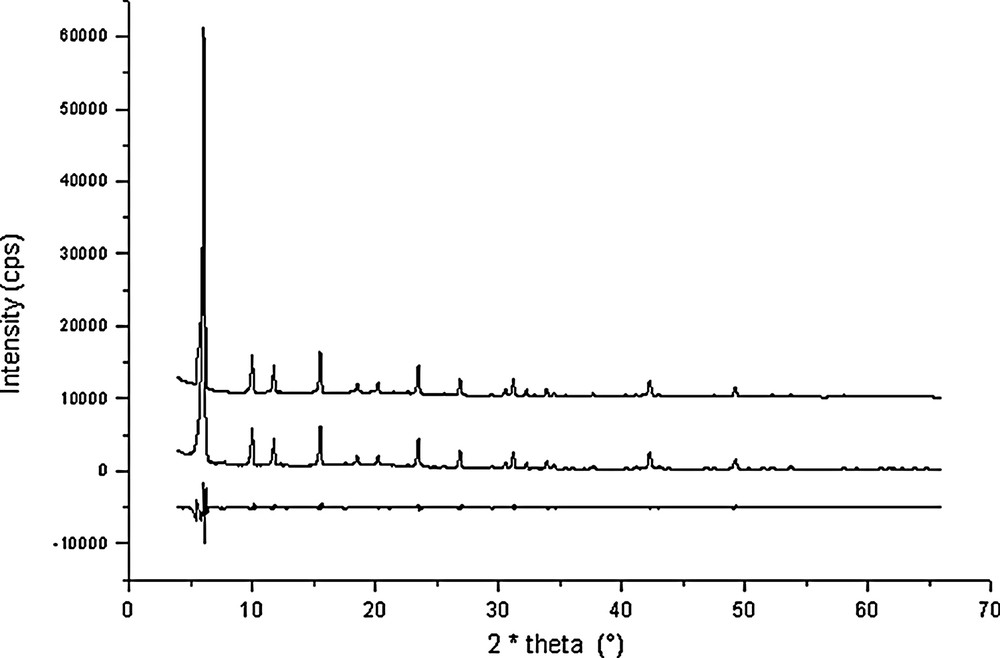
Rietveld plots for Na56Al56Si136O384·1.3 C6H6 + 18 H2O (point 11 in Fig. 1).
Point 12
Sample label: PL52_BZ10
Sample formula: Na56Al56Si136O384·15 C6H6 + 18 H2O
Sample origin: LZY-52 (Sigma–Aldrich)
Diffractometer: Philips – X′Pert – in air-tight brass sample-holder
Wavelength (Å): Cu Kα
Angular range (°2θ): 4–66
Angular step (°2θ): 0.025
Unit-cell parameter (Å): 24.705(1)
Number of observables: 2481 + 16 = 2497
Number of hkl triplets: 165
Rp/Rwp/Rex/RI (%): 6.0/8.4/3.4/6.5
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0540(3) | .0353(3) | .1247(3) | 0.8 | 192 |
| O1 | –.1073(4) | 0 | .1073(4) | 2.5 | 96 |
| O2 | –.0023(4) | –.0023(4) | .1438(6) | 2.5 | 96 |
| O3 | –.0330(7) | .0755(4) | .0755(4) | 2.5 | 96 |
| O4 | –.0713(6) | .0715(4) | .1785(4) | 2.5 | 96 |
| NaI | 0 | 0 | 0 | 3.3 | 5(1) |
| NaI' | .0679(9) | 25(1) | |||
| NaII | .2395(6) | 26(1) | |||
| C1 | .258 | .338 | .298 | 9.0 | 8.1(5) |
| H1 | .227 | .369 | .298 | 9.0 | |
| C2 | .477 | .477 | .546 | 9.0 | 6.9(5) |
| H2 | .459 | .459 | .582 | 9.0 | |
| OW1 | .167 | .167 | .171 | 9.0 | 1(1) |
| H11 | .181 | .134 | .191 | 9.0 | |
| H21 | .134 | .181 | .191 | 9.0 | |
| OW2 | .211 | .326 | .326 | 9.0 | 17(1) |
| H21 | .171 | .331 | .323 | 9.0 | |
| H22 | .221 | .337 | .366 | 9.0 |

Rietveld plots for Na56Al56Si136O384·15 C6H6 + 18 H2O (point12 in Fig. 1).
Point 13
Sample label: PL52_BZ20
Sample formula: Na56Al56Si136O384·29 C6H6 + 18 H2O
Sample origin: LZY-52 (Sigma – Aldrich)
Diffractometer: Philips – X′Pert – in air-tight brass sample-holder
Wavelength (Å): Cu Kα
Angular range (°2θ): 4–66
Angular step (°2θ): 0.025
Unit-cell parameter (Å): 24.693(1)
Number of observables: 2481 + 16 = 2497
Number of hkl triplets: 165
Rp/Rwp/Rex/RI (%): 5.4/7.3/3.6/5.8
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0543(2) | .0364(2) | .1256(2) | 0.8 | 192 |
| O1 | –.1066(3) | 0 | .1066(3) | 2.5 | 96 |
| O2 | –.0033(3) | –.0033(3) | .1428(5) | 2.5 | 96 |
| O3 | –.0327(5) | .0759(3) | .0759(3) | 2.5 | 96 |
| O4 | –.0722(4) | .0716(3) | .1784(3) | 2.5 | 96 |
| NaI | 0 | 0 | 0 | 3.3 | 3(1) |
| NaI' | .0621(5) | 26(1) | |||
| NaII | .2413(6) | 27(1) | |||
| C1 | .258 | .338 | .298 | 9.0 | 19(1) |
| H1 | .227 | .369 | .298 | 9.0 | |
| C2 | .477 | .477 | .546 | 9.0 | 10(1) |
| H2 | .459 | .459 | .582 | 9.0 | |
| OW1 | .167 | .167 | .171 | 9.0 | 3(1) |
| H11 | .181 | .134 | .191 | 9.0 | |
| H21 | .134 | .181 | .191 | 9.0 | |
| OW2 | .211 | .326 | .326 | 9.0 | 15(1) |
| H21 | .171 | .331 | .323 | 9.0 | |
| H22 | .221 | .337 | .366 | 9.0 |
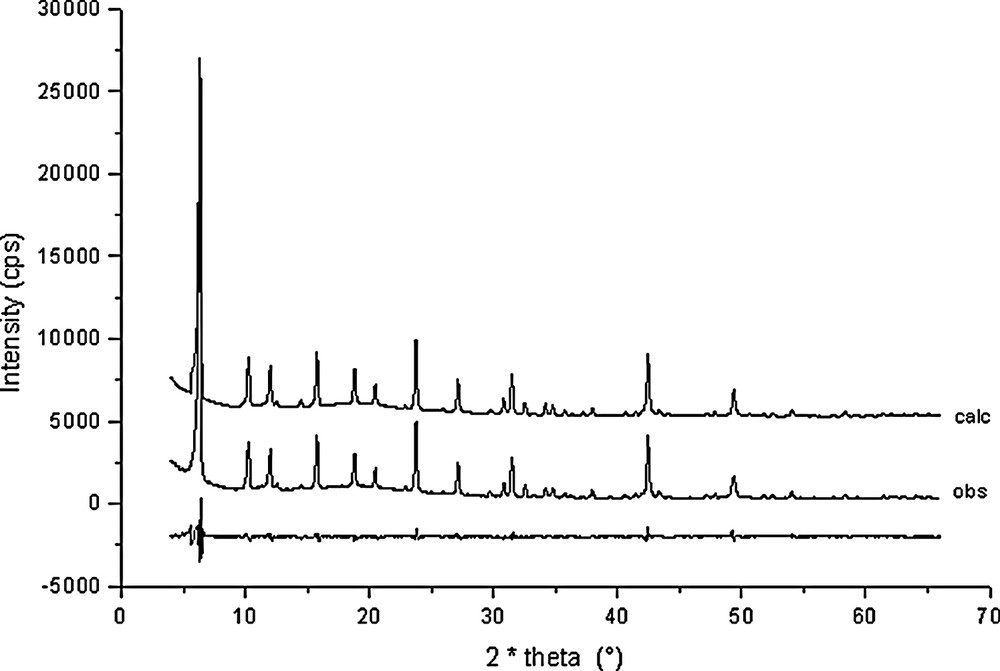
Rietveld plots for Na56Al56Si136O384·29 C6H6 + 18 H2O (point 13 in Fig. 1).
Point 14
Sample label: PL52_BZ40
Sample formula: Na56Al56Si136O384·43 C6H6 + 18 H2O
Sample origin: LZY-52 (Sigma–Aldrich)
Diffractometer: Philips – X′Pert – in air-tight brass sample-holder
Wavelength (Å): Cu Kα
Angular range (°2θ): 4–66
Angular step (°2θ): 0.025
Unit-cell parameter (Å): 24.690(1)
Number of observables: 2481 + 16 = 2497
Number of hkl triplets: 165
Rp/Rwp/Rex/RI (%): 6.0/8.4/3.4/6.5
| Atom | x/a | y/b | z/c | B (iso) | population/uc |
| Si | –.0543(2) | .0367(2) | .1264(2) | 0.8 | 192 |
| O1 | –.1070(3) | 0 | .1070(3) | 2.5 | 96 |
| O2 | –.0026(3) | –.0026(3) | .1416(5) | 2.5 | 96 |
| O3 | –.0347(5) | .0762(3) | .0762(3) | 2.5 | 96 |
| O4 | –.0732(4) | .0726(3) | .1774(3) | 2.5 | 96 |
| NaI | 0 | 0 | 0 | 3.3 | 1(1) |
| NaI' | .0592(5) | 25(1) | |||
| NaII | .2381(5) | 30(1) | |||
| C1 | .258 | .338 | .298 | 9.0 | 30(1) |
| H1 | .227 | .369 | .298 | 9.0 | |
| C2 | .477 | .477 | .546 | 9.0 | 13(1) |
| H2 | .459 | .459 | .582 | 9.0 | |
| OW1 | .167 | .167 | .171 | 9.0 | 8(1) |
| H11 | .181 | .134 | .191 | 9.0 | |
| H21 | .134 | .181 | .191 | 9.0 | |
| OW2 | .211 | .326 | .326 | 9.0 | 10(1) |
| H21 | .171 | .331 | .323 | 9.0 | |
| H22 | .221 | .337 | .366 | 9.0 |
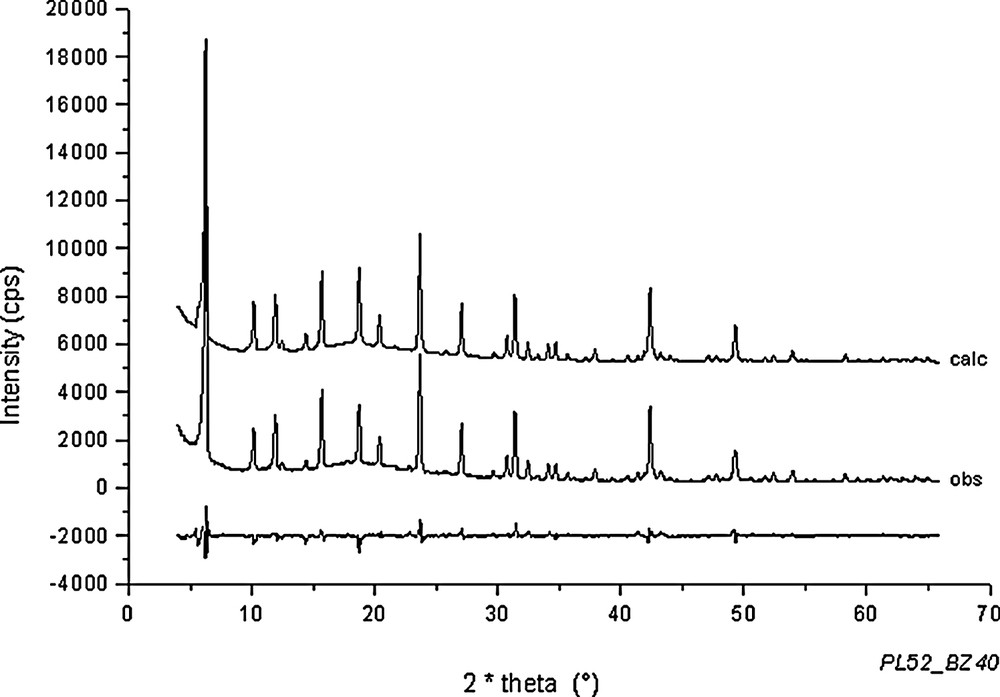
Rietveld plots for Na56Al56Si136O384·43 C6H6 + 18 H2O (point 14 in Fig. 1).


