1 Introduction
For decades, chemists, mineralogists and material scientists have been employing powder diffraction as the most powerful (analytical and structural) method in the characterization of metals, alloys, salts, rocks and ores, i.e. of classic inorganic compounds. At variance, until the mid nineties, the realm of molecular materials (such as organics and pharmaceutically active species) was largely colonized by single crystal diffraction, given that their structural complexity seemed to restrict the use of powder diffraction to phase identification (which is, nevertheless, a highly profitable activity: indeed, quantification and detection of polymorphs and solvates have consequences of high economical value). Once the recent improvements in radiation sources, optics, instrumentation, detectors, computers and software were made available to the wide community of structural chemists, the derivation of a structural model for such species (from powder diffraction data ‘only’) came within reach [1]. Nowadays, the increase of instrumental resolution and new efforts in devising indexing algorithms make it possible to detect, even from polyphasic mixtures [2], the correct unit cell of an unknown species, and, eventually, to solve (by a combination of direct- or reciprocal-space techniques, brutal force [3], and more advanced methods [4]) their crystal and molecular structures. Recently, also the structures of a number of organometallic species and covalent polymers [5] have been successfully retrieved, leading to the discovery of new stoichiometries, connectivities and geometries, unforeseen [6], unexpected [7] or even badly postulated [8], throughout the years, on the basis of weak spectroscopic evidence.
The use of powder diffraction in the field of organic–inorganic hybrids (which is larger than that of simple organometallics) presents a series of problems which, being somewhat characteristic of the very nature of these species (see Fig. 1), cannot be overcome by increasing the radiation flux and the instrumental resolution, but can be only circumvented by using additional (experimental or computational) information.
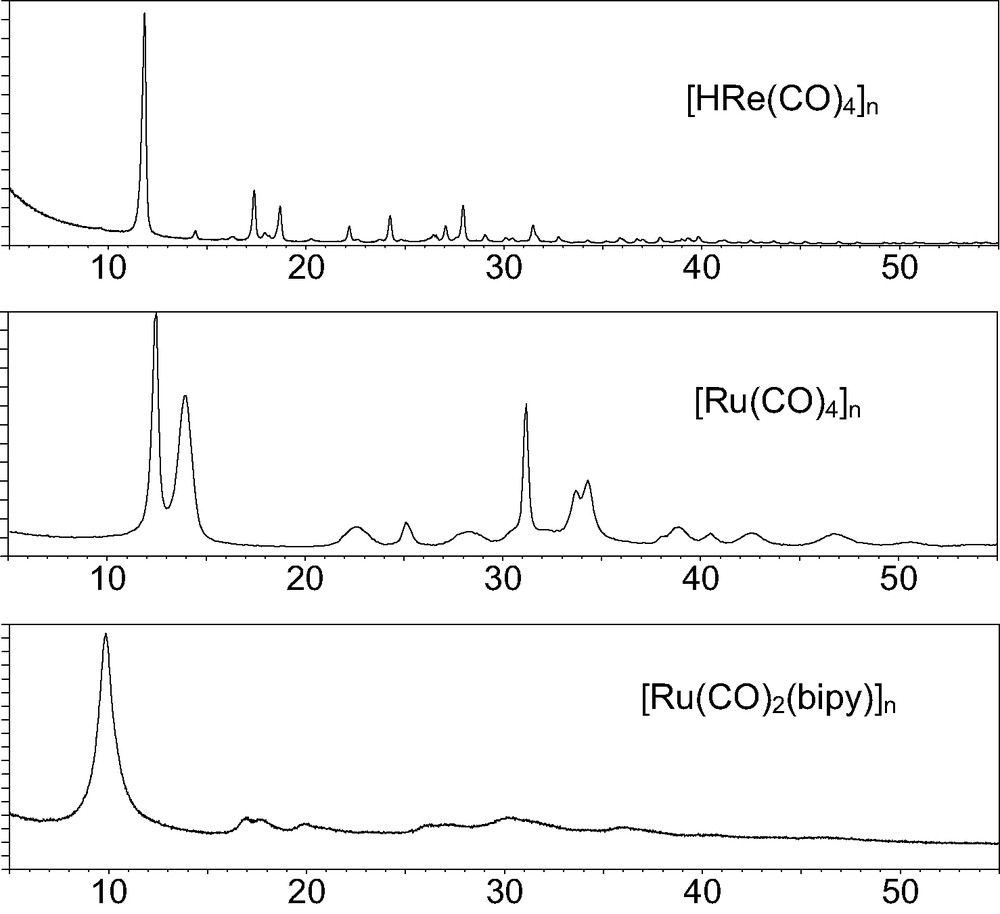
Raw XRPD patterns for three 1D organometallic polymers, showing different degrees of crystallinity, and markedly anisotropic peak widths, up to 1.5° 2θ.
Indeed:
- • 1. Molecular compounds (and ‘salts’ containing large polyatomic ions) are bound by weak intermolecular forces, hence have high thermal parameters, large peak widths and a rapid fall-off of the scattering power with the scattering angle. A large intrinsic peak width is known to hamper the indexing process (the key step in ab initio X-ray powder diffraction (XRPD)), while the absence of significant reflections above sinθ/λ = 0.4 Å–1 dramatically decreases the attainable resolution, leading often to uninterpretable Fourier maps (for light atoms linked by short bonds) and instabilities in the Rietveld refinement.
- • 2. While solution of the phase problem is often simplified by the presence of heavy scatterers [the metal(s)], completion of the structural model is more difficult, because of the weaker contribution to the whole scattering power of light atoms, which can be then easily missed, or poorly located, in difference Fourier maps. Worthy of note, these maps suffer of a further inherent problem, in that |Fobs| are normally extracted (for overlapping reflections) through a partitioning algorithm based upon the already found (partial) model: this artificially lowers the pertinent RBragg and ΔF values, thus affecting the overall quality of the difference Fourier map.
- • 3. Most organometallic species contain ligands with a wide conformational flexibility, which make the different steps of structure solution, model completion and/or theoretical crystal structure predictions even more difficult.
2 Discussion
In the early nineties we started a project on the structural characterization of co-ordination compounds from PD data measured on conventional equipment [9], and soon realized the necessity of adding ‘external’ (i.e. not present in the diffraction pattern) information in order to improve the quality of the results, because the independent atom models often converge to unphysical bonding values. Typically, the detailed knowledge of the most common stereochemistries (available from databases) and the hidden assumption that harmonic wells (of arbitrary curvature) about ‘reference’ values can be added in a generalized cost function, allow to include geometrical restraints in the refinement procedure. Accordingly, the widely used programs for Rietveld refinement, in their presently available versions (May 2004), GSAS [10], Fullprof [11], Rietan [12], and TOPAS [13], all include a wide spectrum of possible restraints, on distances, angles, torsions, planarity and even chirality.
While the most simple geometric approximations (interatomic distances and angles) hold for intramolecular contacts, parameterization of nonbonding (intra- and inter-molecular) interactions by this technique is not viable, because the flatness of their potential energy wells and their asymptotic behavior for large separations can hardly be reproduced by restraining a number of interatomic distances. Notwithstanding, the correct structural model should correspond to a packing energy minimum and, simultaneously, be consistent with the experimental diffraction data; therefore, as briefly described in the following, we employed Energy + Rietveld (uncoupled, but iterated) refinements, in search for a valuable tool for obtaining and/or validating ab initio XRPD crystal structures.
2.1 Molecular mechanics (MM) in the crystal lattice as a tool for solving structures
While solving the crystal structure of [(CO)2Rh(μ-Cl)2Rh(C8H8)], 1 [14] (see Fig. 2) location of two crystallographically independent Rh atoms (Patterson) and two bridging Cl ions (difference Fourier) was easily achieved. At this point, although the Rh(I) atoms were likely in square planar environments (an η2-ligand simulating a single donor site), no easily distinguishable C and O atoms (of the carbonyl or cyclooctadiene ligands) could be found in a further difference map. However (unconventionally) resorting to packing considerations, i.e. to the qualitative analysis of the empty volumes about the Rh2Cl2 core, we clearly detected which metal was bound to cyclooctadiene and which to carbonyls.
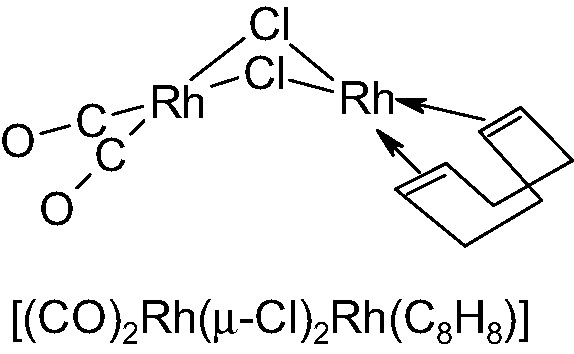
Schematic drawing of the roofed structure of [(CO)2Rh(μ-Cl)2Rh(C8H8)].
Therefore, the location and orientation of the chelating diolefin were initially determined by rough standard molecular building procedures (performed by SMILE [15]); this step, in which the C8H8 fragment was attached to the pertinent metal atom in a very approximate conformation (and disregarding the crystal environment), was followed by a steric energy minimization of the whole flexible molecule within its crystal lattice (thanks to a locally developed program [16]), which eventually afforded a good starting point for the final (restrained) Rietveld refinement (Rp and RF = 0.116 and 0.085, respectively).
Finally, the roof-shape of the Rh2Cl2 fragment and the overall feasibility of Rietveld/MM refinements were checked by comparing the (two) one-dimensional cuts of Rwp (along the Rh···Rh and Cl···Cl directions, respectively) with the two-dimensional section (Rh···Rh/Cl···Cl) of the potential energy hypersurface, PES (see Fig. 3). Interestingly, but not exceptionally, even if the minima of the two independent cost functions are close (which is not always true), Rwp is much more sensible to high Z atoms (Rh vs. Cl) displacements, while the PES is softer along the Rh···Rh direction than along Cl…Cl. As a direct consequence, joint refinements should face the non-trivial problem of relative scaling of different ‘observations’ which, at present, is not uniquely defined.
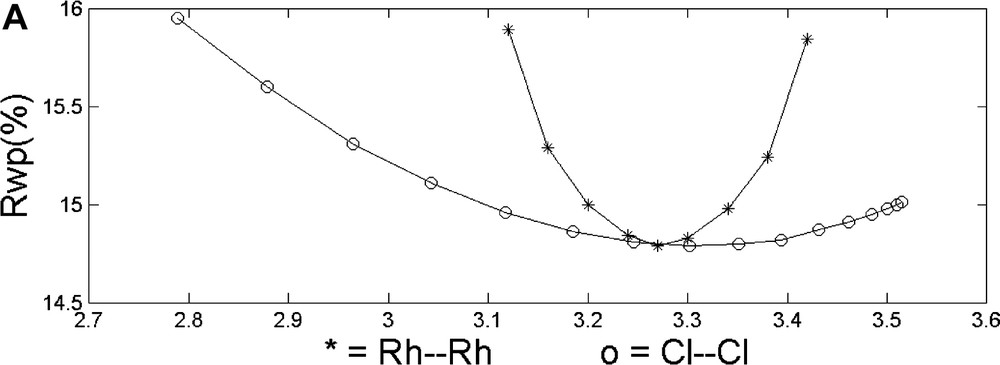
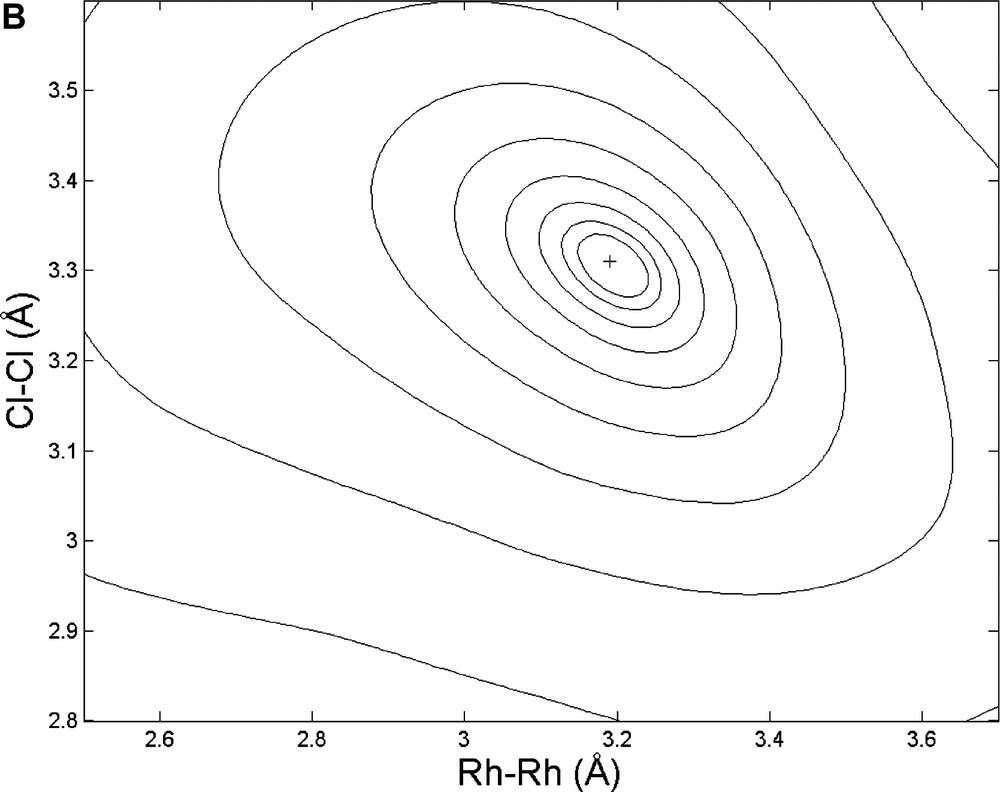
Top: Monodimensional cuts of the Rwp hypersurface along the Rh···Rh and Cl···Cl directions, respectively. Bottom: 3D view of the potential energy hypersurface, projected onto the Rh···Rh vs. Cl···Cl plane (values in Å).
2.2 MM in the crystal lattice as a tool for validating structures
A ‘standard’ ab-initio XRPD structure determination of {(phen)Pd[C(=O)ON(-CH3)C(=O)]}, 2 (phen = 1,10 phenanthroline) [17], was undertaken to determine the controversial [18] connectivity pattern of this complex organometallic species. Briefly: (i) peak search and indexing of data collected on a conventional powder diffractometer afforded an orthorhombic unit cell of approximate dimensions a = 7.09; b = 10.66 and c = 17.27 Å, space group Pna21, Z = 4, M(24) = 17, F(24) = 33 (0.013, 57); (ii) interpretation of the Patterson map allowed location of the unique Pd atom; (iii) the lack of a center of symmetry and what was later interpreted as a remarkable preferred orientation determined a noisy and not easily interpretable difference Fourier map; (iv) the orientation of a planar (phen)PdC2 fragment was determined by a rotational grid search about the (refinable) Pd atom position, using P-RISCON [19] and optimized by a rigid-body Rietveld refinement, using a Z-matrix formalism implemented by us into a local version of the program PREFIN [20] (now incorporated into DEBVIN [21]); (v) completion of the structure with the few missing light atoms was possible by a surprisingly informative difference Fourier map (see Fig. 5) obtained on newly collected data free of texture effects; (vi) the correct stereoisomer (2a in Fig. 4) was clearly identified by the position of the missing substituent in the metallacycle.
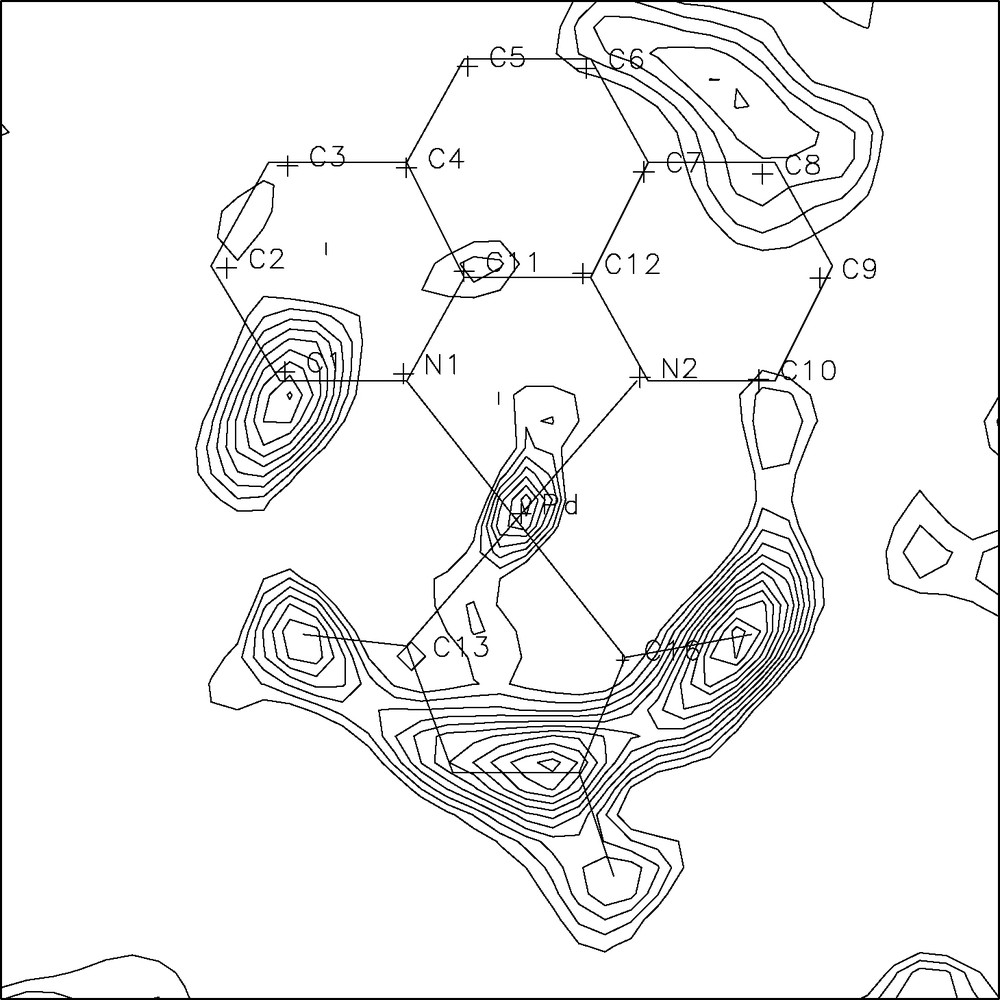
Difference Fourier map in plane with the Pd(phen) moiety (sketched by thin straight lines); the residual electron density clearly indicates which of the four moieties (2a) was present in the crystal of 2.
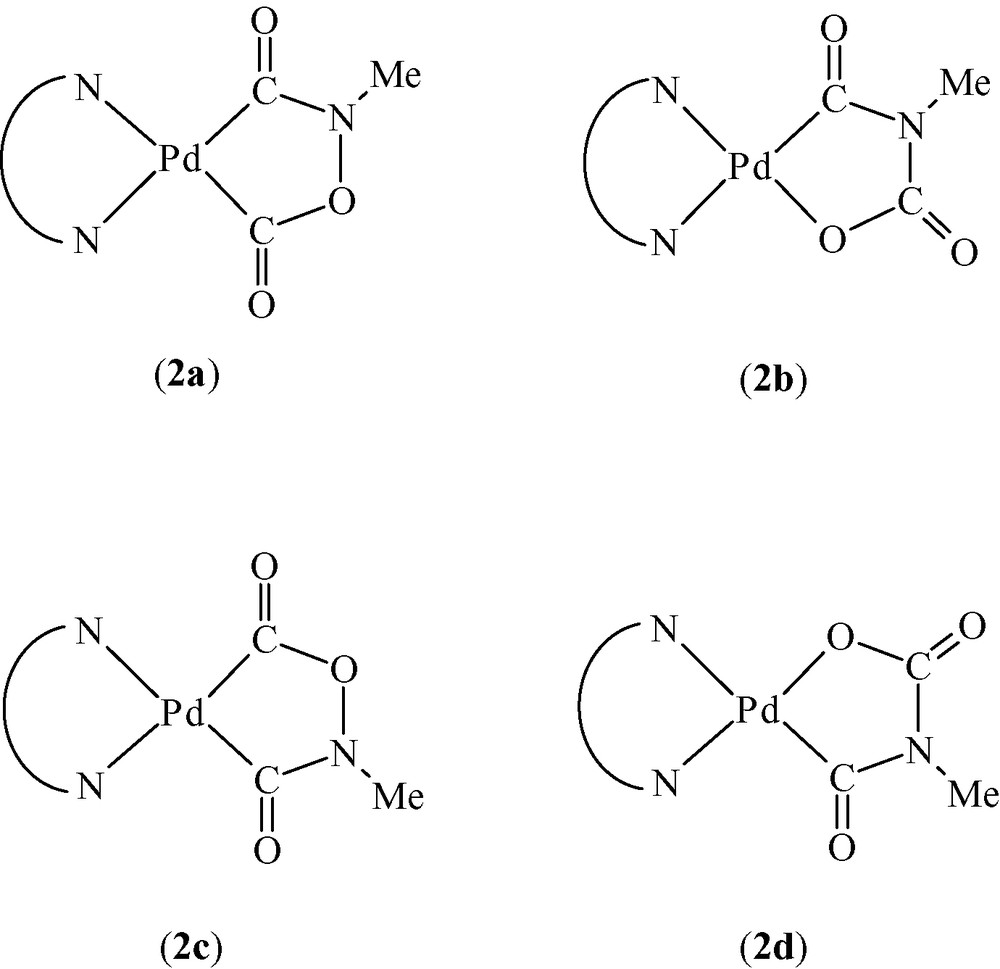
Possible stereoisomers of species 2. Note that the (2a, 2c) or (2b, 2c) couples represent crystallochemically, not chemically, distinct ‘isomers’.
The relevant stereochemical task of this structural study was to discriminate between two different stereoisomers of 2, each one possibly occurring in the crystal in two different orientations (see Fig. 4); therefore, a cross-validation of the XRPD results (structure 2a) was achieved by MM [16].
Given the significantly different energy values reported in Table 1, our computations differentiated among the four plausible structures depicted in Fig. 4, reinforced the XRPD results and showed that subtle information of the molecular shape, hidden in the lattice metrics, symmetry operations and heavy atom locations (obtained from XRPD without a priori information), can successfully be retrieved by MM. Note that, given the quality of the Fourier map in Fig. 5, this validation may appear redundant. However, because the original textured data did not allow the successful completion of steps (v) and (vi), we actually employed MM well before resynthesizing our product. It was indeed this computational evidence which stimulated us to attempt such difficult synthesis again, in search for a less textured sample.
Results of the steric energy computations (kcal mol–1) for molecules 2a–2d
| Fragment (as in Fig. 4) | 2a | 2b | 2c | 2d |
| Total steric energy, SEi | –24.0 | –17.4 | +26.6 | +7.1 |
| Intramolecular energy, IEi | +25.2 | +25.4 | +38.5 | +35.0 |
| Packing energy, PEi | –49.2 | –42.8 | –11.9 | –27.9 |
| SEi–SE2a | 0.0 | +6.6 | +50.6 | +31.1 |
2.3 MM in the crystal lattice as a tool for incorporating ‘previous stereochemical knowledge’
Here we discuss the structures of three organometallic polymers [22]2, namely [ReH(CO)4]n [23] [Ru(CO)4]n [24] and [Ru(CO)2bipy]n [25] (bipy = 2,2′-bipyridine) for which the representative XRPD patterns have been presented above in Fig. 1.
In all three cases there are two kinds of problems which are deeply entangled: (i) the structural complexity of the materials, for which XRPD alone is not able to afford accurate atomic positions, particularly when strong scatterers are present (Re, Ru), and (ii) the sample contribution, which is a clear manifestation of the presence of defects, inherent in the actual phase. Interestingly, and at variance from conventional single crystal studies, XRPD affords, in some cases, some extra-information of microstructural parameters, such as strain and coherence lengths, which are normally overlooked.
The analyses of the XRPD traces of very different ‘quality’ (as shown above) clearly resulted in structural models of different accuracy; modeling and geometrical restraints were necessary in the first two cases to help convergence in the final Rietveld refinement cycles; differently, the very limited amount of information present in the bottom trace of Fig. 1 required the knowledge of the previously determined ruthenium tetracarbonyl structure in order to assess the few ‘accessible’ structural features (cell parameters hence crystal packing) of the ruthenium polymers containing diazaaromatic ligands.
In the first of our examples, the [HRe(CO)4]n polymer, the three crystallographically independent metal atoms, each one defining its own infinite 31 (homochiral) helix, were unambiguously located by Direct Methods (EXPO [26]); however, due to the intrinsic limitations of XRPD, we were unable to complete the starting model by Fourier methods; thus, we had to rely on MM and on some previous stereochemical knowledge to complete the whole structure. It is of particular interest that the preliminary information afforded by powder diffraction (i.e. lattice constants, space group symmetry and ‘good’ heavy atom locations) uniquely determine the shape of the ‘cavity‘ containing the molecule, and, hence, the overall stereochemistry of the polymer (see Fig. 6). Finally, even the hydrogen locations were assessed (within the helical metal cores, screened by the carbonyl ligands).
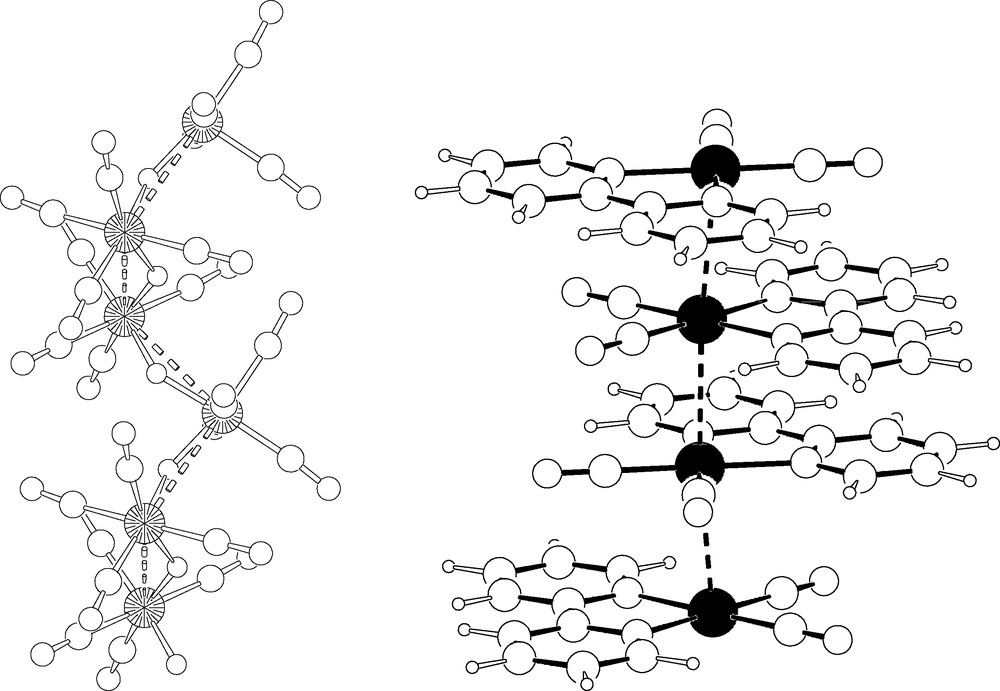
Left: A fragment of the 31 helix of [HRe(CO)4]n. Rhenium atoms as large circles. Right: Stacking of staggered Ru(CO)2(bipy) fragments in the 1D polymer (for the crystal disorder, see text).
In this species, as well as in the related [HRe(CO)4]6 hexamer (also solved ab initio from XRPD data), it might be considered odd to speak about hydrogen locations when we barely see the metal centers; however, it is well known that the location of the hydrides may be determined, at the molecular level, from those of the other atoms [27].
Among the first efforts we spent in the field of powder diffraction characterization of organometallic polymers, the determination of the crystal structure of [Ru(CO)4]n holds a specific role: from its rather poorer XRPD trace (see Fig. 1), we still managed to determine its crystal and molecular structure, which was unexpectedly different from that guessed by IR spectroscopy [28]: instead of a zig-zag polymer built by cis-C2v fragment, linear chains, containing the staggered, trans D4h monomers (with Ru atoms 2.94 Å apart) were found. In addition, its microstructural analysis allowed the determination of the average chain length (ca. 150 monomers) and of the lateral strain induced by the pseudohexagonal packing of parallel polymeric rods.
The structural features determined for [Ru(CO)4]n significantly helped in unravelling the nature, and the crystal packing, of the nearly amorphous [Ru(CO)2(bipy)]n polymer, an efficient catalyst for electrochemical carbon dioxide reduction and water gas shift reaction [29]. In this case, we had to ‘manually’ guess the lattice parameters by observing the systematicity of the d* ratios of the few observable bumps, as well as by detecting their subtle splitting.
Once the correct cell and lattice centering were detected, model building and allowance for an extremely (but, eventually, easily interpretable) disordered structure allowed a rather decent, yet unexpected, matching between the observed and calculated XRPD traces. The final model confirmed the polymeric nature of the sample, which shows stacking of C2v–Ru(CO)2(bipy) fragments (ca. 3.0 Å apart), staggered (by ±45° or ±135°, as in the parent [Ru(CO)4]n), but disordered in four equivalent orientations about z.
2.4 Selected area electron diffraction (SAED) as a tool for indexing large cells
Two-dimensional systems are common to many aspects of material chemistry. The variety of the available organic ligands (and the tendency of certain inorganic substrates to afford well defined layers) can be used to design low-dimensional hybrid inorganic-organic systems with a high stereochemical control, exploiting (strong) covalent bonding, weaker dipolar effects, segregation or intercalation processes.
The crystal morphology of Magnetic Cobalt Soaps, as shown in Fig. 7, clearly shows that, more than ever, preferential orientation effects are likely at work. This is a rather annoying problem, both in the indexing, but particularly in the structure solution (and refinement) stages. Nevertheless, careful sample preparation 3, the use of a highly monochromatized soft radiation (Co–Kα1), and particularly the metric information gathered from SAED on a single platelet (Fig. 7, bottom) allowed the structural analyses of a number of (monoclinic) cobalt soaps with cell parameters as large as 58 Å. Due to their structural complexity, neither direct nor Patterson methods afforded unique (refinable) cobalt atom locations, that could be later used for model completion by Fourier methods. However, direct space simulated annealing techniques, using two independent rigid all-trans alkanoate groups and one cis-Co(H2O)2 fragment, eventually afforded reasonable starting models. Thus, coupling SAED with tailored XRPD measurements, we successfully characterized a number of mono- and dicarboxylato(diaqua)cobalt(II) species [30].
These compounds belong to the same structural class, with long chain organic ligands segregated from the polar heads and metal ions connected by RCO2 bridges in the rare anti–anti conformation (see Fig. 8). Based on the structures determined from XRPD data, the interpretation of the low-temperature magnetic behavior and of the coupling constants of a two-dimensional magnetic lattice was then possible.

Schematic plot (down b, horizontal axis = c) of the crystal structure of cis-Co(H2O)2(C20H39O2)2, showing the elongated organic ligands running nearly parallel to the c axes; cobalt atoms in black, oxygen atoms cross-hatched.
2.5 Merging optical and structural data into a comprehensive structural model
[DAMS+][Cu5I6] ([DAMS+] = [trans-4-(4-dimethylaminostyryl)-1-methylpyridinium]) has a very simple XRPD pattern corresponding to a rather elongated rhombohedral lattice (a = 4.25, c = 38.24 Å), with approximate cell volume of 600 Å3, the asymmetric unit of which cannot obviously host the large [DAMS+] cation. What conventional diffraction sees is the stacking (along the trigonal axis with a spacing of ca. 12.75 Å) of CuI slabs formed by two parallel slightly corrugated sheets (similar to those present in the room temperature γ-CuI phase, but with a certain amount of CuI vacancies in order to balance the charges of the guest anions) which are suitably translated in order to grant the tetrahedral co-ordination of the CuI ion. The ‘empty’ space within the slabs (per slab, per unit cell) is 96 Å3. This implies that each [DAMS+] cation (estimated volume 262 Å3, length ca. 17 Å) extends over three contiguous unit cells, does not conform to any translational or point symmetry operator of the host lattice, does not actually contribute to Bragg intensities except for low angle 00ℓ reflections and cannot be detected in the XRPD experiment 4. Nevertheless, by coupling structural, optical and spectroscopic information we were able to suggest (see Fig. 9) that, within two host Cu-defective slabs, the intercalated [DAMS+] cations must be: (i) ‘edge-on’ oriented (the interslab spacing being 12.75 Å); (ii) dipole ordered (given the observed SHG activity); (iii) densely packed (as J-aggregates, given the red-shifted visible absorption band); but iv) translationally disordered (given the lack of supercell hk0 reflections). Finally, we were also able to propose a physical explanation for the highly crystalline rhombohedral stacking of the host lattice by observing that anion alignment of adjacent slabs must be due to favorable coupling of charges (I–)(⊕[DAMS+]⊕)(–I) originated by the substantial bilateral symmetry of [DAMS+] nearby the charged N atom. Actually, the crucial factor controlling the formation of a macroscopic ordering is the intrinsic polarity of the ‘first’ [DAMS+] guest layer, which imparts a definite ‘order’ to the host vacancies and, simultaneously, determines the orientation of the next guest add-layer.
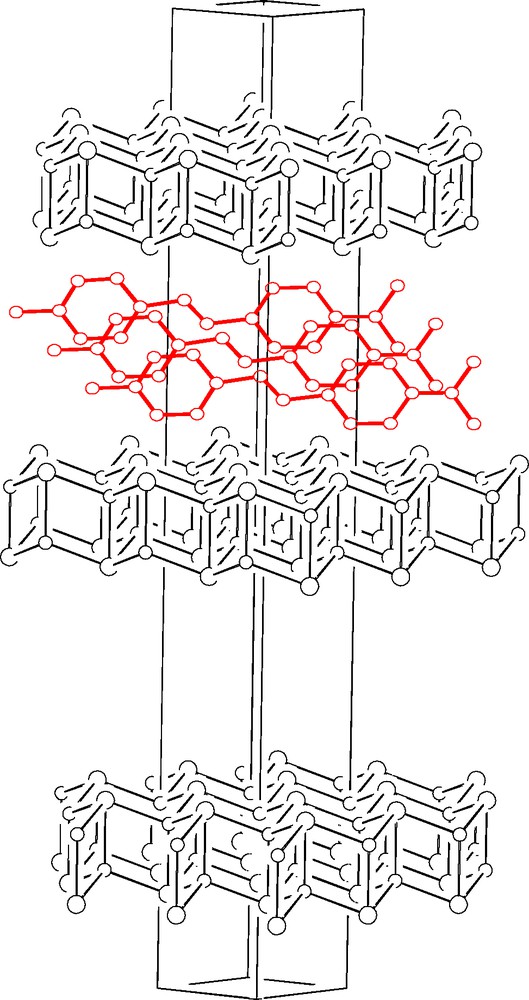
Unit cell diagram for [DAMS+][Cu5I6] (or DAMS+@CuI), showing the defective (see text) CuI layers and the intercalated DAMS+ ions. The latter are edge-on, with respect to the layers, and translationally disordered over three adjacent cells.
2.6 Merging neutron and X-ray diffraction data to obtain a superior structural model
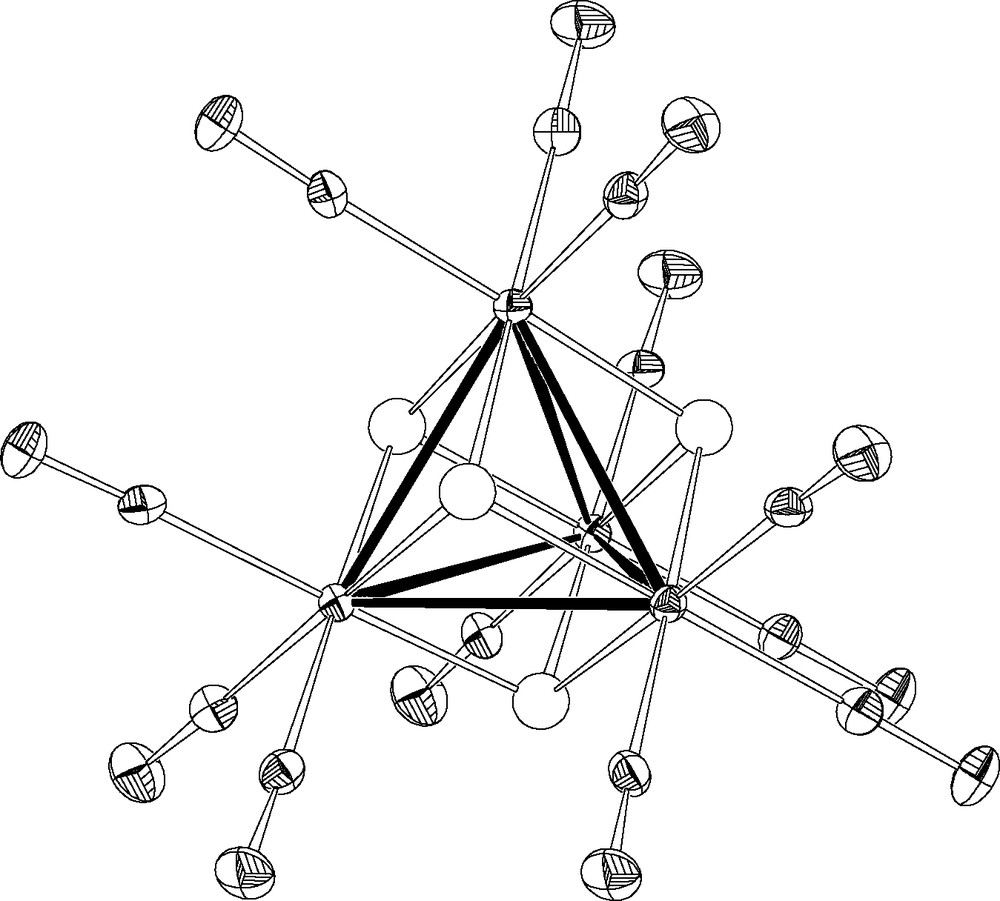
[(μ3-H4)Re4(CO)12], 3, is unusual among metal cluster compounds, being one of the few known ‘unsaturated’ carbonyl clusters (56 vs. 60 cluster valence electrons) [31]; its conventional X-ray single crystal structure has been previously reported by Wilson and Bau [32] and the μ3-H character inferred from local stereochemical considerations and an ‘image-enhanced’ (i.e. symmetry-averaged) difference Fourier map (estimated average Re–H 1.77 Å). However, while studying the reactivity of solid 3 with gases (NH3, CO and H2O), using XRPD we observed a new ‘pseudo-polymorphic’ 3·2C6D6 crystal phase, isomorphous with Re4(CO)12(μ3-OH)4·2C6H6 [33]. The availability of sizeable amounts of this new phase (but not of large single crystals) and our experience with XRPD on co-ordination and organometallics systems prompted us to attempt the viability of a new approach to hydrides location where: (i) the burden of the structure determination lies on a single crystal X-ray experiment; (ii) the accurate location of the hydrides are essentially rescued from neutron powder diffraction; and (iii) the final structural parameters are obtained from a joint refinement [34]5.
Eventually we demonstrated that (μ3-H4)Re4(CO)12 in 3·2 C6D6 has a crystallographically imposed Td symmetry (see Fig. 10), with a Re4(CO)12 core virtually identical to that found in 3 and confirmed the μ3-nature of the hydrido ligands; however, we observed significant differences in the H bonding parameters (Re–Hx 1.88(12) vs. 1.77 Å, Re–Hn 1.99(2) Å), where Hx and Hn labels address the ‘X’ and ‘N’ components of the split H atom 6.
2.7 Using NMR information to drive XRPD toward the correct solution
The first efficient low voltage driven organic light emitting devices (OLEDs), reported by Tang and Van Slyke [35], were based on Alq3. Fifteen years later, Alq3 is still a key compound widely investigated and used in electroluminescent devices. The class of tris-chelate oxyquinoline octahedral metal complexes (Mq3), of which Alq3 is a member, may exist in the fac or mer isomeric forms, of C3 and C1 symmetry, respectively. Mer-Alq3 crystallizes in the α and β phases (and in a number of clathrates), whose optical properties are determined by the nature of π–π intermolecular contacts (the shorter the contacts, i.e. the denser the crystal, the more the fluorescence is red-shifted) [36]. The first report proving the existence of fac-Alq3 appeared in 2002 [37] and was immediately followed by other topical publications [39–41]. Noteworthy, the ‘discovery’ of the fac-isomer was perhaps delayed by the fact that Mq3 species were invariably found in mer stereochemistry, as extensively documented in [38].
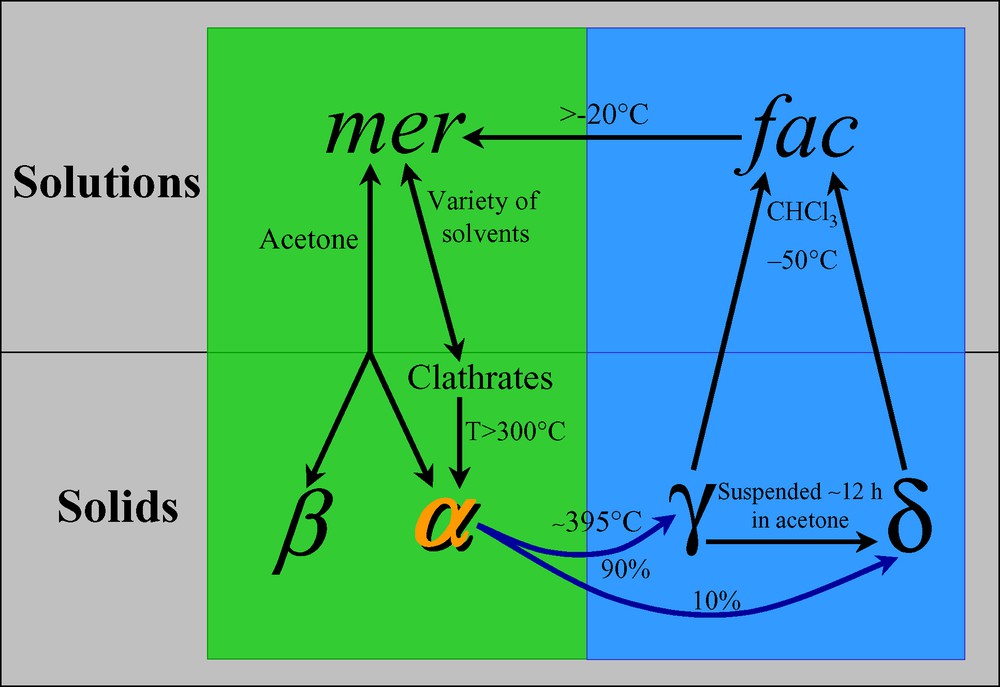
α-Alq3 polycrystalline powders can be easily transformed into a so called γ phase upon heating at ca 400 °C under atmospheric pressure [36], while ‘train’ sublimation leads to, among others fractions, the blue emitting δ phase, originally suggested to contain the fac-Alq3 isomer [41]. Notably the δ phase can be quantitatively obtained by suspending γ-Alq3 in a few drops of liquid acetone (at RT); in addition, the observation that seeding of supersaturated mer-Alq3 solutions with γ (or δ) nuclei does not yield the δ phase, suggests that γ- and δ-Alq3 share the same isomer [37,40].
Conventional 1H and 13C NMR investigations at RT revealed that, regardless of the starting material (α, (β), γ or δ phases), only the mer-Alq3 species is present in solution; however, when γ- or δ-Alq3 are suspended in CDCl3 at –50 °C, the pure fac-isomer can be observed. Indeed, fac-Alq3 is inert at –50 °C for several hours and starts to convert in mer-Alq3 at –20 °C (see Fig. 11) [37]. Intramolecular ligand scrambling in the mer isomer has been recently studied by dynamic NMR in CDCl3 solution (283–310–K temperature range) [42]; the activation parameters derived therein for the mer/mer and mer/fac interconversions confirmed either the impossibility to directly observe fac-Alq3 resonances at room temperature and its inertness at lower temperatures.
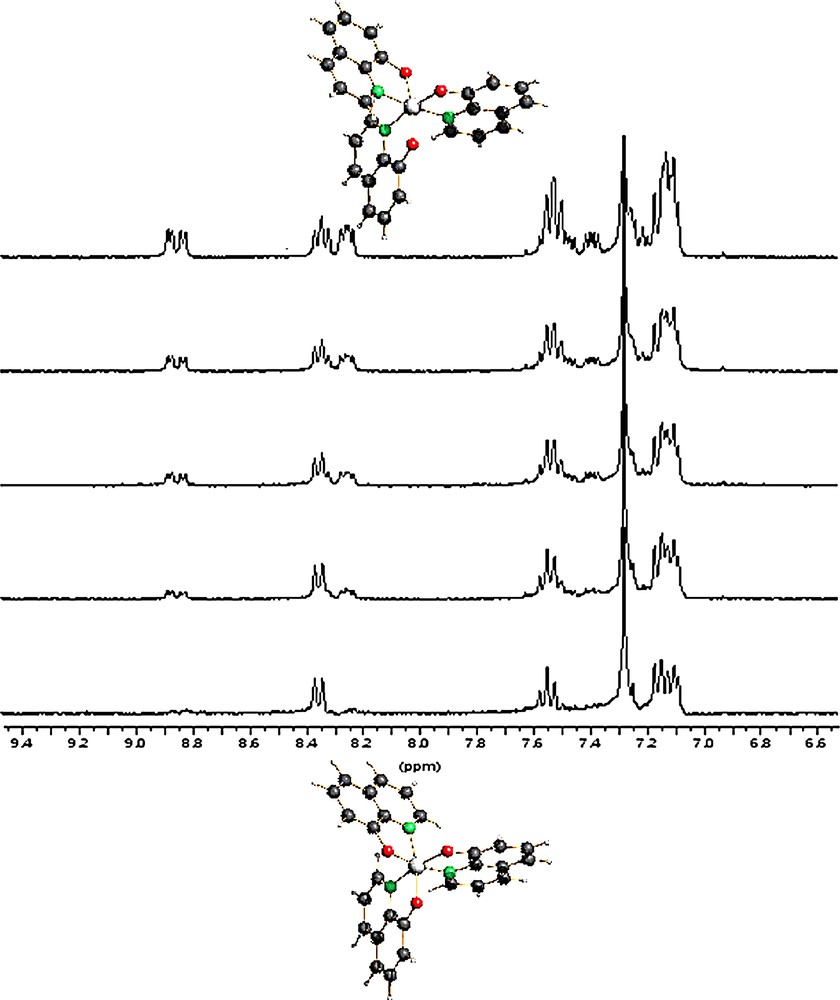
Time-evolution of the 1H NMR spectra (6.5–9.5 ppm range) of δ-Alq3 dissolved in CDCl3 at –50 °C, measured at –10 °C. Bottom to top: t = 0, 20, 40, 60, 120 min. Initially, the absence of ‘unperturbed’ H2 signals (near δ 8.9 ppm), coupled with the fact that only the signals of three magnetically equivalent H4 nuclei are observed, shows that only the fac-isomer (bottom) is present. After a while, peaks of the mer isomer (top trace) progressively appear. The increase of the overall proton resonance intensities observed during isomerization is due to the higher solubility of mer-Alq3 leading to a progressive dissolution of some ‘floating’ fac-Alq3. Masquer
Time-evolution of the 1H NMR spectra (6.5–9.5 ppm range) of δ-Alq3 dissolved in CDCl3 at –50 °C, measured at –10 °C. Bottom to top: t = 0, 20, 40, 60, 120 min. Initially, the absence of ‘unperturbed’ H2 signals (near δ 8.9 ppm), coupled with ... Lire la suite
Our studies led to the phase transformation diagram reported in Fig. 12 and to the selective production of ‘pure’ polycrystalline δ-Alq3, the XRPD pattern of which was easily indexed. At this point simulated annealing techniques, in conjunction with the fundamental information provided by the variable temperature NMR spectroscopy (see Fig. 11), made it possible to obtain a suitable structural model for the δ-Alq3 phase. After the deposit of our patent [37] and our first attempt to publish these results 7 many other studies on this subject appeared (including an XRPD structural characterization [38], a single crystal X-ray diffraction study [40] and a solid-state 27Al CP/MAS NMR spectroscopic study [43]), while we faced substantial, perhaps unreasonable difficulties in publishing our results [44].
One may question whether XRPD alone would have led to the correct structural model in the absence of ‘external information’ The fortunate availability of two independent XRPD ab initio structural characterizations of the δ-Alq3 phase and of experimental patterns of different origins and quality [37,44] allows us to build Table 2, where subtle, but significant differences can be appreciated.
Comparison of final refinement results for two different steroisomers and three independent data collections. All computations were performed using TOPAS and rigid bodies hinged about the aluminum atom as described in Refs. [37,40]
| D8–Kα12 | Stoe–Kα1 | X3B1 | ||||
| Typical fwhm (°) | 0.14 | 0.14 | 0.034 | |||
| Maximum peak-to-background | 147 | 15 | 26 | |||
| Refined % of γ-Alq3 | 5.0 | 1.4 | 1.2 | |||
| Agreement indices | Rwp | RB | Rwp | RB | Rwp | RB |
| Fac-Alq3 | 0.071 | 0.030 | 0.063 | 0.020 | 0.075 | 0.045 |
| Mer-Alq3 | 0.185 | 0.105 | 0.112 | 0.078 | 0.134 | 0.079 |
The results reported in Table 2 clearly show that, in principle, all three experiments may discriminate (with a different degree of certainty) between the two structural hypotheses. However, what is difficult to ascertain is the role of external knowledge during the ‘solution’ process. Indeed, as nicely suggested by Dinnebier [44], “it turned out, that global optimization algorithms in direct space run into severe problems in localizing the global minimum except if the correct isomer is used as starting model allowing the torsion angles to vary within certain limits. Only the high angle part of the powder pattern contains the information which is necessary to distinguish between different isomers. Nevertheless, the correct solution (if found) can be clearly identified.”
In this particular case, the agreement indices of the mer-stereoisomers alone could have easily led to an unfortunate misinterpretation, taking also into account that these values can further be lowered by data massaging, for example by releasing some restraints or by introducing texture or other microstructural effects. Worthy of note, the presence of one short intermolecular contact allows to discard the mer isomer hypothesis on a stereochemical basis. However, since the intrinsic limitations of the XRPD method may result in a slight misorientation of the refined fragment(s), the presence of such bad contact could also have been tolerated and considered either as: (i) a fake intermolecular contact or, of even more dramatic consequences, (ii) an unduly elongated bond of a new C–C bonded polymer, obtained by high-temperature (ca. 400 °C) H2 elimination 8.
Thus, since it is only the crystallographer who eventually decides whether or not the ‘best available solution’ well approximates reality, the larger the external information the easier and reliable the solution will be.
3 Conclusions and outlook
The validation of structural results of low quality on adding external observations is a customary behavior in protein crystallography; analogously, combination of EXAFS with PD data has also been reported [45]. All these approaches are ultimately based on the assumption that, if the structural model is optimized vs. data of different origins (diffraction, theory, spectroscopy, database frequencies, etc.), it is likely that systematic errors are cancelled or greatly limited.
The use of MM significantly increases the confidence in the final model; indeed, the coupling of XRPD with MM computations in the crystal lattice can successfully discriminate between a few alternative models by actively using experimental, i.e. accessible, information on lattice metrics, space group symmetry operations and heavy atom location. This approach, provided that a proper force field is available, is thought to increase the resolution inherent in the diffraction method and, therefore, to act as a lens capable to rescue subtle structural details which XRPD data alone cannot afford. In addition, the use of a joint, or even uncoupled, Rietveld/MM refinement supersedes the common behavior of introducing arbitrarily weighted restraints, since it weighs on a physical basis the different energetic contributions, leaving, as the only arbitrary choice, the relative importance of the two (partial) cost functions (Rwp and E), to be possibly equipartitioned.
In this mini-review we have also shown the importance of tailored experiments (such as SAED, NPD, NLO, NMR and other spectroscopic measurements) which, alone, cannot afford the structural information sought, but which invaluably assist the development of the ‘true’ model.
Obviously, single crystal X-ray diffraction still is the most powerful structural tool in the organometallic and co-ordination chemist's hands. Without this technique the whole branch of structural physical chemistry, as well as many fields of synthetic chemistry where spectroscopy alone is of little use, would not exist. However, it would be extremely unfortunate if the stereochemistry of important organometallic species, or of entire classes of compounds, would remain unknown because of the lacking of suitable well-diffracting single crystal specimens.
The number of molecular (or, more generally, covalent) structures solved and refined from powder diffraction data are steadily increasing. A quick survey in the most recent CSD release (April 2004) shows indeed about 700 entries under the ‘powder’ flag, 347 of which contain metal atoms 9. If compared to the pioneering ages, where a handful of structures were solved (yearly) by this method (mostly exploiting the newly available synchrotron sources), we can safely state that the number of scientists using this technique in they daily work has definitely grown, with the obvious consequence that new classes of compounds have been characterized, opening the way to new (and significant) chemistry. However, there is still a gap between the number of actual users of the method and the multitude of chemists which would greatly benefit from it. Thus, in accordance with our original goal, and particularly after it has been shown that the interplay between experiments of different origins give the highest confidence to the obtained results, we easily foresee, for structural powder diffraction from conventional laboratory data, a bright, not far, future.
Acknowledgements
We thank all co-workers who have participated in this project for their continuous support and helpful discussions. Funding from the Italian MURST and CNR is also acknowledged.
1 When dealing with (i) insoluble, thermally unstable, compounds which cannot be (re)crystallised from solution or from the melt; (ii) metastable phases destroyed or modified upon manipulation; (iii) twins; (iv) very small crystals and/or crystal aggregates; (v) gas/solid, liquid/solid and solid state reactions fragmenting and misorienting the coherent domains of the starting crystals but conserving the (poly)crystalline nature of the sample [9].
2 One-dimensional and ‘pseudo’ one-dimensional materials have since long fascinated physicists and chemists because of their unusual properties. There is a recent renaissance of research in the area of 1D polymers with metal-containing backbones possibly in the light of the explosion of interest in nanoscale electronic devices.
3 If possible, the side-loading technique should be used (H.F. Mc Murdie, M.C. Morris, E.H. Evans, B. Paretzkin, W. Wong-Ng, Powder Diffr. 1 (1986) 40), unless only a small quantity of material is available (in such case, the capillary mounting is desirable).

4 Note that a single crystal structure determination would not perform better in this respect, since diffraction, in the presence of disordered vacancies and cations, can at most observe the averaged host lattice.
5 A similar approach has been used for the analysis of the cation distribution in doped KTiOPO4 (S.J. Crenell, J.J. Owen, C.P. Grey, A.K. Cheetham, J.A. Kaduk, R.H. Jarman, J. Mater. Chem. 1 (1991) 113) and of the incommensurately modulated structure of Bi2Sr2CaCu2O8+y (Y. Gao, P. Coppens, D.E. Cox, A.R. Moodenbaugh, Acta Crystallogr. A49 (1993) 141). The combined use of X–N data from either two single-crystal datasets (F.A. Cotton, L.F. Chen, A.J. Schultz, C. R. Acad. Sci. Paris, Ser. II 323 (1996) 539) or two powder-diffraction experiments (R.E. Morris, W.T.A. Harrison, J.M. Nicol, A.P. Wilkinson, A.K., Cheetham, Nature 359 (1992) 519 has also been reported).
6 A split atom model was used to refine the μ3-H atoms by invoking two ‘new’ elements, Hx and Hn, with null contribution to the N and X structure factors, respectively. This makes, inter alia, their locations substantially unsensitive to the intrinsic overweight of the X dataset (in terms of quality and, perhaps, number of observations).
7 Manuscript N° 1075213 sent to Science on 16.06.2002.
8 Obviously this would contrast the observation that upon dissolution of δ-Alq3, followed by solvent removal, pure α-Alq3 is retrieved.
9 These values include also pure refinements, without ab initio structure solution. A more indicative figure, although not disaggregated among the different classes of compounds can be found at http://sdpd.univ-lemans.fr/iniref.html.


