1 The ligand close-packing model
In 1960, Bartell and Bonham [1], from an electron diffraction study of isobutene (2-methyl propene) (Fig. 1) found that the non-bonding distances between the three carbon atoms surrounding the central carbon were all the same, in other words they form an equilateral triangle. They proposed that these three atoms are close-packed and that this is the most important factor determining the geometry of this molecule. They pointed out that the observed CH3–C–CH3 angle of 112° was not in agreement with the prevailing belief that the central carbon atom is sp2 hybridized which should lead to a 120° bond angle. Moreover, this unexpectedly small angle could not be explained as being due to repulsion between bulky CH3 groups which should lead to a larger angle than 120°. According to Bartell and Bonham the small CH3–C–CH3 angle is due to the close packing of the three ligand C atoms and the fact that the C=CH2 bond is shorter than the other two C–C bonds. The central carbon atom is therefore not at the center of the equilateral triangle of carbon atoms but is displaced towards the CH2 carbon so that the opposing bond angle is necessarily smaller than 120°. A later more accurate electron diffraction study [2], however, gave the slightly different bond lengths and angles shown in parentheses in Fig. 1, which show that all three distances between the carbon atoms are not the quite the same. However, Bartell's slightly inaccurate data fortunately led him to investigate other ligand–ligand distances in both three and four coordinated molecules with a central carbon atom [3,4]. He found that these distances were also very nearly constant so that these ligands also appeared to be close-packed around the central carbon. So he proposed that each of these ligands could be assigned a characteristic radius such that the sum of two ligand radii gave the distance between any two given ligands [3,4]. Unfortunately, Bartell's proposal that the bond angles in these molecules are determined by ligand packing and differences in bond lengths was contrary to conventional thinking at the time, which was in terms of hybridization, and so was not widely accepted.

The structure of 2-methyl propene as determined by Bartell and Bonham.
Later, when other investigators, such as Glidewell [5], attempted to apply Bartell's radii (which have been referred to by Glidewell and others as 1, 3 radii) to molecules with other central atoms they found that they did not give good predictions of inter-ligand distances so that Bartell's model was gradually forgotten. Nevertheless, several authors, including Hargittai [6] in particular, continued to emphasize that ligand–ligand repulsions could be of importance in determining molecular geometry. For example, in his study of the geometry of the SO2 group in a variety of XYSO2 molecules he noted that “The oxygen–oxygen distance is strikingly constant at about 248–249 pm” and he went on to conclude “The constancy of the oxygen–oxygen distance of the SO2 group indicates that non-bonded atom–atom interactions may be at least as important in determining the geometry of the sulfone group as the electron pair repulsions considered in the VSEPR model”.
In 1997 Gillespie and Robinson [7,8], in the course of an investigation of bond lengths to fluorine, found exactly the same constancy of inter-ligand distances in other molecules with a central carbon atom as well as with other central atoms, such as Be and B, as Bartell had found for molecules with a central carbon atom. Some typical examples are given in Table 1 for F ligands. Similar data for Cl and H ligands are given in Tables 2 and 3. The ligand radii (one-half the X–X distance) obtained from this data and similar data are given in Table 4. The values for O and N were obtained from O–X and N–X distances. The radii for C, N and O are for these atoms, as it is considered that it is these atoms that are close-packed, and not for the complete groups such as CH3, NH2, and OH. These radii have been found to be nearly independent of the nature of the other atoms attached to the central atom. The effect of replacing H by other atoms such as F in a group such as CH3 has not been investigated but it is possible that such substitution would cause a change in the size of the carbon atom, so that a different ligand radius would have to be used.
Average bond lengths, bond angles, and F–F distances in some molecules containing BeFn, BFn, and CFn groupsa,b
| Molecule | CN | A–F | < FAF | F–F |
| BeF3– | 3 | 149 | 120 | 258 |
| BeF42– | 4 | 155.4 | 109.5 | 254 |
| Mean | 256 (2) | |||
| BF3 | 3 | 130.7 | 120.0 | 226 |
| F2B–OH | 132.3 | 118.0 | 227 | |
| F2B–NH2 | 132.5 | 117.9 | 227 | |
| F2B–Cl | 131.5 | 118.1 | 226 | |
| F2B–H | 131.1 | 118.3 | 225 | |
| BF4– | 4 | 138.2 | 109.5 | 226 |
| F3B–CH3– | 142.4 | 105.4 | 227 | |
| F3B–CF3– | 139.1 | 109.9 | 228 | |
| F3B–PH3 | 137.2 | 112.1 | 228 | |
| Mean | 226 (1) | |||
| CF3+a | 3 | 124.4 | 120 | 216 |
| F2C=CF2 | 131.9 | 112.4 | 219 | |
| F2C=CCl2 | 131.5 | 112.1 | 218 | |
| F2C=CH2 | 132.4 | 109.4 | 216 | |
| F2C=CHF | 133.6 | 109.2 | 218 | |
| [F2C–N]2 | 130.4 | 110.8 | 215 | |
| CF4 | 4 | 131.9 | 109.5 | 215 |
| F3C–CF3 | 132.6 | 109.8 | 217 | |
| F3C–BF3– | 134.7 | 104.9 | 214 | |
| F3C–OF | 131.9 | 109.4 | 215 | |
| F3C–O– | 139.2 | 101.3 | 215 | |
| Mean | 216 (1) |
a Ab initio structure.
b Distances in pm, angles in degrees.
Average bond lengths, bond angles, and Cl–Cl distances in some molecules containing BeCln, BCln, and CCln groupsa,b
| Molecule | CN | A–X | XAX | X–X |
| BeCl3– a | 3 | 194.2 | 120.0 | 336 |
| Cl2Be(NCMe)2 | 4 | 197.8 | 116.8 | 337 |
| Cl2Be(OEt2)2 | 197.8 | 116.6 | 337 | |
| BeCl4– a | 210.4 | 109.5 | 344 | |
| Mean | 339 | |||
| BCl3 | 3 | 174.2 | 120.0 | 301 |
| Cl2B–BCl2 | 175.0 | 118.7 | 301 | |
| BCl4– | 4 | 183.3 | 109.5 | 299 |
| Cl3B–NH3 | 183.8 | 111.2 | 303 | |
| Cl3B–NH5C5 | 183.7 | 110.1 | 301 | |
| Cl3B–NMe3 | 1831 | 109.3 | 299 | |
| Cl3B–PPh3 | 185.1 | 109.5 | 302 | |
| Mean | 301 (1) | |||
| CCl3+ a | 3 | 165.8 | 120.0 | 287 |
| Cl2CO | 173.8 | 111.8 | 288 | |
| Cl2C=CH2 | 171.8 | 112.4 | 286 | |
| CCl4 | 4 | 177.1 | 109.5 | 289 |
| Cl2CH2 | 176.5 | 112.0 | 293 | |
| Cl2CF2 | 174.4 | 112.5 | 290 | |
| Cl2CMe2 | 179.9 | 108.3 | 292 | |
| Cl3C–CCl3 | 176.9 | 108.9 | 288 | |
| Cl3CH | 175.8 | 111.3 | 290 | |
| Cl3CF | 176 | 109.7 | 291 | |
| Mean | 290 (2) |
a Ab initio structure.
b Distances in pm, angles in degrees.
Average bond lengths, bond angles and H–H distances in some molecules containing BHn, CHn, and NHn groupsa,b
| Molecule | CN | A–H | < HAH | H–H |
| BH3 | 3 | 118.5 | 120.0 | 205 |
| H2B–NH2a | 118.4 | 121.3 | 206 | |
| H2B–NH2a | 119.0 | 116.0 | 202 | |
| BH4– a | 4 | 123.7 | 109.5 | 202 |
| H3B–F– a | 124.7 | 108.2 | 202 | |
| H3B–Cl – | 120.3 | 113.5 | 201 | |
| H3B–CO | 122.1 | 114.5 | 205 | |
| H3B–NMe3 | 121.1 | 113.6 | 203 | |
| H3B–PH3 | 121.2 | 114.6 | 204 | |
| H3B–PMe3 | 121.2 | 113.5 | 203 | |
| H3B–PF3 | 120.7 | 115.0 | 203 | |
| Mean | 203 (1) | |||
| CH3+ | 3 | 108.7 | 120.0 | 188 |
| H2C=CH2 | 108.7 | 117.4 | 186 | |
| H2C=C=CH2 | 108.2 | 118.4 | 186 | |
| H2C=CF2 | 109.1 | 122.0 | 191 | |
| H2C=CMe2 | 109.5 | 117.4 | 187 | |
| H2C=C(Cl)CN | 108.6 | 116.5 | 185 | |
| H2C=CHF | 108.5 | 114.7 | 183 | |
| H2C=NH | 109.2 | 109.8 | 179 | |
| H2C=O | 110.1 | 116.3 | 187 | |
| H2C=S | 109.2 | 117.2 | 186 | |
| Mean | 186 (2) | |||
| CH4 | 4 | 108.4 | 109.5 | 177 |
| H3C–CH3 | 109.4 | 107.8 | 177 | |
| H3C–F | 110.5 | 109.9 | 181 | |
| H2CF2 | 109.2 | 111.9 | 181 | |
| H3C–Cl | 109.6 | 110.9 | 181 | |
| H2CCl2 | 108.7 | 111.5 | 180 | |
| H2CClF | 107.8 | 111.9 | 179 | |
| H3C–Br | 109.5 | 111.6 | 181 | |
| H2CBr2 | 107.1 | 110.9 | 175 | |
| H3C–I | 109.6 | 111.8 | 181 | |
| H3C–CN | 110.3 | 109.4 | 180 | |
| H3C–NC | 110.2 | 109.8 | 180 | |
| H3C–NH2 | 111.2 | 108.4 | 180 | |
| H3C–OH | 109.8 | 109.1 | 179 | |
| H3C–CF3 | 108.5 | 110.6 | 178 | |
| H3C–SiH3 | 109.3 | 107.7 | 177 | |
| H3C–GeH3 | 108.3 | 108.4 | 176 | |
| FCH2–CF3 | 109 | 108.9 | 177 | |
| ClCH2–CF3 | 109.5 | 108 | 177 | |
| Mean | 178 (2) | |||
| H2N=BH2b | 3 | 99.5 | 112.6 | 166 |
| H2N=BF2 | 100.3 | 106.9 | 161 | |
| NH4+Cl– | 4 | 103.2 | 109.5 | 169 |
| NH4+Br– | 103.1 | 109.5 | 168 | |
| NH3 | 101.6 | 107.3 | 164 | |
| ND3 | 101.4 | 107.1 | 163 | |
| D3N–BF3 | 100.7 | 107.6 | 163 | |
| NH2– | 103.4 | 104 | 163 | |
| H2N–CH3 | 103.1 | 106 | 165 | |
| H2N–NH2 | 102.2 | 107 | 164 | |
| H2N–F | 102.3 | 103.5 | 161 | |
| H2N–Cl | 101.7 | 107 | 164 | |
| H2N–SHa | 99.5 | 110.1 | 163 | |
| Mean | 164 (2) |
a Ab initio structure.
b Distances in pm, angles in degrees.
Ligand Radii (pm)
| Ligand | Central atom | ||||
| Be | B | Ca | N | ||
| H | 102 | 89 | 82 | ||
| C | 137 | 125 | 125 | 120 | |
| N | 144 | 124 | 119 | 114 | |
| O | 133 | 119 | 114 | 113 | |
| F | 126 | 113 | 108 | 108 | 107 |
| Cl | 168 | 151 | 145 | 144 | 140 |
a Bartell radii in italics.
Each of the radii for ligands bonded to Be, B and N differ from those for ligands bonded to C which are very close to the radii deduced by Bartell. These ligand radii decrease across the periodic table with increasing electronegativity of the central atom and therefore decreasing ligand charge. This expected decrease in charge is confirmed by the ligand charges calculated by the atoms in molecules (AIM) method [9,10] (Table 5). Figs. 2 and 3 show that the ligand radius of fluorine and of hydrogen increases with increasing ligand charge, as would be expected. The form of this variation would not necessarily be expected to be the same for F and for H but there is no obvious reason why it appears to be linear for H. This increase of the ligand radius with the ligand charge is the principal reason why the use of the Bartell radii for central atoms other than carbon was found to be unsatisfactory and the reason therefore that the concept of ligand close packing (LCP) fell into disuse.
AIM ligand charges
| Ligand | F | Cl | H |
| LiX | –0.92 | –0.91 | –0.91 |
| BeX2 | –0.88 | –0.84 | –0.87 |
| BX3 | –0.81 | –0.64 | –0.70 |
| CX4 | –0.61 | –0.09 | –0.04 |
| NX3 | –0.28 | +0.08 | +0.35 |
| OX2 | –0.13 | +0.23 | +0.63 |
| FX | 0 | +0.38 | +0.78 |
| BeX3– | –0.91 | ||
| BeX42– | –0.94 | ||
| BX4– | –0.86 | –0.70 | –0.67 |
| CX3+ | –0.53 | +0.33 | +0.16 |
| NF4+ | –0.08 | +0.48 |

Plot of fluorine ligand radius against the fluorine charge for period-2 molecules.
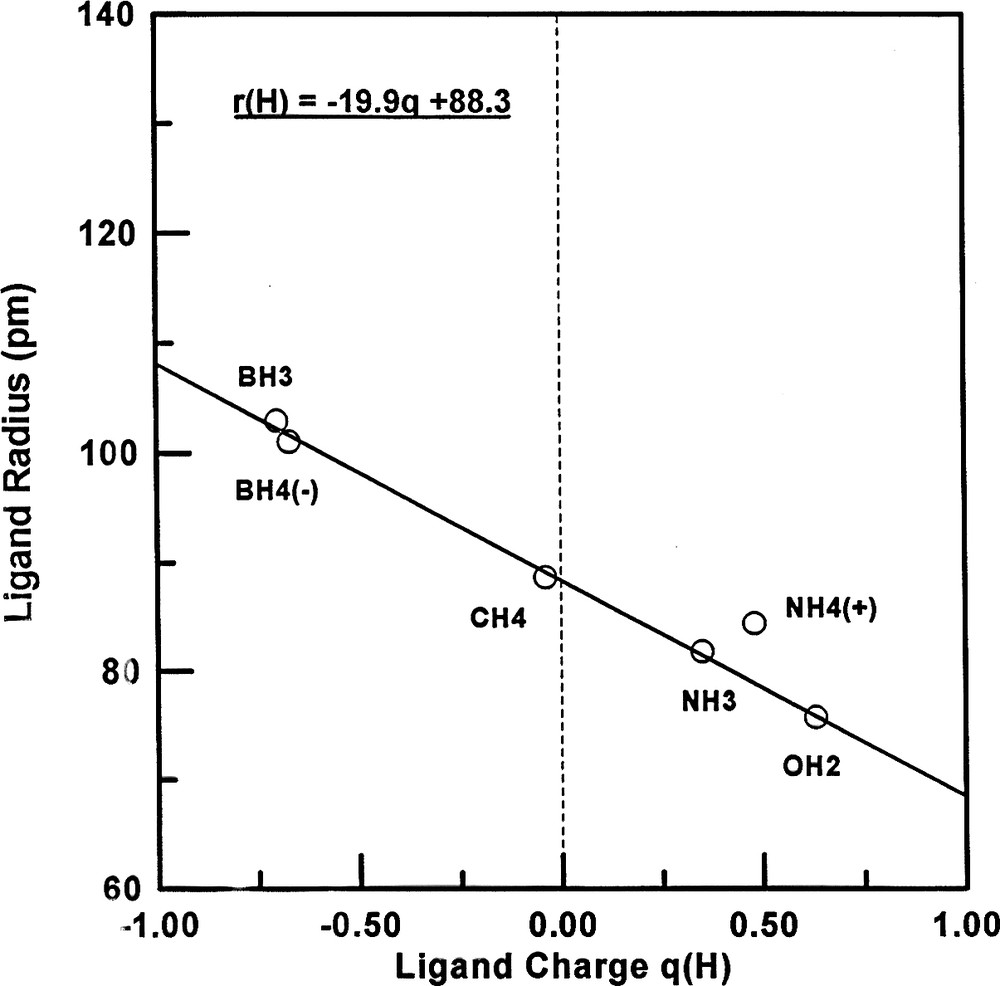
Plot of the hydrogen ligand radius against the hydrogen charge for period-2 molecule.
We have confirmed Bartell's finding that in molecules with two or more different ligands, X, Y, … bonded to the central atom the X–Y distances are given to a good approximation by the sum of the X and Y radii. In other words ligand radii are additive to a good approximation. Some examples are given in Tables 6–8. Because the ligands are close-packed the ligand radii given in Table 4 are independent of the coordination number of the central atom, which is either three or four. Thus the substantial difference in the length of the BF bonds in BF4– (138.2 pm) and BF3 (130.7 pm) is simply accounted for by the change in coordination number, in other words three ligands pack more closely around the central atom than four. There is no reason to assume that the bond length difference is due to back-bonding from fluorine to boron giving the BF bond some double bond character (Fig. 4) as has often been suggested on the grounds that in this way the otherwise empty 2pz orbital is occupied and the octet rule is obeyed. However, there is no reason that the octet rule (to which there are many exceptions) has to be obeyed or why the 2pz orbital has to be occupied.
Inter-ligand O–F distances in some oxofluoro boron and carbon moleculesa,b
| Molecule | A–F(O) | <FAO | O–F |
| F3B–OH2 | 1 138.2 BF | 1–3 105.9 | 233 |
| 2 138.3 BF | 2–3 106.5 | 234 | |
| 3 153.2 BO | |||
| F3B–O(H)Me | 1 139.9 BF | 1–3 105.7 | 233 |
| 2 135.5 BF | 2–3 106.0 | 230 | |
| 3 152.4 BO | |||
| F3B–OPPh3 | 1 135.7 BF | 1–4 105.7 (3) | 229 |
| 2 135.3 BF | 2–4 108.1 (4) | 233 | |
| 3 133.4 BF | 3–4 109.2 (4) | 233 | |
| 4 151.6 BO | |||
| F3B–OAsPh3 | 1 135.4 BF | 1–4 106.4 (3) | 228 (1) |
| 2 136.2 BF | 2–4 109.0 (3) | 232 (1) | |
| 3 135.2 BF | 3–4 109.0 (3) | 231 (1) | |
| 2 148.6 BO | |||
| F2B–OH | 1 132.3 BF | 1–2 122.8 | 234 |
| 2 134.4 BO | |||
| F2B–O– a | 1 140.5 BF | 1–2 126.8 | 234 |
| 2 120.7 BO | |||
| Mean O–F | 232 (2)c | ||
| CF3OCF3 | 1 132.7 BF | 110.2 | 221 |
| 2 136.9 BO | |||
| CF3O– | 1 139.2 BF | 116.2 | 223 |
| 2 122.7 BO | |||
| CF3OF | 1 131.9 BF | 109.6 | 222 |
| 2 139.5 BO | |||
| COF2 | 1 131.7 BF | 126.2 | 222 |
| 2 117 BO | |||
| MeC(O)F | 1 134.8 BF | 121.4 | 221 |
| 2 118.1 BO | |||
| FC(O)OF trans | 1 132.4 BF | 126.5 | 223 |
| 2 117 BO | |||
| FC(O)OF cis | 1 132 BF | 126.4 | 223 |
| 2 117.2 BO | |||
| FC(O)NO3 | 1 132 BF | 128.8 | 224 |
| 2 116.5 BO | |||
| [F(O)C–]2 | 1 132.9 BF | 124.2 | 222 |
| 2 118BO | |||
| Mean | 222 (1)d |
a Ab initio structures.
b Distances in pm, angles in degrees.
c Radius sum 232 pm.
d Radius sum 222 pm.
Inter-ligand C–F and C–Cl distances in some fluorocarbon and chlorocarbon moleculesa
| Molecule | C–X | <CCF | C–F |
| F3C–CF3 | 1 132.6 CF | 109.8 | 234 |
| 2 154.5 CC | |||
| (CF3)3CH | 1 133.6 CF | 110.9 | 237 |
| 2 156.6 CC | |||
| (CF3)3CHCl | 1 133.3 CF | 111 | 237 |
| 2 154.4 CC | |||
| H3C–C(O)F | 1 136.2 CF | 110.5 | 236 |
| 2 150.5 CC | |||
| F2C=CF2 | 1 131.9 CF | 123.8 | 232 |
| 2 131.1 CC | |||
| F2C=CCl2 | 1 131.5 CF | 124 | 235 |
| 2 134.5 CC | |||
| F2C=CH2 | 1 131.6 CF | 125.2 | 234 |
| 2 132.4 CC | |||
| FCH=CFH trans | 1 134.1 CF | 119.3 | 231 |
| 2 132.9 CC | |||
| Mean | 234 (2)b | ||
| Molecule | C–X | <CCCl | C–Cl |
| (CH3)2CCl2 | 1 179.9 CCl | 108.9 | 271 |
| 2 152.3 CC | |||
| CH3CH2Cl | 1 174.6 CCl | 110.7 | 274 |
| 2 152.8 CC | |||
| CH3C(O)Cl | 1 179.8 CCl | 112.2 | 275 |
| 2 150.8 CC | |||
| [O(Cl)C]2 | 1 174.6 CCl | 111.7 | 272 |
| 2 153.6 CC | |||
| Cl2C=CCl2 | 1 171.9 CCl | 122.2 | 270 |
| 2 135.5 CC | |||
| H2C=CHCl | 1 172.8 CCl | 121.1 | 269 |
| 2 135.5 CC | |||
| Cl2C=C=CH2 | 1 173.3 CCl | 122.2 | 269 |
| 2 132.6 CC | |||
| Mean | 271 (2) c |
a Distances in pm, angles in degrees.
b Radius sum 233 pm.
c Radius sum 270 pm.
Comparison of predicted and calculated H–H inter-ligand distances a
| Molecule | A–H | A–X | ∠H–A–X | H–X | |
| obs. pred.b | |||||
| Boron | |||||
| BHF2 | 118 | 131.1 | 120.9 | 216 | 215 |
| Carbon | |||||
| CH3F | 110.5 | 138.5 | 109 | 203 | 197 |
| CH2F2 | 109.2 | 135.8 | 108.1 | 200 | 197 |
| CHF3 | 108.8 | 134.5 | 110.5 | 200 | 197 |
| CH3Cl | 109.6 | 178.1 | 108 | 236 | 234 |
| CH2Cl2 | 108.7 | 176.5 | 108.1 | 234 | 234 |
| CHCl3 | 107.3 | 176.7 | 108.5 | 234 | 234 |
| CH3Br | 109.5 | 193.9 | 107.2 | 249 | 248c |
| CH2Br2 | 107.1 | 192.1 | 108.3 | 248 | 248c |
| CHBr3 | 106.8 | 193 | 108.1 | 248 | 248c |
| Nitrogen | |||||
| NH2F | 102.3 | 143 | 101.1 | 191 | 188 |
| NHF2 | 102.9 | 140 | 99.8 | 187 | 188 |
| NH2Cl | 101.2 | 174.8 | 103.7 | 222 | 224 |
| Oxygen | |||||
| HOF | 96.4 | 144.2 | 97.2 | 183 | 186 |
| HOCl | 95.9 | 169 | 102.5 | 212 | 215 |
| HOCl | 96.4 | 170 | 103 | 213 | 215 |
a Distances in pm and bond angles in degrees.
b From sum of ligand radii r(H) + r(X) in Table 5.
c r(Br) = 159 pm.

The structures of BF3 and BF4– and resonance structures for BF3 describing the supposed π-back-donation from F to B producing double bond character in the BF bonds.
In any case, it seems unreasonable to expect that there can be any substantial donation of electron density from a very strongly electronegative fluorine atom to a much more weakly electronegative boron atom. That ligand packing could determine bond lengths does not seem to have been very seriously considered in the past and bond length variations have very often been attributed simply to changes in double or triple bond character, particularly in the case of carbon–carbon bonds, but this is not necessarily the case for other bonds or even always for carbon–carbon bonds.
The ligand radii in Table 4 include data for N as a central atom for both approximately tetrahedral NX3E molecules as well as triangular planar NX3 molecules derived from the bond lengths and angles for these molecules given in Table 9. Clearly no radius can be assigned to a lone-pair that spreads out around the core, as much as possible occupying a spherical domain in the absence of any ligands. In NX3E molecules the lone-pair spreads out around the core pushing the ligands together until they ‘touch’, that is until the X–X distance is equal to the sum of the ligand radii.
Bond lengths, bond angles, and X–X distances in NX3E trigonal pyramidal and NX4+ tetrahedral moleculesa
| N–X | <XNX | X–X | |
| NH3 | 101.6 | 107.3 | 164 |
| NF3 | 136.5 | 102.3 | 213 |
| NMe3 | 145.1 | 110.9 | 240 |
| NH4+ | 103.2 | 109.5 | 168 |
| NF4+ | 130.5 | 109.5 | 213 |
| bArNMe3+ | 146.5 | 109.5 | 239 |
| NMe4+ Br– | 148.7 | 109.5 | 243 |
a Bond lengths in pm, angles in degrees.
b D.J. Evans, D.L. Hughes, Acta Crystallogr. 46C (1990) 1452.
In series of related molecules such as the hydrides and halides of N, P, O and S, bond angles increase with increasing size (i.e. ligand radius) of the halogen as can be seen in Table 10. Similarly, in a series of hydrides, fluorides chlorides, or bromides of the elements in a given group the bond angle decreases with increasing size of the central atom. There are two exceptions in Table 10, namely that the bond angle in NH3 is larger than in the NF3 molecule and the bond angle in H2O is larger than F2O even though H is smaller than F. This apparent anomaly shows that bond lengths must also be taken into account. The ligands in both NH3 and NF3 are both close-packed, so that the slightly smaller bond angle in NF3 than in NH3 must be due to the greater length (136.5 pm) of the NF bonds than the NH bonds (99.7 pm). The same explanation may be given for the larger bond angle in H2O than in F2O.
Bond angles in trigonal pyramidal AX3E and angular AX2E2 moleculesa,b
| N | P | As | Sb | |
| AH3 | 107.2 | 93.5 | 92.1 | 91.6 |
| AF3 | 102.3 | 97.7 | 96.1 | |
| ACl3 | 107.1 | 100.3 | 98.6 | 97.2 |
| ABr3 | 101.1 | 99.8 | 98.2 | |
| AMe3 | 110.9 | 98.6 | 96.1 | 94.1 |
| AI3 | 102 | 100.2 | 99.3 | |
| O | S | Se | Te | |
| AH2 | 104.5 | 92.1 | 90.6 | 90.3 |
| AF2 | 103.1 | 98 | ||
| ACl2 | 110.9 | 102.7 | 99.6 | 97 |
| AMe2 | 111.8 | 99.1 | 96.3 | 94 |
a Data taken from Gillespie and Hargittai.
b Angles in degrees.
The effect of bond length is also evident in other hydrides and is particularly evident in molecules such as HOF which has an H–F distance of 183 pm which is close to the average (186 pm) of the H–H distance in H2O (151 pm) and the F–F distance in F2O (221 pm) as would be expected if the ligands are close-packed in each case. But the H–F distance corresponds to the small bond angle of 97.3° which is smaller than the angles in both H2O (104.5°) and F2O (103.3°) because of the short length of the O–H bond compared to that of the O–F bond (Fig. 5).

The structures of F2O, FOH, and H2O.
2 Bond angles and the VSEPR model
The LCP model gives a different explanation for bond angles than the VSEPR model. According to the VSEPR model XAX bond angles decrease with increasing electronegativity of the ligand and the consequent reduction in size of the AX bonding domain. In most cases ligand size decreases with increasing electronegativity of the ligand. For example, in the halogens ligand size increases from F to Br while the ligand electronegativity decreases from F to Br, so that the predictions of the two models often agree. However, the inadequacy of the electronegativity rule is illustrated clearly by the examples in Fig. 6 where according to this rule we would expect the bond angles in the HOX molecules to be between the values for the HOH and XOX angles instead of smaller than either. In the next section we mention some further examples for which the two models do not make the same predictions and where the predictions of the LCP model are in agreement with experiment whereas those of the VSEPR model are not.

Plot of fluorine ligand radius against fluorine charge for period-2 and-3 molecules.
3 Period-3 molecules
Because the period-3 elements are larger than the corresponding period-2 elements and the AX bonds are correspondingly longer it is natural to wonder if their molecules are also close-packed. In fact, as is not surprising, it has been shown that only six-coordinated molecules are close-packed [11]. The vast majority of the six-coordinated molecules of the period-3 elements are either AF5X or AF6 molecules. The only known homoleptic six-coordinated molecule with ligands other than fluorine are PCl6– and Si(OH)62–. PCl6– is only found in solid PCl5 which consists of PCl4+ and PCl6– ions and only one example of the Si(OH)62– ion is known [12]. It would appear that, with the exceptions of PCl6– and Si(OH)62–, six-coordinated molecules with more than one or two ligands that are larger than fluorine are too crowded to be stable. Hydrogen is the only ligand that is smaller than F and hydrides of the higher oxidation states of P, S and Cl are unknown as they are unstable with respect to the lowest oxidation state hydride and H2. Table 11 gives the F–F distances in a number of six-coordinated fluorides of Si, P, S and Cl. These inter-ligand distances are very nearly constant confirming that these ligands can be regarded as close-packed. The fluorine ligand radii given in Table 12 were obtained from the data in Table 11. These ligand radii decrease across period-3 from 119 pm for fluorine bonded to silicon to 110 pm for fluorine bonded to chlorine as expected from the increasing electronegativity of the central atom and the consequent decrease in the ligand negative charge. This expected decrease in the ligand charge is confirmed by the AIM calculated ligand charges given in Table 5. These ligand radii agree well with the radii deduced for the period-2 fluorides taking into account the differences in the fluorine charge as shown in Fig. 6. The points for the six-coordinated period-3 molecules fit very well on the curve for the four-coordinated period-2 fluorides, showing that the six-coordinated period-3 fluorides are indeed close-packed.
Bond lengths, bond angles, and F–F inter-ligand distances in some period-3 six coordinate fluoridesa,b
| Molecule | A–F | <FAF | F–F* |
| Silicon | |||
| SiF62– | 1 168.4 a | 1–2 90 | 238 |
| 2 168.4 e | 2–2 90 | 238 | |
| SiF4(dipy)-trans | 1 165.7 a | 1–2 93.1 | 239 (245)c |
| 2 163.1 e | 2–2 97.4 | ||
| SiF5NH3– | 1 168 a | 1–2 90.4 | 238 |
| 2 167.8 e | 2–2 90.1 | 237 | |
| SiF4(NH3)2 | 2 167.1 e | 2–2 90 | 236 |
| Mean | 238 (1) | ||
| Phosphorus | |||
| PF6– | 1 158 a | 1–2 90 | 224 |
| 2 158 e | 2–2 90 | 224 | |
| PF5·py | 1 158.2 a | 1–2 91.8 | 228 |
| 2 158.9 e | 2–2 88.4 | 222 | |
| PF5H– | 1 159.4 a | 1–2 88.8 | 223 |
| NMe4+ | 2 159.5 e | 2–2 90.0 | 226 |
| PF5·NH3 | 1 158.2 a | 1–2 91.5 | 228 |
| 2 159.5 e | 2–2 89.6 | 225 | |
| Mean | 225(2) | ||
| Sulfur | |||
| SF6 | 1 156.2 a | 1–2 90 | 221 |
| 2 156.2 e | 2–2 90 | 221 | |
| SF5Cl | 1 158.8 a | 1–2 89.3 | 222 |
| 2 156.3 e | 2–2 90 | 221 | |
| SF5OCl | 1 156.0 a | 1–2 89.6 | 221 |
| 2 156.0 e | 2–2 90 | 221 | |
| SF5OCN | 1 155.4 a | 1–2 90.4 | 221 |
| 2 155.4 e | 2–2 90 | 221 | |
| SF5NCO | 1 156.7 a | 1–2 89 | 220 |
| 2 156.7 e | 2–2 90 | 222 | |
| SF5CF3 | 1 157.0 a | 1–2 89.5 | 220 |
| 2 156.0 e | 2–2 90 | 221 | |
| SF5C≡CH | 1 157.0 a | 1–2 88.9 | 221 |
| 2 156.0 e | 2–2 90 | 221 | |
| Mean | 221(1) | ||
| Chlorine | |||
| ClF5 | 1 157.1 a | 1–2 86 | 221 (235)d |
| 2 166.9 e | 2–2 89.7 | ||
| ClF6+ | 1 155 a | 1–2 90 | 219 |
| 2 155 e | 2–2 90 | 219 |
a Data from Robinson and Gillespie, Inorg. Chem. 42 (2003) 3865.
b All structures included in this table have bond lengths accurate to 1 pm or better and angles accurate to 1° or better.
c The NSiN angle is only 80.0° so the two fluorine atoms in this plane are not close-packed and the F–F distance is accordingly larger than 238 pm.
d The lone-pair increases the length of the adjacent bonds in the base of the square pyramid so these ligands are not close-packed with each other but only with the axial ligand.
Fluorine ligand radii, rF (pm). For the period-3 non-metals
| Si | P | S | Cl |
| 119 | 112 | 111 | 110 |
4 Five-coordinated molecules
It is not possible to pack five ligands around a central atom so that they are all close-packed and at equal distances from each other and from the central atom. The points-on-a-sphere model shows that either the trigonal bipyramid or the square pyramid is the preferred structure depending on the value of the exponent n in the assumed force law F = 1/dn, where d is the distance between the points. However, this model is only an approximation as five ligands cannot all be at the same distance from the central atom core. In fact the vast majority of five-coordinated molecules of the non-metals have the trigonal bipyramidal geometry with two longer axial bonds and three shorter equatorial bonds in which the axial ligands are close-packed with the equatorial ligands, but the equatorial ligands are not close-packed with each other giving six close-packed Feq–Fax distances and three longer Feq–Feq distances. Because the axial ligands are close-packed with the equatorial ligands the ligand radius can be obtained from the Fax–Feq distances as shown in Table 13. These values are close to, but very slightly smaller than, the radii obtained from the six-coordinated molecules. This small discrepancy suggests that the ligands in these molecules are not quite as incompressible as the LCP model assumes. A free ligand, such as a fluoride ion, is relatively compressible. As ligands are attracted to the central atom the inter-ligand distances decrease and the inter-ligand repulsive force increases until an equilibrium situation is reached in which the attractive force between the ligands and the central atom is just balanced by the repulsive forces. The constant inter-ligand distances in these molecules show that when, in the four-coordinated molecules of period-2 and the six-coordinated molecules of period-3, the equilibrium situation is reached, the ligands have been compressed to such an extent that the repulsive force between them would increase very rapidly with any further decrease in the inter-ligand distance and so the ligands have become essentially incompressible. In five-coordinated molecules the three equatorial ligands are not close-packed with each other and so it is reasonable to suppose that they are a little more compressible than in the corresponding six-coordinated molecules so that the Feq–Fax distances are very slightly shorter than in the corresponding six-coordinated molecules.
Axial (a) and equatorial (e) bond lengths, bond angles, and inter-ligand F–F distances in some five-coordinated fluorides a
| Molecule | A–F | < XAX | X–X |
| SiF5– | 1 166 a | 1–2 90.2 | 232 |
| BzlNMe3+ | 2 162.2 e | ||
| SiF4Ph– | 1 169.1 a | 1–1 87.3 | 229 |
| NPr4+ | 2 162.6 e | ||
| SiF4Mes– | 1 171.7 a | 1–2 89.3 | 233 |
| K+* | 2 156.2 e | ||
| SiF4C6H2tBu3– | 1 167.7 a | 1–2 89.5 | 233 |
| K+ * | 2 162.1 e | ||
| SiF3Xyl2– | 1 171.4 a | 1–2 87.9 | 234 |
| K+ * | 2 165.2 e | ||
| SiF3(Ph)tBu– | 1 170 a | 1–2 86.1 | 228 |
| K+* | 2 163.9 e | ||
| SiF3(Ph)Me– | 1 169.5 a | 1–2 87.9 | 230 |
| N(nBu)4+ | 2 162.1 e | ||
| SiF3Ph2– | 1 170.5 a | 1–2 86.2 | 230 |
| NMe4+ | 2 156.2 e | ||
| SiF3(o-Tol)2– | 1 170.1 a | 1–2 87.2 | 230 |
| K+ * | 2 164 e | ||
| SiF3(phen) | 1 162.1 a | 1–2 93.7 | 234 |
| 2 159 e | |||
| SiF4NH2– | 1 167.8 a | 1–2 90 | 237 |
| NH4+ | 2 167.8 e | ||
| Mean | 232 (2) | ||
| PF5(g) | 1 157.7 a | 1–2 90 | 220 |
| 2 153.4 e | |||
| PF5(s) | 1 158.5 a | 1–2 90 | 220 |
| 2 152.2 e | |||
| PF4Cl | 1 158.1 a | 1–2 90.3 | 221 |
| 2 153.5 e | |||
| PF3Cl2 | 1 159.3 a | 1–2 90 | 221 |
| 2 153.8 e | |||
| PF3Cl2 | 1 159.3 a | 1–2 89.3 | 221 |
| 2 154.6 e | |||
| PF4Me | 1 161.2 a | 1–2 89.1 | 221 |
| 2 154.3 e | |||
| PF4(2-mp) | 1 160.1 a | 1–2 88.1 | 218 |
| 2 153.9 e | |||
| PF3Me2 | 1 164.3 a | 1–2 89.9 | 226 |
| 2 155.5 e | |||
| PF3(NH2)2 | 1 161.9 a | 1–2 89.5 | 224 |
| 2 156 e | |||
| Mean | 221 (2) | ||
| SF4 | 1 164.6 a | 1–2 87.9 | 222 |
| 2 154.5 e | |||
| F3SCH3 | 1 168.1 a | 1–2 87.6 | 226 |
| 2 157.5 e | |||
| F3SCF3 | 1 167.9 a | 1–2 84.1 | 219 |
| 2 159.6 e | |||
| F3SCN | 1 165.7 a | 1–2 86.9 | 221 |
| 2 155.2 e | |||
| F4S=O | 1 158.4 a | 1–2 85.8 | 213 |
| 2 152.8 e | |||
| F4S=CH2 ED | 1 159.5 a | 1–2 86.6 | 217 |
| 2 157.5 e | |||
| XR | 3 159.3 a | 3–4 86.8 | 217 |
| 4 156.1 e | |||
| F4S=C (CF3)Me | 1 159 a | 1–2 86.8 | 217 |
| 2 157 e | |||
| F4S=NF | 1 161.5 a | 1–2 89.1 | 219 |
| 2 156.4 e | |||
| 3 153.5 a | 3–4 87.2 | 214 | |
| 4 156.4 e | |||
| F4S=NH ** | 1 161.1 a | 1–2 85.8 | 215 |
| 2 155.0 e | |||
| 3 156.9 a | 3–4 85.9 | 213 | |
| 4 155.0 e | |||
| F4S=NMe | 1 164.3 a | 1–2 85.9 | 219 |
| 2 156.7 e | |||
| 3 154.6 a | 3–4 85.9 | 212 | |
| 4 156.7 e | |||
| Mean | 217(4) |
a Distances in pm and bond angles in degrees. Data from Robinson and Gillespie, Inorg. Chem. 42 (2003) 3865.
The A–X bonds in four-coordinated molecules of period-3 are shorter than in the corresponding six-coordinated molecules just as the A–X bonds in three-coordinated period-2 molecules are shorter than in the corresponding AX4 molecules they are not short enough to reduce the inter-ligand distance to the close packing distance so that the period-3 AF4 molecules are not close-packed. Consistent with this conclusion we see in Fig. 7 that the points for these molecules lie clearly above the curve for the close-packed molecules for both period-2 and 3. The reduction in bond length from SiF62– to SiF4 has sometimes been ‘explained’ by invoking double bond resonance structures for SiF4 just as such structures have been invoked to explain the decrease in bond length from BF4– to BF3. However, there is no other evidence in support of this supposed double bond character. The difference in the bond lengths in SiF62– and SiF4 are more reasonably explained on the basis that four ligands can pack more closely than six, even though in these period-3 AX4 molecules the attraction between the central atom core and the ligands is not strong enough to bring them into close packing.

Plot of hydrogen ligand radius against hydrogen charge for period-2 and-3 molecules.
5 Bond angles in PH3 and H2S
One of the exceptions to the VSEPR model to which attention has frequently been drawn 13 is that the very small bond angles in PH3 (93.3°) and H2S (92.1°) are even smaller than in the corresponding fluorides PF3 (97.8°) and SF2 (98.0°) and therefore in disagreement with the VSEPR electronegativity rule which predicts that the hydrides should have larger angles than the fluorides. These small angles are, however, consistent with the smaller ligand radius of hydrogen than that of fluorine [14]. Because there are no known six-coordinated hydrides of P and S the ligand radius of hydrogen bonded to these elements cannot be obtained from experimental data. However, these radii can be estimated from the calculated ligand charge (Table 5) and the linear relationship between the ligand radius of hydrogen and the ligand charge shown in Fig. 3. Fig. 7 shows the same plot with the addition of the hydrides of the elements of period-3. The experimental H–H distance in SiH4 is much larger than the distance obtained from the calculated ligand charge showing that the hydrogen ligands are clearly not close-packed, as is also shown by the position of the point for SiH4 which lies well off the close-packed plot. In contrast the calculated H–H distances in PH3 and H2S are quite close to the experimental value and the corresponding points in Fig. 7 lie close to the linear plot, showing that the hydrogen ligands in these two molecules are very nearly close-packed as a result of the repulsion exerted by the lone-pair, giving the observed small bond angles of 93.3° (PH3) and 92.1° (H2S). For true close packing these angles would be 88° (PH3) and 87° (H2S).
6 Fluorides of the elements of period-4 and beyond
Because the atoms of the main group elements of period-4 are only a little larger than the atoms of the corresponding elements of period-3 as judged, for example, by their covalent radii, it is not surprising that the maximum coordination number of these elements is also six and is again limited mainly to the fluorides. The A–X bonds are longer than in the corresponding period-3 molecules so that the ligands are not close-packed even in the six-coordinated molecules. Nevertheless there is not sufficient space in the valence shells of these elements to pack more than six ligands. It is only for the period-5 elements that coordination numbers higher than six are found. The seven-coordinated TeF7–, TeF6(OMe)–, TeF5(OMe)2–, IF7, and IOF6– molecules all have a pentagonal bipyramidal geometry in which the axial bonds are shorter than the equatorial bonds and the five equatorial ligands are close-packed (Fig. 8). The geometry of these molecules has been discussed in more detail in a recent paper [11].
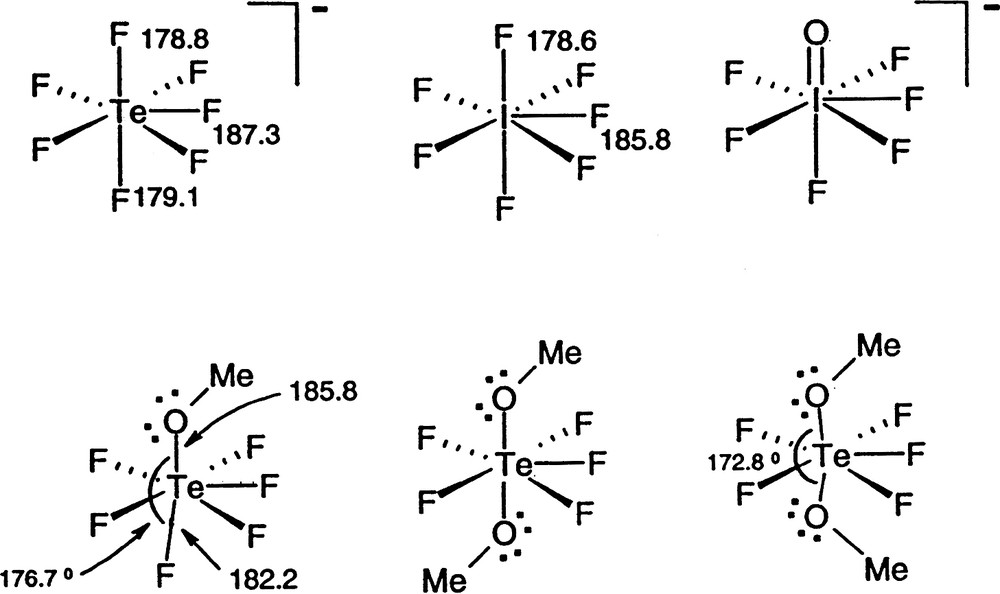
Pentagonal bipyramidal AX7 molecules, The axial bonds are shorter than the equatorial bonds and the equatorial ligands are close-packed.
AX6E molecules, such as XeF6 are of particular interest as they have often been cited as exceptions to the VSEPR rules and as examples of what have been called molecules with ‘stereochemically inactive or weak lone-pairs’ [15,16]. According to the VSEPR model they would be expected to have a geometry based on the pentagonal bipyramid with a lone-pair in an axial position, giving an overall pentagonal pyramidal geometry. However, all the chlorides, bromides and iodides of this type such as SeCl62– and the fluoride BrF6– have a regular octahedral (Oh) geometry, whereas the three fluorides SeF62–, IF7–, and XeF6 have a C3v distorted octahedral geometry in which three of the bonds are longer than the other three and are spread out to give FAF angles larger than 90° (Fig. 9). This geometry is consistent with presence of a lone-pair in a position between the long bonds but having only a weak distorting effect. In the remaining molecules of this type, which have an octahedral geometry, the non-bonding electrons which would normally form a lone-pair appear to have no influence on the geometry. These unexpected geometries can, however, be understood in terms of the LCP model. For the relatively large ligands Cl, Br, I for which the AX6E molecules of Sn, Pb, Sb, Bi, Se, and Te all have octahedral geometries it is reasonable to suppose that the ligands are close-packed or at least nearly close-packed leaving no space in the valence shell for a lone-pair. The two non-bonding electrons remain in a spherical domain surrounding the core (from the point of view of the orbital model they occupy the 4 s or 5 s orbital) giving rise to considerably longer AX bonds than in all the other halides of these elements [1l,15]. For the period-3 AF6E molecules BrF6– also has an octahedral geometry but SeF62– has the C3v distorted octahedral geometry which can be attributed to the larger size of the core leaving enough space in the valence shell for some of the non-bonding electron density to move into the valence shell to form a ‘partial’ lone-pair (Fig. 10). The three bonds surrounding the supposed position of the partial lone-pair are considerably longer than the other three and also the Se–F bonds in molecules with less crowded valence shells, and the angles between these bonds are larger than 90°. All these dimensions are consistent with the supposed position of the lone-pair (Table 14). Because the central iodine atom in IF6– is larger than the selenium atom in SeF62– there is more space for some “lone-pair” density and the molecule is more distorted from an octahedral geometry as shown by the smaller angle between opposite bonds and a relatively smaller lengthening of the bonds compared with IF5 for example. XeF6 is similarly distorted.

AF6E molecules. BrF6– has a regular octahedral geometry. The other molecules have C3v distorted ‘octahedral’ geometries in which the lone-pair only partially occupies the position shown thereby increasing the length of the adjacent bonds and increasing the angles between them to greater than 90°.
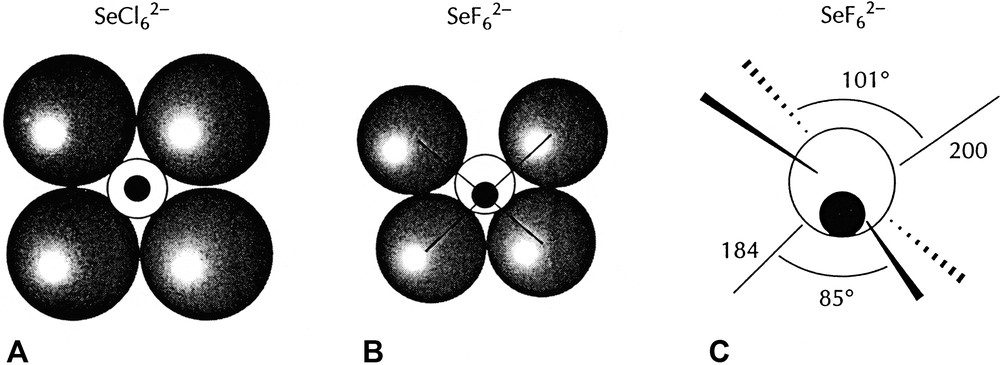
Diagrams of a symmetry plane though the Se atom in SeCl62– and SeF62– showing how the larger Cl ligands fully occupy the Se valence shell so that the two non-bonding electrons remain surrounding the core whereas the smaller fluorine ligands allow a partial penetration of the non-bonding pair into the valence shell producing a C3v distortion of the molecule.
Structural data for AX6E molecules and the corresponding AX5E and AX4E2 molecules a
| BrF6– | SeF62– | IF6– | XeF6 | |
| Long bond | 185 | 202 | 204 | 191 |
| Short bond | 185 | 184 | 186 | 186 |
| Opposed bond angle | 182 | 172 | 164 | |
| BrF5 | SeF4 | IF5 | XeF5+ | |
| Type | AX5E | AX4E2 | AX5E | AX5E |
| Long bond | 177 | 177 | 187 | 186 |
| Short bond | 169 | 168 | 181 | 182 |
a Bond lengths in pm, bond angles in degrees.
The only other known examples of molecules with weakly active or inactive lone-pairs are XeF7– and XeF82–. XeF7– has C3v geometry similar to that of XeF6 but with the seventh ligand opposite the supposed position of the lone-pair in XeF6 forming a long bond of 210 pm (Fig. 11). In this molecule the lone-pair must again be mainly surrounding the core but also part of the valence shell and sufficiently stereochemically active to increase the length of the unique axial bond and also to distort the symmetry of the remaining bonds to C3v. XeF82– has the square antiprism geometry observed for IF8– and TeF82– which are AX8 molecules. So this is another example of a molecule with an inactive ‘lone-pair’ that remains in the core and is unable to penetrate into the valence shell because of the large number of closely packed ligands. As a consequence of the large core the bonds, which have an average length of 202 pm, are considerably longer than the bonds in XeF6 which have an average length of 189 pm.

The C3v geometry of the XeF7– ion.
7 Structural and chemical consequences of close packing
The maximum coordination number of the atoms in a given period increases from four in period-2, to six in period-3 and 4, and eight in period-5. This increase is primarily a consequence of the increasing atomic size down any group of the periodic table. Molecules of the main group elements with coordination numbers of greater than four, i.e. the elements of period-3 and beyond, have often been called hypervalent with the implication that the bonding in these molecules is in some way different from that in the ‘ordinary’ period-2 molecules. There is, however, as has been discussed elsewhere [15,16], no good reason to suppose that the bonding in these molecules (which in the VB theory has been described in terms of spd hybrid orbitals, or in MO language as involving three-center four-electron bonds) is in any way of a different nature from the bonding in period-2 molecules. The term ‘hypervalent’ is therefore no longer of any value except as a term, albeit a not very necessary term, for describing molecules with a higher coordination number than four [16,17].
The OH ligand is very similar in size to an F ligand, so it would be expected that there would be a similar large number of high coordination number hydroxides of the main group elements of period-3 and beyond. However, there are only a very few such molecules. The theoretically possible hydroxides of P, S and Cl, and of, As, Se and Br such a P(OH)5, S(OH)6, and Cl(OH)7 are only known as their four-coordinated oxo acids PO(OH)3, SO2(OH)2, and ClO3(OH). Thus it would appear that these hexahydroxides are unstable because the close packing of the ligands facilitates the elimination of water to give the much less crowded and more stable four-coordinated molecules. In contrast the period-5 six-coordinated Te(OH)6 and IO(OH)5 are stable molecules because the hydroxide groups in these molecules are not close-packed. We would not, however, expect the seven-coordinated Te(OH)7– and I(OH)7 to be stable molecules because if they were to have the pentagonal bipyramidal structures of TeF7– and IF7 in which the five equatorial ligands are close-packed they would be expected to eliminate water to give the more stable six-coordinated TeO(OH)5– and IO(OH)5.
It is interesting to note that although S(CH3)6 and Se(CH6) are not known, Te(CH3)6 is a stable molecule and that although P(CH3)5 is not known, the four-coordinated H2C=P(CH3)3 is a stable molecule that can be imagined as being formed from P(CH3)5. As(CH3)5 is, however, a stable molecule, consistent with the larger size of the As atom. This molecule is stable, whereas Se(CH3)6 is not, presumably because the Se atom is smaller than the Te atom and because crowding of the ligands is not so severe in a trigonal bipyramidal molecule since only the axial ligands are close-packed.
8 Limitations of the LCP model
The LCP model strictly applies only to the three-and four-coordinated molecules of period-2 and the six-coordinated molecules of period-3 in which the ligands may be described as truly close-packed, and in which the size of the ligand as described by its ligand radius can be determined. It can also be applied to the axial ligands in a trigonal bipyramidal molecule which are close-packed with the equatorial ligands, and the equatorial ligands in a pentagonal bipyramidal molecule. However, ligand–ligand repulsions are important in all molecules and it is reasonable to assume that the magnitude of ligand–ligand repulsions are proportional to the size of the ligand, although this can only be regarded as a qualitative concept for ligands for which the ligand radius cannot be determined.
The LCP model, like the VSEPR model, cannot be used to explain the geometry of transition metal molecules because there are no lone-pairs in the valence shell of the transition metal and because the ligands are generally not close-packed. When the core is spherical the geometry is determined by ligand–ligand repulsions. In molecules in which the core is not spherical it has been shown that the distortions of the core from a spherical shape are the most important factor in determining deviations from the shape predicted by ligand–ligand repulsions 18.
9 Comparison of the VSEPR and LCP models: advantages of the LCP model
Both models the VSEPR and the LCP models emphasize the importance of non-bonding electrons (lone-pairs) in determining molecular geometry. The VSEPR model places emphasis on repulsions between bonding electron pairs and between bonding pairs and lone-pairs, whereas the LCP model emphasizes repulsions between ligands and between ligands and lone-pairs. Both models lead to the same predictions of geometry for homoleptic molecules and, for such molecules, the two models cannot be distinguished. They may, however, give different predictions for molecules with two or more different ligands. The VSEPR model explanation is based on the relative electronegativities of the ligand and the central atom and on how this affects the sizes of bonding pairs whereas the LCP model is based on the sizes of ligands. Whereas the size of a bond pair is a purely qualitative property that cannot be defined or measured, the size of ligand can be defined and measured by means of the ligand radius. Thus the LCP model is more quantitative than the VSEPR model. It can, for example predict bond angles when the bond lengths are known. The size of a lone-pair cannot be measured or defined in either model but its effect can be made more quantitative in the LCP model, in that in the four-coordinated molecules of period-2 and the six-coordinated molecules of period-3 a lone-pair pushes the ligands together until they reach their close-packed inter-ligand distance. Moreover, as we have seen, the LCP model can explain almost all the exceptions to the VSEPR model. The LCP model can be regarded as a development from, and an improvement on, the VSEPR model, but in recognition of the widespread use of the VSEPR model for discussing molecular geometry over a period of almost 50 years, and the common features of both models, what we have been describing as the LCP model should perhaps be called the VSEPR-LCP model.



Vous devez vous connecter pour continuer.
S'authentifier