Traitement de données pour la vélocimétrie RMN d'écoulement rapides : étude par simulation numérique de la mesure en rhéométrie « Couette »

Hassan Kassem; Stéphane Rodts

doi:10.1016/j.crci.2005.06.031

Traitement de données pour la vélocimétrie RMN d'écoulement rapides : étude par simulation numérique de la mesure en rhéométrie « Couette »

Hassan Kassem ¹ ; Stéphane Rodts ¹

¹ Laboratoires des matériaux et structures du génie civil (UMR 113 LCPC–ENPC–CNRS), 2, allée Kepler, 77420 Champs-sur-Marne, France

Comptes Rendus. Chimie, Volume 9 (2006) no. 3-4, pp. 539-547.

Résumés

Français
Anglais

La qualité des mesures de vitesse par RMN dans les expériences de rhéomètrie « Couette » requiert normalement que le fluide étudié ne subisse que des petits déplacements durant la séquence. Nous montrons que lorsque cette condition ne peut pas être remplie, des mesures précises peuvent néanmoins être obtenues. Nous décrivons une approche de traitement de données qui, sans changer de séquence, repousse d'un facteur 10 la limite supérieure des vitesses mesurables. La méthode est validée sur des signaux RMN non bruités, simulés numériquement. La méthode de simulation, qui tient compte des problèmes de sélection de chemin de cohérence, est présentée. .

Data processing for NMR velocimetry of fast flow: a numerical study of ‘Couette’ rheo-NMR measurements. NMR velocimetry in Couette rheo-NMR experiments is known to be accurate within the limit that the fluid undergoes small displacements during the sequence. In this work, it is shown that even when this last requirement can not be fulfilled, some good-quality measurements may however be extracted from raw data. A data processing method is developed, which increases the range of measurable velocity by a factor of 10, without any necessary change in the sequence. The method is validated on simulated, noise-free, NMR data. The simulation method, which takes into account coherence pathway selection, is also described. .

Métadonnées

Reçu le : 2005-03-29
Accepté le : 2005-06-23
Publié le : 2005-08-29

DOI : 10.1016/j.crci.2005.06.031

Mot clés : IRM du proton, Vélocimétrie, Rhéomètre, Mécanique des fluides, Écoulement Couette, Traitement de données
Mots clés : Proton MRI, Velocimetry, Rheometry, Fluid mechanics, Couette flow, Data processing

Affiliations des auteurs :

Hassan Kassem ¹ ; Stéphane Rodts ¹

¹ Laboratoires des matériaux et structures du génie civil (UMR 113 LCPC–ENPC–CNRS), 2, allée Kepler, 77420 Champs-sur-Marne, France

@article{CRCHIM_2006__9_3-4_539_0,
     author = {Hassan Kassem and St\'ephane Rodts},
     title = {Traitement de donn\'ees pour la v\'elocim\'etrie {RMN} d'\'ecoulement rapides : \'etude par simulation num\'erique de la mesure en rh\'eom\'etrie {{\guillemotleft}~Couette~{\guillemotright}}},
     journal = {Comptes Rendus. Chimie},
     pages = {539--547},
     publisher = {Elsevier},
     volume = {9},
     number = {3-4},
     year = {2006},
     doi = {10.1016/j.crci.2005.06.031},
     language = {fr},
}

TY  - JOUR
AU  - Hassan Kassem
AU  - Stéphane Rodts
TI  - Traitement de données pour la vélocimétrie RMN d'écoulement rapides : étude par simulation numérique de la mesure en rhéométrie « Couette »
JO  - Comptes Rendus. Chimie
PY  - 2006
SP  - 539
EP  - 547
VL  - 9
IS  - 3-4
PB  - Elsevier
DO  - 10.1016/j.crci.2005.06.031
LA  - fr
ID  - CRCHIM_2006__9_3-4_539_0
ER  -

%0 Journal Article
%A Hassan Kassem
%A Stéphane Rodts
%T Traitement de données pour la vélocimétrie RMN d'écoulement rapides : étude par simulation numérique de la mesure en rhéométrie « Couette »
%J Comptes Rendus. Chimie
%D 2006
%P 539-547
%V 9
%N 3-4
%I Elsevier
%R 10.1016/j.crci.2005.06.031
%G fr
%F CRCHIM_2006__9_3-4_539_0

Hassan Kassem; Stéphane Rodts. Traitement de données pour la vélocimétrie RMN d'écoulement rapides : étude par simulation numérique de la mesure en rhéométrie « Couette ». Comptes Rendus. Chimie, Volume 9 (2006) no. 3-4, pp. 539-547. doi : 10.1016/j.crci.2005.06.031. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2005.06.031/

Version originale du texte intégral

1 Introduction

Connaître le champ de vitesse dans un fluide en mouvement est une préoccupation récurrente en rhéologie et en mécanique des fluides. Au fil des ans, la vélocimétrie par imagerie par résonance magnétique nucléaire (vélocimétrie IRM) [1] s'est imposée parmi les techniques non intrusives qui permettent d'obtenir expérimentalement des informations quantitatives sur la forme des écoulements. Ne nécessitant de la part des échantillons aucune propriété d'homogénéité ou de transparence optique particulière, elle supplante parfois les techniques plus répandues de PIV [2], de diffusion de rayonnements [3] ou d'ondes sonores [4] dès qu'il s'agit d'étudier des milieux opaques, et/ou finement divisés.

L'IRM a ainsi trouvé un vaste terrain d'utilisation dans le domaine de la rhéologie des fluides dits « complexes », en sachant mesurer des champs de vitesse directement à l'intérieur d'échantillons tels que des mousses, des suspensions argileuses, du ciment frais, ainsi que divers produits cosmétiques ou agroalimentaires [5–13]. Grâce au développement de rhéomètres, souvent de géométrie Couette, insérables dans les IRM [5–8], une information essentielle est ainsi recueillie, permettant notamment d'observer avec précision les phénomènes de thixotropie et de seuil d'écoulement, propriétés souvent difficiles à bien appréhender avec un rhéomètre « classique » [6,7].

La caractérisation d'un écoulement par RMN peut se faire par différentes approches : temps de vol, spin tagging… [1,5,8–12]. Cependant, la méthode du « codage de phase », qui consiste à introduire dans la séquence une paire de gradients de champ pulsés pour déphaser le signal RMN proportionnellement aux composantes du vecteur vitesse, offre certainement la manière la plus robuste de procéder pour avoir une information quantitative [9]. Les séquences fondées sur cette technique demandent en principe que le fluide ne subisse que des petits déplacements pendant la séquence. Or la durée minimum d'une séquence comportant des gradients est typiquement de quelques millisecondes. On peut ainsi estimer que pour un écoulement qui se joue à l'échelle du centimètre, on ne peut tolérer que des déplacements millimétriques, et donc que seules les vitesses inférieures à quelques 10 cm/s peuvent être mesurées correctement. Au-delà, des écarts significatifs sont susceptibles d'apparaître entre les mesures et le « vrai » champ de vitesse.

Le raisonnement que nous tenons, fortement inspiré de l'école de pensée des « problèmes inverses » [14], est que même en présence de ces écarts, le signal RMN mesuré contient toujours des informations sur la vitesse. L'apparition des biais de mesure tiendrait essentiellement au fait que les méthodes de traitement des données utilisées ne sont conçues que pour des contextes simples de mise en œuvre des séquences. La mise au point de traitements de données « améliorées », tenant compte des imperfections expérimentales, devrait en revanche permettre de restaurer la qualité des mesures, et d'étendre la technique à des gammes de vitesses plus importantes, sans remettre en cause les séquences utilisées.

Cet article aborde le problème de cette restauration du champ de vitesse dans le cadre restreint de la mesure de profils d'écoulements en cellules rhéologiques de type « Couette ». Dans notre étude, qui n'est pour nous qu'une première étape, nous nous sommes affranchis du problème du bruit de mesure en travaillant sur des signaux RMN simulés. Dans un premier temps, après un rappel des caractéristiques du système et de la séquence étudiés, nous exposons la méthode de simulation numérique mise en œuvre, en insistant sur les précautions particulières nécessitées par la sélection du chemin de cohérence. Nous montrons ensuite que le traitement « classique » des données conduit, passée une vitesse d'écoulement seuil, à l'apparition de biais de mesure, avec notamment un défaut de positionnement spatial du champ de vitesse sur les profils obtenus. Nous présentons enfin une méthode de traitement de données pour corriger ces erreurs de localisation, et discutons de son efficacité sur quelques exemples.

2 Vélocimétrie RMN en géométrie Couette

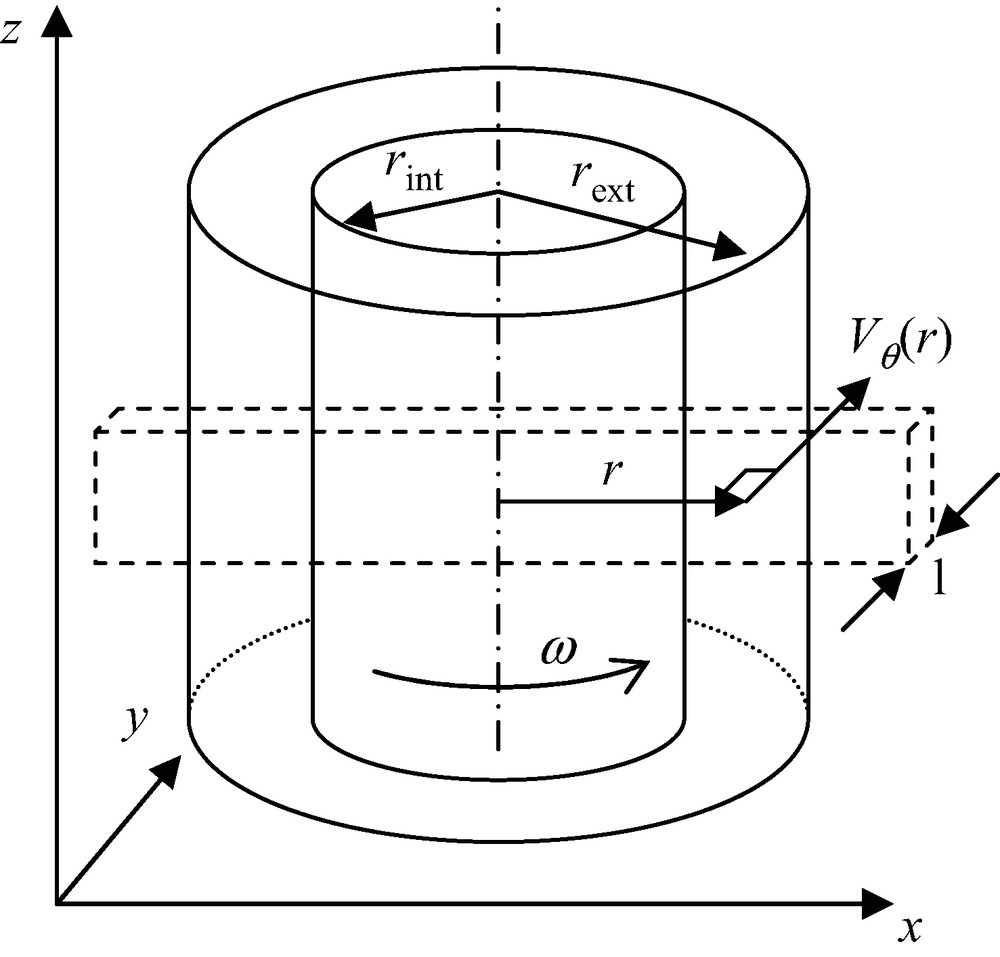
La rhéométrie en cellule Couette consiste à cisailler un fluide dans l'entrefer de deux cylindres concentriques [7]. Nous considérerons ici le cas d'une cellule dans laquelle le cylindre extérieur, de rayon $R_{ext}$ est fixe, et le cylindre intérieur, de rayon $R_{int}$ tourne à une vitesse angulaire ω (Fig. 1). Lorsque l'écoulement créé est stable, il existe généralement une large zone centrée sur la mi-hauteur du dispositif, dans laquelle le champ de vitesses est à symétrie cylindrique. Dans cette zone la seule composante non-nulle des vitesses est la composante orthoradiale $V_{θ}$ , et ne dépend que de la positon radiale $r$ .

Fig. 1
Schéma du rhéomètre « Couette » insérable dans l'IRM. Les rayons des cylindres intérieur et extérieur sont de 4 et 6 cm, respectivement. Le barreau en pointillé indique la zone sélectionnée par la séquence RMN de mesure de vitesse.

En rhéométrie assistée par RMN, c'est ce « profil de vitesse » $V_{θ} (r)$ que l'on cherche à mesurer. L'information recueillie se révèle précieuse de renseignements sur les propriétés d'écoulement du fluide étudié.

Différentes approches RMN ont été proposées pour mesurer ce profil de vitesse [5,8–13]. Celle introduite par Hanlon et al. [9], modifiée par Raynaud et al. [8] et Rodts et al. [13], du fait de sa rapidité, sa robustesse, et sa simplicité de mise en œuvre, a depuis quelques années trouvé une application en routine. Elle a récemment contribué à plusieurs avancées dans le domaine de la rhéologie [6,7] (Fig. 2). Fondée sur une séquence d'imagerie profil en écho de spin [15], elle comporte deux impulsions radiofréquences sélectives successivement dans les directions z et y de l'espace, de manière à découper virtuellement un barreau le long d'un diamètre de la cellule (Fig. 1). Un gradient de lecture dans la direction x permet de recueillir des profils d'aimantation complexes le long de ce barreau. La sensibilité à la vitesse est donnée par deux impulsions de gradient supplémentaires dans la direction y. Dans l'hypothèse où chaque point du fluide à l'intérieur du volume sélectionné se déplace en ligne droite pendant la séquence, ces gradients induisent sur les profils un déphasage, dépendant de la positon radiale :

φ (r) = γ G δ Δ V_{θ} (r)

(1)

où γ est le rapport gyromagnétique du noyau étudié,

G

l'amplitude des gradients de codage, δ leur durée et Δ leur temps de séparation. Du fait de la trajectoire circulaire de chaque point du fluide, cette hypothèse n'est en fait valide que si la durée de la séquence est suffisamment brève devant la période de rotation du cylindre intérieur. Lorsque cette condition est vérifiée, le profil de vitesse proprement dit s'obtient en réalisant successivement deux mesures utilisant deux valeurs différentes de gradient de codage, toutes choses égales par ailleurs, et en comparant point par point les phases des deux profils d'aimantation obtenus.

Fig. 2
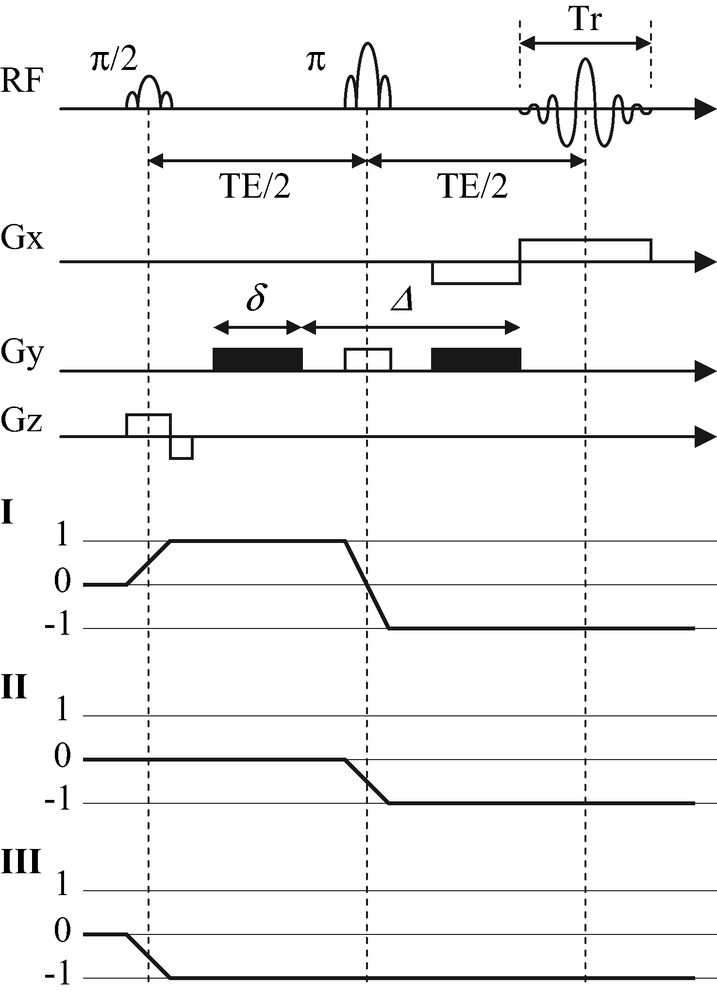
En haut : séquence RMN utilisée pour la mesure de vitesse en géométrie Couette. Les impulsions de gradient permettant spécifiquement le codage de la composante orthoradiale du champ de vitesse sont en noir. En bas : les trois chemins de cohérence susceptibles de générer des signaux lors de la simulation.

3 Simulation numérique de la mesure RMN

Pour étudier le comportement de la séquence dans différentes conditions de réglage et d'écoulement, nous avons choisi de procéder par simulation numérique. Cette approche permet simultanément de bénéficier de données non bruitées, afin de ne pas aborder ensemble toutes les difficultés, et surtout d'avoir une parfaite connaissance du profil de vitesse à l'intérieur du fluide au moment de l'expérience.

Nous nous plaçons dans le cadre de la RMN du proton. Nous supposons que notre échantillon n'exhibe qu'une seule raie, et que les cohérences de second quanta et plus ne peuvent pas être excitées, de sorte que la description de l'état local des spins par un vecteur classique d'aimantation soit valide. L'objet des simulations est de calculer, au fil du déroulement de la séquence, l'évolution locale de l'aimantation en chaque point de la cellule Couette, puis, par sommation des aimantations locales, de reconstituer le signal RMN globalement émis par l'échantillon au moment du gradient de lecture. Comme la direction verticale n'intervient pas dans le processus de mesure, nous nous restreignons à calculer l'aimantation pour des points de l'échantillon situés dans un plan d'orientation xy, localisé à la mi-hauteur du barreau. Différentes approches sont rencontrées dans la littérature pour effectuer le calcul du champ d'aimantation à travers l'échantillon. Celles fondées sur une approche « différences finies temporelles » où « éléments finis temporels » [16], dans lesquelles le champ d'aimantation est calculé sur un maillage fixe. Une faiblesse de ces techniques vient cependant de leur difficulté à bien rendre compte des phénomènes d'advection [17], ce qui les rendait inadaptées à notre étude dans laquelle un écoulement est justement mis en jeu. Nous avons ainsi choisi une autre approche, consistant à calculer le champ de vitesse en des points mobiles, ou « particules virtuelles », qui se déplacent avec l'écoulement. Cette approche a notamment déjà été utilisée dans des travaux où des mouvements complexes de la matière étaient mis en jeu, en particulier pour les phénomènes de diffusion dans lesquels les trajectoires des particules étaient de type Brownien [18]. Dans notre étude, nous avons utilisé un grand nombre de particules (64 000), réparties de sorte à recouvrir de manière homogène la zone d'écoulement d'où le signal RMN est émis (Fig. 3).

Fig. 3
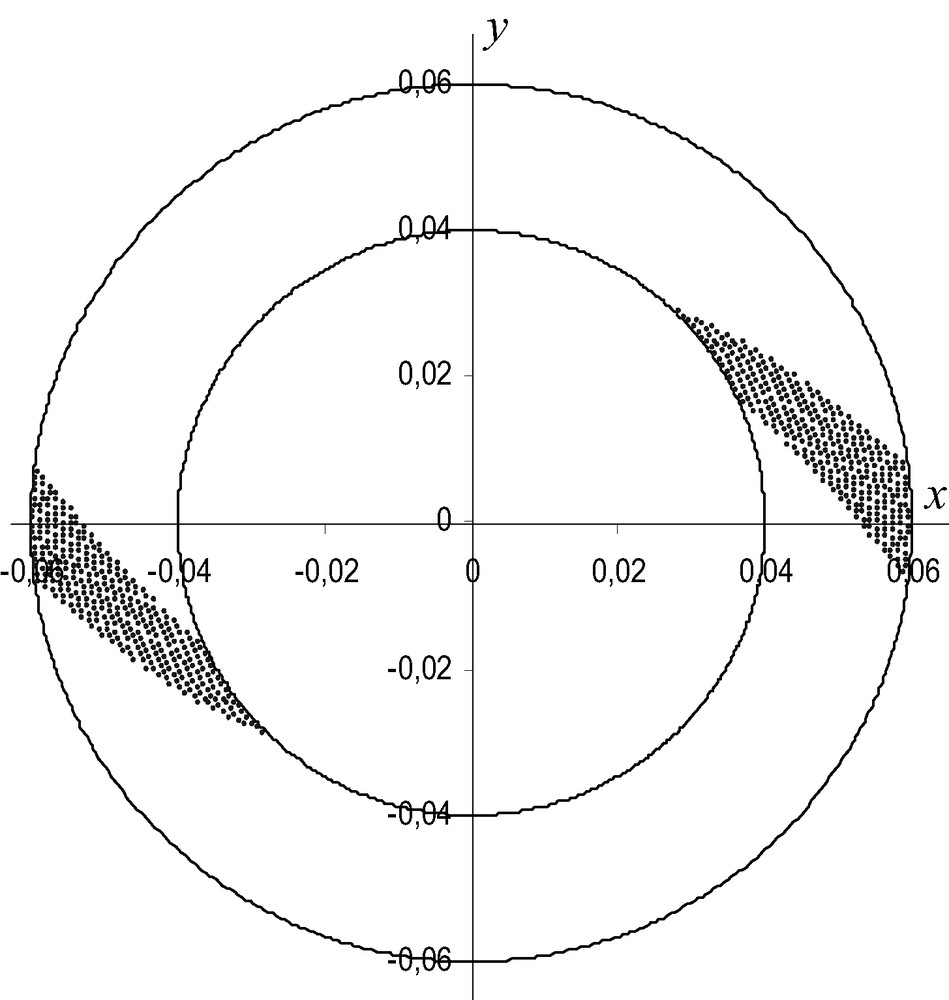
Points d'échantillonnage du signal RMN local dans le plan d'étude, au moment de l'acquisition du signal, pour les conditions expérimentales décrites au § 5. Chaque point représente une particule virtuelle introduite dans l'écoulement. Les cercles indiquent les surfaces des cylindres interne et externe de la cellule Couette. Seule une zone qui englobe de manière large le barreau de sélection est échantillonnée. Pour préserver la lisibilité du schéma, toutes les 64 000 particules n'ont pas été représentées.

Un profil de vitesse $V_{θ} (r)$ ayant été choisi pour la simulation, une particule située à $t = 0$ en des coordonnées polaires $(r_{0}, θ_{0})$ suit la trajectoire :

{\begin{cases} r (t) = r_{0} \\ θ (t) = θ_{0} + \frac{V_{θ} (r_{0})}{r_{0}} t \end{cases}

(2)

L'aimantation $\vec{M} (t)$ portée par la particule est calculée au cours du temps, en résolvant les équations de Bloch dans le repère tournant :

{\begin{matrix} \frac{d M_{x}}{d t} = γ \vec{G} (t) · \vec{r} (t) M_{y} - γ B_{1 y} (t) M_{z} \\ \frac{d M_{y}}{d t} = - γ \vec{G} (t) · \vec{r} (t) M_{x} + γ B_{1 x} (t) M_{z} \\ \frac{d M_{z}}{d t} = γ B_{1 y} (t) M_{x} - γ B_{1 x} (t) M_{y} \end{matrix}

(3)

et avec la condition initiale d'une aimantation complètement relaxée :

M_{x} = 0 M_{y} = 0 M_{z} = M_{0}

(4)

Dans les équations ci-dessus, $\vec{G} (t)$ représente le gradient de champ magnétique, et rend compte des gradients appliqués dans les trois directions d'espace en cours de séquence. $\vec{r} (t)$ représente le vecteur position de la particule suivie. $B_{1 x} (t)$ et $B_{1 y} (t)$ représentent le cas échéant les deux composantes transverses du champ radiofréquence. Les phénomènes de relaxation pourraient également être pris en compte, mais nous n'en parlerons pas, car ils sont sans effet sur le processus de mesure de vitesse proprement dit.

Le système d'équation est résolu par la méthode de Runge et Kutta [19], avec un pas de temps petit devant tous les autres temps caractéristiques de la séquence, à savoir : temps d'application des gradients, temps d'échantillonnage du signal RMN pendant le gradient de lecture, période de précession autour du champ $B_{1}$ , et période de précession autour des gradients de champ dans les zones de l'échantillon éloignées du centre.

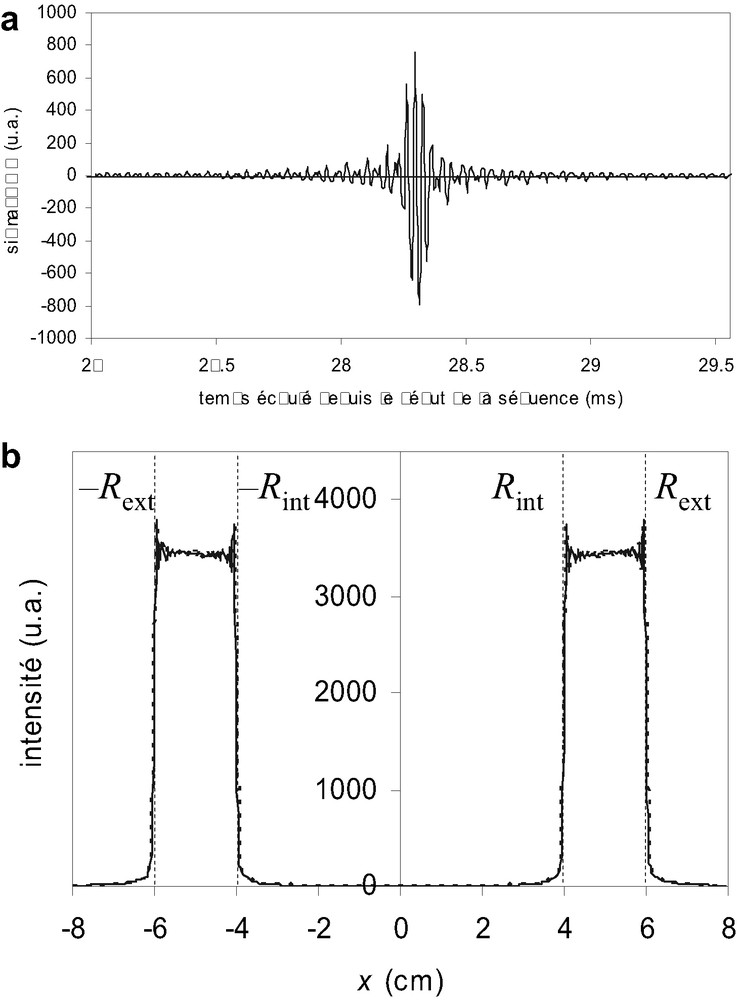
Le signal RMN global de l'échantillon est finalement obtenu en sommant les composantes $M_{x}$ et $M_{y}$ d'aimantation transverse de toutes les particules, chaque particule ayant été au préalable affectée d'une pondération représentative de la surface qu'elle occupe dans l'échantillon, en fonction de sa distance aux particules plus proches voisines (Fig. 4a).

Fig. 4
(a) Un des deux signaux RMN mesurés pendant le gradient de lecture, pour une vitesse de rotation du rhéomètre de 2,5 rad/s (simulation). Seule la partie réelle du signal est représentée. (b) Profils d'intensité de signal obtenus après transformée de Fourier de chacun des deux signaux RMN impliqués dans le processus de mesure. Les deux profils apparaissent respectivement en ligne continue et en pointillés, et sont presque superposés.

Parallèlement à la résolution des équations de Bloch, nous avons dû porter un soin tout particulier à la sélection des chemins de cohérence [20]. Du fait que nous procédons par simulation numérique, les signaux simulés sont exempts de toute erreur de ligne de base ou d'erreurs de quadratures. Dans le cadre d'une RMN du proton simple quanta, trois signaux sont néanmoins encore susceptibles d'être présents dans le résultat de nos simulations (Fig. 2). Le signal I est celui que nous souhaitons mesurer. Le signal II provient du transfert dans le plan transverse de composantes longitudinales d'aimantation existant avant l'impulsion $π$ . Dans notre situation où la relaxation n'est pas prise en compte, ces composantes peuvent résulter d'imperfections de l'impulsion $π / 2$ . Le signal III provient enfin de toutes les zones de l'échantillon dans lesquelles l'impulsion $π$ n'a pas été parfaite, c'est-à-dire, dans le cas d'une impulsion sélective, de pratiquement tout l'échantillon. En situation expérimentale, les impulsions de gradient dans la direction y ont une action défocalisante qui élimine presque totalement les signaux II et III. Au plan numérique cependant, notre échantillon n'est pas continu, mais se présente comme un échantillonnage de particules discrètes. Ainsi, de forts signaux parasites, a priori défocalisés, peuvent parfois réapparaître en cours de séquence par phénomènes de type « pic de diffraction », en fonction de l'écartement entre particules voisines.

Nous avons ainsi dû éliminer explicitement les signaux II et III de nos simulations. L'élimination du signal II se fait en mettant à zéro toutes les composantes $M_{z}$ de l'aimantation juste avant le début de l'impulsion $π$ . Le signal III est quant à lui éliminé par cyclage de phase [20] : une intensité de gradient ayant été choisie pour le codage de vitesse, la simulation est menée deux fois, en changeant entre les deux simulations l'orientation du champ $B_{1}$ de l'impulsion $π$ d'un angle $π / 2$ dans le plan transverse du repère tournant. Cette opération inverse le signe du signal I, tout en laissant inchangé le signal III. En retranchant les signaux obtenus dans les deux simulations, on obtient ainsi le signal I pur.

4 Mesure dans l'hypothèse de petits déplacements

Nous simulons sur les Figs. 4 et 5 le processus de mesure RMN d'un profil de vitesse dans les conditions suivantes : $R_{ext} = 6 cm$ , $R_{int} = 4 cm$ , $ω = 2,5 rad/s$ , soit 23,9 tr/min. Le timing des gradients de vitesse est : $δ = 11 ms$ , $Δ = 13.4 ms$ . La largeur de barreau sélectionnée dans la direction y est de $ℓ = 1 mm$ . Le temps d'écho, qui sépare l'impulsion $π / 2$ du centre du gradient de lecture est de $T E = 27,9 ms$ , et le temps de lecture du signal pendant ce gradient est de $T r = 2,56 ms$ (Fig. 2). Ces conditions d'expérience sont proches de celles couramment rencontrées sur l'IRM du LMSGC. Les réglages choisis pour le timing de la séquence ne correspondent cependant pas à un réglage optimum. Il s'agit pour nous d'un choix qui nous permettrait ultérieurement, en l'état actuel des gammes de vitesse accessibles sur notre matériel, d'étudier expérimentalement les biais de mesure discutés dans cet article.

Fig. 5
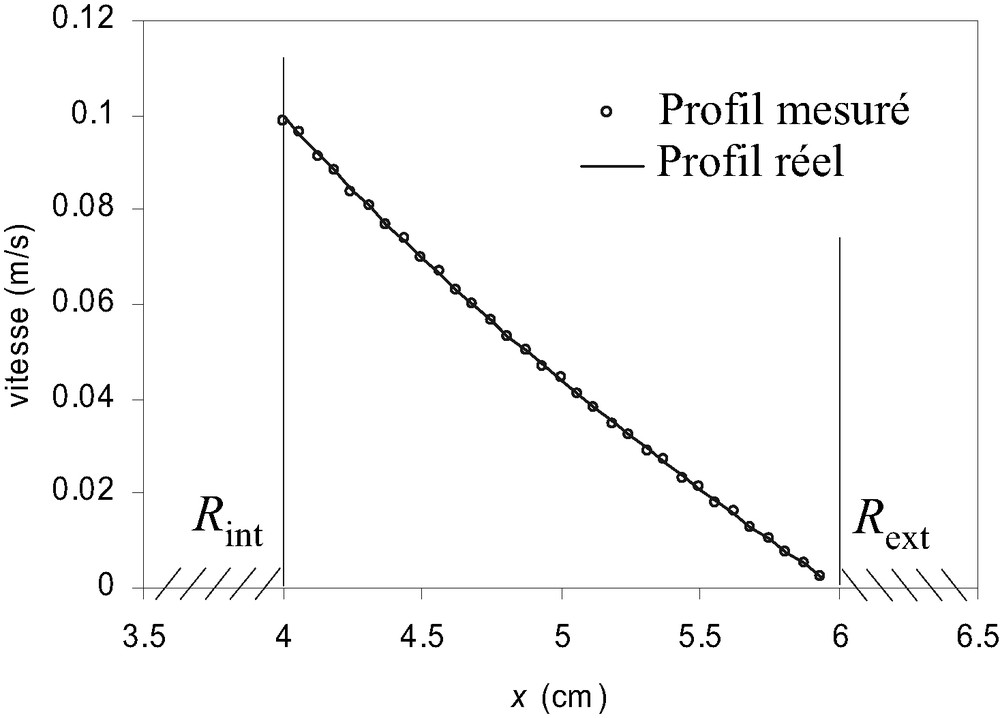
Comparaison des profils de vitesse réels et mesurés pour une vitesse de rotation du rhéomètre de 2,5 rad/s.

Pour les simulations, le profil de vitesse imposé dans l'échantillon est de forme newtonienne :

V_{θ} (r) = r \times \frac{V_{\max}}{R_{int}} \frac{1 - {(\frac{R_{ext}}{r})}^{2}}{1 - {(\frac{R_{ext}}{R_{int}})}^{2}}

(5)

$V_{\max}$ désigne la vitesse d'écoulement imposée par la surface du cylindre interne :

V_{\max} = ω R_{int}

(6)

Elle vaut ici $V_{\max} = 10 cm/s$ . Durant la séquence, c'est près de cette surface que l'échantillon subit les plus grands déplacements. Ceux-ci sont de l'ordre de $T E \times V_{\max} \approx 2.79 mm$ , et du fait de leur petitesse, se font quasi-exclusivement selon la direction y. Bien que plus importants que la largeur du barreau, ils restent extrêmement modestes face aux dimensions de la cellule Couette, et l'hypothèse de petits déplacements en ligne droite, pour laquelle la séquence de mesure a été initialement conçue, est valide.

La Fig. 4a montre dans le signal temporel un écho bien centré. En Fig. 4b, le profil spatial d'intensité du signal RMN recueilli s'inscrit quasi-exactement dans les zones d'entrefer de la cellule Couette délimitées par les rayons $R_{int}$ et $R_{ext}$ . Enfin, sur la Fig. 5, le profil d'écoulement, déduit de la simple comparaison des phases des deux profils complexes d'aimantation obtenus pour les deux valeurs différentes des « gradients de vitesse », se superpose presque parfaitement avec le profil newtonien (équation (5)). Une analyse quantitative des résultats montre que l'erreur relative entre mesure et profil réel est de l'ordre de 1 %. Ce résultat, qui apporte une validation à la méthode de simulation utilisée, illustre ainsi la robustesse de la méthode constatée au plan expérimental.

Nous avons observé, qu'avec notre timing de séquence et nos dimensions de cellule, ce bon accord mesure–profil réel se maintenait jusqu'à des vitesses de rotation de l'ordre de $ω = 5 rad/s$ , soit 47,8 tr/min.

5 Mesure en présence de grands déplacements

L'objet de notre travail est d'étudier le processus de mesure lorsque la condition de petits déplacements n'est plus remplie. Dans ce but, nous confrontons à nouveau les champs de vitesse réels et mesurés, mais pour une vitesse de rotation de $ω = 50 rad/s$ , soit 477 tr/min. L'écoulement pris en compte dans la simulation du processus de mesure est toujours newtonien, et le timing de la séquence reste le même. La vitesse de surface du cylindre intérieur est maintenant de $V_{\max} = 2 m/s$ , et le déplacement associé pendant la séquence devient de l'ordre de $5,58 cm$ . Cela est du même ordre que le rayon $R_{int}$ , et la condition de petit déplacement n'est clairement plus vérifiée. Des disfonctionnements de la séquence apparaissent alors.

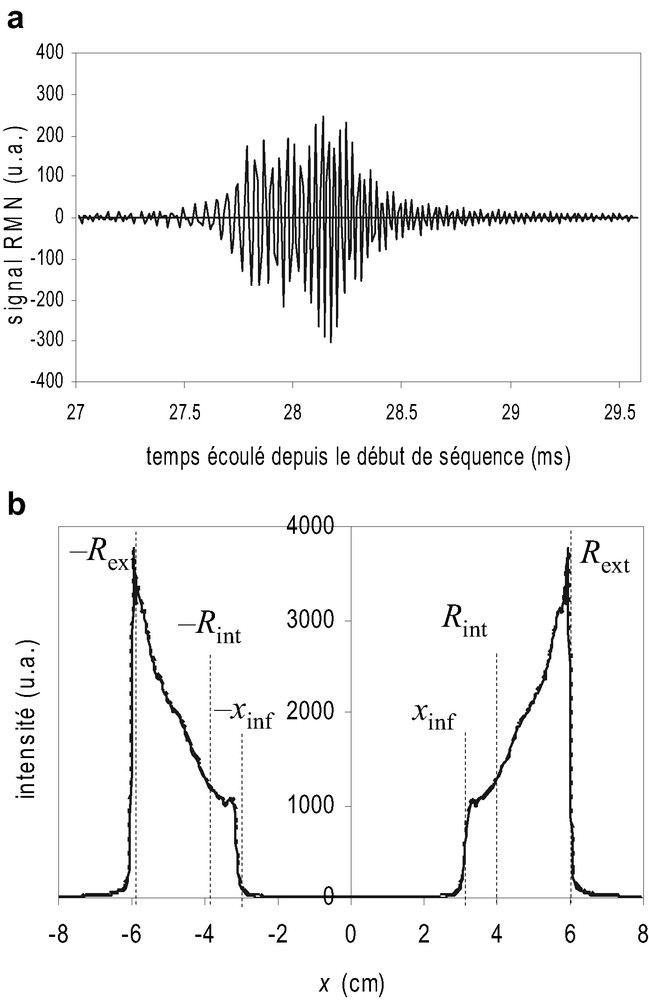
Le signal temporel mesuré (Fig. 6a) prend toujours la forme d'un écho, mais qui n'est plus totalement centré, et qui est sensiblement « étiré » vers la gauche. Par ailleurs, le profil spatial d'intensité du signal RMN, obtenu par transformée de Fourier du signal temporel, n'est plus strictement contenu dans la zone d'entrefer de la cellule Couette (Fig. 6b) : la limite d'échantillon imposée par $R_{ext}$ est toujours respectée, mais un signal significatif est en revanche recueilli en deçà du rayon $R_{int}$ , jusqu'à une position que nous notons $x_{\inf}$ .

Fig. 6
(a) – Un des deux signaux RMN mesurés pendant le gradient de lecture, pour une vitesse de rotation du rhéomètre de 50 rad/s (simulation). Seule la partie réelle du signal est représentée. (b) – Profils d'intensité de signal obtenus après transformée de Fourier de chacun des deux signaux RMN impliqués dans le processus de mesure. Les deux profils obtenus apparaissent respectivement en ligne continue et en pointillés, et sont presque superposés. Les échelles verticales pour les deux graphiques sont les mêmes que dans la Fig. 4.

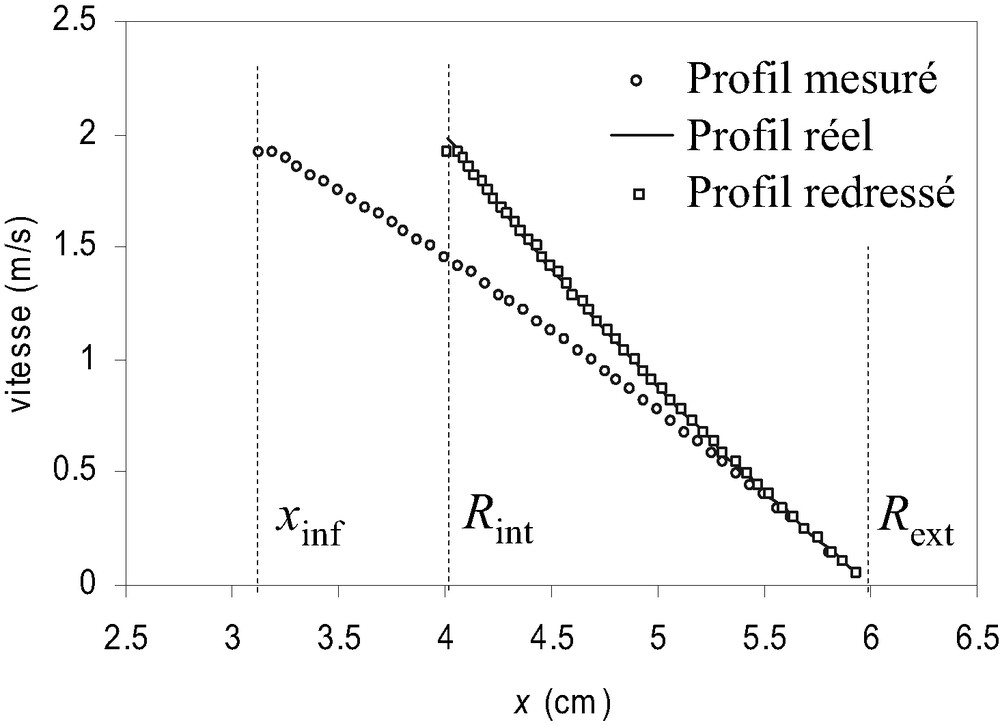
Sur la base de la formule (1), un profil de vitesse peut néanmoins être calculé dans la zone $[x_{\inf}, R_{\max}]$ d'émission de signal. Le résultat de ce calcul, que nous nommons « profil mesuré », est présenté sur la Fig. 7. Outre le fait qu'un champ de vitesse apparaît virtuellement en dehors de la zone d'entrefer de la cellule Couette, le profil mesuré s'éloigne considérablement du profil d'écoulement réel à l'intérieur de cette zone, ce d'autant plus que l'on s'approche du cylindre intérieur.

Fig. 7
Comparaison des profils réels, mesurés, et redressés pour une vitesse de rotation du rhéomètre de 50 rad/s. Les profils réels et redressés sont presque superposés.

De tels écarts entre les mesures RMN et le champ de vitesse réel dans l'échantillon n'ont à notre connaissance jamais été décrits dans les conditions normales d'utilisation de la séquence de vélocimétrie, et résultent donc manifestement du fait que l'hypothèse de petits déplacements n'est plus vérifiée.

La non-validité de cette hypothèse peut avoir à notre sens plusieurs effets :

• celui que pendant la séquence, le barreau, initialement excité de manière resserrée autour de l'axe des x par l'impulsion sélective $π$ , puisse avoir tourné considérablement autour du cylindre intérieur au moment où s'effectue le gradient de lecture (Fig. 3). Le profil recueilli ne sera donc pas celui d'un barreau contenu dans l'intervalle $[R_{int}, R_{\max}]$ , mais celui d'un barreau « enroulé » autour du cylindre interne. Ceci expliquerait en particulier pourquoi du signal apparaît sur les profils pour des valeurs de x inférieures à $R_{int}$ ;
• celui que pendant le temps de séquence, la trajectoire des points du fluide proches du cylindre interne ne peut plus être assimilée à une trajectoire rectiligne uniforme. Des corrections doivent donc en toute rigueur être apportées à la relation (1) ;
• une perturbation plus générale du processus d'imagerie de profil, car on effectue des mesures sur un échantillon en fort mouvement, avec une séquence qui n'est compensée ni en vitesse, ni en accélération.

6 Redressement des biais de mesure

Nous avons constaté, sur plusieurs séries de simulations mettant en jeu des « grandes » vitesses de rotation, que les vitesses mesurées, même dans les zones erronées du profil, restaient du même ordre de grandeur que les vitesses réelles à l'intérieur de l'échantillon. Notamment, la vitesse mesurée à l'extrémité gauche du profil erroné est extrêmement proche de la vitesse réelle d'écoulement à la surface du cylindre interne (Fig. 7). Par ailleurs, en dépit de la déformation des signaux RMN pendant le gradient de lecture, les profils d'intensité calculés par transformée de Fourier gardent des limites nettes, qualitativement compatibles avec l'effet d'enroulement du barreau autour du cylindre interne. Cela suggère que le processus d'imagerie, bien que présentant quelques signes de perturbation, n'est pas pour autant remis en cause par la forte rotation de l'échantillon.

Nous avons ainsi jugé que l'effet d'enroulement du barreau dans la direction x devait tenir le rôle prépondérant dans l'apparition des écarts entre mesure et profil réel d'écoulement. C'est ainsi de la correction de cet unique effet que nous nous sommes actuellement préoccupés.

À un plan quantitatif, nous appréhendons le décalage d'abscisse de la manière suivante. Considérons un point situé dans le barreau de mesure, de coordonnée radiale $r$ , et de vitesse $V_{θ}$ . C'est au moment de l'impulsion $π$ que le barreau est délimité dans la direction y. Notre point est alors situé – à la largeur du barreau près, qui est ici très fin – sur l'axe des x, et son abscisse est $r$ . La lecture du signal RMN n'a lieu qu'un instant $T$ plus tard. À ce moment-là, le point se sera déplacé, entraîné dans l'écoulement selon la trajectoire circulaire (2), et se retrouvera en une abscisse :

x_{mes} (r, V_{θ}, T) = r \cos (\frac{V_{θ}}{r} T)

(7)

Si nous négligeons les biais dans la mesure de vitesse proprement dite, le profil mesuré indiquera bien pour notre point la vitesse d'écoulement $V_{θ} (r)$ . Mais au lieu d'indiquer que cette vitesse a lieu à l'abscisse $r$ , il la placera en la coordonnée $x_{mes}$ , c'est-à-dire en une position décalée vers le centre de la cellule Couette. Cela est effectivement constaté, au moins qualitativement, sur la Fig. 7, où le profil mesuré se trouve entièrement à gauche du profil réel d'écoulement.

Pour corriger les mesures, nous souhaitons utiliser la relation (7) et recalculer, pour l'ensemble des couples de valeurs $(V_{θ}, x_{mes})$ qui décrivent le profil erroné, la coordonnée $r$ en laquelle la vitesse doit réellement apparaître pour représenter le profil réel d'écoulement dans l'échantillon.

Une difficulté provient de l'estimation du temps $T$ . En effet, l'acquisition du signal n'est pas ponctuelle dans le temps, et la seule chose que l'on puisse postuler a priori, compte tenu du timing de séquence (Fig. 2), est que :

\frac{T E}{2} - \frac{T r}{2} < T < \frac{T E}{2} + \frac{T r}{2}

(8)

Afin d'affiner cette estimation, nous avons recherché, pour différents jeux de données obtenus dans différentes simulations d'expériences « haute vitesse », quelle valeur de $T$ permettait d'obtenir le meilleur accord, au sens d'un critère de moindres carrés, entre le profil réel d'écoulement et les mesures redressées. De manière invariable, nous avons trouvé que les valeurs optimales étaient toujours très proches du centre de l'intervalle (équation (8)).

Ce résultat nous permet de proposer comme formule de redressement la relation simplifiée :

x_{mes} (r, V_{θ}) = r \cos (\frac{V_{θ} \times T E}{2 r})

(9)

Cette relation est uniquement régie par le temps d'écho $T E$ , c'est-à-dire par une grandeur connue de la séquence. Elle pourrait donc être mise en œuvre en l'état dans un contexte expérimental, sans besoin d'information supplémentaire.

Cette méthode de redressement a été appliquée aux données de mesure présentées sur la Fig. 7. Pour chaque point $(V_{θ}, x_{mes})$ du profil erroné, l'équation (9) a été résolue numériquement par une méthode de Newton–Raphson [19], afin de calculer la position radiale corrigée $r$ . Le profil de vitesse redressé se trouve pratiquement superposé au profil réel d'écoulement. Sur cet exemple, une analyse quantitative des écarts subsistants indique une erreur relative maximale de 3 %.

Nous avons testé cette méthode de redressement pour différentes valeurs de vitesse de rotation du rhéomètre, sans changer le timing de notre séquence. Des redressements satisfaisants ont pu être obtenus jusqu'à une vitesse de rotation de $ω = 620 tr/min$ , soit une vitesse de surface du cylindre intérieur de $V_{\max} = 2,6 m/s$ , 13 fois supérieure à la limite de validité de l'hypothèse de petits déplacements.

7 Discussion – Conclusion

Nous avons montré, sur la base de données simulées non bruitées d'écoulements newtoniens, que l'hypothèse de petits déplacements était essentielle pour la bonne marche générale de la séquence de vélocimétrie de type « profilométrie radiale » en cellule Couette, du moins dans son contexte « normal » d'utilisation. Si l'écoulement étudié est trop rapide par rapport au timing de la séquence, de sévères biais de mesure apparaissent. Les cas étudiés ont montré que l'enroulement du barreau de mesure pendant la séquence, qui conduit à une mauvaise localisation des vitesses mesurées sur l'axe des abscisses, constituait la principale source de biais.

Nous avons proposé une méthode de post-traitement des données apportant une correction à ce défaut. La seule réparation de l'effet de décalage des abscisses, indépendamment des autres sources possibles d'artefacts, nous a permis de restaurer de manière très satisfaisante la qualité des mesures jusqu'à des vitesses d'écoulement 13 fois supérieures aux vitesses pour lesquelles les premiers biais apparaissent.

Des études ultérieures porteront sur l'influence des autres sources d'artefacts, ainsi que sur la robustesse de la méthode de correction proposée sur des données bruitées. Elles seront publiées à part. Le succès de cette approche pourrait à terme étendre considérablement le champ d'application de la technique de vélocimétrie par IRM.

Bibliographie

[1] A. Caprihan; E. Fukushima Annu. Rev. Fluid Mech., 31 (1999), p. 95

[2] M. Raffel; C. Willert; J. Kompenhans Particle Image Velocimetry, a practicle guide, Springer Verlag, 1998, p. 253

[3] S. Poncet; M.-P. Chauve; P. Le Gal J. Fluid Mech., 522 (2005), p. 253

[4] S. Manneville; L. Bécu; A. Colin Eur. Phys. J. Appl. Phys., 28 (2004), p. 361

[5] P.T. Callaghan Rep. Prog. Phys., 62 (1999), p. 599

[6] N. Huang, G. Ovarlez, F. Bertrand, S. Rodts, P. Coussot, D. Bonn, Phys. Rev. Lett. 94 (2005) 028301 ; (b) P. Coussot, J. S. Raynaud, F. Bertrand, P. Moucheront, J. P. Guilbaud, H. T. Huynh, S. Jarny, D. Lesueur, Phys. Rev. Lett. 88 (21) (2002) 218301.

[7] P. Coussot Rheometry of pastes, suspensions and granular materials: Applications in industry and environment, Wiley, New York, 2005, p. 264

[8] J.-S. Raynaud; P. Moucheront; J.-C. Baudez; F. Bertrand; J.-P. Guilbaud; P. Coussot J. Rheol., 46 (2002) no. 3, p. 709

[9] A.D. Hanlon; S.J. Gibbs; L.D. Hall; D.E. Haycock; W.J. Frith; S. Ablett Magn. Reson. Imaging, 16 (1998), p. 953

[10] K.W. Moser; L.G. Raguin; A. Harris; H.D. Morris; J. Georgiadis; M. Shannon; M. Philpott Magn. Reson. Imaging, 18 (2000), p. 199

[11] J. Götz; W. Kreibich; M. Peciar; H. Buggisch J. Non-Newtonian Fluid Mech., 98 (2001), p. 117

[12] A. Corbett; R.J. Philipps; R.J. Kauten; K.L. McCarthy J. Rheol., 39 (1995), p. 907 (n°5)

[13] S. Rodts; F. Bertrand; P. Poullain; P. Moucheront C.R. Chimie, 7 (2004), p. 275

[14] J. Idier Approche bayésienne pour les problèmes inverses, Hermès Science Publications, Lavoisier, 2001, p. 367

[15] P.T. Callaghan Principles of Nuclear Magnetic Resonance Microscopy, Clarendon, Oxford, 1991, p. 492

[16] C. Yuan; G.T. Gullberg; D.L. Parker Med. Phys., 14 (1987) no. 6, p. 914

[17] G. Allaire; S.M. Kaber Algèbre linéaire numérique, Ellipses, Paris, 2002, p. 256

[18] S. Bobroff, G. Guillot, Magn. Reson. Imag. 14 (7/8) (1996) 819; (b) S. Majumdar, J.C. Gore, J. Magn. Reson. 78 (1988) 41.

[19] W.H. Press; S.A. Teukolsky; W.T. Vetterling; B.P. Flannery Numerical Recipes in Fortran. 2nd edition, University Press, Cambridge, 1992

[20] R.R. Ernst; G. Baudenhausen; A. Wokaun Principles of Nuclear Magnetic Resonance in one and two dimensions, Clarendon Press, Oxford, 1987, p. 610

Commentaires - Politique

Ces articles pourraient vous intéresser

Développements récents dans l'application de l'IRM à la rhéologie et à la mécanique des fluides

Stéphane Rodts; François Bertrand; Sébastien Jarny; ...

C. R. Chim (2004)

Réduction de la traînée avec une solution de CTAC-NaSal : Étude du glissement à la paroi en géométrie de Couette

Ferhat Hadri; Anthony Besq; Sylvain Guillou; ...

C. R. Méca (2010)

Sur la mesure de l'intensité du champ magnétique terrestre et la distribution du magnétisme dans les aimants

Bernard Leprêtre; Jean-Louis Le Mouël

C. R. Géos (2005)