Macromolecular reactions in polymer blends: interchain effects

Arkady D. Litmanovich; Nikolay A. Platé; Yaroslav V. Kudryavtsev; Elena N. Govorun

doi:10.1016/j.crci.2006.07.001

Résumé

Interchain interactions affect both reactivity and mobility of macromolecules and hence influence such processes as interdiffusion and phase separation. Three types of reactions in polymer blends proceeding without participation of low molecular reagents and leading to different kinds of copolymers are considered. For polymeranalogous reaction leading to statistical copolymers, the evolution of the blend structure under concerted action of the reaction and interdiffusion is described. For end-coupling reaction leading to a diblock copolymer formation, the competition between the reaction and spinodal decomposition is considered. For interchain exchange reaction in a homogeneous melt leading to multi-block and eventually to random copolymers, an analytical description of the molecular weight and block length transient distributions of the reaction product is developed. For the interchain exchange in a quasi-homogeneous blend, the competition between the reaction and spinodal decomposition is considered. Some important unsolved problems are mentioned.

1 Introduction

Recent advances both in experimental and theoretical studies of reactions in polymer blends were achieved by using relatively simple model systems: homogeneous and quasi-homogeneous melts as well as bi- and trilayer films with well-defined interfaces [1]. Homogeneous blends of the compatible polymers keep homogeneity during the reaction between functional groups and are used to estimate the kinetic parameters: rate constant, activation energy [2]. Quasi-homogeneous blends, being fine dispersed or even highly interpenetrated, are thermodynamically unstable and may be used to study a competition between the reaction and phase separation [3]. Also the studying an early stage of the reaction enables one to estimate an influence of the initial blend structure on the reaction kinetics [4]. Heterogeneous blends with sharp, in particular planar, interface are employed to estimate the contributions of the reactivity and diffusion into the process [5]. Studying such model systems is an unavoidable stage in the development of the theory of reactions in mixers where a forced mixing affects greatly the reaction kinetics and the product structure.

For reactions in a polymer bulk state, one needs to take account of the chemical interchain effect, that is, a direct influence of interchain interactions on the reactivity of polymer functional groups [6]. For example, decomposition of poly(tert.butylacrylate) in a melt proceeds with acceleration caused mainly by interchain interactions of ester and carboxylic groups [7]. The interchain effect is very pronounced in blends [1]. However interchain interactions affect not only reactivity but also a mobility of macromolecules and hence influence such processes as interdiffusion and phase separation. A reacting blend structure changes under concerted action of these chemical and physical factors. Therefore an analysis of interchain interactions is a key approach in the theory of reactions in polymer blends.

In this paper we present the results concerning three types of reactions in polymer blends proceeding without participation of low molecular reagents and leading to different kinds of copolymers. For polymeranalogous reaction leading to statistical copolymers, the evolution of the blend structure under concerted action of the reaction and interdiffusion is described. For end-coupling reaction leading to a diblock copolymer formation, the competition between the reaction and spinodal decomposition is considered. For interchain exchange reaction in a homogeneous melt leading to multi-block and eventually to random copolymers, an analytical description of the molecular weight and block length transient distributions of the reaction product is developed. For the interchain exchange in a quasi-homogeneous blend, the competition between the reaction and spinodal decomposition is considered.

2 Polymeranalogous reaction

Consider a two-dimensional blend composed of two films of compatible polymers A and B initially separated with a narrow boundary. At a proper temperature both the interdiffusion and polymeranalogous reaction proceed: A units transform irreversibly into B ones, both inner and external B neighbors accelerate the reaction. Reactivity of an A group depends upon its microenvironment; the latter is changed due to the reaction itself and due to interdiffusion as well. Hence, there is a need to involve interdiffusion in a theory.

There are essential differences between interdiffusion processes in non-reacting and reacting blends. A binary blend structure is described by a concentration profile of A chains, ϕ. For the reacting blend, some new phenomena appear on the scene.

First, in polymer systems these are chains that diffuse but these are units that react. Therefore the concentration profile of reacting chains, ϕ, and that of transforming units A, ρ, do not coincide and such a divergence affects both driving forces of interdiffusion and the reaction kinetics. Second, the products of polymeranalogous reaction are heterogeneous in composition, so during the process an initial binary blend becomes essentially multicomponent. Third, partly transformed chain may diffuse either to the left or to the right (one-dimensional interdiffusion is considered). As a consequence, beside two opposite flows of reacting and accelerating chains, a new kind of diffusive movement arises: diffusive intermixing of reacting chains of different composition.

Thus the problem is significantly complicated. However, for a relatively slow reaction so that a local equilibrium is maintained in the system due to diffusion, the task may be solved using methods of the linear non-equilibrium thermodynamics.

Yashin et al. [8] derived reaction–diffusion equations containing the free energy of the system, F, Onsager coefficients, Λ, and reaction kinetics contribution, f; these constituents reflect all peculiarities mentioned. Figs. 1 and 2 demonstrate the most considerable results of calculations.

Fig. 1
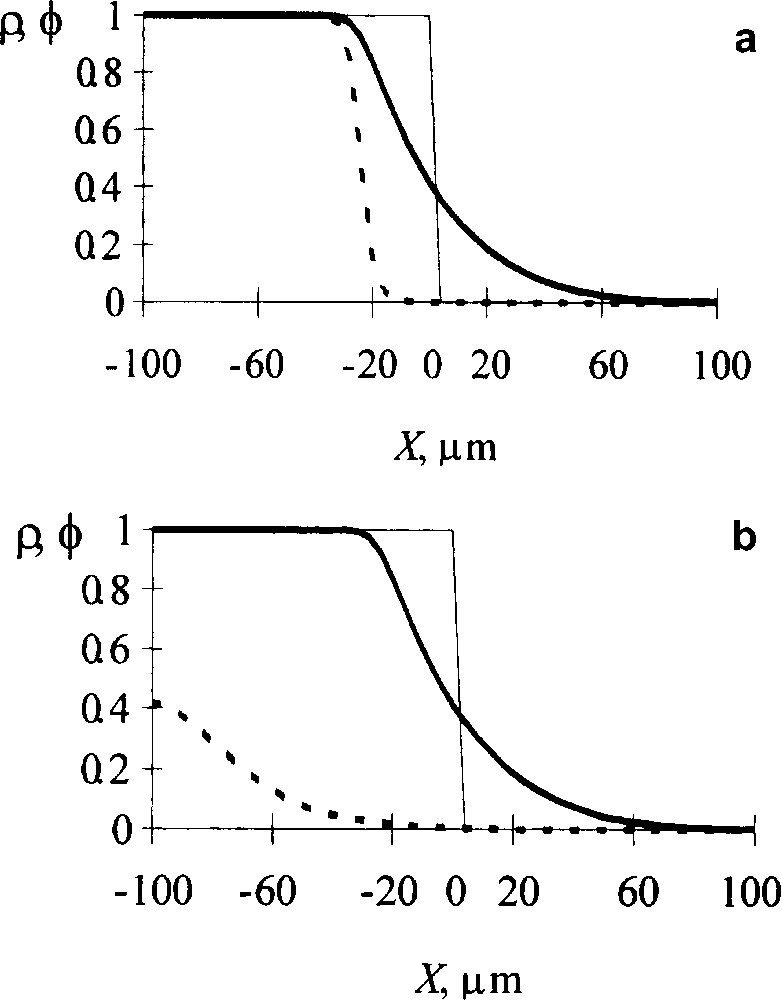
Influence of diffusion intermixing of reacting chains on the reaction kinetics. Volume fraction profiles of A units (ρ, dotted line) and reacting chains (ϕ, solid line): (a) intermixing is ignored; (b) intermixing is counted for. Dashed line indicates the initial interface profile. N_A = 500, N_B = 2000, rate constant γ = 5 × 10⁻⁵ s⁻¹, Flory–Huggins parameter χ = 0, time 17.5 × 10⁴ s [9].

Fig. 2
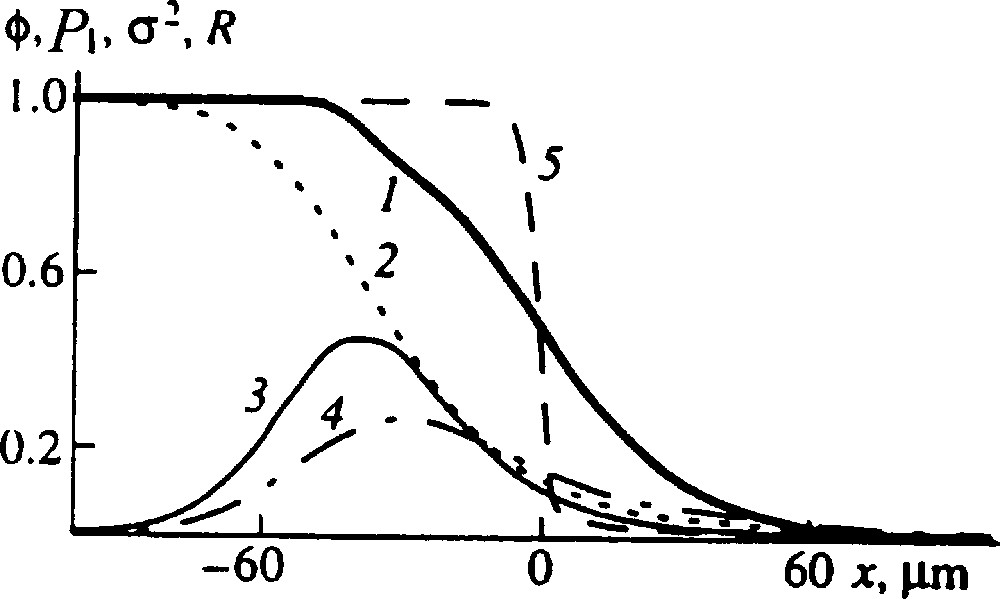
Detailed description of the blend structure: (1) volume fraction of the reacting chains, ϕ; (2) the mean fraction of A units in the reacting chains, P₁; (3) the dispersion of the reacting chains distribution in composition, σ²; (4) the probability of a boundary between the A and B sequences, R = 2P(AB); (5) the initial interface profile. N_A = 500, N_B = 2000, χ = −0.01, the rate constants β = γ = 2 × 10⁻⁵ s⁻¹, time 1 × 10⁵ s [9].

Fig. 1 shows a contribution of diffusive intermixing for a strong interchain acceleration. If the intermixing is ignored (top picture), the reaction appears to proceed only in the regions where B chains have penetrated. However correct calculations show (bottom picture) that due to intermixing, the reaction for the same time interval extends throughout a whole region occupied by reacting chains. So the degree of conversion increases markedly.

The principal aim of a theory in this field is to describe the blend structure. Indeed, the primary structure of a polymer blend characterized by the spatial distribution of macromolecules of different composition determines the blend properties (like the distribution of units along the chain determines the copolymer properties). It is worth to emphasize that the theory does permit to calculate a detailed structure of the blend. It is seen in Fig. 2 not only profiles of reacting chains concentration, ϕ , and their mean composition, P₁, but also the profiles of such characteristics as the dispersion of compositional heterogeneity of reacting chains, σ², and the probability of a boundary between the A and B sequences, R = 2P(AB). Note that it is extremely difficult to obtain such detailed information by experiment.

3 End-coupling

End-coupling reaction leading to the formation of a diblock copolymer is an effective method of the reactive compatibilization. Schulze et al. [5] studied the reaction between deutero-polystyrene with amino end groups and polymethylmethacrylate with anhydride end groups at 174 °C using forward recoil spectroscopy to establish whether the reaction is chemically or diffusion controlled. They employ bilayer and trilayer films with well-defined interfaces as the proper (pure) model systems. Especially impressive results were obtained using trilayer system. In this case, the polystyrene active (dPS-NH₂) chains have to diffuse through the inert polystyrene layer before to react with poly(methyl methacrylate) active (PMMA-Anh) chains at the interface between PS and PMMA-Anh. The authors [5] established that dPS-NH₂-22 chains crossed the PS/PMMA interface many times before to react with PMMA-anh. In other words, the reaction is chemically controlled.

Taking into account this result we tried to describe theoretically a competition between spinodal decomposition and relatively slow, chemically controlled end-coupling reaction [9].

Consider artificially prepared quasi-homogeneous blend of incompatible polymers A and B. Let the spinodal decomposition proceeds after a proper temperature jump. It is convenient to describe a blend morphology in terms of structure factor, S, since this quantity is measured experimentally using light or neutron scattering. The structure factor dependence on the wave vector, k, reflects non-homogeneity of the system. Permanent growth of S corresponds to the progressive phase separation.

Now let each A and B chain bear one proper active end-group, so that diblock copolymer AB is forming via end-coupling. The reaction competes with phase separation since the diblock copolymer is a compatibilizing agent. Our goal is to analyze how the reaction affects the initial stage of the possible spinodal decomposition. During this stage fluctuations of concentrations arise, grow and disperse due to interdiffusion. For a slow reaction, approaches of linear non-equilibrium thermodynamics may be applied. The evolution of structure factor matrix is described by the following general equation.

\frac{d \hat{S}}{d t} = - (\hat{D} + \hat{R}) \hat{S} - \hat{S} {(\hat{D} + \hat{R})}^{T} + 2 \hat{Λ}

Here D and R describe contributions of interdiffusion and reaction, respectively, 2Λ does a diffusion noise. The equation may be solved numerically using expressions for the free energy, Onsager coefficients and the reaction kinetics. Fig. 3 shows reduced structure factor S_AA/S₀ versus reduced wave vector (k R_c)² for various moments of time. It is seen that first, while volume fraction of copolymer is small, structure factor grows; then begins to decrease and the blend approaches homogeneity.

Fig. 3
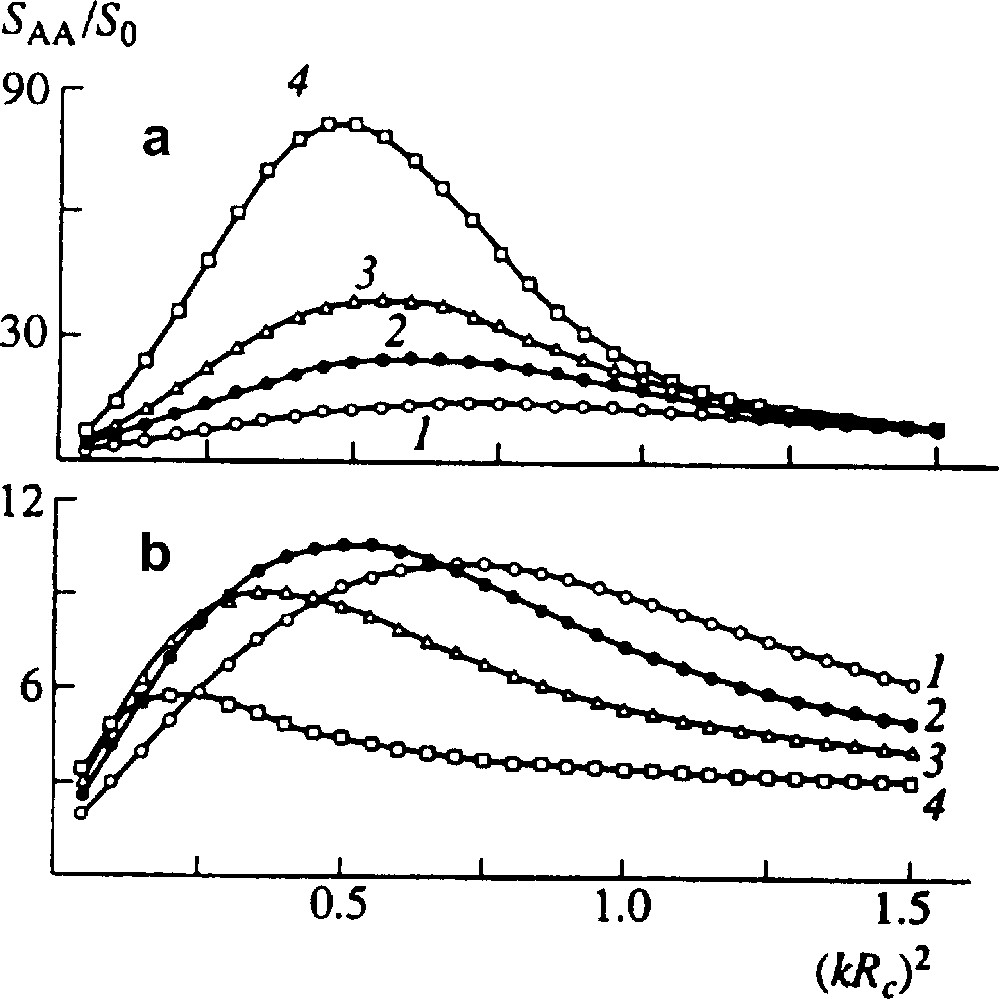
Reduced structure factor for an initially quasi-homogeneous blend of two incompatible homopolymers A and B at time t = 20 (1), 35 (2), 50 (3), and 80 s (4). S₀ = S_AA (t = 0). (a) No reaction, (b) end-coupling proceeds, N_A = N_B = 500, N_c = 1000, D_A = D_B = 2 × 10⁻¹³ cm² s^–1, rate constant α = 0.01 s⁻¹ [9].

We studied also some problems concerning a diblock copolymer influence both on thermodynamic equilibrium and particle growth in dispersed blends of incompatible polymers [10,11]. It is worth noting however that studies related to a block copolymer stabilizing effect should be regarded as preliminary stages. The topical problem is a complete description of the process, which includes end-coupling reaction and phase separation as well as various mechanisms of particles growth.

4 Interchain exchange

Another important problem is a reactive compatibilization via reactions of interchain exchange. The reaction proceeds either between two inner bonds (direct exchange, say, transesterification) or between end-group and inner bond (end-group interchange, say, alcoholysis). During the reaction, homopolymers transform gradually into block copolymers, multi-block copolymers and eventually into random copolymers. It seems extremely difficult to describe the process in extruders or other mixers. To solve the problem, we have to advance step by step.

4.1 Homogeneous systems: the product structure

It is reasonable to consider at first the reaction in a homogeneous system. Using the kinetic approach Kudryavtsev [12] recently derived equations for an evolution of the molecular weight distribution (MWD) during direct interchange. Moreover, Kudryavtsev et al. [13–15] described for the first time an evolution of the weight distribution in block length (BWD) of the reaction products for both direct and end-group interchange. Besides, MWD and BWD for direct interchange have been studied using Monte Carlo simulations [13].

Calculations comprised both direct and end-group interchange for initially monodisperse components as well as for components having Flory MWD.

Fig. 4 demonstrates the transient MWD for both kinds of an interchange, the initial blend being monodisperse. Different curves correspond to the different conversion, which was measured in the number of interchanges per number average chain τ, this quantity being proportional to real time. It is seen that although the initial and final distributions in the systems are the same, the transient distributions are essentially different. In principle, it gives the possibility to determine the most contributing type of interchange for the concrete blend studied.

Fig. 4
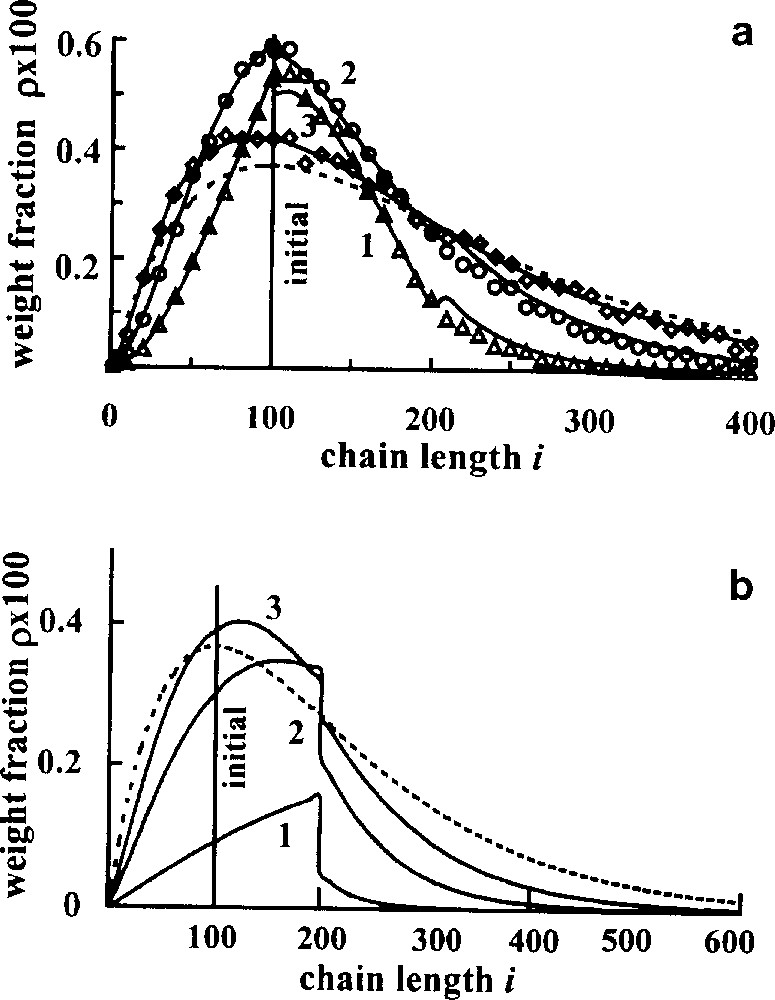
Transient MWDs. Initially all chains consist of 100 units. Mole fraction of A units ϕ_A = 0.5, points – Monte Carlo results; theoretical curves correspond to the different number of interchanges per average chain, τ; (a) direct interchange, τ = 1(1), 3(2), 10(3); (b) τ = 0.2(1), 1(2), 2(3); dotted lines – equilibrium distribution [12,13].

In Fig. 5 the distributions of A blocks in the copolymer and in the blend as a whole are compared. The corresponding curves in Fig. 5a, b plots differ noticeably at short time although the distributions eventually tend to the Flory form, which is shown by thin lines. Hence the averaged blend structure studied in experiments does not correspond to the copolymer formed structure till the homopolymers are present in the blend. It is worth to emphasize that the theoretical curves fit fairly well Monte Carlo results – points shown in Figs. 4 and 5.

Fig. 5
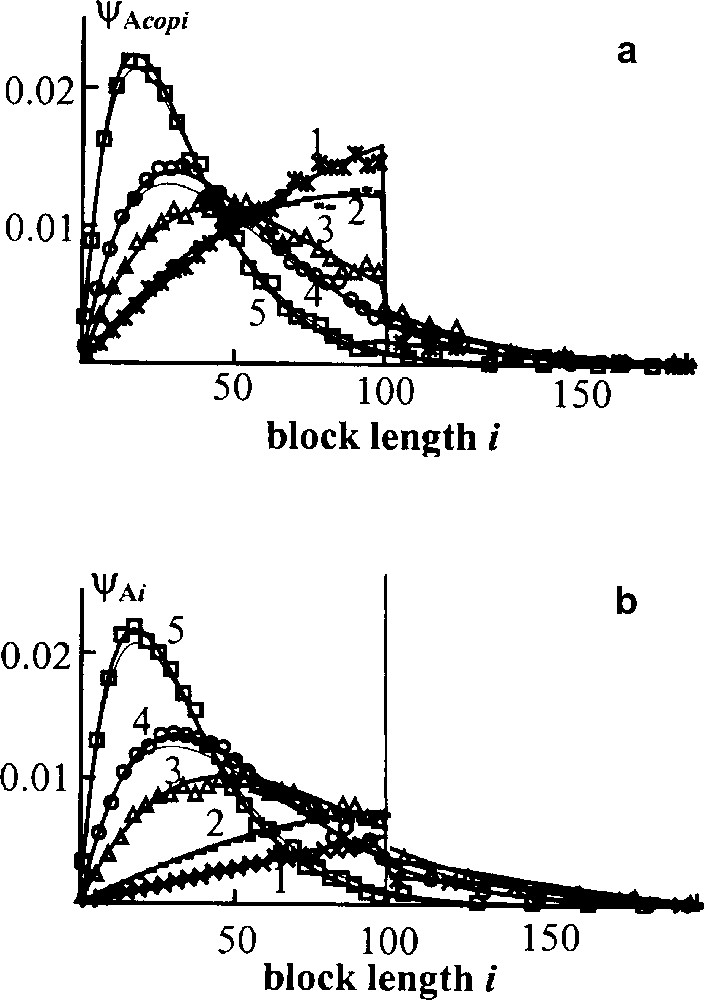
Transient block weight distributions for direct interchange. Initially all chains consist of 100 units. ϕ_A = 0.5, points – Monte Carlo results; curves – theoretical calculations for the whole blend (a) and for copolymer only (b); thin lines – Flory distribution; τ = 0.5(1), 1(2), 3(3) 5(4), 10(5) [13,14].

Based on our studies of interchange kinetics for both mechanisms and various initial conditions, we may divide any interchange process into two stages: fast and slow. The fast stage takes the time enough for an average chain to undergo several interchanges; under the typical experimental conditions, it would be a few minutes. At this stage the MWD of the blend takes the form of the Flory distribution, homopolymer chains are almost exhausted, the copolymer composition is nearly equalized with the composition of the whole blend. In the course of the slow stage, the average copolymer block length decreases gradually until it reaches the value characteristic of the completely random copolymer. The full randomization is attained when each interchangeable group in the copolymer reacts on average one time. In real experiments, it usually takes more than an hour.

4.2 Quasi-homogeneous systems

Next step in our studies relates to fine dispersed quasi-homogeneous blend.

For such a blend, the ratio of reaction and phase separation rates determines an evolution of the blend structure. Such a competition has been studied by Tanaka et al. [3] by the example of transesterification in systems polycarbonate/polyethyleneterephthalate and polycarbonate/polyarylate. If the reaction rate prevails, the blend remains fine dispersed and approaches homogeneity. If the phase separation rate prevails, coarse particles are formed and further the reaction proceeds at the interface.

Recently Govorun and Kudryavtsev [16] considered a competition between transesterification and spinodal decomposition for initially quasi-homogeneous blend. The reaction is assumed to be slow enough, so that a chain does not undergo the reaction during its diffusive displacement equal to its size (radius of gyration). The process is described in terms of the structure factor, like for end-coupling reaction (see above), however the task is more complex because the initial binary blend becomes multicomponent. The dynamic structure factor obeys the equation

\hat{S} (q, t) / q^{2} = - (\hat{D} (q) \hat{S} (q, t) + \hat{S} (q, t) D^{T} (q)) + 2 \hat{Λ} (q)

The matrices of diffusion coefficients $\hat{D} (q) = \hat{Λ} (q) {\hat{G}}^{- 1} (q)$ , pair correlation functions $\hat{G} (q) = \hat{G} (q, φ = 0)$ , and Onsager coefficients $\hat{Λ} (q)$ were calculated using the random phase approximation [17]. All these characteristics change slowly with time due to the reaction. The reaction contribution is described using Kudryavtsev [12] kinetic equations.

Consider first a spinodal decomposition in an unreacted blend to elucidate the effect of polydispersity [16]. It is shown in Fig. 6 that structure factor grows more slowly for polymers having Flory MWD than for monodisperse components.

Fig. 6
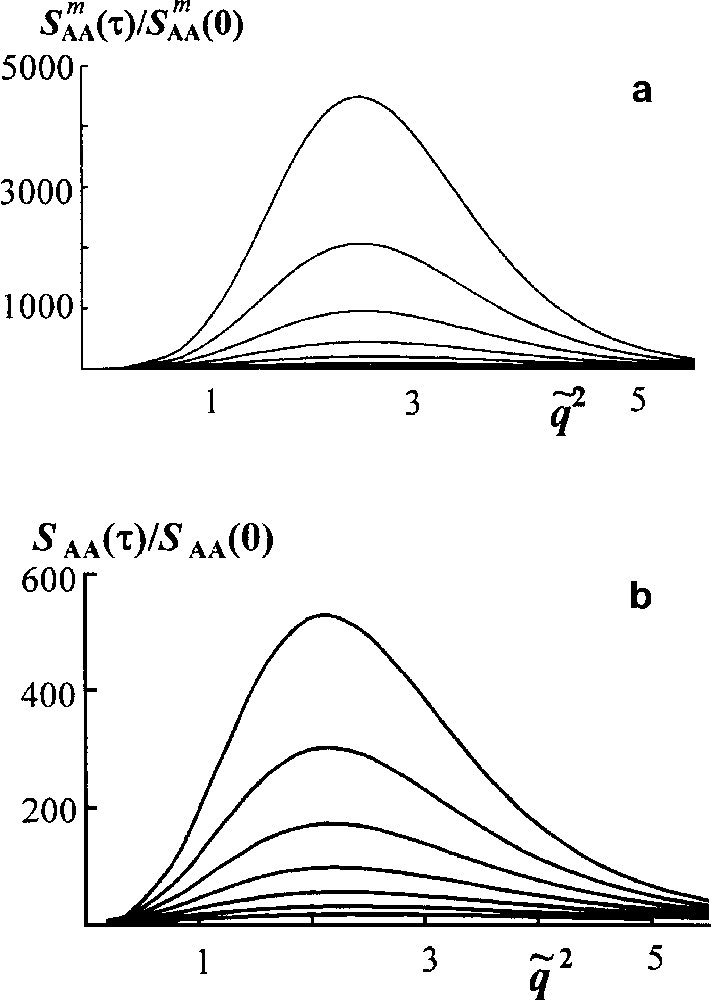
Spinodal decomposition in mono- and polydisperse blends. Scaled structure factor $S_{AA} (\tilde{q}, τ) / S_{AA} (\tilde{q},0)$ versus scaled wave vector ${\tilde{q}}^{2} = q^{2} {N a}^{2} / 6$ . Curves reflecting the structure factor growth are plotted for the dimensionless time τ = t/t_R from 0.6 to 1.5 by Δτ = 0.15 (t_R is the Rouse time for a number average chain). (a) Monodisperse blend N_A = N_B = 20; (b) blend of homopolymers A and B having Flory MWD, ${\bar{N}}_{A} = {\bar{N}}_{B} = 20$ . In both cases ϕ_A = 0.5, χ = 0.4 [16].

If a blend of polydisperse polymers A and B as a whole is incompatible, the most thermodynamically incompatible are the longest chains. However such chains are of the least mobility. Therefore the phase separation proceeds more slowly.

Now consider a linear stage of spinodal decomposition in a reacting blend, where the components have Flory MWD. Fig. 7 demonstrates that the reduced structure factor $S_{AA} (\tilde{q}, τ) / S_{AA} (\tilde{q},0)$ first grows, then diminishes slowly, its maximum value being of the order of magnitude less than for unreacted blend (Fig. 6). Thus transesterification retards phase separation from the very beginning of the process. According to calculations, a phase separation in the system studied is suppressed when the average block length becomes two or three times smaller than the length of initial homopolymers.

Fig. 7
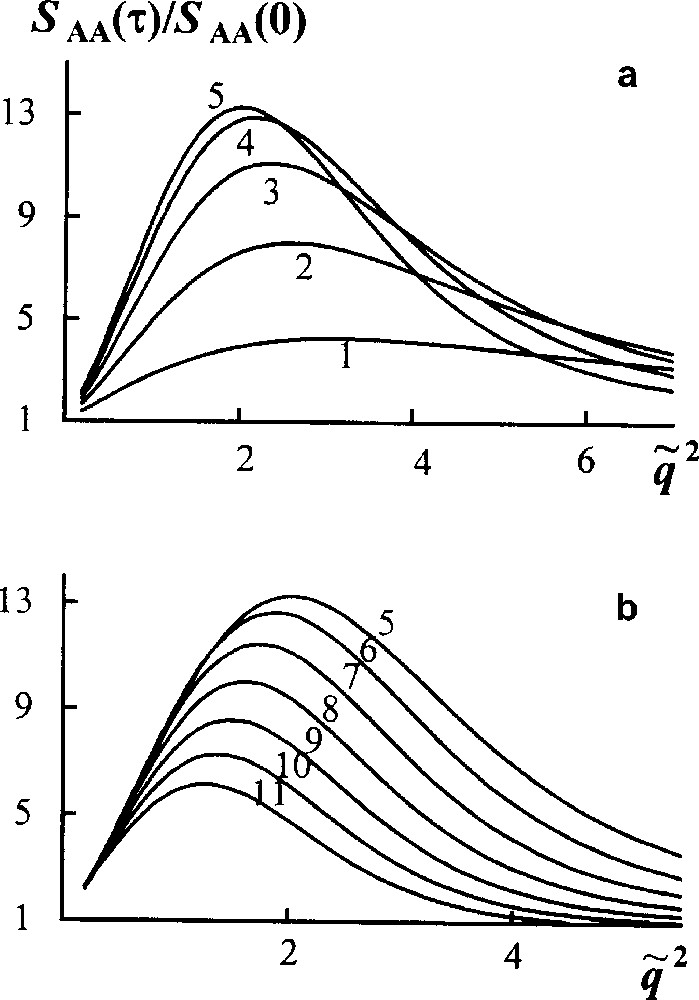
Reaction − spinodal decomposition in the reacting blend. Scaled structure factor $S_{AA} (\tilde{q}, τ) / S_{AA} (\tilde{q},0)$ versus scaled wave vector ${\tilde{q}}^{2} = q^{2} {N a}^{2} / 6$ . Curves 1–11 are plotted for τ = t/t_R from 0.3 to 3.3 by Δτ = 0.3. ${\bar{N}}_{A} = {\bar{N}}_{B} = 20$ , ϕ_A = 0.5, χ = 0.4 [16].

The present approaches elaborated for homogeneous and quasi-homogeneous systems might be useful to a certain extent for describing the initial stage of the interchange kinetics at the interfaces of real heterogeneous blends. However the topical problems in this field are to describe the broadening of the interface during interchange reaction and, ultimately, to embed the forced mixing in the theory. It is especially desirable to describe an evolution of the heterogeneous blend structure in terms of MWD and BWD of the reaction products. This is a good challenge.

Acknowledgements

Financial aid by the program of President of the Russian Federation for Leading Research Schools is acknowledged. Y.K. is also grateful to the Russian Science Support foundation.