1 Introduction
Reactive processing involves the difficulties of molten polymer processes, such as twin-screw extrusion for example, and the problems of controlling a chemical reaction in very specific conditions (high viscous medium, high temperatures, short residence times). Consequently, reactive processing developments require basic research in the fields of chemistry, rheology, flow modelling and mixing, in line instrumentation and process control. The aim of this short review is to give an overview of the works carried out in our laboratory in the field of the reactive processing. The present topic is focused on the rheology developments for reactive systems. From a processing point of view, rheology can be viewed as the interface between chemistry and flow modelling. The work of the rheologist is then to predict the variation of the viscoelastic parameters versus the extent of the reaction (rheo-chemistry). Another task of the rheologist is to contribute to the understanding of the macromolecular architecture development following a chemical modification. This approach is generally named molecular dynamic from rheo-physics.
On the other hand, numerous typical reactive systems [1] can be considered in reactive processing, as for example: chemical modification of molten polymers, bulk polymerisation, reactive blending of immiscible polymer blends by reaction at the interface, and in situ polymerisation and/or crosslinking of one of the two phases. In reactive extrusion, there is still a fundamental question to be solved: what is the local concentration of reactants at the different length scale of mixing from macro-mixing to micro-mixing? Actually, the role of diffusion and mixing is emphasised by the high viscosity of the molten polymers and the drastic variation of the viscosity with the extent of the reaction. The typical cone and plate or parallel plate geometries fail in homogenising low-viscosity-ratio fluid mixtures. To overcome these problems when mixing is a determinant step, non-conventional geometry can be designed and developed [2] for a conventional rheometer in order to have a quantitative analysis of shear rate/stress data of different mixing systems (rheo-mixing).
Lastly, a control process based on measurements of the pressure gradient inside the die was developed, as the pressure sensor turned out to be a pertinent sensor that allows the in-line control of the process (rheo-processing).
In order to illustrate in more details the contribution of the rheology to reactive processing, we will mainly focus the present review on the polymerisation of ε-caprolactone in bulk and dispersed media.
2 Mixing–diffusion reaction
We will consider hereafter the case of the bulk polymerisation. With regard to the bulk polymerisation of ε-caprolactone (PCL) and linear polyurethane (PU), for example, the quality of mixing in terms of concentration of monomers at the monomer scale can be really supposed perfect [3]. In other words, the reactive media is homogeneous from the reactant concentrations’ point of view. Actually, the monomers (ε-CL/initiator or diols/diisocyanate) are miscible and have low viscosities so that it is extremely easy to reach homogeneous conditions before the beginning of the chemical reaction. Furthermore, although the diffusion coefficient of monomers drastically increases with the extent of the reaction owing to the variation of the bulk viscosity, no variation of the reaction kinetics was observed with the viscosity. From a processing point of view, the monomers are pre-mixed at room temperature before their introduction into the reactor (the reactor is here either the gap between the plates of the rheometer or the extruder) so that the mixing step is separated from the reaction step. Actually, the mixing capability of the extruder is not the key parameter for these systems and the originality of the reactive extrusion must rely on the continuous aspects offered by a twin-screw extruder. Nevertheless the kinetics of the polymerisation must be fitted to the residence times in extruder of the order of 1 min. But, this important aspect of the reactive extrusion is the scope of the chemist, since he must develop new catalyst systems for high-temperature processing in order to avoid side reactions.
Note that a quite different behaviour (Tromsdorff effect) is observed for free-radical polymerisation of methyl methacrylate (MMA). Indeed, the viscosity of the reaction mixture becomes higher with the polymer chain formation. This high viscosity hinders the diffusion of chains because on entanglements, so the rate of termination slows down considerably. Consequently, the rates of initiation and propagation come out of balance. Chains grow without termination, so that the conversion is accelerated.
The situation is quite different when carrying out the polymerisation in melt dispersed media.
The dispersion and/or dissolution at a molecular scale of low-viscosity reactants in a polymer of high viscosity is a key for the control of the final macromolecular architecture when one considers a reactive polymer processing technology in the molten state. Such a reactive process in polymer blending can be for example the in situ polymerisation of one phase in the presence of another or the grafting of a functional species onto a polymer chain [4]. Generally speaking, the mixing time must be lower than the time of chemical modification and/or polymerisation; otherwise the local stoichiometry may be different from what is desired, resulting in non-controlled materials.
For example, we studied [5] the formation of a polyethylene/polyurethane polymer blend via in situ polymerisation of diols and diisocyanate monomers dispersed in a molten polyethylene. It was observed that high solubility of isocyanate monomers and low solubility of alcohols in molten PE induce an imbalance stoichiometry that limits the degree of polymerisation (molecular weight) during the blending process. In addition, the difference in viscosity between the minor and major phase has a controlling influence on the qualitative compounding behaviour exhibited. Such a reactive system is then controlled by the solubility parameters of the different reactants and their diffusion in the reactive media. In other words, the concentration in monomers is not homogeneous any more compared with the bulk conditions. Actually, such a situation always occurs in most of reactive systems in dispersed media.
3 Bulk ε-caprolactone polymerisation
A ‘coordination–insertion’ process can be assumed in the polymerisation of the caprolactone, using an alcoxymetallic compound such as titanium n-propoxide [6,7]. This two-step mechanism consists of the monomer coordination to the initiator, followed by monomer insertion into the metal oxygen bond (Fig. 1). A selective acyl oxygen bond scission is observed during the ring-opening reaction. The polymer chain grows from the initiator titanium atom by successive insertion of the monomer, and the initiator molecule is included into the growing polymer chain. This polymerisation is considered as a living polymerisation. In addition, the n-propoxide titanium is tetrafunctional. Therefore, each molecule of initiator could theoretically generate four polymer chains. A 1H NMR study has proved that more than two sites in one catalyst molecule could generate the growth of a polymer chain.
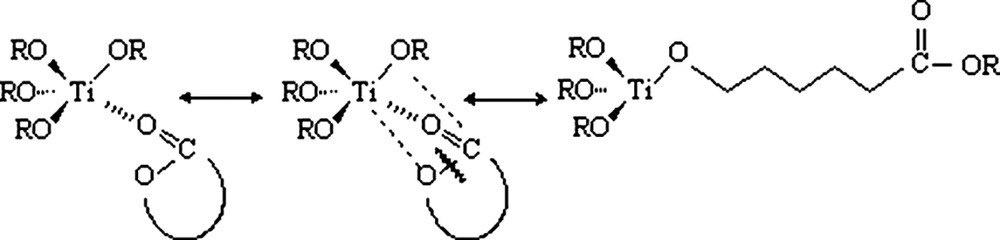
Mechanism of the ε-caprolactone polymerisation by the titanium n-propoxide.
Moreover, this type of polymer is very sensitive to degradation because of the rapid hydrolysis of Ti–O–polymer bonds included in the chain, as shown in Fig. 2. FTIR and 1H NMR studies have unambiguously shown that the second end group of the polymer, namely hydrolysed, is a hydroxyl function resulting from the hydrolysis of the living growing chain. Obviously, the first end group consists of the propoxide group of the initiator.
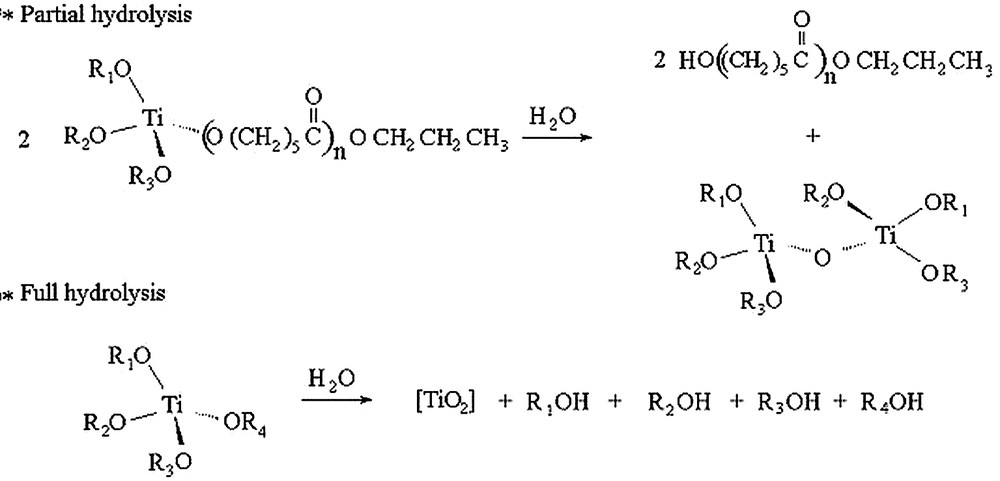
Hydrolysis mechanism of the alcoxy–metallic polymer bond.
Bulk polymerisation was carried out in situ in the rheometer using parallel plate geometry. Nitrogen was used to prevent thermal oxidation. As the polymerisation is living, different molar ratios [Monomers]/[Initiator] (ratios [M]/[Io]) were used in order to obtain poly(ε-caprolactone) of different molecular weights. The sample (Monomer/Initiator) was injected between the plates with a syringe, and was then heated by conduction through the plates. Rheological kinetics were carried out in real time at a temperature of 140 °C and at a frequency of 1 rad s–1. During polymerisation, the modulus varies over about four orders of magnitude (Fig. 3a). At the end of the polymerisation process, frequency sweep experiments (10−2 < ω(rad s–1) < 102) were carried out in dynamic oscillatory mode at various temperatures (80 < T(°C) < 160) in order to apply the time–temperature superposition principle (Fig. 3b).
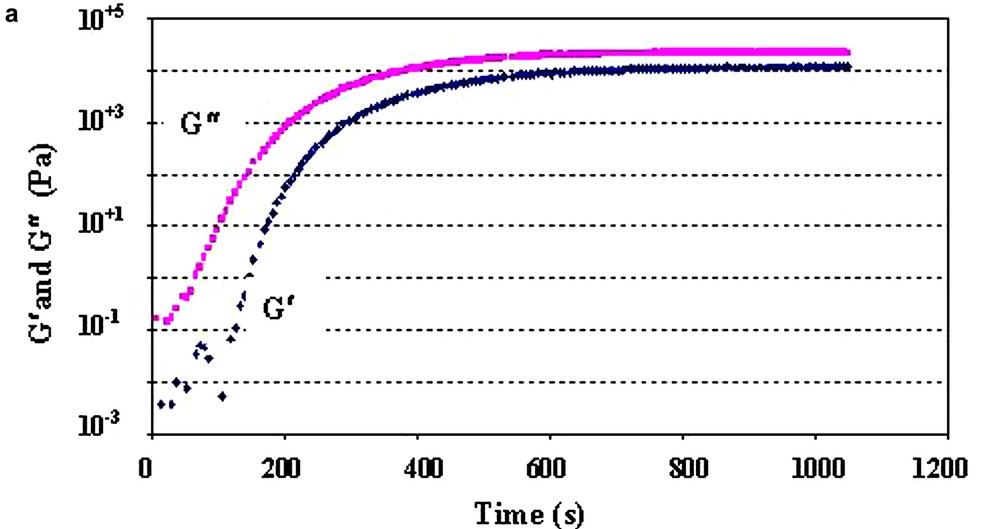
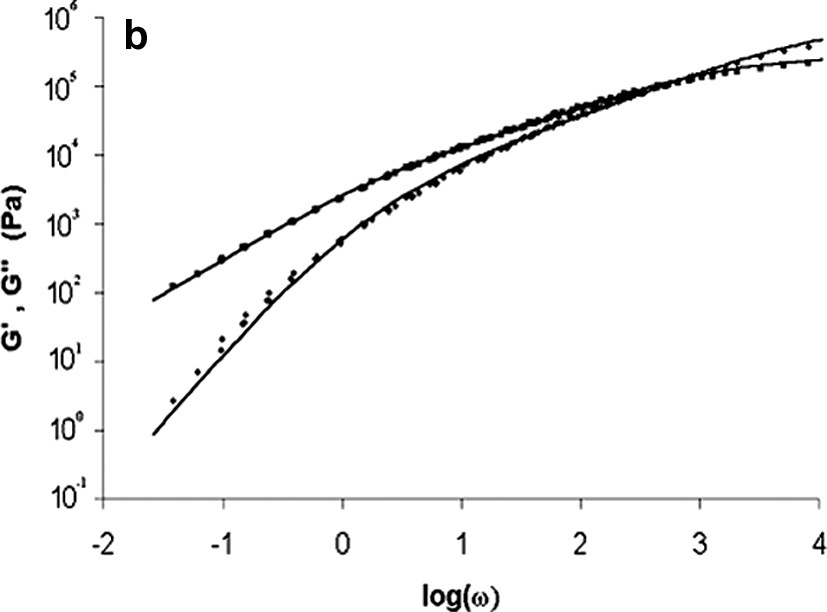
In situ bulk polymerisation of ε-caprolactone between the plates of the rheometer.
(a) Variation of the complex shear modulus versus the extent of the reaction. T = 140 °C, ω = 1 rad s–1.
(b) Master curve built at the end of the polymerisation process, T = 140 °C.
3.1 Rheo-physics
As previously explained, the dynamic characterisations of ‘in situ’ polymers were carried out directly on samples at the end of the polymerisation process. However, the molecular weight characterisation of the samples by SEC requires, on the one hand, to remove the sample from the rheometer plates and, on the other hand, to put it in THF. From this simple procedure, hydrolysis of the polymer by the mechanisms described earlier is inevitable. Consequently, the molecular weight distribution measured by SEC is not representative of the true MWD of the polymer chains of the polymer synthesised in situ between the plates. In order to explain the dynamics and the structure of poly(ε-caprolactone) chains synthesised in situ in the rheometer, inverse calculation of the MWD was used [8].
A model based on a mixing rule of the relaxation function was used to predict the linear viscoelastic behaviour of polydisperse poly(ε-caprolactone). Few parameters are needed in the model, namely the scaling law for the zero-shear viscosity of narrow fractions, the plateau modulus and the value of the molecular weight between entanglements Me. One of the main applications of the present approach, already developed in a discrete relaxation spectrum form by Carrot and Guillet [9], is to provide a relation between MWD and rheological properties precise enough to investigate the way towards a prediction of the MWD shape from viscoelastic measurements. The inverse problem of the determination of the MWD was treated using the a priori shape (Wesslau or bimodal Wesslau) of the MWD.
For example, Fig. 4 shows, in full line, the bimodal MWD obtained from the minimisation process, in comparison with the MWD of the hydrolysed form in dotted line. Note that the hydrolysed sample originates from the hydrolysis reaction of a sample, that has been synthesised in situ. Therefore, these two samples can be directly compared for the study of their chemical structure from a rheological point of view. The global MWD is plotted in full line and obviously exhibits a great tail at high molecular weights. It can be observed from Fig. 4 that the main MWD is close to the MWD of the hydrolysed polymer. This result suggests that the main contribution to the global MWD is due to the poly(ε-caprolactone) chains, for which the hydrolysis mechanism does not perturb the viscoelastic properties (relaxation mechanisms). Then, at polymerisation, these chains have the structure shown in Fig. 5 (structure 1).
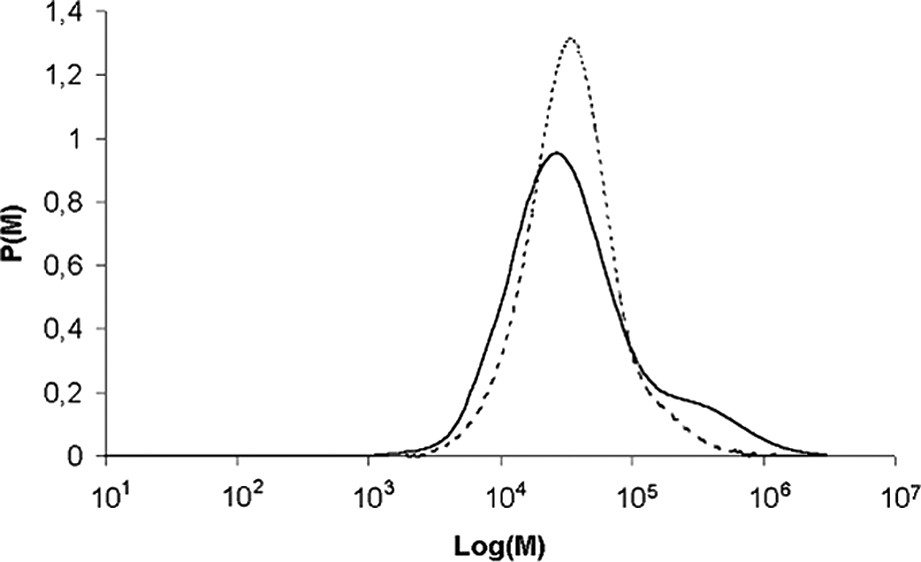
MWD of the in situ synthesised polymer from the rheological inverse calculation. Dotted line: MWD of the hydrolysed sample determined from SEC analysis.
Chemical structure of the in situ synthesised poly(ε-caprolactone).
Structure 1: one polymer chain by titanate group.
Structure 2: two polymer chains by titanate group.
Structure 3: three or four chains by titanate group (star structures).
This means that only one polymer chain grows per titanate group. During the hydrolysis process, the Ti–O–polymer bond is destroyed without modification of the relaxation mechanisms of the hydrolysed chain.
The origin of the second distribution that contributes to about 15% of the total distribution can be found in the potential functionality of the titanium n-propoxide. Moreover, from the structure of the titanium group, the functionality of the initiator is 4 and so four chains can grow from the initiator. The discussion of the above section concludes that about 85% of the titanium tetrapropoxide has an apparent functionality of one. Therefore the most probable apparent functionality of the last 15% is two, leading to the structure of the chains shown in Fig. 5 (structure 2).
However, the star structures of the chains, shown in Fig. 5 (structure 3), can be present in the system. NMR analysis has shown that more than two polymer chains could grow from each catalyst molecule. In fact, the tail of the distribution can consist of structures 2 and 3. Structure 2, which leads to a linear chain, can be assumed to have the same molecular dynamic as the chains of structure 1. In other words, the Ti(OR)2 group involved in the chains does not modify the mechanism of relaxation of the chains.
3.2 Rheo-chemistry
The aim of the rheo-chemistry is to build models able to predict the evolution of the rheological behaviour of reactive systems in the bulk at any reaction time and under any processing conditions of temperature, initiator concentration and shear rate. First of all, the kinetic model giving the evolution of the conversion rate and the molecular parameters, namely average molecular weight and molecular weight distribution as a function of time, was taken from extensive work done on the polymerisation of ε-caprolactone.
Secondly, rheological models characterising the melt viscoelactic behaviour of poly(ε-caprolactone), the complex viscosity, the storage modulus G′ and the loss modulus G″ were built on the basis of phenomenological models such as Yasuda et al.’s [10] relaxation spectrum models [11] or molecular dynamic models [12,13] based on a blending law of the relaxation function.
Lastly, during the ε-caprolactone polymerisation, the reactive mixture must be considered as a solution of polymer because the monomer is present until the end of the reaction. The terminal viscoelastic parameters are strongly affected by this dilution effect. A free volume correction was brought in order to take into account the dilution effect caused by the presence of the monomer.
The combination of both models (kinetic and rheological) enables the evolution of the viscosity during bulk polymerisation to be calculated. In both cases, the overall calculation [14] was shown to depict reasonably the variation of the modulus of the complex viscosity and loss modulus G″(t). The storage modulus G′(t) was well depicted when the reactive blend follows the entangled regime laws. Although rough approximations were made on relaxation times and on MWD, a generally good depiction of the rheological evolution of the present polymerising system is obtained. For example, Fig. 6a–c shows the prediction of our different models.
Experimental data and modelling of rheological curves as a function of the polymerisation time. [M]/[Io] = 1300, T = 140 °C.
(a) Modelling of the absolute viscosity ||η*|| from Carreau Yasuda model (■): experimental data at ω = 1 rad s–1; (●): experimental data at ω = 10 rad s–1.
(b) Modelling curves of G′ and G″ from the relaxation time spectrum model (♦, ■): experimental data at ω = 1 rad s–1; (◊, □): experimental data at ω = 10 rad s–1.
(c) Modelling curves of G′ and G″ from the blend of relaxation function model (♦, ■): experimental data at ω = 1 rad s–1, (◊, □): experimental data at ω = 10 rad s–1. Reprinted with permission from Gimenez et al. [14].
However, the models are able to predict reasonably well the evolution of rheological behaviour of the reactive system for any processing conditions such as temperature, frequency and initiator concentration ([M]/[Io] ratio). This is of great importance for an application to reactive extrusion processes. Indeed, a general modelling strategy using the kinetics of polymerisation and molecular weight distribution to predict the time-dependent rheology during the bulk polymerisation of a system such as ε-caprolactone offers new control for processing operations.
3.3 Rheo-mixing
Rheology is often used for the study of complex systems because, at macroscopic scale, it shows phenomena that appear at microscopic scale. Until now, rheology is generally devoted to the study of dynamic rheology systems at low strain and for linear viscoelastic response. Actually, the rheological properties during a mixing stage have not been much studied, probably because the characterisation of complex fluids may be a challenging task when conventional rheometers are used. The typical cone and plate or parallel plate geometries fail low-viscosity-ratio fluid mixtures. Also, a rheological study is complicated by several difficulties such as the fact that the medium is not homogeneous, at least at the early stages of the process. To overcome these problems when mixing is a key step, the general approach is the following: a batch mixer is used and the viscosity and shear rate are deduced from the speed and torque measurements. Nevertheless, due to the amount of polymer introduced in such a mixer (about 60 g) and the low conductivity of polymer components, self-heating phenomenon by viscous dissipation is an important non-well-controlled parameter. In a previous work [15], we developed a new mixing device (rheo-mixer) in order to collect interesting data about mixing in unusual molten polymer systems. This non-conventional geometry was put on a conventional rheometer in order to have a quantitative analysis of shear rate/stress data of different mixing systems. The rheo-mixer is constituted by a cylindrical vessel of 24.5-mm diameter, mounted on the motor, and a plate mounted on the torque transducer of the rheometer. Actually, this mixing device is based on a parallel plate analogy with some vertical obstacles like spikes in the gap for breaking up the streamlines of the fluid. Thus, the upper plate presents spikes of 2-mm height.
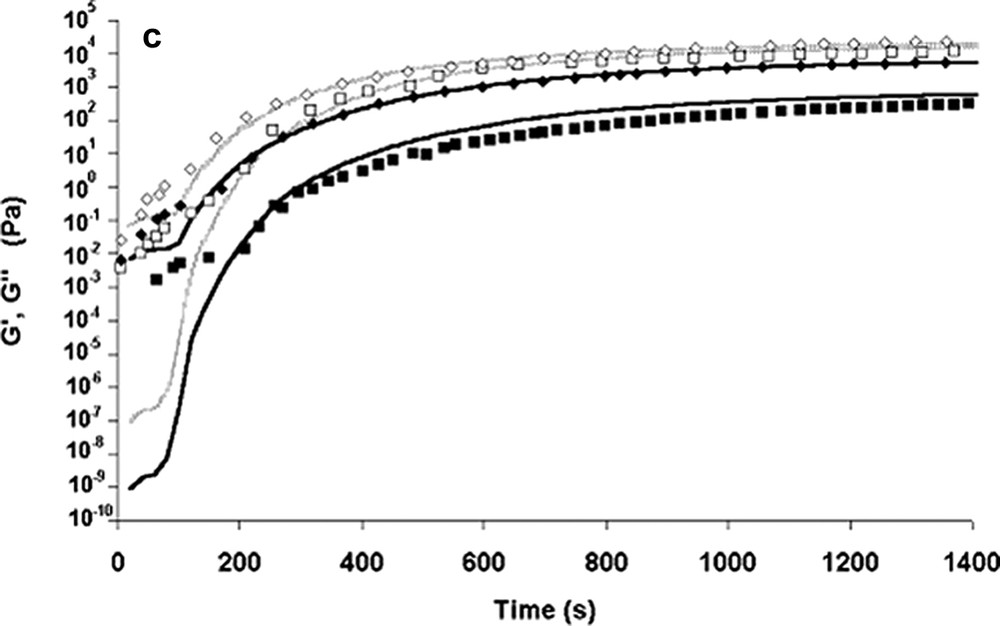
In the previous part (rheo-chemistry), the rheological behaviour during the bulk polymerisation of ε-caprolactone with titanium n-propoxide as the initiator was studied directly in the rheometer with parallel plate geometry and in the domain of the linear viscoelasticity. Thus, the low deformation applied could not promote mechanical mixing. The influence of high deformations and mixing conditions on the rheo-kinetics of ε-CL bulk polymerisation (T = 102 °C, [M]/[Io] ≈ 600) was then studied using the rheo-mixer. Fig. 7 shows that the same evolution of the viscosity (rheo-chemistry) during the polymerisation is obtained for shear rates in the range 1.5–150 s−1. Besides, it can be pointed out that the PCL samples completely polymerised exhibit a Newtonian behaviour over the whole range of shear rate investigated here. For the different processing conditions, we observed the same molecular weights of the samples within an experimental error of 10%: and , that is a polydispersity index of Ip = 1.6. Consequently, the fact that the viscosity–kinetic curves depict the same curve at different shear rate is not surprising, since the system is thoroughly mixed before its introduction into the mixer. In other words, the polymerisation process is carried out in a perfectly homogeneous medium, as previously assumed.
Bulk polymerisation of ε-caprolactone in the rheo-mixer at different shear rates.
Rheo-kinetics at T = 102 °C.
Reprinted with permission from Cassagnau and Fenouillot [16].
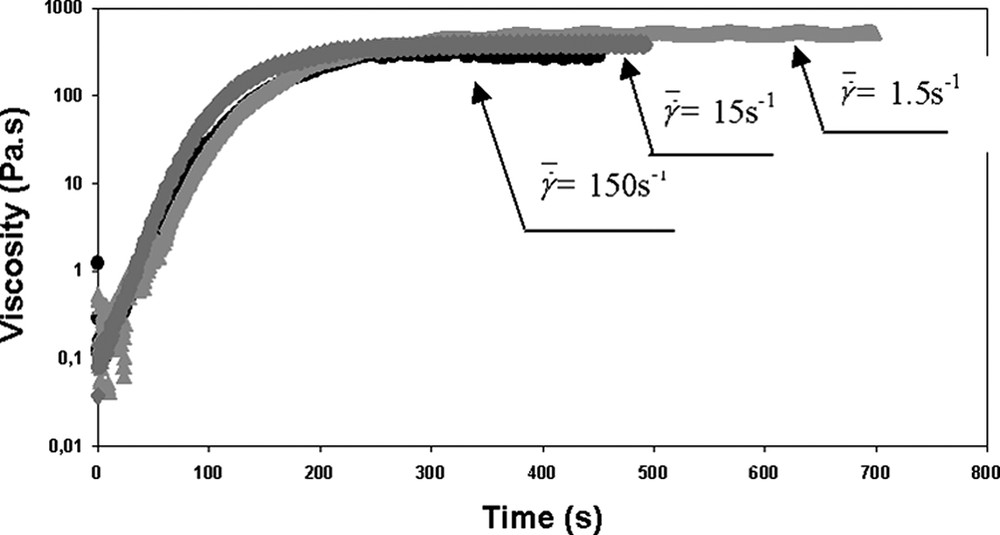
The polymerisation of the ε-CL was then carried out in a molten EVA matrix [16] according to the experimental conditions used in bulk polymerisation (T = 102 °C, [M]/[Io] ≈ 600). Fig. 8 shows the variation of the apparent viscosity versus the mixing time (or reaction time) for different shear rates. This figure shows that the time of polymerisation of ε-CL in EVA is around 300–400 s, which is close to the time observed in bulk. The comparison of these characteristic times indicates that the polymerisation rate is not really slowed down when the ε-CL polymerises in presence of the EVA. Thus, the monomer does not completely incorporate to EVA prior to reacting.
Polymerisation of ε-caprolactone in the rheo-mixer during mixing with EVA at different shear rates. T = 102 °C.
EVA/PCL at the end of the mixing and polymerisation processes: 60/40 wt.%.
Reprinted with permission from Cassagnau and Fenouillot [16].
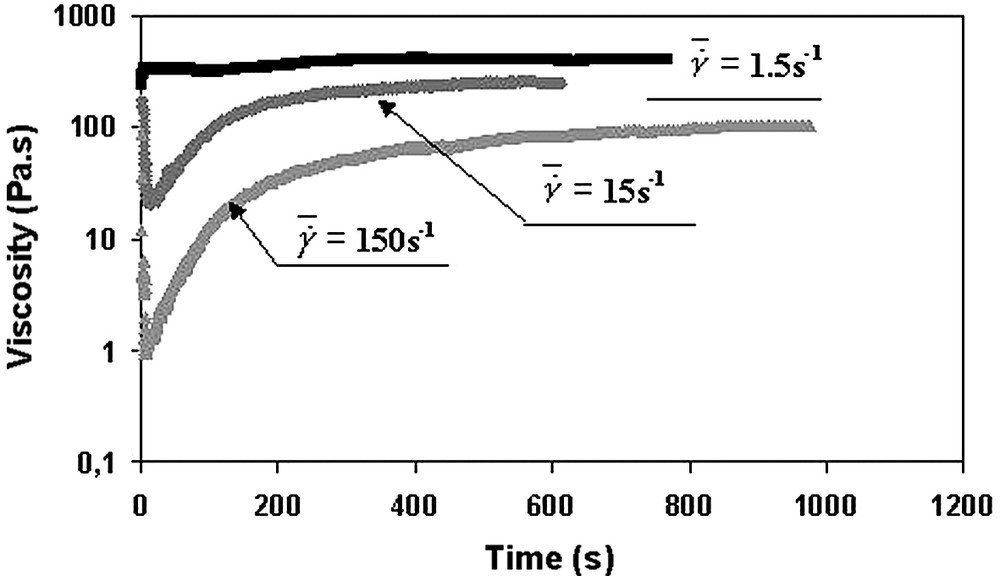
Fig. 9 shows that the molecular weight distribution of the PCL is broader in dispersed media (, Ip = 2.6) than in bulk (, Ip = 1.6) and that the molecular weight distribution is not dependent on the mixing conditions (shear rate), as observed in Fig. 8. Actually, the PCL and EVA phases are PCL- and EVA- rich phases containing ε-caprolactone, since the monomer is present until the end of the reaction, and can diffuse in EVA. Thus, the broadening of the molecular weight distribution in dispersed media can be explained by two facts: (1) the ε-CL monomer is partitioned between the EVA and PCL phases, leading to a concentration gradient of the ε-CL in the reactive phase; (2) the initiator in presence of the ester function of EVA is able to lead to alkoxide exchange reaction. This new initiator bearing O-polymer ligand with difference activity in ε-Cl polymerisation can lead to a broader poly (ε-caprolactone) molecular weight distribution.
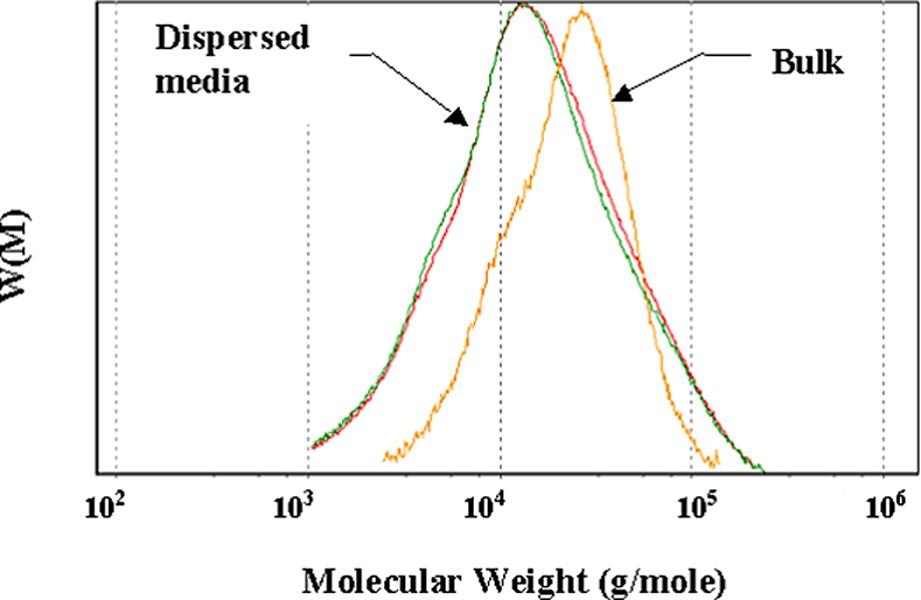
Molecular weight distributions of poly(ε-caprolactone) synthesised in bulk and in EVA dispersed media (1.5 and 15 s−1).
Reprinted with permission from Cassagnau and Fenouillot [16].
3.4 Rheo-processing
The bulk polymerisation was carried out [17] in an intermeshing self-wiping co-rotating extruder (Leistritz LSM 30–34, centreline distance: C1 = 30 mm, screw diameter: D = 34 mm, barrel length: L = 1.2 mm, L/D = 35). A ‘conveying screw element’ geometry was used for the bulk polymerisation. The extruder was equipped with a slit rheometer as shown in Fig. 10, where the position of thermal and pressure transducers can be seen. The dimensions of the slit die are W = 50 mm, L = 44 mm and H = 1 mm. The pressure sensors (P1, P2, P3 and P4) allow us to determine the gradient pressure ΔP inside the die, and the infra-red temperature sensor gives the bulk temperature. The residence time distribution (RTD) at the die exit (slit rheometer), which describes the history of the polymer inside the extruder, was determined with an in-line ultraviolet fluorescence method using anthracene methanol as a tracer. The solution of tracer (ε-caprolactone plus anthracene methanol) was injected in the feed stream by means of a syringe and a septum at the head of the extruder.
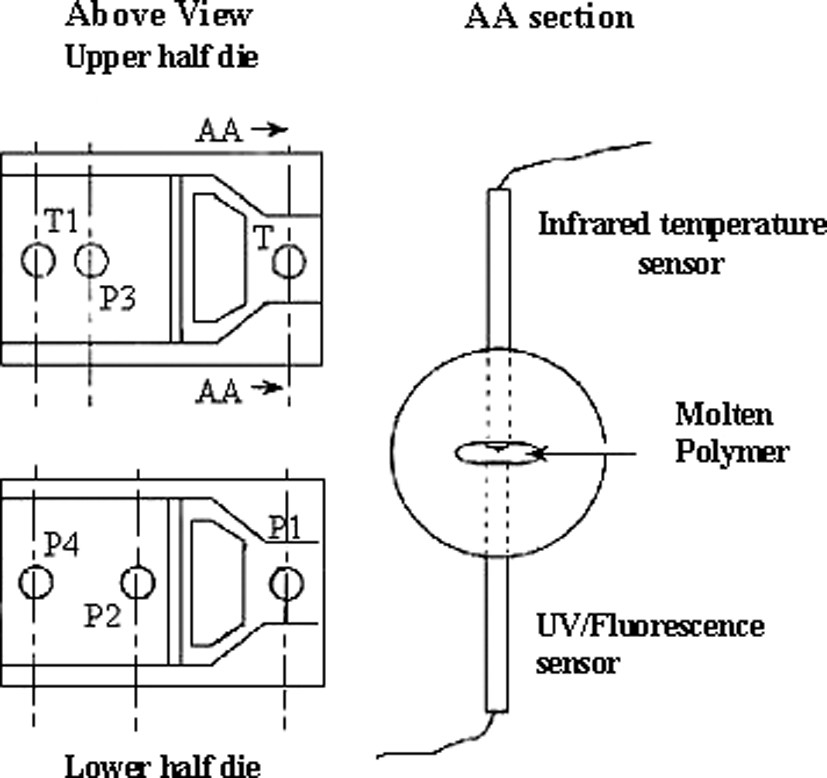
Geometry of the slit rheometer. Location of the pressure transducers (P1, P2, P3 and P4), location of the infrared temperature transducer (T) and location of the UV-fluorescence transducer (T1).
The polymerisation were carried out at 160 °C and with a global reactive feeding flow of Q = 3 kg h–1. The [M]/[Io] ratio of the reactive system varied in the range 400–1200, as such a ratio was expected to give reaction times compatible with residence times (results deduced from the kinetic study).
Fig. 11a shows the variation of temperature and pressure at the exit die as a function of the screw rotation speed. It was observed a material self-heating in the barrel and in the die with the increase of the screw rotation speed. This material self-heating caused by viscous dissipation corresponds to the shear rate increase between screws and barrels. The decrease of pressure observed at the same time is exclusively related to a temperature effect, as the pressure is correlated to the viscosity and therefore to the temperature. The temporary large increase of temperature and pressure observed after the change of the screw rotation speed is attributed to local changes of the flow at the die, which disappears with the regime balancing. Fig. 11b shows the effects of the flow variation (N = 100 rpm, Q = 1.5, 3 and 6 kg h–1) on temperature and pressure at the die exit. The temperature increase results from the material self-heating consequent to the shear rate increase due to the variation of the flow. In the same way, the pressure as a function of the wall stress and therefore the viscosity increase with flow.
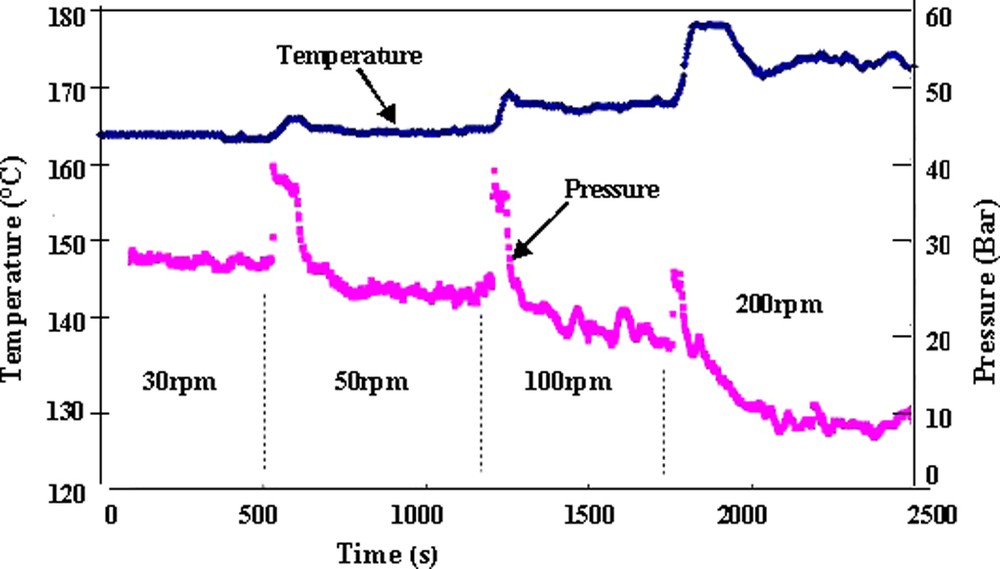
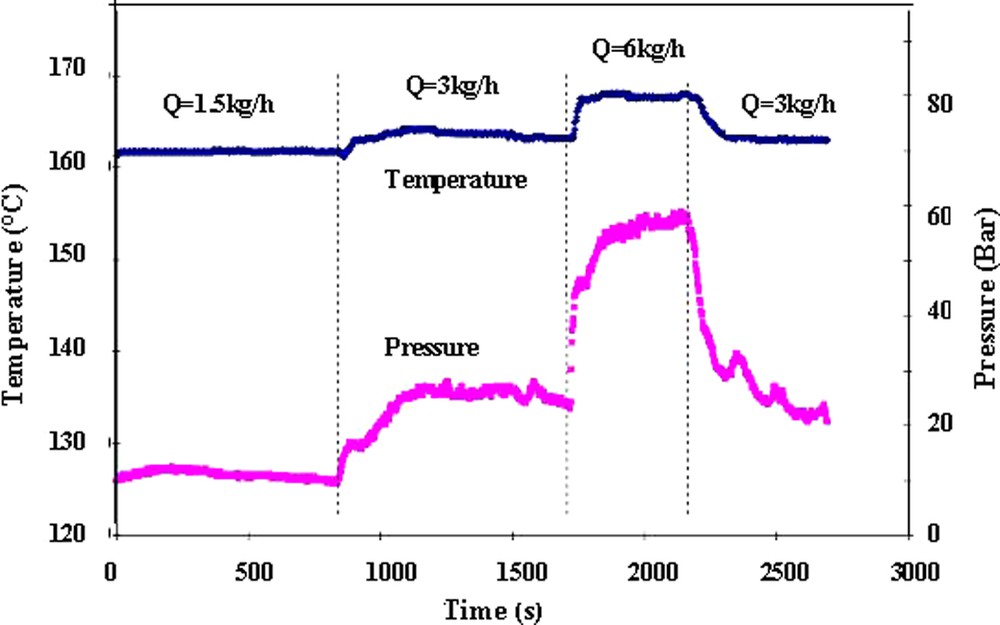
Pressure and temperature variations at the slit die. [M]/[Io] = 800.
Temperature set-point T = 160 °C.
(a) Influence of the screw rotational speed on pressure and temperature Q = 3 kg h–1.
(b) Influence of the flow rate Q on pressure and temperature N = 100 rpm.
Reprinted with permission from Gimenez et al. [17].
Starting from the rheological modelling of the polymerisation that gives the evolution of the viscosity whatever the process conditions are (namely temperature, initiator concentration and shear rate), the pressure at the die exit can be predicted, using the well-known equations of the gradient pressure as a function of the flow parameters.
The modelling procedure previously developed is able to predict the pressure of the stabilised regime whatever is the [M]/[Io] ratio of the reactive system. A model of the process dynamic can be established, taking into account the system dynamic, which can be determined owing to the RTD E(t), and more precisely the cumulative RTD obtained at the die exit by ultra-violet fluorescence measurements.
The transfer function [17] corresponds to the dynamic modelling of the process (see Fig. 12). Assuming that, the transfer function can be applied to each ratio [M]/[Io]:
Modelling of the variation of the ratio [M]/[Io] versus time at the slit die.
Dynamic function transfer.
Reprinted with permission from Gimenez et al. [17].
Fig. 13 shows that a good correlation is obtained between experimental data (variation of pressure versus time by changing the ratio [M]/[Io]) and the dynamic modelling. As it was already observed, the accuracy of the modelling depends on the coefficient αv of the zero shear-rate viscosity scaling law.
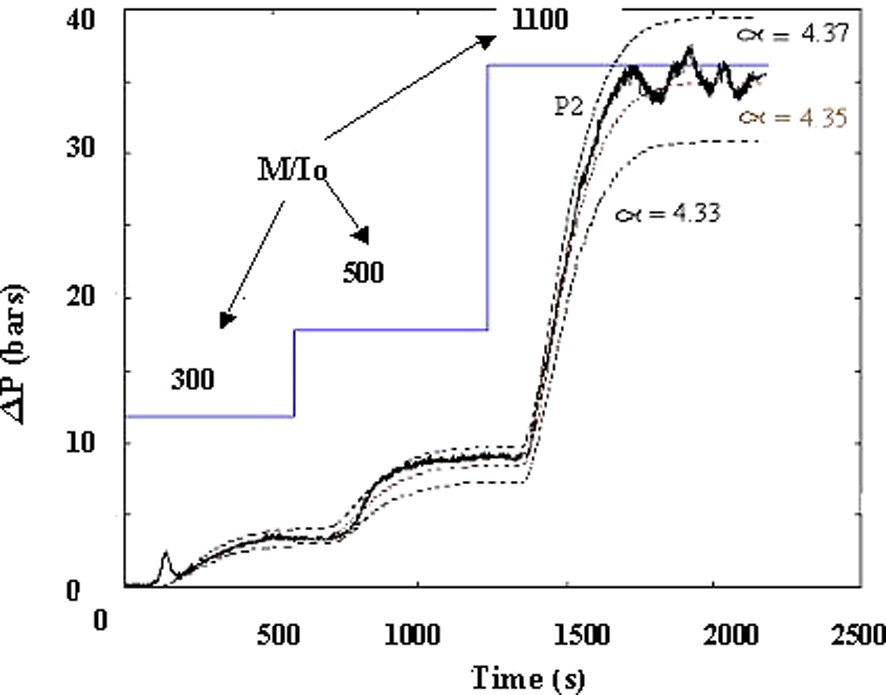
Dynamic modelling of the pressure variations versus time resulting from step variation of [M]/[Io] ratio.
T = 160 °C, Q = 3 kg h–1 and N = 100 rpm.
Reprinted with permission from Gimenez et al. [17].
4 Conclusion
This short review aims at showing the integrated activity that we have developed over the last years in the field of reactive processing. The different sections of this article illustrate the ε-caprolactone polymerisation in bulk and in dispersed media. Our approach is based on original, combined developments in chemistry, in-line instrumentation and rheology. Rheological works have been divided into four important contributions: rheo-physics, rheo-chemistry, rheo-mixing, and rheo-processing. The aim of rheo-physics studies is to calculate the molecular weight distributions and chain structures of in situ polymerised poly(ε-caprolactone) samples. From rheo-chemistry works we are now able to predict the variation of the complex shear modulus versus the extent of polymerisation. Complex mixing situations encountered in reactive polymer blends have been investigated from developments of new rheological tools such as rheo-mixer. Lastly, a rheo-processing approach based on the in-line measurement of the viscosity in a slit rheometer at the die exit of the extruder allows us to envisage its application to the experimental control of the process.
Furthermore, a strong cooperation with other groups working in the fields of flow modelling [18] and chemical engineering [19] allows us to envisage a complete modelling of the reactive extrusion based on fundamental aspects. In addition, scale-up considerations for polymerisation in a twin-screw extruder using 3-D numerical simulation based on our rheological modelling have been recently reported in the literature [20].
However, a lot of reactive systems can be explored by reactive processing and this integrated approach should be reconsidered for each typical system.