1 Introduction
1.1 Presentation of the reactive-extrusion process
Reactive extrusion is not a recent process, but it has rapidly developed during the last 10 years and is more and more used today for the chemical modification of existing polymers. It consists in using an extruder (single or twin-screw) as a continuous chemical reactor [1]. Besides the classical functions of a screw extruder (solid conveying, melting, mixing, pumping), additional functions are requested, such as the development and the control of a chemical reaction. Compared to a classical batch process in solution, reactive extrusion provides the following advantages [2]:
- ● the reaction is conducted in the melt, in absence of any kind of solvent;
- ● an extruder is able to work with very viscous products, which is not the case for batch reactors;
- ● processing conditions are much wider and flexible in an extruder (mixing conditions, high temperatures, modular geometry…).
However, some drawbacks are also to be mentioned:
- ● the main one is the residence time, which is very short in an extruder (of the order of a few minutes). Consequently, only fast reactions are possible in reactive extrusion, even if the temperature and concentration of reagents are very often more important in molten state than in solution;
- ● the cooling capacity of an extruder is limited and reactions with high exothermicity could be difficult to manage in reactive extrusion.
Among the existing extrusion systems, co-rotating twin-screw extruders are the most widely used in reactive extrusion, due to many advantages compared to the single screw machines:
- ● twin-screw extruders have a modular geometry, which allows one to adapt the screw profile to the reaction to be carried out. The profile can be divided into successive independent sections, with specific functions: feeding and melting of the polymer, injection of the reagents, mixing, reaction development, devolatilization, pumping and shaping;
- ● twin-screw extruders are starve fed. The fill ratio of the screws is only partial, that permits to easily introduce or remove different ingredients along the barrel, either in liquid or solid form;
- ● mixing capacities are more important in a twin-screw extruder, and the mixing conditions (distributive or dispersive) can be easily controlled according to the geometry of the kneading discs sections (number of discs, disc thickness, staggering angle).
1.2 Examples of industrial applications
As explained before, all the chemical modifications conducted in batch reactors cannot be transposed to reactive extrusion. However, a number of applications are already developed and used industrially:
- ● radical polymerization of styrene: polymerization is initiated in a pre-polymerizer (batch reactor) until reaction rates of 20–40%. Then, the prepolymerized system is introduced in an extruder to achieve the polymerization and to remove residual monomers [3]. Other polymers, like polyesters [4], polyamides [5] or polyacrylates [6] can also been produced by reactive extrusion;
- ● chemical modifications: the objective is to modify chemical or physico-chemical properties of existing polymers, without altering the other physical or mechanical properties. The most popular example is the grafting of maleic anhydride onto polypropylene [7]. Other modifications such as exchange reactions or modification of functional groups [8] can also be conducted in extruders. An example will be developed in Section 3;
- ● rheological modifications: the controlled degradation of polypropylene is used for many years for adjusting the molecular weight distribution of these resins, and thus their rheological properties. This is achieved by the use of peroxide initiators and will also be developed in Section 3;
- ● reactive blending: polymer blends have been largely studied during the last years to produce new materials with enhanced properties. As many polymers are incompatible, it is necessary to add a compatibilizer to obtain satisfactory properties. This compatibilizer can be created in situ, by an interfacial reaction conducted during the extrusion process [9];
- ● dynamic vulcanization: thermoplastic elastomers are obtained by the dispersion of a vulcanized elastomer in a thermoplastic matrix. Elastomer is the major phase and a phase inversion takes place during the vulcanization process. All these products are traditionally produced using reactive extrusion [10].
1.3 Interest and principles of reactive extrusion process modeling
As it can be seen from the previous examples, reactive extrusion is an important way to modify and develop new polymeric systems. However, it is a complex process, which involves many aspects, and the optimization of a such system addresses a lot of questions, due to the high number of operating variables and their interactions during the process [11]. For example, local flow conditions (residence time, temperature, mixing) will govern the reaction development, which will modify the material (viscosity change, exothermicity), leading to changes in flow conditions. Moreover, the geometry and the kinematics of a twin-screw extruder may be very complex, compared to a batch reactor. Consequently, it seems important to develop theoretical approaches, able to provide useful tools to define the best conditions for conducting an operation of reactive extrusion and to control the process. For that, different approaches may be developed, that we can roughly classify into two main categories: the approaches based on chemical engineering and those based on continuum mechanics.
The first ones consist in considering the twin-screw extruder as a series of ideal chemical reactors, generally continuous stirred-tank reactors (CSTR) and plug-flow reactors (PFR). According to its geometry, the screw profile is described by a certain number of these reactors, connected through direct flows and possible backflows. A global mass balance for each reactor allows defining a set of equations, whose resolution leads to an approximation of the flow conditions. Energy balances and kinetic equations are similarly written, which permit to calculate, in steady or unsteady conditions, the reactive extrusion process. Such models have been proposed by Ganzeveld et al. [12] for the polymerization of n-butylmethacrylate, Kim and White [13] for the transesterification of EVA copolymer, Michaeli et al. [14,15] for the polymerization of polystyrene and polyamide and, more recently, by Choulak et al. [16,17] for the polymerization of ε-caprolactone. These methods consider an oversimplification of the flow conditions, leading to rapid computations able to be used for process control applications. But they necessitate to adjust the parameters (principally the number and the type of chemical reactors) to each situation considered, before being able to calculate the process. In that sense, they cannot be used as predictive tools and are totally inefficient to solve scale-up problems.
The second approach is based on continuum mechanics. In this case, flow conditions are calculated by solving classical continuum mechanics equations (mass, momentum, energy balances), according to local geometry, kinematics and boundary conditions. As the calculation is based on the real conditions, and not on an ideal representation, it is theoretically not necessary to adjust parameters and these models can be totally predictive, as soon as the physical data are known. Consequently, they can be used not only to calculate a certain configuration, but also to optimize it and to predict what could happen when changing processing conditions or screw profile. These models are more flexible and accurate than the chemical engineering models, but they are also more time consuming and are generally inappropriate for direct process control.
In this paper, we will only focus on this last approach that we have chosen to develop in our laboratory. This way has also been followed by Kye and White [18] for the polymerization of ε-caprolactam, Kim and White [19] for the grafting of maleic anhydride onto polypropylene, Fukuoka [20] for the grafting of vinylsilane onto polyethylene and Zhu et al. [21,22] for the polymerization of ε-caprolactone.
2 Principles and challenges of the modeling based on continuum mechanics
To develop a theoretical model of reactive extrusion, different sub-models are necessary:
- ● a model for the description of the flow conditions in the complex geometry of a twin-screw extruder;
- ● a model for the description of the chemical reaction, as a function of local values of time, temperature, mixing conditions, concentration of reagents…;
- ● a model for the description of the physical and rheological changes induced in the material by the reaction development.
All these sub-models have then to be coupled in order to provide the desired results.
2.1 Twin-screw flow model
The first ingredient of a reactive extrusion model is a tool for computing the flow conditions along the twin-screw extruder. In such a machine, the geometry and the local flow conditions are complex: the flow is unsteady, non-isothermal and three-dimensional (3D). Of course, even if 3D simulations are now possible [23,24], simplifications are necessary to obtain a user-friendly software. It has been done a few years ago in our laboratory, to develop the Ludovic© model [25]. This commercialized software is based on a one-dimensional (1D) approach. It allows one to calculate the main thermomechanical parameters of the process (pressure, temperature, residence time, shear rate, filled ratio…), from the hopper to the die exit, including solid conveying, melting and melt conveying. It has obviously been validated through comparisons with more developed numerical simulations and with experiments [26]. As it is a 1D model, it only provides average local values of temperature and residence time. But we will see later on that it is largely sufficient for the prediction of the reaction extent along the screws.
2.2 Kinetic equations
A chemical reaction is usually described by one or many kinetic equations, controlled by kinetic constants. Balance equations written on the different chemical species generally allow one to define a conversion degree or a rate of advancement as a function of time and temperature. Depending on the complexity of the case, it can be obtained by calculating a simple analytical function or by solving a set of partial differential equations. In the last case, numerical resolutions are necessary at each step of the reaction development along the screws.
For this part, the most difficult is often to define accurately the different kinetic constants involved in the kinetic equations. We have shown that, in some cases, a small error in the values of such constants may induce large discrepancies in the simulation of the whole process [27].
2.3 Rheokinetic model
In some cases (for instance exchange reactions), the modifications induced by the reaction on the rheological behavior of the material are negligible. The properties of the unmodified polymer can then be used during all the process. In other cases (controlled degradation, polymerization), these changes are dominant. For example, in a polymerization process, the viscosity may increase from 10−3 Pa s (monomer) to 103 Pa s (polymer) between the hopper and the die exit. This is, obviously, to take into account. It is thus necessary to develop rheokinetic models, which will describe the change in the viscosity (and eventually other material parameters) as a function of the reaction extent. Examples will be provided in Section 3 concerning the controlled degradation of polypropylene and the polymerization of ε-caprolactone. In these cases, the kinetic equations allow one to calculate the average molecular weight and the viscosity law is described with parameters being functions of this molecular weight [28].
2.4 Coupling
Once the preceding models have been established, it is necessary to ensure the coupling existing between the different parameters: reaction develops according to the local values of temperature and residence time, this modifies the viscosity of the material, which in turn affects the local flow conditions. To handle with these complex couplings, the following procedure is adopted: a first simulation is performed without coupling, to define a first guess of fill ratio, residence times, temperatures and reaction extents. The viscosities are then defined according to these values. Then, a second simulation is started, coupling at each location flow conditions, reaction development and viscosity changes. Detailed information on this method can be found elsewhere [29]. A general scheme describing the principle of the computation is presented in Fig. 1.
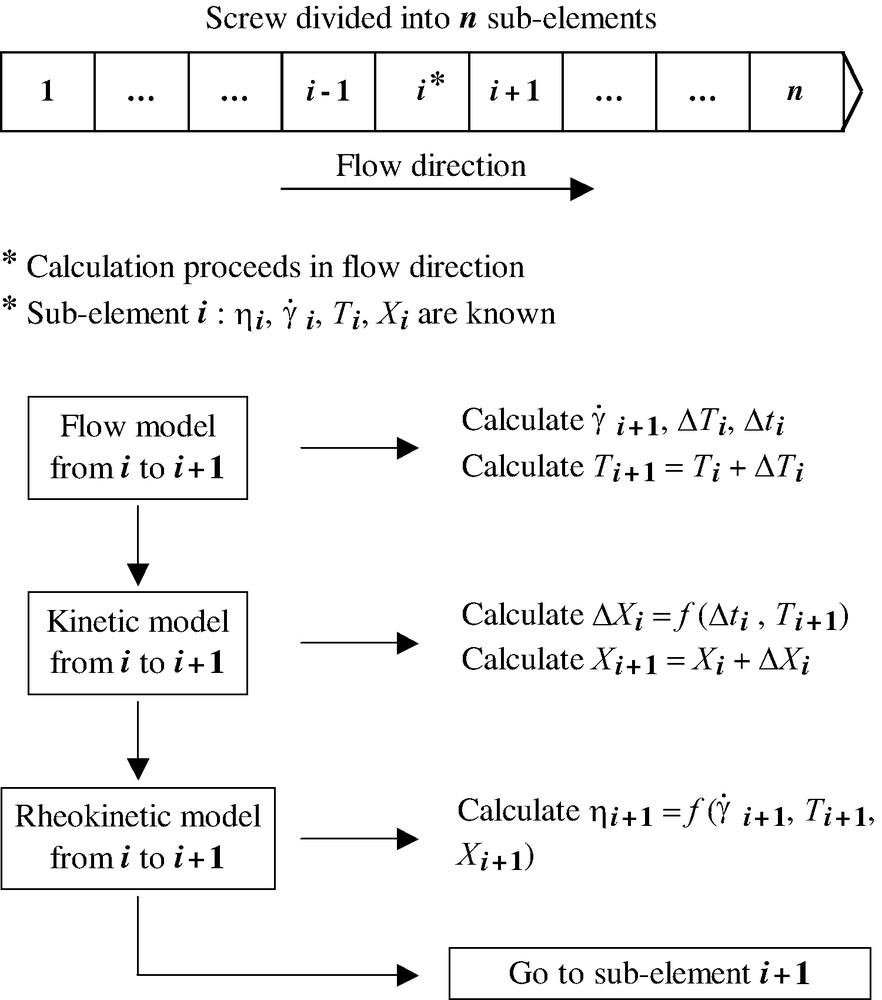
Scheme describing the principle of the computation.
2.5 Problems and challenges
As explained before, the simulation proposed is based on a number of approximations and assumptions. We will see in Section 3 that the results are often satisfactory, but important questions remain open to the discussion. They indicate the challenges that are to be faced to develop these models and also the resulting limitations of the actual simulations.
- ● Kinetic equations are generally established in static and isothermal conditions, very far away from the strong conditions encountered in the extruder. Are the values of kinetic constants measured in these conditions still valid for the extrusion simulation? How would it be possible to define accurate kinetics in real extrusion conditions?
- ● The reactive medium is assumed to be homogeneous in the model. The reagents are supposed to be instantaneously perfectly mixed with the molten polymer. It is clear that, in some cases, local mixing should be evaluated and introduced as a parameter in the kinetic equations to account for the heterogeneity of the real system. How could we handle heterogeneous systems? How can be considered the case of a low viscous phase dispersed in a very viscous medium?
- ● Degradation of reagents, side or parasitic reactions induced by the high temperatures are difficult to take into account, even if they play a role in the real process. They are generally neglected, as it is difficult to calculate many different reactions at the same time, having complex effects on the material;
- ● The examples presented hereafter concern chemical modifications of single-phase materials. In the case of reactive blends for example, a new difficulty arises from the morphology of the system. Depending on the flow and reaction conditions, the blend morphology (dispersed or co-continuous phase, dimensions of droplets or fibrils) will change during the process. It is thus necessary to take this change into account, which poses important problems for the modeling. If some models exist for calculating the morphological changes of a polymer blend along a twin-screw extruder [30], they are limited to the case of a minor phase dispersed in a matrix. The phase inversion, encountered for example during the dynamic vulcanization of thermoplastic elastomers, is far away to be modeled, as the corresponding changes in rheological behavior.
3 Examples of modeling
3.1 Esterification of EVA copolymer [29,31]
This first example concerns the modification by a transesterification reaction of an ethylene–vinyl acetate copolymer by an aliphatic primary alcohol (octanol-1). This reaction, catalyzed by an organometallic compound, leads to the substitution of vinyl acetate groups of EVA by hydroxyl groups of the alcohol. It is an equilibrated reaction, with a maximum of 65% conversion at the equilibrium, whose kinetics is well known and documented [32]. As no important changes are induced in the EVA structure, the reaction does not influence the viscosity and a rheokinetic model is not necessary in this case.
Fig. 2 shows the evolution along the screws of the local temperature, the cumulative residence time and the conversion rate, for the following conditions: EVA flow rate 10 kg/h, reagents (alcohol and catalyst) 2.35 kg/h, screw speed 150 rpm, barrel temperature 185 °C. The extruder is a Clextral BC45 (Firminy, France) with following characteristics: centerline distance 45 mm, screw diameter 50 mm, length 1200 mm. As shown in Fig. 2, the screw profile includes two left-handed elements and a block of kneading discs. Reagents are injected after the melting of the EVA, i.e. after the first left-handed element. We can see that the extent of the reaction follows the evolution of the residence time. It increases mainly in the filled sections of the extruder, i.e. in the second left-handed element and in the block of kneading discs. These zones are also characterized by a local increase in temperature, due to viscous dissipation, which accelerates the reaction.

Esterification of EVA copolymer; evolution along the screws of temperature, cumulative residence time and reaction extent.
In Fig. 3 is shown the influence of the screw speed (50, 100 and 150 rpm) for a total flow rate of 4 kg/h and a barrel temperature of 185 °C. An increase in rotation speed induces both a decrease in residence time and an increase in product temperature by viscous heating. Thus, the parameters controlling the reaction vary in opposite directions and it is consequently impossible to intuitively foresee the final influence on reaction extent. The model gives the answer: it can be seen in Fig. 3 that the reaction is more developed at a higher screw speed. It can be checked that it is effectively due to a higher product temperature all along the screws, leading to a higher reaction extent despite the shorter residence time. These results have been validated by comparison with experiments where the reaction extent was measured by infrared measurements. It can be seen in Fig. 3 that the agreement is pretty good, both at the die exit and along the screws. General validation has been made for various feed rates, barrel temperatures, stoichiometry and extruder size [31]. In all situations, this model, without any adjustable parameter, is very close to the reality.

Esterification of EVA copolymer; influence of screw speed on reaction extent at constant feed rate. Symbols represent experimental measurements by infrared spectroscopy (● 50 rpm; ○ 100 rpm; ◆ 150 rpm).
3.2 Controlled degradation of polypropylene [29,33,34]
As explained previously, peroxide-induced degradation is used to adjust the level of viscosity of polypropylene polymerized using Ziegler–Natta catalysis. The kinetic models describing the degradation are taken from the literature [35,36]. They include peroxide decomposition, hydrogen abstraction, β-scission, intermolecular chain transfer, thermal degradation and termination by disproportionation. They necessitate using an adjustable parameter, which is the efficiency of the peroxide f. It is the ratio of free radicals leading to β-scissions to the whole number of free radicals. The solution of the kinetic scheme, through a Runge–Kutta procedure, provides the values of the average molecular weights [36]. As the viscosity is directly linked to the molecular weight, we have conducted a specific study on the rheological behavior of these products [28]. We have shown that the viscosity can be described by a Carreau–Yasuda law, whose parameters are function of the weight average molecular weight.
Fig. 4 shows the influence of peroxide content on the evolution of the weight average molecular weight, for the following processing conditions: flow rate 10 kg/h, screw speed 225 rpm, barrel temperature 170 °C. The extruder is a Werner ZSK 30 (centerline distance 26 mm, screw diameter 30.85 mm, length 1160 mm). The peroxide is injected with a pump after the polypropylene melting. The symbols in Fig. 4 show the experimental molecular weights measured by size exclusion chromatography. We have adjusted the values of efficiency to obtain a good agreement with the simulation: f decreases from 0.95 to 0.45 when the peroxide content increases from 250 to 4000 ppm. These values are in agreement with the choices usually made in the literature [35,37]. Once this determination of f has been made, we assume in the following simulations that the efficiency is only a function of the peroxide content.

Controlled degradation of polypropylene; influence of peroxide content on average molecular weight. Symbols represent experimental measurements by size exclusion chromatography.
In Fig. 5, we show the influence of feed rate (2.5, 10 and 20 kg/h) at constant screw speed for a peroxide content of 1000 ppm. We observe that the degradation is more important at low feed rate. This is directly related to the increase in residence time [38]. The agreement with the experimental points at the die exit is fairly nice. It has also been checked that it remains valid for samples collected along the screws: it can be seen in Fig. 6, for two amounts of peroxide, that the strong decrease provided by the model after the injection of peroxide is also observed in the experiments [39]. The agreement when varying other parameters (screw speed, barrel temperature, screw profile, extrusion size) has also proven to be satisfactory [29,33,39].

Controlled degradation of polypropylene; influence of feed rate on average molecular weight at constant screw speed (● 2.5 kg/h; ○ 10 kg/h; ◆ 20 kg/h). Symbols represent experimental measurements by size exclusion chromatography.

Controlled degradation of polypropylene; evolution of weight average molecular weight along the screw profile. Comparison between computation and experimentation (2.3 kg/h; 75 rpm; 200 °C) for two levels of peroxide (● 0.05 phr; ○ 0.10 phr).
3.3 Polymerization of ε-caprolactone [27]
Polycaprolactone is a synthetic polymer, which is both biodegradable and biocompatible. It is mainly used in the medical domain for applications as artificial skin, resorbable prostheses and sustained release systems for drugs. It can be obtained from the polymerization of ε-caprolactone, initiated by organometallic compounds, such as metal alkoxides and carboxilates. In the present case, using tetrapropoxy-titanium as initiator, a two-step coordination–insertion process is assumed for the polymerization [40,41]. It consists in monomer coordination onto the initiator, followed by monomer insertion into the titanium–alcoxy bond. The polymer chain grows from the titanium atom by successive insertion of the monomer. This polymerization is living as long as the reactive sites are not destroyed.
In the extrusion process, the reactive system (monomer and initiator) is injected with a pump into the barrel, just before a block of kneading discs. Two other kneading blocks downstream allow mixing and homogenization of the polymerizing material.
The global kinetic equation was determined by Gimenez et al. [41,42]. They showed that the conversion rate is a function of time, temperature, partial order related to the initiator and ratio, where and are, respectively, the initial concentrations of monomer and initiator. From the conversion rate, the weight average molecular weight can be determined. Obviously, the polymerization reaction induces a huge variation in viscosity. Consequently, the definition of an evolutionary viscosity is necessary. Details can be found elsewhere [43]. To summarize, depending on the critical molecular weight of the polymer and the polymer concentration, two regimes are considered: under a critical mass, a Rouse regime is observed, with a Newtonian viscosity; above this critical mass, an entangled regime is observed, with a shear-thinning viscosity described by a Carreau–Yasuda law, whose parameters are function of molecular weight and concentration.
These different models have been introduced in Ludovic© software to calculate the change in monomer conversion along the screws. An example of results is shown in Fig. 7. It corresponds to the following processing conditions: feed rate = 4 kg/h, screw speed = 100 rpm, barrel temperature = 160 °C, = 1000. The extruder is a Leistritz LSM 30–34 (centerline distance 30 mm, screw diameter 34 mm, length 1200 mm). We observe that the polymerization starts at the injection point, with a very low viscosity (10−4 Pa s), and increases mainly in the blocks of kneading discs, because of the large residence times. The polymerization is achieved just before the die exit, where the viscosity reaches a value of 900 Pa s. In Fig. 8, for a lower barrel temperature (105 °C), we can see the influence of the feed rate at constant screw speed. In these conditions, the polymerization is only partial and is lower at high flow rate, because of the shorter residence time. The experimental measurements of conversion rate by 1H NMR (symbols in Fig. 8) confirm these results. This example has also been studied by Choulak et al. [16,17], who used a chemical engineering approach dedicated to process control.

Polymerization of ε-caprolactone; evolution along the screws of conversion rate and viscosity.
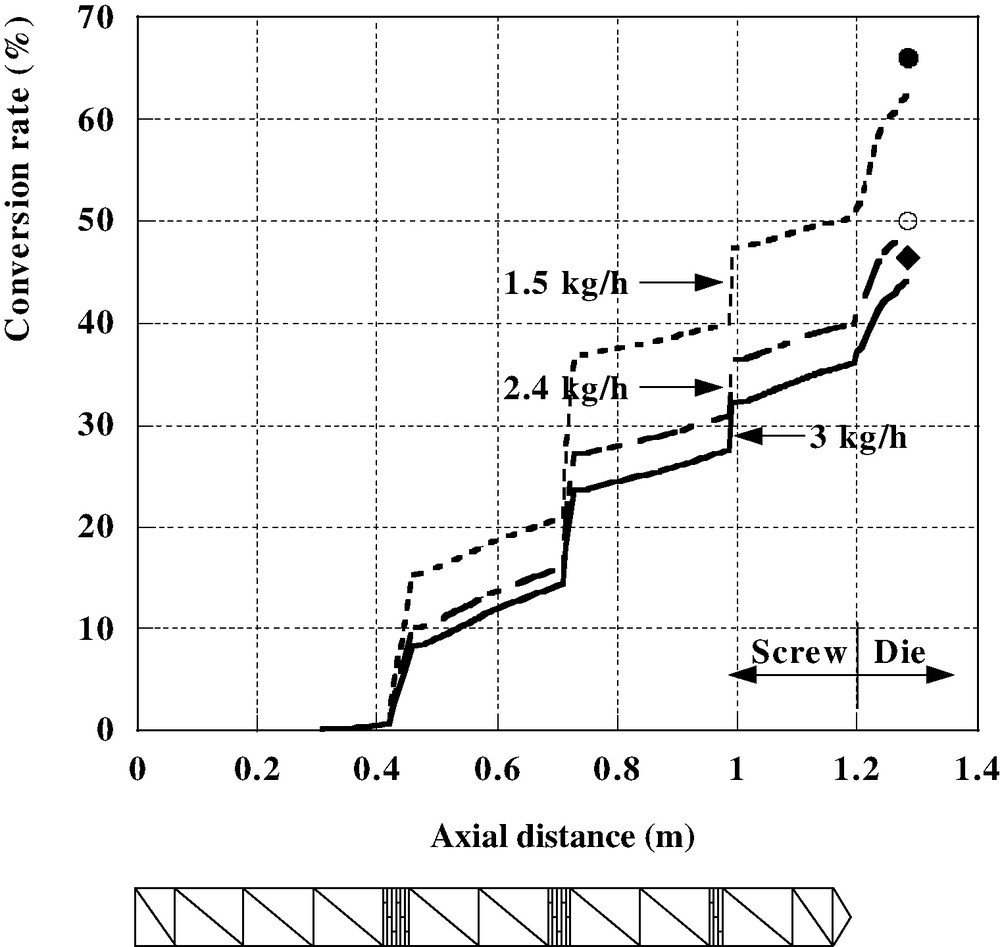
Polymerization of ε-caprolactone; influence of feed rate on conversion rate at constant screw speed (● 1.5 kg/h; ○ 2.4 kg/h; ◆ 3 kg/h). Symbols represent experimental measurements by 1H NMR.
3.4 Starch cationization [44,45]
The last example concerns the chemical modification of a natural polymer. Starch, issuing from natural and renewable resources, is more and more used for industrial applications, for example in packaging industry, instead of synthetic polymers. In papermaking industry, cationic starches can increase strength, filler and fines retention, and drainage rate of the pulp. They can also lower biological oxygen demand (BOD) of the white water when used as wet-end additives. Sizing agents based on cationic starches offer unique advantages due to their electrochemical attraction to cellulosic fibers. Moreover, because of the tenacity of the ionic bonding, these modified starches are not removed during repulping of broke. These cationic starches are produced from starch with reagents containing amino, ammonium, sulfonium, or phosphonium groups, which are able to carry a positive charge. Starch cationization consists in substituting the hydroxyl groups of the glycosyl units by one of these functional groups. The degree of substitution (DS) indicates the average number of sites per anhydroglucose unit on which there are substituent groups. Thus, if one hydroxyl on each of the anhydroglucose units has been cationized, DS is equal to 1. If all three hydroxyls have been cationized, DS is maximum and equal to 3. Cationic starches used in industry usually have DS in the range 0.02–0.10.
Usually, cationic starches are prepared using conventional batch reaction procedures. However, the cationization by chemical process in a batch reactor presents some drawbacks, like discontinuous process with low yield, residual reactive agent elimination, and environment pollution. Thus, to overcome these drawbacks, some tentative has been made to develop starch cationization using reactive extrusion process [46,47]. But, without modeling, it was until now difficult to define optimal conditions for industrial applications.
We started recently a systematic study of this reaction. We used a wheat starch and two reagents: 2,3-epoxypropyltrimethylammonium chloride (Quab 151®) and 3-chloro 2-hydroxypropyl-trimethylammonium (Quab 188®). Starch is plasticized with 40% water. It is fed at the screw start using the hopper, when water and reagent are injected downstream using a pump. The reaction of cationization involves two stages with the Quab 188®, the first stage for transforming the reagent (in alkaline medium) into an active epoxy form, and the second stage for operating the substitution on starch backbone. With the Quab 151®, being initially under epoxy form, the first stage is eliminated. As the reaction is an exchange reaction, it has no influence on starch viscosity [48]. Consequently, we will neglect this aspect. A kinetic study allowed defining an overall kinetic law, permitting to describe, for each reagent, the change in degree of substitution as a function of time and temperature [49]. After implementation in Ludovic© software, we were able to calculate the evolution of the degree of substitution along the screws.
Fig. 9 shows an example of results for a Clextral BC 21 extruder (centerline distance 21 mm, screw diameter 25 mm, length 900 mm) at 400 rpm and 80 °C. We observe that the reaction starts once the reagents have been injected. The increase in degree of substitution is important in the regions where the residence time is long (kneading discs or left-handed element). As seen in the experiments, an increase in feed rate tends to reduce the reaction extent. Moreover, it is clear that the injection of the reagents after the melting zone reduces the residence time and leads thus to a lower degree of substitution.

Starch cationization; variation of degree of substitution along the screws with feed rate at constant screw speed (targeted DS equal to 0.04).
Systematic comparisons have been made between experimental and computed reaction efficiencies. It can be seen in Fig. 10 that, whatever the reagent, its amount or the processing conditions (feed rate, screw speed, barrel temperature), the agreement is good on a wide range of values (efficiencies between 30% and 90%).

Starch cationization; comparison between computed and experimental efficiency (● Quab 151; ○ Quab 188).
4 Conclusion
We have shown in this paper that it is possible, using a continuum mechanics approach, to model with a good accuracy an operation of reactive extrusion. The various examples presented as illustrations (on different systems, different types of reaction and different machines) clearly show the versatility of the method. For that purpose, it is necessary to possess accurate kinetic data and, if requested, rheokinetic laws. Depending on the considered reaction, full predictive models without any adjustable parameter can be derived. They are very useful to understand the conditions of the process and to optimize it, for example by modifying screw profile and/or processing conditions. Optimization can be made simply by trial and error or, more efficiently, using specific optimization procedures, based for example on evolutionary algorithms [50,51]. Moreover, the difficult scale-up problems can be easily solved using such models. In other cases, adjustable parameters remain in the kinetic equations, which have to be estimated through experiments before any application. Nevertheless, even if these models may present some imperfections, they appear as efficient tools on such complex systems, compared to systematic trial and error procedures. Finally, besides these models, another approach is possible, based on classical chemical engineering analysis, which is less efficient for prediction and scale-up, but more appropriate for process control.


