On the structure and relative stability of uranyl(VI) sulfate complexes in solution

Valérie Vallet; Ingmar Grenthe

doi:10.1016/j.crci.2007.03.004

On the structure and relative stability of uranyl(VI) sulfate complexes in solution

Valérie Vallet ¹ ; Ingmar Grenthe ²

¹ Laboratoire PhLAM (CNRS UMR 8523), CERLA (CNRS FR 2416), Université des sciences et technologies de Lille-1, 59655 Villeneuve-d'Ascq cedex, France
² Department of Chemistry, Inorganic Chemistry, Royal Institute of Technology (KTH), Teknikringen 36, 10044 Stockholm, Sweden

Comptes Rendus. Chimie, Volume 10 (2007) no. 10-11, pp. 905-915.

Résumés

Anglais
Français

The mode of coordination, mono-, bidentate, sulfate in UO₂(SO₄) and UO₂(SO₄)₂²⁻, and the relative energy of the various isomers have been studied at the DFT and MP2 levels using DFT-optimized geometry in a CPCM solvent model. The U–S distances in the mono- and bidentate coordination, 3.63 and 3.08 Å, respectively, agree very well with experimental observations from solutions. The U–O_sulfate distance is significantly different in complexes with mono- and bidentate coordination, 2.23, vs. 2.37 Å, an observation difficult to deduce from the experimental studies. The experimental distance between uranium and the equatorial oxygen atoms, U–O_eq, is very close to the calculated average distance in a five-coordination model, but significantly longer in a six-coordination model, indicating a preference for the former; this finding is supported by energy calculations, where the five-coordinated isomers for the UO₂(SO₄) have the lowest Gibbs energy. For UO₂(SO₄)₂²⁻, the calculated Gibbs energy of reaction indicates that the six-coordinated isomer is slightly more stable than the five-coordinated one; however, the difference is small and less than the expected uncertainty in calculations of this type. Bidentate coordination of the sulfate group is always preferred over monodentate coordination. However, all differences in Gibbs energy between the different isomers is small, indicating that the mode of coordination may change with the composition of test solutions used, as observed experimentally. The U–O–S_mono angle is close to 143° in complexes with a monodentate sulfate group; this is traced to steric effects, which overcome the electronic preference for a linear U–O–S bond. This study demonstrates the significant increase in chemical information that may be obtained by combining experimental data on structures and thermodynamics with quantum chemical methods.

Supplementary Materials:
Supplementary material for this article is supplied as a separate file:

mmc1.pdf

Le mode de coordination, monodentate ou bidentate, de l'ion sulfate dans UO₂(SO₄) et UO₂(SO₄)₂²⁻ et la stabilité relative des différents isomères conformationels en phase aqueuse ont été étudiés par des calculs de chimie quantique au niveau DFT et MP2, utilisant des géométries optimisées au niveau DFT avec le modèle de solvant CPCM. Les distances U–S sont de 3,63 Å et 3,08 Å pour une coordination monodentate et bidentate, respectivement, et sont en très bon accord avec les mesures expérimentales en solution. La distance U–O_sulfate est sensiblement plus courte dans les complexes monodentés, 2,22 Å, que dans les complexes bidentés, 2,37 Å, une disparité qu'il est difficile de déduire des données expérimentales. La distance expérimentale entre l'uranium et les oxygènes coordinés dans le plan équatorial, U–O_eq, est très proche de la valeur calculée dans les isomères pentacoordinés, alors que cette distance est plus longue dans les modèles hexacoordinés, indiquant une préférence pour une coordinence 5. Cette observation est corroborée par les valeurs calculées des énergies libre relatives, qui indiquent que les isomères pentacoordinés ont l'énergie libre la plus basse pour le complexe UO₂(SO₄). Pour UO₂(SO₄)₂²⁻, l'énergie libre de réaction indique que l'isomère hexacoordiné est légèrement plus stable que celui pentacoordiné; cependant, la différence est, très faible et plus petite que l'incertitude des calculs de ce type. Nous observons aussi une préférence pour la coordination bidentate des ions sulfate dans les deux composés mono- et bisulfate. Or, l'énergie libre de réaction entre les différents isomères structuraux est faible, indiquant que le mode de coordination de l'ion sulfate peut changer avec la composition chimique de la solution ionique utilisée. Dans les complexes monodentés, l'angle U–O–S_mono est proche de 143°; ceci est attribué aux effets stériques qui dominent les effets d'interaction électronique tendant à rendre la liaison linéaire. Cette étude illustre comment l'analyse des données expérimentales concernant les structures et la thermodynamique, couplée aux calculs de chimie quantique, permet d'accroître la compréhension de la chimie des actinides en solution.

Compléments :
Des compléments sont fournis pour cet article dans le fichier séparé :

mmc1.pdf

Métadonnées

Reçu le : 2006-08-14
Accepté le : 2007-03-08
Publié le : 2007-05-02

DOI : 10.1016/j.crci.2007.03.004

Keywords: Structure, Bonding, Equilibria, Uranyl, Sulfate, Complexes, Quantum chemistry
Mots clés : Structure, Liaison, Équilibres chimiques, Uranyl, Sulfate, Complexes, Chimie quantique

Affiliations des auteurs :

Valérie Vallet ¹ ; Ingmar Grenthe ²

¹ Laboratoire PhLAM (CNRS UMR 8523), CERLA (CNRS FR 2416), Université des sciences et technologies de Lille-1, 59655 Villeneuve-d'Ascq cedex, France
² Department of Chemistry, Inorganic Chemistry, Royal Institute of Technology (KTH), Teknikringen 36, 10044 Stockholm, Sweden

@article{CRCHIM_2007__10_10-11_905_0,
     author = {Val\'erie Vallet and Ingmar Grenthe},
     title = {On the structure and relative stability of {uranyl(VI)} sulfate complexes in solution},
     journal = {Comptes Rendus. Chimie},
     pages = {905--915},
     publisher = {Elsevier},
     volume = {10},
     number = {10-11},
     year = {2007},
     doi = {10.1016/j.crci.2007.03.004},
     language = {en},
}

TY  - JOUR
AU  - Valérie Vallet
AU  - Ingmar Grenthe
TI  - On the structure and relative stability of uranyl(VI) sulfate complexes in solution
JO  - Comptes Rendus. Chimie
PY  - 2007
SP  - 905
EP  - 915
VL  - 10
IS  - 10-11
PB  - Elsevier
DO  - 10.1016/j.crci.2007.03.004
LA  - en
ID  - CRCHIM_2007__10_10-11_905_0
ER  -

%0 Journal Article
%A Valérie Vallet
%A Ingmar Grenthe
%T On the structure and relative stability of uranyl(VI) sulfate complexes in solution
%J Comptes Rendus. Chimie
%D 2007
%P 905-915
%V 10
%N 10-11
%I Elsevier
%R 10.1016/j.crci.2007.03.004
%G en
%F CRCHIM_2007__10_10-11_905_0

Valérie Vallet; Ingmar Grenthe. On the structure and relative stability of uranyl(VI) sulfate complexes in solution. Comptes Rendus. Chimie, Volume 10 (2007) no. 10-11, pp. 905-915. doi : 10.1016/j.crci.2007.03.004. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2007.03.004/

Version originale du texte intégral

1 Introduction

Quantitative information on chemical equilibria and the thermodynamics of actinide complex formation in aqueous solution is, in addition to its pure scientific interest, also important in many applications, such as separation technology and speciation in ground and surface water systems. Solution thermodynamic data provide information on the stoichiometry of the complexes formed, but little or no information on the structure of the first coordination sphere, i.e. the mode of coordination of ligands and the possible formation of isomers of various types. There is extensive information [1] on the chemical thermodynamics of actinide complex formation reactions, including the following uranyl(VI) sulfate reactions that will be discussed in this communication:

UO₂²⁺ + SO₄²⁻ ⇌ UO₂(SO₄)

(1)

UO₂²⁺ + 2SO₄²⁻ ⇌ UO₂(SO₄)₂²⁻

(2)

We will use experimental and quantum chemical data to provide information on the mode of coordination of the sulfate ion and the number of coordinated water molecules in the uranyl(VI) sulfate complexes formed in reactions (1) and (2).

Single-crystal X-ray structures of a number of uranyl(VI) sulfate compounds reveal that the sulfate ion can be coordinated both in bidentate [2] and monodentate [3] fashion, but with predominance of the latter type. A characteristic feature of the bond distances in solid compounds that contain both mono- and bidentate sulfate coordination is that the U–O_sulfate bond distance is about 0.15 Å shorter in the former than in the latter. Structure studies of uranyl(VI) sulfate complexes in solution have been made by Moll et al. using EXAFS [4] and by Neuefeind et al. using large-angle X-ray diffraction (LAXS) [5]. Both methods provide accurate information on bond distances, but much less precise information on coordination numbers. These two studies demonstrate that the sulfate ion also in solution can be coordinated both in a monodentate [5] and bidentate fashion [4]. The solution structure determinations are complicated by the fact that the test solutions may contain a mixture of different uranyl species, as will be discussed in the following.

The equilibrium constants for the formation of uranyl(VI) sulfate complexes are moderately large at zero ionic strength, log β⁰₁ = 3.15 and log β⁰₂ = 4.14, respectively [1] for the reactions (1) and (2). These equilibrium constants decrease substantially with increasing ionic strength [1], cf. Appendix, and from their magnitude it is not possible to make a reliable prediction of the mode of coordination of sulfate and the number of donor atoms in the equatorial plane of the UO₂²⁺ ion. We have therefore used quantum chemical methods to determine the structure and bond distances in various isomers of UO₂(SO₄) and UO₂(SO₄)₂²⁻ and their relative electronic and Gibbs energies of formation. The bond distances can be directly compared with experimental data, while the relative energies are used to corroborate the conclusions drawn from the bond distances.

The quantum chemical calculations refer to a model where the complexes are dissolved in a model solvent where the water is described by a conductor-like polarizable continuum model (CPCM) with the macroscopic dielectric constant of water [6]. This differs in two ways from the experimental situation: hydrogen bonding is treated in a simple way and interactions between the dissolved complexes and the counter ions, Na⁺ in most experimental test solutions, are not taken into account, i.e. the calculation refers to a medium with zero ionic strength. For this reason we have tested how sensitive the geometry and the relative energy of the complexes are for different model assumptions.

The M–O–S bond angle in most solid-state structures of metal sulfates differs significantly from 180°, the configuration that is expected to minimize electrostatic repulsion. To rationalize this observation, we have probed the interaction between the uranyl unit and a unidentate sulfate group through the energy decomposition scheme [7] in ADF [8,9] (see Section 2.1) to determine whether the angular preference is driven by electronic or steric effects.

2 Quantum chemical calculations and results

2.1 Computational details

The small-core relativistic effective core potential of the Stuttgart–Bonn group was employed for uranium [10], along with the segmented (14s13p10d8f6g)/[10s9p5d4f3g] basis set [11]. The valence triple-ζ plus polarization basis sets were used for sulfur [12a], oxygen [12b], and hydrogen [12b] atoms. The correlation-consistent double-ζ plus polarization basis set (cc-pVDZ) from Woon et al. [13] was used for the sodium counterion. The structures of the various isomers of UO₂(SO₄) and UO₂(SO₄)₂²⁻ species were optimized with the gradient-corrected hybrid functional B3PW91 [14], as this is known to result in geometries that are close to the experimental values. Single-point MP2 calculations were also performed at the DFT-optimized geometries, with the 1s core orbitals of oxygen, the 1s, 2s, and 2p orbitals of sulfur and 5s, 5p, 5d orbitals of uranium frozen. Thermochemical corrections to the electronic energies to obtain free energies were computed using the geometries and vibrational partition functions computed at the DFT level for a temperature of 25 °C and a pressure of 1 atm. Solvent effects on geometries, partition functions and energies were accounted for through the use of the conductor-like polarizable continuum model (CPCM) [6], with the United Atom Kohn Sham (UAKS) formula for the atomic radii [15]. All calculations were performed with the Gaussian 03 package [16].

2.2 Comment on the energy calculations

There is no significant difference in electronic energy of reaction calculated at the DFT and MP2 levels (Table 2) for reactions that do not involve a change in coordination number. This is not the case for reactions where the coordination number changes from 5 to 6, in which the DFT values are 10–20 kJ/mol higher than the MP2 values. The reason for this is known and related to the known tendency of current exchange correlation functions to underestimate the stability of high coordination numbers. These errors may compensate when comparing two isomers that differ by the number of bound water molecules and the mode of coordination of the sulfate group. Further details have been discussed by Rotzinger [17] for transition metals and by Wåhlin et al. [18] in the context of the uranyl aqua ion. It is thus important to compare DFT-based numbers for energetics to those obtained with wave-function-based correlated methods, such as MP2. The difference between the electronic and Gibbs energy of reaction is strongly dependent on the contribution of low-frequency vibration modes originating from shallow potential wells. In some cases it was not possible to obtain structures with only real frequencies; in other cases, such as [UO₂(SO_4-chelate)₂(OH₂)₂]·(H₂O), the difference between the electronic and Gibbs energy of reaction was fairly large, around 10 kJ/mol. We conclude that the calculated free energy of reaction may have an uncertainty of about the same magnitude.

Chemical model	N^a	DFT-B3PW91	MP2
ΔE	ΔG⁰	ΔE	ΔG⁰
[UO₂(SO₄-chelate)(OH₂)₃],(H₂O)	5	0.0	0.0	0.0	0.0
UO₂(SO₄-mono)(OH₂)₄	5	12.3	13.0	16.3	17.0
[UO₂(SO₄-chelate)(OH₂)₄]	6	22.2	32.4	12.0	22.2
[UO₂(SO₄-chelate)(OH₂)₃],(H₂O),Na⁺	5	0.0	–^b	0.0	–^b
[UO₂(SO₄-mono)(OH₂)₄],Na⁺	5	12.5	–^b	10.3	–^b
[UO₂(SO₄-chelate)₂(OH₂)₂]²⁻,(H₂O)	6	0.0	0.0	0.0	0.0
[UO₂(SO₄-chelate)₂(OH₂)]²⁻,(H₂O)₂	5	12.7	−9.0	26.4	4.7
[UO₂(SO₄-mono)₂(OH₂)₃]²⁻	5	−3.0	−3.1	17.8	17.7
[UO₂(SO₄-chelate)(SO₄-mono)(OH₂)₂]²⁻,(H₂O)	5	−0.3	–^b	18.7	–^b
[UO₂(SO₄-chelate)(SO₄-mono)(OH₂)₃]²⁻	6	21.5	26.5	28.9	33.9

^a N is the coordination number of uranyl(VI).

^b The computation of the thermal contributions was not possible because of spurious imaginary frequencies obtained with the CPCM solvent model.

2.3 Details of the energy decomposition calculations

To analyze the interaction between uranyl and monodentate sulfate groups, we have computed the total interaction energy between the uranyl fragment and one monodentate sulfate group, using the energy decomposition scheme [7] implemented in the Amsterdam density functional (ADF) package [8,9]. For these calculations, we considered a simplified molecular system involving the uranyl unit and one monodentate sulfate group, without additional water molecules in the first coordination sphere. All-electron calculations were performed using the scalar relativistic zero-order regular approximation (ZORA) – DFT method [19] with the hybrid B3LYP functional [20]. All atoms were described with the uncontracted triplet-ζ Slater-type orbital (STO) augmented by two polarization functions (TZ2P) [21]. The various contributions to the total interaction energy are given in Table S3. The geometry was optimized at the B3LYP level without symmetry constraints. We then explored the evolution of the total bonding energy between the uranyl and the monosulfate groups for various U–O–S bending angles ranging from 120° to 180°, with steps of 10°.

2.4 Quantum chemical results

The bond distances for the various isomers of the uranyl monosulfate and uranyl bis-sulfate complexes calculated at the DFT-B3PW91 level in the CPCM solvent are given in Table 1. The total energy and coordinates of the different complexes are given as supporting data, Tables S1 and S2. The only other theoretical data available is that of Craw et al. [22]. They optimized the structure of uranyl monosulfate at the Hartree–Fock level, assuming a bidentate coordination and imposing C_2v symmetry on the structure. They did not consider the lower-symmetry monodentate isomer, certainly because of lack of computational capacity at that time. Our calculated equatorial distances are generally shorter, by 0.20 Å, than those obtained by Craw et al. This is a result of relaxing the symmetry constrains and of the effect of electron correlation and solvent effects, as discussed for other uranyl structures by Wahlgren et al. and Vallet et al. [23]. In the experimental test solutions, there are counterions present (Na⁺ or H⁺), and we therefore explored if the Na⁺ counterions present in the test solutions might influence the quantum mechanical (QM) bond distances in the mono- and bidentate isomers; we found no significant changes. It is noteworthy that it was not possible to optimize the structure of the monodentate isomer in gas phase because of proton abstraction of one non-coordinated oxygen atom in the sulfate from a neighboring coordinated water molecule.

Chemical model	N^a	U–O_yl	U–O_wat	U–O_chel	U–O_mono	U–O_aver	U–S_chel	U–S_mono
[UO₂(OH₂)₅]²⁺·(H₂O)	5	1.746	2.43(1)	–	–	2.43(1)	–	–
EXAFS Ref. [23]	5	1.77	2.41	–	–	–	–	–
UO₂(SO₄-mono)(OH₂)₄	5	1.759	2.48(3)	–	2.22	2.43(8)	–	3.61
[UO₂(SO₄-mono)(OH₂)₄]·Na⁺	5	1.758	2.46(1)	–	2.25	2.42(7)	–	3.64
[UO₂(SO₄-chel)(OH₂)₃]·(H₂O)	5	1.765	2.46(3)	2.37(2)	–	2.42(4)	3.08	–
[UO₂(SO₄-chel)(OH₂)₃]·(H₂O),Na⁺	5	1.760	2.43(2)	2.39	–	2.42(3)	3.07	–
[UO₂(SO₄-chel)(OH₂)₄]	6	1.760	2.52(3)	2.41	–	2.51(6)	3.13	–
[UO₂(SO₄-chel)(OH₂)₃]^b	5	1.74	2.64	2.562	–	–	3.08	–
EXAFS Ref. [4]	5	1.78	–	–	–	2.42	3.12	–
[UO₂(SO₄-mono)₂(OH₂)₃]²⁻	5	1.769	2.49(3)	–	2.29	2.4(1)	–	3.67
[UO₂(SO₄-chel)(SO₄-mono)(OH₂)₂]²⁻·(H₂O)	5	1.769	2.46(1)	2.42(1)	2.27	2.41(6)	3.11	3.67
[UO₂(SO₄-chel)(SO₄-mono)(OH₂)₃]²⁻	6	1.765	2.58(9)	2.47(1)	2.38	2.49(7)	3.17	3.74
[UO₂(SO₄-chel)₂(H₂O)]²⁻·(OH₂)₂	5	1.768	2.43	2.40(1)	–	2.41(1)	3.09	–
[UO₂(SO₄-chel)₂(H₂O)₂]²⁻·(OH₂)	6	1.769	2.54	2.46(1)	–	2.49(3)	3.16(1)	–

^a N is the coordination number of uranyl(VI).

^b From Ref. [22]: structure optimized at the Hartree–Fock level in gas phase.

2.4.1 Five-coordinated UO₂(SO₄) and UO₂(SO₄)₂²⁻

Two different isomers, [UO₂(SO_4-mono)(OH₂)₄] and [UO₂(SO_4-chel)(OH₂)₃] (cf. Fig. 1) were identified for UO₂(SO₄). The U–S distances are 3.61 and 3.08 Å, respectively, the corresponding U–O_sulfate distances 2.22 and 2.37(2) Å are also significantly different. The average U–OH₂ distances in the two isomers are 2.48(3) and 2.46(3) Å, slightly longer than the experimental EXAFS distance, 2.43(1) Å in UO₂(OH₂)₅²⁺ [23a]. The negative Gibbs energy of reaction, ΔG⁰ = −17.0 kJ/mol (cf. Table 2) for:

UO₂(SO_4-mono)(OH₂)₄ → [UO₂(SO_4-chel)(OH₂)₃]

(3)

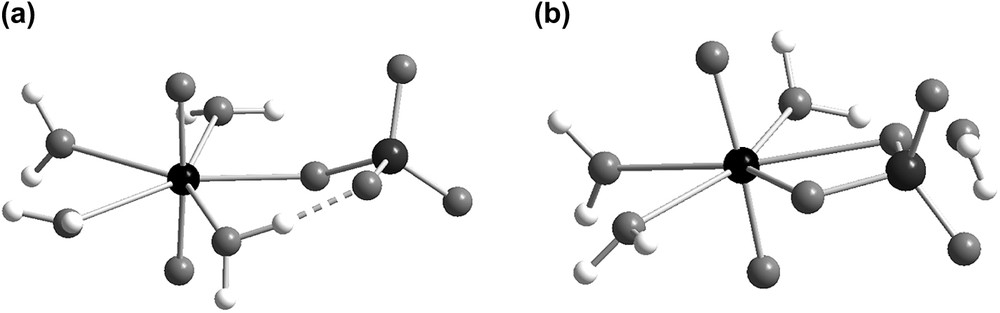
indicates that the complex with chelate bonded sulfate is the most stable isomer.

Fig. 1
The structure of the two five-coordinated isomers of UO₂(SO₄): (a) [UO₂(SO_4-mono)(OH₂)₄] and (b) [UO₂(SO_4-chelate)(OH₂)₃],(H₂O) based on DFT geometry optimizations in the CPCM solvent. The dashed line indicates a hydrogen bond where the distance H_water–O_sulfate is about 1.60 Å and the angle O_water–H–O_sulfate is 168°; the water outside the first coordination sphere in UO₂(SO_4-chelate) forms only very weak hydrogen bonds.

There are three five-coordinated isomers of UO₂(SO₄)₂²⁻, [UO₂(SO_4-mono)₂(OH₂)₃]²⁻, [UO₂(SO_4-chel)₂(OH₂)]²⁻·(H₂O)₂ and [UO₂(SO_4-mono)(SO_4-chel)(OH₂)₂]²⁻·(H₂O), cf. Fig. 2. The U–S distances in the mono- and bidentate sulfate groups are close to those in the UO₂(SO₄) isomers and the same is true for the U–O distances. The quantum chemical bond distances for the isomer [UO₂(SO_4-chel)₂(OH₂)]²⁻·(H₂O)₂ are in good agreement with the experimental EXAFS data [4], indicating that this is the stable isomer. The calculated Gibbs energy of reaction for reaction (4):

[UO₂(SO_4-chel)₂(OH₂)]²⁻·(H₂O)₂ → [UO₂(SO_4-mono)₂(OH₂)]₃²⁻

(4)

is 13 kJ/mol, indicating that the chelate bonded isomer is the most stable one. However, the electronic energy of reaction indicates the reverse as ΔE (MP2) is −8.6 kJ/mol; caution is therefore necessary when using the electronic energy to estimate the relative stability of isomers.

[UO₂(SO_4-chel)₂(OH₂)]²⁻·(H₂O)₂ → [UO₂(SO_4-chel)(SO_4-mono)(OH₂)₂]²⁻·(H₂O)

(5)

It was not possible to calculate the Gibbs energy of reaction for reaction (5) because of the appearance of imaginary frequencies, but as this complex contains two different U–S distances that are not evident in the experimental EXAFS data, we conclude that also this isomer is less stable than [UO₂(SO_4-mono)(SO_4-chel)(OH₂)₂]²⁻·(H₂O).

Fig. 2
The structures of the three different five-coordinated isomers of UO₂(SO₄)₂²⁻: (a) [UO₂(SO_4-mono)₂(OH₂)₃]⁻², (b) [UO₂(SO_4-chelate)₂(OH₂)²⁻]·(H₂O)₂ and (c) [UO₂(SO_4-mono)(SO_4-chelate)(OH₂)₂(H₂O)²⁻]·(H₂O), based on DFT geometry optimizations in the CPCM solvent. The dashed line indicates a hydrogen bond where the distances H_water–O_monosulfate and H_water–O_chel-sulfate are about 1.60, 1.94 Å in structures (a), (b) and (c), respectively. The angles O_water–H–O_monosulfate and O_water–H–O_chel-sulfate are 168° and 177°, respectively.

2.4.2 Six-coordinated UO₂(SO₄) and UO₂(SO₄)₂²⁻

There is only one stable six-coordinated isomer of UO₂(SO₄), [UO₂(SO_4-chel)(OH₂)₄], cf. Fig. S1a; all bond distances are longer than in the corresponding five-coordinated isomer, the U–S distance is 3.13 Å, the U–O_chel, 2.41 Å and the U–OH₂ 2.52(3) Å. The average U–O distance in the first coordination sphere is 2.51(6) Å, larger than the value for the five-coordinated isomer, 2.42 Å, which is in good agreement with the experimental EXAFS distance, 2.40–2.44 Å [4].

There are two stable six-coordinated isomers of UO₂(SO₄)₂²⁻, [UO₂(SO_4-chel)₂(OH₂)₂]²⁻·(H₂O) and [UO₂(SO_4-chel)(SO_4-mono)(OH₂)₃]²⁻, cf. Fig. S1b,c. All bond distances in these isomers are significantly longer than in the corresponding five-coordinated isomers and neither of these structures is consistent with the experimental EXAFS data. The positive Gibbs energy for reaction:

[UO₂(SO_4-chel)₂(OH₂)₂]²⁻·(H₂O) → [UO₂(SO_4-chel)(SO_4-mono)(OH₂)₃]²⁻, ΔG⁰ = 33.9 kJ/mol,

at the MP2 level, indicates that the isomer [UO₂(SO_4-chel)₂(OH₂)₂]²⁻·(H₂O) is the most stable one and confirms that bidentate sulfate coordination is preferred in six-coordinated isomers.

2.4.3 The relative stability of five- and six-coordinated isomers

Five-coordination is preferred for the UO₂SO₄ isomer as indicated by the negative Gibbs energy of reaction for:

[UO₂(SO_4-chel)(OH₂)₄] → [UO₂(SO_4-chel)(OH₂)₃]·(H₂O), ΔG⁰ = −22.2 kJ/mol

(6)

For UO₂(SO₄)₂²⁻, the Gibbs energy of reaction for reaction (7), ΔG⁰(MP2) = 4.7 kJ/mol, indicates that the six-coordinated isomer is more stable. However, the free-energy change is small and we can see no chemical reason why six-coordination should be preferred in UO₂(SO₄)₂²⁻ when this is not the case in UO₂(SO₄). In addition the EXAFS data are in better agreement with the five-coordinated model.

[UO₂(SO_4-chel)₂(OH₂)₂]²⁻·(H₂O) → [UO₂(SO_4-chel)₂(OH₂)]²⁻·(H₂O)₂

(7)

We have made several test of models where additional water molecules have been added to the second coordination sphere, but all of them indicate a small preference for six-coordination.

3 Discussion

The interpretation of experimental EXAFS and LAXS data rests both on assumptions of the chemical composition of the tests solutions and on the physical models used. The chemical composition of the test solutions, that is the stoichiometric concentrations of the various species present, can be estimated from published equilibrium constants. There is extensive information in the literature on the equilibrium constants formed in the uranyl(VI) sulfate system [1] and the species UO₂(SO₄) and UO₂(SO₄)₂²⁻ are well established. The formation of UO₂(SO₄)₃⁴⁻ has been suggested by Ahrland [24], but this proposal has not been accepted in the reviews [1a,1b]. The equilibrium constants for the complex formation reactions depend on the ionic strength and the ionic medium composition, as described in the reviews by Grenthe et al. [1a,25] and Guillaumont et al. [1b]. For the reactions:

UO₂²⁺ + HSO₄⁻ ⇌ UO₂(SO₄) + H⁺

(8)

UO₂²⁺ + 2HSO₄⁻ ⇌ UO₂(SO₄)₂²⁻ + 2H⁺

(9)

in sulfuric acid solutions, the ionic strength/ionic medium variation of the equilibrium constant can be described using the specific ion interaction theory (SIT) as described in the Appendix and Ref. [25]. The relationship between log K⁰ and the log K^I, the equilibrium constants at ionic strengths zero and I, is particularly simple in test solutions where sulfuric acid is the predominant component because here

m_{H^{+}}

≈

m_{{HSO}_{4}}

, resulting in the cancellation of interaction terms, cf. Appendix. We have used this method to re-evaluate the speciation in the EXAFS test solutions used by Moll et al. [4] and find, in agreement with them, that only a minor amount of UO₂²⁺(aq) is present in their test solution A (1.00 M H₂SO₄). However, they have underestimated the amount of UO₂(SO₄)₂²⁻, cf. Appendix. The sulfate concentration in test solutions B (10.0 M H₂SO₄) and C (2.00 M NaClO₄, 0.50 M Na₂SO₄, pH 2.00) is higher than in test solution A and accordingly the relative amount of UO₂(SO₄)₂²⁻ is higher, as suggested by Moll et al. The SIT expression is not accurate in test solutions with ionic strengths larger than 3–4m. It is also difficult to use in uranyl sulfate test solutions that contain other ionic species in high concentrations because of the many ionic interactions that have to be taken into account. The total concentration of uranium in the test solutions used by Neuefeind et al. [5] is so high that the SIT method is inaccurate. However, from the total concentrations of uranium and sulfate in their test solutions, it seems quite clear that the predominant complex is UO₂(SO₄)(aq).

The most straightforward experimental method to determine if sulfate is coordinated through one or two oxygen donors is to determine the U–S distance and this method has been used both by Moll et al. [4] and Neuefeind et al. [5]. Moll et al. find a U–S distance of 3.12 Å in test solutions A, B, and C, indicating that the sulfate is bidentate coordinated in all sulfate complexes present. The number of U–S distances in test solution C is close to 2, confirming the predominance of UO₂(SO₄)₂²⁻. Ahrland [24] has suggested that the complex UO₂(SO₄)₃⁴⁻ is formed at high sulfate concentrations:

UO₂(SO₄)₂²⁻ + SO₄²⁻⇌UO₂(SO₄)₃⁴⁻

(10)

As the stepwise equilibrium constant for the reaction (9) is small, K(9) ≈ 6 M⁻¹, it seems unlikely that a third sulfate ligand forms a chelate; if this complex is formed one would expect to see a second U–S distance for monodentate coordination at about 3.7 Å. There is no such evidence and we conclude that complexes with a maximum of two chelating sulfate groups are formed in the test solutions in accordance with the evaluation made by Grenthe et al. [1a].

Neuefeind et al. [5] used LAXS data from two test solutions containing the same concentration of uranyl(VI), the first without and the second with sulfate present. In this way they could to a large extent eliminate the contributions of the solvent in the difference radial distribution functions, allowing a clear identification of the U–S distance and the difference in the average U–O distances in the two complexes. They find a U–S distance of 3.67 Å, in excellent agreement with the QM value, 3.64 Å, for a complex with monodentate sulfate coordination. In both studies [4,5] there is no evidence of a mixture of mono- and bidentate coordination; however, the experimental method is not sensitive enough to detect small amounts of the two isomers.

In the EXAFS study of Moll et al. [4], only one U–O_eq distance, 2.42 (2) Å, was found for test solutions A, B and C; O_eq denotes the oxygen atoms in the equatorial plane of the uranyl sulfate complex(es). This distance is equal to the average U–O_eq distance, 2.42 Å in the five-coordinated complexes obtained using QM, but significantly shorter than the corresponding average distance, 2.51 Å, computed for the six-coordinated complexes. The average U–OH₂ distance in the five-coordinated complexes, 2.46 Å, is somewhat longer than in aqua ion UO₂(OH₂)₅²⁺, 2.43 Å, obtained in this study using the B3PW91 functional and 2.41 Å, obtained from the experimental EXAFS data [23].

The average difference between the U–O distances in the equatorial plane of UO₂²⁺(aq) ≡ UO₂(OH₂)₅²⁺ and in the sulfate test solutions used by Neuefeind et al. [5] is 0.017 Å. This value is very close to the difference between the average U–O distances in [UO₂(OH₂)₅]²⁺·(H₂O) and [UO₂(SO₄)(H₂O)₄]·(H₂O), 0.008 Å, obtained using the QM optimized structures in the PCM solvent (see Table 1) where systematic errors in the distances will cancel to a large extent. It is not clear to us if the difference method used by Neuefeind et al. is precise enough to identify individual variations in the bond distances, in particular the appearance of one shorter U–O distance in the presence of four longer ones in the uranyl(VI) sulfate solution. The quantum chemical results show a significantly shorter U–O distance, 2.22 Å, in the monodentate sulfate isomer than in the chelate, 2.37 Å, for UO₂(SO₄). The trend is the same in the various isomers of UO₂(SO₄)₂²⁻ and we find it unlikely that this difference is a computational artifact. In this context it is worth noticing that the U–O_mono distance is significantly shorter, about 0.15 Å, than the U–O_chel distance in KNa₅(UO₂)(SO₄)₄·H₂O [3a] and in K₄(UO₂)(SO₄)₃ [3b], which contain both mono- and bidentate coordination.

Both the average U–O_eq distances and the Gibbs energy of reaction suggest that the uranyl(VI) moiety has five donor atoms in the equatorial plane; this is consistent with the fact that there are no known crystal structures in the uranyl(VI) sulfate system with six-coordination [26].

The U–O_sulfate–S angle is 141.5° and 143° in [UO₂(SO₄-mono)(OH₂)₄] and [UO₂(SO₄-mono)₂(OH₂)₃], respectively. These values agree with that obtained by Neuefeind et al. [5], and is in the range of the values, 139° to 146°, with a grand average of 143°, found in crystal structures. Neuefeind et al. [5] suggested that the bent angle might be either an intrinsic property of uranyl–sulfate bonding, or due to hydrogen bond interactions. A screening of structure of crystals with unidentate sulfate and transition metal ions or alkali ions indicate that the M–O–S angle is always bent, around 130° or slightly larger; this property does not seem to be specific for the bonding to uranium. To rationalize this observation, we have probed the interaction between the uranyl unit and a unidentate sulfate group through the energy decomposition scheme [7] in ADF [8,9] (see Section 2.1) to determine whether the angular preference is driven by electronic or steric effects. The total bonding energy (E_B) between the two fragments (the uranyl moiety and the sulfate group) was calculated for various bending angles ranging from 120° to 180° with steps of 10°. It is decomposed into a steric component (sum of the electrostatic and Pauli terms) and an electronic component (so-called orbital interaction). Fig. 3 shows the variation of the various contributions with the U–O–S angle. To facilitate the comparison, we have assigned the binding energy 0 kJ/mol at 180° to each of the contributions and calculated the energy at other angles relative to that reference. From the shape of the curve of the orbital interaction (electronic) component, it is clear that there is an electronic preference for linearity. However, steric interactions favor the bent structure, because the classical electrostatic interaction offsets the unfavorable Pauli repulsion upon bending. A plot of the total interaction energy indicates that there is an energy minimum around 125° and that the energy gain upon bending is about 16 kJ/mol. The bond angle is smaller than observed experimentally, but this might very well be due to the fact that the calculations were made using a model without water in the first coordination sphere. The key point is that the “driving force” for a bent U–O–S angle is the steric interaction energy, which overcomes the electronic preference for a linear U–O–S angle. Such steric interactions are most likely also important for the coordination of monodentate sulfate in other metal complexes and thus provide a rationalization for the general observation of bent M–O–S bonds.

Fig. 3
Contributions to the total bonding energy of UO₂(SO_4-mono) for different U–O–S angles: (a) the steric contribution is the sum of the electrostatic interaction and Pauli repulsion; (b) the total bonding energy is the sum of the steric contributions and orbital interaction and has a minimum around 125°.

It is very clear from the experimental observations that the composition of the test solutions, (total concentration of uranium, ionic strength, and ionic medium) results in different modes of coordination of sulfate. This indicates that the difference in Gibbs energy between the two isomers is small, as also found in the quantum chemical calculation (Table 2) that refers to reactions (4)–(6). These reactions involve a transfer of water from the first to the second coordination sphere of U(VI), while in the test solutions the reactions describe the transfer of water from the first coordination sphere to the bulk solvent, as exemplified by:

UO₂(SO_4-mono)(OH₂)₄⇌UO₂(SO_4-chel)(OH₂)₃ + H₂O

(11)

Reaction (11) shows that the relative stability of the mono- and bidentate isomers depends on the water activity, where a low water activity will favor the chelate. As the water activity decreases with increasing ionic strength and temperature, it seems possible to test this by performing LAXS and EXAFS studies at higher temperatures. A very small change in Gibbs energy of reaction for reaction (11) will result in a substantial change in the relative amounts of the two isomers, as shown in Table 3. With the approximations used in the chemical and quantum chemical models, it seems difficult to claim a higher accuracy than 10 kJ/mol in the Gibbs energy and this uncertainty range spans the range of ΔG⁰ values in Table 3, for which there is a substantial change in the relative amounts of the isomers.

ΔG⁰ (kJ/mol)	[UO₂(SO_4-chel)(OH₂)₃]/[UO₂(SO_4-mono)(OH₂)₄]
−5.0	7.5
0	1.00
+5.0	0.133

4 Conclusions

Standard solution chemical methods give information on the stoichiometry of the complexes with respect to the reactants, in this case UO₂²⁺ and SO₄²⁻, but not on the mode of coordination of the ligand and the number of coordinated water ligands. Structure chemical methods such as EXAFS provide this information, but the structure models are not always unique. In addition, EXAFS methods require information on the speciation, i.e. the concentration of the different species in the test solutions used. In systems where several different complexes occur in comparable concentrations, it is very difficult to deduce structure information. Quantum chemistry provides tools to obtain both the geometry and relative energy of different complexes and this information, combined with experimental solution chemical and EXAFS data, makes it possible to obtain a better understanding of the chemistry of aqueous complex formation than using the experimental or theoretical methods alone. In the present system we conclude that there are several possible isomers of the complexes UO₂(SO₄) and UO₂(SO₄)₂²⁻ that have very near the same energy. These isomers consist both of species where the sulfate ligand is coordinated in bi- and monodentate fashion. However, the number of donor atoms in the equatorial plane of the UO₂ moiety is five in all isomers, as supported both by experimental and calculated average bond distances and the relative energy of isomers with the same mode of coordination of sulfate, but a different number of coordinated water ligands. The relative stability of the different isomers is small and the mode of coordination of the sulfate ligand seems therefore to be dependent on the water activity, as also noted experimentally.

Acknowledgments

This study was supported by the ACTINET network of excellence and through a grant from the Trygger Foundation. Computational resources have been provided by the ‘Institut de développement et de ressources en informatique scientifique’ of the ‘Centre national de la recherche scientifique’, IDRIS (Project 61859), the ‘Centre informatique national de l'enseignement supérieur’ (CINES, Project phl2531), and the ‘Centre de ressources informatiques’ (CRI) of the ‘Université des sciences et technologies’ of Lille. CERLA is supported by the ‘Ministère chargé de la recherche’, the ‘Région Nord-Pas-de-Calais’, and the FEDER.

Appendix

The experimental EXAFS and LAXS investigations have been made in test solutions that contain UO₂²⁺(aq), UO₂(SO₄)(aq) and UO₂(SO₄)₂²⁻(aq), and it is important to know these concentrations for the analysis of the experimental data. Such calculations are based on the known total concentrations of the components and known equilibrium constants for the formation of the two sulfate complexes. The latter are tabulated in data bases [1] and usually refer to standard state conditions; they have therefore to be recalculated to the actual ionic medium of the test solutions. We have reanalyzed the composition of the test solutions described by Moll et al. [4] using the specific ion interaction theory (SIT), as described in the example given below. The theoretical basis for the SIT is described in Refs. [1,25].

The activity coefficient of an ion, i, is described by Eq. (A.1):

\log γ_{i} = - \frac{A Z_{i}^{2} I^{1 / 2}}{1 + 1.5 I^{1 / 2}} + \sum_{j} ɛ_{γ} (i, j) m_{j}

(A.1)

where Z_i is the charge of ion, I the ionic strength and A the Debye–Hückel parameter (A = 0.5100 mol^−1/2 kg^1/2 at 25 °C). ɛ(i, j) is the specific ion interaction parameter between the ions i and j and m_j the molality of the ion j. If i is a cation, the summation involves all anions, j, present in solution, and the reverse if i is an anion. Note that the summation includes all pair ion interactions. The SIT model ignores both binary interactions between species of the same charge, and the contribution of ternary interactions to the activity coefficients.

The activity correction is particularly simple in sulfuric acid solutions, as shown by the following example for the reactions:

UO₂²⁺ + HSO₄⁻ ⇌ UO₂(SO₄) + H⁺

(A.2)

\log γ ({UO}_{2}^{2 +}) = - 4 D + ɛ ({UO}_{2}^{2 +}, {HSO}_{4}^{-}) m_{{HSO}_{4}}

(A.3)

\log γ ({HSO}_{4}^{-}) = - D + ɛ ({HSO}_{4}^{-}, {UO}_{2}^{2 +}) m_{{UO}_{2}^{2 +}} + ɛ ({HSO}_{4}^{-}, H^{+}) m_{H^{+}}

(A.4)

\log γ (H^{+}) = - D + ɛ (H^{+}, {HSO}_{4}^{-}) m_{{HSO}_{4}}

(A.5)

The relationship between the standard state equilibrium constant at zero ionic strength, K⁰, and in m molal H₂SO₄, K^(m) is then:

\log K^{0} (A.2) = \log K^{(m)} + 4 D + ɛ (H^{+}, {HSO}_{4}^{-}) m_{{HSO}_{4}} - ɛ ({HSO}_{4}^{-}, {UO}_{2}^{2 +}) m_{{UO}_{2}} - ɛ ({HSO}_{4}^{-}, H^{+}) m_{H} - ɛ ({UO}_{2}^{2 +}, {HSO}_{4}^{-}) m_{{HSO}_{4}}

(A.6)

D is the Debye–Hückel term A√I/(1 + 1.5√I); in pure sulfuric acid

m_{H^{+}} = m_{{HSO}_{4}}

. As the concentration [UO₂²⁺] is often much smaller than [HSO₄⁻], the term

ɛ ({HSO}_{4}^{-}, {UO}_{2}^{2 +}) m_{{UO}_{2}^{2 +}}

can be neglected and Eq. (A.6) is then:

\log K^{0} (A.2) = \log K^{(m)} + 4 D - ɛ ({UO}_{2}^{2 +}, {HSO}_{4}^{-}) m_{{HSO}_{4}}

(A.7)

The interaction coefficient ɛ(HSO₄⁻,UO₂²⁺) has been estimated to be 0.35 ± 0.11 based on the experimental interaction coefficients ɛ(UO₂²⁺, ClO₄⁻) and ɛ(UO₂²⁺, NO₃⁻).

The equilibrium constant for the reaction:

UO₂²⁺ + 2HSO₄⁻ ⇌ UO₂(SO₄)₂²⁻ + 2H⁺

(A.8)

is obtained in the same way:

\log K^{0} (A.8) = \log K^{(m)} + ɛ ({UO}_{2}^{2 +} {{(SO}_{4})}_{2}^{2 -}, H^{+}) m_{H} + 2 ɛ (H^{+}, {HSO}_{4}^{-}) m_{{HSO}_{4}} - 2 ɛ ({HSO}_{4}^{-}, H^{+}) m_{H} - ɛ ({UO}_{2}^{2 +}, {HSO}_{4}^{-}) m_{{HSO}_{4}^{-}}

The specific ion interaction parameters used are taken from Ref. [1b] and are listed in Table A.1.

Using the equilibrium constants at zero ionic strength from Ref. [1] (log K⁰(A.2) = 1.17 and log K⁰(A.8) = 0.18) and the interaction coefficients from Table A.1, we obtain the following equilibrium constants valid in 1.0 M H₂SO₄: log K(A.2) = 0.71 and log K(A.8) = 0.56; the uncertainty in these quantities is at least 0.10 log units. The composition of test solution A in the paper by Moll et al. [4] is then [UO₂²⁺(aq)] = 5.6 ± 1.4 mM, [UO₂(SO₄)(aq)] = 26.5 ± 0.2 mM and [UO₂(SO₄)₂²⁻] = 17.8 ± 1.7 mM; the uncertainty ranges have been estimated using the uncertainty in the equilibrium constants. In their calculation of the composition of test solution A, Moll et al. do not seem to have taken the formation of UO₂(SO₄)₂²⁻ into account. It seems clear that the predominant complex in the test solution is UO₂(SO₄)(aq), but with a significant amount of UO₂(SO₄)₂²⁻. It is not possible to make an accurate estimate of the speciation in test solution B because of the high ionic strength in 10 M H₂SO₄; however, as a result of the higher total concentration of HSO₄⁻, it seems clear that the predominant complex is UO₂(SO₄)₂²⁻. It is not possible to make an accurate analysis of the speciation in test solution C using the SIT, as the test solution contains large amounts of both ClO₄⁻ and HSO₄⁻ and has a high ionic strength. To conclude: the reanalysis of the test solutions used in the EXAFS measurements of Moll et al.[4] are only to a minor degree affected by the presence of UO₂²⁺(aq), and the predominant complexes are UO₂(SO₄)(aq) and UO₂(SO₄)₂²⁻.

Ion interaction coefficient	E(i, j) (kg mol⁻¹)	Comments
ɛ(UO₂²⁺, HSO₄⁻)	0.35 ± 0.11	The interaction coefficient is estimated from the known values ɛ(UO₂²⁺, ClO₄⁻) = 0.46 and ɛ(UO₂²⁺, NO₃⁻) = 0.24.
ɛ(HSO₄⁻, H⁺)	0.15	The interaction coefficient is estimated from the known value ɛ(HSO₄⁻, Li⁺) = 0.15.
ɛ(H⁺, HSO₄⁻)	0.15	ɛ(HSO₄⁻, H⁺) ≡ ɛ(H⁺, HSO₄⁻)
ɛ(UO₂(SO₄)₂²⁻, H⁺) ≈ ɛ(UO₂(SO₄)₂²⁻, Li⁺)	−0.02 ± 0.06	The interaction coefficient is estimated by increasing the known value ɛ(UO₂(SO₄)₂²⁻, Na⁺) = −0.12 ± 0.06 by 0.10, the difference found between Li⁺ and Na⁺.

Bibliographie

[1] Chemical Thermodynamics of Uranium (I. Grenthe; J. Fuger; R.J.M. Konings; R.J. Lemire; A.B. Muller; C. Nguyen-Trung; H. Wanner; R. Guillaumont; T. Fanghänel; J. Fuger; I. Grenthe; D. Palmer; M. Rand; V. Neck, eds.), Update of the Chemical Thermodynamics of Uranium, Neptunium, Plutonium, Americium and Technetium, NEA/OECD, North Holland, 1992

[2] L. Niinistö; J. Toivonen; J.A. Valkonen; A. Zalkin; H. Ruben; D.H. Templeton; N. van der Putte; B.O. Loopstra Struct. Commun., 32 (1978), p. 647

[3] L.A. Hayden; P.C. Burns; Y.N. Mikhailov; L.A. Kokh; V.E. Kuznetsov; T.G. Grevtseva; S.K. Sokol; G.V. Ellert Koord. Khim. (USSR), 163 (2002), p. 313

[4] H. Moll; T. Reich; C. Hennig; A. Rossberg; Z. Szabó; I. Grenthe Radiochim. Acta, 88 (2000), p. 559

[5] J. Neuefeind; S. Skanthakumar; L. Soderholm Inorg. Chem., 43 (2004), p. 2422

[6] V. Barone; M. Cossi J. Phys. Chem. A, 102 (1998), p. 1995

[7] K. Morokuma; T. Ziegler; A. Rauk; T. Ziegler; A. Rauk; F.M. Bickelhaupt; E.J. Baerends Inorg. Chem. (K.B. Lipowitz; D.B. Boyd, eds.), Review of Computational Chemistry, 55, Wiley-VCH, New York, 1971, p. 1236

[8] ADF2006.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com.

[9] G. te Velde; F.M. Bickelhaupt; E.J. Baerends; C. Fonseca Guerra; S.J.A. van Gisbergen; J.G. Snijders; T. Ziegler J. Comput. Chem., 22 (2001), p. 931

[10] W. Küchle; M. Dolg; H. Stoll; H. Preuss J. Chem. Phys., 100 (1994), p. 7535

[11] X. Cao; M. Dolg; H. Stoll J. Chem. Phys., 118 (2003), p. 487

[12] A. Schäfer; C. Huber; R. Ahlrichs; A. Schäfer; H. Horn; R. Ahlrichs J. Chem. Phys., 100 (1994), p. 5829

[13] D.E. Woon, K.A. Peterson, T.H. Dunning, Jr., in preparation.

[14] A.D. Becke Phys. Rev. A, 38 (1988), p. 3098

[15] V. Barone; M. Cossi; J. Tomasi; M. Cossi; N. Rega; G. Scalmani; V. Barone J. Comput. Chem., 102 (1998), p. 102

[16] M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, J.A. Montgomery, Jr., T. Vreven, K.N. Kudin, J.C. Burant, J.M. Millam, S.S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G.A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J.E. Knox, H.P. Hratchian, J.B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R.E. Stratmann, O. Yazyev, A.J. Austin, R. Cammi, C. Pomelli, J.W. Ochterski, P.Y. Ayala, K. Morokuma, G.A. Voth, P. Salvador, J.J. Dannenberg, V.G. Zakrzewski, S. Dapprich, A.D. Daniels, M.C. Strain, O. Farkas, D.K. Malick, A.D. Rabuck, K. Raghavachari, J.B. Foresman, J.V. Ortiz, Q. Cui, A.G. Baboul, S. Clifford, J. Cioslowski, B.B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R.L. Martin, D.J. Fox, T. Keith, M.A. Al-Laham, C.Y. Peng, A. Nanayakkara, M. Challacombe, P.M.W. Gill, B. Johnson, W. Chen, M.W. Wong, C. Gonzalez, J.A. Pople, Gaussian, Inc., Wallingford CT, Gaussian 03, Revision C.02, 2004.

[17] F.P. Rotzinger J. Phys. Chem. B, 109 (2005), p. 1510

[18] P. Wåhlin, C. Danilo, V. Vallet, F. Réal, J.-P. Flament, U. Wahlgren, J. Chem. Theory Comput., submitted for publication.

[19] E. van Lenthe; E.J. Baerends; J.G. Snijders; E. van Lenthe; E.J. Baerends; J.G. Snijders; E. van Lenthe; E.J. Baerends; J.G. Snijders; E. van Lenthe; A.E. Ehlers; E.J. Baerends; R.G. Parr; W. Yang J. Chem. Phys., Density Functional Theory of Atoms and Molecules, 99, New York, Oxford, 1993, p. 4597

[20] A.D. Becke J. Phys. Chem., 98 (1993), p. 5648

[21] ADF STO basis set database available online at http://tc.chem.vu.nl/SCM/DOC/atomicdata/.

[22] J.S. Craw; M.A. Vincent; I.H. Hillier; A.L. Wallwork J. Phys. Chem., 99 (1995), p. 10181

[23] U. Wahlgren; H. Moll; I. Grenthe; B. Schimmelpfennig; L. Maron; V. Vallet; O. Gropen; V. Vallet; U. Wahlgren; B. Schimmelpfennig; H. Moll; Z. Szabó; I. Grenthe Inorg. Chem., 103 (1999), p. 8257

[24] S. Ahrland Acta Chem. Scand., 5 (1951), p. 1151

[25] I. Grenthe; A. Plyasunov; K. Spahiu Modelling in Aquatic Chemistry (I. Grenthe; I. Puigdomenech, eds.), NEA/OECD, 1997

[26] FIZ/NIST Inorganic Crystal Structure Data Base, Version 1.3.3, Fachinformationszentrum, Karlsruhe, National Institute of Standards and Technology, Gaithersburg, 2005

Commentaires - Politique