Plan
Comptes Rendus
no. 10-11

Liquid–liquid extraction: An adsorption isotherm at divided interface?
Fabienne Testard1 ; Laurence Berthon2 ; Thomas Zemb3 
1 LIONS at CEA/DSM/DRECAM/SCM, CEA Saclay, F91191 Gif-sur-Yvette, France
2 CEA/DEN/DRCP, 30207 Bagnols-sur-Cèze cedex, France
3 Institut de chimie séparative de Marcoule, UMR5257, BP 171 71, 30207 Bagnols-sur-Cèze cedex, France
Comptes Rendus. Chimie, Volume 10 (2007) no. 10-11, pp. 1034-1041.

Résumés

We show that liquid–liquid extraction can be described as the equilibrium between two pseudophases of ions: the hydrated state in the water phase and the solvation state when the ions are adsorbed on an organized interface. The extractant is considered as a potential surface where the ions can adsorb. Unlike phenomenological binding “constants”, ion extraction/stripping can be seen as the sum of Langmuir isotherms. The number of aggregated extractants in one reverse micelle in the solvent is at least equal to or higher than the number of extracting molecules complexed at a given instant to the ion to be extracted. Considering extraction equilibrium as a sum of isotherms corresponding to the different states of aggregation of extractant molecule in the solvent, the resulting constant is representative of both the efficiency of the extraction and the structure of the solution. This is a first step toward the development of predictive models for the apparent distribution coefficients.

Nous montrons que l'extraction liquide–liquide peut être décrite comme un équilibre entre deux pseudophases d'ions : les ions hydratés dans la phase aqueuse et les ions « solvatés », qui sont dispersés dans les cœurs polaires des micelles inverses. Les ions sont alors considérés comme adsorbés sur une interface eau–huile dispersée. Le nombre d'agrégation d'une micelle donnée est supérieur ou égal au nombre de liaisons complexantes impliquant un ion extrait. Considérant l'équilibre d'extraction comme une somme d'isothermes correspondant aux différents états d'agrégation dans le solvant, les constantes obtenues permettent de quantifier l'efficacité de l'extraction en relation avec la structure de la solution. Ceci est un premier pas vers le développement de modèles prédictifs des coefficients de distribution apparents.

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crci.2007.04.014
Mots clés : Complex fluid, Liquid–liquid extraction, Langmuir isotherm, Binding constant, Aggregation number, Supramolecular organization, Fluide complexe, Extraction liquide–liquide, Isothermes de Langmuir, Constante d'association, Nombre d'agrégation, Organisation supramoléculaire
Fabienne Testard 1 ; Laurence Berthon 2 ; Thomas Zemb 3

1 LIONS at CEA/DSM/DRECAM/SCM, CEA Saclay, F91191 Gif-sur-Yvette, France
2 CEA/DEN/DRCP, 30207 Bagnols-sur-Cèze cedex, France
3 Institut de chimie séparative de Marcoule, UMR5257, BP 171 71, 30207 Bagnols-sur-Cèze cedex, France 
@article{CRCHIM_2007__10_10-11_1034_0,
     author = {Fabienne Testard and Laurence Berthon and Thomas Zemb},
     title = {Liquid{\textendash}liquid extraction: {An} adsorption isotherm at divided interface?},
     journal = {Comptes Rendus. Chimie},
     pages = {1034--1041},
     publisher = {Elsevier},
     volume = {10},
     number = {10-11},
     year = {2007},
     doi = {10.1016/j.crci.2007.04.014},
     language = {en},
}
TY  - JOUR
AU  - Fabienne Testard
AU  - Laurence Berthon
AU  - Thomas Zemb
TI  - Liquid–liquid extraction: An adsorption isotherm at divided interface?
JO  - Comptes Rendus. Chimie
PY  - 2007
SP  - 1034
EP  - 1041
VL  - 10
IS  - 10-11
PB  - Elsevier
DO  - 10.1016/j.crci.2007.04.014
LA  - en
ID  - CRCHIM_2007__10_10-11_1034_0
ER  - 
%0 Journal Article
%A Fabienne Testard
%A Laurence Berthon
%A Thomas Zemb
%T Liquid–liquid extraction: An adsorption isotherm at divided interface?
%J Comptes Rendus. Chimie
%D 2007
%P 1034-1041
%V 10
%N 10-11
%I Elsevier
%R 10.1016/j.crci.2007.04.014
%G en
%F CRCHIM_2007__10_10-11_1034_0
Fabienne Testard; Laurence Berthon; Thomas Zemb. Liquid–liquid extraction: An adsorption isotherm at divided interface?. Comptes Rendus. Chimie, Volume 10 (2007) no. 10-11, pp. 1034-1041. doi : 10.1016/j.crci.2007.04.014. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2007.04.014/

Version originale du texte intégral

1 Introduction

In recent years similarities have been suspected between surfactant molecules and extractants. Asare was the first to review all the experimental evidence of the presence of aggregates in TBP extracts used in the PUREX process [1]. Several publications evidence the supramolecular organization of extractants in organic solvent [2–6] (referred to as the “diluent” in the liquid–liquid extraction field). The similarities between surfactant and extractant range from the molecular to the macroscopic level [1,2]. At the molecular scale, all efficient extractants show amphiphilicity in the chemical formula [1]: a polar chelating part linked to long alkyl chains to increase the solubility in the diluent. At the macroscopic scale, the presence of extractants decreases the water–oil surface tension [3]. Moreover, application of the Gibbs equation is consistent with values around 0.4 nm2 per hydrophobic chain in the extractant, the same order of magnitude as surfactants and lipids. In the last 10 years, progress in the sensitivity of small-angle X-ray scattering has opened the possibility of direct measurement of the average “aggregation number” of the reverse micelles, host of the extracted ions [4]. Since the number of molecules weakly bound by long-range interactions in one “reverse micelle” is usually less than 10, the intensity of the produced X-ray scattering is slightly higher than the one produced by pure alkane (a signal related to the compressibility). However, SANS [5] or coupled SAXS and SANS [6] experiments can determine the exact microstructure of any reverse aggregate made by extracting molecules: polar core volume, attraction between cores, micelle volume, average distance between micelles.

In a similar way to more classical amphiphilic molecules [7], when the concentration of extractant molecules is increased, several states of aggregation are encountered with the extractant in organic solvent [8]:

  • (1) When the chemical potential is beyond a certain threshold, the molecules are present mainly as monomers.
  • (2) Above a certain threshold known as the critical micellar concentration (CMC)—even if there is nothing “critical” in this transition—progressive aggregation occurs in distinct aggregates containing an average number N (the aggregation number) of extractants. The geometrical centre of these aggregates contains all the polar species present: extracted salt and co-extracted water (Fig. 1-B1). In the nuclear field, the most used extractant agent is a triple-chain phosphate, tributyl phosphate (TBP).
  • (3) When co-surfactants or few “modifiers” are present in the diluent, the reverse micellar aggregates are mixed aggregates. Each aggregate involves a number N of complexing agents around a polar core, but also a number N′ of another type of amphiphilic molecule. Fatty acids or alcohol are often used in industrial processes (Fig. 1-B2).
  • (4) Hydrotropes or solvo-surfactants (“modifiers”) can also structure the solvent. The microstructure is then a three-dimensional network of hydrogen bonds connecting polar parts of the extractant molecules. This three-dimensional network gives a very characteristic peak in the small-angle scattering spectrum. This peak may be conserved even in the presence of extractant agents [9]. No distinct “reverse micelles” are formed (Fig. 1-C). Structural investigation is necessary for predictive modeling of phase instability in this aggregation state.
  • (5) When both extractant and solute concentration are increased, a “gel” can be obtained [3a] and broad X-ray scattering peaks are detected. The microstructure can be seen either as a microemulsion, with locally connected cylinders or bilayer, or as a “molten” liquid-crystal state: a hexagonal, cubic, or smectic phase with very small domain size (Fig. 1-D). These small domains are referred to as “tactoids” in classical colloidal-state textbooks [10].

Fig. 1

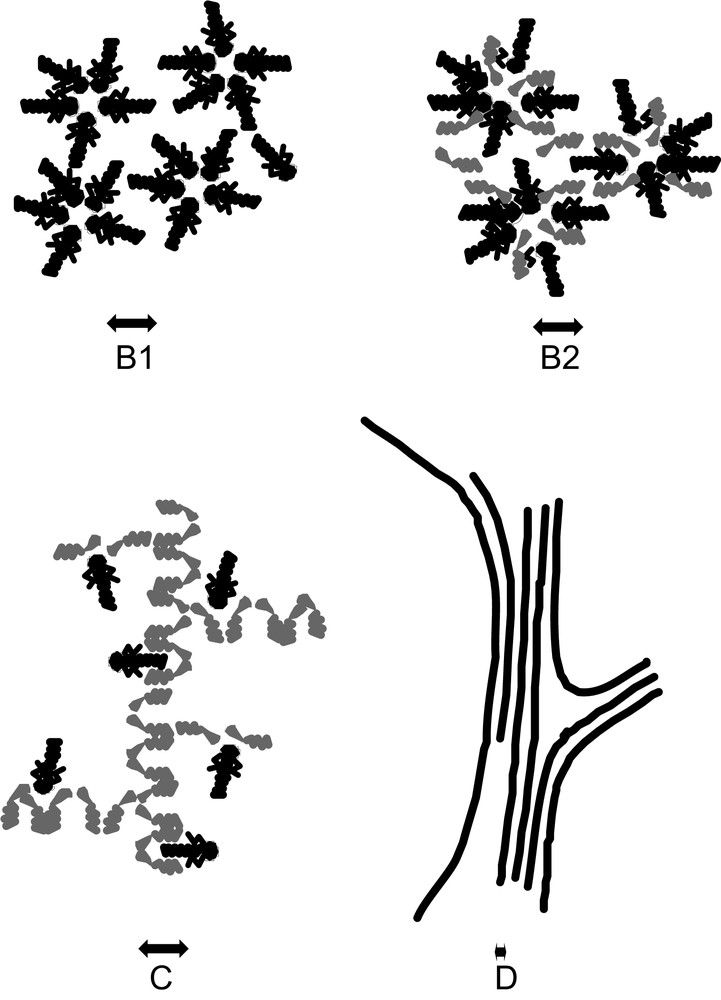
Schematic representation of the four organized microstructures detected for extractant solutions in solvents (black: extractant molecule, grey: co-surfactant or co-solvent); (B1) Water–oil micelles or reverse aggregates of surfactant molecules; (B2) water–oil micelles with another solute acting like a co-surfactant; (C) random dynamic networks in organized solvent, acting like adsorption sites for solubilized complexing molecules; (D) microphase separation containing “tactoids” i.e. co-existence of locally condensed structures such as a hexagonal phase.

These four microstructural states of extracting molecules apart from molecular dispersion are compared in Fig. 1. The extraction is usually less efficient at low extractant concentrations in a monomer state. In the pure or mixed reverse micellar state, extraction is more efficient because the number of extractant molecules linked to a given ion can increase up to the aggregation number. In the molten liquid crystalline state, the extracting power continues to increase, since the aggregation number diverges while the coordination number must remain constant. The coordination number is relative to the extracted ions and is limited, while the aggregation number is related to the amphiphilicity of both the extractant and the complexes. In this state, there is a possible instability and a certain increase in viscosity. Progresses in the understanding of liquid–liquid extraction will be obtained when it will be possible to quantify the coordination number and the aggregation number separately.

In most cases known today, the number of surfactants/extractants in one reverse micelle—i.e. the aggregation number—is larger than (or at least equal to) the stoichiometric coefficient of the extractant in the extracted complexes derived from approximating liquid–liquid extraction as a stoichiometric equilibrium. In Appendix, the classical procedure used for deriving apparent reaction “constants” as well as the stoichiometry of the complexes is precisely described. The number of equilibria involved in the complexation and aggregation phenomena is quite important and difficult to solve. The aggregation state of the extractant must be determined to obtain the speciation of the extractant, but the supramolecular state is often given independently of the nature of the complexes present in the diluent. There is a need for a complete description of both the structural organization and the nature of the complexes in the diluent.

In this paper, we extend the pseudophase concept developed for micelles and microemulsions to the extraction process [11]. The basis of the pseudophase model is the conceptual separation in solution between all the molecules dispersed in an aggregate of aggregation number N and all monomers present. The aggregate is treated as a pseudophase in which surfactants and solubilized substances reside, the other phase being the so-called monomer phase. Since rapid equilibrium occurs for a given molecule that is exchanged between these two “pseudophases”, the chemical potential must be the same in both pseudophases. The measurement of the number of monomers isolated in the solvent thus gives access to the chemical potential, since monomers can be considered as an ideal solution.

Thirty years ago, Evans and co-workers used the concept of pseudophases to develop the chemical potential of a surfactant molecule as a function of the radius of curvature of the aggregate, hence the aggregation number [12]. For ionic surfactants, counterions seen as decorating the surface have led to the first predictive model of counterion exchange in micelles [13]. In the systems implemented industrially in the nuclear industry, extraction is used to separate cations (actinides) from the dissolution liquor arising from spent nuclear fuel. Liquid–liquid extraction systems are classified into four types [14]: (a) extraction through cation exchange, (b) solvation, (c) ion-pair formation, and (d) formation of complexes with synergistic extraction. Extractants are chosen to extract certain cations specifically. However, micellar systems based on cationic surfactant can be used for separating actinides as anionic complexes [15]. These systems could not be understood in terms of “binding constants” since these micellar systems were extracting ions without direct complexation and have not been implemented industrially to our knowledge.

Considering the use of solvation for extraction, we want to apply the adsorption isotherm approach to treat the liquid–liquid extraction. This approach is used in the micellar field to quantify the solubilization of a neutral solute in direct block co-polymer micelles [16]. Considering ion extraction as a sum of extraction isotherms in pseudophase equilibrium would allow us to consistently describe all types of self-organized extracting systems. This paper offers a new approach for investigating liquid–liquid extraction considering both the extraction efficiency and the supramolecular organization.

2 Adsorption isotherm: definition

Let us consider the ion equilibrium as an adsorption isotherm. The system is an extractant organic solution in contact with an aqueous solution containing solute. After equilibrium, the solute is extracted in the organic phase. The receiving “surface” for the extracted ion is offered by each extractant present in the organic phase. To be self-consistent, the surface area per molecule must be considered. This is defined thermodynamically and can be determined experimentally. However, the surface area per molecule may have different affinities, depending on the pseudophase considered: monomers, micelles, bicontinuous networks, and nuclei of liquid crystals.

Rather than referring to a constant corresponding to a unique identified equilibrium implying different stoichiometric coefficients and neglecting water co-extraction, an isotherm of adsorption is considered. The ions are considered to adsorb on a surface Σ, which is related to the area per extractant molecule σ simply by: Σ = cextσ, where cext is the extractant concentration in the solvent, excluding the macroscopic solvent–water interface in the case of emulsified systems. If it is assumed that no more than one ion can be extracted by one extractant molecule, the saturation limit of the ion isotherm is given simply by the 1/1 molar ratio. This limit cannot generally be obtained experimentally because phase instabilities, due, for example, to the weak “long-range” Van der Waals interaction between micelles, induce a phase separation in the fluid (the so-called “third phase”). However, this saturation limit has a well-defined thermodynamic meaning.

If “lateral” interactions between adsorbed ions can be disregarded, the general isotherm is then given in the Langmuir form by Eq. (1):

θ=KadM1+KadM(1)
where θ is the relative occupancy of “sites”, each site being the polar side of the extractant seen as a single site molecule; θ is thus defined by the molar ratio of ion over extractant in the organic phase. The numerical value of the constant Kad depends on whether molar fraction or concentration units are used for the variable M characterizing the ions in the water solution at equilibrium. The water in excess imposes a chemical potential for the salt.

The same approach of a long-range interaction-driven binding isotherm of ions on organized weak natural ligands—in this case, common phospholipids—has led to a quantitative explanation of the long-lasting mystery of electrophoretic mobility and swelling of lipids observed in the presence of chaotropic salts [17].

3 Application to uranyl nitrate extraction by diamide–hexane solution

A typical example is shown in Fig. 2 for the extraction of uranyl nitrate from a 1 M LiNO3 water solution to an organic solution of diamide in hexane. The diamide is N,N′-dimethyl-N,N′-dibutyl tetradecylmalonamide DMDBTDMA. The uranyl concentration in the solvent phase is determined by titration (X-ray fluorescence). The vertical line represents the formation of a third phase, a practical limit above which titration is impossible. Before this limit of three-phase instability, the adsorption isotherm follows a Langmuir behavior that allows phenomenological description in terms of binding constants.

Fig. 2

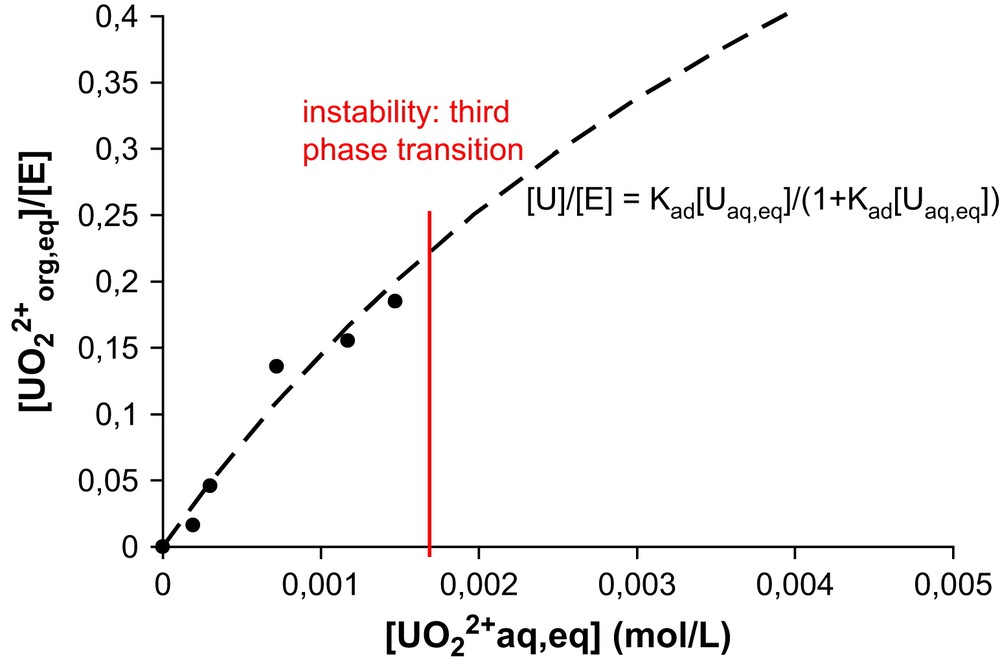
Isotherm of extraction of uranyl nitrate by diamide (noted “E”) in hexane. The organic phase (DMDBTDMA–hexane) is contacted and equilibrated by water–LiNO3 (1 M)–UO2(NO3)2 with an initial 1/1 volume ratio. The sample is biphasic. The vertical red line represents the third phase instability. (For interpretation of the references to color in figure legends and text, the reader is referred to the web version of this article.)

However, if we now consider the same extraction isotherm for different concentrations of extractant molecules, we obtain the results shown in Fig. 3.

Fig. 3

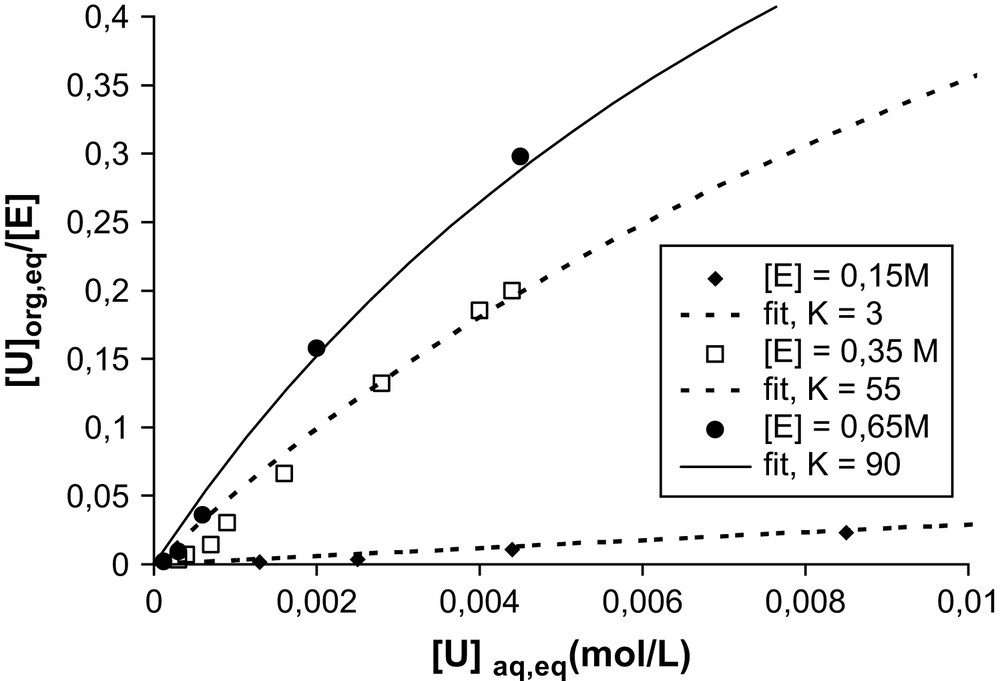
Effect of the extractant concentration on the extraction isotherm for uranyl extraction by a solution of diamide (noted “E”) in hexane. Experimental conditions: DMDBTDMA–hexane is contacted and equilibrated by water–LiNO3 (1 M)–UO2(NO3)2) with initial 1/1 volume ratio. K is the constant “Kad” defined in the text.

Taking into account that the extractants can exist in four different states of aggregation, the adsorption isotherm has now to be written as the simultaneity of four adsorption isotherms (Eq. (2)):

θ=1[E]tot∑pp[E]ppKadppMpp1+KadppMpp(2)
where “pp” stands for the sum of the contributions of the four pseudophases: monomers, micelles, networks and tactoids, seen as nuclei of liquid-crystal precursors.

When only an average organization is considered, the adsorption isotherm is defined by an average adsorption constant (Eq. (3)):

θ=〈Kad〉Mpp1+〈Kad〉Mpp(3)

The four constants Kadpp represent the affinities of the four different interfaces for the ions to be extracted.

These constants can be converted to a free energy ΔG as given by Eq. (4):

ΔG=−RTlnKadpp(4)
where ΔG represents the free energy associated with the transfer of ions from water to the organic phase and its adsorption on the polar ligand “surface” σ in the aggregation state of one given pseudophase (pp).

Expressed in L mol−1, the binding constant Kadpp can be converted [18] to a binding energy given by Eq. (5), which is valid if the entropy variation associated with the micelle reorganization due to the presence of a given ion in a given site can be neglected.

Kadpp=σδexp(−U/RT)(5)

The product σδ decomposes the binding volume into an area σ and a layer thickness δ. The ion potential U is a step function with a width δ. In the case of micelles, δ is typically the radius of the polar core. The attractive potential U can be considered as the combination of one short-range and one long-range term. The short-range term would be the energy of complexation between the ion and the complexing “site” of the ligand (amide, phosphate) and the long-range term would itself be the combination of the Van der Waals (dispersion) interaction and the dehydration mechanism active between the ion and the microscopic polar–apolar interface. These three mechanisms are combined in a typical aggregate which is in this sense an active interface.

As indicated in Fig. 3, the affinity of the same DMDBTDMA molecule depends on the supramolecular speciation of the extractant in the solvent. For example, in the monomeric state, i.e. below the CMC, for an extractant concentration in the solvent of 0.15 M, monoKad ∼ 3 L mol−1. All other parameters being equal, and using the extractant mainly in the micellar state (0.65 M), micKad ∼ 90 L mol−1, i.e. the concentration at which half the target ions are complexed varies by two orders of magnitude depending on the supramolecular organization state of the extraction. Taking into account the molecular equilibrium of complexation without the aggregation state of the extractant will thus never be sufficient to develop predictive models.

4 Maximum of solubilization

The concentration range indicated in the preceding paragraph does not permit the exploration of high extractant concentrations. For this we can use the known values of the maximum of solubilization (LOC) used by chemical engineers designing extractant plants. The LOC represent the Limiting Organic Concentration: maximum of solubilization of a solute limited by phase separation or a solubility limit (asymptotic behavior). For the uranyl extraction limit, the LOC is given by the limit of third phase apparition. The same coordinates can be used to replot these values, as in Fig. 4 for the extraction of uranyl nitrate by diamide in dodecane. One point is obtained on each isotherm; hence only an order of magnitude of an average adsorption constant is determined by this way. This average association constant is defined only as a rough practical approximation. It assumes that the adsorption isotherm, disregarding the affinity differences of monomers, micelles, bicontinous networks and tactoids, is expressed by Eq. (3).

Fig. 4

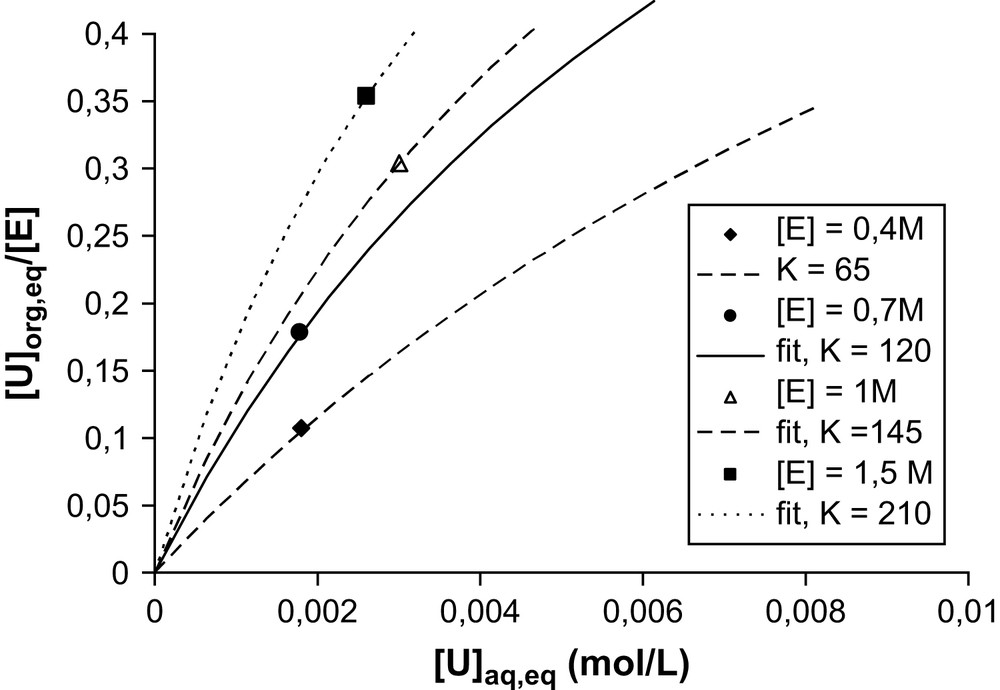
Position of the maximum of solubilization, replotted from the LOC value ([3a]) in the form of specific points of the adsorption isotherm. Experimental condition: DMDBTDMA–dodecane contacted and equilibrated by water–LiNO3 (1 M)–UO2(NO3)2) with initial 1/1 volume ratio until third phase apparition. “E” is for DMDBTDMA.

Table 1 summarizes the values of this average constant at various concentrations. Typically, half the interface available for ion adsorption is in the form of monomers at the lowest concentration, and only 10% at the highest concentration [3a]. At the highest concentration, it is likely that association in the form of tactoids intervene for a non-negligible fraction.

Table 1

Constants associated with the Langmuir adsorption isotherm for variable ligand concentrations

[C14] M0.40.711.5
〈Kad〉 (L mol−1)65120145210

5 Discussion in the case of neodymium nitrate

Adopting the same approach in the case of a lanthanide salt (neodymium nitrate) gives the result indicated in Table 2 using one average Langmuir constant.

Table 2

Average Langmuir constants 〈Kad〉 in the case of neodymium nitrate (DMDBTDMA–dodecane contacted with water–LiNO3 (1 M)–Nd(NO3)3)

[C14] M0.120.40.711.5
〈Kad〉 (L mol−1)<10−3 M0.0450.180.170.28

For a given diamide concentration (0.7 M), the average binding of the lanthanides is much weaker than in the case of uranyl: 0.18 L mol−1 for neodymium and 120 L mol−1 for uranyl. This property—which can also be immediately detected by measuring partition coefficients or preparing a system with mixed uranyl and lanthanide—is of course necessary to use a micellar fluid for ion separation. Considering only the complexation part (Uc), and water-soluble ligands, a stronger affinity of diamides is already detectable since the partition coefficients differ by roughly two orders of magnitude [19].

Depending on the nature of the ions to be extracted, the shape of the isotherm can change. In that case, a Langmuir isotherm will not describe the adsorption isotherm. This will be particularly true if a large variation of supramolecular organization is observed over the salt concentration range in determining the isotherm. A complete description with a precise identification of the pseudophases in the solution and very precise in the titrations will therefore be necessary to decompose the data as a sum of adsorption isotherms.

6 Conclusion

We have shown that a description of ion extraction equilibria can be rationalized using the adsorption isotherm approach. All ions present in the two-phase systems equilibrate between their hydrated state and “adsorbed” states. The “adsorbed” states are the sum of all ions adsorbed on “interfaces” formed by the self-assembly of extractants in the oil. This situation is shown schematically in Fig. 5. The simplest general method for characterizing the association of extractants uses the concept of pseudophases, initially developed for water-soluble surfactants. One of the consequences of pseudophase approximation is to formalize and give a theoretical background to the co-existence of several pseudophases in a given sample. For instance, above the CMC, a concentration of monomers equivalent to the CMC is always in equilibrium with aggregated species. Another advance introduced by this view is to make a clear distinction between the coordination number, i.e. the number of extractants bound to a given extracted ion at any given instant, and the aggregation number, which is the number of extractants bound by weak interactions at a given instant in a given aggregate. The aggregation number is always larger than or equal to the number of extractant linked to a given ion.

Fig. 5

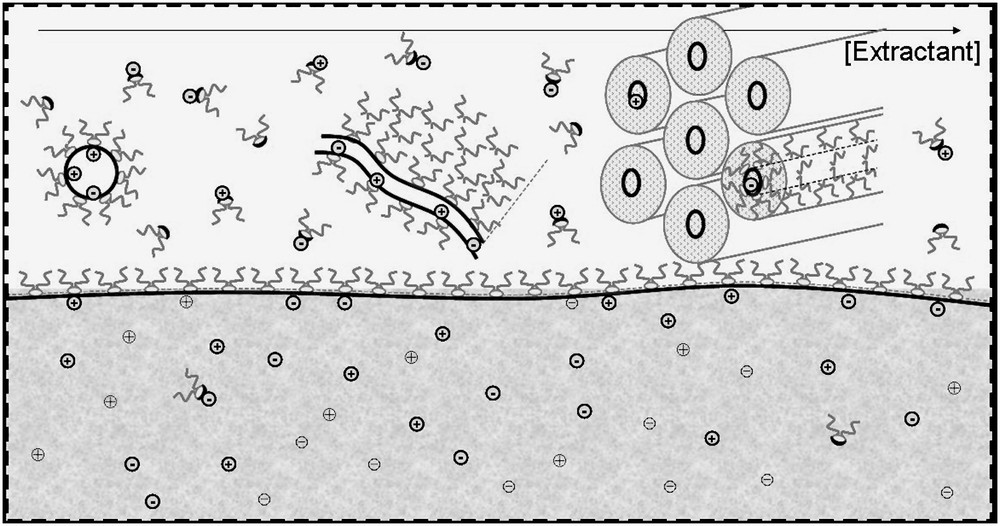
Schematic view at nanometric scale of the oil–water interface covered by an active monolayer of ligands, considered as surfactants, and hence assembling as represented in a ternary phase diagram. Several organizations, in the form of pseudophase equilibrium, co-exist in the oil. Ion extraction is represented quantitatively by the superposition of four extraction isotherms (drawn by S. Lassiaz).

With the adsorption isotherm approach, surprising variations are obtained for the average binding constants for the different aggregation states. The different isotherms are driven as well by short-range nearest neighbor interactions and by long-range terms, such as the dispersion [20] or hydration [21] interaction. Since all these interactions, as well as the ligand self-assembly itself, are driven by curvature of the polar–apolar interface, we can expect that this description will evidence the efficiency of the extraction related to the structure of the organic phase.

This approach in terms of isotherms could also be important for solvent formulation. The transient “reservoir” of ions that are adsorbed at the macroscopic oil–water interface at a given instant could give some insight into the kinetics of the extraction process.

Acknowledgements

The authors wish to thank Prof. C. Madic for fruitful discussions, S. Lassiaz for Fig. 5, and the Nuclear Fission Safety Program of the European Union for support under the EUROPART (F16W-CT-2003-508854).

Appendix Ion extraction seen as a stoichiometric complexation equilibrium

To illustrate the classical ion extraction approach in liquid–liquid extraction, we present here the extraction equilibrium according to a solvation mechanism. Other mechanisms such as ion exchange, i.e. extraction of metal ion by dialkyl phosphoric acid, exist but are not presented here. The overall way is the same. In the case of liquid–liquid extraction by a solvation mechanism, solutes are extracted according to the equilibrium:

xMa++yXb−+zE¯⇌MxXyEz¯
where overlines indicate organic species, E is the extractant, M the cation of the solute (H+, UO22+, …) and X the counterion; x, y and z are the stoichiometric coefficients of the extracted complex. Several species can be present in solution as a function of the experimental conditions; in this case parallel equilibria must be written. The extraction equilibrium is characterized by the constant K:
K=aMxXyEz¯aE¯zaMa+xaXb−y(A1)
where aA is the activity coefficients of species A, which can be expressed in molarity:
K=[MxXyEz¯]γMxXyEz¯[E¯]zγE¯z[Ma+]xγMa+x[Xb−]yγXb−y(A2)
where γA is the activity coefficient of species A and [A] is the molar concentration of species A.

It is important to note that the number of ligands complexing a given extracted ion does not have to be identified systematically with an aggregation number when the extractant is in a micelle. This is particularly true for high aggregation states (high aggregation numbers).

The activity of the species in the aqueous and organic phases must be known in order to calculate the constant K. The basic difficulty in this approach is that any real situation implies ions extracted at high concentration. The mean stoichiometric activity coefficient of a constituent mixture in aqueous phase can be calculated from the physicochemical data of the binary electrolyte solutions it contains [22,23]. In general, the ratio of the activity coefficients in the organic phase γMxXyEz¯/γE¯z is assumed to be constant. The apparent constant K′ is thus:

K′=[MxXyEz¯][E¯]z[Ma+]xγMa+x[Xb−]yγXb−y(A3)

Moreover, in practical applications, the solute transfer between the two phases is characterized by the distribution ratios DM:

DM=∑[M¯]∑[M](A4)
where ∑[M¯] is the sum of all ions present in the solvent, whatever their form, and ∑[M] the sum of ions present in the water phase, including possible complexation with ions in the aqueous phase.

From the extraction equilibrium, the distribution ratio can be expressed by:

DM=x[MxXyEz¯][Ma+](A5)

The distribution ratio is then linked to the apparent constant K′ by the general relation:

DM=xK′[Ma+]x−1[E¯]z[Xb−]yγMa+xγXb−y(A6)

The first step of the data analysis is to determine the complex stoichiometry. Two complementary methods are currently used: “organic phase saturation” or the “slope analysis method”. The slope analysis method assumes that only one species is extracted, that the extractant concentration in the organic phase and aggregation state (monomer, aggregate, protonated, etc.) are known for all species. Distribution ratios are measured as a function of one parameter (ionic strength, solute concentration, extractant concentration, etc.), keeping all other parameters constant. The stoichiometric coefficients (x, y and z) are then determined by measuring the distribution ratio, as shown in the following equation, where k is a constant:

log(DM)=k+(x−1)log([Ma+])+zlog([E¯])+ylog([Xb−])+xlog(γMa+)+ylog(γXb−)

The extraction of uranyl nitrate by malonamide diluted in alkane has been investigated by this method [24]. First, the aggregation of the malonamide was studied without uranyl nitrate: small aggregates are formed with an aggregation number of about four [25]. The associated constant determined as K = 3.7 × 103 (mol/L)−3. From these data, the speciation diagram of the extractant was calculated (determination of the monomer and aggregate concentration). The slope analysis method was applied (Fig. A1). The slope indicates an average number of ligands around the uranyl nitrate is equal to nine molecules. Assuming that, without ions, molecules that are present in the solvent mainly as tetramers yield the following equilibrium:

2.25E¯4+UO22++2NO3−⇌E9UO2(NO3)2¯

Fig. A1

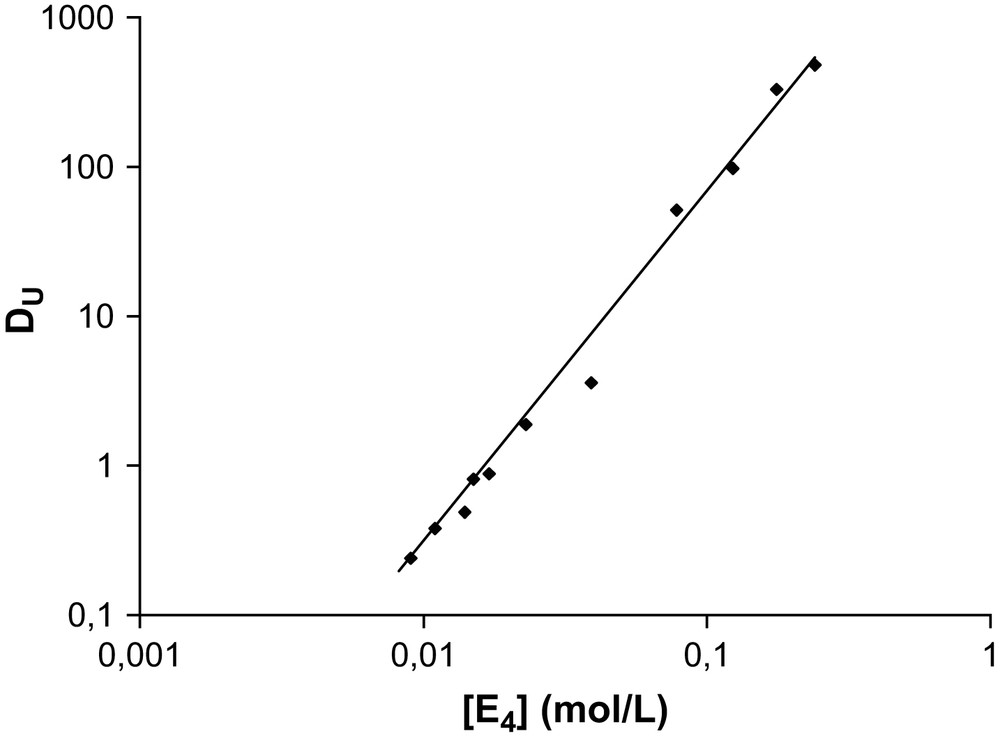
Distribution coefficient of uranyl nitrate as a function of aggregate concentration of DMDBTDMA. Organic phase: DMDBTDMA diluted in TPH, aqueous phase: uranyl nitrate in 2 M of LiNO3.

From the slopes determined and within the approximations used, the binding constant K′ appears as shown in Table A1 [26].

Table A1

Apparent constant of formation of E9UO2(NO3)2¯ in industrial solvent (TPH)

Aqueous phase
LiNO3 2 mol/LLiNO3 4 mol/L
K′ (mol−4.25 L4.25)1.3 × 1041.4 × 103

Bibliographie

[1] K. Osseo-Asare Adv. Colloid Interface Sci., 37 (1991), p. 123

[2] G. Cote Radiochim. Acta, 91 (2003), p. 639

[3] G.F. Vandegrift; E.P. Horwitz J. Inorg. Nucl. Chem., 42 (1980), p. 119

[4] C. Erlinger; L. Belloni; T. Zemb; C. Madic Langmuir, 15 (1999), p. 2290

[5] R. Chiarizia; M.P. Jensen; P.G. Rickert; Z. Kolarik; M. Borkowski; P. Thiyagarajan; R. Chiarizia; K.L. Nash; M.P. Jensen; P. Thiyagarajan; K.C. Littrell Langmuir, 20 (2004), p. 10798

[6] S. Nave; G. Modolo; C. Madic; F. Testard; S. Nave; C. Mandin; L. Martinet; L. Berthon; F. Testard; C. Madic; T. Zemb Phys. Chem. Chem. Phys., 22 (2004), p. 527

[7] H.F. Eicke Top. Curr. Chem., 87 (1980), p. 85

[8] F. Testard; L. Martinet; L. Berthon; S. Nave; B. Abécassis; C. Madic; T. Zemb Conference Proceedings Atalante (2004) http://www-atalante2004.cea.fr (Available from:)

[9] B. Abecassis; F. Testard; T. Zemb; L. Berthon; C. Madic Langmuir, 19 (2003), p. 6638

[10] H.R.E. Kruyt, Colloid Science, vols. 1 and 2, Elsevier Press, New York, 1952

[11] Y. Chevalier; T. Zemb Rep. Prog. Phys., 53 (1990), p. 279

[12] D.F. Evans; D.J. Mitchell; B.W. Ninham; D.F. Evans; H. Wennerstroem J. Phys. Chem., The Colloidal Domain: Where Physics, Chemistry, Biology and Technology Meet, 88, Wiley-CVH, 1984, p. 6344

[13] J.B. Hayter Langmuir, 8 (1992), p. 2873

[14] M. Cox Principles and Practices of Solvent Extraction (J. Rydberg; C. Musikas; G.R. Choppin, eds.), M Dekker, Inc., New York, Basel, Hong Kong, 1992, p. 357

[15] J. Strnad; K. Heckmann J. Radioanal. Nucl. Chem., 163 (1992), p. 47 (and references cited therein)

[16] A. Chouciar; A. Eisenberg JACS, 125 (2003), p. 11993

[17] H. Petrache; T. Zemb; L. Belloni; V.A. Parsegian Proc. Natl Acad. Sci. USA, 103 (2006), p. 7982

[18] A.W. Adamson; A.P. Gast Physical Chemistry of Surfaces, John Wiley Son Press, USA, 1997

[19] S.I. Sinkov; B.M. Rapko; G.J. Lumetta; B.P. Hay; G.J. Lumetta; B.M. Rapko; P.A. Garz; B.P. Hay JACS, 43 (2004), p. 8404

[20] V.A. Parsegian Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers and Physicists, Cambridge University Press, New York, USA, 2006

[21] R.P. Rand; V.A. Parsegian Biochim. Biophys. Acta, 988 (1989), p. 351

[22] N. Charrin; P. Moisy; P. Blanc Radiochim. Acta, 88 (2000), p. 25

[23] A.C. Kappenstein; P. Moisy; G. Cote; P. Blanc Phys. Chem. Chem. Phys., 2 (2000), p. 2725

[24] L. Nigond; C. Musikas; C. Cuillerdier Solvent Extr. Ion Exch., 12 (1994), p. 261

[25] L. Nigond; C. Musikas; C. Cuillerdier Solvent Extr. Ion Exch., 12 (1994), p. 297

[26] L. Nigond, PhD thesis, Université Clermont-Ferrand-2, Report CEA-R-5610, 1992.

Commentaires - Politique

Ces articles pourraient vous intéresser

Influence of the extracted solute on the aggregation of malonamide extractant in organic phases: Consequences for phase stability

Laurence Berthon; Fabienne Testard; Laurence Martinet; ...

C. R. Chim (2010)

Molecular mechanisms induced by phase modifiers used in hydrometallurgy: consequences on transfer efficiency and process safety

Asmae El Maangar; Sylvain Prévost; Sandrine Dourdain; ...

C. R. Chim (2022)

Solvent extraction of uranium from an acidic medium for the front-end of nuclear fuel cycle: from mechanisms understanding to innovative process design

Fabrice Giusti; Elise Guerinoni; David Lemire; ...

C. R. Chim (2024)