1 Introduction
Observations of three-dimensional crystalline structures with large cells have pointed out the limitation of classical crystallography as the study of periodic organizations of objects such as atoms or molecules, object without dimension in the topological sense. In the particular case of three-dimensional liquid crystalline structures built by amphiphilic molecules, specific concepts have been introduced, considering them as organizations of two-dimensional objects, surfaces or films. The crystallographic properties of these structures could then be studied from an intrinsic point of view, using operations of symmetry groups defined by displacements on the surfaces.
We consider here the liquid crystalline phases with cubic symmetry formed by amphiphilic molecules in the presence of water. These phases are present in some phase diagrams in the immediate vicinities of lamellar and hexagonal phases, as shown in Fig. 1 [1–4]. Although their structures, shown in Figs. 2 and 3, have topologies and symmetries strikingly different from those of the two other phases, they can all be understood within the same geometrical frame if we consider that the amphiphile/water interface is determinant structurally. They all are periodic systems of fluid films separated by interfaces: lamellar phases are periodical stackings of flat interfaces at constant distances, and cubic or hexagonal phases can be seen as periodical stackings of symmetrically curved interfaces. We focus our attention on cubic phases which are indeed spectacular examples of how molecules having a liquid-like behavior in their respective domains, i.e. exhibiting no short-range order, can build crystalline structures with long-range order.
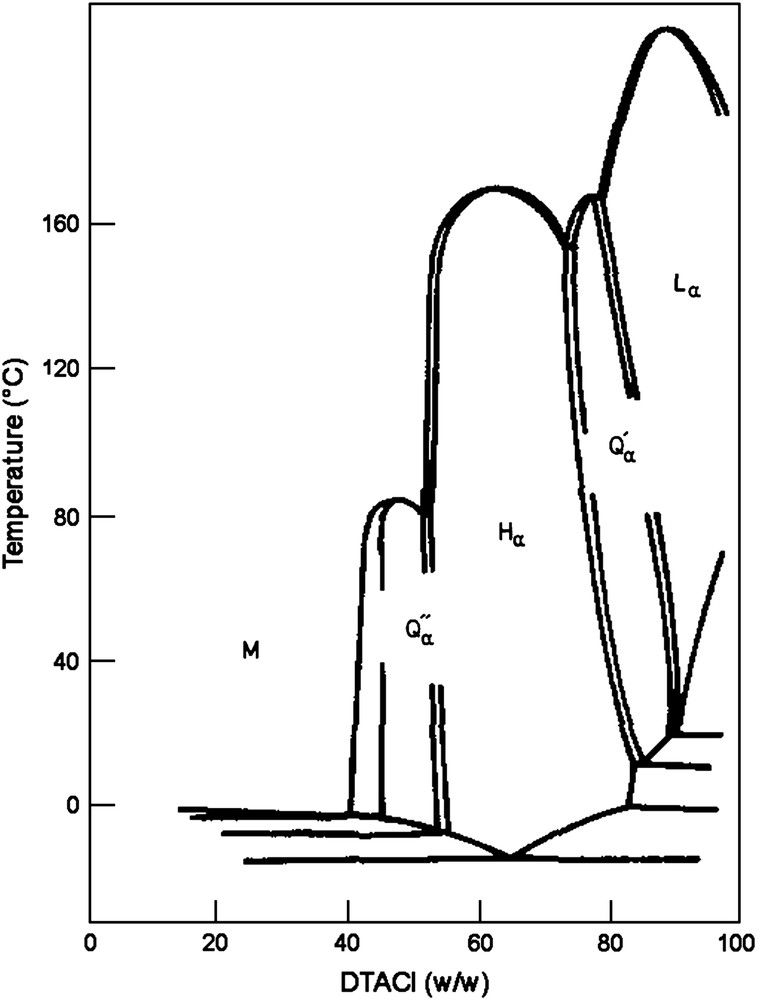
Phase diagram for the dodecyltrimethylammonium chloride/water system, Lα = lamellar, Hα = hexagonal, M = micellar, Q′α and Q″α = cubic (from Ref. [1]).
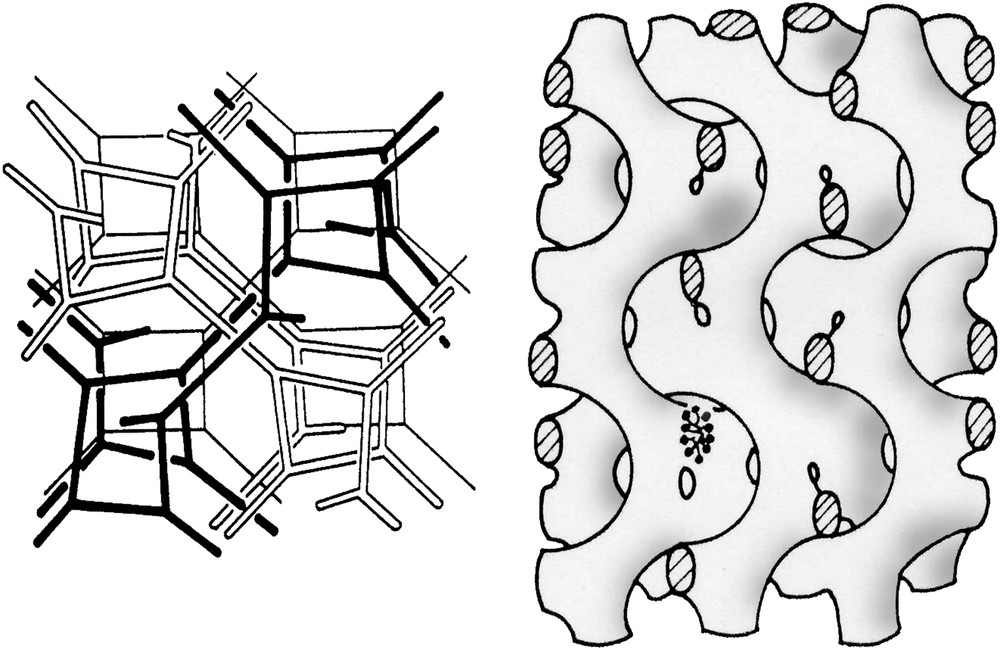
The structure proposed for cubic phase Q′α of space group Ia3d, the amphiphilic molecules build short rods connected three-by-three in two interwoven infinite networks.

The structure proposed for the cubic phase Q″α of space group Pm3n, the amphiphilic molecules build micelles either in an isotropic environment on the black sites or in an anisotropic environment on the white sites.
This work illustrates the role played by the notion of defect in the analysis of complex structures in soft condensed matter, one of the favorite problems among all those investigated by Yves Bouligand. It is a pleasure for us to acknowledge here his most original views and most stimulating contributions in throwing bridges between physico-chemical and biological structures.
2 Competition of physical forces and frustration
The concept of geometrical frustration [5] applies to systems in which several ordering forces have contradictory effects. It is clearly the case for amphiphile/water systems. We do not detail the forces acting in these systems. We only consider that they have components normal to the interfaces that impose constant distances between them when moving along them, and components parallel to the interfaces, whose values in the aqueous and paraffinic media control the interfacial curvature. The structures of these fluid films must therefore conciliate constant interfacial distances and curvatures, and we want to understand them investigating the geometrical configurations which satisfy these constraints. When the thermodynamical conditions are such that the interfaces are flat, the obvious configuration is that of the periodical stacking along one dimension of the lamellar phase shown in Fig. 4. When these conditions deviate from the above, the interfaces become curved and a typical case of geometrical frustration is met, as shown in Fig. 4, as the normal forces, which want to maintain a constant distance, are in conflict with the parallel forces, which want to maintain a constant curvature. This frustration has no direct solution in flat Euclidean space R3 but has one in curved space S3, the hyper-sphere. However, the real systems exist in R3 and the possible configurations are to be found in this space. They will be obtained by introducing defects of rotation, or disclinations, to suppress the curvature of S3 [6]. Following this process the structures of amphiphile/water liquid crystals can be looked at as structures of disclinations. We study here the particular processes leading to configurations having the topologies of cubic phases [7,8].
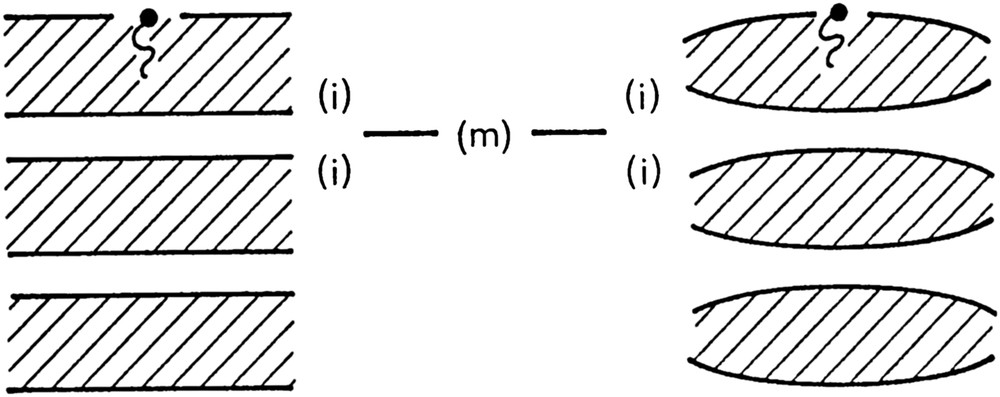
Schematic representation of the frustration: flat interfaces, this situation is compatible with a constant distance between them, this is the case in lamellar phases (left), curved interfaces (right), this is not compatible with a constant distance if the lamellar symmetry is kept and this imposes changes of topology and symmetry.
3 Relaxation of the frustration in S3
The whole periodic system of frustrated fluid films can be represented without frustration in S3 by transferring the middle surface of the film in one cell onto surfaces separating S3 in two identical sub-spaces. Doing so, the symmetry of the film and the periodicity (defined as generated by displacements along geodesics of the space, here great circles of S3 normal to the interfaces) are preserved. There are two surfaces separating S3 in two identical sub-spaces: the spherical torus T2 and the great sphere S2. The spherical torus can be obtained by identifications of the opposite sides of a square sheet in S3, as shown in Fig. 5, and, therefore admits a {4, 4} regular tiling.1 The great sphere S2 is an ordinary sphere embedded in the hyper-sphere, it is equivalent to the equator of the sphere when two-dimensional spaces are considered. Now, being a curved space, the hyper-sphere presents an angular deficit around each of its points with respect to the flat Euclidean space where we live, and correcting this deficit by angular defects, i.e. disclinations, bringing the necessary angular complements is a way to map S3 onto R3. But the nature and the mode of introduction of the disclinations must respect the symmetries of the relaxed structures in S3 [9].
4 Disclinations normal to the spherical torus and “bicontinuous” cubic structures
Disclinations are to be introduced around the symmetry axes of the relaxed structure in a manner respecting the symmetries. The process for introducing a disclination in a material is known as the Volterra's process. As shown in Fig. 6, a cut is made ending on a symmetry axis of the material and an angular sector of the same material is introduced in-between the lips of the cut, matching the symmetries on either sides of them in order to avoid any distortion along the surfaces in contact. After relaxation, the stress, hence the energy of the defect, is concentrated along the line ending the cut. When applied to the spherical torus, the Volterra process leads to a configuration which has a bicontinuous topology similar to that of the cubic phases Q′α. In the course of this process, the squares of the {4, 4} tiling of the spherical torus are transformed into hexagons without any modification of the number of polygons per vertex, or the π/2 values of the angles, as shown in Fig. 7. A new surface is therefore generated by this disclination process which admits a {6, 4} tiling. Obviously such a tiling is not Euclidean, or planar, and the new surface has a constant negative Gaussian curvature, it is a hyperbolic plane. A hyperbolic plane, a bi-dimensional space with constant negative Gaussian curvature, cannot be embedded in R3 without metric distortions. However, the properties of such hyperbolic planes can be studied using the Poincaré model in the Euclidean plane [10]. A hyperbolic plane with a {6, 4} tiling is represented in Fig. 8a, together with its orthoscheme triangles or asymmetric units. These triangles have angles of π/2, π/4, and π/6 and are not Euclidean. The analysis of their possible configurations, straight or curved sides, informs about the possible surfaces in R3. We consider only one case here, when the two sides of the right angle are straight; other cases are discussed in Ref. [7]. These straight sides build a lattice of intersecting straight lines whose element is a non-planar quadrangle (α, β, γ, δ) with three angles of π/2 and one of π/3. These elements can be assembled four-by-four in a more symmetrical skew quadrangle (δ, ɛ, φ, χ) with four angles of π/3 and four equal sides (Fig. 8b). These quadrangles are regularly organized on the hyperbolic plane and it was shown by Schoenflies [11] and Schwarz [12] that, when embedded in R3, they build a cubic lattice whose translation cell is shown in Fig. 8c. Schwarz has shown that this cubic lattice is the support of an infinite periodic minimal surface (IPMS), called F or D, separating R3 into two identical sub-spaces whose labyrinths are the two interwoven, but not connected, lattices of rods shown in Fig. 9. These two interwoven labyrinths are indeed identical to those which were determined for the cubic phase built by lipids extracted from insect cuticles [13] and more recently for that built by glycerol monooleate [14]. (In these cases the labyrinths are channels of water separated by a bilayered film of amphiphile whose middle surface should follow the F-surface very nearly).
A Volterra defect inserted in a volume of matter.

A -π-disclination in a square transforms it into an hexagon, the four-connectivity is preserved at every vertex; if the original square is in a plane with zero Gaussian curvature, the plane transforms into a hyperbolic surface with negative Gaussian curvature.
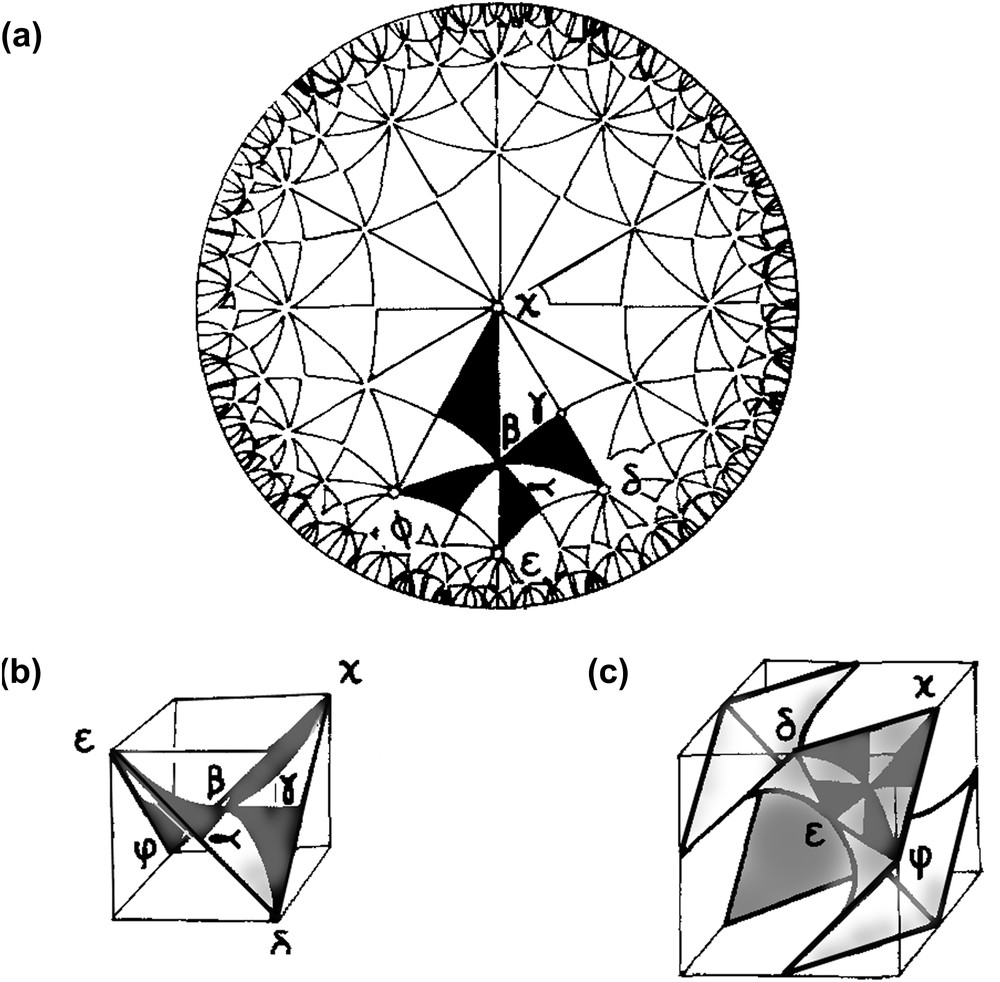
Poincaré's representation of a hyperbolic plane with {6, 4} tiling and its orthoscheme triangles with angles π/2, π/4, π/6 (top), the organization of quadrangles (α, β, γ, δ) in the saddle (δ, ɛ, φ, χ) in R3 (left), the monkey saddle cell with a set of six quadrangles (δ, ɛ, φ, χ) (right).
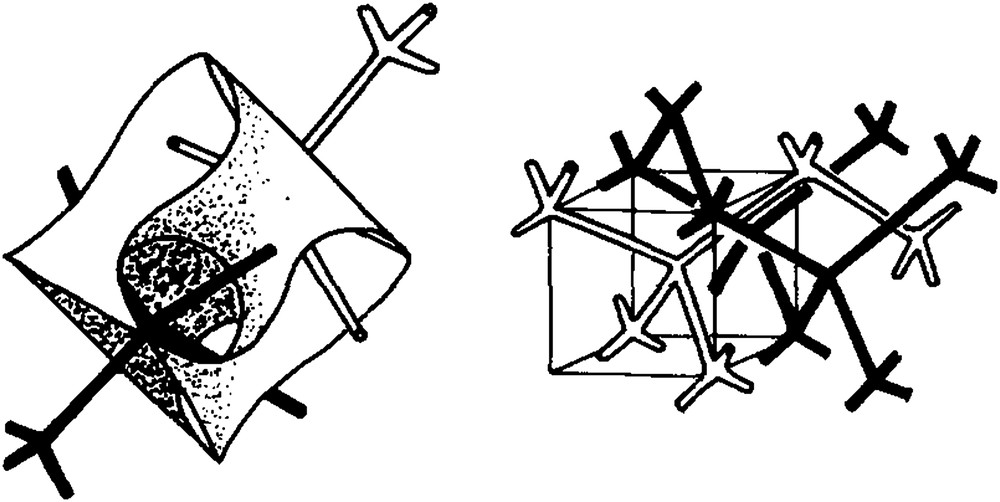
The translation cell for the F-surface of Schwarz and the labyrinths of the Pn3m cubic structure separated by this surface.
The two other configurations possible for the orthoscheme triangle, one with a straight hypotenuse and another with all sides curved, permit to build two other cubic phases [8]: one with Im3m symmetry, where it is the P surface of Schwarz which separates labyrinths of rods connected six-by-six, another with Ia3d, where two labyrinths of rods connected three-by-three are separated by a surface G calculated more recently by Schoen [15] (see also Fig. 2).
5 Infinite periodic minimal surfaces, “bicontinuous” cubic structures and the hyperbolic plane
Using intrinsic operations of symmetry groups defined by displacements inside the surface, we take advantage of the relation existing between these groups and those characterizing the tilings of the hyperbolic plane. The three IPMS of negative curvature admit a {6, 4} tiling. It is therefore tempting to associate these IPMS with a surface of constant negative Gaussian curvature, the hyperbolic plane also admitting a {6, 4} tiling [16]. It is possible to show that the relationships existing between the hyperbolic plane and the IPMS are indeed of the same nature as those existing between the Euclidean plane and other surfaces, such as a cylinder or a torus. A cylinder is obtained by cutting a strip from a plane and identifying the two boundaries, a torus of genus g = 1 is obtained by cutting a square, or a rectangle, in a plane and identifying the opposite edges 2 by 2. If a Euclidean {4, 4} net of unit cells is defined on the original plane, the identifications needed for building the cylinder and the torus are identical to the application of Born–von Karman conditions preserving the translational periodicity of the plane. Thus, new surfaces can be built from the plane by substituting some operations of translation by identifications.
Symmetry operation of a tiling like the {6, 4} are obtained by combinations of the reflections into the sides of the orthoscheme triangles [17]. If two reflections defined by two non-intersecting sides are combined, the resulting operation is, like in Euclidean space, a translation. It is possible to define translation sub-groups in the {6, 4} hyperbolic [18].
In the example of the {4, 4} lattice in two-dimensional flat space, identification of all translations to the identity leads to a torus of genus g = 1. In the case of the {6, 4} hyperbolic tiling, the identification of all translations to the identity leads to a torus with a genus g = 3. This is also the property of the three cubic IPMS P, F, G. If only well-chosen translations are forced to the identity, it is possible to get surfaces embedded in R3 that are the three cubic IPMS. Obviously, this can be seen as some kind of surgery, in which some parts of the hyperbolic plane are cut and lips of the cut reglued. This method is an interesting tool to study symmetry of networks in R3 [19].
The three cubic IPMS P, F, G have the topologies and symmetries of the Q′α structures observed in-between lamellar and hexagonal phases. Among these three structures, Ia3d is the most commonly observed, followed by Pn3m then Im3m structures. In fact, the choice between one of these three structures results from subtle changes of physico-chemical parameters (see for instance [20]). It is interesting to quote here that biological membranes can eventually build bicontinuous cubic structures with similar symmetries; they, however, differ from those of physico-chemical origin described above by the fact that they exhibit parameters larger by about one order of magnitude: coarsely, 102 nm against 10 nm [21]. Most likely, forces related to the specificities of biological membranes and their molecules are to be taken into account [22].
6 Disclinations on the great sphere and “micellar” cubic structures
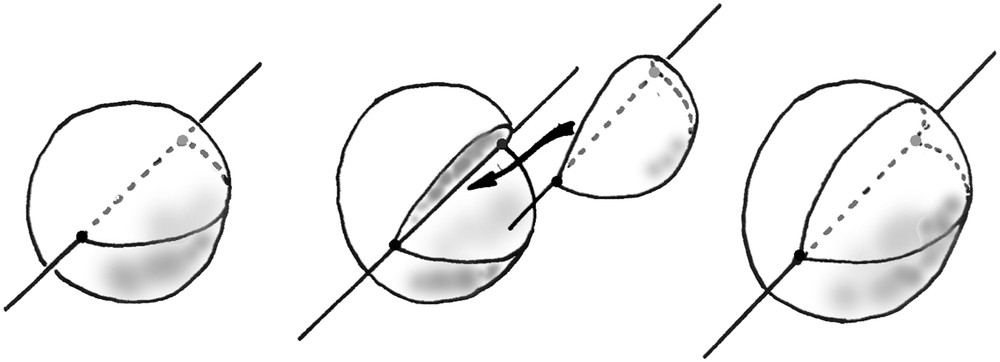
The relaxed structure admits C2 symmetry axes which are great circles of S2 and the Volterra's process corresponding to the creation of a disclination along one of these axes brings in a third finite sub-space, as illustrated in Fig. 10. The development of this process in order to map S3 onto R3 leads to a space filling packing of identical finite cells. The law of topological stability imposes the search for eventual space filling assemblies of regular polyhedra, or polytopes, having three faces per edge and four edges per vertex or, having three faces belonging to the same polyhedron around one vertex and three polyhedra around one edge [23]. These are, in Schafli's {p, q, r} notation, the polytopes of the {p, 3, 3} family. They are four which, unfortunately, exist in curved spaces only [24], those being in spherical spaces with constant positive Gaussian curvatures {3, 3, 3}, {4, 3, 3}, and {5, 3, 3}, and in a hyperbolic space with constant negative curvature {6, 3, 3}. As there is no {p, 3, 3} polytope in a flat Euclidean space, our problem admits no solution with identical regular polyhedral cells2 [25]. We are therefore driven to search for eventual non-regular but, nevertheless, periodic solutions. For this it is useful to consider the fact that the regular {p, 3, 3} polytopes are found in spaces of decreasing curvatures and are therefore met one after the other during the progressive introduction of disclinations needed to map S3 onto R3. The polytope of interest is obviously {5, 3, 3}, which exists in the space of lowest positive curvature. We must start from this and add in new disclinations in order to realize the final mapping of S3 onto R3. To maintain the cellular structure disclinations cannot be contained in the surfaces. Symmetries impose to choose new disclinations perpendicular to cell faces. Indeed it is known that disclinations perpendicular to pentagonal faces of a dodecahedron transform it into the tetrakaidecahedron and hexakaidecahedron shown in Fig. 11.
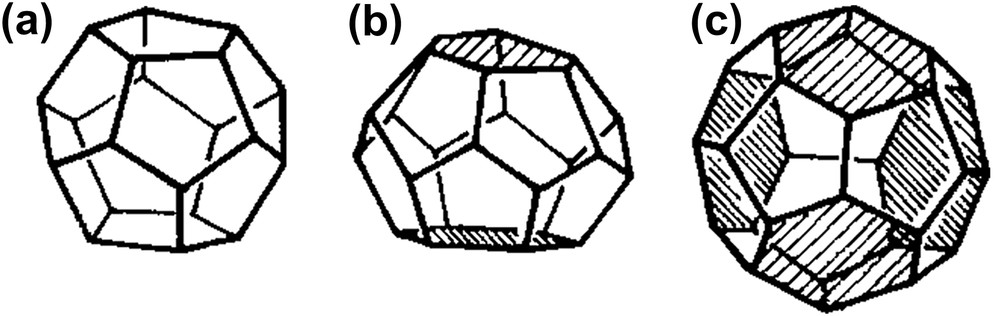
Transformation of a dodecahedron (a) into a tetrakaidecahedron (b) by one 2π/5 disclination along an axis normal to pentagonal faces and into a hexakaidecahedron (c) by four half disclinations; hexagons created from pentagons by disclinations are hatched.
These non-regular polyhedra are particularly interesting here as it is known that when slightly distorted they can be packed so that they build periodic space filling assemblies of cells [26]. These organizations should be those of the film and micelles permitted by the properties of our Euclidean space, the film being supported by the faces of the polyhedra, and each cage delimited by it contains a micelle. Several structures can be built along the above principle and, among them, we can distinguish two large families according to the fact that their dihedral and edge angles stay close to those of fluid films, whether they balance their tensions or not. If we limit ourselves to the first case, we are left with two relatively simple structures: firstly, the type-I structure has space group Pm3n and its crystallographic unit cell contains 2 dodecahedra and 6 tetrakaidecahedra, the local arrangement of its polyhedra being shown in Fig. 12. The second, type-II structure has space group Fd3m and its crystallographic unit cell contains 16 dodecahedra and 8 hexakaidecahedra. These structures have the topologies and symmetries of the structures of the Q″α cubic phases found in-between hexagonal and micellar phases. The faces of the polyhedra support the film and the micelles are contained within the polyhedra. As there are two types of polyhedra, there are two types of micelles.
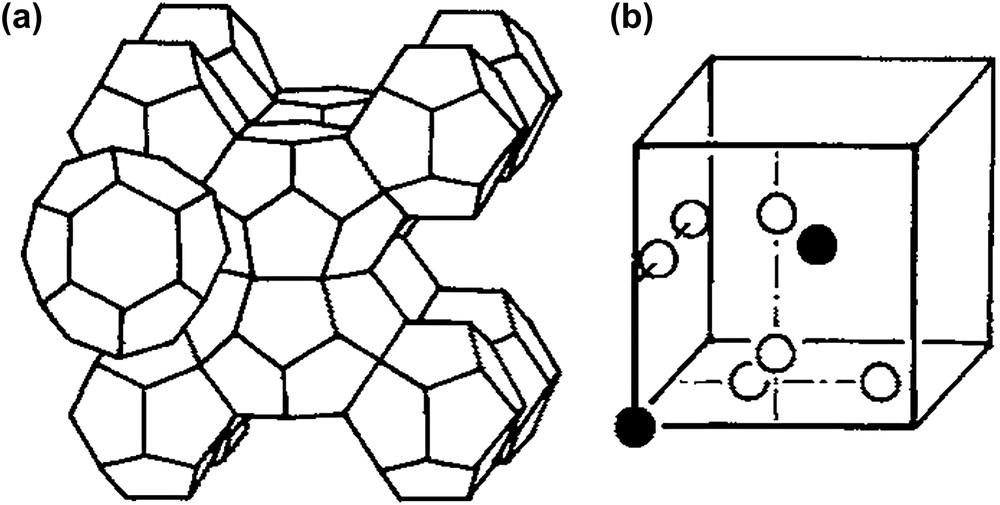
Aggregation of slightly distorted dodecahedra (black sites) and tetrakaidecahedra (white sites) in a periodic structure with Pm3 symmetry (from Ref. [26]).
This agreement shows the importance of the space filling term in the formation of these structures. However, observations of a few cases of micellar cubic phases with other symmetries, for instance compact hexagonal P663/mmc [27], show that other constraints may intervene. At last, the well-defined localizations of bicontinuous and micellar cubic phases in the phase diagrams, on either sides of the hexagonal phase, can also be analyzed within the frame of this geometrical approach [28].
7 Comment
Two incompatible topological requirements are confronted in the systems under study: that looked for by the local configuration and that imposed by the structure of our Euclidean space, the second preventing the propagation of the first. This incompatibility vanishes if the systems are considered as embedded in adequate curved spaces; ideal structures can be built there in which the local configuration propagates freely. Mapping the curved spaces onto the Euclidean one with disclinations correcting their angular deficit leads to structures which can be seen as the best compromises between the two requirements. In these optimal structures, regions where the local configuration is kept ideal and regions where it is distorted by disclinations, illustrated in Fig. 13, are organized regularly. The energy cost is concentrated in the latter and their interaction, most likely repulsive, organizes and stabilizes the structures. These optimal structures being similar to the observed ones, the complexity of the latter is not to be analyzed as the packing of individual molecules but as that of these regions, each of which being made of large numbers of molecules. This explains the changeover from the liquid-like disorders of the molecules in their respective domains to the formation of crystalline structures and justifies the jump by one order of magnitude at least from the characteristic molecular size to the structural parameter. By this last point, this problem is not far from that of the crystalline structures with large cells formed by certain alloys [29].
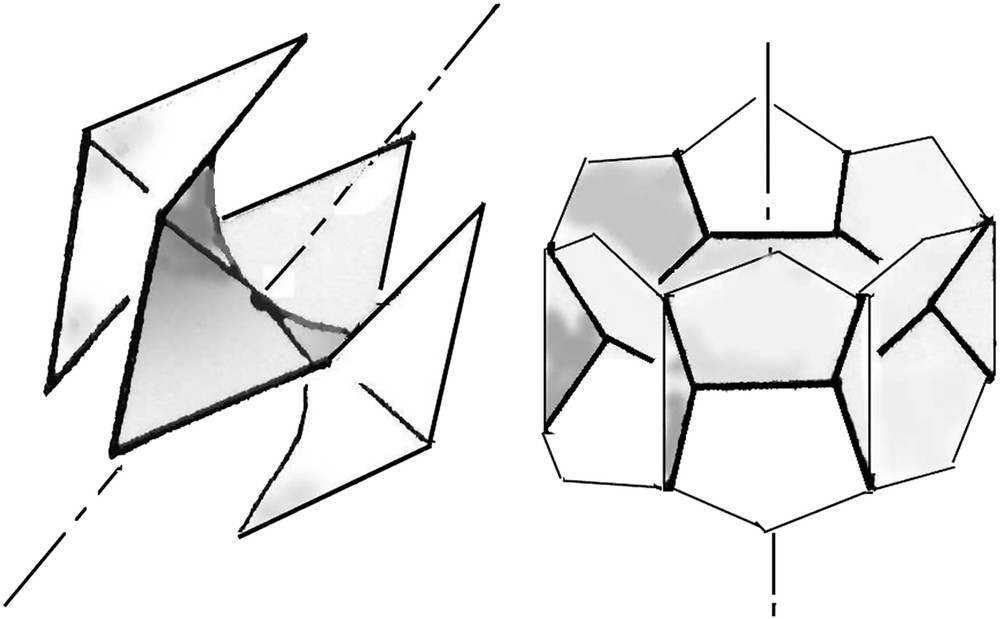
A disclination surrounded by saddles, memories of the spherical torus, in the Pn3m bicontinuous cubic structure (left), a disclination surrounded by junctions of films, memories of the {5, 3, 3} polytope in the Pm3 micellar cubic structure (right).
1 The Schlafli notation {p, q} for a two-dimensional tiling means that the tiling is made of regular polygons having p edges that meet q by q at vertices. Notation {p, q, r} for a three-dimensional packing means that the packing is made of regular polyhedra having faces with p edges, each polyhedron has q faces around one vertex and there are r polyhedra around one edge.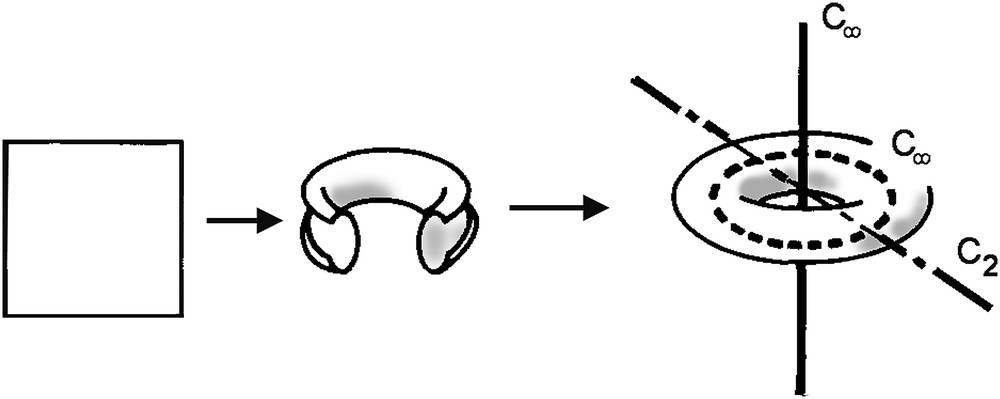
2 Soap bubble froth are macroscopic examples of the impossibility of filling R3 with {p, 3, 3}.


