1 Introduction
Yves Bouligand's stunning interpretation of bow-shaped fibers (arceau) as a structure fibrillaire torsadée [1] launched the field of cholesteric liquid crystal defects in physics [2,3], polymeric liquid crystals [4] and biology [2,4,5]. Why cholesterics? Because they are chiral, nematic liquid crystals with a length scale. Nematic liquid crystals, now on every laptop in the universe, have no length scale. While triggering a roaring avalanche, Bouligand gently noted: Ce phénomène est trop irrégulier pour qu'on puisse adopter avec certitude cette interprétation… [1].
A group theoretic treatment of defects in systems with broken continuous symmetries lead Volovik and Mineev to class multiplication tables for cholesteric defects [6]. They argued that cholesterics could belong to the same group as the biaxial nematics of Toulouse [7] and Mermin [8]. But, cholesterics have a length scale thus limiting the rigor of a group theoretic treatment. One can summarize: Ce phénomène est trop régulier pour qu'on puisse adopter avec certitude cet interprétation.
Because nematics have no length scale, we can adopt with certainty, the Class Multiplication Table for nematic defects1 (Table 1). Only two characters are needed to completely describe a uniaxial nematic's symmetry group: the identity, E, and C2, an 180° rotation of the nematic director, n. Because two 180° rotations recover the identity (C2 × C2 ↔ E in Table 1), S = ±1 disclinations are not line defects in 3D, i.e. they are homotopic to the uniform state (E) [9].
| C2(2) | E | C2 |
| E | E | C2 |
| C2 | C2 | E |
As Toulouse enunciated in his talk at Bell Labs (∼1977): “You cannot lasso a basket ball”, the basketball being a hemisphere (because n = −n) of allowed orientations for n and the lasso, a closed loop on that surface, can shrink to a point representing a uniform state. The only other closed line on this surface joins two diametrically opposite but physically equivalent points. It topologically describes a Möbius line defect, S = +1/2 or S = −1/2. Each can turn into the other just by “going over the top” of the hemisphere [4,10]. Or, in a Toulouse corollary, each Möbion is its own anti-defect.
I was delighted. Just before I left Orsay in 1972 for Bell Labs, Yves and I had been studying the optical contrasts of defects in thin slices of polymerized liquid crystals. I had made a calculation to understand the bright focused lines often associated with S = ±1/2 defects when viewed between glass plates. The calculation was considered WRONG, because it showed an S = +1/2 turning into an S = −1/2 when it “turned a corner” in a cube.
Without benefit of homotopic theory of defects, Yves had to fight long and vigorously to convince formidable experts [4]. A similar, but not exact, David and Goliath scenario comes to mind. Not exact because, 5 years later, Toulouse still did not know about Ref. [4].
In his 1981 Christmas card, Yves illustrated S = ±1/2 homotopy (Fig. 1) showing the inclusion of edge disclinations. With his permission, I submitted Fig. 1 for our popular article in Physics Today on defects in liquid crystals [10]. To my great regret, it was edited out for reasons I never knew. It is a good example of Bouligand's talents for sharing with the rest of us the power and beauty of complex liquid crystalline structures in 3D [11,12].
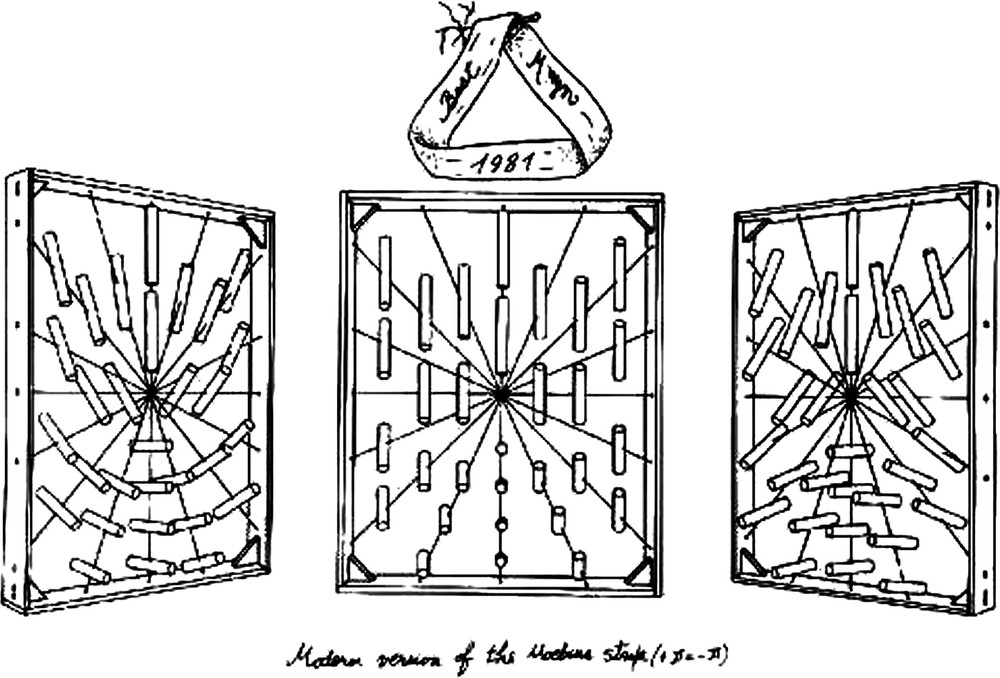
In nematics, there is only one line defect – includes edge disclinations [11].
2 Arceau
One of Bouligand's most impressive talents is that he is not afraid of complexity. In fact, one might say, he relishes deciphering and discussing complicated images that tend to immobilize lesser mortals. Then, he “magically” pulls out of his hat beautiful drawings of the linchpins to his ideas thus clarifying everything for everyone.
A good example is his early drawing to account for the observation of arceau in chromosome fibers (Fig. 2). The arceau is an idea accessible to many that came out of observations of a series of very complicated patterns [1,2].

The arceau in chromosome fibers [1].
As Yves Bouligand is a champion of complexity, I would like to share with him some of our recent observations and thoughts on the B7 phase formed by Weissflog's banana-shaped molecule [13]. Fig. 3 is a snapshot showing B7's resemblance to the biological branch of the liquid crystal family [14,15].
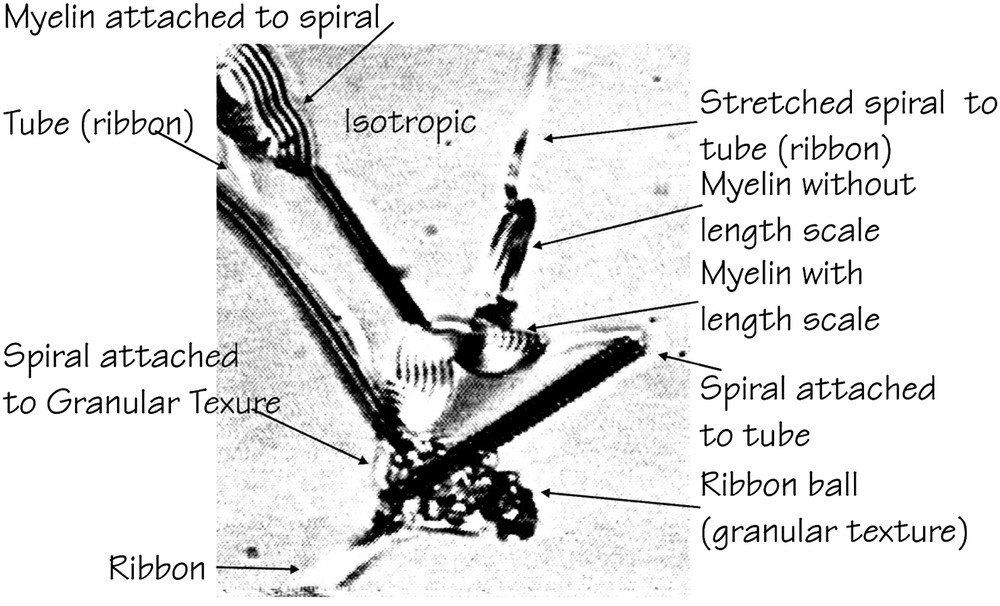
The many textures observed in thin (1–4 μm) B7 sample about 12 K below a transition to the isotropic liquid state after cycling many times in an electric field. The field of view is ∼170 × 150 μm [14].
We distinguish between Weissflog's B7 bananas, from other similarly named banana phases, because its X-ray diffraction pattern does not show a simple layered structure, or indeed, any structure known up to now in classical liquid crystals [13]. We do not know the ground state of Weissflog's B7. In its B7 phase, many different birefringent objects come and go in an isotropic (tetrahedratic?) sea, even quite far from the transition temperature2 to the usual isotropic liquid state [14,15]. What if the isotropic liquid in Fig. 3 is tetrahedratic [16]? Let's go to a thicker sample [15].
3 Tetrahedratic banana LCs
While thinking of achiral biaxial smectic liquid crystals, Helmut Brand, Harald Pleiner and myself came up with banana liquid crystals [17–19]. We found that even though these objects were achiral (no asymmetric carbons) they could, by symmetry, have a polarization, P, when stacked in layers.
To our surprise, when achiral banana liquid crystals were first synthesized [20,21], they spontaneously exhibited ambidextrous chirality – both left- and right-handed structures were observed. Ambidextrous chirality is unknown in quadrupolar (Qij) liquid crystals [22].
Before achiral banana-shaped liquid crystals had been synthesized, Leni Fel went beyond quadrupolar liquid crystals (Qij) to consider liquid crystal phases with tetrahedratic (octupolar) order, Tijk [16] (Fig. 4). Tetrahedratics lack inversion symmetry and are optically isotropic.
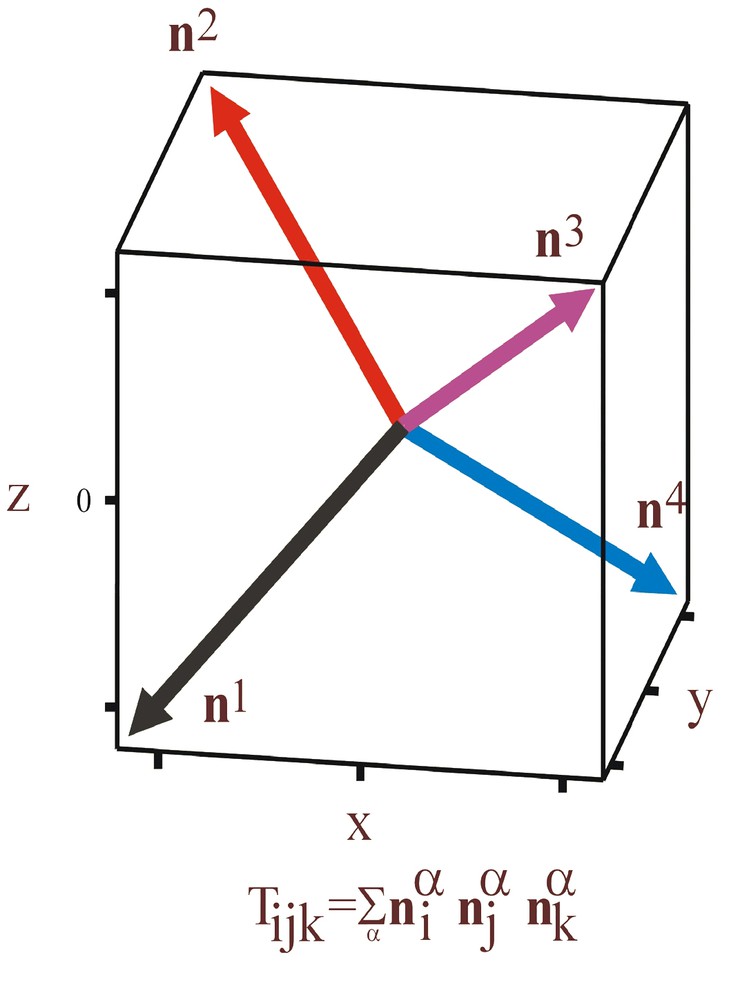
The tetrahedratic order parameter, Tijk, where α = 1, 2, 3 or 4 refers to the 4 vectors in the cube. Tetrahedratics are isotropic and lack inversion symmetry.
After banana LCs were synthesized [13,20,21], Rhadzihovsky and Lubensky argued [23,24], that banana symmetry required the usual quadrupolar order parameter, Qij [22], a vector order parameter, P [17–19], and also, Fel's octupolar order parameter, Tijk [16], all coexisting at every spot in space and all at the same time.
A daunting proposition. However, such coexistence is possible as the different moments of the mass distribution (the second moment for nematics, the third one for tetrahedratics) are independent of each other [25].
A simplifying feature for analysis is that the free energy gradient terms in Qij and Tijk can couple at lower order [25,26] than spatially homogenous ones, rather similar to cholesterics. While Tijk lacks inversion symmetry, it has no preferred sense of rotation. Consequently, this lowest order gradient term accounts for ambidextrous chirality in achiral banana liquid crystals by reducing the energy of ambidextrous twist in both fields below that of the uniform state [26].
Recently we found that the same lowest order coupling term could account for the biaxial myelin in Fig. 5 by facilitating the spontaneous appearance of biaxial Bouligand arceau with an average length scale [25].

Biaxial myelin observed in a free drop of Weissflog's B7 about 7 K below TB7-I [15]. Polarizers crossed 45° to the border.
Nevertheless, the coexistence of the two order parameters, Tijk and Qij, at each point in space, poses many questions. For example, how does one draw the picture?
Our solution is to embed a uniaxial nematic director in the tetrahedral field (Fig. 6) and draw many pictures (or phase portraits) when the order parameters vary spatially.

The well-known side view of n in a Bouligand arceau alone and superposed on the computed Tijk. The less familiar top view, an arceau for n alone and superposed on Tijk, is the view looking down on Fig. 5. Embedding a uniaxial field (n) in an isotropic field that lacks inversion symmetry (Tijk) can lead to biaxiality [25].
Fig. 6 shows for spontaneous splay-bend that the tetrahedratic vectors are not symmetric around n [25], making the net field biaxial.
We interpret Fig. 5 as a spontaneous splay-bend texture viewed from “the top” as in Fig. 6. Its remarkable features include thick continuous black lines, marked 0, 1, 2 and weak biaxiality as evidenced by the extinction asymmetry when one of the optic axes is perpendicular (nearly ordinary ray) to the polarizer compared to when it is parallel (only one extraordinary ray), and the bright focused spot at the top left of line “0” from one of the extraordinary rays focusing to the center of the defect line. The average distance between the black lines is 16.3 ± 1.8 μm. The biaxiality in Fig. 5 is a consequence of the lowest order coupling between gradients in quadrupolar and tetrahedral (Fig. 4) order [25].
4 Biaxial arceau
Birefringent optics is rich and complex. An extraordinary ray refracts when its index of refraction changes in space while ordinary rays, having only one index of refraction, travel in straight lines [27,28]. It might help to think of the biaxiality in Fig. 5 as weak so that one of its extraordinary rays is close to ordinary.
In Fig. 7, we take the side view of a biaxial arceau (Fig. 5) and consider how extraordinary rays travel through a splay-bend texture when viewed from the top. We assume that all the black lines, even the faint ones, are where the optic axis is parallel to the incident rays. The fact that they are not uniformly black is likely due to slight irregularities in sample flatness as it travels. We assume every black line is where the optic axes are parallel to the incident beam (i.e. 0, π, 2π… in the side view of Fig. 6, or, homeotropic). Between every black line in Fig. 5, we imagine a 0–π splay-bend wall (Fig. 7).

Optical path for the side view of Bouligand arceau in Fig. 6.
When the polarization is parallel to the splay-bend texture, the extraordinary wave front bends towards the region with higher index of refraction i.e. away from the black lines. When the incident ray is exactly parallel to n, it bends to either side perpendicular to the dark lines, doubling when it is a single extraordinary [27,28] ray. This accounts for the zig-zaggy extinction lines in the top left quadrant of Fig. 5. The bright white spot at the end of line “0”, is because the single extraordinary ray in this polarization focuses a little bit more towards the end of line “0” because of the defect curvature.
As there is relatively little spatial variation in the nearly ordinary index of refraction when the polarization is perpendicular to the splay-bend texture, it travels pretty much straight through. It refracts parallel to the dark lines. This accounts for the nearly uniform blackness of the extinction brush (only a little bit of blackness leaks out) in the top right quadrant of Fig. 5. A pure ordinary ray would not leak.
5 Questions
Fig. 5 may be the first observation of a biaxial nematic defect, predicted to come in three flavors [6–8]. Question: what is the group multiplication table for a uniaxial nematic embedded in an achiral tetrahedratic field? Does it differ from biaxial nematics?
Is a biaxial nematic with an average length scale sufficiently irregular to satisfy Yves Bouligand [1] for biological systems?
Acknowledgements
It was a great pleasure, and honor, to participate in this Festival Honoring Yves Bouligand, champion of new ideas, complexity and life. Once again, the arceau opens a treasure chest.
Vive l'arceau ! I thank Françoise Livolant, Marie Madeleine Giraud and Françoise Gaill for lively and friendly discussions during the stimulating and fascinating conference they organized to honor Yves Bouligand.
1 Notation from M. Tinkham, Group Theory and Quantum Mechanics, McGraw Hill Book Company (1964) p. 324.
2 Large latent heat 7.5 cal/g, TB7-I = 180 °C, DSC tested stable over several days of temperature cycling [14].


