Limit of detection of cerebral metabolites by localized NMR spectroscopy using microcoils

Nicoleta Baxan; Herald Rabeson; Guillaume Pasquet; Jean-François Châteaux; André Briguet; Pierre Morin; Danielle Graveron-Demilly; Latifa Fakri-Bouchet

doi:10.1016/j.crci.2007.07.002

Limit of detection of cerebral metabolites by localized NMR spectroscopy using microcoils

Nicoleta Baxan ¹ ; Herald Rabeson ¹ ; Guillaume Pasquet ² ; Jean-François Châteaux ² ; André Briguet ¹ ; Pierre Morin ² ; Danielle Graveron-Demilly ¹ ; Latifa Fakri-Bouchet ¹

¹ Laboratoire CREATIS – LRMN UMR CNRS 5220, INSERM U630, INSA de Lyon, UCB Lyon-1, 3, rue Victor-Grignard, 69616 Villeurbanne, France
² Laboratoire INL CNRS UMR 5270, UCB Lyon-1, bâtiment Léon-Brillouin, 43, bd du 11-Novembre-1918, 69622 Villeurbanne cedex, France

Comptes Rendus. Chimie, Volume 11 (2008) no. 4-5, pp. 448-456.

Résumés

Anglais
Français

NMR has the ability to investigate biological systems non-destructively; however, its low sensitivity has primarily hampered their investigation compared to other techniques. Therefore, optimizing radiofrequency coils to improve sensitivity do offer benefits in NMR spectroscopy. Sensitivity may be improved for mass and volume limited samples if the size of the detection RF coils matches the sample size. In this paper, the mass and concentration limits of detection (LOD_m, LOD_c) for a microcoil will be estimated by MRS measurements and then compared with analytical values. For the Choline case, the LOD_c is close to 4.4 mM. These preliminary results enable us to open largely the biomedical applications based on cerebral metabolism investigation by experiments in small animals.

La nouvelle génération de microantennes fabriquées par des techniques de microélectronique offre une approche intéressante pour l'analyse par spectroscopie localisée d'échantillons de faibles concentrations et de faibles volumes. En effet, l'adaptation des dimensions de l'antenne aux échantillons permet l'amélioration du rapport signal sur bruit et, par conséquent, l'optimisation de la résolution spatiale et temporelle des acquisitions. Dans cette étude, les limites de détection LOD_m et LOD_c, établies comme figures de mérite, sont estimées expérimentalement et comparées à leurs valeurs analytiques. Dans le cas de la choline, LOD_c est de 4.4 mM. Ces résultats préliminaires prometteurs offrent une nouvelle voie de recherche pour les applications biomédicales in vivo chez le petit animal.

Métadonnées

Reçu le : 2007-04-27
Accepté le : 2007-07-17
Publié le : 2007-11-28

DOI : 10.1016/j.crci.2007.07.002

Keywords: Magnetic resonance localized spectroscopy, Microcoil, Concentration sensitivity, Mass-limited sensitivity, Limit of detection LOD, Cerebral metabolites, Quantification
Mots clés : Spectroscopie localisée par résonance magnétique, Microantennes, Sensibilité en fonction de la concentration S_c, Sensibilité en fonction de la masse S_m, Limites de détection LOD, Métabolites cérébraux, Quantification

Affiliations des auteurs :

Nicoleta Baxan ¹ ; Herald Rabeson ¹ ; Guillaume Pasquet ² ; Jean-François Châteaux ² ; André Briguet ¹ ; Pierre Morin ² ; Danielle Graveron-Demilly ¹ ; Latifa Fakri-Bouchet ¹

@article{CRCHIM_2008__11_4-5_448_0,
     author = {Nicoleta Baxan and Herald Rabeson and Guillaume Pasquet and Jean-Fran\c{c}ois Ch\^ateaux and Andr\'e Briguet and Pierre Morin and Danielle Graveron-Demilly and Latifa Fakri-Bouchet},
     title = {Limit of detection of cerebral metabolites by localized {NMR} spectroscopy using microcoils},
     journal = {Comptes Rendus. Chimie},
     pages = {448--456},
     publisher = {Elsevier},
     volume = {11},
     number = {4-5},
     year = {2008},
     doi = {10.1016/j.crci.2007.07.002},
     language = {en},
}

TY  - JOUR
AU  - Nicoleta Baxan
AU  - Herald Rabeson
AU  - Guillaume Pasquet
AU  - Jean-François Châteaux
AU  - André Briguet
AU  - Pierre Morin
AU  - Danielle Graveron-Demilly
AU  - Latifa Fakri-Bouchet
TI  - Limit of detection of cerebral metabolites by localized NMR spectroscopy using microcoils
JO  - Comptes Rendus. Chimie
PY  - 2008
SP  - 448
EP  - 456
VL  - 11
IS  - 4-5
PB  - Elsevier
DO  - 10.1016/j.crci.2007.07.002
LA  - en
ID  - CRCHIM_2008__11_4-5_448_0
ER  -

%0 Journal Article
%A Nicoleta Baxan
%A Herald Rabeson
%A Guillaume Pasquet
%A Jean-François Châteaux
%A André Briguet
%A Pierre Morin
%A Danielle Graveron-Demilly
%A Latifa Fakri-Bouchet
%T Limit of detection of cerebral metabolites by localized NMR spectroscopy using microcoils
%J Comptes Rendus. Chimie
%D 2008
%P 448-456
%V 11
%N 4-5
%I Elsevier
%R 10.1016/j.crci.2007.07.002
%G en
%F CRCHIM_2008__11_4-5_448_0

Nicoleta Baxan; Herald Rabeson; Guillaume Pasquet; Jean-François Châteaux; André Briguet; Pierre Morin; Danielle Graveron-Demilly; Latifa Fakri-Bouchet. Limit of detection of cerebral metabolites by localized NMR spectroscopy using microcoils. Comptes Rendus. Chimie, Volume 11 (2008) no. 4-5, pp. 448-456. doi : 10.1016/j.crci.2007.07.002. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2007.07.002/

Version originale du texte intégral

1 Introduction

Nuclear Magnetic Resonance Spectroscopy (MRS) is one of the most often used techniques to study the metabolism changes in different biological and chemical samples. NMR spectroscopy fulfils an important role through its ability to produce structural information and also to provide data on intermolecular dynamics. Current studies are concentrated on the analysis of limited sample volumes (of the order of the microlitre) – tissues, cell cultures, protein structures [1]. The field of NMR has developed a large array of experimental capabilities, but NMR sensitivity still lags significantly behind most other analytical methods by a factor of 100–1000, especially for many important mass-limited and concentration-limited samples. The observation of metabolites with short spin–spin relaxation decay becomes possible using short echo-time localization pulse-sequences. However, quantification of spectra is hampered by overlapping metabolite resonances and certainly by low signal-to-noise ratio (SNR) due to the limited size of the observed volume. Thus, the analysis of sample volumes of nanolitre order implies the development of NMR coils having dimensions of several micrometres [2,3] by microelectronics technology.

This paper presents the concept and the spectroscopic performances of a micro-NMR probe particularly suited to the analysis of such concentration-limited and mass-limited samples.

The originality of NMR microspectroscopy calls for a discussion of certain pertinent definitions and concepts to define the performance and design criteria essential to planning experimental strategies that maximize signal-to-noise ratio measurement. Consequently, in the first part we provide a brief overview of the figures of merit [4,5] which are important to determine the feasibility of our experiment using MR microprobes. Next, a comparison between the measured limits of detection by MR microspectroscopy and their estimated values based on analytical considerations will be described. The analytical estimation is based on several parameters like the nuclear precession frequency, the sample concentration and volume, the number of magnetically equivalent nuclei, which give rise to a particular resonance, the linewidth of the resonance and also the scan time, t_scan. The limits of detection of the acquired spectroscopic data are quantified based on the prior knowledge of the signals which will be analyzed by the QUEST method [6]. Additionally, performance criteria will be established based on the described figures of merit being very useful in choosing a probe for a particular analysis.

1.1 MR probe miniaturization

Research carried out during the last decade showed the possibility to implement NMR instrumentation at small scale, especially with radiofrequency resonators, which can be used as NMR signal detectors. The actual tendency in the MR spectroscopy field is the analysis of limited mass and concentration samples; the main limitation is represented by the low signal-to-noise ratio. Conventional MR instruments used for small volume analysis give a small signal-to-noise ratio (SNR) because of their large dimensions compared to the sample size. The amplitude of the MR signal is maximized when the size of the detection RF coil matches the sample's size. Therefore, a micro-MR device designed for microsamples is required to improve the signal-to-noise ratio (SNR) and consequently to increase the sensitivity [7]. Considering, the need of examining by spectroscopy (or by NMR microimaging) small quantities of tissue, it is possible to create probes with working volume compatible with such limitations [2]. Thus, to analyze samples with volume of the order of the nanolitre, it is necessary to build, by microelectronics technology, antennas having dimensions of several micrometres [3]. At this scale, susceptibility effects may modify considerably the static magnetic field spatial distribution in the microantenna vicinity. This problem seems to be circumvented by deposition of suitable substrates (for example As–Ga) on circuits, or by the use of microcircuit supports for which the choice of materials (copper–chromium, copper–beryllium) should guarantee the magneto-compatibility of the whole device. In addition, the use of materials with large gap may offer stability in temperature and frequency and may guarantee good conditions of biocompatibility. In such situation, the use of the MESFET (metal, semi-conductor field effect transistor) technology is certainly possible [8]. The construction of such resonators must be supplemented by the installation of the preamplifier on the same substrate in order to optimize the signal-to-noise ratio [9], which may be more efficient and less space consuming than external preamplifier devices as proposed formerly by Magin and coworkers in their pioneering work [10]. This way requires investigations essentially based on the present state of the art of microelectronics and it can turn into profit from nano-techniques' design processes. On the biomedical scope, accurate metabolites variations' quantification associated with spatial localization of small resonators placed directly into a well-defined region of interest (ROI) appears essential.

1.2 Figures of merit for MR microspectroscopy

The investigation of mass-limited and concentration-limited samples by MRS requires several performance criteria in order to validate the feasibility of the experiment using MR microprobes. These criteria allow computing the approximate mass or concentration of sample needed to acquire a desired SNR for a specific peak acquired during a specific scan time. These figures of merit [4,5] are the concentration sensitivity S_c, the mass sensitivity S_m, the concentration limit of detection LOD_c, and the mass limit of detection LOD_m, respectively. The sensitivity refers to the probe behaviour once the sample is placed in its active volume. Actually the sensitivity is the slope of the calibration curve of SNR versus the amount of sample in the detection region, here termed as the active volume V_active [10]. The concentration sensitivity is a figure of merit appropriate to compare the microcoils' performances using a sample of fixed concentration. It is defined as the ratio between the SNR and the concentration of the sample, S_c = SNR/C, where C is a chosen unit of concentration for the sample within the active volume of the microprobe [4]. S_c is a suited criterion of performance for a sample of fixed concentration. The mass sensitivity, S_m is defined as the ratio between the SNR and the amount of mass (or moles) of the sample in the active volume V_active, S_m = SNR/mol, where the mol refers to the number of moles of sample in the probe active volume. S_m is more appropriate in comparing probe performance for a sample of fixed mass. Both S_c and S_m are relaying on the signal-to-noise ratio value, as we can easily notice from their analytical expressions. SNR is an important factor that determines the ability of the instrument to perform measurements on the sample in reasonable time. There are a multitude of factors which contribute to the signal strength as well as to the noise factor of the equivalent electronic system. Time-domain SNR can be calculated as follows:

{SNR}_{t} = \frac{(\frac{B_{1}}{i}) ω_{0} M_{0}^{⊥} V_{s}}{\sqrt{4 k T_{s} R_{noise} Δ f}}

(1)

where B₁/i is the magnitude of the unitary magnetic field (i = 1 A), ω₀ denotes the Larmor frequency,

M_{0}^{⊥}

is the net magnetization of the sample, V_s is the sample volume, k is the Boltzmann constant, T_s is the coil's temperature,

Δ

f is the receiver bandwidth; at this scale, R_noise is mainly due to the coil's electrical resistance. This expression does not depend on spectral linewidth, but only on probe characteristics. However, MRS signals are generally analyzed as spectra. Consequently, it is necessary to determine an expression for normalized SNR in the frequency domain as well. Its expression depends on several parameters [8,11–13] as follows:

{SNR}_{f} = \frac{(B_{1} / i) ω_{0} M_{0}^{⊥} V_{s} T_{2}^{*} \sqrt{N_{acc}}}{F \sqrt{4 k T_{s} R_{noise}} \sqrt{2 t_{acq}}} = \frac{1}{F} {SNR}_{t} \sqrt{Δ f} \frac{T_{2}^{*} \sqrt{N_{acc}}}{\sqrt{2 t_{acq}}},

(2)

where

T_{2}^{*}

is the apparent spin–spin relaxation time, N_acc is the number of acquisitions and t_acq is the acquisition time. F represents the noise factor of the detection electronics comprising the attenuation of the printed circuit board (PCB), the cable attenuation from the board to the spectrometer and the noise figure of the spectrometer.

T_{2}^{*}

is a function both of the relaxation time T₂, of static field inhomogeneities and of the sample itself. We do not have a model to predict the magnetic field B₀ perturbations at our disposal, and consequently the

T_{2}^{*}

will be estimated from the measured linewidth (LW) of the acquired spectra as follows:

T_{2}^{*} = \frac{1}{π LW}

(3)

The amplitude of the magnetization at equilibrium is given by:

M_{0}^{⊥} = \frac{N_{s} γ^{2} ℏ^{2} I (I + 1) B_{0}}{3 k T}

(4)

where T is the sample temperature, N_s the number of spins per unit volume. N_s is a function of both the number of molecules, N_A (N_A is Avogadro's number) and of magnetically equivalent spins per molecule, n_eq and of molar concentration C [mol l⁻¹]:

N_{s} = 10^{3} C N_{A} n_{eq}

(5)

The ratio between the analytically estimated SNR value and the measured one will represent the noise factor F. The noise factor F or the equivalent noise figure NF (dB) (F = 10^NF/10, NF = 10 log (F)) is influenced for our system by several parameters: attenuation of the printed board PCB (A_PCB), attenuation of the cable from the board to the spectrometer (A_cable) and from the conventional spectrometer preamplifier input. Neither the noise factor introduced by the PCB nor the noise factor coming from the electronic system is taken into account in the SNR analytical value.

The difference between the analytical SNR value and the one obtained by measure could be defined as an estimation of the noise figure NF (dB) coming from the PCB and other electronic losses additionally to the known noise figure coming from the cable and the spectrometer (NF_cable ≅ 0.6 dB, NF_spectrometer ≅ 1 dB).

Assuming the coil resistance as the principal noise source, a value for the theoretical noise V_n was found to be V_n = 14.66 × 10⁻¹⁰ V (Eq. (1)), with R_noise = 1.27 $Ω$ , Δf = 4 kHz, t_acq = 0.512 s.

An additional figure of merit is the limit of detection LOD, representing the minimum concentration and sample mass necessary to yield an SNR of 3 [4,5]. These limits of detection depend on the concentration of the sample in the active volume of the probe LOD_c, LOD_c = 3/S_c, where S_c is the concentration sensitivity, and on the amount of moles contained in the probe V_active, LOD_m = 3/S_m, where S_m is the mass sensitivity. The analysis of mass-limited samples requires the accumulation of a number of acquisitions; in this case the MR microprobe gives rise to a significantly higher SNR for a given scan time, t_scan. Consequently, these performance parameters can be more explicitly defined as time-normalized concentration sensitivity and time-normalized mass sensitivity:

n S_{c} = \frac{SNR}{C \cdot t_{scan}^{1 / 2}}

(6)

n S_{m} = \frac{SNR}{mol \cdot t_{scan}^{1 / 2}}

(7)

The time-normalized limits of detection in terms of concentration and of mass become:

n {LOD}_{c} = \frac{3 \cdot C \cdot t_{scan}^{1 / 2}}{SNR}

(8)

n {LOD}_{m} = \frac{3 \cdot mol \cdot t_{scan}^{1 / 2}}{SNR}

(9)

The figures of merit described here could be considered as important performance indicators for MR microprobes employed under different situations, such as the amount of sample and the concentration range for a given experiment.

2 Materials and methods

2.1 MR microcoil

The microcoil (needle: the most active part of the NMR device) extends with 40-μm-thick cooper tracks on 10-mm length. Tracks, realised jointly with the coil, convey the detected signal. The implantable part of the probe looks like a 9-mm-long, 550-μm-thick and 600-μm-wide needle (500 μm for coil diameter plus 50 μm on each side left for dicing). Notice that the needle is quite fragile [14].

A capacitive network must be associated with the microcoil to tune the antenna at the nucleus Larmor frequency of interest (200 MHz for ¹H in a magnetic field of 4.7 T) and to match the impedance of the transmission channel (50-Ω cable). Considering size constraints for implantation, the adjustable capacitors are fixed on a printed circuit board (PCB) which remains out of the sample. The antenna is glued on the PCB circuit and electrical connections are realised by microbonding of 50-μm-diameter aluminium wires (Fig. 1a–c).

Fig. 1
(a) First realisation of microcoil with tuning/matching circuit, (b) SEM view of needle coils and (c) needle coil scheme.

During experiments, the transmitted RF field is generated by a bird-cage Rapid Biomedical coil (inner diameter Φ = 6.9 cm, Ettlingen, Germany) producing a uniform field. The receiving microcoil must be detuned during excitation with a PIN diode also mounted on the PCB substrate [15]. This described circuit [14,16] is currently used to evaluate performances in vitro but must be still improved for in vivo applications since the equivalent series resistance of the coil depends on sample or intrinsic characteristics (conductivity and imaginary part of permittivity).

2.2 Localised ¹H spectroscopy

The observation of metabolites with short spin–spin relaxation decays is possible using free induction decay or short echo-time pulse-sequences. However, quantification of spectra is hampered by overlapping metabolite resonances and certainly by low signal-to-noise ratio (SNR) due to the small size of the observed volume. Fitting of time or frequency-domain model function to such low-SNR in vivo data requires extensive prior knowledge. The method QUEST, which includes spectral estimation in the time domain, uses a basis-set of expected metabolites signals. A simulated basis-set of the theoretical metabolite signals can be quantum mechanically simulated according to the employed sequence [6]. The signals with low signal-to-noise ratio and the large amplitude of the water peak have to be removed. The water signal was suppressed by variable power RF pulses with optimized relaxation decays (VAPOR) [17]. Outer volume suppression (OVS) combined with a short echo-time PRESS was used for localization. The removal of residual water components was performed in a pre-processing step using the Hankel–Lanczos Singular Value Decomposition algorithm – HLSVD. ¹H spectrum of a solution of cerebral metabolites has been acquired with a short echo-time PRESS sequence used for localization of the excitation close to the active part of the antenna. The phantom solution contains a mixture of three MR-observable ¹H metabolites in human brain: choline [100 mM], N-acetylaspartate (NAA) [100 mM] and creatine [50 mM] [18]. Experiments were conducted on a 4.7-T Bruker magnet (Biospec System, 270 mT/m gradient set). The localization was made with a PRESS sequence (bandwidth 4 kHz, 4096 complex points, 256 averages, TR = 7000 ms, TE = 20 ms, scan time t_scan = 30 min). Eddy current compensation and static magnetic field drift correction were applied during the acquisition.

2.3 Microcoil sensitivity

Knowing the coil RF field cartography in terms of uniformity and amplitude and its corresponding sensitivity distribution, the signal-to-noise ratio in the frequency domain can be analytically evaluated.

The active volume of the planar microcoil was determined by MRI measurements [16] using a MSME sequence (Fig. 2) (FOV = 2.2 cm, isotropic resolution 172 μm/pixel, slice thickness 0.5 mm, six slices).

Fig. 2
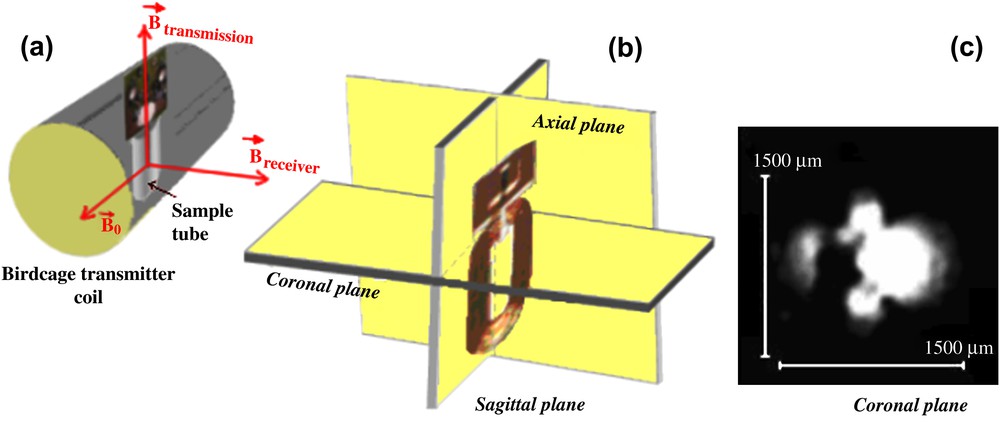
MR setup with the microcoil positioning in the sample tube (a) and the slice selection (b) for the microimaging part, coronal plane of the microcoil obtained with a MSME (Multi Slice/Multi Echo) sequence (c).

The active volume of the planar microcoil is determined from the MR signal intensity value in Fig. 2 if it is not less than 70% of the maximum observed intensity (threshold = 30%) (V_active = spatial resolution (x, y) × slice thickness). Along the coil length (six slices of 0.5-mm thickness each) the MR signal intensity occurs in a volume having approximately V_active = 2.07 μl. The signal intensity deceases from the coil centre to a distance close to d = 960 μm. The unitary magnetic field distribution B₁ will also be calculated from the coil centre to the distance d = 960 μm.

The magnitude of the unitary field in the active volume was estimated from the magnetic field iso-lines from the sensitivity map of the microcoil (Fig. 3a) obtained using the Biot–Savart law (Matlab 7.0 software) as we have reported in our previous work [16]. A mean value for B₁ of 1.34 mT/A was obtained (Fig. 3b).

Fig. 3
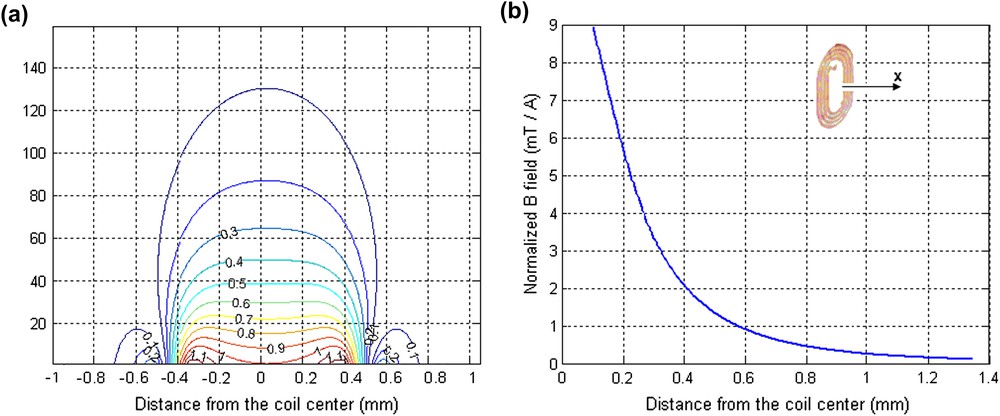
(a) Magnetic field B₁ distribution produced in the xy plane by a unit current flowing through the microcoil. The value of the magnetic field was normalized to a value of 1.0 at the centre of the microcoil, (b) calculated unitary magnetic field B₁ along the coil axis.

We can notice that for a given static magnetic field, volume and sample, the SNR value strongly depends on the unitary magnetic field B₁.

3 Results

The limits of detection were calculated based on the SNR expression in the frequency domain according to the model described in Section 1. $T_{2}^{*}$ values were estimated from the measured linewidth of the acquired signals (Fig. 4) of choline and NAA: $T_{2}^{*} [Cho] = 11.2 ms$ and $T_{2}^{*} [NAA] = 11.1 ms$ , respectively.

Fig. 4
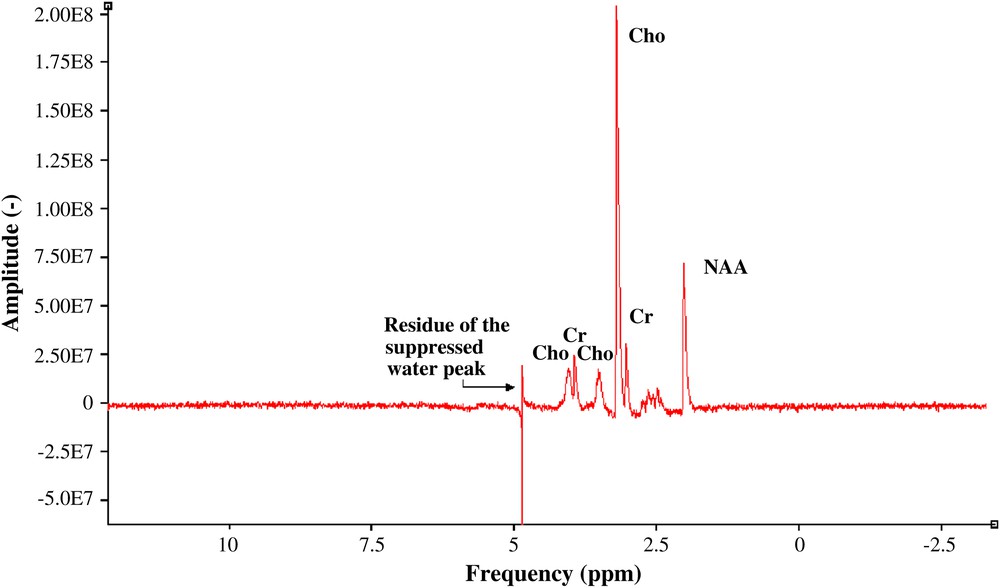
¹H spectrum of three cerebral metabolites: choline, and NAA (50 mM), creatine (50 mM), pH = 7.0 ± 0.1, no pre-treatment was performed.

There are 13 non-exchangeable protons in Choline, nine from a trimethylamine group and four from two methylene groups. The nine protons of the trimethylamine group –(CH₃)₃ are magnetically equivalent and give rise to the prominent singlet at 3.19 ppm. For this group, the spin density is $N_{s}^{Cho} = 54.21 \times 10^{25} m^{- 3}$ (n_eq^Cho = 9). NAA has seven protons that give NMR signals between 2.0 and 8.0 ppm. It typically provides the most prominent resonance, a singlet at 2.01 ppm, from the three protons of an N-acetyl CH₃ group. In this case, the spin density is $N_{s}^{NAA} = 4.07 \times 10^{25} m^{- 3}$ (n_eq^NAA = 3). The net magnetization becomes ${}^{Cho}M_{0}^{⊥} = 12.23 \times 10^{- 5} A/m$ and ${}^{NAA}M_{0}^{⊥} = 7.75 \times 10^{- 5} A/m$ , respectively (Eq. (4)). The estimated SNR for the choline case is close to 52.1 and for the NAA close to 17.4 after 256 averages (Eq. (2)). This brings to a ${LOD}_{c}^{Cho}$ value close to 5.7 mM and a ${LOD}_{c}^{NAA}$ value close to 17.2 mM. These analytical results will be compared with the limits of detection obtained from the acquired data quantified using jMRUI (http://www. mrui.uab.es/mrui), and the ratio between their analytical and their measured values will be summarized afterwards. In the SNR measurement of both acquired signals (choline and NAA) using jMRUI, no pre-treatment was performed, in order to have a rigorous comparison of the limits of detection of the estimated and the acquired spectroscopic data. The ratio between them makes it possible to estimate the noise factor F (Eq. (2)) representing the signal-to-noise losses coming from different electronic stages to the spectrometer input.

The SNR values as well as the sensitivity and their corresponding limits of detection (non-normalized) for both analytical and acquired data are displayed in Table 1. The mass sensitivity and the mass limit of detection were calculated for both metabolites (Cho, NAA) of the phantom solution within the active volume measured by MR imaging (Fig. 2) V_active = 2.07 μl of the microcoil ( ${LOD}_{m} = V_{active} \times {LOD}_{c}$ ) [5]. Actually V_active represents the proportionality constant that relates mass limit of detection to the concentration limit of detection.

Métabolite mean ± SD	SNR_estim	SNR_meas	S_c^estim (mM)	S_c^meas (mM)	LOD_c^estim (mM)	LOD_c^meas (mM)	LOD_m^estim (10⁻⁹ mol)	LOD_m^meas (10⁻⁹ mol)
Choline	52.1	20 ± 0.2	521	200 ± 2	5.7	15 ± 0.33	11.8	31.05 ± 0.7
NAA	17.4	7.1 ± 0.3	174	71 ± 3	17.2	42.2 ± 0.3	35.6	87.3 ± 0.6

The normalized sensitivities and their corresponding limits of detection were also calculated and are summarized in Table 2.

Metabolite	nS_c^estim (mM)	nS_c^meas (mM)	nLOD_c^estim (mM)	nLOD_c^meas (mM)	nLOD_m^estim (10⁻⁸ mol)	nLOD_m^meas (10⁻⁸ mol)
Choline	12.3	4.71 ± 0.04	241.8	636.3 ± 14	50.05	131.7 ± 30
NAA	4.1	1.7 ± 0.07	729.6	1790 ± 12	151	370.3 ± 25

A method to increase the SNR is the application of a weighting function of exponential decay (principle of adapted filtering), which causes line broadening (LB) of additional Lorentzian broadening. Maximum SNR is obtained with LB = LW. An LB of 10 Hz was performed on the acquired data [6] and the SNR for both metabolite signals are close to 68 (choline) and 23 (NAA) (Fig. 5). The following values for the concentration limits of detection have been obtained for the choline and the NAA case: ${LOD}_{c}^{Cho} = 4.4 mM$ and ${LOD}_{c}^{NAA} = 13 mM$ , respectively (Fig. 5). The mass limit of detection is: 9.1 × 10⁻⁹ mol (choline) and 29.6 × 10⁻⁹ mol (NAA).

Fig. 5
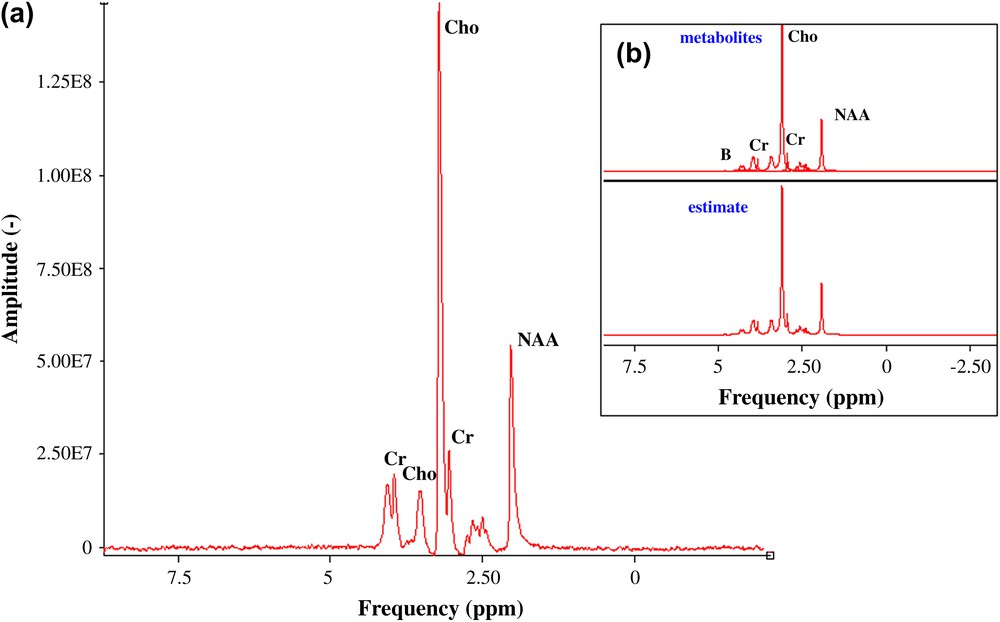
(a) Acquired ¹H spectrum, apodisation LB of 10 Hz, of three cerebral metabolites: choline, and NAA (100 mM), creatine (50 mM), pH = 7.0 ± 0.1, (b) QUEST quantification.

4 Discussions

We can notice that the acquired data measurements are below the analytical ones. The degradation of the measured SNR compared to its estimated SNR value accounts for a noise factor F ∼ 2.6 corresponding to a noise figure NF ∼ 4.1 dB. Actually the SNR degradation is due to additional noise coming from different sources: the detection of electronic losses like the printed circuit board (wire bounding, tuning/matching capacitors), cable attenuation and conventional spectrometer attenuation. Finally, our Bruker imaging system is not installed inside a Faraday cage for RF shielding and this could account for an additional SNR damage. All these parameters induce signal-to-noise losses and have to be taken into account in the estimated model (Eq. (2)).

The obtained values of the limits of detection show that the investigation of small volumes implies a poor concentration limit of detection $(V_{obs} ↓ \Leftrightarrow {LOD}_{c} ↑)$ . So, the smaller is the volume, the harder will be its detection. These results bring us to an important conclusion that a concentration-limited sample will yield a higher SNR in a probe with a higher active volume, a smaller volume implies a roughly estimation of the concentration limit of detection. A mass-limited sample is most effectively analyzed using a probe with the smallest active volume (largest S_m) [5]. S_c is particularly appropriate in comparing probe performances using a sample with a fixed concentration. In contrast to S_c, S_m is especially useful to compare probe performance for a sample of fixed mass. The normalized limit of detection is a useful figure of merit which can provide significant insight to assist in the validation of a micro-NMR probe with an optimal temporal resolution.

5 Conclusion

In this paper a ¹H spectrum containing several cerebral metabolites acquired with a receiver planar microcoil is presented. The limit of detection for this microprobe is significantly improved compared with our previous work [16]. A comparison between the theoretical estimation and the acquired data limits of detection was achieved and shows that probe-induced perturbation reduces the performances of these microcoils. To improve the overall efficiency of the detection microprobe, the additional noise of 4.1 dB occurring from the parameters discussed above (PCB, magnetic field inhomogeneities, etc.) have to be minimized. However, the actual values for LOD_c in both choline and NAA cases of 4.4 and 13 mM are close to the concentrations found in the rat brain [19] where they are about 2 mM for the choline and about 8.5 mM for the NAA case. These preliminary results make it possible to validate the sensitivity performances of the microcoils used in MR spectroscopy and make it possible to largely open the biomedical applications' field based on experiments in small animals (rodents).

Bibliographie

[1] A.G. Webb J. Pharm. Biomed. Anal., 38 (2005), p. 892

[2] J.S. Schoeniger; S.J. Blanckband JMR B, 104 (1994), p. 127

[3] T.L. Peck; R.L. Magin; P.C. Lauterbur JMR B, 108 (1995), p. 114

[4] D.L. Olson; J.A. Norcross; O'Neill-Johnson; T.L. Peck Anal. Chem., 76 (2004), p. 2966

[5] M.E. Lacey; R. Subramanian; D.L. Olson; A.G. Webb; J.V. Sweedler Chem. Rev., 99 (1999), p. 3133

[6] H.H. Ratiney; M. Sdika; Y. Coenradie; S. Cavassila; D. van Ormondt; D. Graveron-Demilly NMR Biomed., 18 (2005), p. 1

[7] D. Hoult; R. Richards JMR, 24 (1976), p. 71

[8] C. Massin; F. Vincent; A. Homsy; K. Ehrmann; G. Boero; P.-A. Besse; A. Daridon; E. Verpoorte; N.F. de Rooij; R.S. Popovic J. Magn. Reson., 164 (2003), p. 242

[9] L. Fakri-Bouchet, T. Cherifi, L. Quiquerez, J.-F. Châteaux, A. Briguet, 13th ISMRM International Society of Magnetic Resonance, Miami Beach Florida, 2005, p. 409.

[10] R. Magin; A.G. Webb; T.L. Peck IEEE Spectrum (1997), p. 51

[11] C. Massin, S. Erlogu, F. Vincent, B.S. Gimi, P.A. Besse, R.L. Magin, R.S. Popovic, The 12th International Conference on Solid State Sensors, Actuators and Microsystems, Boston, 2003.

[12] C. Massin; G. Boero; F. Vincent; J. Abenhaim; P.-A. Besse; R.S. Popovic Sens. Actuators A, 97–98 (2002), p. 280

[13] K. Ehrmann; M. Gersbach; P. Pascoal; F. Vincent; C. Massin; D. Stamou; P.-A. Besse; H. Vogel; R.S. Popovic J. Magn. Reson., 178 (2006), p. 96

[14] B. Sorli; J.-F. Chateaux; M. Pitaval; H. Chahboune; B. Fabre; A. Briguet; P. Morin Meas. Sci. Technol., 15 (2004), p. 877 (Institute of Physics Publishing)

[15] E.B. Boskamp Radiology, 157 (1985), p. 449

[16] N. Baxan, A. Rengle, J.-F. Chateaux, A. Briguet, G. Pasquet, P. Morin, L. Fakri-Bouchet, IEEE-EMBC, New York, 2006, p. 4314.

[17] I. Tkac; Z. Starcuk; I.Y. Choi; R. Gruetter Magn. Reson. Med., 41 (1999), p. 649

[18] C. Cudalbu; S. Cavassila; H. Ratiney; D. Grenier; A. Briguet; D. Graveron-Demilly C.R. Chim., 9 (2006), p. 534

[19] V. Govidanraju; K. Young; A. Maudsley NMR Biomed., 13 (2000), p. 129

Commentaires - Politique

Ces articles pourraient vous intéresser

Conception de microbobines radiofréquence pour la RMN : apport d’une simulation électromagnétique

Mircea Armenean; André Briguet; Hervé Saint-Jalmes

C. R. Biol (2002)

Relaxation measurements by magnetic resonance force microscopy

Olivier Klein; Vladimir V. Naletov

C. R. Phys (2004)

Rat brain metabolite relaxation time estimates using magnetic resonance spectroscopy at two different field strengths

Cristina Cudalbu; Adrian Rengle; Olivier Beuf; ...

C. R. Chim (2008)