NMR experimental procedure for obtaining 3Q and 5QMAS spectra from the same multiplex SPAM acquisition

Redouane Hajjar; Yannick Millot; Pascal P. Man

doi:10.1016/j.crci.2007.07.003

NMR experimental procedure for obtaining 3Q and 5QMAS spectra from the same multiplex SPAM acquisition

Redouane Hajjar ¹ ; Yannick Millot ¹ ; Pascal P. Man ¹

¹ Université-Pierre-et-Marie-Curie – Paris-6 Systèmes interfaciaux à l'échelle nanométrique (SIEN), 4 place Jussieu, 75252 Paris cedex 05, France

Comptes Rendus. Chimie, Volume 11 (2008) no. 4-5, pp. 380-386.

Résumés

Anglais
Français

Since the discovery of the MQMAS method applied to quadrupolar nuclei with half-integer spin by Frydman and coworkers, this method has been considerably developed. Recently, Malicki and coworkers combined the multiplex phase cycling approach with the new SPAM method. This multiplex SPAM MQMAS sequence increases the signal-to-noise ratio by about a 2.5 factor. Additionally, this sequence can simultaneously record 3Q and 5QMAS spectra with the same acquisition. However, it is not easy to obtain experimentally, at the same time, a good signal-to-noise ratio in the two spectra. We propose a procedure for optimizing the pulse durations and finding a good compromise to record the two MQMAS spectra without peak aliasing in the F1 dimension. For this, we simulate the echo and the anti-echo amplitudes of a spin I with increasing pulse durations in a powder rotating at the magic angle, using Mathematica and SIMPSON. We apply this method to obtain the 3Q and 5QMAS spectra of ²⁷Al in TEABEA-11 zeolite. The latter spectrum shows two tetrahedral sites for the aluminium atoms.

Depuis la découverte de la méthode MQMAS appliquée aux noyaux quadripolaires de spin demi-entier par Frydman et collaborateurs, cette méthode a été énormément développée. Récemment, Malicki et collaborateurs ont combiné l'approche du cyclage de phases multiplex avec la nouvelle méthode SPAM. Cette séquence multiplex SPAM MQMAS augmente le rapport signal sur bruit d'environ un facteur 2,5. De plus, elle permet l'enregistrement simultanément des expériences 3Q et 5QMAS à partir des mêmes données d'acquisition. Mais expérimentalement il n'est pas toujours aisé d'obtenir, en même temps, un bon rapport signal sur bruit dans les deux spectres. Nous proposons une procédure pour optimiser les durées d'impulsions et choisir un bon compromis pour sélectionner efficacement les deux MQ sans repliement des signaux dans la dimension F1. Pour cela, nous avons simulé les amplitudes de l'écho et de l'anti-echo d'un spin I en fonction de l'augmentation des durées d'impulsion dans une poudre tournant à l'angle magique, en utilisant les notebooks Mathematica-5 et les scriptes Tcl de SIMPSON1.1.1. Nous avons appliqué cette méthode pour obtenir des spectres 3Q et 5QMAS de ²⁷Al dans une zéolithe TEABEA-11. Le dernier spectre montre deux sites tétraédriques pour les atomes d'aluminium.

Métadonnées

Reçu le : 2007-04-25
Accepté le : 2007-07-11
Publié le : 2007-11-05

DOI : 10.1016/j.crci.2007.07.003

Keywords: MQMAS, SPAM, Multiplex, SIMPSON, Mathematica, NMR, Simulation
Mots clés : MQMAS, SPAM, Multiplex, SIMPSON, Mathematica, RMN, Simulation

Affiliations des auteurs :

Redouane Hajjar ¹ ; Yannick Millot ¹ ; Pascal P. Man ¹

¹ Université-Pierre-et-Marie-Curie – Paris-6 Systèmes interfaciaux à l'échelle nanométrique (SIEN), 4 place Jussieu, 75252 Paris cedex 05, France

@article{CRCHIM_2008__11_4-5_380_0,
     author = {Redouane Hajjar and Yannick Millot and Pascal P. Man},
     title = {NMR experimental procedure for obtaining {3Q} and {5QMAS} spectra from the same multiplex {SPAM} acquisition},
     journal = {Comptes Rendus. Chimie},
     pages = {380--386},
     publisher = {Elsevier},
     volume = {11},
     number = {4-5},
     year = {2008},
     doi = {10.1016/j.crci.2007.07.003},
     language = {en},
}

TY  - JOUR
AU  - Redouane Hajjar
AU  - Yannick Millot
AU  - Pascal P. Man
TI  - NMR experimental procedure for obtaining 3Q and 5QMAS spectra from the same multiplex SPAM acquisition
JO  - Comptes Rendus. Chimie
PY  - 2008
SP  - 380
EP  - 386
VL  - 11
IS  - 4-5
PB  - Elsevier
DO  - 10.1016/j.crci.2007.07.003
LA  - en
ID  - CRCHIM_2008__11_4-5_380_0
ER  -

%0 Journal Article
%A Redouane Hajjar
%A Yannick Millot
%A Pascal P. Man
%T NMR experimental procedure for obtaining 3Q and 5QMAS spectra from the same multiplex SPAM acquisition
%J Comptes Rendus. Chimie
%D 2008
%P 380-386
%V 11
%N 4-5
%I Elsevier
%R 10.1016/j.crci.2007.07.003
%G en
%F CRCHIM_2008__11_4-5_380_0

Redouane Hajjar; Yannick Millot; Pascal P. Man. NMR experimental procedure for obtaining 3Q and 5QMAS spectra from the same multiplex SPAM acquisition. Comptes Rendus. Chimie, Volume 11 (2008) no. 4-5, pp. 380-386. doi : 10.1016/j.crci.2007.07.003. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2007.07.003/

Version originale du texte intégral

1 Introduction

The Multiple-Quantum Magic-Angle-Spinning (MQMAS) method is very much used in solid-state NMR to obtain high-resolution 2D spectra of quadrupolar nuclei. In these spectra, an isotropic dimension is correlated to the anisotropic dimension that gives the usual MAS-broadened pattern of each resolved site. Since the discovery of MQMAS by Frydman and Harwood in 1995 [1], this experiment has been developed mainly in two ways. First, several pulse sequences have been proposed to improve the efficiencies of MQ excitation and conversion [2–15]. Second, two acquisition methods were introduced to obtain 2D MQMAS spectra with pure-adsorption lineshapes [16]: the amplitude-modulated method which generally includes a z-filter part [17] and the phase-modulated method which is associated with full-echo MQMAS [18,19]. In 2004 Gan and Kwak [20] introduced Soft-Pulse-Adding-Mixing (SPAM) as a solution to the efficiency and 2D-lineshape problems. Amoureux et al. [21] gave a complete description of this method which consists in adding several coherence transfer pathways constructively. Moreover, Gan and Kwak suggested the possibility of introducing into the SPAM MQMAS experiment the multiplex phase cycling initiated by Ivchenko et al. [22]. Very recently, Malicki et al. [23] proposed a multiplex SPAM MQMAS sequence (Fig. 1). One of the main advantages is the possibility, with the same acquisition, of recording 3Q and 5QMAS NMR spectra. However, the problem is the difference in pulse duration for the two MQ [24–27]. In this communication, we present a method based on the simulation of signal intensity depending on the pulse duration to find a compromise between the 3Q and 5QMAS spectra.

Fig. 1
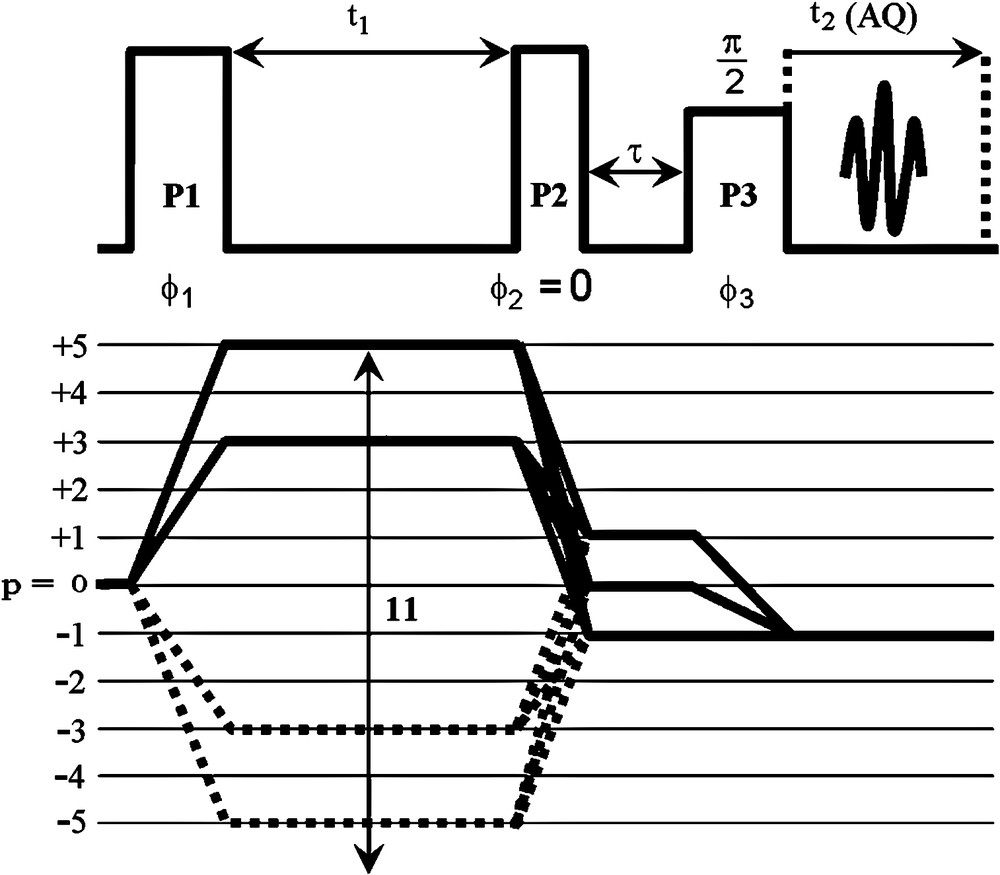
Multiplex SPAM MQMAS sequence for a spin I = 5/2.

2 Multiplex SPAM MQMAS sequence

This sequence [23] consists of three pulses: two strong pulses (P1 and P2) and one selective pulse (P3) (Fig. 1). The P1 pulse generates simultaneously all coherences available for the excited spin I, and after the MQ evolution period (t₁), the P2 pulse puts this spin system along the z-axis of the laboratory frame. There is no phase cycling for the P2 pulse, and the receiver phase is always set to zero. The P3 pulse selects 0Q and ±1Q coherences, and the signal increase comes from transfers through these three coherence levels. To select individually all coherences, it is necessary to apply N1 (= 4I + 1) phases to the P1 pulse. For each value of this phase, two Free Induction Decay (FID) signals are recorded separately: a signal with a phase zero and a second with a phase π for the P3 pulse. These two phases for P3 are necessary to add the 0Q and ±1Q coherences in a constructive way: one of these two phases is for echo pathway, the other phase for anti-echo pathway. The time between P2 and P3 is short (1 μs) to avoid dephasing of the ±1Q coherences [23]. FID signals are stored in a 3D data file and when the acquisition is finished, the processing program “MSM” [28] reorganizes them in a normal 2D data file. This program treats signals according to:

s (t) = \frac{1}{2 N_{1}} \sum_{m = 0}^{2 N_{1} - 1} s (t, m) \exp (- ⅈ ϕ_{num} (m)) .

(1)

The signal s(t) is phase-modulated. The choice of ϕ_num allows us to select the different coherence pathways to generate a 2D MQMAS spectrum with pure-adsorption lineshapes, and this without using the States acquisition. Transformation by shearing is necessary to obtain an isotropic spectrum in the F1 dimension. Optimal pulse durations were always found to be identical to the best values in a z-filtered MQMAS experiment [21,23], thus to optimize the pulse duration of multiplex SPAM MQMAS experiment, we will use a z-filter sequence.

3 Echo and anti-echo amplitude simulation

The pulse durations of P1 and P2 that provide maximum line intensity are not identical for the two coherences 3Q and 5Q. To study this difference, we developed [29] Mathematica-5 notebooks and SIMPSON1.1.1 Tcl scripts [30] to optimize the echo and anti-echo amplitudes for a z-filtered MQMAS experiment applied to a half-integer quadrupole spin. We start by determining the expressions of the irreducible spherical tensors V_(2,0), W_(2,0) and W_(4,0) of the first- and second-order quadrupolar Hamiltonians $H_{Q}^{(1)}$ and $H_{Q}^{(2)}$ using the Wigner rotation matrix [31]. From these expressions we develop a Mathematica-5 notebook to simulate the intensity of the central line of a spin I excited by a MQMAS sequence (in our case the z-filter sequence). The first- and second-order quadrupolar interactions for a powder rotating at the magic angle are taken into account during the pulses. We consider that the NMR line intensity, which depends on the various interactions involved during the RF pulses, is proportional to the echo amplitude. This program calculates the theoretical line intensities of the central transition versus the variable duration and for various experimental parameters (spin I, RF amplitude Ω_RF/2π, variable pulse duration, rotation rate, MQ desired) and estimated values of C_Q and η. This simulation can also be performed with the SIMPSON program. The agreement between our simulations and those obtained with SIMPSON is excellent, the values of these simulations being identical with an accuracy of 10⁻⁹. SIMPSON gives 9 digits after dot for a real number.

To illustrate the difference between P1 and P2 pulse durations, we use our Mathematica-5 notebooks applied to ²⁷Al (I = 5/2) (parameters are given in the caption of Fig. 2). We simulate (Fig. 2) the intensity of the central line according to each pulse, and this for a 3Q and 5QMAS experiment. We observe that for the three pulses the intensity of the 5QMAS experiment is always lower than that of the 3QMAS experiment. This is foreseeable since coherence leap for a 5Q is larger than for a 3Q. The line intensity variation versus the P3 pulse duration is identical for the two experiments, and 8 μs is the best intensity (not shown). This is also expected because this pulse makes the same jump $0 Q \to - 1 Q$ in the two experiments. This 8-μs pulse duration corresponds to the 90 selective pulse for the central transition at Ω_RF/2π = 10 kHz (which is exactly 8.33 μs). For P2 and P1 pulses the maximum durations are different:

t_{P 2}^{3 QMAS} (max) = 1.5 μs \neq t_{P 2}^{5 QMAS} (\max) = 2.5 μs,

(2)

and

t_{P 1}^{3 QMAS} (max) = 4.5 μs \neq t_{P 1}^{5 QMAS} (max) = 5.5 μs .

(3)

In all cases, durations

t_{P 2}^{5 QMAS} (max)

and

t_{P 1}^{5 QMAS} (max)

are higher than

t_{P 2}^{3 QMAS} (max)

and

t_{P 1}^{3 QMAS} (max)

, respectively. The intensity of the 3QMAS experiment decreases markedly (≈80%) when we choose the ideal conditions for P2 of the 5QMAS experiment (

t_{P 2}^{5 QMAS} (max)

). However, it decreases much less when

t_{P 1}^{5 QMAS} (max)

are used. Finally, concerning the pulse durations and in order to extract from the same acquisition the 3Q and 5QMAS 2D spectra, we propose to use: P1, pulse duration equal to

t_{P 1}^{5 QMAS} (max)

and P2, pulse duration which will be appropriate for the two experiments. In this example, this is 2.25 μs.

Fig. 2
Maximum echo amplitude optimization by simulation of P2 and P1 pulse durations for the z-filtered MQMAS sequence obtained with Mathematica-5 notebooks for ²⁷Al (I = 5/2). The simulation parameters are rotor spinning speed: 5 kHz; Larmor frequency: 104.309 MHz; amplitude of the strong radio-frequency pulse (P1 and P2): 90 kHz; amplitude of selective pulse P3: 10 kHz; quadrupolar coupling constant: 1.75 MHz; asymmetry parameter η = 0.5; quadrupolar interaction: first- and second-order. t_P3 = 8 μs. (A) t_P1 = 4 μs for 3Q (■) and 5Q (▴); (B) t_P2 = 1.5 μs for 3Q (■) and t_P2 = 2.5 μs for 5Q (▴).

The echo amplitude for the 5QMAS experiment is much lower than for 3QMAS and thus optimization is much longer. To limit the latter, we propose to use our simulation program. We start by optimizing the echo amplitude experimentally according to the pulse durations for the 3QMAS experiment. From this study and by estimating the quadrupolar coupling, we can simulate the variation of the echo amplitude according to the pulse duration for the 5QMAS experiment.

4 Experimental considerations

It is fairly easy to avoid peak aliasing in the F2 dimension of a 2D spectrum but it is more difficult to anticipate this problem in the F1 dimension. For a 2D MQMAS spectrum, on the one hand, it is not easy to predict the positions of the various crystallographic sites in the isotropic F1 dimension and, on the other hand, the off-resonance position in F1 differs from that of F2 by a factor (k − p) [32]. Thus, it is necessary to determine by simulation or a brief experiment which is the smallest spectral width in the F1 dimension SW(F1). We will then be able to deduce the maximum increment usable for the F1 dimension.

Moreover, the smallest spectral width in the F1 dimension SW(F1), which avoids peak aliasing during the acquisition of a 5QMAS spectrum, is five times larger than for a 3QMAS spectrum. The position $ω_{F_{1}} (I, p)$ of the center of gravity of the peak relative to the carrier frequency $ω_{cf}$ in the F1 dimension is given by [32]:

ω_{F_{1}} (I, p) = δ_{CS}^{iso} ω_{cf} [k (I, p) - p] + ω_{- 1 / 2, 1 / 2}^{(2) iso} [k (I, p) + λ (I, p)],

(4)

where the quantity λ(I, p) relates to the second-order quadrupolar shifts for a pQ spectrum,

ω_{- p / 2, p / 2}^{(2) iso}

and a −1Q spectrum,

ω_{- 1 / 2, 1 / 2}^{(2) iso}

, as:

ω_{- p / 2, p / 2}^{(2) iso} = λ (I, p) ω_{- 1 / 2, 1 / 2}^{(2) iso},

(5)

with:

ω_{- 1 / 2, 1 / 2}^{(2) iso} = - \frac{3 {(2 π C_{Q η})}^{2}}{10 ω_{cf} {[2 I (2 I - 1)]}^{2}} [I (I + 1) - \frac{3}{4}],

(6)

C_{Q η} = \frac{e^{2} q Q}{h} \sqrt{\frac{η^{2}}{3} + 1} = C_{Q} \sqrt{\frac{η^{2}}{3} + 1} .

(7)

The parameters C_Qη, C_Q and η are called the quadrupolar product, the quadrupolar coupling constant and the asymmetry parameter, respectively. The values of k and λ for the three half-integer quadrupole spins I (5/2, 7/2 and 9/2) and the coherence order p are reported in Table 1. We see that for any half-integer quadrupole spin I, we have the following relation:

ω_{F_{1}} (I, | p | = 5) = 5 \times ω_{F_{1}} (I, | p | = 3) .

(8)

Finally, like Amoureux and Trébosc [33], we observed that the intensity of the 5Q coherences decrease more quickly with the t₁ than for the 3Q coherences. In other words, the minimum number of increments necessary to acquire a 5QMAS 2D spectrum correctly, to have a null signal at the end of acquisition, is not sufficient for a 3QMAS experiment. This causes the truncation of the signal for the latter.

I	pQ	$λ (I, p)$	$k (I, p)$	$k (I, p) - p$	$k (I, p) + λ (I, p)$
5/2	3Q	−3/4	19/12	−17/12	5/6
−5Q	−25/4	25/12	85/12	−25/6
7/2	3Q	−9/5	101/45	−34/45	4/9
5Q	1	11/9	−34/9	20/9
9/2	3Q	−9/4	91/36	−17/36	5/18
5Q	−5/4	95/36	−85/36	25/18

5 Experimental

MAS NMR experiments were performed on a Bruker AVANCE400 spectrometer at 9.4 T and with a 4-mm zirconia rotor. ²⁷Al 3Q and 5QMAS spectra were acquired with the multiplex SPAM MQMAS sequence [28]. The P1 and P2 pulse durations were 4.5 and 2.0 μs, respectively (Ω_RF/2π = 92 kHz). The P3 pulse duration was 6.5 μs (Ω_RF/2π = 10 kHz). The multiplex spectra were acquired at a spinning rate of ν_Rot = 14 kHz, with a 0.25-s recycle delay, 2 μs for the increment of the t1 period, 210 sections and 140 accumulations. Data processing was performed using the “MSM” program [28]. Shearing transformation and scaling of the F1 axis was realized with “xfshear” [28] or with Grandinetti's RMNFAT program [34]. Tetraethylammonium BEA (TEABEA) zeolite (with Si/Al = 11 and Na/Al < 0.1) was provided by Dzwigaj et al. [35]. More details are given in Section 6.

6 Results and discussion

From the same acquisition, the multiplex SPAM sequence allows us to extract 2D spectra corresponding to various pQMAS experiments. For a spin I = 5/2 the “MSM” program will generate 3Q and 5QMAS 2D spectra. In practice, it is unfortunately not easy to obtain good signal-to-noise ratios for both spectra. There are differences in the optimal experimental parameters to obtain MQ coherences of orders 3 and 5.

By using the previous considerations (spectral width in the F1 dimension and number of increments) and pulse duration optimization, it is possible to extract from the same acquisition 3Q and 5QMAS 2D spectra. We will apply the multiplex SPAM sequence to the case of aluminium-27 (I = 5/2) in TEABEA-11 zeolite to demonstrate our method.

We start by optimizing the pulse durations for the two experiments (3Q and 5QMAS) with a 1D z-filtered MQMAS sequence. The pulse duration P3, corresponding to the best intensity, is identical for the two experiments (6.50 μs for Ω_RF/2π = 10 kHz). Fig. 3A–D presents experimental optimizations of the pulse durations P2 and P1, respectively. It shows, as expected, that the durations t₂ (max) and t₁ (max) corresponding to the best intensities for the two experiments are different. Indeed:

t_{P 2}^{3 QMAS} (max) = 1.50 μs \neq t_{P 2}^{5 QMAS} (max) = 2.25 μs,

(9)

and

t_{P 1}^{3 QMAS} (max) = 3.5 μs \neq t_{P 1}^{5 QMAS} (max) = 4.5 μs .

(10)

The pulse durations of the 3QMAS experiment are shorter than those of 5QMAS. A good compromise to record the multiplex SPAM experiment under the best conditions is to apply pulse durations P1 and P2 of 4.5 and 2 μs, respectively.

Fig. 3
Experimental optimizations of P2 and P1 pulse durations of the z-filtered MQMAS sequence obtained for ²⁷Al in TEABEA-11 zeolite with 240 scans and t_P3 = 6.5 μs. (A) t_P1 = 3.0 μs for 3Q, (B) t_P1 = 3.5 μs for 5Q, (C) t_P2 = 3.5 μs for 3Q and (D) t_P2 = 4.5 μs for 5Q.

For the 3QMAS 2D experiment, the smallest spectral width of the F1 dimension, which avoids peak aliasing during the acquisition of TEABEA-11, is equal to 24 kHz, but this is not sufficient for the 5QMAS experiment. The minimum width which will be appropriate for both experiments is SW(F1) = 120 kHz.

Now we will determine the minimum number of sections ${TD}_{F 1}^{min}$ necessary to the F1 dimension and this without having a truncated signal. The maximum delay (t₁) between the first two pulses, for which we always observe a signal, is 320 and 420 μs for 5Q and 3Q coherences, respectively.

The signal of 5Q coherences decreases more quickly than that of 3Q coherences. Thus, for a 2-μs increment, we will use 210 sections for ${TD}_{F 1}^{min}$ , to obtain a value of at least t₁ = 420 μs.

Fig. 4A–B represents the 3Q and 5QMAS 2D multiplex SPAM spectra, respectively and are obtained from the same acquisition with a good signal-to-noise ratio. In the 3QMAS spectrum, we observe two resonances which correspond to the octahedral ${Al}_{O_{h} (1)}$ and tetrahedral ${Al}_{T_{d} (2)}$ environments of the aluminium atoms. With 5Q coherences, which give a better resolution, we observe two sites ${Al}_{T_{d} (2 a)}$ and ${Al}_{T_{d} (2 b)}$ from the F1 projection. Omegna et al. [36] and Capek et al. [37] also observed these tetrahedral sites. The resolution increase obtained with the 5QMAS experiment seems to indicate that the homogeneous interactions are not weak. Indeed, 3QMAS experiments are more sensitive to homogeneous broadening than 5QMAS [33,38,39].

Fig. 4
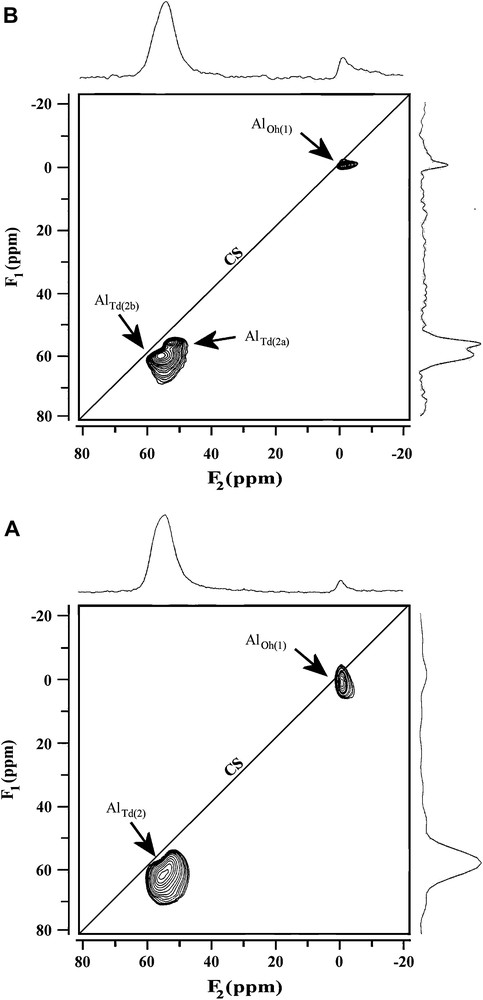
²⁷Al 3QMAS (A) and 5QMAS (B) multiplex SPAM MQMAS spectra of TEABEA-11 zeolite obtained with the same acquisition.

For our sample, the signal of 5Q coherences decreases much faster than that of 3Q coherences. In this case, we could record 3Q and 5Q spectra separately and obtain for the same experimental time a slightly better sensitivity. Indeed, we will use P1 and P2 durations corresponding to the maximum of the signal for each experiment and not to intermediate values. Moreover, we will be able to increase the increment of the 3Q experiment to reduce the spectral width and obtain overall the same number of sections as previously. It seems that recording 3Q and 5QMAS experiments simultaneously and handling of one data file is interesting in the case of samples where the decreases versus t₁ in 3Q and 5Q coherences are not too different.

7 Conclusion

We proposed a procedure to obtain simultaneously 3Q and 5QMAS 2D spectra from the multiplex SPAM sequence. This method indicates how to choose the experimental parameters to obtain good sensitivity in both experiments. More generally, to reduce the time for pulse duration optimization in the 5QMAS experiment, we propose to use our simulation programs. Moreover, we indicate and discuss the precautions to be taken to go from a 3QMAS spectrum to a 5QMAS spectrum avoiding peak aliasing and a truncated signal. We apply this method to TEABEA-11 zeolite and obtain good 3Q and 5QMAS spectra.

Bibliographie

[1] L. Frydman; J.S. Harwood J. Am. Chem. Soc., 117 (1995), p. 5367

[2] F.H. Larsen; N.C. Nielsen J. Chem. Phys. A, 103 (1999), p. 10825

[3] P.K. Madhu; A. Goldbourt; L. Frydman; S. Vega J. Chem. Phys., 112 (2000), p. 2377

[4] A. Goldbourt; P.K. Madhu; S. Vega Chem. Phys. Lett., 320 (2000), p. 448

[5] P. Zhao; P.S. Neuhoff; J.F. Stebbins Chem. Phys. Lett., 344 (2001), p. 325

[6] C.M. Morais; M. Lopes; C. Fernandez; J. Rocha Magn. Reson. Chem., 41 (2003), p. 679

[7] J. Gu; W.P. Power Solid State Nucl. Magn. Reson., 27 (2005), p. 192

[8] A.P.M. Kentgens; R. Verhagen Chem. Phys. Lett., 300 (1999), p. 435

[9] H. Schafer; D. Iuga; R. Verhagen; A.P.M. Kentgens J. Chem. Phys., 114 (2001), p. 3073

[10] D. Iuga; H. Schafer; R. Verhagen; A.P.M. Kentgens J. Magn. Reson., 147 (2000), p. 192

[11] G. Wu; D. Rovnyak; R.G. Griffin J. Am. Chem. Soc., 118 (1996), p. 9326

[12] P.K. Madhu; M.H. Levitt J. Magn. Reson., 155 (2002), p. 150

[13] H.T. Kwak; S. Prasad; Z. Yao; P.J. Grandinetti; J.R. Sachleben; L. Emsley J. Magn. Reson., 150 (2001), p. 71

[14] H.-T. Kwak; S. Prasad; T. Clark; P.J. Grandinetti J. Magn. Reson., 160 (2003), p. 107

[15] Z. Gan J. Am. Chem. Soc., 122 (2000), p. 3242

[16] T. Vosegaard; P. Florian; D. Massiot; P.J. Grandinetti J. Magn. Reson., 143 (2000), p. 217

[17] J.-P. Amoureux; C. Fernandez; S. Steuernagel J. Magn. Reson. A, 123 (1996), p. 116

[18] D. Massiot; B. Touzo; D. Trumeau; J.P. Coutures; J. Virlet; P. Florian; P.J. Grandinetti Solid State Nucl. Magn. Reson., 6 (1996), p. 73

[19] S.P. Brown; S. Wimperis J. Magn. Reson., 124 (1997), p. 279

[20] Z. Gan; H.-T. Kwak J. Magn. Reson., 168 (2004), p. 346

[21] J.P. Amoureux; L. Delevoye; S. Steuernagel; Z. Gan; S. Ganapathy; L. Montagne J. Magn. Reson., 172 (2005), p. 268

[22] N. Ivchenko; C.E. Hughes; M.H. Levitt J. Magn. Reson., 160 (2003), p. 52

[23] N. Malicki; L. Mafra; A.-A. Quoineaud; J. Rocha; F. Thibault-Starzyk; C. Fernandez Solid State Nucl. Magn. Reson., 28 (2005), p. 13

[24] A. Goldbourt; P.K. Madhu Monatsh. Chem., 133 (2002), p. 1497

[25] J.-P. Amoureux; C. Fernandez; L. Frydman Chem. Phys. Lett., 259 (1996), p. 347

[26] J.P. Amoureux; C. Fernandez Solid State Nucl. Magn. Reson., 10 (1998), p. 211

[27] J.-P. Amoureux; C. Fernandez Solid State Nucl. Magn. Reson., 16 (2000), p. 339

[28] C. Fernandez, <http://www-lcs.ensicaen.fr/article.php?id_article=88&ids=16>.

[29] P.P. Man, <http://www.pascal-man.com/tensor-quadrupole-interaction/spam.shtml>.

[30] M. Bak; J.T. Rasmussen; N.C. Nielsen J. Magn. Reson., 147 (2000), p. 296

[31] P.P. Man, <http://www.pascal-man.com/tensor-quadrupole-interaction/Hamiltonian.shtml>.

[32] Y. Millot; P.P. Man Solid State Nucl. Magn. Reson., 21 (2002), p. 21

[33] J.P. Amoureux; J. Trébosc J. Magn. Reson, 179 (2006), p. 311

[34] P.J. Grandinetti, <http://www.grandinetti.org/Software/RMN/index.html>.

[35] S. Dzwigaj; M.J. Peltre; P. Massiani; A. Davidson; M. Che; T. Sen; S. Sivasanker Chem. Commun. (1998), p. 87

[36] A. Omegna; M. Vasic; J.A. Van Bokhoven; G. Pirngruber; R. Prins Phys. Chem. Chem. Phys., 6 (2004), p. 447

[37] L. Capek; J. Dedecek; B. Wichterlova J. Catal., 227 (2004), p. 352

[38] K.J. Pike; R.P. Malde; S.E. Ashbrook; J. McManus; S. Wimperis Solid State Nucl. Magn. Reson., 16 (2000), p. 203

[39] J.-P. Amoureux; M. Pruski, Encyclopedia of Nuclear Magnetic Resonance, vol. 9, 2002 (p. 226)

Commentaires - Politique