1 Introduction
In the last few years, mesoporous materials attracted much attention due to their potential applications in several fields, including catalysis, polymerization, photochemistry…[1]. The silica-based MCM-41 structure is known to act as a bioactive material. Indeed, the intrinsic porosity of such material offers a wide range of possibilities for hosting molecules and the ability for drug delivery [2,3]. Recently, several researchers have been interested in the incorporation of bisphosphonates [4] in the pores of mesostructured silica, which may inhibit bone resorption. Confinement of such molecules could offer new opportunities such as bone reconstruction. The direct synthesis of Si–O–P mesoporous materials has been very rarely reported in the literature [5,6] and has received little attention.
In the field of materials, the local structure of nuclei can be probed efficiently by solid-state NMR spectroscopy. A large panel of techniques can be implemented for establishing connectivities between nuclei. It includes cross-polarization and J-derived experiments. The CP MAS (cross-polarization magic-angle spinning) sequence [7] relies on dipolar interaction. Such experiment establishes spatial proximities between X and Y nuclei. For X = 31P and Y = 29Si, very few results have been reported so far in the literature. These results are related to silicon phosphide (involving direct 31P–29Si bonds) [8] and silicophosphates involving 31P–O–29Si groups [9]. J-derived experiments based on the isotopic scalar J coupling constants establish X–Y through-bond connectivities. In the early 1990s, such solid-state NMR sequences were implemented successfully by Fyfe et al. [10] and Eckert et al. [11]. More recently, several groups showed that a large number of J experiments could be easily transposed to solid-state NMR. Among these, we find the HMQC (heteronuclear multiple quantum coherence) sequence, which has been adapted for the following spin pairs: 1H/13C, 1H/15N, 31P/27Al, 27Al/17O, 31P/29Si and 31P/71Ga [11–17]. The INEPT (insensitive nuclei enhanced by polarization transfer) sequence [18] is one of the most important pulse blocks in modern solution state experiments [19]. In solid-state NMR, the INEPT sequence was adapted for the study of mobile [20] and rigid [21] organic and hybrid systems. Examples related to inorganic components have been rarely reported in the literature [22–26].
In this paper, the complete study of silicophosphate phases such as Si5O(PO4)6 and various SiP2O7 polymorphs is presented. The efficiency of 31P → 29Si CP MAS, MAS-J-HMQC and MAS-J-INEPT experiments involving the {31P,29Si} spin pair is demonstrated. The 31P → 29Si CP MAS experiment has been then successfully applied for the structural characterization of Si–O–P derived mesoporous materials. Such materials were obtained via an aerosol process. The incorporation of phosphorus in the silica network at atomic level was clearly demonstrated.
2 Experimental: syntheses and solid-state NMR
Solid-state NMR experiments were performed on a Bruker Avance 300 spectrometer at B0 = 7 T with ν0 (31P) = 121.49 MHz and ν0 (29Si) = 59.63 MHz, using a 4-mm triple resonance Bruker MAS probe. Samples were spun at the magic angle using ZrO2 rotors (5–14 kHz). 31P chemical shifts were referenced to 85% aqueous H3PO4. 29Si chemical shifts were referenced to TMS. In the case of mesoporous materials, all experiments were obtained at low temperature (T = 238 K), thanks to a cooling unit (BCU-X), a control temperature unit, and a DVT probe. The calibration of the temperature was performed using lead nitrate, Pb(NO3)2. Full experimental details are given in the figure captions. The X-ray diffraction patterns of mesoporous materials were obtained using a D8 Advance Bruker diffractometer (Cu Kα radiation: λ = 1.54718 Å, 1–6° in 2θ with a step size of 0.02° in 2θ, scan rate: 5 s/step). For TEM experiments (Philips Technai 12), samples were dispersed in ethanol and dropped onto a copper grid covered with carbon.
The synthesis protocols are the following: Si5O(PO4)6: TEOS (Si(OCH2CH3)4), ethanol and distilled water were used as precursors (TEOS/EtOH/H2O = 1:4:3). The phosphorus precursor H3PO4 (85%) was added (Si/P = 1:1) at room temperature. The reaction was slightly exothermic. The addition of 1% (molar ratio) of a paramagnetic complex (NiCl2·6H2O) was performed for NMR relaxation purposes, leading to a slightly green solution. After stirring at 25 °C, a transparent green wet gel was obtained (2 h). The final powder was obtained after heat treatment at 800 °C for 2 h. The structure of Si5O(PO4)6 described by Mayer [27] (trigonal,
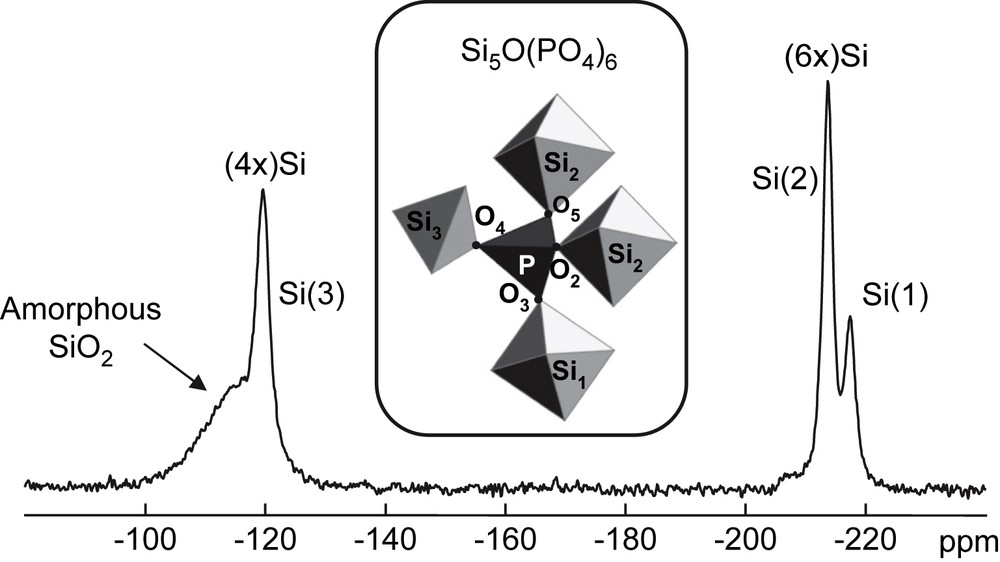
Part of the structure of Si5O(PO4)6 around the unique P atom. The labelling scheme of atoms is given according to Ref. [27]. 29Si MAS spectrum (single pulse experiment) (∅ = 4 mm, rotation frequency (RO) = 14 kHz, number of scans (NS) = 1760, recycle delay (RD) = 10 s, 90° (29Si) = 4.5 μs, LB = 10 Hz).
31P and 29Si isotropic chemical shifts for the mixture of Si5O(PO4)6 and SiP2O7 polymorphs [15]
| Phase (JCPDS) | δiso (ppm) | |
| 29Si (Fig. 1) | 31P (Fig. 2) | |
| Si5O(PO4)6 (70-2071) | −119.3 | −43.8 |
| −213.5 | ||
| −217.3 | ||
| SiP2O7 tetragonal (22-1320) | −45.5 | |
| −52.8 | ||
| SiP2O7 monoclinic 1 (39-0189) | −47.6 | |
| −55.3 | ||
| SiP2O7 monoclinic 2 (25-0755) | −46.1 | |
| −49.4 | ||
| SiP2O7 cubic (22-1321) | ∼−50 | |
| ∼−58 | ||
| ∼−70 |
2.1 Mixture of SiP2O7 polymorphs and Si5O(PO4)6
After the dissolution of NiCl2·6H2O (1%) in ethanol, H3PO4 (85%) was added, followed by TEOS (Si/P = 1:2). A gel was obtained after 2 h at room temperature, heated at 100 °C for 48 h, and further heat-treated at 1000 °C for 2 h. The X-ray diffraction (XRD) powder pattern of the sample (not shown here) indicates that besides the Si5O(PO4)6 crystalline phase presented above, three polymorphs of SiP2O7 were synthesized as major constituents, namely a tetragonal (JCPDS: 22-1320) [28] and two monoclinic forms (JCPDS: 39-0189 and 25-0755) [29,30]. As shown in Fig. 2, the 31P MAS NMR spectrum reveals also the presence of the SiP2O7 cubic form (JCPDS: 22-1321), but as a very minor component. This particular phase was not clearly evidenced by XRD. For the SiP2O7 polymorphs, it is known from XRD data that the pyrophosphate groups (involving generally two non-equivalent P sites) are linked exclusively to SiVI atoms (Fig. 2). The 31P and 29Si isotropic chemical shifts of the various SiP2O7 polymorphs are reported in Table 1.
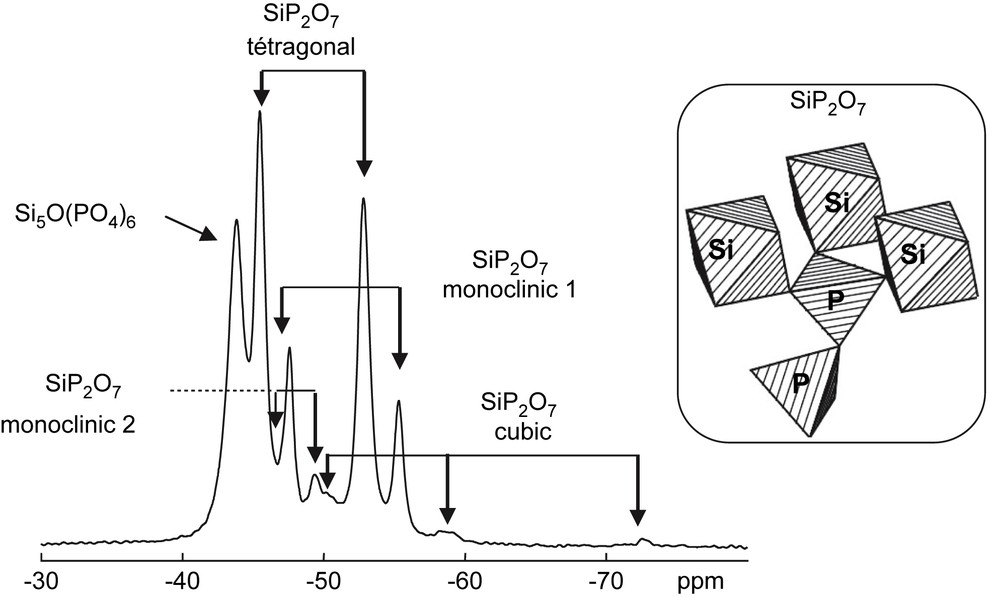
Structural scheme for SiP2O7 pyrophosphate phases: one given P atom is bonded to one P atom and three equivalent 6-fold coordinated Si atoms. 31P MAS spectrum of the mixture of Si5O(PO4)6 and several polymorphs of SiP2O7 (tetragonal, monoclinic 1, monoclinic 2, and cubic) (∅ = 4 mm, RO = 14 kHz, NS = 8, RD = 5 s, 90° (31P) = 6 μs, LB = 0 Hz).
2.2 SiP0.1-aerosol mesoporous derivative
At room temperature, 5 g (13.7 mmol) of the surfactant (CTAB, C16H33N+(CH3)3Br−) were dissolved in a solution of distilled water/ethanol. Then, 0.8 ml (11.6 mmol) of H3PO4 (85%) was added. The pH was then adjusted to 2.1 with HCl (2 M) before the addition of 23 ml of TEOS. The molar ratio was CTAB/TEOS/H3PO4: 0.14:1.0:0.10. The solution was then treated using the aerosol process. Some works have been already dedicated to the synthesis of mesoporous spheres obtained by this method [31]. The nanoparticles were produced in a reactor consisting of a spraying chamber combined with a tubular furnace and a filter. The final powder was heated at 310 °C and 500 °C in air to remove efficiently the surfactant and to obtain the final mesoporous silicophosphate materials.
3 Results and discussion
The various pulse schemes used in this work will be first presented. The full characterization of Si5O(PO4)6 and SiP2O7 polymorphs by CP MAS, MAS-J-HMQC and MAS-J-INEPT experiments are first shown, followed by the structural characterization of Si–O–P mesoporous materials.
3.1 Solid-state NMR methodology
3.1.1 31P → 29Si HETCOR CP MAS experiment
The 31P → 29Si 2D HETCOR sequence presented in Fig. 3a is an extension of the 1D 31P → 29Si CP MAS experiment. For the set-up, the MAS rotation frequency was fixed at 5 kHz. Even at this moderate MAS rate, the Hartmann–Hahn (H–H) profile must split into sharp spinning sidebands (because of the small heteronuclear dipolar interaction involving 31P and 29Si). A VACP profile (variable amplitude cross-polarization) [32] was used during the contact time (tCP), in order to broaden the H–H profile. The 29Si acquisition was obtained under 31P CW decoupling. A saturation loop (characterized by Δ and n) was applied on the 31P channel before the first 90° pulse.

(a) Pulse sequence for the 2D 31P → 29Si CP MAS HETCOR experiment. (b) 2D 31P → 29Si HETCOR CP MAS spectrum of the mixture of Si5O(PO4)6 and several polymorphs of SiP2O7 (∅: 4 mm, RO = 5 kHz, NS = 104 for each t1 increment, RD = 10 s, 90° (31P) = 5.3 μs, tCP = 40 ms, State mode with 384 t1 increments, LB = 10 Hz in F2 (29Si), LB = 20 Hz in F1 (31P)). The zoomed region corresponds to the 6-fold coordinated 29Si nuclei.
3.1.2 31P–29Si MAS-J-HMQC experiment
The 2D 31P–29Si MAS-J-HMQC sequence is presented in Fig. 4a. T2′ time constants [15] were measured by spin-echo experiments (90°–τ′–180°–τ′) under fast MAS for the unique 31P signal. Such time constants are characteristic of the lifetime of the involved coherences. The experimental curve was fitted by a single exponential decay in time domain according to:
| (1) |
| (2) |
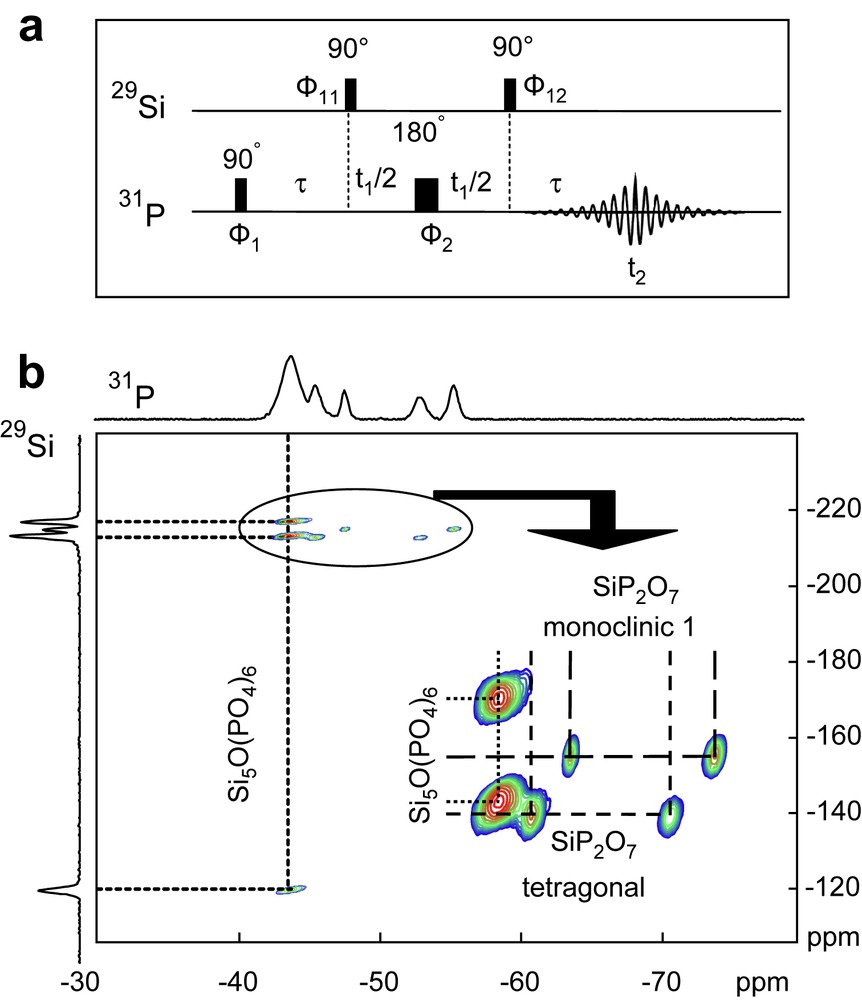
(a) 2D 31P–29Si MAS-J-HMQC pulse sequence. Φ1 = +x; Φ2 = +x, +x, +y, +y, −x, −x, −y, −y; Φ11 = +x; Φ12 = +x, −x; receiver = +x, −x, −x, +x, +x, −x, −x, +x. (b) 31P–29Si 2D MAS-J-HMQC spectrum of the mixture of Si5O(PO4)6 and SiP2O7 polymorphs (∅ = 4 mm, RO = 14 kHz, NS = 136 for each t1 increment, RD = 5 s, 90° (31P) = 6.8 μs, 90° (29Si) = 5.3 μs, τ = 25 ms, State mode with 208 t1 increments, LB = 0 Hz in F2 (31P), LB = 0 Hz in F1 (29Si), presaturation on the 31P channel). Below: expansion of the oval region. Masquer
(a) 2D 31P–29Si MAS-J-HMQC pulse sequence. Φ1 = +x; Φ2 = +x, +x, +y, +y, −x, −x, −y, −y; Φ11 = +x; Φ12 = +x, −x; receiver = +x, −x, −Lire la suite
3.1.3 31P–29Si MAS-J-INEPT experiment
The pulse sequence for refocused 2D 31P–29Si MAS-J-INEPT experiment is shown in Fig. 5a. The original solution state technique [18] was adapted here for rotating solids and for a new pair of nuclei {31P,29Si}. Fast magic-angle spinning (usually 14 kHz) averages the chemical shift anisotropy and the heteronuclear dipolar couplings to zero, leaving only the scalar couplings and the isotropic chemical shifts [21]. The refocused INEPT pulse sequence consists of the following steps: a 90° pulse is applied to the 31P channel, followed by an evolution delay optimized to achieve 31P anti-phase magnetization. The refocusing of the isotropic chemical shifts is obtained by the simultaneous application of 180° pulses on both phosphorus-31 and silicon-29 channels (only the 2JP–O–Si couplings have to be taken into account). For a pair of 31P and 29Si nuclei involved in a 31P–O–29Si group, anti-phase phosphorus-31 coherence with respect to silicon-29 is created after the first τ–π–τ period. The two simultaneous 90° pulses lead to anti-phase silicon-29 coherence. The refocusing period τ′–π–τ′ is then applied to obtain in-phase 29Si magnetization. 31P decoupling is finally applied during the acquisition of the 29Si signal.

(a) 31P–29Si 2D refocused MAS-J-INEPT pulse sequence. Φ1 = +x, +x, +x, +x, +x, +x, +x, +x, −x, −x, −x, −x, −x, −x, −x, −x; Φ2 = +x, −x; Φ3 = +y, +y, −y, −y; Φ4 = +x, −x; Φ5 = +x, +x, +x, +x, +y, +y, +y, +y, −x, −x, −x, −x, −y, −y, −y, −y; Φ6 = +x, −x, +x, −x, +y, −y, +y, −y; receiver = +x, +x, −x, −x, +y, +y, −y, −y. (b) 2D 31P–29Si refocused MAS-J-INEPT spectrum of the mixture of Si5O(PO4)6 and SiP2O7 polymorphs (∅ = 4 mm, RO = 14 kHz, NS = 496 for each t1 increment, RD = 5 s, 90° (29Si) = 5.7 μs, 90° (31P) = 4.3 μs, τ = 11.4 ms, τ′ = 4.6 ms, State mode with 128 t1 increments, LB = 20 Hz in F2 (29Si), LB = 20 Hz in F1 (31P)). The expansion of the boxed region is presented in the figure. The projections of the 2D spectrum are also given. Masquer
(a) 31P–29Si 2D refocused MAS-J-INEPT pulse sequence. Φ1 = +x, +x, +x, +x, +x, +x, +x, +x, −x, −x, −x, −x, −x, −x, −x, −Lire la suite
In the MAS-J-INEPT experiment, τ and τ′ delays must be carefully optimized. Such parameters involve not only the value of the 2JP–O–Si coupling constants, but also the relaxation time T2′ associated with each site. Table 2 presents an estimation of the T2′ (29Si) and T2′ (31P) values. For the refocused INEPT experiment, and considering a unique 2JP–O–Si coupling constant, the signal intensity is given by [19,34]:
| (3) |
3.1.4 Results
Figs. 3b, 4b and 5b present the 2D 31P–29Si CP MAS HECTOR (with tCP = 40 ms), 2D 29Si–31P MAS-J-HMQC (τ = 25 ms) and 2D 31P–29Si MAS-J-INEPT (τ = 11.4 ms and τ′ = 4.6 ms) spectra of the Si5O(PO4)6SiP2O7 mixture, respectively (see the synthesis above). Three cross-peaks associated Si5O(PO4)6 phase are systematically observed (the unique 31P site at −43.8 ppm is J and D coupled to the three 29Si resonances – Fig. 1). Moreover, the 2D spectra reveal the presence of numerous cross-peaks (shown in the expansions in Figs. 3b, 4b and 5b), located in the 6-fold coordinated 29Si chemical shift range (∼−215 ppm). These cross-peaks are safely assigned to SiP2O7 polymorphs. Therefore, D and J 2D experiments are suitable to edit the 31P MAS spectra in terms of pairs involved in each SiP2O7 pyrophosphate phase (Fig. 2). Moreover, the unique 29Si isotropic shift corresponding to each SiP2O7 polymorph is determined with great accuracy. All 31P and 29Si isotropic chemical shifts are reported in Tables 3 and 4 (HECTOR and HMQC/INEPT experiments, respectively). Comparing the three experiments, we note that in the 2D 29Si–31P MAS-J-HMQC and MAS-J-INEPT spectra, no cross-peaks corresponding to the monoclinic 2 form of SiP2O7 are observed. Such cross-peaks are observed in the case of the 2D HETCOR experiment (Fig. 3b). It is assumed that the J coupling constants are markedly different for the various SiP2O7 phases, leading to the underestimation of the monoclinic 2 form in J-derived experiments. The absence of observable cross-peaks for the cubic forms in the three experiments is due to the low amount of this particular phase (Fig. 2).
31P and 29Si isotropic chemical shifts corresponding to the projections in the 2D 31P–29Si CP MAS HETCOR experiment for the mixture of Si5O(PO4)6 and SiP2O7 polymorphs
| Phase (JCPDS) | δiso (ppm) | |
| 31P HETCOR (Fig. 3b) | 29Si HETCOR (Fig. 3b) | |
| Si5O(PO4)6 (70-2071) | −43.8 | −119.6 |
| −213.8 | ||
| −217.6 | ||
| SiP2O7 tetragonal (22-1320) | −45.4 | −213.2 |
| −52.9 | ||
| SiP2O7 monoclinic 1 (39-0189) | −47.6 | −215.5 |
| −55.4 | ||
| SiP2O7 monoclinic 2 (25-0755) | −46.0 | −215.4 |
| −49.4 | −215.6 |
31P and 29Si isotropic chemical shifts corresponding to the projections in the 2D 31P–29Si MAS-J-HMQC and 31P–29Si MAS-J-INEPT experiments for the Si5O(PO4)6/SiP2O7 polymorph mixture
| Phase (JCPDS) | δiso (ppm) | |||
| 31P HMQC (Fig. 4b) [15] | 29Si HMQC (Fig. 4b) [15] | 31P INEPT (Fig. 5b) [26] | 29Si INEPT (Fig. 5b) [26] | |
| Si5O(PO4)6 (70-2071) | −43.8 | −119.1 | −43.9 | −119.3 |
| −213.3 | −213.5 | |||
| −217.0 | −217.3 | |||
| SiP2O7 tetragonal (22-1320) | −45.5 | −212.8 | −45.6 | −213.0 |
| −52.9 | −52.9 | |||
| SiP2O7 monoclinic 1 (39-0189) | −47.6 | −214.9 | −47.7 | −215.3 |
| −55.4 | ||||
| −55.3 |
Si5O(PO4)6 acted also as a model compound for the measurement of individual 2JP–O–Si coupling constants via the MAS-J-INEPT experiment. The INEPT build-up curves obtained vs τ′ (at fixed τ = 11.4 ms) for Si(1), Si(2) and Si(3) are presented in Fig. 6a, b and c, respectively. The variation of the intensity is clearly dependent on both the number of P atoms bonded to the silicon atoms (n = 6 for Si(1), Si(2); n = 3 for Si(3)) and the crystallographic characteristics of the various sites (for Si(1) and Si(2)). Eq. (3), as well as the T2′ constants presented in Table 2, were used for the fitting of the experimental curves for Si(1) and Si(3) (with n = 6 and n = 3, respectively). For both Si sites, a unique 2JP–O–Si coupling constant is involved. The extracted J value corresponds to 2JP–O–Si ≈ 15 and 12 Hz for Si(1) and Si(3), respectively [26]. Obviously, the Si(2) build-up curve differs drastically from the one obtained for Si(1), even though Si(1) and Si(2) correspond both to 6-fold coordinated silicon atoms. In the case of Si(2), two different 2JP–O–Si coupling constants have to be a priori considered corresponding to Si(2)–O(2)–P and Si(2)–O(5)–P bonding paths (Fig. 6b). Considering two distinct J coupling constants (J1 and J2, SI3I′3 spin system), the product operator formalism [19] leads to:
| (4) |

(a–c) Experimental evolution of the 31P–29Si MAS-J-INEPT intensities as function of τ′ (with fixed τ = 11.4 ms) for Si(1), Si(2) and Si(3) (Si5O(PO4)6 phase), respectively. The experimental data (o) were fitted by Eq. (3) for Si(1) and Si(3) and Eq. (4) for Si(2). The fixed T2′ constants are extracted from spin echo experiments (Table 2) (∅ = 4 mm, RO = 14 kHz, NS = 656, RD = 5 s, 90° (31P) = 5 μs, 90° (29Si) = 5.3 μs). Each Si site is depicted schematically.
MAS-J-HMQC, MAS-J-INEPT and HETCOR CP MAS experiments are comparable in terms of experimental time. However, it must be noted that very long contact times (up to 40 ms) have to be used for efficient CP transfer (the 31P/29Si dipolar coupling is estimated to be ∼340 Hz in Si–O–P groups). The HMQC and INEPT sequences are obviously less demanding in terms of RF power, as short pulses are involved. Nevertheless, care must be taken when choosing the evolution periods, as T2′ relaxation processes have to be taken into account.
3.2 Mesoporous Si–O–P materials
Fig. 7a shows the X-ray diffraction pattern of the SiP0.1-aerosol sample (see Section 2). The two observed peaks can be indexed as (100) and (110) reflections of a 2D hexagonal mesostructure. The TEM image of the powder presented in Fig. 7b shows the spherical morphology of the obtained nanoparticles (with diameters ranging from ∼50 to 300 nm).

(a) X-ray diffraction pattern (at low angle) of the SiP0.1-aerosol sample. (b) TEM picture of the SiP0.1-aerosol sample. (c) 31P MAS NMR spectrum of SiP0.1-aerosol sample at T = 238 K (∅ = 4 mm, RO = 8 kHz, NS = 1080, RD = 20 s, 90° (31P) = 3.9 μs, TPPM 15 decoupling). (d) 1H → 31P CP MAS spectrum of SiP0.1-aerosol sample at T = 238 K (∅ = 4 mm, RO = 8 kHz, NS = 112, RD = 2 s, 90° (1H) = 5.3 μs, tCP = 2 ms, TPPM 15 decoupling, LB = 20 Hz). (e) 29Si MAS spectrum of SiP0.1-aerosol sample at T = 238 K (∅ = 4 mm, RO = 8 kHz, NS = 184, RD = 60 s, 90° (29Si) = 5.1 μs, TPPM decoupling, LB = 30 Hz). (f) 1H → 29Si CP MAS spectrum of SiP0.1-aerosol sample at T = 238 K (∅ = 4 mm, RO = 8 kHz, NS = 2040, RD = 3 s, 90° (1H) = 5.3 μs, tCP = 10 ms, TPPM 15 decoupling, LB = 50 Hz). (g) 31P → 29Si CP MAS spectrum of SiP0.1-aerosol sample at T = 238 K (∅ = 4 mm, RO = 8 kHz, NS = 22456, RD = 10 s, 90° (31P) = 5.1 μs, tCP = 10 ms, CW {31P} decoupling, LB = 100 Hz, presaturation on the 31P). Masquer
(a) X-ray diffraction pattern (at low angle) of the SiP0.1-aerosol sample. (b) TEM picture of the SiP0.1-aerosol sample. (c) 31P MAS NMR spectrum of SiP0.1-aerosol sample at T = 238 K (∅ = 4 mm, RO = 8 kHz, NS = 1080, RD = 20 s, 90° (31P) = 3.9 μs, TPPM 15 decoupling). (d) 1H → 31P ... Lire la suite
1H → X CP MAS experiments performed at room temperature showed systematically poor efficiency of polarization transfer. It is assumed that proton mobility strongly reduces the efficiency of the CP process. CP efficiency was indeed regained at low temperature (T = 238 K). The following spectra were recorded at T = 238 K. The 31P MAS spectrum of the SiP0.1-aerosol sample is shown in Fig. 7c. Four resonances at ∼2.5, −9.5, −23.0 and −38.3 ppm are evidenced, which can be assigned to Q′N species, N ranging from 0 to 3 (see Table 5 for the definition of Q′N and for the assignments). Protonated phosphate groups are evidenced by 1 H→ 31P CP MAS experiment at tCP = 2 ms (Fig. 7d). At this contact time, the resonance at ∼2.5 ppm corresponding to the Q′0 specie is underestimated due to fast molecular motion even at low temperature. The other three resonances are assigned safely to protonated species, in agreement with notations presented in the literature [35]. The 29Si MAS spectrum is presented in Fig. 7e. Two broad resonances at δ ∼−103 and ∼−111 ppm correspond to Q3 and Q4 species (Table 5). The corresponding 1H → 29Si CP MAS experiment is presented in Fig. 7f. Q3 units are overestimated, as it is usually the case in the case of silica gels and derivatives. Moreover, a weak amount of Q2 units is evidenced: the corresponding resonance is located at ∼−91 ppm. It has to be noticed that the notations used in Table 4 are rather loose. Indeed, various combinations of 29Si–O–Si/29Si–OH/29Si–O–P bonds can lead to the same isotropic chemical shift value. Therefore, 31P–29Si CP MAS experiments appear as a valuable tool of investigation for the characterization of dipolar couplings within the mesoporous structure. The corresponding spectrum of the aerosol sample is presented in Fig. 7g. The signal-to-noise ratio is rather low due to the low amount of phosphorus used in the synthesis. Nevertheless, two resonances located at δ ∼−101 (hardly discernable) and ∼−113 ppm can be detected. Such observations indicate the presence of Si⋯P dipolar contacts. These preliminary results are encouraging for an in-depth characterization of the structure of the Si–O–P mesoporous materials. 1H → 29Si → 31P CP MAS experiments, as well as J experiments, should permit complete editing and assignment of both 31P and 29Si resonances in such materials.
Proposed assignments for 31P and 29Si isotropic resonances
| δ (ppm) | Assignment |
| (31P) | |
| ∼0 | OP(OH)3 |
| −10/−20 | OP(OH)2(OP/OSi) |
| −20/−25 | OP(OH)(OP/OSi)2 |
| −30/−35 | OP(OP)n(OSiIV)m |
| ∼−45 | OP(OSiIV)n(OSiVI)m |
| (29Si) | |
| −90/−95 | Si(OSi)2(OH)2 Q2 |
| ∼−100 | Si(OSi)3(OH) Q3 or Si(OSi)(OH)2(OP) |
| ∼−110 | Si(OSi)4 Q4 or Si(OSi)2(OP)(OH) |
| −110/−120 | Si(OSi)4−x(OP)x with x = 1–3 |
4 Conclusions
This paper has been devoted to the methodological characterization of the {31P,29Si} spin pair by solid-state MAS NMR techniques. Experiments based on J and heteronuclear dipolar interaction were implemented using crystalline silicophosphate phases as model compounds. Si5O(PO4)6 and various polymorphs of SiP2O7 were studied systematically by 2D 31P → 29Si CP MAS HETCOR, MAS-J-HMQC and MAS-J-INEPT experiments. The editing role of such experiments was clearly demonstrated. The 31P–29Si INEPT build-up curves allowed the measurement of 2JP–O–Si coupling constants. An unexpected dependence on both the coordination mode of the Si nuclei and the involved crystallographic paths has been demonstrated. Finally, 31P → 29Si CP MAS experiments were adapted to the characterization of Si–O–P mesoporous materials obtained by aerosol process. The results showing 31P···29Si dipolar contacts are encouraging and will be compared in a near future to those obtained by MAS-J-derived techniques.



Vous devez vous connecter pour continuer.
S'authentifier