Preliminary <sup>1</sup>H NMR investigations of local dynamics in interface of polymers grafted on silica

Tahar Tajouri; Ghazi Kassab

doi:10.1016/j.crci.2007.10.008

Preliminary ¹H NMR investigations of local dynamics in interface of polymers grafted on silica

Tahar Tajouri ¹ ; Ghazi Kassab ¹

¹ Université de Tunis, IPEIT, Unité de recherche UR 0113-04, 2, rue Jawhar-Nahrou, Montfleury, 1008 Tunis, Tunisia

Comptes Rendus. Chimie, GERM 2007, Volume 11 (2008) no. 4-5, pp. 407-414.

Abstracts

English
French

The ¹H NMR technique is used to study the behaviour and dynamics of the poly(ethylene oxide) chains grafted chemically on silica. A noticeable influence of the different physicochemical parameters on the dynamics and the conformation of the grafted macromolecules is evidenced. The grafting ratio, the temperature, the solvent can all in well-chosen situations modify the configurations and dynamics of the chains.

The temperature dependence of the ¹H NMR spin–lattice relaxation time is analyzed for preliminary evaluation of the correlation time of the local dynamics of the polymeric chains and for three significant grafting ratios.

The magic-angle spinning technique is used to study the dynamics of the macromolecules at the interface. It permits to determine two correlation times for each grafting ratio: τ_sl characteristic of an environment with a slow motion and τ_fa characteristic of the local segmental motion. This last correlation time is compared to that obtained by measurements of T₁.

La technique de RMN a été utilisée pour étudier le comportement et la dynamique des chaînes de polyoxyéthylène greffées sur silice. Une influence notable de différents paramètres physicochimiques sur la dynamique et les conformations adoptées par les macromolécules greffées a été mise en évidence. Le taux de greffage, la température, le solvant peuvent, dans des situations bien choisies, modifier les configurations et la dynamique des chaînes.

La dépendance des temps de relaxation spin-réseau avec la température a été analysée pour une évaluation préliminaire des temps de corrélation de la dynamique locale des chaînes de polymères pour trois taux de greffage significatifs.

La technique de la rotation à l'angle magique a été utilisée pour étudier la dynamique des macromolécules à l'interface. Elle a permis de déterminer deux temps de corrélation pour chaque taux de greffage : τ_sl, caractéristique des mouvements lents, et τ_fa, caractéristique du mouvement local des segments. Ce dernier temps a été comparé à celui obtenu par des mesures de T₁.

Metadata

Received: 2007-04-29
Accepted: 2007-10-25
Published online: 2008-02-21

DOI: 10.1016/j.crci.2007.10.008

Keywords: NMR, Relaxation times, Magic angle spinning, Poly(ethylene oxide), Grafted polymer, Interfaces
Mots-clés : RMN, Temps de relaxation, Rotation à l'angle magique, Polyoxyéthylène, Polymères greffés, Interfaces

Author's affiliations:

Tahar Tajouri ¹; Ghazi Kassab ¹

¹ Université de Tunis, IPEIT, Unité de recherche UR 0113-04, 2, rue Jawhar-Nahrou, Montfleury, 1008 Tunis, Tunisia

@article{CRCHIM_2008__11_4-5_407_0,
     author = {Tahar Tajouri and Ghazi Kassab},
     title = {Preliminary {\protect\textsuperscript{1}H} {NMR} investigations of local dynamics in interface of polymers grafted on silica},
     journal = {Comptes Rendus. Chimie},
     pages = {407--414},
     publisher = {Elsevier},
     volume = {11},
     number = {4-5},
     year = {2008},
     doi = {10.1016/j.crci.2007.10.008},
     language = {en},
}

TY  - JOUR
AU  - Tahar Tajouri
AU  - Ghazi Kassab
TI  - Preliminary 1H NMR investigations of local dynamics in interface of polymers grafted on silica
JO  - Comptes Rendus. Chimie
PY  - 2008
SP  - 407
EP  - 414
VL  - 11
IS  - 4-5
PB  - Elsevier
DO  - 10.1016/j.crci.2007.10.008
LA  - en
ID  - CRCHIM_2008__11_4-5_407_0
ER  -

%0 Journal Article
%A Tahar Tajouri
%A Ghazi Kassab
%T Preliminary 1H NMR investigations of local dynamics in interface of polymers grafted on silica
%J Comptes Rendus. Chimie
%D 2008
%P 407-414
%V 11
%N 4-5
%I Elsevier
%R 10.1016/j.crci.2007.10.008
%G en
%F CRCHIM_2008__11_4-5_407_0

Tahar Tajouri; Ghazi Kassab. Preliminary ¹H NMR investigations of local dynamics in interface of polymers grafted on silica. Comptes Rendus. Chimie, GERM 2007, Volume 11 (2008) no. 4-5, pp. 407-414. doi : 10.1016/j.crci.2007.10.008. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2007.10.008/

Version originale du texte intégral

1 Introduction

In order to modify the interactions between a solid and the surrounding medium, one way consists in grafting polymers at the interface. In turn these interactions depend on the conformations and mobilities of the chains. The interfaces formed by polymers grafted on silica are the continuous objects of considerable interest for both practical and fundamental reasons [1–4]. The configuration and the properties of chain polymer should depend essentially on the polymer surface density [5,6], length (molecular weight), and the nature of the solid surface. Less information is available on short grafted polymeric chains [7,8]. The knowledge of the dynamics of grafted polymer may also provide essential data for the understanding of global surface properties like wetting, adhesion… The study of the molecular dynamics is very important to understand how the motions of polymer chains are affected by different anchoring points on the solid surface. It has appeared that the grafting ratio becomes a very significant parameter in the characterisation of such systems [9,10].

Only few data concerning the chain segment dynamics are available. The dynamics of the macromolecules is a complex process, extended in a large temporal and spatial range, going from the fast motions of the monomeric unit to the slow process of the reorientation of monomer units to each other [1,10–12].

Poly(ethylene oxide) (PEO) is a simple polymer, that can be used as a model system, since all the CH₂ are chemically identical (with the exception of the terminal group), and the NMR spectrum of the polymer has one simple line. The solid support is silica (Aerosil) with a high degree of chemical purity [9].

It has already been shown that only the dipolar interaction between the nuclei is the cause of relaxation and that the motion of the monomer units is very anisotropic [9,13]. The strong PEO/silica interactions cause the polymer to adopt a flat configuration by spreading on the solid surface.

NMR is one of the most sensitive methods to investigate the dipolar interaction between the nuclear spins on the polymeric chain, and thus it is an important source of information concerning the polymeric dynamics.

In this work our interest was to observe the modification of the dynamics of the polymeric chain induced by grafting. For this purpose, the ¹H NMR spin–lattice and the spin–spin relaxations were observed in a large temperature range, for poly(ethylene oxide) PEO with molecular weight 2000 grafted on silica with different grafting ratios. An important parameter for characterising the dynamics of the polymeric chain is the correlation time of the local segmental motions. This parameter was evaluated from spin–lattice relaxation time versus temperature (T₁(T)) data.

2 Experimental

2.1 Materials

The silica is pyrogenic, Aerosil 300 (from Degussa), prepared at high temperature in a flame [9,14]. This material was selected because it has a high degree of chemical purity and it is not porous. It consists of large aggregates formed by small spheres, each sphere being about 7–12 nm in diameter. Its specific surface area, measured by nitrogen adsorption, is of about 300 m² g⁻¹.

The silica surface is mainly reactive with the surrounding through its silanol groups. The number of silanols on a silica surface is about 5 per square nanometers for a fully dehydrated silica. They are assumed to be rather randomly distributed and therefore it seems a fair approximation to assume that the density of grafting points is constant.

The polymer is poly(ethylene oxide) PEO. The molecular weight and polydispersity was determined by gel permeation chromatography. The length of the chains is always that corresponding to a molecular weight of 2000 with a polydispersity of 1.04.

Grafting reaction: the silica was dried, agglomerated in acetone (RP) and brought to 150 °C in an oven. It was then dispersed in a PEO solution to achieve the desired impregnation ratio. The solvent was evaporated in a rotating evaporator under a pressure of 2 × 10³ Pa. The powder was again dried and degassed in a vacuum of 0.1 Pa and then kept in nitrogen. For the grafting reaction the vessel was maintained in an oil bath at a temperature fixed at ±3 °C. The reaction time was varied for the chosen temperature between 4 h at 113 °C and 1 h 30 min at 234 °C. This last case corresponds to the highest coverage achieved. Once the grafting was performed, the unbounded polymer was removed by a long extraction in a Soxhlet. The grafted silica was first dried in air to remove most of solvent and finally put in a dynamic vacuum of 0.1 Pa for 24 h in an oven kept at 60 °C to avoid the degradation of the polymer. The grafting ratio was evaluated by elemental analysis or by pyrolysis weight loss between 25 and 750 °C under oxygen.

The grafting ratio, τ_G, is expressed in weight%. It is the weight of polymer irreversibly fixed on 100 g of silica. When using pyrolysis procedure, τ_G is given by the following relationship:

τ_{G} = \frac{Δ m}{m_{i} - Δ m} \times 100

(1)

where m_i is the weight of the initial sample and Δm is the weight loss after pyrolysis.

Three significant grafting ratios for different ranges were studied:

- low grafting ratio: 5%,
- medium grafting ratio: 19%,
- high grafting ratio: 53%.

2.2 NMR technique

Experimental ¹H measurements were carried out on a Bruker CXP 300 Fourier transform NMR spectrometer operating at 300 MHz.

Each spectrum was obtained by fast Fourier transforming the averaged free induction decay (FID) occurring after a π/2 radiofrequency pulse. The π/2 pulse width was less than 1.5 μs, which corresponds to a B₁ rotating field of more than 40 Gauss. The dead time of the detection was less than 4 μs.

Experimental measurements of T₁ (¹H) were carried out by using the inversion-recovery pulse sequence (π–τ–π/2).

Experiments were carried out over the temperature range 220–380 K, with the latter being controlled by a variable temperature regulator from Bruker.

This spectrometer was equipped with a “double- bearing” probe head allowing magic angle spinning (at 54°44′) at rates going from 0 to 4.5 kHz. Rotation at room temperature was achieved by an air-driven turbine in which the rotor itself was supported by gas bearing. Experiences at low temperature were achieved by using cold nitrogen gas as propulsor. The experimental spectra were fitted with calculated Lorentzian or Gaussian lines, with the program Linefit from Bruker.

The samples were prepared as follows:

- relaxation time experiment: the samples were all prepared in Pyrex spheres of 5-mm diameter, which gave greater field homogeneity. Before the experiment the grafted silica was dried by direct pumping.
- MAS experiment: the powder samples (PEO grafted on silica) were placed in zirconia cylindrical rotors of 5-mm diameter, volume about 0.3 cm³ (about 0.15 g), spinning at the magic angle (54°44′).

3 Result and discussion

3.1 Effect of the dipolar interaction for PEO

For polymer grafted on silica, dipolar interaction between adjacent nuclei is considered to be the only interaction responsible for nuclear relaxation processes. There exist two contributions due to intermonomer unit and intramonomer unit interactions. The interaction can therefore be decomposed into two parts of the Hamiltonian [13,15]:

H_{D} = H_{D}^{intra} + H_{D}^{inter}

(2)

To investigate more thoroughly the influence of the second term, the Hamiltonian can be rewritten as follows [15]:

H_{D} = H_{D}^{1} + H_{D}^{2}

(3)

H_{D}^{1} = H_{D}^{intra} + H_{D}^{inter} - {\bar{H}}_{D}^{inter}

(4)

H_{D}^{2} = {\bar{H}}_{D}^{inter}

(5)

H_{D}^{1}

is a fluctuating interaction giving rise to a narrowing of the line. The local motion of monomer units is relatively fast in comparison with the evolution to the equilibrium of the transverse magnetisation (≪T₂); the average of

H_{D}^{1}

is approximately zero (i.e.

{\bar{H}}_{D}^{1} \neq 0

).

$H_{D}^{2}$ is a static interaction (i.e. ${\bar{H}}_{D}^{2} \neq 0$ ) giving the residual interaction (nonzero average dipolar spin coupling). This interaction is due to the very slow anisotropic reorientation process of the monomer units relative to one another. This interaction depends on the local density of monomer units. It is not averaged because the motion of the segments relative to each other is strongly hindered. The local motion of segments on the other hand is rapid enough to average the Hamiltonian ${\bar{H}}_{D}^{1}$ . The effects of these two terms on the relaxation times T₁ and T₂ of the spin system are very different. The spin–lattice relaxation time T₁ depends only on $H_{D}^{1}$ , whereas the spin–spin relaxation function T₂ depends on both $H_{D}^{1}$ and $H_{D}^{2}$ .

3.2 Spin–lattice relaxation time study

The dominant mechanism which governs the spin–lattice relaxation process of the proton of macromolecules is the dipolar interaction between the nuclear spins located within one given chain segment. The expression of the spin–lattice relaxation rate 1/T₁ for identical spins is given by the relation [16]:

\frac{1}{T_{1}} = K [\frac{τ_{c}}{1 + ω^{2} τ_{c}^{2}} + \frac{4 τ_{c}}{1 + 4 ω^{2} τ_{c}^{2}}]

(6)

where

K (K \propto 1 / r^{6})

is a parameter depending on the distance between the interacting spins, ω is the resonance frequency of the protons, and τ_c is the correlation time of the spins' motion.

The observation of the longitudinal magnetisation in a large domain of temperature gives the possibility to evaluate the correlation time τ_c of the local fluctuations of the chain segments [17]. This evaluation becomes very simple when the minimum of the spin–lattice relaxation time versus temperature T₁(T) is observed.

The mathematical expression for τ_c is derived from a specific model for the chain dynamics. Unfortunately, there is no general theory of NMR relaxation for such complex systems as polymers yet. Different models are used. The BPP model [18], usually used for simple liquids and developed for the interpretation of the experimental data, introduces, for a simple isotropic and random motion of the lattice, a rotational correlation time of the supposedly thermally activated process. The Kramer and Helfand model [19,20] is based on the passage of a particle over a potential energy barrier. Two different stable conformations/structures of the polymeric chain are separated by a potential energy barrier of height E_a. The energy required for conformational transition is provided by thermal activation.

For a quantitative estimation of the correlation time of molecular dynamics, the Kramer and Helfand model is used. The temperature dependence of the correlation time is:

τ_{c} = B \exp (\frac{E_{a}}{R T})

(7)

where B is a parameter depending on the nature of polymer, E_a is the activation energy required for conformational transition, R is the universal constant of the gases. Both parameters B and E_a are unknown. We will try to estimate the values of those parameters by analyzing the experimental data T₁(T).

By combining Eqs. (6) and (7), we obtain the temperature dependence of the spin–lattice relaxation rate:

\frac{1}{T_{1}} = K B \exp (\frac{E_{a}}{R T}) [\frac{τ_{c}}{1 + ω^{2} {(B \exp (\frac{E_{a}}{R T}))}^{2}} + \frac{4 τ_{c}}{1 + 4 ω^{2} {(B \exp (\frac{E_{a}}{R T}))}^{2}}]

(8)

In this relation there are three unknown parameters: K, B, E_a. From experimental data we are trying to determine these parameters in order to evaluate the correlation time τ_c. Neverthless some situations are of great interest:

- the extreme narrowing limit $ω τ_{c} ≺ ≺ 1$ ,
- the minimum of the spin–lattice relaxation time.

The first situation is fulfilled in the domain of high temperatures and leads to a simplification of Eq. (8):

\frac{1}{T_{1}} = 5 K B \exp (\frac{E_{a}}{R T})

(9)

This relation can be used to evaluate the activation energy E_a.

Concerning the second situation, the minimum of the spin–lattice relaxation time implies the condition: $\partial T_{1} / \partial T = 0$ . From Eq. (8), by derivation, we can obtain the simplest relation corresponding to the minimum of the spin–lattice time:

ω τ_{c} \approx 0.616

(10)

It is possible to estimate the correlation time for the temperature which corresponds to the minimum of the spin–lattice relaxation time. For other temperatures, the correlation time can be calculated using Eq. (7) when the parameters B and E_a are known.

If we substitute Eq. (8) into Eq. (6), we can obtain a direct relation between the minimum value of the relaxation time T_{1_min} and the parameter K:

\frac{1}{T_{1_{\min}}} = K \times 5.035 \times 10^{- 9}

(11)

Hence B is the only unknown parameter. If the activation energy E_a and the parameter K are known, the parameter B can be evaluated from the best fit of experimental data T₁(T) to (3). Then the values of the parameters B and E_a can be used to calculate the correlation time at any temperature with Eq. (7).

We measured the spin–lattice relaxation time for the polymer grafted on silica at different grafting ratios in the temperature range 220–380 K; this domain includes the temperature corresponding to the minimum of the relaxation time (Fig. 1). The values of T_{1_min} and corresponding temperature are listed in Table 1.

Fig. 1
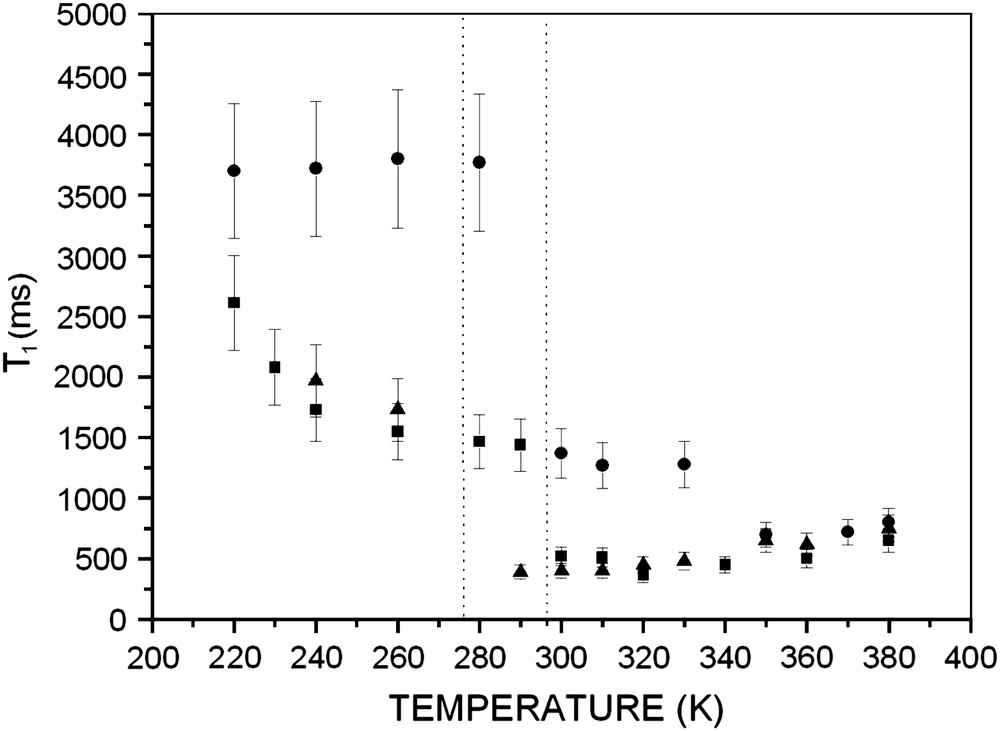
Temperature dependence of the spin–lattice relaxation time T₁ for PEO 2000 grafted on silica with molecular weight 2000 for different grafting ratios: (●) 5%, (■) 19%, (▴) 53%. Data obtained from ¹H NMR spectroscopy (300 MHz) (without sample rotation).

	T_{1 min} (s)	T(T_{1 min}) (K)	10⁻³/T_{1 min}	K (s⁻²)	E_a (kJ/mol)	B (s)
5%	0.7	350	2.85	0.27 × 10⁹	5.9	9.9 × 10⁻¹⁰
19%	0.36	320	3.12	0.55 × 10⁹	9.56	1.4 × 10⁻¹⁰
53%	0.4	310	3.22	0.45 × 10⁹	8.65	1.9 × 10⁻¹⁰

From the minimum of the relaxation time we calculated the values of parameter K for all grafting ratios with Eq. (11). These values are also listed in Table 1.

It was already demonstrated by measurements of relaxation times [9] that there exists a transition situated between 270 and 290 K. The transition is not a vitreous transition of poly(ethylene oxide) because the latter (for free PEO macromolecules) is situated at 210 K. It is of a dynamic nature, and corresponds to a modification of the motion of the monomer units, which is influenced by the grafting ratio. This transition is observed for all grafting ratios. It is more important when the grafting ratio is low.

For each grafting ratio we calculated the activation energy E_a from the Arrhenius plot of the experimental data in this temperature range (Fig. 2).

Fig. 2
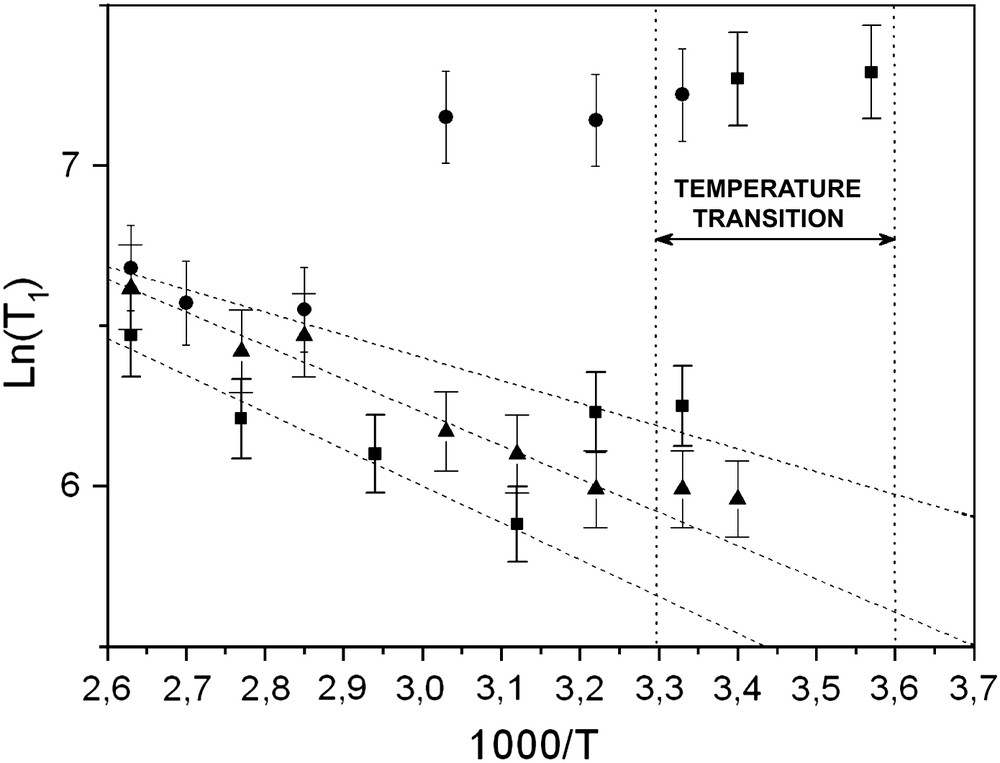
¹H NMR. Arrhenius plot of the experimental T₁(T) data for PEO 2000 grafted on silica with molecular weight 2000 at different grafting ratios: (●) 5%, (■) 19%, (▴) 53%.

The values of parameters K and E_a were introduced in Eq. (8). We fitted the experimental results T₁(T) to this equation in order to obtain the parameter B. We retained the value of B that corresponds to the relatively best fit.

To a first approximation we do not obtain a good fit for all samples (Fig. 3). In fact, we obtain an agreement for the temperatures located after the zone of transition. We were interested in the high temperatures, i.e. after the zone of transition. Let us note that for the low grafting ratio, the results are in disagreement.

Fig. 3
¹H NMR. The fit plot of the experimental 1/T₁(T) data using Eq. (3) for PEO 2000 grafted on silica with molecular weight 2000 at different grafting ratios: (●) 5%, (■) 19%, (▴) 53%.

The simplest dynamic model is very well suited to a system with great mobility. In the domain of high temperature, above the transition temperature range, the dynamic of the polymeric segment is high and this model can be applied with good results. We calculated the parameter E_a in this temperature domain, and used this value to fit the experimental data T₁(T) in the entire temperature domain.

At low temperature, in particular in the vicinity of the transition temperature range, the dynamics of the polymeric chain is very much reduced compared with the dynamics at high temperature. In this situation, it is possible that the simple model of the potential energy barrier could not explain the behaviour of the polymeric segment. For this reason, some deviations of the fit from the experimental data may be observed. However, this model can be used for preliminary investigation of the local dynamics.

Using the parameters E_a and B obtained in this way, we generated the correlation time at any temperature after the transition temperature range using Eq. (2) as shown in Fig. 4. These values of τ_c were calculated.

Fig. 4
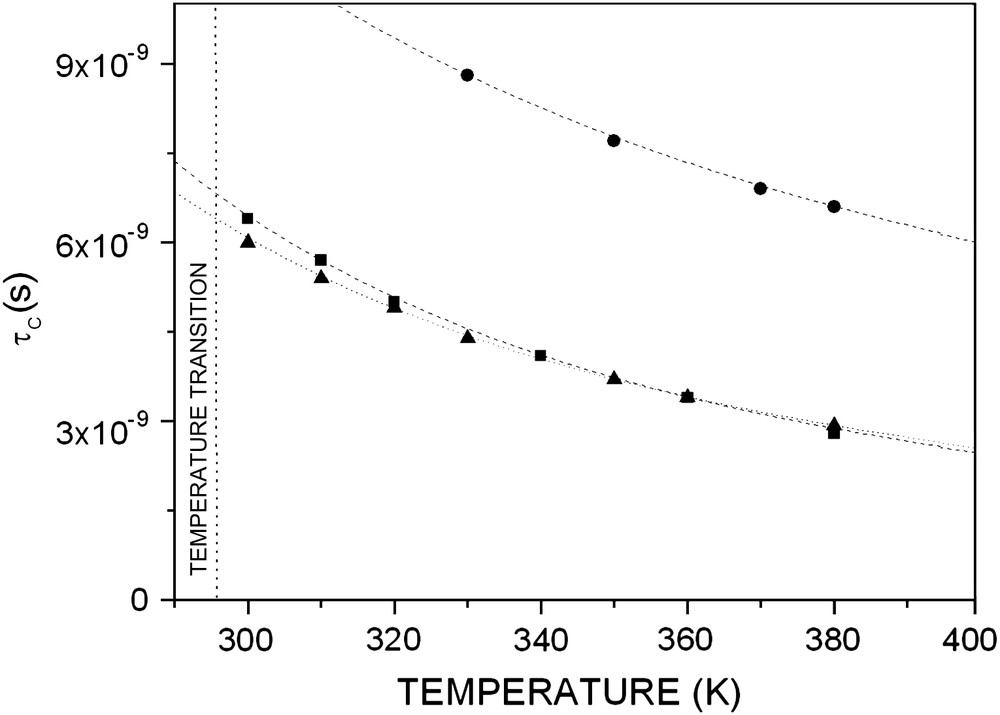
¹H NMR. The values of τ_c generated with Eq. (2) for PEO 2000 grafted on silica with molecular weight 2000 at different grafting ratios: (●) 5%, (■) 19%, (▴) 53%.

3.3 Rotation effect and limit linewidth study

The magic-angle spinning technique was used to study the dynamics of the polymeric chain and to determine two correlation times (τ_sl and τ_fa) for each grafting ratio. In fact, we assume that the fluctuation of local dipolar field arises from two contributions [21,22]:

- the reorientation motion of monomer units relative to each other described by the $H_{D}^{inter}$ Hamiltonian and characterised by the relatively longer correlation time τ_sl;
- the local motion of monomer units, relatively fast, and described by the $H_{D}^{intra}$ Hamiltonian and characterised by the short correlation time τ_fa.

We are interested essentially in the last correlation time, which corresponds to the local segmental motion. It can be evaluated from the analysis of the experimental results and can be compared to the correlation time determined by T₁.

Some experiments have been performed on PEO grafted on silica at room temperature at different grafting ratios [23]. In Fig. 5, experimental ¹H NMR spectra showing the effect of sample rotation on the narrowing of the central line is presented. Fig. 6 shows the evolution of the linewidth versus the rate of rotation. The NMR line narrowing effect by high speed rotation is observed in the same samples with different grafting ratios. As previously, the same evolution is observed in our experiences. In fact, when the rotation frequency increases, one observes a line narrowing for ω_r ≈ 1/τ_sl. After this transition, the linewidth will be limited to (δω)_li independently of the rotation rate, because of the very large value of 1/τ_fa. This behaviour is characteristic of the coexistence of two fast and slow motions, described, respectively, by $H_{D}^{intra}$ and $H_{D}^{inter}$ , characterised by the respective correlation times τ_fa and τ_sl. The resulting spectral density is illustrated in Fig. 6 (inset). The study of the NMR linewidth as a function of ω_r is therefore interesting for evaluating the correlation time τ_fa in PEO/silica systems. The linewidth, when the sample rotates at ω_r, can be written as [22,23]:

{(δ ω_{r})}^{2} = \frac{2}{π} {(δ ω_{fa})}^{2} τ_{fa} δ ω_{r} + \frac{{(δ ω_{s})}^{2}}{π} \frac{2}{3} [arctg (ω_{r} + δ ω_{r}) τ_{sl} - arctg (ω_{r} - δ ω_{r}) τ_{sl}] \frac{1}{3} arctg [(2 ω_{r} + δ ω_{r}) τ_{sl} - arctg (2 ω_{r} - δ ω_{r}) τ_{sl}]

(12)

We can notice that the evolution of the linewidth with the rotation frequency deduced from the expression (12) is in agreement with all our experiences.

Fig. 5
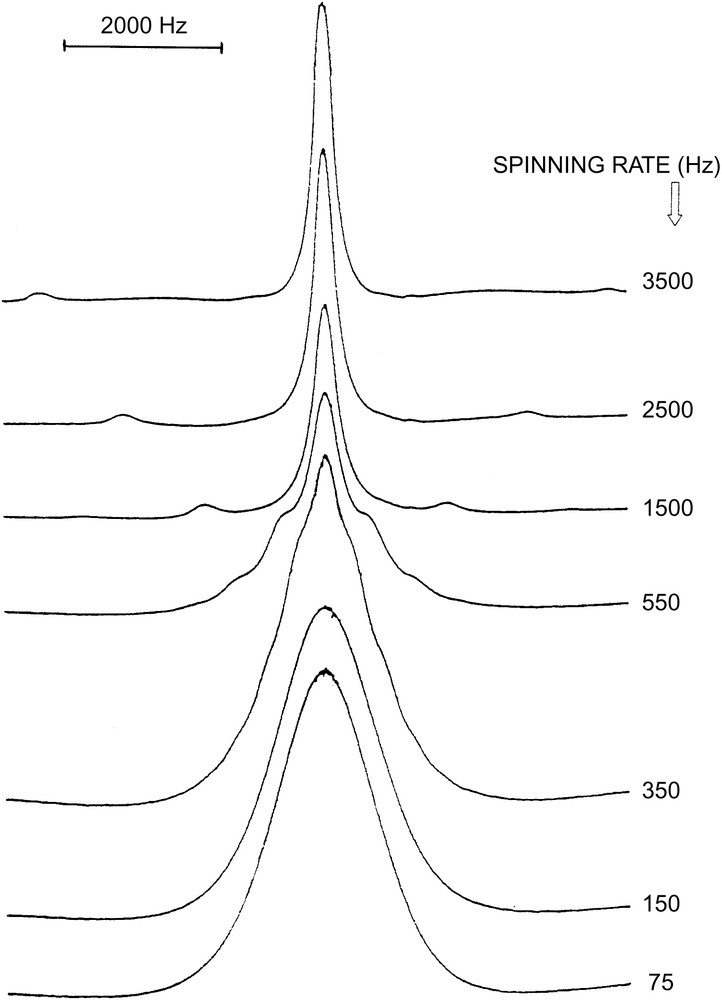
¹H NMR. Spectra recorded during sample rotation. Spectra correspond to an increasing spinning rate (from 0 to 3500 Hz); PEO 2000 grafted on silica (grafting ratio 53%); room temperature.

Fig. 6
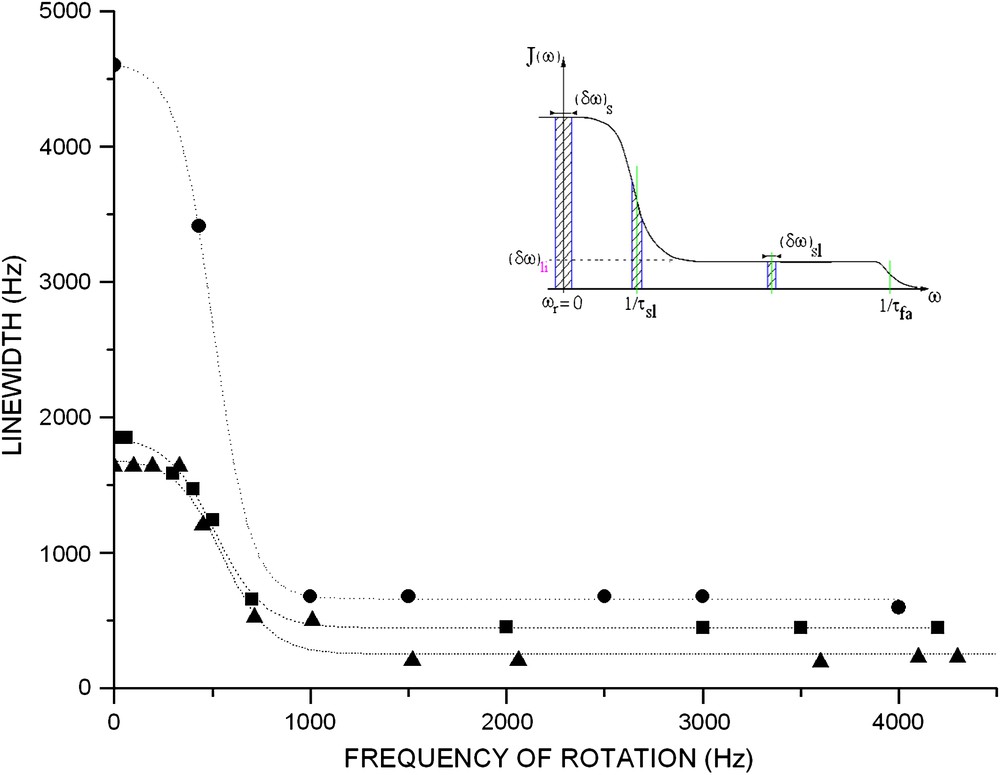
Evolution of linewidth versus rotation frequency of sample. Different grafting ratios at room temperature for grafted poly(ethylene oxide). (●) 5%, (■) 19%, (▴) 53%. Data obtained from ¹H NMR spectroscopy (300 MHz). Inset: effects of sample rotation on linewidth when two molecular motions τ_fa and τ_sl are present in a sample.

Particularly, when ω_r > 1/τ_sl, the linewidth reaches a limiting value:

{(δ ω)}_{li} = \frac{2}{π} {(δ ω_{fa})}^{2} τ_{fa}

(13)

The residual linewidth must therefore give the fast correlation time of fast internal motion. From this expression, we can confirm that the more the segmental motion is fast, the more the linewidth is small. In order to study this motion, we adopt Andrew's approach [24] introduced above. A computing program has been elaborated using the previous expressions. The last relation (12) permits to plot a theoretical curves and to fit it by varying τ_fa and τ_sl. τ_fa is deduced from the expression (13). A good agreement between theoretical curves and experimental results by varying the value of τ_sl is obtained. τ_fa and τ_sl are determined in this way. Table 2 shows the experimental results concerning the measurement of these correlation times for different grafting ratios.

	Correlation time τ_c (s) (by spin–lattice relaxation time T₁)	τ_c (s) (by MAS technique)
5%		1.7 × 10⁻⁶
19%	6.4 × 10⁻⁹	1 × 10⁻⁶
53%	6 × 10⁻⁹	0.9 × 10⁻⁶

We obtained two correlation times characteristic of the fast segmental motion by two different techniques. The comparison of the values obtained at 300 K shows a great difference. We observe a ratio of approximately 100. This variation can be explained as follows.

The spin–lattice relaxation which limits the life time of spin in a given state can lead to a linewidth of about 1/T₁. In the polymer grafted system, the local motion of the monomer units, which is relatively fast, represents a significant mechanism of relaxation. According to the BPP [18] model, the components of the order of the Larmor frequency ω₀ (and 2ω₀) of the local motion could produce transitions between the states of nuclear spins and thus to support the transfer of energy between the spins and the lattice.

The macroscopic rotation of the sample does not have a significant effect on this type of mechanism of relaxation. In fact, the macroscopic frequency of the rotation reached is much weaker than ω₀. The spin–lattice relaxation time T₁ and the linewidth which results from it are not modified by the rotation of the sample. Thus, we can notice that the linewidth generated by the spin–lattice relaxation mechanism is generally negligible when compared to the limiting linewidth.

4 Conclusion

The local mobility of the polymeric chain can be investigated by analyzing the temperature dependence of the NMR spin–lattice relaxation time and magic-angle spinning. An important parameter used to characterise this process is the correlation time of the local dynamics of the polymeric segments. This parameter can be evaluated, in a first approximation, using the dynamic model of the passage of a particle over a potential barrier. The mathematical relation used for this evaluation requires an analysis of the T₁(T) data for a wide range of temperatures, including the extreme narrowing and the minimum of the T₁(T). The correlation time is dependent on the temperature. For a given grafting ratio, the correlation time decreases with increasing the temperature, which indicates an increase of the polymer mobility.

The correlation time of the local dynamics determined by the MAS technique lies in the range of 10⁻⁶–10⁻⁷, but it is greater than the correlation time obtained by the spin–lattice relaxation method (about 10⁻⁹–10⁻⁸). The comparison of the values obtained by the two techniques shows a great difference. A ratio of one hundred is obtained. Indeed, the macroscopic rotation does not have an effect on the mechanism of relieving of T₁. It is necessary to reach the frequency of rotation close to the frequency of Larmor, which is impossible.

References

[1] M. Wang; M. bertmer; D.E. Demco; B. Blumich; V.M. Litvinov; H. Barthel Macromolecules, 36 (2003), p. 4411

[2] M. bertmer; L. Gasper; D.E. Demco; B. Blumich; V.M. Litvinov Macromol. Chem. Phys., 205 (2004), p. 83

[3] M. Zeghal; P. Auroy; B. Deloche Macromolecules, 32 (1999), p. 4947

[4] E. Papirer Adsorption on Silica Surfaces, Marcel Dekker, Inc., New York, 2000

[5] Polymers and Surfaces: A Versatile Combination (H. Hommel, ed.), Research Signpost, Trivandrum, India, 1998

[6] P.G. De Gennes Adv. Colloid Interface Sci., 27 (1987), p. 189

[7] V.M. Litvinov; H. Barthel; J. Weis Macromolecules, 35 (2002), p. 4364

[8] M. bertmer; M. Wang; D.E. Demco; B. Blumich Solid State Nucl. Magn. Reson., 30 (2006), p. 45

[9] T. Tajouri; H. Bouchriha Polymer, 37 (1996), p. 3185

[10] K. Yamamoto; A. Maruta; S. Shimata Polymer, 33 (2001), p. 584

[11] T.Tajouri; H. Bouchriha; H. Hommel Polymer, 44 (2003), p. 6825

[12] K. Saalwächter; P. Ziegler; O. Spyckerelle; B. Haidar; A. Vidal; J. Sommer J. Chem. Phys., 6 (2003), p. 3468

[13] L. Facchini; A.P. Legrand Macromolecules, 17 (1984), p. 2405

[14] The Surface Properties of Silica (A.P. Legrand, ed.), John Wiley and Sons, Chichester, 1998

[15] T. Tajouri; H. Bouchriha J. Colloid Interface Sci., 252 (2002), p. 450

[16] A. Abragam Principles of Nuclear Magnetism, Oxford Univ. Press, London, 1961

[17] J.P. Cohen-Addad NMR and Fractal properties of Polymeric Liquids and Gels, Pergamon Press, London, 1992

[18] N. Bloembergen; E.M. Purcell; R.V. Pound Phys. Rev., 73 (1948), p. 679

[19] H.A. Kramer J. Chem. Phys., 7 (1940), p. 284

[20] E. Helfand J. Chem. Phys., 54 (1971), p. 4651

[21] S. Azizi; T. Tajouri; H. Bouchriha Polymer, 41 (2000), p. 5921

[22] E.R. Andrew; A. Jasinski J. Phys. C: Solid State Phys., 4 (1971), p. 391

[23] T. Tajouri; H.Hommel Magn. Reson. Chem., 45 (2007), p. 488

[24] E.R. Andrew Philos. Trans. R. Soc. Lond. Ser. A, 292 (1981), p. 505

Comments - Policy