Spin-polarization in 1,3,5-trihydroxybenzene-bridged first-row transition metal complexes

Thorsten Glaser; Hubert Theil; Maik Heidemeier

doi:10.1016/j.crci.2008.05.016

Spin-polarization in 1,3,5-trihydroxybenzene-bridged first-row transition metal complexes

Thorsten Glaser ¹ ; Hubert Theil ¹ ; Maik Heidemeier ¹

¹ Fakultät für Chemie, Universität Bielefeld, Universitätsstr. 25, 33615 Bielefeld, Germany

Comptes Rendus. Chimie, Volume 11 (2008) no. 10, pp. 1121-1136.

Résumé

The late Olivier Kahn formulated a research objective for molecular magnetism: ‘The normal trend for the molecular state is the pairing of electrons […] with a cancellation of the electron spins. The design of a molecule-based magnet requires that this trend be successfully opposed.’ One strategy for enforcing ferromagnetic interactions is the spin-polarization mechanism. While this mechanism is almost always working in organic chemistry, the application to transition metal complexes is not straight-forward. We have established a structurally related series of trinuclear complexes bridged by modified 1,3,5-trihydroxybenzene (phloroglucinol) ligands. The trinuclear Cu^II complexes all exhibit weak, but ferromagnetic interactions. The trinuclear V^IV complex exhibits even smaller ferromagnetic interactions, while a trinuclear Mn complex exhibits antiferromagnetic interactions. The correlation between structural and magnetic parameters in the series of Cu complexes gives experimental insight into the spin-polarization mechanism. The crucial parameter for an efficient spin-polarization mechanism through the bridging benzene unit seems to be the amount of spin density in the p_z^π orbitals of the phenolic oxygen atoms. This spin density crucially depends on the remaining coordination sites and on the ligand folding at the central Cu–phenolate bond. The spin transfer from the metal to the phenolate oxygen atom occurs by two different mechanisms, namely spin-polarization and spin-delocalization, which can provide opposing contributions. The main conclusion of this study is that for a more efficient spin-polarization through the central benzene ring the spin density in the phenolate O p_z^π orbital must be maximized, which can mainly be achieved by increasing the covalency of the metal–phenolate bond.

Métadonnées

Reçu le : 2008-01-30
Accepté le : 2008-05-26
Publié le : 2008-08-20

DOI : 10.1016/j.crci.2008.05.016

Mots clés : Molecular magnetism, Ferromagnetic interactions, Spin polarization, Ligand design

Affiliations des auteurs :

Thorsten Glaser ¹ ; Hubert Theil ¹ ; Maik Heidemeier ¹

¹ Fakultät für Chemie, Universität Bielefeld, Universitätsstr. 25, 33615 Bielefeld, Germany

@article{CRCHIM_2008__11_10_1121_0,
     author = {Thorsten Glaser and Hubert Theil and Maik Heidemeier},
     title = {Spin-polarization in 1,3,5-trihydroxybenzene-bridged first-row transition metal complexes},
     journal = {Comptes Rendus. Chimie},
     pages = {1121--1136},
     publisher = {Elsevier},
     volume = {11},
     number = {10},
     year = {2008},
     doi = {10.1016/j.crci.2008.05.016},
     language = {en},
}

TY  - JOUR
AU  - Thorsten Glaser
AU  - Hubert Theil
AU  - Maik Heidemeier
TI  - Spin-polarization in 1,3,5-trihydroxybenzene-bridged first-row transition metal complexes
JO  - Comptes Rendus. Chimie
PY  - 2008
SP  - 1121
EP  - 1136
VL  - 11
IS  - 10
PB  - Elsevier
DO  - 10.1016/j.crci.2008.05.016
LA  - en
ID  - CRCHIM_2008__11_10_1121_0
ER  -

%0 Journal Article
%A Thorsten Glaser
%A Hubert Theil
%A Maik Heidemeier
%T Spin-polarization in 1,3,5-trihydroxybenzene-bridged first-row transition metal complexes
%J Comptes Rendus. Chimie
%D 2008
%P 1121-1136
%V 11
%N 10
%I Elsevier
%R 10.1016/j.crci.2008.05.016
%G en
%F CRCHIM_2008__11_10_1121_0

Thorsten Glaser; Hubert Theil; Maik Heidemeier. Spin-polarization in 1,3,5-trihydroxybenzene-bridged first-row transition metal complexes. Comptes Rendus. Chimie, Volume 11 (2008) no. 10, pp. 1121-1136. doi : 10.1016/j.crci.2008.05.016. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2008.05.016/

Version originale du texte intégral

1 Introduction

1.1 Molecule-based magnetic materials and ferromagnetic interactions

The considerable interest in the synthesis of magnetic materials based on molecular entities with its potential application in fields like molecular electronics [1–5] started with the observation that [Cp^∗₂Fe]⁺[TCNE]⁻, 1, exhibits a spontaneous long-range ferromagnetic ordering with a Curie temperature T_C of 4.8 K [6,7]. The structure of 1 consists of chains of alternating [Cp^∗₂Fe]⁺ and [TCNE]⁻ units both having an S = 1/2 ground state. The intra-chain interaction is ferromagnetic with J = +13 cm⁻¹. (All coupling constants J in this manuscript are related to the Heisenberg–Dirac–van Vleck–Hamiltonian in the form of H = −2JS₁S₂.) Below 4.8 K, weak but ferromagnetic dipolar interactions between the chains lead to the observed spontaneous magnetization. This 3D long-range magnetic order in a system constructed from molecular building blocks initiated world-wide research activities to prepare quasi-1D, 2D, and 3D molecule-based magnets. Prominent examples with T_Cs above room temperature are V(TCNE)₂·y(CH₂Cl₂), 2 [8], and some members of the family of Prussian Blue analogues like KV^II[Cr^III(CN)₆], 3 [9], or V^II_0.42V^III_0.58[Cr^III(CN)₆]_0.86·2.8H₂O, 4 [10,11]. This last class provides a convenient approach for the design of new interesting materials because the high symmetry of the M–CN–M′ exchange pathway allows the prediction of the nature of the exchange interactions [12,13] by the use of the Goodenough–Kanamori rules [14–18].

Another milestone in the field of molecule-based magnets was the observation that [Mn₁₂O₁₂(O₂CCH₃)₁₆(OH₂)₄], Mn₁₂ [19], exhibits a hysteresis in the magnetization of purely molecular origin and has been the first member of a new class of molecular materials called single-molecule magnets (SMMs) [20–22]. In contrast to the above mentioned molecule-based magnets exhibiting a long-range ferromagnetic order, SMMs possess an energy barrier for spin reversal which causes a slow relaxation of the magnetization at low temperatures. The energy barrier originates from a high-spin ground state and a magnetic anisotropy of the easy-axis type (negative zero-field splitting parameter D). This magnetic anisotropy barrier results in a magnetic bistability at low temperatures which attracts a great deal of scientific attention [23,24] and some reports on potential application of SMMs appeared in the literature [23–28]. Mn₁₂ is a high-spin molecule with an S_t = 10 spin ground state which shows a zero-field splitting D of −0.5 cm⁻¹ resulting in an anisotropy barrier D·S_t² of ∼50 cm⁻¹. While high-spin ground states, combined with a strong negative zero-field splitting, are necessary conditions for an SMM, they are not sufficient. In order to reduce relaxation pathways and to diminish interstate mixing, the ground states should be energetically well separated, i.e. strong exchange couplings are highly desirable. Additionally, the serendipitous increase of the nuclearity of polynuclear transition metal complexes by using small ligands results in compounds with symmetries that approach the cubic limit. In this situation, the local anisotropies cancel each other by projecting on the global spin ground state.

The above given summary of the two major directions in the field of molecule-based magnets, namely long-range ordered magnets and single-molecule magnets, clearly defines one important research objective in molecular magnetism, which is not yet realized: synthetic strategies to building blocks which enforce ferromagnetic interactions and/or high-spin ground states. This objective was already formulated by the late Olivier Kahn: ‘The normal trend for the molecular state is the pairing of electrons […] with a cancellation of the electron spins. The design of a molecule-based magnet requires that this trend be successfully opposed’ [29].

In order to establish synthetic recipes for parallel spin alignments we are exploring three different strategies:

(1) the double exchange mechanism [30–33] in face-sharing octahedra [34,35],
(2) the use of orthogonal magnetic orbitals [15,36,37] (second Goodenough–Kanamori rule),
(3) the spin-polarization mechanism [38,39] in meta-phenylene-bridged complexes [40–43], which is the subject of the work described herein.

1.2 The spin-polarization mechanism

It is well established in organic chemistry that the meta-phenylene linkage of organic radicals and carbenes leads to ferromagnetic interactions, while in the corresponding ortho- and para-phenylene linkages, the interaction is antiferromagnetic [44–49]. This simple, heuristic phenomenon is usually attributed to a general mechanism termed spin-polarization and some concepts concerning this spin-polarization will be summarized here.

The archetype compounds are the alternant hydrocarbons 5–7 (Scheme 1, top row) [50]. Alternant hydrocarbons are conjugated systems in which the atoms can be divided into two groups, starred and unstarred, in such a way that no two atoms with like parity are directly linked. If the number of atoms in the two sets differs, the more numerous set should be the starred one [51]. It is easy to see from Scheme 1 that 5 and 7 have four starred and four unstarred carbon atoms, while in the meta-isomer 6 there are five starred and three unstarred carbon atoms (Scheme 1, middle row).

For the ortho- and para-phenylene-bridged diradicals 5 and 7, resonance structures can be formulated (Scheme 1, bottom row) where each carbon atom possesses an electron octet by three σ-bonds and one π-bond (Kekulé-type structure [38]). For the meta-phenylene-bridged diradical 6 no such resonance structure can be formulated (excited structures [38] or non-Kekulé compounds [51]). At least one carbon atom is connected to its three neighbors by single bonds only [38]. From these resonance structures, it is quite evident that the ortho-isomer 5 and the para-isomer 7 possess closed-shell singlet ground states while the meta-isomer 6 has an open-shell diradical ground state. However, from this simple picture it is not yet evident whether the two radicals in 6 couple ferromagnetically (S_t = 1) or antiferromagnetically (S_t = 0).

From LCAO-MO considerations based on simple Hückel theory (one-electron theory), it follows that an alternant hydrocarbon with n starred atoms and m unstarred atoms has n − m non-bonding MOs (NBMOs). Thus, in 5 and 7 the eight π-electrons are in four bonding MOs resulting in the closed-shell ground states, while in 6 two NBMOs are degenerate at ‘zero’ energy each occupied by only one π-electron. Application of Hund's rule for atoms on this molecule predicts therefore a ferromagnetic S_t = 1 ground state in 6 [49,51].

A simple generalization is provided in Eq. (1) which gives an easy way to obtain the spin ground state S_t of an alternant hydrocarbon with n starred and m unstarred atoms [49,52–54].

S_{t} = \frac{n - m}{2}

(1)

Increasing the level of theory, i.e. going from Hückel MO theory to many-electron MO theory at the SCF level, a new phenomenon arises [55]. In a one-electron theory or in closed-shell many-electron SCF MO theory it is assumed that the two-paired electrons in one MO with α- and β-spin share the same spatial part of the MO. The treatment of an open-shell system by many-electron MO theory results in a situation that the two-paired electrons in one MO do not possess the same spatial distribution. A simple explanation is the following: an unpaired electron of say α-spin interacts differently with the two-paired electrons in a bonding MO. While the unpaired electron experiences a Coulomb repulsion by both electrons in the bonding MO, some exchange stabilization occurs for the electrons of like spin, i.e. the α-spin electrons. This leads to different potentials felt by the two electrons in the bonding MO due to the presence of the unpaired electron. Thus the two electrons in the bonding orbital are not equal anymore and therefore the spatial distribution and the energy of the MOs they occupy must differ; the two electrons are spin-polarized by the unpaired electron.

Theoretically [56], this phenomenon can be treated in the so-called unrestricted Hartree–Fock (UHF) formalism, where each electron occupies a spin-MO consisting of a space-part and a spin-part. In this unrestricted approach, the two electrons of ‘one’ MO of the restricted level may have different orbital parts of the MO. A different method is based on the restricted Hartree–Fock (RHF) formalism followed by configuration interaction with excited electron configurations (RHF + CI). Both treatments lead to two major conclusions [51,56]:

(1) In contrast to Hückel MO theory, spin density is not only distributed at the starred atoms in alternant hydrocarbons but also at the unstarred atoms.
(2) The unstarred atoms may possess negative spin density (β-spin density) even for a wave function describing an α-spin electron.

This treatment provides a simple picture for explaining the observed ferromagnetic S_t = 1 ground state in the meta-isomer 6 as compared to the antiferromagnetic ground state in the ortho- and para-isomer 5 and 7, respectively: the sign of the spin density in the bridging unit of the atoms alternates [57]. This is illustrated in Scheme 2 and provides the opportunity to develop high-spin organic radicals and carbenes on the back of an envelope.

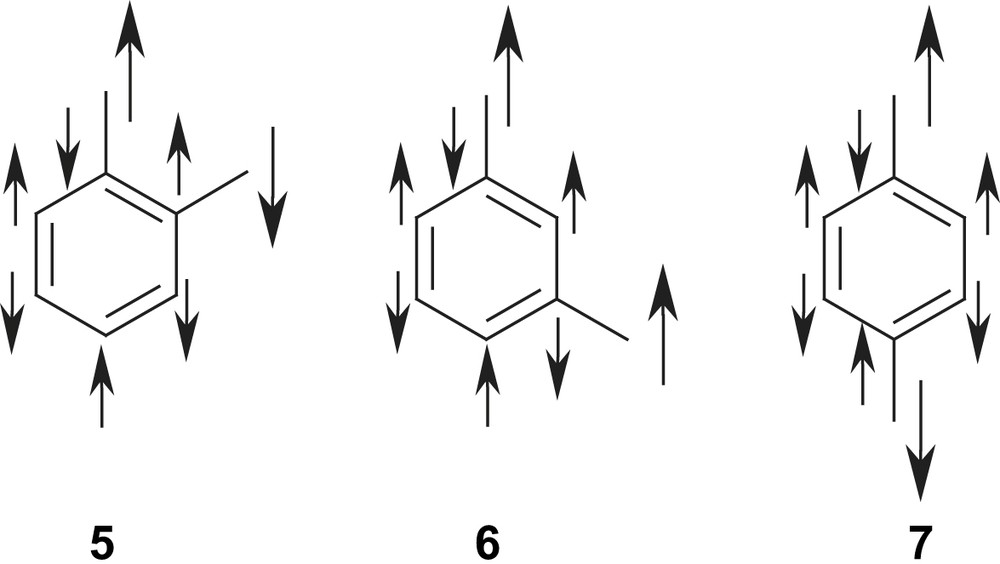
It should be noted that the simple Hückel picture with two non-bonding orbitals at ‘zero-energy’ may be misleading in that respect that it might imply that there would be no interaction between these two electrons. This interpretation is not correct. There is a strong interaction through the intervening π-orbitals, resulting in a strong stabilization of the ferromagnetic ground state in 6 (exchange integral K).

1.3 Applications of the spin-polarization mechanism to transition metal complexes

This concept was applied to transition metal complexes by using various bridging units. Pyrimidine 8 has been frequently used as an m-phenylene bridging unit. Mitsubori et al. synthesized dinuclear vanadyl complexes with variously substituted pyrimidines as bridging units and they obtained ferromagnetic interactions between the two V^IV ions with coupling constants of 1–2 cm⁻¹ [58,59]. In an extension they used these substituted pyrimidine rings for the preparation of 1D Cu^II coordination polymers and they obtained again ferromagnetic couplings between the Cu^II ions [60]. Lloret et al. used pyrimidine for the preparation of a 2D Co^II network. The ferromagnetic interactions between the Co^II ions through the pyrimidine bridging units over two dimensions lead to a ferromagnet with a Curie temperature T_C of 8.2 K [61]. Additionally they could show by using the para-isomer pyrazine 9 that the interactions between the Co^II ions are antiferromagnetic.

While these reports seem to show that the spin-polarization mechanism, originally developed for organic radicals and carbenes, can be adapted in coordination chemistry, the first drawback becomes evident in the coupling constants, which are tremendously lower in comparison to the pure organic molecules. However, more irritating is the larger number of reports, where a bridging pyrimidine unit 8 facilitates antiferromagnetic couplings in Cu^II [62–67], Mn^II [62,67], Fe^II [68,69], Co^II [62,67–70], Ni^II [62,67], and Ti^III [71] complexes.

The same holds true for the C₃-symmetric μ₃-bridging ligand 1,3,5-triazine 10, which may be regarded as the triangular extension of the μ₂-bridging ligand pyrimidine 8. Hendrickson and coworkers used 2,4,6-trihydroxy-1,3,5-triazine (cyanuric acid) 11 and the corresponding thiol analogue trithiocyanuric acid 12 to prepare trinuclear Ti^III complexes. The coordination sphere of the Ti^III ions is saturated by cyclopentadienyl ligands. Interestingly, the cyanuric acid 11 bridged compounds show antiferromagnetic couplings [72], while the trithiocyanuric acid 12 bridged complexes exhibit ferromagnetic couplings [73].

To the best of our knowledge, the first meta-phenylene bridging unit, which is not comprising nitrogen donor atoms as part of the benzene ring, was reported by Oshio using the resorcinol (1,3-dihydroxybenzene)-based ligand 13 [74,75]. The dinuclear Fe^IIIFe^III complex was reported to have a ferromagnetic coupling of J = +0.62 cm⁻¹. However, the dinuclear Cu^II complex showed antiferromagnetic interactions.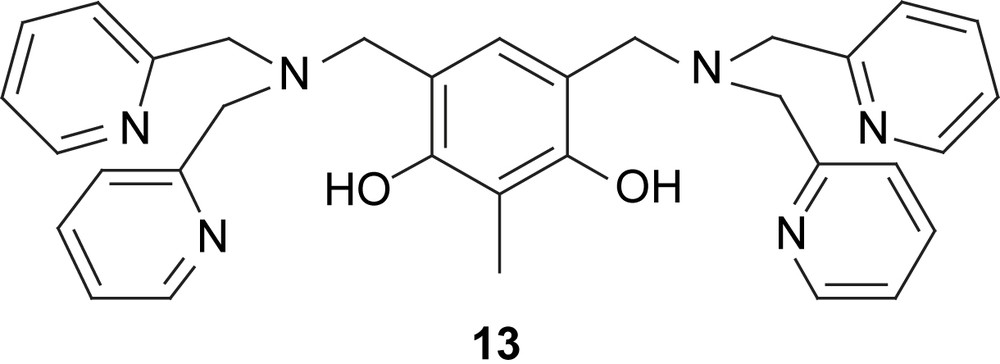

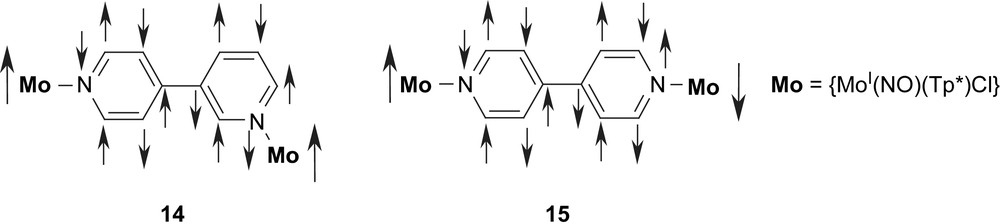
In a systematic study [76], McCleverty, Ward, and coworkers have been able to correlate the exchange couplings in dinuclear Mo complexes of extended polypyridyl and polyphenol ligands with the bridging topology by the spin-polarization mechanism [77–82]. In their classical paper they used extended polypyridyl-type ligands as bridges between two Mo^I complex fragments [77]. Depending on the relative orientation of the substitution they have shown that the coupling in 14 is ferromagnetic while it is antiferromagnetic in 15. The intuitive spin-polarization picture provided in Scheme 3 easily allows a prediction of this coupling behavior. It should be noted that the spin densities indicated in 14 and 15 are taken as provided in the classical paper [77]. As described in more detail below we prefer to draw the spin densities on the coordinating nitrogen atoms in the same direction as the spin on the metal atom due to the prevalence of spin-delocalization in this bond as compared to spin-polarization. However, either kind of drawing results in the same overall coupling. The coupling in 15 was established as J = −16.5 cm⁻¹, while the ferromagnetic coupling in 14 is again quite low at J = +0.4 cm⁻¹ [77].

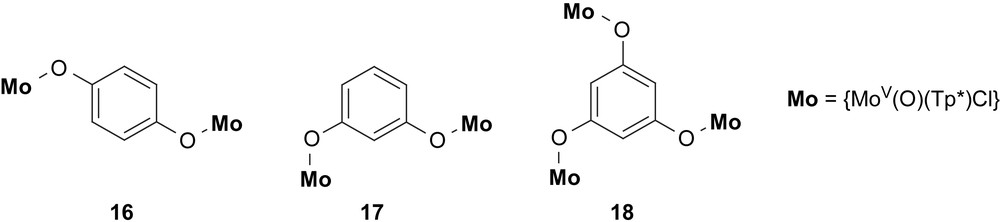
Hereupon they extended their bridging units to dihydroxobenzene units, namely 1,3-dihydroxy- and 1,4-dihydroxybenzene (Scheme 4). Using Mo^V complex fragments bound to these bridging units they observed again in agreement with the spin-polarization mechanism antiferromagnetic interactions in the 1,4-para-isomer 16 and ferromagnetic coupling in the meta-isomer 17 [79]. The coupling constants in these Mo^V complexes are stronger in comparison to the Mo^I-polypyridyl complexes: J = −40 cm⁻¹ in the para-isomer 16 and J = +4.9 cm⁻¹ in the meta-isomer 17. In the contents of this account, the first application of 1,3,5-trihydroxybenzene (phloroglucinol) should be highlighted, which they used as bridging ligand for three Mo^V complex fragments in 18. Interestingly, the coupling constant increases from 17 to 18 to J = +7.2 cm⁻¹ [79]. They extended their studies to naphthalene-based dihydroxy systems where also the exchange interactions could be rationalized by the spin-polarization mechanism [81].

Parallel to our efforts to employ phloroglucinol as bridging unit in trinuclear complexes of first-row transition metal ions, Journaux and coworkers developed bridging units based on 1,3-diaminobenzene and 1,3,5-triaminobenzene. The amino function allows the attachment of chelating arms directly at the nitrogen donor atoms. Two of the N-functionalized ligands 19 coordinate two Cu^II ions in a meta-phenylene fashion resulting in the formation of a metallacyclophane [83]. This bridging unit results in a ferromagnetic coupling of J = +8.4 cm⁻¹. The oxamate units of the ligand allow the coordination of a second metal ion to each unit, resulting in polynuclear complexes with interesting magnetic behavior [84–88]. The use of 1,3-diaminobenzenes bearing other N-substituents also resulted in dinuclear Cu^II complexes with ferromagnetic interactions [89,90]. Especially interesting in the context of this account is the use of a μ₃-extended version with a 1,3,5-trisoxamate benzene bridging ligand, which allows the synthesis of a trinuclear Cu complex with a coupling constant of J = +5.8 cm⁻¹ [91].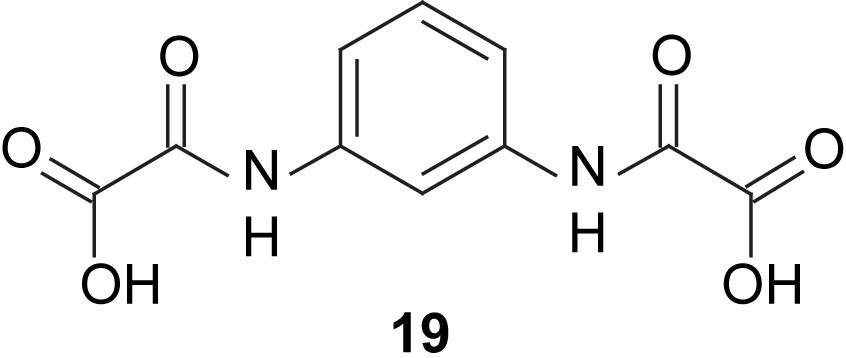

The above given examples indicate that the concept of spin polarization, which almost always works in organic chemistry to predict ferromagnetic interactions and to rationally develop new high-spin compounds, cannot be applied in a straight-forward manner to transition metal complexes.

Several theoretical investigations were performed to get insight into the question why the concept of spin-polarization cannot be applied that simply to transition metal complexes [63,67,92,93]. Karafiloglou already showed for organic diradicals that not only the spin polarization, but also exchange and superexchange interactions contribute to the overall coupling [56]. Analogously, Cano et al. emphasized the contribution of both spin-polarization and spin-delocalization in transition metal complexes [94]. This was also demonstrated by Bencini et al. for the meta-isomer 17 and the para-isomer 16. They showed that the orientation of the magnetic orbital on each metal site relative to the plane of the bridging benzene ring is crucial for a ferromagnetic or an antiferromagnetic contribution of the superexchange interaction as well as of the spin-polarization mechanism [82].

Takano et al. investigated dinuclear Cu^II and Mn^II complexes with a bridging pyrimidine ligand using DFT and post-Hartree–Fock methods [92]. They concluded that superexchange interactions leading to antiferromagnetic interactions are more important in meta-phenylene-bridged transition metal complexes as compared to meta-phenylene-bridged organic carbenes and radicals. Finally, ferromagnetic interactions are proposed in pyrimidine-bridged dinuclear Cu^II complexes if the pyrimidine-nitrogen donor of one Cu^II center is coordinated equatorially and the pyrimidine-nitrogen donor of the other Cu^II center is coordinated axially. Antiferromagnetic interactions were proposed if both nitrogen atoms are coordinated equatorially [67].

In order to obtain more experimental insight into the spin-polarization mechanism in transition metal complexes, we summarize here a series of trinuclear complexes which are bridged by the meta-phenylene bridging unit phloroglucinol. Based on the nature of the remaining coordination sphere, the influence of the electron-density on the metal ions and on the spin-polarization mechanism can be studied. Additionally, this series allow us to correlate the relative orientation of the magnetic orbitals to the plane of the bridging benzene ring to the experimentally observed exchange coupling.

2 1,3,5-Trihydroxy-bridged trinuclear complexes with first-row transition metal ions

We have reacted the parent phloroglucinol with numerous first-row transition metal complex fragments in order to obtain trinuclear phloroglucinol-bridged complexes in analogy to the formation of 18. Despite the variation of the reaction conditions and the coligands on the transition metal complex fragments we have not been able to isolate a pure sample of a trinuclear complex. In this respect, it should be noted that the preparation of 18 required the chromatographic separation of mono-, di-, and trinuclear phloroglucinol complexes [79]. We attribute these problems to a lower thermodynamic and a kinetic stability of a phenolate first-row transition metal ion bond due to lower covalency in comparison to a bond of a phenolate to a second- or third-row transition metal ion. We had to overcome these problems by attaching pendant arms with additional coordinating groups in the 2,4,6-position of phloroglucinol, thereby enhancing the stability by use of the chelate effect. An analogous approach was used by Abrahams et al. with azophenyl groups in 2,4,6-position [95].

The ligand preparation is based on the condensation of 2,4,6-trisacetyl-1,3,5-trihydroxybenzene with three equivalents of N,N-dimethylethylenediamine which affords the trisimine ligand H₃L in reasonable yields. The reaction of H₃L with Cu^II ions under basic conditions yielded a green solution that is typical of Cu^II-phenolato complexes. In order to complete the preferred penta-coordination of the three copper ions, three equivalents of a bidentate chelate ligand were added: the use of bipyridine (bpy) resulted in the isolation of [L(Cu^II(bpy))₃](BF₄)₃ (20(BF₄)₃) and the use of salicylaldehyde (Hsal) provided [L(Cu^II(sal))₃] (21) [40].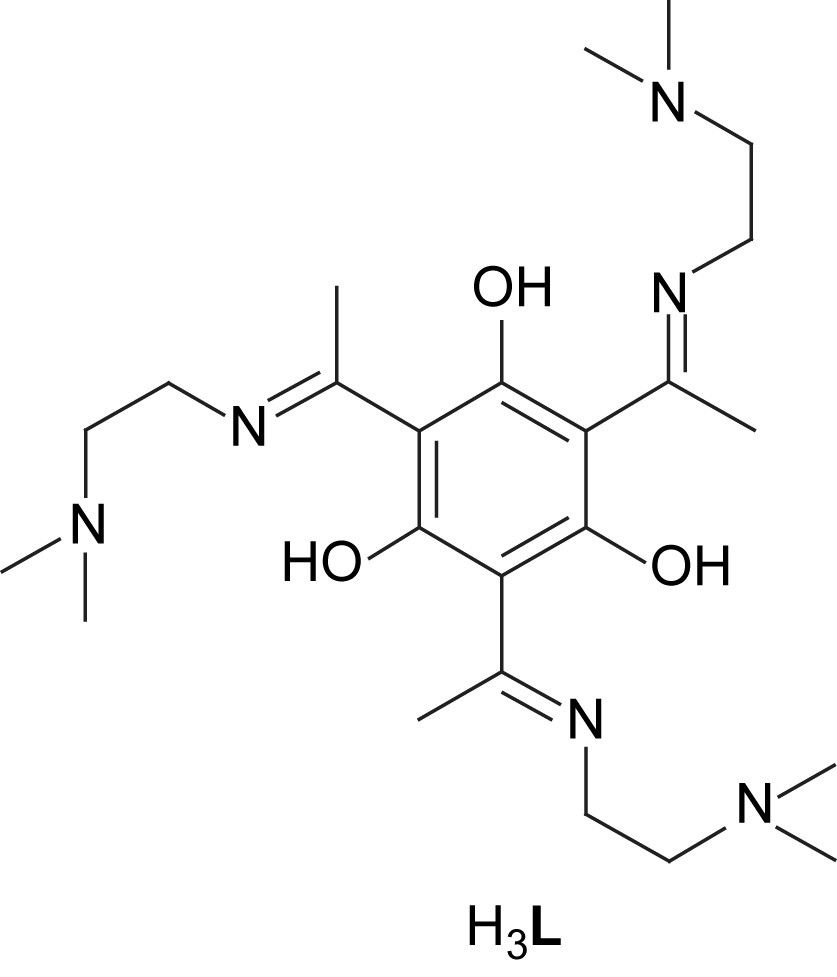

Fig. 1 shows the molecular structure of the trinuclear trication 20³⁺ and illustrates the ability of the ligand L³⁻ to bridge three metal ions. Each of the three copper ions is coordinated by one phenolato oxygen donor and two nitrogen donors of the ligand L³⁻, and two nitrogen donors of bpy. The coordination geometry of the three copper ions is square pyramidal, however, two copper ions show considerable distortions towards trigonal bipyramidal.

Fig. 1
Molecular structure of the trication 20³⁺ [40].

The temperature-dependent magnetic susceptibility measurements on 20(BF₄)₃ and 21 revealed an increase of the effective magnetic moment (μ_eff) with decreasing temperature indicating ferromagnetic interactions between the three Cu^II ions. We have simulated the experimental data using a full-matrix diagonalization approach of the appropriate spin-Hamiltonian (Eq. (2)). The best fit results in J = + 1.96 cm⁻¹ for 20(BF₄)₃ and J = + 3.31 cm⁻¹ for 21 [40]. Thus, the phloroglucinol bridging unit is able to propagate ferromagnetic couplings in trinuclear Cu^II complexes. However, the magnitude of the coupling is not comparable to the strong couplings obtained for organic radicals and carbenes.

H = - 2 J (S_{1} S_{2} + S_{2} S_{3} + S_{1} S_{3}) + \sum_{i = 1}^{3} [g_{i} μ_{B} S_{i} B]

(2)

3 Trinuclear first-row transition metal triplesalen complexes

3.1 Design of the triplesalen ligand

In order to meet the two necessary requirements for SMMs, we have designed the ligand triplesalen C (Scheme 5) [96] which combines the phloroglucinol bridging unit A for ferromagnetic couplings and thus high-spin ground states with the coordination environment of a salen ligand B which is known to establish a pronounced magnetic anisotropy by its strong ligand field in the basal plane [97–99]. A well studied example is the Jacobsen catalyst [(salen′)Mn^IIICl] (H₂salen′ = (R,R)-N,N′-bis(3,5-di-tert-butylsalicylidene)-1,2-cyclohexanediamine) [100] which is a Mn^III (S = 2) species with a zero-field splitting of D ≈ −2.5 cm⁻¹ [97,101,102]. In this respect, it is interesting to note that already dimeric Mn^III salen complexes behave as SMMs [103,104] and can be used as building blocks for the rational synthesis of other SMMs and single-chain magnets (SCM) [105–109].

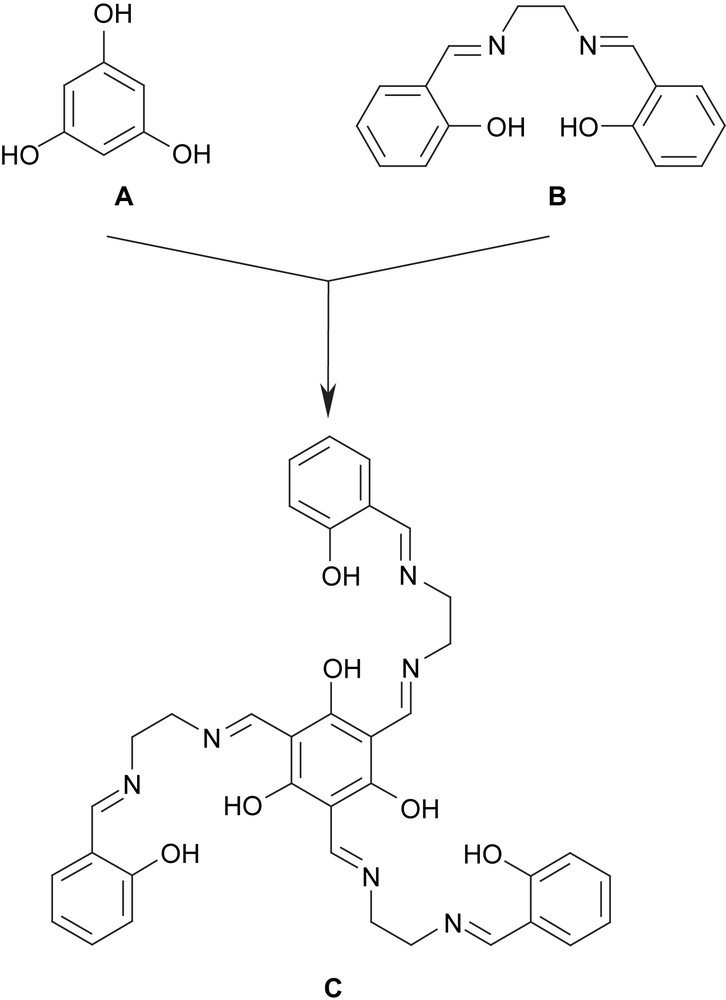
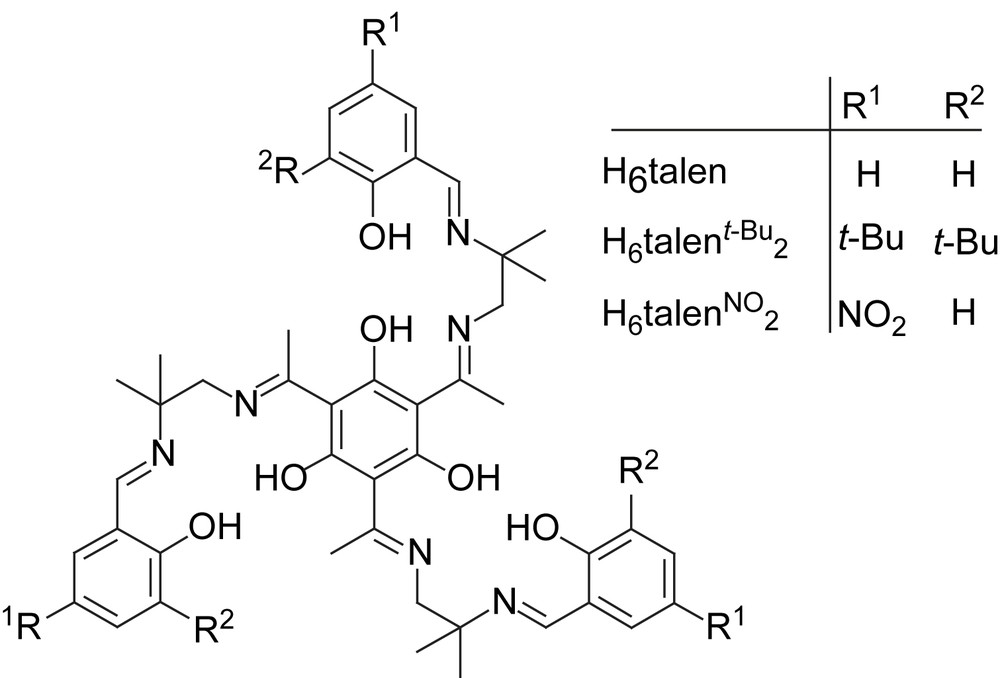
The requirement for a successful synthesis was a differentiation of the reactivity of the two amine functions of the ethylene diamine component. Based on the work by Elias and coworkers we used 1,2-diamino-2-methylpropane. The sterically more crowded amino function does not react with ketones while the sterically less crowded amino function does react with ketones and aldehydes [110]. In this respect we have been able to synthesize triplesalen ligands with different terminal substituents (Scheme 6) [96,111].

We have shown in a series of trinuclear nickel triplesalen complexes that variation of the terminal substituents in triplesalen ligands provides a control of the electronic communication between the metal salen subunits [111]. Additionally, a severe ligand folding was observed in $[({talen}^{t {-Bu}_{2}}) {Ni}_{3}]$ resulting in an overall bowl-shaped molecular structure.

While the square-planar coordinated Ni^II ions in these trinuclear triplesalen complexes are diamagnetic, we have been able to synthesize, crystallize, and characterize the following triplesalen complexes with paramagnetic ions: [(talen)Cu^II₃] (22) [41,42], $[({talen}^{t {-Bu}_{2}}) {Cu}_{3}^{II}]$ (23) [42], $[({talen}^{{NO}_{2}}) {Cu}_{3}^{II}]$ (24) [42], $[({talen}^{t {-Bu}_{2}}) {(V^{IV} O)}_{3}]$ (25) [43], and $[({talen}^{{NO}_{2}}) {{Mn}^{III} {(DMSO)}_{2}}_{3}] {({ClO}_{4})}_{3}$ (26 (ClO₄)₃) [112].

3.2 Structural properties of the trinuclear triplesalen complexes

The molecular structure of 23 is provided as a general example for the molecular structures of the trinuclear triplesalen complexes in Fig. 2. The triplesalen ligand acts as a triple tetradentate ligand, connecting three salen-like coordination compartments by the meta-phenylene coupling unit phloroglucinol. In the trinuclear Cu complexes, the Cu^II ions are coordinated square-planar by the N₂O₂ coordination environment of a salen-like ligand compartment. In 25, the V^IV ions are square-pyramidally coordinated where the basal plane comprises the N₂O₂ donor set of a salen-like ligand compartment and the apical position is occupied by the vanadyl oxygen atom. In the trinuclear Mn^III complex 26³⁺, the Mn^III ions are six-coordinate in an axially elongated octahedral coordination polyhedra. The basal plane is provided by the N₂O₂ donor set of the salen-like coordination compartment while the axial positions are occupied by oxygen atoms of coordinated DMSO solvent molecules.

Fig. 2
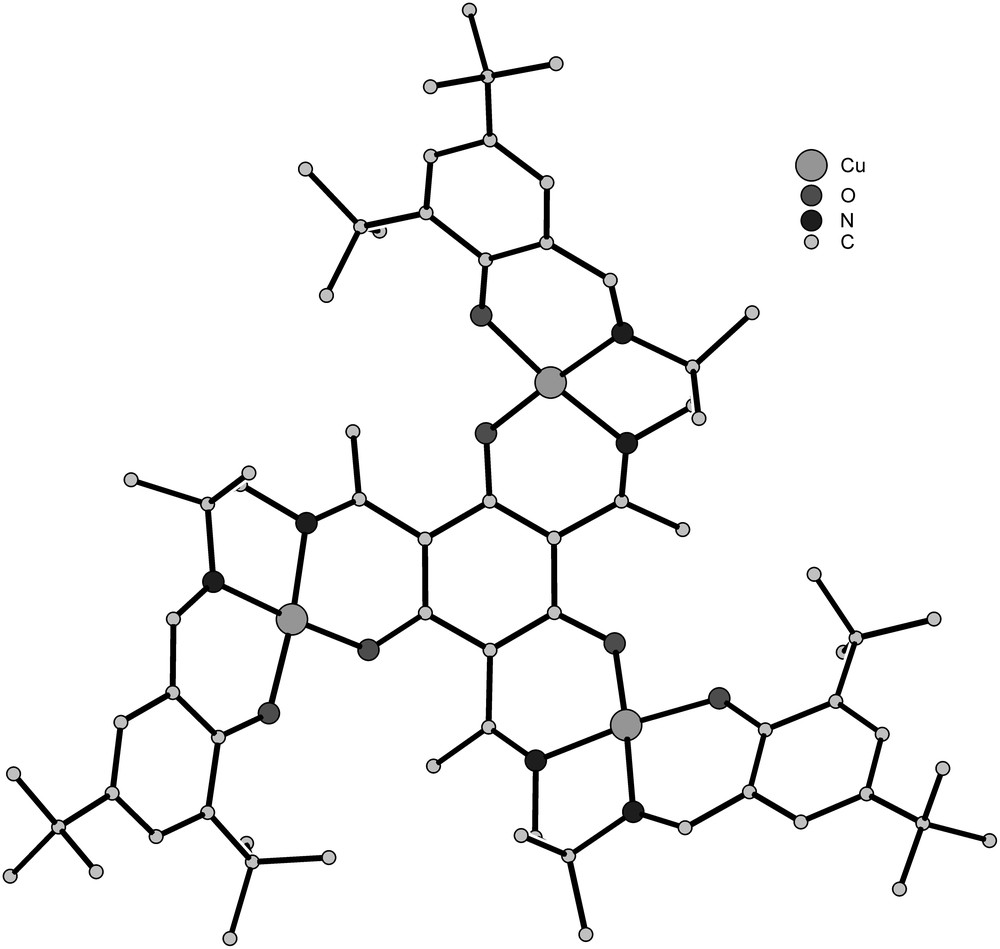
Molecular structure of 23 in crystals of 23·CHCl₃ [42].

While the drawing in Fig. 2 might imply that the triplesalen complexes are planar molecules, the view provided in Fig. 3 indicates that the compounds exhibit severe distortions of the metal salen units. It is interesting to note that the degree of the ligand folding depends not only on the exact nature of the ligand but also on the metal ion used. We have been able to crystallize 23 as three different solvates, each exhibiting a different kind of ligand folding (23·hexane, 23·CH₂Cl₂, and 23·CHCl₃; the exact composition including the crystal solvent molecules is more complex; the given description is only used for a simple differentiation of the three solvates of 23).

Fig. 3
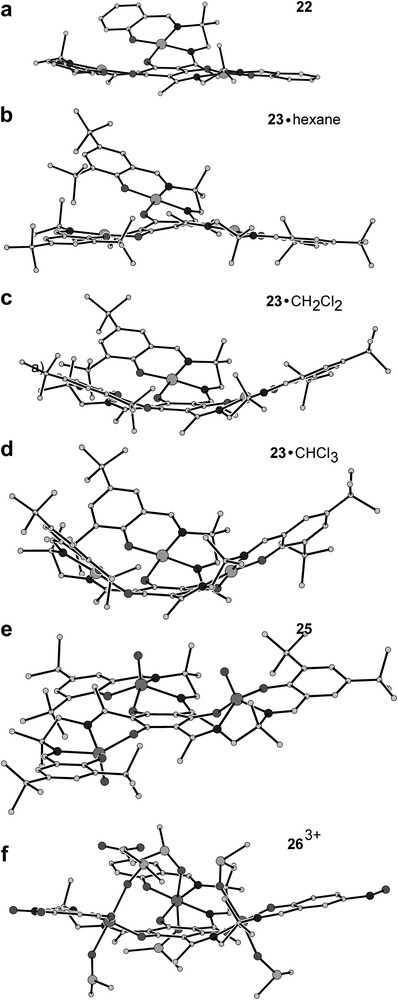
Side-view on the molecular structures of (a) [(talen)Cu^II₃] (22) [41,42], (b)–(d) $[({talen}^{t {-Bu}_{2}}) {Cu}_{3}^{II}]$ (23) [42], (e) $[({talen}^{t {-Bu}_{2}}) {(V^{IV} O)}_{3}]$ (25) [43], and (f) ${[({talen}^{{NO}_{2}}) {{Mn}^{III} {(DMSO)}_{2}}_{3}]}^{3 +}$ (26³⁺) [112] close to perpendicular to the central phloroglucinol unit to illustrate the varying degrees of ligand folding.

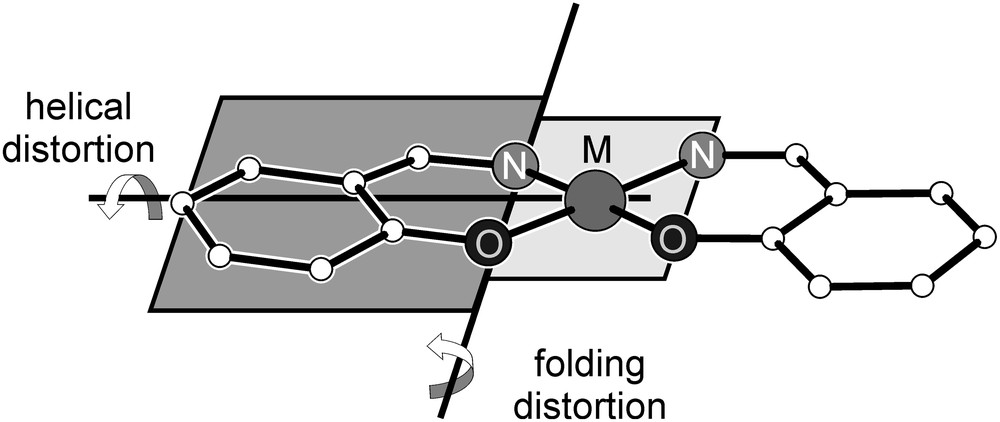
As described in Section 1, an important geometrical parameter influencing the spin-polarization mechanism was recognized to be a rotation of the plane of the magnetic orbitals relative to the plane of the meta-phenylene bridging unit [82]. The interactions between the metal ions are propagated through the oxygen atoms of the bridging phloroglucinol unit. Therefore, a geometric parameter describing the different degrees of ligand folding should consider the bonding of the oxygen p orbitals with the metal ions. Therefore, we used the parameter φ introduced by Cavallo and Jacobsen [113]. The bent angle φ is defined by φ = 180° − ∠(M–X_NO–X_R) (X_NO = midpoint of adjacent N and O donor atoms, X_R = midpoint of the six-membered chelate ring, containing the N and O donor atoms). By this definition the angle φ describes mainly the folding distortion and only minor effects of the helical distortion (Scheme 7). The values for these bent angles are provided in Table 1.

		Ref.	φ^cent/deg^a	φ^term/deg^a	S_i	J/cm^−1,^b
20(BF₄)₃		[40]	n.a.	n.a.	1/2	+1.96

21		[40]	n.a.	n.a.	1/2	+3.31

22		[41,42]			1/2	+1.52
	Cu1		17.0	2.0
	Cu2		7.5	1.2
	Cu3		12.1	3.1

23·Hexane		[42]			1/2	+1.08
	Cu1		20.7	6.8
	Cu2		16.4	8.3
	Cu3		22.0	10.4

23·CH₂Cl₂		[42]			1/2	+1.17
	Cu1		24.4	7.5
	Cu2		18.4	2.9
	Cu3		16.7	8.5

23·CHCl₃		[42]			1/2	+1.55
	Cu1		30.2	8.6
	Cu2
	Cu3

24					1/2	+1.02
	Cu1
	Cu2		n.d.	n.d.
	Cu3

25		[43]			1/2	+0.44
	V1		33.8	12.8
	V2		29.6	16.7
	V3		36.9	10.1

26³⁺		[112]			2	−(0.30 ± 0.05)
	Mn1					D = -(4.0 ± 0.4)cm⁻¹
	Mn2		29.7	−20.0
	Mn3

^a Definition of the bent angles for the central phenolate units (φ^cent) and the terminal phenolate units (φ^term). φ = 180° − ∠(M–X_NO–X_R) with X_NO = midpoint of adjacent N and O donor atoms, X_R = midpoint of the six-membered chelate ring containing the N and O donor atoms.

^b Errors are ±0.10 cm⁻¹ if not provided otherwise.

^c n.a. = not applicable; n.d. = not determined.

3.3 Magnetic properties of the trinuclear complexes

We have measured the temperature dependence of the magnetic susceptibility of all trinuclear complexes and fitted the temperature dependence of μ_eff vs. T using the spin-Hamiltonian in Eq. (2). We have determined the coupling constant J for the triplesalen complexes 20–26³⁺ (Table 1). For the trinuclear Mn^III complex 26³⁺ we added a term in the spin-Hamiltonian accounting for the zero-field splitting of the S_i = 2 Mn^III (Eq. (3)). In order to obtain a meaningful value for the coupling constant in this trinuclear Mn^III complex, we also measured the VTVH (variable temperature–variable field) magnetization data for 26³⁺ at 1 T, 4 T, and 7 T. The simultaneous fitting of the μ_eff vs. T and the VTVH data allowed the analysis of both J and D for complex 26³⁺.

H = \sum_{i = 1}^{3} [D_{i} ({\hat{S}}_{z i}^{2} - \frac{1}{3} S_{i} (S_{i} + 1))]

(3)

While all coupling constants for the trinuclear Cu^II complexes exhibit ferromagnetic interactions, the same holds true for the trinuclear V^IVO complex 25, but not for the trinuclear Mn^III complex 26³⁺. Interestingly, the different solvates of the trinuclear Cu complex 23 exhibit different coupling constants.

4 Discussion

The zeroth-order description for meta-phenylene-bridged diradicals corresponds to a localization of the unpaired electron, i.e. the spin density, in p_z^π orbitals of the benzylic carbon atoms. By switching on the interaction, as described in Section 1, the strong stabilization of the ferromagnetic ground state occurs. Our discussion for the phloroglucinol-bridged trinuclear complexes is based on the argument that the higher the spin density in the related phloroglucinol O p_z^π orbitals is, the stronger the stabilization of the ferromagnetic ground state will be. In other words, an efficient spin-polarization in phloroglucinol-bridged transition metal complexes requests a preferable high spin-density in the p_z^π orbitals of the coordinating oxygen atoms. The first simple conclusion is therefore that the spin-polarization of phloroglucinol-bridged transition metal ions can never be as high as for organic radicals because the main spin-density is localized on the transition metal ion and the O p_z^π orbital possesses only a small fraction of the spin-density.

Therefore, the remaining fundamental issue concerns the mechanism of the spin transfer from the paramagnetic metal ion onto the ligand, i.e. in our case onto the phloroglucinol oxygen atom. It is important to note that the spin transfer from a transition metal ion to its ligating atoms is more complex than that assumed in a simple (restricted) MO diagram [94]. This description implies that the covalent overlap of a magnetic (singly occupied) d orbital with the p orbitals of the ligand atoms leads to a delocalized molecular orbital, where the unpaired electron and hence the spin-density is partially transferred from the metal ion onto the ligands. Therefore, the spin-density on the coordinating ligand atoms is of the same sign as the spin-density on the transition metal ion (spin-delocalization mechanism).

The open-shell treatment described in Section 1 must be applied also to transition metal complexes. This results in a splitting of the d manifold. The d orbitals with spin-up (α-spin) electrons are energetically stabilized in comparison to the d orbitals with spin-down (β-spin) electrons. This is the basis for the usually applied UHF scheme or unrestricted calculations based on density functional theory (DFT). The magnitude of the splitting of spin-up and spin-down d orbitals depends obviously on the number of unpaired electrons. The larger the number of unpaired electrons the stronger is this exchange stabilization (spin-polarization). Understanding the spin transfer from the metal to the ligand atoms becomes more complicated by going from the restricted scheme (simple MO diagram as described above) to an unrestricted treatment implying spin-polarization.

The influence of an open-shell system for the treatment of the spin-transfer from metal to ligand atoms (spin polarization vs. spin delocalization) complicates the simple analysis by a qualitative MO diagram. Figgis et al. studied experimentally the interplay between spin-delocalization and spin-polarization for the spin transfer from the metal ion to the ligand atoms by polarized single-crystal neutron diffraction [114–120]. It becomes evident that the sign of the spin-density depends on the dⁿ electron configuration on the metal and of the nature of the σ- and π-binding characters of the ligand. An important result was the determination of the anisotropy of the metal–ligand covalency. Furthermore, the sign of the spin-density can and usually does vary for different orbitals of the same atom.

The covalent interaction of a filled ligand orbital with a magnetic orbital on the metal usually leads to a positive spin-density on this ligand orbital due to spin-delocalization. On the other hand, the covalent interaction of a filled ligand orbital with an empty metal orbital (e.g. the 4s/4p orbitals for a 3d metal) usually leads to a negative spin-density in these ligand orbitals due to spin polarization. (The two electrons of the donor MO are spin-polarized in that respect that the probability of the α-spin electron to be close to the metal ion is higher than that of the β-spin electron.) Depending on the strength of the covalent interaction and the σ- and π-characteristic of the ligands the sum of the spin-densities of an individual ligand atom can therefore be positive, negative, or cancel each other close to zero. However, related to the Cu^II–OPh system discussed here, it is important to summarize that σ- and π-donor ligands usually obtain an overall positive spin density if the transition metal ion possesses electrons in the e_g orbitals.

We want to apply these principles to understand the observed couplings in our trinuclear phloroglucinol-bridged complexes.

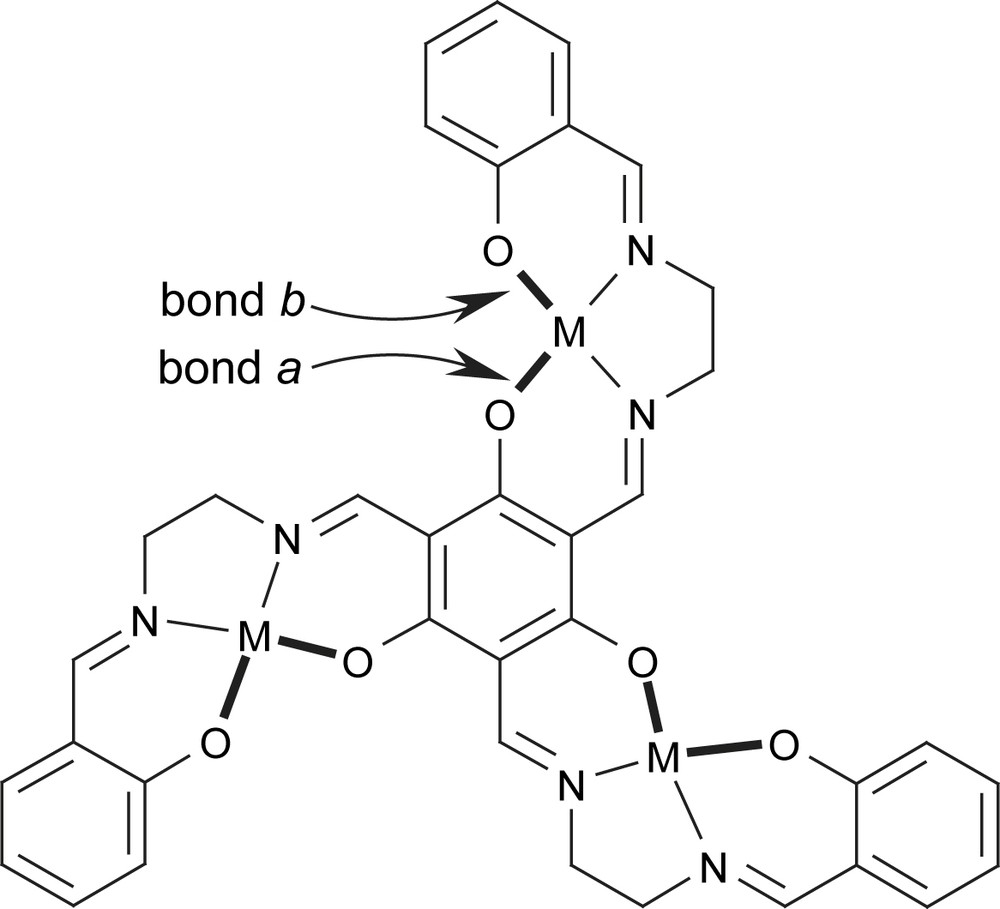
In the study of the trinuclear nickel triplesalen complexes [111] we established a communication between the nickel salen subunits which can be influenced by the choice of the terminal substituents of the phenol moieties. As the electronic communication between the three metal ions is mediated by the central metal-phenolate bonds (bonds a in Scheme 8), the strengthening of these bonds would increase the interaction between the metal ions. An indirect handle for influencing the central metal-phenolate bonds a is provided by a variation of the strengths of the terminal metal phenolate bonds (bonds b in Scheme 8). In accordance with Pauling's electroneutrality principle a weakening of the terminal bonds b (less charge donation of the terminal phenolates) strengthens the central bonds a (more charge donation of the central phenolates), and vice versa [121]. In this respect, we found that the introduction of tert-butyl groups in $[({talen}^{t {-Bu}_{2}}) {Ni}_{3}]$ leads to stronger bonds b and weaker bonds a as compared to those of [(talen)Ni₃]. On the other hand the use of the nitro groups in $[({talen}^{{NO}_{2}}) {Ni}_{3}]$ resulted in weaker bonds b and thus stronger bonds a. However, we envisioned a second modulating effect induced by the ligand folding which opposes the electronic control described above. The degree of ligand folding, which shows the strongest effect at the central phenolate units, increases in the order $[({talen}^{{NO}_{2}}) {Ni}_{3}]$ < [(talen)Ni₃] < $[({talen}^{t {-Bu}_{2}}) {Ni}_{3}]$ .

To better understand the spin-polarization mechanism in phloroglucinol-bridged complexes, we analyzed the trinuclear Cu^II triplesalen complexes with respect to the terminal substituents and to the ligand folding. This provides experimental insight into the influence of the orientation of the magnetic orbitals on the spin-polarization properties.

Figgis et al. studied the spin-density in divalent hexaaqua complexes of the first transition metal row. They found that for the Jahn-Teller distorted Cu^II complex the spin-density of the coordinating water oxygen atoms in the basal plane exhibits positive spin-density [119]. This confirms that in Cu^II complexes with π-donor ligands the spin-delocalization mechanism prevails the spin-polarization mechanism. This spin-delocalization was experimentally demonstrated by Kahn and coworkers, using polarized neutron diffraction [122,123]. In this respect, increasing the covalency of the bonds a should increase the spin-density on the phenolate oxygen atom.

In the hypothetical limit of a frozen ligand folding irrespective of the nature of the terminal substituents, the tert-butyl substituents in 23 strengthen the bonds b, resulting in weaker bonds a. On the other hand, introduction of the nitro substituent in 24 decreases the strength of bond b and therefore increases the strength of bond a. The overall ferromagnetic coupling should therefore follow the trend 24 > 22 > 23. However, the experimental trend is 22 ∼ 23·CHCl₃ > 23·CH₂Cl₂ > 23·hexane > 24 (Table 1). This fact is again attributed to an opposing effect introduced by the varying degree of ligand folding.

In a rigorous coplanar orientation of the CuN₂O₂ plane and the plane of the phloroglucinol (coplanarity of the xy-plane of the salen subunit and the x′y′-plane of phloroglucinol, Scheme 9a) the magnetic ${Cu d}_{x^{2} - y^{2}}$ orbital and the O p_z_′ orbital (the π orbital with regard to the O–C^benzene bond) are orthogonal and the overlap integral is zero (Scheme 9a). Thus, no spin delocalization occurs by this bonding pathway.

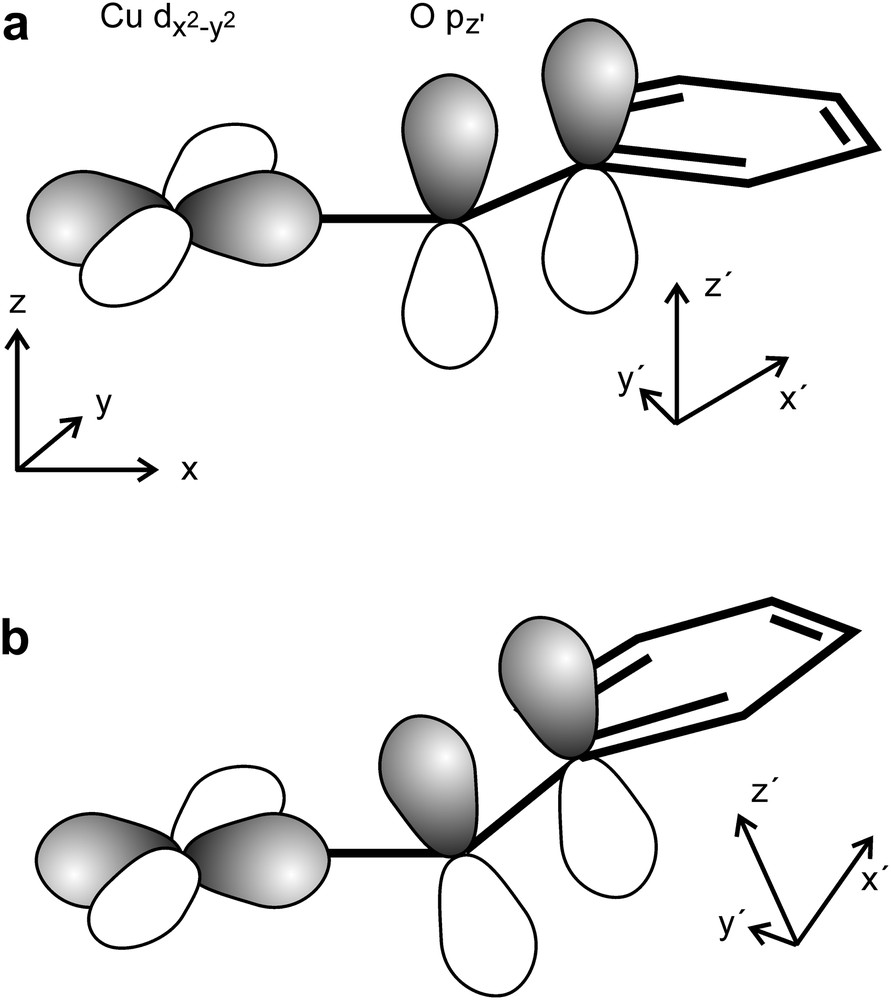
Folding at the central Cu^II–phenolate bond (non-coplanarity of the xy and the x′y′ planes, Scheme 9b) results in a non-orthogonal overlap of the O p_z_′ orbital with the magnetic ${Cu d}_{x^{2} - y^{2}}$ orbital and therefore to a direct delocalization of spin-density into the O p_z_′ orbital. The higher spin-density in the O p_z_′ orbitals should result in a stronger spin-polarization through the central benzene ring as compared to the coplanar arrangement described above. As the ligand folding is higher in the tert-butyl derivative 23 this ligand folding opposes the effect by the terminal substituents. This is corroborated by the fact that the 23·CHCl₃ with the strongest ligand folding has the highest J value in the solvates of 23.

On the other hand, the interaction of oxygen orbitals with the metal 4s and 4p orbitals should result in negative spin-density by the spin-polarization mechanism and it is difficult to estimate the variation on this pathway by the ligand folding.

We have performed DFT calculations for the quartet ground state on simplified models in order to quantify these qualitative considerations. The ligand folding was mimicked by rotation of the CuN₂O₂ planes either along the central O–N vector or along the Cu–O vector. We have used several model geometries. In all cases, ligand folding opens a direct bonding pathway between the ${Cu d}_{x^{2} - y^{2}}$ orbital and the O p_z_′ orbital. This is evidenced by an increased positive spin-density in the O p_z_′ orbital. However, a close inspection of the atomic spin-densities of the central benzene ring and of the distribution of the spin-densities in the p_z_′, p_x_′, and p_y_′ orbitals demonstrates that not only the spin-delocalization but also the spin-polarization is increased due to the ligand folding. The spin-densities for two similar model structures are shown in Fig. 4. The structure in Fig. 4a shows an increase of the absolute atomic and p_z_′ spin densities of alternating sign in the central benzene ring while for the slightly changed geometry in Fig. 4b an overall increase of positive spin-densities at all carbon atoms can be observed. These findings are consistent with the theoretical studies summarized in Section 1 [56,82,94], which reveal that both spin-polarization and spin-delocalization contribute to the overall coupling between the transition metal ions. Thus, assigning the experimentally observed stronger ferromagnetic coupling in the molecular structures exhibiting stronger ligand folding to spin-polarization or spin-delocalization is not justified.

Fig. 4
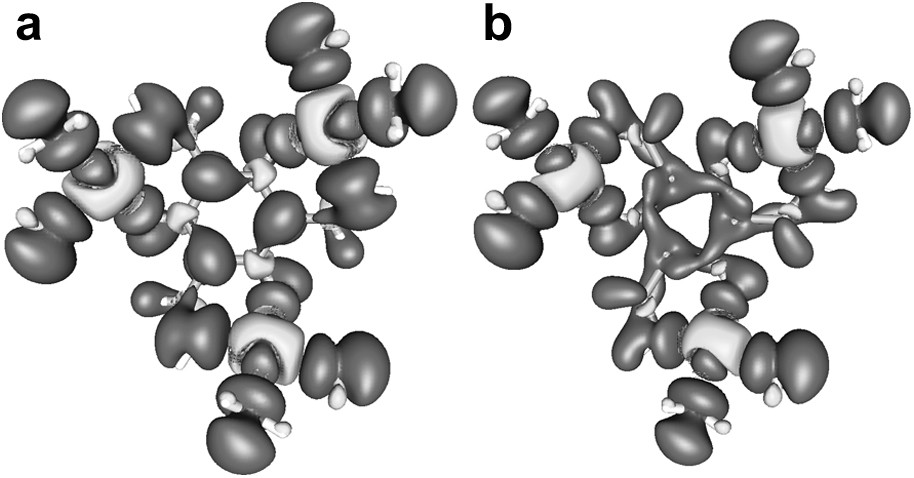
Spin-density plots for structural models of [(talen)Cu^II₃]. While there are only small differences in the ligand folding panel (a) shows mainly spin polarization and panel (b) shows mainly spin delocalization on the central benzene ring [reproduced from Ref. [42] with permission/copyright Wiley-VCH].

In the trinuclear V^IV complex 25 the magnetic orbitals are of the d_xy type. The local environment of the V phenolate bond is more distorted due to the vanadyl group, which pulls the V out of the basal plane by ∼0.7 Å. In combination with the ligand folding at the central phloroglucinol oxygen bond this opens various bonding pathways between the O p_z^π orbital and the metal d orbitals. This leads to strong opposing spin-delocalization and spin-polarization effects. The spin-polarization due to the overlap of the magnetic orbital with the phenolate orbitals is opposed by the spin-polarization due to very strong interactions of the O p_z^π orbital with the empty $d_{x^{2} - y^{2}}$ and d_xy/d_yz orbitals (Scheme 10). The strengths of these bonding interactions have been demonstrated by electronic absorption spectroscopy. These bonding interactions of the occupied ligand p orbital with the empty metal d orbitals lead to a polarization of this bonding in that respect that positive spin-density is induced at the metal site, whereas negative spin-density is induced on the ligand atom. This conflicting spin-delocalization and spin-polarization effect leads to the overall small observed coupling of J = +0.44 cm⁻¹ [43].

An interesting case is the trinuclear Mn^III complex 26³⁺. The d⁴ electronic configuration should enable covalent interactions of filled ligand orbitals with magnetic σ- and π-orbital. However, this simple MO description is not straight-forward. Figgis et al. already pointed out that in the isoelectronic Cr^II ion the spin density on the oxygen atom should be negative [119]. The increase of covalency going from Cr^II to Mn^III should provide some more spin delocalization in the Mn complex resulting in competing spin-polarization and spin-delocalization pathways. This conflicting mechanism may explain the very low coupling constant observed in 26³⁺ of only J = −0.30 cm⁻¹ [112].

5 Conclusion

The spin-polarization mechanism is a straight-forward recipe in organic chemistry to construct high-spin molecules. The application of this mechanism to transition metal complex is not straight-forward. The strengths of the exchange coupling are orders of magnitudes lower in transition metal complexes and antiferromagnetic couplings prevail. Our investigation on a series of structurally related trinuclear complexes with a bridging phloroglucinol unit found that an efficient spin-polarization in phloroglucinol-bridged complexes requires the full spin-density in the p_z^π orbitals of the phenolate oxygen atoms. However, in transition metal complexes the spin-density is mainly localized on the metal atoms and therefore, the interaction must be smaller than in the organic counterparts. Additionally, the possibility of multiple bonding pathways between the ligand orbitals and empty or filled metal orbitals results in complicated competitions between spin-polarization and spin-delocalization contributions. These opposing spin-delocalization and spin-polarization effects are another reason for the diminished coupling in meta-phenylene-bridged transition metal complexes.

The main conclusion is that for a pronounced positive spin-density in the p_z^π orbital of the phenolate oxygen atom, the covalency of the metal–phenolate bond must be increased. This conclusion is corroborated by the oxamate benzene ligand system 19 and its μ₃-extended version. In the trinuclear Cu^II complex the coupling constant was determined to be +5.8 cm⁻¹ [91]. The π-orbitals of the amide donor are energetically higher than the phenolate donor orbitals. This results in a better overlap of these ligand orbitals with the Cu^II d orbitals, and hence, a stronger covalency of the metal ligand bond. This should provide a stronger spin-delocalization into the N p_z^π orbitals, which results finally in a stronger coupling through the benzene ring by spin-polarization.

This research has established a useful starting point for investigating future applications of the spin-polarization mechanism of transition metal complexes. The design, synthesis, and characterization of ligands of the second generation based on the phloroglucinol backbone are the focus of continuing studies by our research group.

Bibliographie

[1] D. Gatteschi; O. Kahn; J.S. Miller; F. Palacio Adv. Mater., 3 (1991), p. 161

[2] J.S. Miller; A.J. Epstein Angew. Chem., Int. Ed. Engl., 33 (1994), p. 385

[3] Molecular Magnetism: From Molecular Assemblies to the Devices (E. Coronado; P. Delhaès; D. Gatteschi; J.S. Miller, eds.), Kluwer Academic Publishers, Dordrecht, 1996

[4] J.S. Miller; M. Drillon, Magnetism: Molecules to Materials, vols. I–IV, Wiley-VCH, Weinheim, 2001–2005

[5] J.S. Miller Inorg. Chem., 39 (2000), p. 4392

[6] J.S. Miller; J.C. Calabrese; A.J. Epstein; R.W. Bigelow; J.H. Zhang; W.M. Reiff J. Chem. Soc., Chem. Commun. (1986), p. 1026

[7] J.S. Miller; J.C. Calabrese; H. Rommelmann; S. Chittipeddi; A.J. Epstein; J.H. Zhang; W.M. Reiff J. Am. Chem. Soc., 109 (1987), p. 769

[8] J.M. Manriquez; G.T. Yee; R.S. McLean; A.J. Epstein; J.S. Miller Science, 252 (1991), p. 1415

[9] S.M. Holmes; G.S. Girolami J. Am. Chem. Soc., 121 (1999), p. 5593

[10] S. Ferlay; T. Mallah; R. Ouahes; P. Veillet; M. Verdaguer Nature, 378 (1995), p. 701

[11] E. Dujardin; S. Ferlay; X. Phan; C. Desplanches; C.C.D. Moulin; P. Sainctavit; F. Baudelet; E. Dartyge; P. Veillet; M. Verdaguer J. Am. Chem. Soc., 120 (1998), p. 11347

[12] M. Verdaguer; A. Bleuzen; V. Marvaud; J. Vaissermann; M. Seuleiman; C. Desplanches; A. Scuiller; C. Train; R. Garde; G. Gelly; C. Lomenech; I. Rosenman; P. Veillet; C. Cartier; F. Villain Coord. Chem. Rev., 190–192 (1999), p. 1023

[13] T. Mallah; S. Thiebaut; M. Verdaguer; P. Veillet Science, 262 (1993), p. 1554

[14] J.B. Goodenough Magnetism and the Chemical Bond, Interscience, New York, 1963

[15] J. Kanamori J. Phys. Chem. Solids, 10 (1959), p. 87

[16] P.W. Anderson Phys. Rev., 115 (1959), p. 2

[17] Magnetism (P.W. Anderson, ed.), Academic Press, New York, 1963

[18] H. Weihe; H.U. Güdel Inorg. Chem., 36 (1997), p. 3632

[19] T. Lis Acta Crystallogr., 36 (1980), p. 2042

[20] R. Sessoli; D. Gatteschi; A. Caneschi; M.A. Novak Nature, 365 (1993), p. 141

[21] R. Sessoli; H.L. Tsai; A.R. Schake; S.Y. Wang; J.B. Vincent; K. Folting; D. Gatteschi; G. Christou; D.N. Hendrickson J. Am. Chem. Soc., 115 (1993), p. 1804

[22] J.R. Long Chemistry of Nanostructured Materials (P. Yang, ed.), World Scientific, Hong Kong, 2003, p. 291

[23] L. Thomas; F. Lionti; R. Ballou; D. Gatteschi; R. Sessoli; B. Barbara; J.R. Friedman; M.P. Sarachik; J. Tejada; R. Ziolo Phys. Rev. Lett., 383 (1996), p. 145

[24] G. Christou; D. Gatteschi; D.N. Hendrickson; R. Sessoli MRS Bull., 25 (2000), p. 66

[25] J. Tejada; E.M. Chudnovsky; E. del Barca; J.M. Hernandez; T.P. Spiller; J. Tejada Polyhedron, 12 (2001), p. 181

[26] M.N. Leuenberger; D. Loss Nature, 410 (2001), p. 789

[27] A. Cornia; A.C. Fabretti; M. Pacchioni; L. Zobbi; D. Bonachi; A. Caneschi; D. Gatteschi; R. Biagi; U. Del Pennino; V. De Renzi; L. Gurevich; H.S.J. Van der Zant Angew. Chem. Int. Ed., 42 (2003), p. 1645

[28] E.D. Dahlberg Phys. Today, 48 (1995), p. 34

[29] O. Kahn Acc. Chem. Res., 33 (2000), p. 647

[30] C. Zener Phys. Rev., 82 (1951), p. 403

[31] P.W. Anderson; H. Hasegawa Phys. Rev., 100 (1955), p. 675

[32] G. Blondin; J.-J. Girerd Chem. Rev., 90 (1990), p. 1359

[33] T. Glaser; K. Rose; S.E. Shadle; B. Hedman; K.E. Hodgson; E.I. Solomon J. Am. Chem. Soc., 123 (2001), p. 442

[34] T. Glaser; T. Beissel; E. Bill; T. Weyhermüller; V. Schünemann; W. Meyer-Klaucke; A.X. Trautwein; K. Wieghardt J. Am. Chem. Soc., 121 (1999), p. 2193

[35] L.F. Chibotaru; J.-J. Girerd; G. Blondin; T. Glaser; K. Wieghardt J. Am. Chem. Soc., 125 (2003), p. 12615

[36] O. Kahn Inorg. Chim. Acta, 62 (1982), p. 3

[37] T. Glaser; H. Theil; I. Liratzis; T. Weyhermüller; E. Bill Inorg. Chem., 45 (2006), p. 4889

[38] H.C. Longuet-Higgins J. Chem. Phys., 18 (1950), p. 265

[39] H.M. McConnell J. Chem. Phys., 39 (1963), p. 1910

[40] T. Glaser; M. Gerenkamp; R. Fröhlich Angew. Chem. Int. Ed., 41 (2002), p. 3823

[41] T. Glaser; M. Heidemeier; S. Grimme; E. Bill Inorg. Chem., 43 (2004), p. 5192

[42] T. Glaser; M. Heidemeier; J.B.H. Strautmann; H. Bögge; A. Stammler; E. Krickemeyer; R. Huenerbein; S. Grimme; E. Bothe; E. Bill Chem.—Eur. J, 13 (2007), p. 9191

[43] H. Theil; C.-G. Frhr. v. Richthofen; A. Stammler; H. Bögge; T. Glaser Inorg. Chim. Acta, 361 (2008), p. 916

[44] H. Iwamura Adv. Phys. Org. Chem., 26 (1990), p. 179

[45] A. Rajca Chem.—Eur. J, 8 (2002), p. 4834

[46] K. Yoshizawa; R. Hoffmann J. Am. Chem. Soc., 117 (1995), p. 6921

[47] H. Iwamura; N. Koga Acc. Chem. Res., 26 (1993), p. 346

[48] D.A. Dougherty Acc. Chem. Res., 24 (1991), p. 88

[49] A.A. Ovchinnikov Theor. Chim. Acta, 47 (1978), p. 297

[50] M.S. Platz Diradicals (W.T. Borden, ed.), Wiley & Sons, New York, 1982, p. 195

[51] M.J.S. Dewar The Molecular Orbital Theory of Organic Chemistry, McGraw-Hill Book Company, New York, 1969

[52] D. Döhnert; J. Koutecký J. Am. Chem. Soc., 102 (1980), p. 1789

[53] D. Maynau; J.-P. Malrieu J. Am. Chem. Soc., 102 (1982), p. 3029

[54] J.-P. Malrieu; D. Maynau J. Am. Chem. Soc., 104 (1982), p. 3021

[55] W.T. Borden Diradicals (W.T. Borden, ed.), Wiley & Sons, New York, 1982, p. 1

[56] P. Karafiloglou J. Chem. Phys., 82 (1985), p. 3728

[57] M. Okamoto; Y. Teki; T. Takui; T. Kinoshita; K. Itoh Chem. Phys. Lett., 173 (1990), p. 265

[58] S.-i. Mitsubori; T. Ishida; T. Nogami; H. Iwamura Chem. Lett. (1994), p. 285

[59] T. Ishida; S.-i. Mitsubori; T. Nogami; N. Takeda; M. Ishikawa; H. Iwamura Inorg. Chem., 40 (2001), p. 7059

[60] T. Ishida; K. Nakayama; M. Nakagawa; W. Sato; Y. Ishikawa; M. Yasui; F. Iwasaki; T. Nogami Synth. Met., 85 (1997), p. 1655

[61] F. Lloret; G. De Munno; M. Julve; J. Cano; R. Ruiz; A. Caneschi Angew. Chem. Int. Ed., 37 (1998), p. 135

[62] T. Ishida; S.-i. Mitsubori; T. Nogami; H. Iwamura Mol. Cryst., Liq. Cryst., 233 (1993), p. 345

[63] M. Yasui; Y. Ishikawa; N. Akiyama; T. Ishida; T. Nogami; F. Iwasaki Acta Crystallogr, B57 (2001), p. 288

[64] R. Feyerhem; S. Abens; D. Günther; T. Ishida; M. Meißner; M. Meschke; T. Nogami; M. Steiner J. Phys.: Condens. Matter, 12 (2000), p. 8495

[65] T. Ezuhara; K. Endo; K. Matsuda; Y. Aoyama New J. Chem., 24 (2000), p. 609

[66] J. Omata; T. Ishida; D. Hashizume; F. Iwasaki; T. Nogami Inorg. Chem., 40 (2001), p. 3954

[67] T. Ishida; T. Kawakami; S.-i. Mitsubori; T. Nogami; K. Yamaguchi; H. Iwamura J. Chem. Soc., Dalton Trans. (2002), p. 3177

[68] T. Kusaka; T. Ishida; D. Hashizume; F. Iwasaki; T. Nogami Chem. Lett. (2000), p. 1146

[69] K. Zusai; T. Kusaka; T. Ishida; R. Feyerherm; M. Steiner; T. Nogami Mol. Cryst. Liq. Cryst., 343 (2000), p. 127

[70] K. Nakayama; T. Ishida; R. Takayama; D. Hashizume; M. Yasui; F. Iwasaki; T. Nogami Chem. Lett. (1998), p. 497

[71] D.R. Corbin; L.C. Francesconi; D.N. Hendrickson; G.D. Stucky Inorg. Chem., 20 (1981), p. 2084

[72] B.F. Fieselmann; D.N. Hendrickson; G.D. Stucky Inorg. Chem., 17 (1978), p. 1841

[73] L.C. Francesconi; D.R. Corbin; D.N. Hendrickson; G.D. Stucky Inorg. Chem., 18 (1979), p. 3074

[74] H. Oshio J. Chem. Soc., Chem. Commun. (1991), p. 240

[75] H. Oshio; H. Ichida J. Phys. Chem., 99 (1995), p. 3294

[76] J.A. McCleverty; M.D. Ward Acc. Chem. Res., 31 (1998), p. 842

[77] A.M.W. Cargill Thompson; D. Gatteschi; J.A. McCleverty; J.A. Navas; E. Rentschler; M.D. Ward Inorg. Chem., 35 (1996), p. 2701

[78] S.R. Bayly; E.R. Humphrey; H. de Chair; C.G. Paredes; Z.R. Bell; J.C. Jeffery; J.A. McCleverty; M.D. Ward; F. Totti; D. Gatteschi; S. Courric; B.R. Steele; C.G. Screttas J. Chem. Soc., Dalton Trans. (2001), p. 1401

[79] V.A. Ung; A. Thompson; D.A. Bardwell; D. Gatteschi; J.C. Jeffery; J.A. McCleverty; F. Totti; M.D. Ward Inorg. Chem., 36 (1997), p. 3447

[80] V.A. Ung; S.M. Couchman; J.C. Jeffery; J.A. McCleverty; M.D. Ward; F. Totti; D. Gatteschi Inorg. Chem., 38 (1999), p. 365

[81] S.R. Bayly; J.A. McCleverty; M.D. Ward; D. Gatteschi; F. Totti Inorg. Chem., 39 (2000), p. 1288

[82] A. Bencini; D. Gatteschi; F. Totti; D.N. Sanz; J.A. McCleverty; M.D. Ward J. Phys. Chem. A, 102 (1998), p. 10545

[83] I. Fernández; R. Ruiz; J. Faus; M. Julve; F. Lloret; J. Cano; X. Ottenwaelder; Y. Journaux; C. Munoz Angew. Chem. Int. Ed., 40 (2001), p. 3039

[84] C.L.M. Pereira; E.F. Pedroso; H.O. Stumpf; M.A. Novak; L. Ricard; R. Ruiz-Garcia; E. Rivière; Y. Journaux Angew. Chem. Int. Ed., 43 (2004), p. 956

[85] E. Pardo; K. Bernot; M. Julve; F. Lloret; J. Cano; R. Ruiz-Garcia; J. Pasán; C. Ruiz-Perez; X. Ottenwaelder; Y. Journaux Chem. Commun. (2004), p. 920

[86] E. Pardo; K. Bernot; M. Julve; F. Lloret; J. Cano; R. Ruiz-Garcia; F.S. Delgado; C. Ruiz-Perez; X. Ottenwaelder; Y. Journaux Inorg. Chem., 43 (2004), p. 2768

[87] E. Pardo; I. Morales-Osorio; M. Julve; F. Lloret; J. Cano; R. Ruiz-Garcia; J. Pasan; C. Ruiz-Perez; X. Ottenwaelder; Y. Journaux Inorg. Chem., 43 (2004), p. 7594

[88] E. Pardo; R. Ruiz-Garcia; F. Lloret; M. Julve; J. Cano; J. Pasan; C. Ruiz-Perez; Y. Filali; L.-M. Chamoreau; Y. Journaux Inorg. Chem., 46 (2007), p. 4504

[89] S.P. Foxon; G.R. Torres; O. Walter; J.Z. Pedersen; H. Toftlund; M. Hüber; K. Falk; W. Haase; J. Cano; F. Lloret; M. Julve; S. Schindler Eur. J. Inorg. Chem. (2004), p. 335

[90] A.R. Paital; T. Mitra; D. Ray; W.T. Wong; J. Ribas-Ariño; J.J. Novoa; J. Ribas; G. Aromi Chem. Commun. (2005), p. 5172

[91] X. Ottenwaelder; J. Cano; Y. Journaux; E. Riviere; C. Brennan; M. Nierlich; R. Ruiz-Garcia Angew. Chem. Int. Ed., 43 (2004), p. 850

[92] Y. Takano; T. Onishi; Y. Kitagawa; T. Soda; Y. Yoshioka; K. Yamaguchi Int. J. Quantum Chem., 80 (2000), p. 681

[93] F. Mohri; K. Yoshizawa; T. Yamabe; T. Ishida; T. Nogami Mol. Eng., 8 (1999), p. 357

[94] J. Cano; E. Ruiz; S. Alvarez; M. Verdaguer Comments Inorg. Chem., 20 (1998), p. 27

[95] B.F. Abrahams; S.J. Egan; R. Robson J. Am. Chem. Soc., 121 (1999), p. 3535

[96] T. Glaser; M. Heidemeier; T. Lügger Dalton Trans. (2003), p. 2381

[97] B.J. Kennedy; K.S. Murray Inorg. Chem., 24 (1985), p. 1552

[98] S. Mitra Prog. Inorg. Chem., 22 (1977), p. 309

[99] A. Bencini; I. Ciofini; M.G. Uytterhoeven Inorg. Chim. Acta, 274 (1998), p. 90

[100] W. Zhang; E.N. Jacobsen J. Org. Chem., 56 (1991), p. 2296

[101] K.A. Campbell; M.R. Lashley; J.K. Wyatt; M.H. Nantz; R.D. Britt J. Am. Chem. Soc., 123 (2001), p. 5710

[102] J. Krzystek; J. Telser J. Magn. Reson., 162 (2003), p. 454

[103] H. Miyasaka; R. Clerac; W. Wernsdorfer; L. Lecren; C. Bonhomme; K.-i. Sugiura; M. Yamashita Angew. Chem. Int. Ed., 43 (2004), p. 2801

[104] Z. Lu; M. Yuan; F. Pan; S. Gao; D. Zhang; D. Zhu Inorg. Chem., 45 (2006), p. 3538

[105] R. Clérac; H. Miyasaka; M. Yamashita; C. Coulon J. Am. Chem. Soc., 124 (2002), p. 12837

[106] H. Miyasaka; R. Clérac; K. Mizushima; K.-i. Sugiura; M. Yamashita; W. Wernsdorfer; C. Coulon Inorg. Chem., 42 (2003), p. 8203

[107] H. Miyasaka; T. Nezu; K. Sugimoto; K.-i. Sugiura; M. Yamashita; R. Clérac Inorg. Chem., 43 (2004), p. 5486

[108] H. Miyasaka; T. Nezu; K. Sugimoto; K.-i. Sugiura; M. Yamashita; R. Clérac Chem.—Eur. J, 11 (2005), p. 1592

[109] C. Coulon; H. Miyasaka; R. Clérac Struct. Bonding, 122 (2006), p. 163

[110] A. Böttcher; H. Elias; B. Eisenmann; E. Hilms; A. Huer; R. Kniep; C. Röhr Z. Naturforsch., B, 49 (1994), p. 1089

[111] T. Glaser; M. Heidemeier; R. Fröhlich; P. Hildebrandt; E. Bothe; E. Bill Inorg. Chem., 44 (2005), p. 5467

[112] T. Glaser; M. Heidemeier; R. Fröhlich C.R. Chim., 10 (2007), p. 71

[113] L. Cavallo; H. Jacobsen Eur. J. Inorg. Chem. (2003), p. 892

[114] B.N. Figgis; P.A. Reynolds; G.A. Williams J. Chem. Soc., Dalton Trans. (1980), p. 2348

[115] B.N. Figgis; P.A. Reynolds; R. Mason Inorg. Chem., 23 (1984), p. 1149

[116] B.N. Figgis; P.A. Reynolds; R. Mason J. Am. Chem. Soc., 105 (1983), p. 440

[117] B.N. Figgis; P.A. Reynolds; A.H. White Inorg. Chem., 24 (1985), p. 3762

[118] B.N. Figgis; J.B. Forsyth; P.A. Reynolds Inorg. Chem., 26 (1987), p. 101

[119] G.S. Chandler; G.A. Christis; B.N. Figgis; P.A. Reynolds J. Chem. Soc., Faraday Trans., 88 (1992), p. 1961

[120] S.P. Best; B.N. Figgis; J.B. Forsyth; P.A. Reynolds; P.L.W. Tregenna-Piggot Inorg. Chem., 34 (1995), p. 4605

[121] T. Glaser; B. Hedman; K.O. Hodgson; E.I. Solomon Acc. Chem. Res., 33 (2000), p. 859

[122] V. Baron; B. Gillon; O. Plantevin; A. Cousson; C. Mathoniere; O. Kahn; A. Grand; L. Ohrstrom; B. Delley J. Am. Chem. Soc., 118 (1996), p. 11822

[123] V. Baron; B. Gillon; A. Cousson; C. Mathoniere; O. Kahn; A. Grand; L. Ohrstrom; B. Delley; M. Bonnet; J.X. Boucherle J. Am. Chem. Soc., 119 (1997), p. 3500

Commentaires - Politique

Ces articles pourraient vous intéresser

The first trinuclear manganese triplesalen complex: Synthesis, structural, and magnetic characterization of $[({talen}^{{NO}_{2}}) {{Mn}^{III} {(DMSO)}_{2}}_{3}] {({ClO}_{4})}_{3}$

Thorsten Glaser; Maik Heidemeier; Roland Fröhlich

C. R. Chim (2007)

Supramolecular networks based on octacyanometallates of Mo and W

Barbara Sieklucka; Robert Podgajny; Tomasz Korzeniak; ...

C. R. Chim (2002)

3d and 4d coordination complexes and coordination polymers involving electroactive tetrathiafulvalene containing ligands

Fabrice Pointillart; Stéphane Golhen; Olivier Cador; ...

C. R. Chim (2013)