1 Introduction
Microscopic interactions between oppositely charged surfactant molecules control the phase behavior and microstructure in cationic–anionic surfactant mixtures [1,2]. Above the critical aggregate concentration, depending on the relative ratio of the two surfactants, these mixtures can yield a variety of aggregate morphologies such as micelles, worm-like micelles, vesicles and bilayers. The optimal geometry of the aggregates is governed by a balance between two opposing forces, namely the attractive and the hydrophobic interactions which favor the aggregation process and the repulsive (electrostatic and/or steric), chain packing and interfacial forces which oppose aggregation. The magnitude of these forces can be tuned by changes in external variables such as temperature or ionic strength and thus can induce changes in the equilibrium structure of the aggregates. The synergistic attraction between oppositely charged surfactant molecules offers a convenient way to alter the electrostatic behavior of surfactant head groups and thus tailor the aggregate geometry. This approach is particularly useful in the design of various practical surfactant formulations as it provides a cost effective means of manipulating the morphology of aggregates.
Alkyl poly-oxyethylene sulfate (AOES) is an important class of anionic surfactants. Their head groups consist of a hybrid uncharged oxyethylene group and a terminal charged sulfate group, so the head group interactions can be changed by the addition of salt or oppositely charged surfactant and the conformation of the head group can be altered by changes in temperature. This interplay between electrostatic and conformation effects at the micellar surface could lead to interesting microstructural changes in mixtures containing this class of surfactants.
Previous reports describing the aggregation of AOES surfactants have mostly used commercially available AOES which contains a distribution of ethylene oxide groups in the hydrophilic head group [3–10]. This polydispersity in ethylene oxide groups can significantly affect the solution properties of these surfactants. Zoeller and Blankschtein reported the salt-induced growth of micelles made with monodisperse dodecyl ethoxy sulfates having one, two, four and six ethoxy groups [11]. Here we examine the association behavior in mixtures of cetyltrimethylammonium bromide (CTAB) and sodium dodecyl tri-oxyethylene sulfate (C12E3S) in water. The aggregation behavior is probed by surface tension measurements and is analyzed in terms of the regular solution approximation. The growth behavior of the micelles at the CTAB-rich and C12E3S-rich sides of the phase diagram is monitored using viscosity, quasielastic light scattering (QLS), small angle neutron scattering (SANS), and cryogenic transmission electron microscopy (cryoTEM) measurements.
2 Materials and methods
Cetyltrimethylammonium bromide (CTAB) was purchased from Aldrich and tri-ethylene glycol mono n-dodecyl ether (C12E3) was obtained from Nikko chemicals. Sodium dodecyl tri-oxyethylene sulfate (C12E3S) was prepared by sulfating C12E3 with chlorosulfonic acid followed by neutralization with sodium hydroxide [12]. Extraction with pentanol and further stripping with water purified the sodium salt of the product and the solvent was removed by vacuum evaporation. The purity was checked by NMR and surface tension measurements. Chlorosulfonic acid was obtained from Fisher Scientific, pentanol from Fluka and sodium hydroxide pellets from J.T. Baker Chemicals. All chemicals were used as-received.
Surface tension measurements were made with a Kruss K10T digital tensiometer using the Wilhelmy plate method. The glassware was acid washed and the platinum plate was flamed prior to use. Measurements were carried out at 25 °C.
The phase behavior was identified combining weight stock solutions of CTAB and C12E3S in nanopure water. The mixtures were equilibrated in a water bath for one day at various temperatures and the phase boundaries were identified by visual observation.
Viscosity measurements were made using a Cannon-Ubbelohde viscometer. The viscometer containing the surfactant solution was immersed in a constant temperature bath and equilibrated for 15 min before measurement. The flow times were kept sufficiently high (by choosing appropriate diameter capillaries) to avoid the need for any kinetic energy correction.
Quasielastic light scattering (QLS) measurements were made using a Brookaven light scattering instrument including a BI200SM goniometer and a BI-9000AT digital correlator. The light source was a Lexel (model 95) argon ion laser having a maximum output power of 300 mW at 488 nm. The scattering angle was varied from 40° to 130°. The flame sealed ampules containing the surfactant solutions were immersed in a thermostated index matching fluid (decalin). The data were analyzed by the method of cumulants [13].
Small angle neutron scattering (SANS) experiments were performed using the NG-3 spectrometer at the Cold Neutron Research Facility of the National Institute of Standards and Technology (NIST) in Gaithersburg, MD. The incident neutron wavelength was 6 Å. Samples were held in quartz cells with 2 mm path lengths and maintained at 25 °C. Measurements were made at different sample to detector distances to cover a scattering vector (q) range of 0.005–0.6 Å−1. The scattering spectra were corrected for background scattering, empty cell contributions, sample transmission and detector efficiency, and the corrected data were radially averaged and placed on an absolute scale using NIST protocols and calibration standards. The incoherent background was determined by Porod extrapolation of the data in the high q region and was subtracted before data evaluation. Corrections due to instrumental smearing were taken into account throughout the data evaluation. For SANS measurements samples were prepared in D2O (Cambridge Isotopes).
Samples for cryoTEM were examined using a Tecnai G2 12 TEM (FEI, Hillsboro, Oregon) at an acceleration voltage of 120 keV. Specimens were prepared using a Vitrobot Mark II (FEI, Hillsboro, Oregon), a semi-automated preparation apparatus that allows for computer controlled blotting of grids in a temperature and humidity controlled environment. Quantifoil grids (SPI Supplies, West Chester, PA) were submerged in liquid samples and blotted up to five times for a period of 2 s for each blot to produce a thin liquid film. After blotting, an adequate relaxation time was provided (see below) to reduce any shear-induced artifacts and then vitrified by rapid immersion into liquid ethane held at its freezing temperature. Here, the time between blotting and vitrification is referred to as the relaxation time. The temperature within the sample preparation chamber was always maintained at 25.0 ± 0.5 °C and at least 95% relative humidity. Vitrified grids were transferred to a Gatan (Pleasanton, CA) single tilt cryogenic holder cooled with liquid nitrogen. The temperature of the grids was maintained below −170 °C during investigation in the TEM. Digital images were recorded using a Gatan multiscan charge coupled device camera and processed with DigitalMicrograph™ software.
Blotting a grid to produce a thin liquid film induces high shear stresses within the liquid on the grid that can alter the microstructure. Relaxation studies were conducted at all surfactant concentrations to identify any shear-induced changes to the observed microstructure. These studies were conducted by preparing separate grids from the same liquid sample using identical preparation parameters and altering the relaxation time from 0 s to 80 s. If no change in microstructure is observed with increasing relaxation time then either no shear-induced artifacts are present or they relax only after minutes. If a change is observed, the minimum relaxation time for accurate imaging is established as the time when any additional relaxation time results in no change to the observed microstructure. The maximum relaxation time is limited by the artifacts caused by evaporation, cooling, and diffusion of surfactant to the air–water interface [14]. All samples were imaged using the shortest required relaxation time.
3 Results and discussion
3.1 Aggregation behavior
Fig. 1 shows the surface tension as a function of surfactant concentration for pure C12E3S and CTAB as well as for solutions containing different mole fractions of C12E3S (α2). The plots show sharp breaks at the critical aggregate concentration (CAC) and the absence of any appreciable minimum indicates that the surfactants are pure. The critical micelle concentration (CMC) of pure C12E3S (0.15 mM) is considerably lower than that of pure CTAB (0.86 mM) because the presence of hydrated oxyethylene groups within an ionic head group enhances the aggregation process. This is further evident from the relatively low value of the ultimate surface tension at the CMC for C12E3S (28 mN/m) compared to that of CTAB (34 mN/m). The CACs as well as the ultimate surface tension at the CAC of the mixtures at intermediate mole fractions are lower than that of either of the pure components, indicating a synergistic enhancement of the surface activity.

Plots of surface tension vs. total surfactant concentration (logarithmic scale) for different mole fractions of C12E3S (α2) in CTAB–C12E3S mixtures at 25 °C.
Fig. 2 shows the experimentally observed CAC of the mixture as well as the surface tension at the CAC as a function of α2. The dotted line is the calculated CAC for ideal mixing within the pseudo phase separation model [15]. The experimental values show a negative deviation from ideal behavior that indicates the expected attractive interaction between the two oppositely charged surfactants. The non-ideal behavior can be quantified using the regular solution approximation [16] that characterizes the interaction between the two components in terms of a parameter β defined as
| (1) |
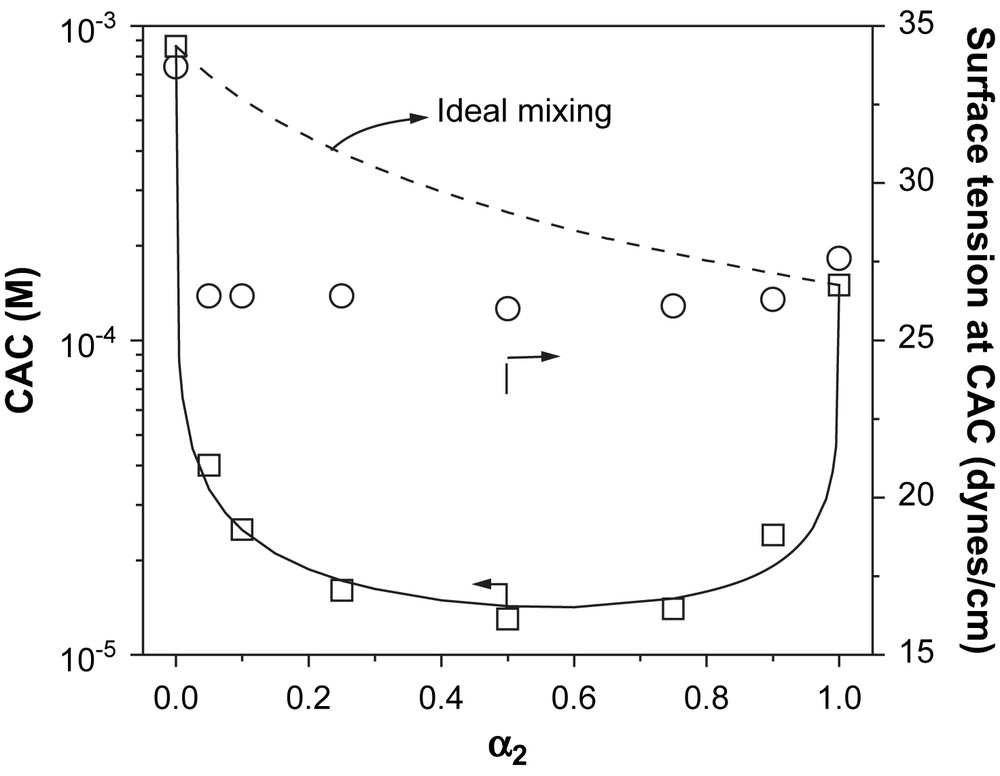
Plot of CAC and the surface tension at the CAC vs. mole fractions of C12E3S (α2). The dashed line represents the ideal solution situation and the solid line is a fit to the data for a β value of −12.7 ± 0.6 within the regular solution approximation. Both the CAC and the ultimate surface tension at the CAC are lower for the mixtures than for either of the pure components.
Here wij is the energy of interaction between molecules of the kind i and j, kB is Boltzmann's constant and T is the absolute temperature. Oppositely charged head groups exhibit attractive interactions and substantially negative values of β are usually observed in such mixtures [17]. The solid line in Fig. 2 gives the calculated CACs of the mixture for a best fit value of β = −12.7 ± 0.6. This value of β is intermediate between those found for similar cationic–anionic mixtures and for ionic–nonionic mixtures [17], and so is consistent with the hybrid nonionic–anionic nature of the head group of C12E3S.
3.2 Phase behavior
The partial pseudo ternary phase map of the catanionic system CTAB–C12E3S–water, at 25 °C, in the water-rich corner is depicted in Fig. 3. Along both binary surfactant–water axes there is a clear isotropic micellar phase region. Addition of C12E3S to the CTAB micellar solution changes the microstructure of the aggregates as the composition approaches the equimolar concentration. In the CTAB-rich side of the phase diagram, the isotropic one-phase region extends up to a mole fraction of α2 ≈ 0.3 for 100 mM total surfactant concentration (CT). When α2 is between 0.3 and 0.35 (CT = 100 mM), the solution phase separates into two coexisting liquid phases (coacervation).

The water-rich corner of the pseudo ternary phase diagram of CTAB–C12E3S–water at 25 °C. The region marked isotropic is a single clear liquid phase. The two-phase region contains two coexisting liquid phases.
As the composition at CT = 50 mM approaches the two-phase region by the addition of C12E3S to CTAB the viscosity of the solution slowly increases, which implies that the spherical CTAB micelles grow to form rod-like micelles by the incorporation of oppositely charged C12E3S molecules (Fig. 4). Close to the two-phase boundary the isotropic solution takes a slight bluish tinge, presumably because of critical scattering.

The relative viscosities of mixtures of CTAB and C12E3S as a function of mole fraction of the C12E3S, α2. The total surfactant concentration is 50 mM.
When α2 is increased further beyond the two-phase region the solution turns turbid. This turbid condition extends over a wide range around the equimolar line. In some cases, a turbid phase remains in equilibrium with a phase-separated precipitate. This precipitate is an indication of the strong attraction of the cationic–anionic pairs leading to the formation of the undissociated and insoluble catanionic salt. Further addition of C12E3S eventually yields another isotropic solution, and for CT = 100 mM this turbid–isotropic transition occurs at α2 ≈ 0.72.
3.3 Structural studies
3.3.1 Viscosity
The above features of the phase diagram are fully analogous to those observed in other cationic/anionic surfactant mixtures [2]. Incorporation of C12E3S into CTAB micelles neutralizes the effective charge on the micelle surface and reduces the repulsive interaction of the head groups. This increases the effective surfactant packing parameter and makes the formation of rod-like micelles energetically favorable due to the relatively higher energy cost of highly curved end caps [18]. Uniaxial growth of spherical micelles is observed as a consequence of suppression of surface charge.
Fig. 4 shows the variation of relative viscosity of a mixture containing CT = 50 mM as a function of α2. The uniaxial growth of CTAB-rich micelles is evident from the rapid increase in the viscosity of the solution with an increase in α2 (open circles). In interesting contrast, there is no significant increase in viscosity in the C12E3S-rich micelles (open squares). In this region of the phase diagram, the viscosity of the solution remains almost constant with only a slight increase in viscosity observed close to the phase boundary. The C12E3S micelles feature both electrostatic and steric repulsions of the head groups. Incorporation of CTAB into the C12E3S micelles reduces the electrostatic repulsion by neutralizing the surface charge, but the remaining steric repulsions of the hydrated oxyethylene groups apparently enable the molecules to continue to occupy a large area per head group. Thus the effective packing parameter remains small and C12E3S-rich micelles do not grow as long as the CTAB-rich micelles. This observation is consistent with the growth behavior seen in other CiEjS micelles caused by the addition of salt [11]. C12E1S and C12E2S micelles grow significantly when salt is added, while C12E4S and C12E6S micelles do not. This is consistent with an increase in steric repulsions between the head groups as the oxyethylene content increases. Further insight into the structure and interactions in these micelles is obtained from the QLS and SANS measurements that follow.
3.3.2 QLS studies
The micellar growth observed in the CTAB–C12E3S mixed micelles in the isotropic region is quantified using QLS measurements assuming a model of stiff rods. The measured diffusion coefficient Da decreases as function of α2 for a mixture containing CT = 50 mM, in the CTAB-rich region (Fig. 5). The diffusion coefficients were corrected for hydrodynamic and osmotic contributions as discussed elsewhere [19]. The corrected diffusion coefficient D0 can be related to the length L of the rod and its axial ratio p by Broersma's relationship [20].
| (2) |

The apparent diffusion coefficient, Da, determined by QLS for 50 mM mixtures of CTAB and C12E3S as a function of the mole fraction α2 at 25 °C.
where η is the solvent viscosity and the shape factor ζ is a function of the axial ratio p. The expressions of Tirado et al., which are valid for axial ratios in the range of 2–30, relate ζ to p [21].
| (3) |
Using the above equations the micellar length L can be evaluated under the assumption that the micelle diameter d is fixed at 43 Å, which is twice the length of the hydrocarbon chain of CTAB. The average length L increases strongly as a function of α2 when α2 is above 0.15 (Fig. 6). When α2 < 0.15, Da is in the range expected for small globular micelles so the reported size is the hydrodynamic diameter obtained using the Stokes–Einstein equation. The length of the rod-like micelles at the overlap concentration [22] (as estimated from the condition that the number density of the rods is equal to L−3) is ∼285 Å, so any value of L calculated using Eq. (2) for 0.25 < α2 < 0.75 is, at best, an upper bound. Moreover, cryoTEM studies indicate the formation of branched micelles at compositions near the phase boundary, which means Eq. (2) is not applicable.

The average length of the rod-like micelle (L) calculated from the QLS data for 50 mM CTAB–C12E3S mixtures as a function of the mole fraction α2 using Eq. (2). The length of the micelles at the overlap concentration is about 285 Å, which is shown by the dotted line.
3.3.3 SANS studies
SANS measurements were carried out to determine the microstructures and interaggregate interactions in the micellar regions of the phase diagram. The evolution of the SANS spectra of C12E3S micelles with added CTAB, at CT = 50 mM, is shown in Fig. 7. For pure C12E3S micelles (α2 = 1) the SANS spectrum resembles that from other ionic micellar solutions and displays a characteristic correlation peak indicating the presence of strong repulsive intermicellar interactions. Successive addition of CTAB to C12E3S micelles decreases the strength of this interaction as a consequence of the decrease of the micellar surface charge density.

The scattering intensity, I(q) as a function of scattering vector q for 50 mM C12E3S–CTAB mixtures at different mole fractions of C12E3S, α2 in the C12E3S-rich region at 25 °C. The solid lines are the best fit to the data using the generalized indirect Fourier transformation (GIFT) method with the HNC closure relation and Yukawa potential for the structure factor.
The SANS spectra were analyzed using the generalized indirect Fourier transformation (GIFT) technique [23,24]. The desmeared scattered intensity is a Fourier transform of the pair distance distribution function (PDDF), p(r), that describes the real space information about the scatterers. Direct Fourier transformation of the measured intensity spectra is impractical due to smearing effects and the finite range of q values accessible by the instrument. Thus an indirect Fourier transformation (IFT) is widely applied to obtain the PDDF. When interparticle interactions are important a suitable model for the structure factor, S(q) has to be introduced in the IFT procedure and the expression for scattered intensity, I(q) becomes
| (4) |
Initial analysis of the SANS data by the IFT method without considering a S(q) showed damped oscillations in the p(r) function for all of the spectra shown in Fig. 7, although the correlation peak almost disappears with decreasing α2. This oscillation is a characteristic of the presence of repulsive intermicellar interactions, and thus it is clear that intermicellar interactions cannot be neglected in any of the samples [26]. The spectra were therefore analyzed by the GIFT method by taking into account S(q), and the resulting PDDFs are depicted in Fig. 8. The PDDF for pure 50 mM C12E3S (α2 = 1) is similar to that expected for globular micelles with diameter ∼55 Å, while that for α2 = 0.72 suggests an elongated micelle with length of about 200 Å. With addition of CTAB to C12E3S micelles, the ratio of maximum dimension to the peak position in the PDDF (a measure of ellipticity of the micelles) increases, reflecting a gradual growth of the micelles to anisotropic structures. The dimensions of the micelles determined by GIFT are consistent with the sizes determined by QLS.
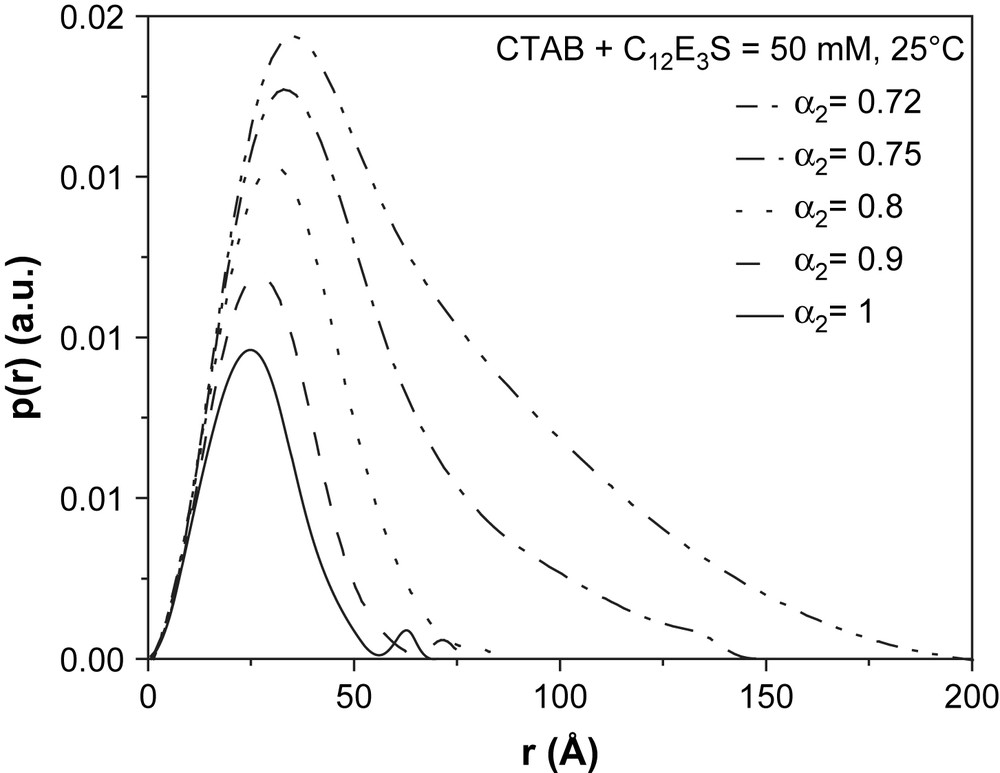
Pair distance distribution functions, p(r) obtained by GIFT analysis of the data in Fig. 7 at different values of α2. The structure factor is calculated assuming a Yukawa form of the potential and HNC closure relation and the parameters are given in Table 1. A globular to cylindrical micelle transition is evident from the change of the p(r) functions.
The parameters obtained from the structure factor model calculations are given in Table 1. The effective equivalent sphere radius of the micelles shows a gradual increase with decreasing α2, consistent with the nature of the p(r) function (Fig. 8). An approximate aggregation number is calculated from the equivalent sphere volume of the micelle, knowing the average volume of surfactant molecule. The fractional charge on the micelle is evaluated from the aggregation number and effective charge per particle. These parameters are included in Table 1 for comparison. The fractional charge on the micelle decreases continuously with decreasing α2, consistent with the expectation that added CTAB molecules partially neutralize the charge on C12E3S-rich micelles.
Parameters of the structure factor obtained from GIFT analysis of the SANS data in Fig. 7 (C12E3S-rich region) using the Yukawa potential and HNC closure relation. The aggregation numbers (Naggs) are derived from the equivalent sphere volume and the volume of surfactant molecule. The fractional charge is the ratio of charge per micelle to Nagg
| Mole fraction of C12E3S (α2) | Equivalent sphere radius (Å) | Charge per micelle | Nagg | Fractional charge |
| 1 | 24 | 29 | 83 | 0.35 |
| 0.9 | 26 | 33 | 112 | 0.30 |
| 0.8 | 31 | 41 | 184 | 0.22 |
| 0.75 | 36 | 44 | 299 | 0.15 |
| 0.72 | 44 | 45 | 539 | 0.08 |
Now, consider the evolution of SANS spectra in the CTAB-rich side of the phase diagram at CT = 50 mM and at 35 °C (Fig. 9). Pure CTAB micelles (α2 = 0) clearly show the expected correlation peak and the peak diminishes with successive addition of C12E3S. IFT of the spectra clearly indicated the presence of intermicellar interactions in all the samples as reflected from the presence of oscillations in the PDDFs. Thus, GIFT analysis is performed with the same model for S(q) as described earlier. The resulting p(r) functions are depicted in Fig. 10 and the fitted parameters are listed in Table 2.

The scattering intensity, I(q) as a function of scattering vector q for 50 mM CTAB–C12E3S mixture in the CTAB-rich region at different values of α2 (T = 35 °C) and the corresponding GIFT analysis (solid lines).
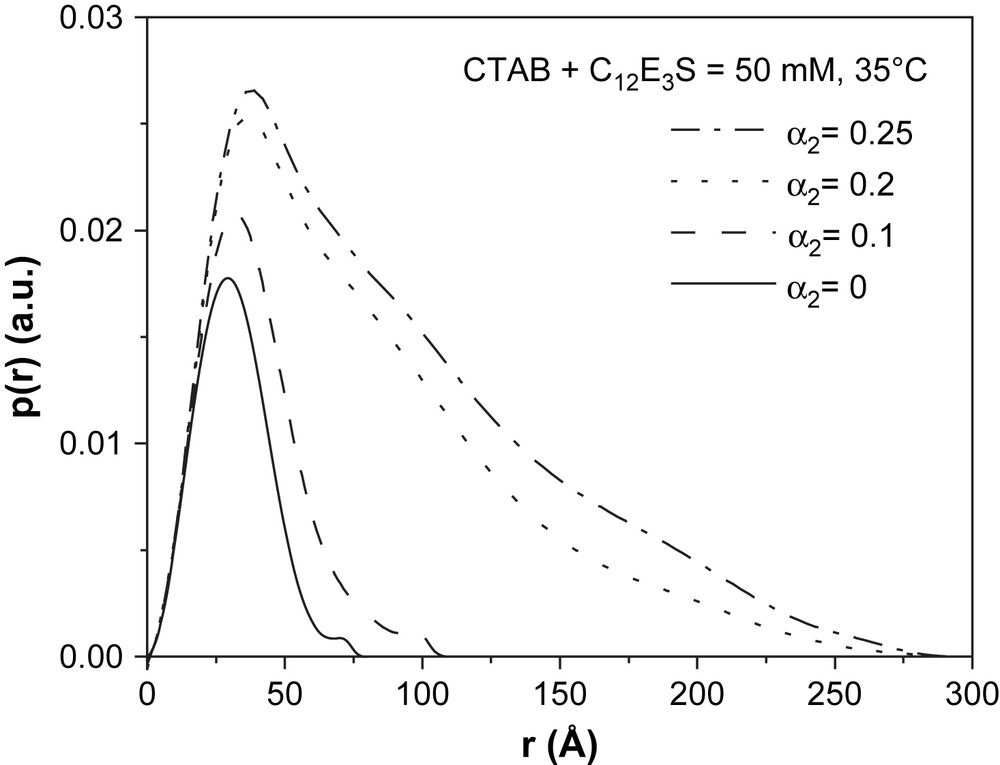
Pair distance distribution functions, p(r) obtained by GIFT analysis of spectra given in Fig. 9. The evolution of long micelles by the addition of C12E3S to CTAB is evident from the changes of the p(r) functions.
Structure factor parameters obtained from GIFT analysis of SANS spectra in Fig. 9 (CTAB-rich region). The notations are same as those used in Table 1
| Mole fraction of C12E3S (α2) | Equivalent sphere radius (Å) | Charge per micelle | Nagg | Fractional charge |
| 0 | 27 | 24 | 139 | 0.17 |
| 0.1 | 31 | 30 | 216 | 0.14 |
| 0.2 | 60 | 66 | 1532 | 0.04 |
| 0.25 | 61 | 69 | 1633 | 0.04 |
In the case of spherical symmetry, the PDDF can be deconvoluted [27] into a cross-section scattering length density profile. Such a process shows that pure C12E3S micelles can be best described in cross-section by a core–shell structure with a core radius of 13 Å and a shell radius of 29 Å. An alternative, but equally good, model for describing the PDDF is in terms of an ellipsoidal micelle with an axial ratio of 33 Å/21 Å. Considering the molecular structure of C12E3S, it is evident that the fully extended chain of this molecule (without including the sulfate head group) can have a total length of 27 Å and the hydrocarbon and oxyethylene part have different scattering length densities. Thus, it is likely that the micelles have a core–shell structure, as the observed shell radius is only slightly larger than 27 Å. However, we cannot neglect the possibility that the micelles are elliptical because the oxyethylene part of the molecule can take different conformations and could give a shell radius much less than 27 Å. It is also possible that a combination of both these effects is present, namely that there are elliptical micelles with a core–shell structure.
For elongated micelles, it is possible to calculate the cross-sectional PDDF, pc(r) and hence obtain the contrast profile of the cross-section of the micelles. The pc(r) function depends mainly on the high q region of the spectra. Thus a low q cut off is established at q = 0.0506 Å−1 and the transformation is repeated by decreasing the cut off to lower q values until the results do not change. Deconvolution of the pc(r) of elongated micelles formed in the CTAB–C12E3S mixture at α2 = 0.72 (CT = 50 mM) also shows that the cross-section can be described by a core–shell structure with core and shell radii 15 Å and 28 Å, respectively. An elliptical cross-section with axis dimensions of 15 Å and 28 Å is an alternative model for this pc(r). Again, either of these two possibilities cannot be neglected based on the geometry of the molecules. A schematic representation of the two alternate possibilities for cross-section of rod-like micelles at α2 = 0.72 is shown in Fig. S1 in the supplementary material.
3.3.4 CryoTEM
The microstructures formed by CATB and C12E3S at 25 °C and different compositions with CT = 50 mM (Fig. 4) were characterized by cryoTEM. Direct imaging of a C12E3S-rich micelles at α2 = 0.9 (Fig. 11, panel A) shows the presence of small spherical micelles and no evidence of elongated micelles. GIFT analysis of SANS spectra (Table 1) also suggests that only small spherical micelles 40–50 Å in diameter are present at α2 = 0.9. At α2 = 0.8 (Fig. 11, panel B) short rod-like micelles ∼50 Å in diameter with apparent lengths of 400 Å or less are observed. Close to the turbid region in phase space at α2 = 0.75 (Fig. 11, panel C), worm-like micelles with contour lengths exceeding 2000 Å are observed. The micelles also exhibit a small degree of branching that is not present at α2 = 0.8. Branch points are identified in cryoTEM as three points of micelle contact and are differentiated from overlapping micelles, which would have four points of micelle contact [28]. No shear-induced artifacts are observed for C12E3S-rich micelles.
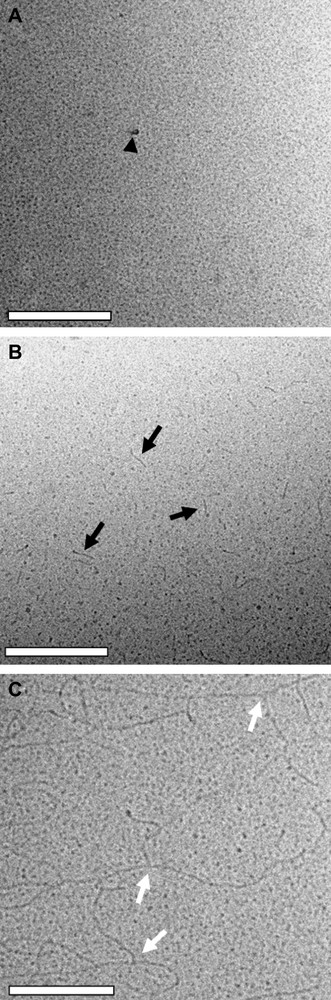
CryoTEM micrographs of C12E3S-rich micelles at α2 = 0.9 (A), 0.8 (B), and 0.75 (C) imaged after 5 s of relaxation time and prepared at 25 °C. Black arrows denote short rod-like micelles, white arrows micelle branch points, and the black arrow head an artifact created when water vapor crystallized on the grid. Scale bar = 200 nm.
CryoTEM micrographs of CTAB-rich micelles at α2 = 0.05 (not shown) show spherical micelles and appear similar to micrographs of samples at α2 = 0.9. The resolution of cryoTEM is not sufficient to detect any difference in size between CTAB-rich and C12E3S-rich spherical micelles. Direct imaging of CTAB-rich micelles at α2 values between 0.05 and 0.24 is complicated by the presence of shear-induced artifacts. A relaxation study conducted at α2 = 0.1 (Fig. 12) reveals the presence of shear-induced ribbon-like micelles. Ribbons are identified in cryoTEM by sections of wide low contrast when viewed with the wide axis of the ribbon parallel to the surface of the grid and narrow high contrast when viewed with the wide axis perpendicular to the surface of the grid. Micelles observed in grids prepared with 5 s of relaxation time (Fig. 12, panel A) exhibit ribbon-like structures approximately 100 Å wide and 50 Å thick. At an intermediate relaxation time of 40 s a mixture of cylindrical and ribbon-like micelles is observed (Fig. 12, panel B). After 80 s of relaxation time cylindrical micelles ∼50 Å in diameter with some contour lengths exceeding 2000 Å are the dominant microstructures. Only a few ribbon-like micelles remain (Fig. 12, panel C). Longer relaxation times were not explored due to the potential for artifacts caused by evaporation, cooling, and diffusion of surfactant to the air–water interfaces.

CryoTEM micrographs representing a relaxation study conducted with CTAB-rich micelles at α2 = 0.1 and prepared at 25 °C. The same sample volume and blotting parameters were used to prepare each grid. The relaxation times between blotting and vitrification are 5 s (A), 40 s (B), and 80 s (C). Black arrows denote ribbon-like micelles viewed on edge, white arrows ribbon-like micelles viewed with the wide axis parallel to the grid surface, and the black arrow head an artifact created when water vapor crystallized on the grid. Scale bar = 200 nm.
Shear-induced artifacts are more prevalent for α2 values closer to the two-phase region. Fig. 13 shows characteristic micrographs for samples measured after short and long relaxation times for α2 = 0.175 and 0.24. At short relaxation times and α2 = 0.175 (Fig. 13, panel A) long twisting ribbon-like micelles are observed. After 80 s of relaxation time, single micelles containing both cylindrical and ribbon-like morphologies are observed. A small number of micelle branch points are also present. At α2 = 0.24 the shear induced during blotting produces a microstructure that appears similar to a lamellar phase (Fig. 13, panel C). The dark lines in the micrograph are wrinkles and edges of the lamellar sheets. Danino et al. [29] reported a similar shear-induced transition from cylindrical micelles to lamellar sheets in aqueous solutions of hexadecylpyridinium chlorate and sodium chlorate. The authors concluded that the close proximity in phase space of the micelle phase to a lamellar phase was responsible for the shear-induced transition. This is consistent with samples at α2 = 0.05 and lower exhibiting no shear-induced artifacts while such artifacts do occur between α2 = 0.1 and 0.24 with the most prevalent at α2 = 0.24. CryoTEM micrographs also suggest the frequency of micelle branching is highest at α2 = 0.24. The C12E3S-rich micelles exhibited less branching even for samples near the turbid region.

CryoTEM micrographs of CTAB-rich micelles prepared at 25 °C and α2 = 0.175 imaged after 5 s (A) and 80 s (B) of relaxation time and at α2 = 0.24 imaged after 5 s (C) and 20 s (D) of relaxation time. Black arrows denote ribbon-like micelles viewed with the wide axis parallel to the grid surface, white arrows micelle branch points, the white arrow head a wrinkle in a lamellar sheet and black arrow heads artifacts created when water vapor crystallized on the grid. Scale bar = 200 nm.
Branched micelles are observed by cryoTEM for both CTAB and C12E3S-rich micelles near respective phase boundaries. The CTAB-rich micelles appear to have a higher density of branching than the C12E3S-rich micelles and the viscosity, as observed in Fig. 4, is greater. Branched micelles observed by cryoTEM are typically reported for solutions that exhibit a peak in zero shear viscosity as a function of a linear increase in a single control parameter [30]. The initial increase in viscosity is often attributed to a linear growth of the micelles while the reduction in viscosity at higher values of the control parameter is attributed to the formation of a branched micelle network. It is interesting to note that no peak in zero shear viscosity is observed in Fig. 4 but branched micelles are observed by cryoTEM. This suggests that with surfactant ratio as the control parameter micelle branching increases the zero shear viscosity for both CTAB and C12E3S-rich micelles until phase separation occurs.
The diameter of micelles observed in cryoTEM for all values of α2 imaged agrees well with the analysis of both light and neutron scattering. The contour length of some cylindrical micelles, particularly for α2 values near phase boundaries, appears greater in cryoTEM than from the scattering analysis. This increase in contour length may be an additional shear-induced artifact that does not recover in the relaxation times used in these studies.
3.4 Effect of temperature
The steric repulsion of the nonionic oxyethylene head groups can be altered by a change in temperature due to dehydration and/or conformational changes of the oxyethylene groups at elevated temperatures. Thus a significant change in the phase boundary of the C12E3S-rich side of the phase diagram is anticipated with a change in temperature. At a given α2, when CT is close to the C12E3S-rich phase boundary, solutions become turbid with an increase in temperature. This is consistent with the well known “clouding” of nonionic surfactant solutions at elevated temperatures. The variation of phase transition temperature (cloud point) as a function of α2 at two different total surfactant concentrations (5 mM and 20 mM) is shown in Fig. 14. Close to the phase boundary electrostatic repulsions between the head groups are neutralized by complexation of oppositely charged surfactant molecules and the mixture behaves like a nonionic surfactant. As α2 increases from the value corresponding to the room temperature phase boundary the surface charge of the micelle increases. This increase of surface charge leads to an increase in the phase transition temperature. The same situation applies to solutions of pure nonionic surfactants, where addition of ionic surfactants increases the cloud point of the micelles [31].
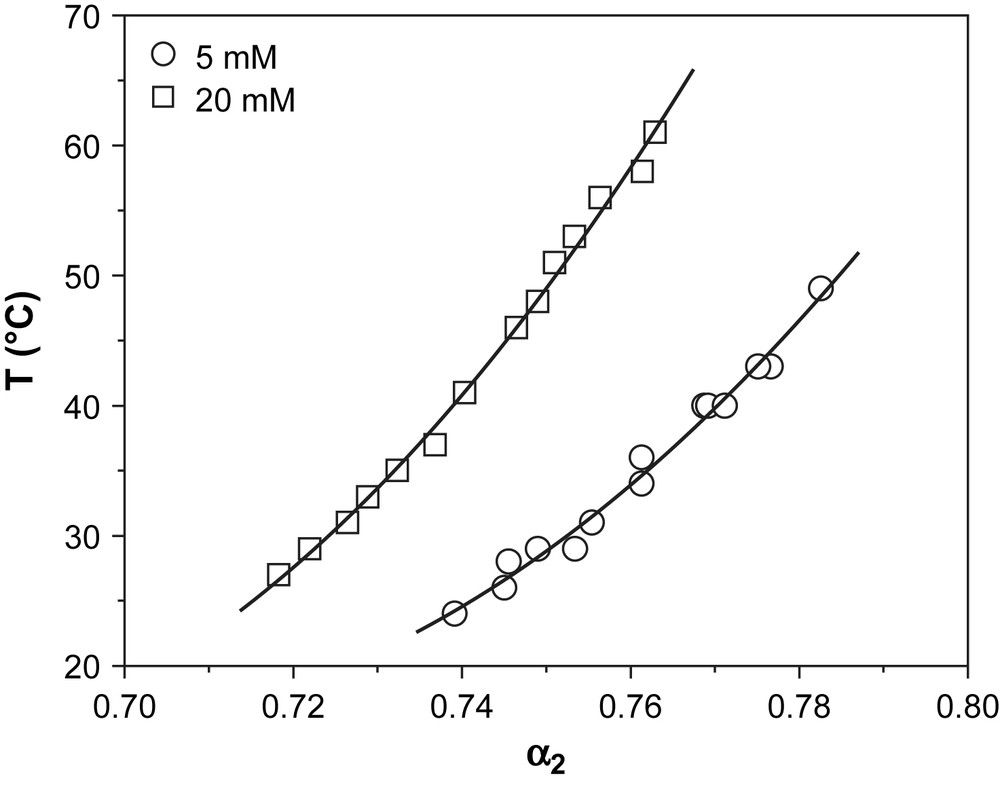
Variation of the phase transition temperature of the mixtures with C12E3S mole fraction (α2) for total concentrations 5 mM and 20 mM. (The solid lines are drawn as a guide to the eye.)
The phase transition temperature is sensitive to the total surfactant concentration and the composition. The variation of mole fraction at the phase boundary with surfactant concentration at 25 °C and 40 °C is shown in Fig. 15. At a given temperature, α2 at the phase boundary decreases initially and then increases beyond a surfactant concentration of ∼25 mM. Such a minimum is observed at all temperatures ranging from 25 °C to 50 °C (data shown only for 25 °C and 40 °C), though the position of the minimum changes slightly with temperature. This non-linear dependence reflects the curvature of the phase boundary on the C12E3S-rich side of the phase diagram.

Variation of the mole fraction at the C12E3S-rich side phase boundary (α2) with total surfactant concentration and at temperatures 25 °C and 40 °C. (The solid lines are drawn as a guide to the eye.)
4 Conclusions
The synergistic interaction between the cationic surfactant CTAB and a hybrid nonionic–anionic surfactant C12E3S is reported. The strength of this attractive interaction is intermediate between those reported for cationic–anionic and ionic–nonionic surfactant mixtures. This synergism leads to a rich phase behavior similar to that found for other catanionic mixtures. A uniaxial growth of CTAB-rich and C12E3S-rich micelles is induced by the addition of the other surfactants due to the suppression of the surface charge and decrease of head group repulsion. Steric repulsion of the oxyethylene groups limits the growth in the C12E3S-rich mixed micelles. The formation of junctions is directly observed by cryoTEM and is more prevalent in CTAB-rich micelles. The formation of shear-induced artifacts makes direct imaging of micelles near the phase boundary difficult. Temperature induced dehydration and/or conformational changes of the oxyethylene groups lead to cloud point phenomenon for solutions rich in C12E3S.
Acknowledgements
P.A.H. is thankful to Dr. C. Manohar, Indian Institute of Technology, Mumbai, India for fruitful discussions. This work was supported by National Science Foundation grant CBET-0436195 and the National Institute of Standards and Technology.


