Plan
Comptes Rendus
no. 1-2

Account / Revue
Flexibility, persistence length and bicontinuous microstructures in microemulsions
Thomas Zemb1
1 Institut de chimie séparative de Marcoule, UMR 5257 CEA/CNRS/UM2/ENSCM, BP 17171 CEA Marcoule, 30207 Bagnols-sur-Cèze, France
Comptes Rendus. Chimie, Volume 12 (2009) no. 1-2, pp. 218-224.

Résumés

Three length scales have to be considered to describe microemulsions: persistence length, spontaneous radius of curvature of the surfactant film as intensive variables and finally the characteristic size imposed by the ratio of volume fraction to available specific area surface. The specific area per unit volume is an intensive variable linked to sizes and topologies that can be built without tearing the surfactant film. We show here that at least four types of bicontinuous microstructures have been detected so far, and that they can be distinguished by a simple experimental determination of the evolution of scattering peak position versus dilution. Besides the classical microstructures dominated by entropy or a priori considered as droplets, the other microstructures identified so far can be approximated as connected cylinders or randomly connected swollen bilayers. All these microstructures can be considered as “molten” precursors of the lyotropic liquid crystalline phases that are adjacent to microemulsions in phase diagrams.

Trois longueurs caractéristiques doivent être considérées dans la microstructure des microémulsions : la longueur de persistance, le rayon de courbure spontané du film ainsi que la taille caractéristique imposée par le rapport des volumes sur les surfaces. Les microstructures possibles sont liées par une contrainte forte de non-déchirure du film. Nous montrons que quatre types de microstructures ont été mises en évidence jusqu'à ce jour. Ces quatre types de microstructures peuvent être discriminées par un tracé simple de la taille caractéristique indiquée par le maximum du pic observé par diffusion en fonction de la fraction de volume. Outre les structures les plus classiques, sous forme de gouttelettes ou celles dominées par l'entropie, les microstructures en cylindres ou bicouches connectés peuvent être considérées comme précurseurs des phases lyotropes qui leur sont adjacentes dans les diagrammes de phases.

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crci.2008.10.008
Keywords: Microemulsion, Microstructure, Swelling, Curvature, Interfacial, Diffusion
Mots clés : Microémulsions, Microstructure, Gonflement, Courbure, Film interfacial, Diffusion
Thomas Zemb 1

1 Institut de chimie séparative de Marcoule, UMR 5257 CEA/CNRS/UM2/ENSCM, BP 17171 CEA Marcoule, 30207 Bagnols-sur-Cèze, France 
@article{CRCHIM_2009__12_1-2_218_0,
     author = {Thomas Zemb},
     title = {Flexibility, persistence length and bicontinuous microstructures in microemulsions},
     journal = {Comptes Rendus. Chimie},
     pages = {218--224},
     publisher = {Elsevier},
     volume = {12},
     number = {1-2},
     year = {2009},
     doi = {10.1016/j.crci.2008.10.008},
     language = {en},
}
TY  - JOUR
AU  - Thomas Zemb
TI  - Flexibility, persistence length and bicontinuous microstructures in microemulsions
JO  - Comptes Rendus. Chimie
PY  - 2009
SP  - 218
EP  - 224
VL  - 12
IS  - 1-2
PB  - Elsevier
DO  - 10.1016/j.crci.2008.10.008
LA  - en
ID  - CRCHIM_2009__12_1-2_218_0
ER  - 
%0 Journal Article
%A Thomas Zemb
%T Flexibility, persistence length and bicontinuous microstructures in microemulsions
%J Comptes Rendus. Chimie
%D 2009
%P 218-224
%V 12
%N 1-2
%I Elsevier
%R 10.1016/j.crci.2008.10.008
%G en
%F CRCHIM_2009__12_1-2_218_0
Thomas Zemb. Flexibility, persistence length and bicontinuous microstructures in microemulsions. Comptes Rendus. Chimie, Volume 12 (2009) no. 1-2, pp. 218-224. doi : 10.1016/j.crci.2008.10.008. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2008.10.008/

Version originale du texte intégral

1 Introduction

Over twenty-five years ago, in a seeding paper dealing with flexibility of oil/water interfaces, de Gennes and Taupin introduced a clear distinction between two length scales in oil/water mixtures: one is the persistence length and the other is given by the ratio of the volume to the available surface [1]. This seeding paper explicitly referred to a surfactant film with a negligible tendency to curve towards water or towards oil, i.e. without spontaneous curvature. The surfactant film is in these conditions close to PIT, “balanced conditions” or equal solubility in water and oil. This is the case with microemulsions of interest in the 1980s, since studies of microemulsions were targeted towards new processes aimed at assisted oil recovery. The persistence length of the film is then defined as:

ξ=texp2πKckT(1)
where t is the film thickness and Kc is a constant coupling the bending energy to the curvature. The easiest way to grab the idea of persistence length is to consider a vector perpendicular to the water/oil interface and linked to the surfactant film. On an average, the direction of this vector with reference to the macroscopic sample would vary by less than one radian due to a linear displacement of less than ξ in the plane of the film. If displacement is much larger than persistence length ξ, the angles of the vector normal to the interfacial layer versus macroscopic sample at the beginning and at the end of displacement are not correlated. Typically, a folded A4 paper in a rubbish bin has a persistence length of the order of 1 cm.

On the other hand, it has been noted by Talmon and Prager that any dispersion of “cells” of size D∗, randomly filled by water and oil, must fulfill the condition between the polar volume fraction ϕ and available surface Σ [2]:

ΣD∗=6ϕ(1−ϕ)(2)
The exact numerical factor has been calculated for tessellation of space compatible with minimum size of Voronoï cells and is not 6, but 5.83 [3,4], a difference not detectable experimentally [5]. Surfactant molecules “missing” from the film and present in the solution as monomers in water or oil have to be taken into account for the determination of the interfacial area Σ per sample volume. In cases where the quantity cs (surfactant molecules located in the film per unit volume of sample) is known in the sample, the specific area can be derived from: Σ = a0cs, where a0 is the usual area per molecule minimizing the free energy of continuous (un-teared) film formation.

On the other hand, the available specific surface Σ can be measured without hypothesis via scattering experiments using the Porod limit as long as the scattering length contrast between the two immiscible fluids present in the microemulsion is known [6]. In favorable cases, the experimental value found from Porod type determination can be compared to the value expected from the known concentrations of surfactants and co-surfactants. This requires that the area per molecule a0 at the oil/water interface is known independently, for example, from surface tension experiments. In the few quantitative experiments published so far, the specific area of contact of oil and water Σ has always been found to be equal to csa0 within experimental error.

In the case considered initially by de Gennes and Taupin, the surfactant film considered had no special tendency to curve towards water or oil. However, the fundamental link between the spontaneous curvature and the molecular packing parameter p had been introduced on a series of classical works by Ninham and co-workers [7,8]. The spontaneous packing parameter p0 of a given film is a combination of the effective volume V of the apolar part of the surfactant including the oil/solvent penetrating into the film and the area per molecule minimizing the free energy [9]. As long as no external constraint imposes a given value of the area per molecule, there is no surface tension of the microscopic oil/water interface. The entropy of molten chains when these ones are in the fluid case imposes a film thickness t, which is usually close to 80% of the crystallographic length [10]. The spontaneous packing parameter p0 is an intrinsic surfactant film property, once the film wetting by the oil and the hydration of head-groups are taken into account.

In any real sample, the effective packing parameter p of the surfactant film is the average over the whole sample of average curvature H and Gaussian curvature K of the film [9]:

p=〈1+Ht+1/3Kt2〉(3)
The bracket indicates an averaging over the whole sample and t is again the interfacial film thickness. This effective packing can be calculated for any sample, once the microstructure is known. It is exactly 1/3 for micelles and exactly 1 for lamellar phases. The difference between spontaneous packing and effective packing has been designed as “frustration” of the surfactant film in order to realize a given microstructure. In the case of nonionic microemulsions, oil-rich microemulsions at temperatures below PIT – i.e. when surfactant film curves towards oil – belong to this category of frustrated microstructures. Attention must be drawn here, since erroneous expressions of effective packing, such as p < 1 for unilamellar vesicles, are copied from paper to paper without reference to original derivation. In the triangle representing complete ternary phase diagrams, spontaneous and effective packing coincide only on defined lines [11]: outside of these lines, the structure is frustrated and there is a bending energy cost of setting up a given microstructure. In the seeding paper [1], de Gennes and Taupin considered only the case where no spontaneous curvature exists and entropy dominates over curvature effects. Generalization of this peculiar case have been considered in Ref. [5]. Hereby, we consider cases where spontaneous curvature cannot be neglected.

In the case of disconnected micelles, it has been shown by Ninham that the difference between spontaneous curvature and effective average curvature in a real sample is related to chemical potential [8]. Extrapolated to the case of microemulsions, the total bending energy of any microstructure consisting of two immiscible fluids separated by a continuous surfactant film surfactant has been shown to be [3,12]:

Gb=1/2k∗<(p−p0)2>(4)
This expression is a generalization of the ubiquitous expression used by Helfrich [13], which considers that there is no coupling between average and Gaussian curvature. Helfrich's approach neglects the topological constraint related to coverage without tearing of the film, given in Eq. (3). At the mostly considered balanced case (PIT etc.), the spontaneous packing parameter is close or equal to 1. Moreover, the “Helfrich” expression of Eq. (4) uses two coupling constants κ and κ′ related to average and Gaussian curvature. This may be inconsistent, specially when κ/κ′ is close to −1/2, as has been demonstrated in Ref. [9].

In the case examined by de Gennes and Taupin, the size of “cells”, alias “domain size”, D∗ has to follow a general relation, including a topological numerical factor τ [1]:

ΣD∗=τϕ(1−ϕ)(5)
In this relation, the peak position corresponds to the domain size via the Bragg relation D∗ = 2π/qmax and ϕ is the volume fraction. Consistently with the suggestion of Talmon and Prager, the topological factor τ can be safely approximated to 6 when films are flexible and constraints linked to spontaneous curvature can be neglected.

If the microstructure is restricted to a dispersion of spherical droplets, the radius of the droplets must be given by:

Rsph=3ϕΣ(6)
Eq. (6) is purely geometric and is the equivalent of Eq. (5), reduced to the case of spherical droplets without coalescence. In order to check the presence of spheres in a liquid–liquid dispersion, area Σ and volume fractions must be known, and the simulation of the full scattering curve for interacting globules of known radius R as derived from Eq. (6) has to be checked for consistency with the scattering observed. Fitting curves with adjustable radii and neglecting the strong constraint is a common mistake and has produced a large number of papers were presence of droplets was assumed, not proved. This has been found to be the case in ternary microemulsions made with AOT with less than 10% volume fraction, even in the presence of solutes [14]. Fitting broad scattering peaks to three parameter expressions such as the formula given by Teubner and Strey [15] will in any case produce a “fit” with three numbers, related to domain size and available area, without insight on the microstructure present. Three parameter-fitting with any type of microstructure extending from interacting droplets to spinodal decomposition indicate some “apparent domain size” without any predictive power about the microstructure present. On the other hand, as shown by Choi and co-workers, precise fitting of the scattering curve allows model-free evaluation of the average curvature [16].

2 Experimenting using dilution and scattering

The situation changes when dilution series are investigated. Indeed, strong relations such as given by Eq. (4) of the relation between size, volume fraction and surfaces behavior made by de Gennes and Taupin has been tested experimentally by SAXS and SANS experiments in the case of microemulsions formulated with a large mole ratio of co-surfactant to surfactant by Guest, Auvray and Langevin [17]. Using data from Guest et al., Fig. 1 shows how well this prediction holds for co-surfactant-rich flexible interfaces. The area was derived from the Porod regime extending into the high-q part of small angle scattering experiments made on absolute scale and taking into account the area brought in by the surfactant and the co-surfactant. The convenient way to test this is to plot the dimensionless quantity D∗Σ versus volume fraction. Precise evaluation of volume fraction requires partition of the surfactant volume into a polar and an apolar part, consistent with scattering length densities used. Other examples of dilution plots are given in Ref. [18]. From the three known volume fractions of water, oil and surfactant, volume fractions of “polar” and “apolar” part including the volume of polar head-groups have to be derived consistently. In Fig. 1, the positions of scattering peak, which would be observed for a microstructure as connected cylinders, is also shown as a discriminating counter-example.

Fig. 1

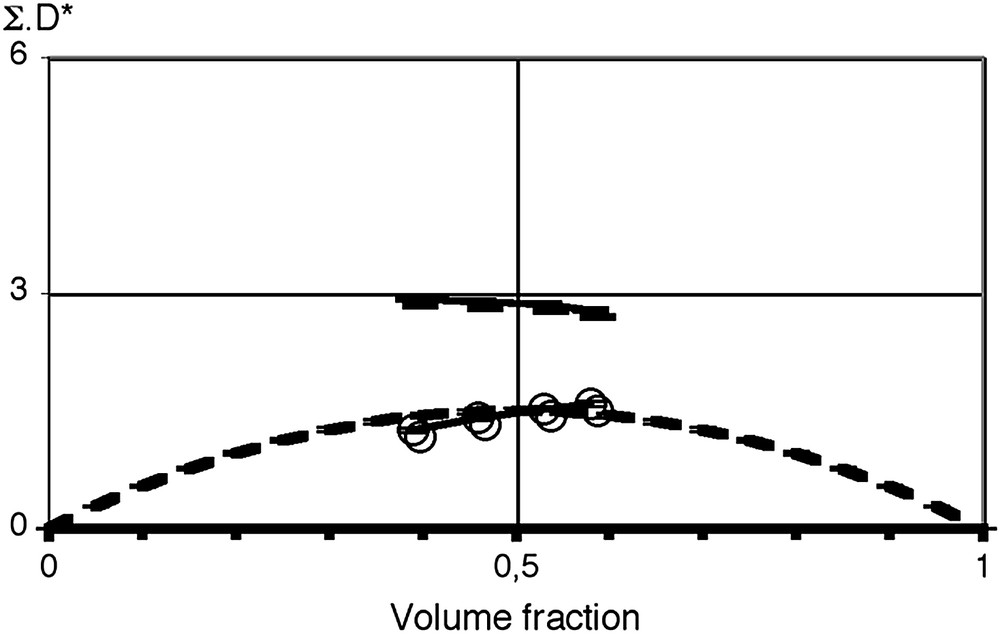
Dilution plot linking volume fraction and scattering peak position scaled by specific surface ΣD∗: data from Ref. [17] with a microemulsion based on SHBS plus co-surfactant; area per surfactant head was measured via the Porod limit 1 nm2/head. Dotted line corresponds to the de Gennes and Taupin prediction with a peak position corresponding to 2π/D∗. The observed peak position in the case of connected w/o cylinders is shown as a discriminating counter-example using a continuous line. Random connected structures without curvature constraints such as considered by Welberry and Milner [19] would give a peak close to the connected cylinders.

The same evolution of the scattering peak position versus volume fraction does not hold at all for ternary microemulsions, even in the case of low spontaneous curvature (i.e. p0 close to 1). In this case, it has been noticed that the peak position corresponds to twice the value derived from the de Gennes–Taupin expression, i.e. one has to introduce a correction in the topological constant τ′ = 2τ, the topological factor τ is taken close to 12. The reason for this behavior has been examined by Welberry and independently with similar results by Milner [19]: the peak in the structure factor moves in reciprocal space from domain size D∗ to larger values due to an effective repulsion between adjacent domains. Such a shift in the peak position by a factor of 2 typically appears when bending constants exceed 0.5kT. This is a good approximation for moderately stiff ternary microemulsions formulated without co-surfactants, such as the ubiquitous “CiEj”-based samples using linear nonionic surfactants, water and oil, with hydrocarbon chain lengths between 8 and 16. Obtaining in a dilution plot twice the value predicted by Talmon and Prager or equivalently by de Gennes and Taupin (i.e. Eq. (5) with a topological factor taken as12 instead of 6 ) is a secure sign that the microstructure is a random tessellation of slightly repulsive domains, with size imposed by the available area and not by spontaneous curvature. In this case, as for most broad peaks, the fitting to the formula introduced by Strey and co-workers [15,16] gives a domain size derived from peak position with a topological factor close to 12 and a coherence length of three times the domain size.

One of the easily observable consequences of de Gennes and Taupin as well as Talmon–Prager models of microemulsions is that conductivity should always increase when water content is increased at constant surfactant weight fraction. This has been noted not to be verified as soon there is no large amount of co-surfactant present [19–21]. The behavior of the conductivity, especially the strong decrease upon addition of water or brine (an anti-percolation), cannot be reconciled with random bicontinuous microstructures such as discussed by de Gennes and Taupin or in a similar manner by Talmon and Prager.

To our knowledge, only one quantitative model of microemulsions is consistent with the non-monotonic conductivity behavior observed: the disordered connected model of microemulsion (DOC) [12]. This model is valid whenever fluctuations are not dominant, but the two typical sizes to take into account are linked to the spontaneous curvature radius and a domain size D∗ imposed by volume to surface ratio of the dispersion. Full scattering curves associated to connected microstructures can be calculated numerically [20]. The position of the scattering peak can be derived explicitly using analytic expressions corresponding to conservation of volume, of surface and curvature.

Two general types of connected microstructures have been identified experimentally so far: connected cylinders and connected locally lamellar structures. Generalized dilution plots ΣD∗ versus volume fraction have demonstrated the existence of a microstructure as connected cylinders or as connected bilayers (bi-liquid foams) [21,22]. Connected cylinders can be considered as structural precursors of hexagonal or cubic mesophases, once the long range ordering typical for lyotropic liquid crystals is lost. The hexagonal case corresponds to a connectivity Z = 2 and the presence of less end-caps than branching points. When end-caps disappear, the connectivity Z can go up to four, i.e. when the microstructure is close to a molten bicontinuous cubic phase. All these microstructures have been demonstrated to exist, based on dilution plots, considering the variation of the product ΣD∗ versus volume fraction. Examples of connected cylinders have been obtained with double chain surfactant and short chain surfactants penetrating the surfactant film. Analytical implicit equations linking volumes, surfaces and curvature allowing the prediction (not fitting) of peak positions for different topologies can be found in Refs. [11,21,22].

To further demonstrate that dimensionless dilution plots can be used to discriminate between microstructures, Fig. 2 shows a dilution plot obtained for a microstructure as connected cylinders, together with the values of ΣD∗ as obtained from de Gennes–Taupin prediction and other models of microemulsions. Several other clear examples of locally lamellar bi-liquid foams have been documented [22–24]. Oil-free versions of connected lamellar phases are the family of sponge phases (including the “asymmetric” sponge) [25] while giant worm-like micelles are the oil-free equivalent of connected cylinders [21].

Fig. 2

Dilution plot linking volume fraction and scattering peak position scaled by specific surface ΣD∗. The case of a synthetic cationic lipid in non-wetting oil (tetradecane). Data taken from Ref. [21]. The experimentally observed scattering peak position is compared to the value expected for connected cylinders (thick line) as well as to the value expected for random domains without curvature effect and an effective topological factor of 12 (shown as grey line). Peak positions expected from dispersion of w/o or o/w interacting spheres (calculated via MSA approximation) are shown as dotted lines for comparison.

It should be noticed that the determination of exact oil/water area per unit volume is crucial to ascertain the presence of a given microstructure: a series of scattering spectra on their own without measure of the specific area cannot distinguish between spheres, randomly connected structures dominated by fluctuations, or curvature imposed microstructures such as “molten” mesophases. Shape of scattering curves alone is not sufficient if volume fractions and specific area are not followed on absolute scale in a dilution experiment. Note that in binary systems, i.e. in the absence of “internal” fluid, the equivalent two-component microstructures to connected bilayers are the family of asymmetric sponge phases and the equivalent of connected cylinders are the giant cylindrical micelles, considered as living polymers.

Fig. 3 shows another example of a dimensionless dilution plot derived from a series of published measurements when temperature is varied in a microemulsion involving an ionic liquid [26]. In the figure, the prediction by de Gennes and Taupin or the random bicontinuous repulsive domain predictions are compared to the values expected for connected cylinders. None of the existing models of microstructures is compatible with the experimental results. Here, the evaluation of the specific area and the volume fraction may be incriminated, because solubility of the surfactant in the two immiscible fluids in contact is not sufficiently known. However, simple random microstructure without local order can be excluded in this case and some type of connected microstructure is more likely to exist.

Fig. 3

Dilution plot linking volume fraction and scattering peak position scaled by specific surface in the case of a microemulsion containing an ionic liquid. Data taken from Ref. [26]. Data are compared to de Gennes and Taupin prediction (shown as a dotted line) and to the values expected from connected cylinders or connected lamellar microstructures (thick and thin dotted lines, respectively).

To our knowledge, only one model of microemulsion takes into account as well fluctuations and the spontaneous curvature constraints. This general model has been developed by Marcelja and Arleth and uses random wavelets [27]. It is not analytic, but requires iterative simulation using Monte-Carlo algorithm of a series of microstructures. This work has allowed one to produce very useful and explicit – as well as unique to our knowledge – pictures of microemulsions, different from the trivial degenerated case where volume fraction is 0.5. Dilution experiments could be simulated using this model based on random wavelets and spontaneous curvature can be taken into account, as well as unequal volumes of water and oil. Figs. 4 and 5 show real-space examples of connected cylinders and locally lamellar microstructures generated in a semi-flexible case (i.e. with κ = 2kT).

Fig. 4

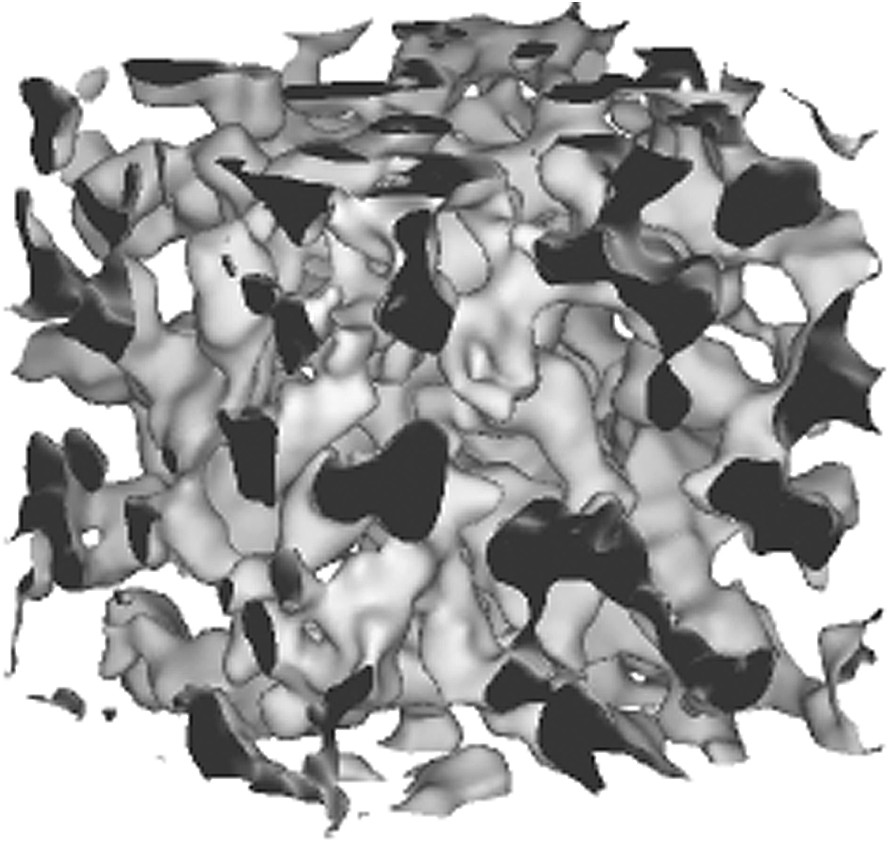
Morphology of a typical non-degenerated microemulsion with a microstructure as connected cylinders, generated using algorithm described in Ref. [27]. This microstructure is expected close to hexagonal phases in the phase diagram. Internal volume fraction is 20%. Spontaneous curvature is chosen towards interior, with a spontaneous packing parameter of 0.9. Bending constant is taken as 2kT versus average curvature and the corresponding – 0.5kT versus Gaussian curvature. The microstructure is thermally equilibrated using the “grf” method as described in Ref. [27] (Lise Arleth, unpublished modelisation).

Fig. 5

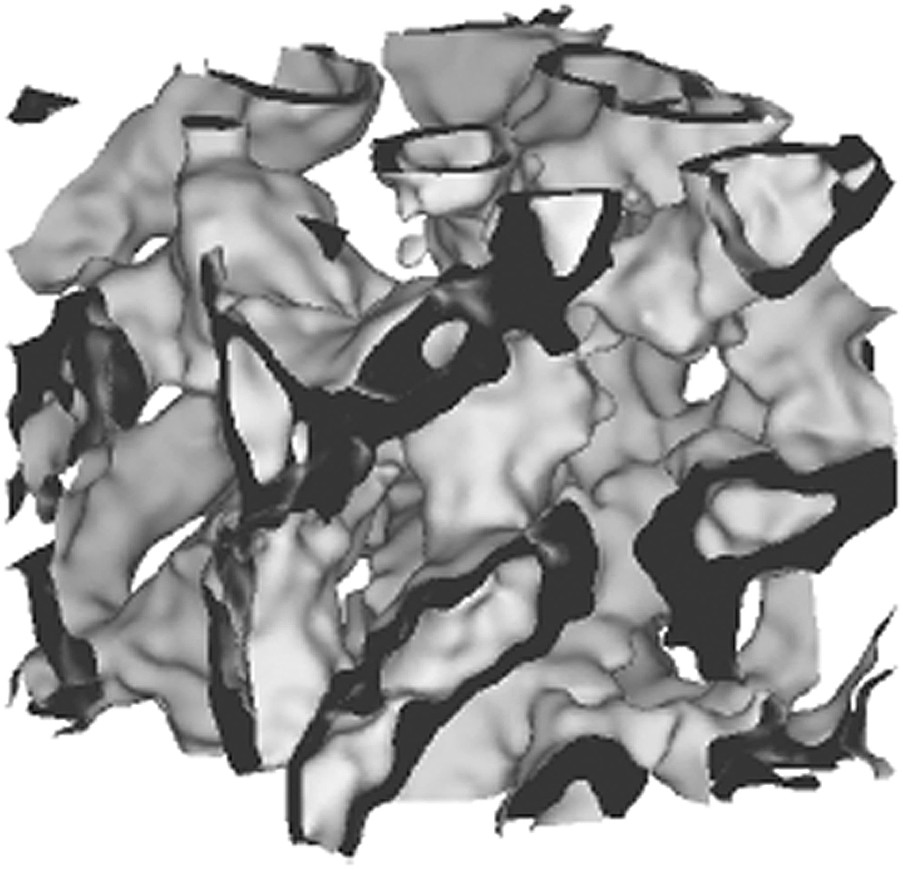
Morphology of a typical connected lamellar microstructure (alias asymmetric oil-swollen sponge phase), generated using algorithm described in Ref. [27]. Parameters are taken as in previous figure, except that spontaneous curvature is taken towards the “external” volume. Internal volume fraction is also 20%. This microstructure is expected for the Winsor IV regime in frustrated regions of the phase diagram [27] (Lise Arleth, unpublished modelisation).

3 Conclusion

In the “diluted” case, i.e. when the volume fraction present lies outside the 0.2–0.8 interval, the pictures of a microemulsion as a dispersion of spherical droplets applies and can be proven either by dilution plots or fitting the scattering expected from a priori known radius of droplets given by surface to volume ratio. However, four types of bicontinuous microemulsions have been shown to exist in concentrated solutions. The only discriminating experiments are dilution plots of systematic measure of the electrical conductivity along the dilution line. The NMR self-diffusion proves the bicontinuity of the microemulsions, but cannot distinguish between the types of microstructure present in a given sample [29]. These can be discriminated by following exact values of conductivities or the dimensionless product ΣD∗ over the largest possible composition range. At the degenerated point with 50% of “internal” and “external” volumes, all expressions degenerate at first order and microstructures cannot be determined unambiguously.

The two oldest recognized types of microstructures are dominated by fluctuations and expected to occur in the presence of short alkyl chains and low co-surfactant content: these are either simple spherical droplets or random domains of size D∗ as proposed by de Gennes and Taupin [1], or in the form of random repulsive domains dominated by fluctuations [18]. In these two cases, conductivity versus water volume fraction is monotonic and the general dilution law as given by Eq. (5) with a topological constant τ of 6 and 12, respectively.

The two other known microstructures are driven by curvature and correspond to the amorphous equivalent of cubic (connected cylinders with connectivity 4), hexagonal (connected cylinders with low connectivity) or lamellar phases (disordered connected lamellar phases). They are all bicontinuous and appear as such on NMR measurement of self-diffusion using spin echo techniques [28]. These microstructures are easier to detect experimentally and to distinguish between themselves by scattering in the case of “stiff” films. Stiff films contain lipids, double chain surfactants, low amount of long chain co-surfactants, charged surfactants at low salinity, co-solutes such as cholesterol, or Gemini-type surfactants. The most studied cases of stiff surfactant describe double chain cationic surfactant (alias synthetic cationic lipids), but the related microstructures have also found also with semi-flexible interfaces, when the packing mode of film is “frustrated”, such as in the case of oil-poor microemulsions at low temperature with nonionic surfactants or water-poor microemulsions at high temperature, i.e. when the radius of curvature points towards the medium with less solubility of the surfactant, which would be described as violation of the so-called “Bancroft” rule in the case of emulsions.

The search for possible microstructures of microemulsions is probably not yet over: one example of dilution plot in a clearly bicontinuous microstructure and incompatible with these four already known types of bicontinuous microemulsions has been described in the case of liquid surfactant containing small amounts of water; in this case, dilution plots do not follow any model prediction, scattering peaks can be fitted to the Teubner–Strey formula, but typical sizes or peak positions do not follow any given dilution law predicted by a model: sterical constraints linked to hydration of head-groups take over the curvature constraints. Up to now, there is to our knowledge no predictive model for the scattering of this type of dispersion, i.e. when the “oil” is mainly made by the chains of the liquid surfactant present [29].

Acknowledgements

Helpful discussions, data availability and gift of figures by L. Arleth, I.S. Barnes, D. Langevin, S. Marcelja, B. Ninham and G.G. Warr are deeply acknowledged.

Bibliographie

[1] P.G. de Gennes; C. Taupin J. Phys. Chem., 86 (1982), p. 2294

[2] Y. Talmon; S. Prager J. Chem. Phys., 69 (1978), p. 2984

[3] Th. Zemb; S.T. Hyde; P.J. Derian; I.S. Barnes; B.W. Ninham J. Phys. Chem., 91 (1987), p. 3814

[4] B.W. Ninham; I.S. Barnes; S.T. Hyde; P.J. Derian; Th. Zemb Europhys. Lett., 4 (1987), p. 561

[5] T.N. Zemb; I.S. Barnes; P.J. Derian; B.W. Ninham Prog. Colloid Polym. Sci., 81 (1990), p. 20

[6] O. Spalla General Theorems (P. Lindner; Th. Zemb, eds.), Neutrons, X-rays and Light: Scattering Methods Applied to Soft Condensed Matter, North-Holland/Elsevier Publ., 2002

[7] J.N. Israelachvilli; D.J. Mitchell; B.W. Ninham J. Chem. Soc., Faraday Trans. 2: Mol. Chem. Phys. (1976)

[8] D.J. Mitchell; B.W. Ninham J. Chem. Soc., Faraday Trans. II, 77 (1981), p. 601

[9] S. Hyde et al. The Language of Shape: The Role of Curvature on Condensed Matter, Elsevier, Amsterdam, 1996

[10] Tanford Charles The Hydrophobic Effect: Formation of Micelles and Biological Membranes, Academic Press, 1980

[11] I.S. Barnes; S.T. Hyde; B.W. Ninham; P.J. Derian; M. Drifford; Th. Zemb; S.T. Hyde; B.W. Ninham; Th. Zemb J. Phys. Chem., 92 (1988), p. 2286

[12] Th. Zemb Colloids Surf. A, 129–130 (1997), p. 435

[13] W. Helfrich Z. Naturforsch. C, 28 (1973), p. 693

[14] M.P. Pileni; T. Zemb; C. Petit Chem. Phys. Lett., 118 (1985), p. 414

[15] M. Teubner; R. Strey J. Chem. Phys., 87 (1987), p. 3195

[16] S.M. Choi; S.H. Chen; T. Sottman; R. Strey; T. Sottman; S.H. Chen; R. Strey J. Chem. Phys., 241–243 (1988), p. 976

[17] D. Guest; L. Auvray; D. Langevin J. Phys. Lett., 46 (1985), p. L-1055

[18] Th. Zemb Scattering by Microemulsions (P. Lindner; Th. Zemb, eds.), Neutrons, X-rays and Light: Scattering Methods Applied to Soft Condensed Matter, North-Holland/Elsevier Publ., 2002

[19] T.R. Welberry; Th. Zemb; S.T. Milner; S.A. Safran; D. Andelman; M.E. Cates; D. Roux; T.R. Welberry; Th. Zemb Prog. Colloid Polym. Sci., 123 (1988), p. 413

[20] I.S. Barnes; T. Zemb J. Appl. Crystallogr., 21 (1988), p. 373

[21] I.S. Barnes; P.J. Derian; S.T. Hyde; B.W. Ninham; T.N. Zemb J. Phys. (Paris), 51 (1990), p. 2605

[22] C. Cabos; P. Delord; J. Marignan Phys. Rev. B: Condens. Matter Mater. Phys., 37 (1988), p. 9796

[23] J. Heil; M. Clausse; J. Peyrelasse; C. Boned Colloid Polym. Sci., 260 (1982), p. 93

[24] D.S. Rushforth; M. Sanchez-Rubio; L.M. Santos-Vidal; K.R. Wormuth; E.W. Kaler; R. Cuevas; J.E. Puigh J. Phys. Chem., 25 (1990), p. 6668

[25] D. Roux; C. Coulon; M.E. Cates J. Phys. Chem., 96 (1992), p. 4174

[26] R. Atkin; G.G. Warr J. Phys. Chem. B, 111 (2007), p. 9309

[27] L. Arleth; S. Marcelja; Th. Zemb J. Phys. Chem., 115 (2001), p. 3923

[28] B. Lindman; U. Olsson Berichte der Bunsenges.-PCCP, 100 (1996), p. 344

[29] I.S. Barnes; M. Corti; V. Degiorgio; Th. Zemb Prog. Colloid Polym. Sci., 93 (1993), p. 205

Commentaires - Politique

Ces articles pourraient vous intéresser

Understanding solubilisation using principles of surfactant self-assembly as geometrical constraints

Fabienne Testard; Thomas Zemb

C. R. Géos (2002)

Microemulsions as model systems

Håkan Wennerström; Ulf Olsson

C. R. Chim (2009)

Effect of the surfactant concentration on the kinetics of oil in water microemulsion polymerization: a case study with butyl acrylate

Klaus Tauer; Alberto G. Ramírez; Raúl G. López

C. R. Chim (2003)