Validation of molecular mass measurements by means of diffusion-ordered NMR spectroscopy: Application to oligosaccharides

Olivier Assemat; Marie-Aude Coutouly; Redouane Hajjar; Marc-André Delsuc

doi:10.1016/j.crci.2009.10.005

Résumé

The validation of molecular mass measurements by using DOSY spectrocopy is presented. A mixture of oligosaccharides has been studied and an extended model has been used. A method has been proposed and applied to correct the imperfections due either to the lock system or the room temperature regulator.

1 Introduction – theory

The DOSY experiment, by separating on two different spectral axes the chemical shift information and the translational diffusion information, is a powerful analytical tool for solution analysis. The possibility of estimating molecular masses by DOSY has recently been investigated in terms of the fractal dimension of the diffusing species [1]. In this work, it is proposed to estimate the molecular mass M of a molecule of interest from its translational diffusion coefficient, by the following relation:

M = {(\frac{C_{r}}{D_{r}})}^{d_{F}}

(1)

where d_F is the fractal dimension of the molecular family, D_r is the diffusivity (ratio of diffusion coefficients of the molecule of interest and of the reference molecule) and C_r a calibration constant. Both C_r and d_F have to be determined experimentally. The reference molecule is usually the solvent residual signal, or some additional small non interacting molecule. In this work, we present an optimisation of the DOSY experiment data processing which allows an accurate mass estimate using Eq. (1), as well as a software implementation of the complete procedure.

2 Mass determination

Equation (1) can be easily used to determine molecular masses from a diffusion experiment. In a DOSY spectrum, each compound is displayed by its 1D spectrum located along the vertical axis at its diffusion coefficient value. The diffusivity D_r of each species is determined by taking the ratio of the diffusion coefficients of the species of interest and of the reference molecule. Inversion of Eq. (1) gives then an estimate of the molecular mass, provided that the reference values C_r and d_F characteristic of the molecule and of the physical conditions, are known. In Augé et al. [1], reference values are given for several molecular famillies (PolyMethylMetacrylate, PolyEthyleneOxyde, PolyStyrene, OligoSaccharides, Globular Proteins, DNA, linear alcanes) in various solvent (HDO, THF, acetone, toluene or CDCl₃). Additionally, this work provides a mean to estimate the uncertainty on the molecular mass from the experimental uncertainties.

A procedure called DOSYtoMW written in python, as been implemented in the NMRnotebook^TM [2] and provides an easy access to this method. This program runs in graphical mode and results are displayed in a dialog box (Fig. 1).

Fig. 1
Using DOSYtoMW, one first draws a line for each species to be analyzed, and a line for the reference molecule (HDO). One then chooses the molecular family and the solvent. Finally, the program provides the mass estimates and the error bars.

The quality of the molecular mass measurement is closely related to the accuracy of the diffusion coefficient values. This means that the NMR experiment must be realized in best conditions. Unfortunately, in spite of the precautions taken by the experimenter, it is common to observe different perturbations due either to the lock system or the room temperature regulator. The instability of such systems leads to poor 2D spectra: generally, chemical shift variations are observed in the indirect dimension F1. The signals shown in Fig. 2 demonstrate the effect of such perturbations. We have developed a method which corrects these imperfections. The proposed method is based on three steps. (1) In the first step, for each 1D row, a peak-picking is done over a small region which contains one signal (ideally, with high signal to noise ratio and coming from a slowly diffusing species). A peak-picking determined from the maximum of a over-zero-filled spectrum was chosen, as it seems to be the best method for small shifts to be estimated accurately. (2) In the second step, the shift from the reference is estimated, the chemical shift of the first row being used as a reference. (3) In the last step, the spectrum is corrected by shifting the whole spectrum. The dataset shift is performed in the time domain by multiplying the reconstructed FID with a complex frequency. This reconstructed FID being obtained with a causality preserving inverse Fourier transform. This procedure has already been described in [3] and used for shearing. The result is shown in Fig. 3 and the signals demonstrate its efficiency.

Fig. 2
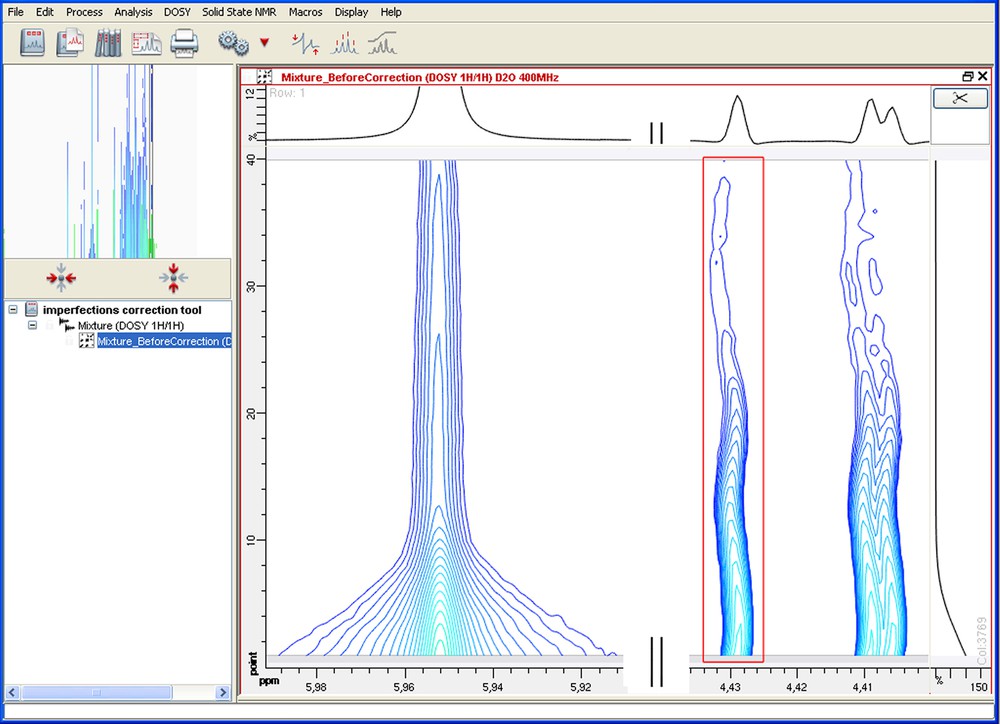
Before correction: imperfections caused by the room temperature regulator. The lock was done on the solvent signal (HDO on the left). Along the indirect dimension, chemical shift variations are observed for the other signals (on the right).

Fig. 3
After correction: now the chemical shift of the solvent varies whereas the chemical shift of the other signals remains stable.

3 Application to oligosaccharides

A mixture of glucose (93 mM), sucrose (26 mM), raffinose (13 mM), and β-cyclodextrin (30 mM) was prepared (all purchased from Sigma) in D₂O (Eurisotop).

DOSY spectra were acquired at room temperature using LED [4] pulse sequence with bipolar field gradients [5] on a Bruker Avance I 400 MHz spectrometer equipped with a 5 mm QNP probehead and a field gradient accessory delivering z-field gradients up to 53.5 G/cm. Sequence delays were Δ = 100 ms (diffusion delay), Δ/2 = 2 ms (gradient duration) and Te = 5 ms (LED) recovery delay. For each data set, 4096 complex points were collected in eight scans, for each 40 experiments in which the gradient strength was linearly incremented from 1.0 to 47.5 G/cm. A 1.5 s recycle delay was used between scans. The spectral axis was processed with an exponential multiplication prior to Fourier transform, which was applied in order to obtain 2048 real points. The procedure described in section 2 was then applied. The diffusion dimension was obtained by performing an inverse Laplace transform using the maximum entropy technique [6]. The DOSY reconstruction was realized with 256 points in the diffusion dimension.

The DOSYtoMW procedure was finally applied in order to estimate the molecular weight of each constituent of the oligosaccharides mixture. An error bar of 5% on measured diffusion coefficients was used.

Those results are summarized in Table 1.

Molecule	Theoretical mass	Experimental determined mass with initial model	Experimental determined mass with extended model
Glucose	180.2	214 ± 48	201 ± 43
Sucrose	342.3	378 ± 82	357 ± 76
Raffinose	504.4	530 ± 117	500 ± 105
β-cyclodextrine	1135	1080 ± 233	1040 ± 219

From this table, it can be seen that the molecular mass estimation method used here allows to determine unambiguously the number of monosaccharide units for oligosaccharides up to seven units, since the error calculated for the ®-cyclodextrin is close to the molecular weight of one sugar unit.

4 Model extension

The molecular weight estimate proposed in [1] for oligosaccharides and used here is based on the work by Viel et al. [7] and was determined on large oligosaccharides with molecular masses ranging from 5.8 to 853 kDa, very different from that presented here. The fact that the molecular masses estimated with this model are correct is a token of the robustness of the model and of the DOSY approach for molecular mass determination.

In return, the newly determined value of diffusion have been used to extend and strengthen the model for low masses. This extended model is now available in the presented software, as well as in the reference web application available at http://abcis.cbs.cnrs.fr/MW/. With this extended model, it can be seen (Table 1) that the mass determination is significantly improved, and the error bars reduced.

5 Conclusion

In conclusion, we have shown that the molecular mass can be estimated by using the DOSY spectroscopy and the extended model. The efficiency of this method and this model is demonstrated through the study of a mixture of oligosaccharides. This new model provides significant improvements in the measurement of molecular mass. We have also shown that our method which corrects the perturbations due either to the lock system or the room temperature regulator, contributes to this improvement. This method is related to the FIDDLE technique proposed by Morris et al. [8] and its improvement [9] which corrects for any kind of global spectrometer perturbations such as phase of shim. The method proposed here, while being much simpler in its implementation, appears to be very efficient on the special case of slight temperature instabilities, which in the case of D₂O lock creates a global shift of the spectrum.