1 Introduction
The study of high temperature liquids is always a technical challenge occurring in many fields of fundamental and industrial research such as geology, metallurgy, glass, energy production… For experimental studies, one has to overcome the problem of the temperature toward the measuring apparatus and the problem of the liquid corrosiveness that may be dramatically increased at high temperature. Therefore, innovative technologies have often to be developed.
Several important thermophysical parameters have been already determined in high temperature liquids, such as density, viscosity, conductivity, surface tension, … Their structure has been more recently investigated thanks to the adaptation of several spectroscopies: NMR [1–3], infrared [4], Raman [5], x-rays [6] and neutron scattering [7,8]. However, these techniques are rarely adapted for the study of the dynamics of high temperature liquids. Among these, one may cite quasi-elastic neutron scattering used for molten bromide [9] and iodide [10], inelastic x-ray scattering used for molten alumina [11] or NMR relaxation time measurements used for the study of molten glasses [12].
However, the understanding of dynamics is a prerequisite to the complete understanding of liquids [13]. Among the dynamical parameters, the self-diffusion coefficient D is fundamental as it represents the ability of atoms or assembly of atoms to move inside their environment. In consequence, D is involved in every model describing dynamical systems.
Initially, D was measured by the capillary method [14]. The principle is to put radioactive salt in a platinum capillary that is immersed in the same molten but non-radioactive salt [15]. The system is left until diffusion occurs, and then is cooled down and solidified. The capillary is cut in several segments and the radioactivity inside each is counted. This method is precise but delicate to handle and requires the use of radioactive species whose period may be short, as for 18F (few hours). Its demanding implementation and the requirement of using radioactive tracers have limited its use and the self-diffusion coefficients are most commonly estimated through electrochemical experiments [16]. In room temperature liquids, diffusion processes have been widely studied thanks to the development of Pulsed Field Gradient NMR (PFG NMR) [17] that allows one to rapidly obtain reliable D in a wide diffusion time range (10−3–101 s). Other advantages of this method are, for example: selectivity toward the isotope, direct access to the D value – no model is required –, in situ experiments…
Few examples have been reported to measure self-diffusion coefficients using PFG NMR at temperature above 400 K. A setup combining high pressure and high temperature (up to 200 MPa and 673 K) has been developed for molten nitrates [18,19], using a titanium alloy combined with a resistance wire. Similarly, the study of molten metals has also stimulated the development of PFG NMR at high temperature up to 640 K [20].
We proposed here a new device to measure self-diffusion coefficients of species in materials with high liquidus temperature (here up to 1500 K). Numerous domains are concerned from fundamental research to industrial applications: molten salts (nuclear molten salt reactor, nuclear waste treatment, fuel cells, solar cells, metallurgy industry…), molten oxides (glass industry, waste storage, magmas…).
In this paper, we present results obtained on molten fluorides. They represent a technical challenge because of their melting temperatures (500 K < Tliquidus < 1800 K) and because of their corrosiveness. Indeed there are very few materials inert toward molten fluorides. One consequence is the scarcity of the data of all kinds on these molten salts. Some spectroscopy techniques have been plied for their structural characterization such as Raman [21–23], NMR [24–26] and Extended x-Rays Absorption Fine Structure (EXAFS) [27,28] along with numerical simulations [29,30]. However, to our knowledge, it is not the case for their dynamics.
2 Experimental section
2.1 Samples preparation
The samples studied here are sensitive to moisture and oxygen. They are therefore prepared in glove boxes under argon.
The salt is put in boron nitride (BN) (AX05, certified without oxide binder) crucible of 6 mm diameter and 14 mm height. The salt is mixed with millimetric BN pieces that have two functions. First, even if the crucible is completely filled with the salt powder, once molten the sample occupies less place than available inside the crucible. Due to the low wetability of the BN toward molten fluorides, the liquid has the shape of a ball (Fig. 1) that turns rapidly over itself. The BN pieces prevent the ball formation. Second, the BN pieces act as a porous network toward the molten salt, for they break any convection flux that could occur. Moreover, the BN is inert toward molten fluorides and has a high thermal conductivity. The mass of the BN (crucible + pieces) is approximately 450 mg and the mass of the salt is 50 mg.

Schematic drawing of the crucible with the millimeter sized piece of boron nitride (BN). The picture shows the ball formed when there is no BN piece.
2.2 NMR
The High Temperature NMR (HT NMR) spectra were recorded using a Bruker Avance II WB 400 MHz spectrometer, operating at 9.40 T. The NMR probe specially built by the Bruker company is based on a 10 mm axial liquid NMR probe equipped with a gradient coil (5.5 gauss/cm/A) coupled with gradient amplifier Great 10A (10 A). We used common NMR pulse sequence with bipolar gradients and stimulated echoes [31].
The sequence is repeated eight times with increased gradient strength. Self-diffusion coefficients are obtained by regression on the signal attenuation curve (Fig. 3).

NMR Signal as function of gradient strength for the experimental point (diamonds) and for the fitted point (stars) with D as parameter. The dotted line represents a schematic evolution of the NMR signal that may occur when convection occurs [35].
NMR relaxation times T1 and T2 strongly vary from one isotope to another. For example, in molten cryolite (Na3AlF6) 23Na and 27Al T1 is about 50 ms whereas in molten LiF–KF 7Li T1 and 19F T1 are about 25 s and 1 s, respectively. Therefore, the NMR pulse sequence has to be adapted depending on the nucleus. In particular, in the case of 7Li, a pre-saturation cycle has been added in order to shorten the experiment time (from 4 hours to 20 min). We have checked on a LiCl 1 M solution at room temperature that the same self-diffusion coefficient value is obtained with or without the pre-saturation cycle.
2.3 Heating method
The in situ HT PFG NMR setup presented here and displayed in Fig. 2 is based on the CO2 laser heating system developed for NMR structural studies at CEMHTI-CNRS in Orléans (France) [32,33]. The crucible is heated here by a symmetrical irradiation using two CO2 lasers (Coherent, 250 W) as presented on Fig. 2.
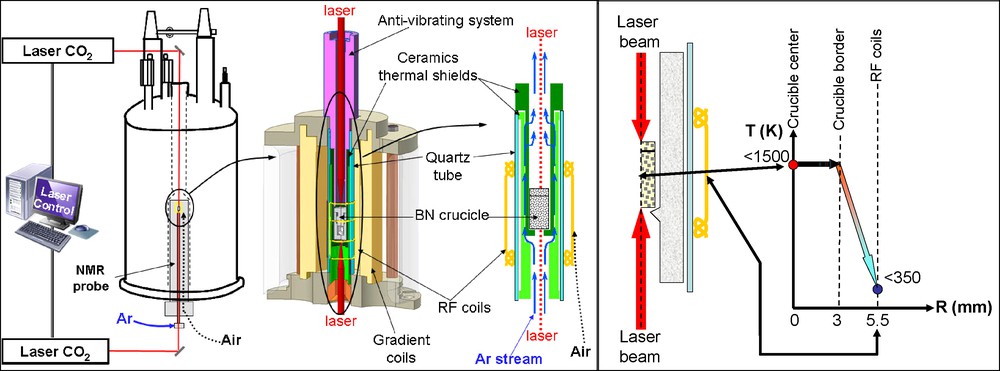
Experimental setup with the heating device and the ceramics assembly on the left. On the right, temperature at different position R: from 1500 K at the crucible to 350 K at the RF coils.
Thanks to the BN high thermal conductivity, the crucible acts as a small furnace. The power of the lasers (thus the temperature) is increased slowly up to the liquidus in order to insure a stabilized and homogeneous temperature in the sample. The heating rate is estimated at 100 °C/min, which is slow, compared with the usual one for a laser heating system. Typically, the temperature increase takes 15 min and the sample is at equilibrium when the diffusion measurement begins.
Up to 900 °C approximately, the variation of the sample temperature is linear versus the laser power and thanks to several compounds whose melting temperature is well-defined temperature calibration can be made. Hence the temperature accuracy is better than 10 °C. Above 900 °C, the sample temperature varies in a parabolic way versus the laser power due to the radiation of the crucible and more cautions have to be taken as for example to decrease the heating rate. In this second domain, we have evaluated the temperature accuracy to 10 °C.
2.4 Thermal shielding of the coils
The difficulty of performing PFG NMR at high temperature lies on the small space available (Fig. 2). Indeed there are only 2.5 mm between the border of the heated crucible and radiofrequency coils. In our setup presented on Fig. 2, the thermal shielding of the radiofrequency and gradient coils is insured by several ceramic barriers. Heat can be transferred to the coils by two ways: contact and above 800 °C radiation. Preliminary tests have shown that the ceramic directly in contact with the crucible can reach a temperature higher than 800 °C at the hottest point and heat radiation occurs. In consequence, at least two ceramic shields are required. The crucible is inserted in a mullite cradle whose function is to stop most of the heat transferred by contact; it is surrounded by an alumina tube that stops the radiation coming from the mullite cradle. A quartz tube is placed between the alumina tube and the coil as an additional protection in quartz. An argon stream at room temperature between the mullite cradle and the alumina tube cools down the ceramics and prevents the BN crucible from oxidizing. The radiofrequency and gradient coils are also cooled down by an additional nitrogen stream.
3 Results
3.1 Does convection occur?
The first point is to check that no convection occurs during the measurement. There are several indicators of this kind of motion [34]. The first one is the shape of the signal attenuation curve with the gradient strength. An increase of magnetization at high gradient strength (Fig. 3) may be the signature of a collective motion in a cycle [35,36]. Our experimental attenuation curve does not present any increase at high gradient strength.
A second manner to detect convection is to measure the self-diffusion coefficient versus diffusion time Δ. In non-confined liquids, the value must be the same whatever Δ. On the contrary, if convection occurs, D may decrease with Δ. Therefore, we have measured the self-diffusion coefficient of fluorine in LiF–NaF (eutectic composition) for several Δ. The results, reported in Table 1, show that the values are not dependent upon Δ. Moreover, these values give an indication on the accuracy of our measurement: it is about 10%. Moreover, an estimation of the precision of this experimental setup can be given with the measurement of DF in pure LiF that has been done 10 times with different samples. The averaged value is 7.3 × 10−9 m2/s and the standard deviation is 0.3 × 10−9.
Values of fluorine self-diffusion coefficient in LiF–NaF (eutectic composition) measured for several diffusion time Δ.
| Diffusion time Δ (ms) | D (m2/s) |
| 25 | 4.4 × 10−9 |
| 50 | 4.7 × 10−9 |
| 75 | 4.6 × 10−9 |
| 100 | 4.7 × 10−9 |
| 150 | 4.8 × 10−9 |
3.2 Cryolite and NaF
The first system presented here is cryolite, Na3AlF6. Its use in the aluminium industry has stimulated numerous studies [37] in electrochemistry, thermophysics, and spectroscopy. Hence data are available to compare with ours. Electrochemistry allows one to obtain self-diffusion coefficients by two ways. The first one is the use of the limiting current (by diffusion) of electroactive species. The second one is to measure the conductivity and to derive D using the Nernst–Einstein relation. The values are obtained using a driving force (non equilibrium state) for one and for another; they are not precise, especially in the case of conductivity [38]. These techniques have often been used because many laboratories possess the electrochemical experimental setup and they rapidly provide an estimation of D in comparison with the reference method i.e., capillary method. The last method allows one to measure directly and precisely self-diffusion coefficients (accuracy about 5%). Our NMR method is well complementary to the capillary method as 19F is a good NMR nucleus with a suitable relaxation time for easy diffusion measurements. The values obtained by several methods for molten cryolite and NaF are reported in Table 2. Our values are in very good agreement with those obtained by the capillary method. It testifies that our experimental setup makes it possible to measure reliable self-diffusion coefficients relatively easily and rapidly (about 30 min for fluorine, 20 min for aluminium and sodium and 50 min for lithium including temperature increase).
Values of self-diffusion coefficients obtained by several methods in cryolite and NaF.
| System | Ion | Method | Reference | Temperature (K) | D (m2/s) |
| Na3AlF6 | 19F | HT PFG NMR | – | 1293 | 5.3 × 10−9 |
| Na3AlF6 | 27Al | HT PFG NMR | – | 1293 | 4.1 × 10−9 |
| Na3AlF6 | 23Na | HT PFG NMR | – | 1293 | 10.8 × 10−9 |
| Na3AlF6 | 22Na | Capillary | Lantelme and Chemla 1968 [39] | 1325 | 9.28 × 10−9 |
| Na3AlF6 | 18F | Capillary | Lantelme and Chemla 1968 [39] | 1325 | 5.81 × 10−9 |
| NaF | 19F | HT PFG NMR | – | 1275 | 9.4 × 10−9 |
| NaF | 23Na | HT PFG NMR | – | 1275 | 9.4 × 10−9 |
| NaF | 18F | Capillary | Harari et al. 1970 [40] | 1322 | 9.67 × 10−9 |
| NaF | 22Na | Capillary | Harari et al. 1970 [40] | 1322 | 9.80 × 10−9 |
| NaF | 22Na | Capillary | Grojtheim and Zuca 1968 [41] | 1295 | 10.3 × 10−9 |
| NaF | Na | Theory | Koishi and Tamaki 2005 [42] | 1300 | 9.14 × 10−9 |
| NaF | F | Theory | Koishi and Tamaki 2005 [42] | 1300 | 9.44 × 10−9 |
It is particularly interesting to compare cryolite and NaF because their liquidus temperature is approximately the same: 1283 K for cryolite and 1279 K for NaF. In pure NaF, we found DNa = DF = 9.4 × 10−9 m2/s. By considering their ionic radius [43], rNa+ = 1.1 Å and rF− = 1.2 Å, it shows that Na+ and F− moves freely as simple charged spheres in molten NaF. On the contrary in cryolite the self-diffusion coefficients of Na+, Al3+ and F− are rather different. DNa is nearly the same as in pure NaF showing that Na+ also moves freely in molten cryolite. In contrast, DAl and DF are about half of DNa. Aluminium cations are known to form complexes with fluorine anions ALFxx − 3 (AlF63, AlF52− and AlF4−). In molten cryolite it has been shown by Raman and NMR spectroscopy that AlF52− was the main species present in the melt [44]. In consequence, the diffusive species are not isolated Al3+ and F− but mainly AlF52−. According to the Stokes-Einstein law D is proportional to the inverse of the radius R of the diffusing entity; it explains the lower values DAl and DF compared with DNa in molten cryolite and DF in molten NaF.
3.3 LiF–NaF
The self-diffusion coefficients of fluorine, lithium, and sodium have been measured in alkali fluoride mixtures: LiF–KF and LiF–NaF over the whole range of compositions. The DF values have been plotted as function of temperature in Fig. 4a. The striking point is that all the values are located in a narrow domain and they are approximately superimposed whatever the alkali fluorides. The ratio Li/Na or Li/K in the salt mixture weakly influences DF compared with the temperature. In a previous paper [45], we have shown that it was the signature of the liquid structure. Indeed, molten alkali fluoride salts can be described in a first approximation as simple baths of polarizable hard charged spheres.

(a) Fluorine self-diffusion coefficient as a function of temperature in LiF–NaF (black square), in LiF–KF (diamond) and in the eutectic composition of LiF–NaF–KF (circle). (b) Self-coefficient of fluorine (black square), sodium (triangle) and lithium (circle) as function of temperature in molten LiF–NaF.
We have also measured the self-diffusion coefficients of lithium and sodium in LiF–NaF at the liquidus temperature (Fig. 4b). The evolutions of DF, DNa and DLi versus temperature are very close. The similarity of these three evolutions can be compared with those in LiF–BeF2 molten salt [46]. DF, DLi, and DBe follow different evolutions from each other because the addition of BeF2 leads to a network-like liquid with Be–F connections [47]. In molten LiF–NaF, the cations diffuse slightly more rapidly than fluorine anions except in pure NaF. Surprisingly, lithium seems to diffuse as rapidly as sodium despite its smaller size. Recent numerical simulations [48] conclude at the existence of Li+ ions clusters in molten LiF–KF, LiF–NaF and LiCl−KCl meaning that the local concentration in Li+ ions fluctuates in the liquid. Are these local distribution heterogeneities the reason why DF < DNa = DLi in LiF–NaF?
An interesting point with Figs. 4 and 5 is that they supply an approximate of DF, DLi, and DNa for any LiF–NaF–KF system for a given temperature.
4 Conclusion
We have developed a new device to measure self-diffusion coefficients at high temperature (up to 1500 K) in corrosive liquids. It is based on classical PFG NMR but with a coupled laser heating system. The results (attenuation echo curve, non-dependence of D versus diffusion time Δ and agreement of values with the capillary method) show that reliable self-diffusion coefficients can be obtained quite easily and rapidly without convection perturbation. We have measured the self-diffusion coefficients in alkali fluorides mixtures. It has been shown that the nature and proportion of the alkali Li, Na or K influence weakly DF, DLi, and DNa compared with temperature. This setup provides the opportunity to study the dynamics in a wide range of high temperature liquids: molten fluorides, chlorides or carbonates and it can be also extended to molten oxides…
Acknowledgements
The authors are indebted to F. Engelke, E. Naumann and K. Zick from Bruker Company for the NMR probe. They are greatful to E. Labrude and P. Melin for their technical support and NMR group members of CEMHTI for valuable discussions especially F. Fayon. This work has been supported by GdR PARIS and by PCR ANSF of programme PACEN.


