1 Introduction
Tautomerism, a particular case of isomerism, plays an important role in modern organic chemistry, biochemistry, medicinal chemistry, pharmacology, molecular biology and life itself [1–9]. Fundamentally, tautomers are isomers possessing distinct structures that arise from migration of a hydrogen atom [10]. The determination of the tautomeric preferences of heterocyclic compounds is a challenging task with direct implications for the interpretation and prediction of chemical reactivity and identification of molecular recognition patterns [11]. Particularly interesting are hetero-π conjugated systems in which the transfer of a proton is accompanied by the formation of strong intramolecular hydrogen bonds [1]. In general, π-electron delocalization plays a driving role in the stabilization of tautomeric systems and so affects tautomeric preferences. However, other internal effects (such as aromaticity, the kind and the location of substituting groups [12–14], concentration of substrates [15] and the surrounding medium [4,16–18]) may change this general behavior.
Reactions of primary amines and aliphatic diamines with dehydroacetic acid (DHA) lead to various heterocyclic compounds of biological interest. Indeed, derivatives of these heterocyclic compounds containing pyronic-like rings could enter in several pharmacological drugs [19,20]. The migration of labile hydrogen atoms in these compounds generates several tautomeric forms and most of their biological activities are expected to depend on these tautomeric equilibria.
In the present article, we investigate the tautomeric equilibria of five series of substituted pyronic derivatives depicted on Scheme 1, the substituting groups being: H, CH2CH2NH2, C6H5, NH2 and OH respectively for series 1, 2, 3, 4 and 5.
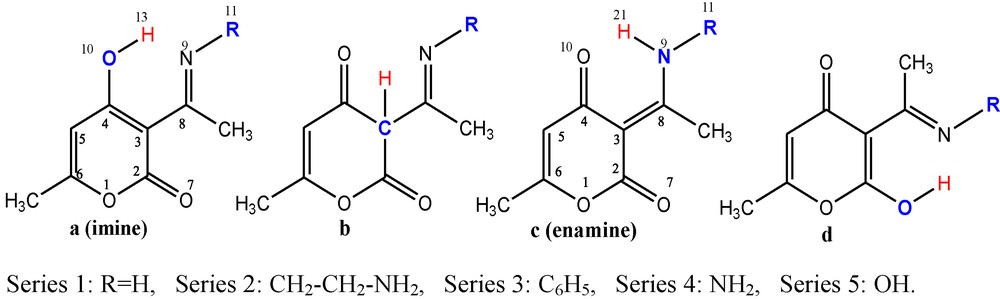
Tautomers under consideration.
Some of the considered heterocycles enter as precursors for the synthesis of compounds which exhibit important pharmacological properties [19,20] such as diazepines which are used as an antidepressive drug for the central nervous system, but also as an anticonvulsive and anti-inflammatory. As it will be seen later in the text, these compounds come predominantly in two tautomeric forms: the imine (a) and the enamine (c) ones of Scheme 1. The imine–enamine tautomerism has been the subject of continuous interest in chemistry and the effects of substituting functional groups on this equilibrium [21] have been the focus of several computational investigations.
Experimental studies carried out on series 4 (RNH2) and 5 (ROH) indicate the predominance of such an imine form [22] whereas in the case of series 1 (RH) [23] and 3 (RC6H5) [23,24], the predominating tautomer is the enamine form. Thus, a question which deserves investigation, is why some substituting groups favour the enamine and why others the imine's form?
Moreover, it is worth noting that the synthesis of compounds exhibiting a pharmacological activity needs an imine's form of the pyronic precursor.
For our part, we carried out first IR and NMR spectroscopy measurements on series 2 (RCH2CH2NH2) which has not yet been studied experimentally, to get an insight into the corresponding tautomeric equilibria. Then, we studied theoretically using standard Density Functional Theory (DFT) calculations the influence of substituting groups and solvents on the relative stability of the different tautomeric forms for the five series of heterocyclic compounds of Scheme 1. Our aim is to investigate how to drive, via the choice of substituting groups and/or solvents, the equilibria in order to get the desired tautomeric form.
2 Results and discussion
The labels of the species under consideration are given in Table 1.
Numbering and names of the tautomers.
| Numbering | Name |
| 1a | 3-ethanimidoyl-4-hydroxy-6-methyl-2H-pyran-2-one |
| 1b | 3-ethanimidoyl-6-methyl-2H-pyran-2,4(3H)-dione |
| 1c | 3-(1-aminoethylidene)-6-methyl-2H-pyran-2,4(3H)-dione |
| 1d | 3-ethanimidoyl-2-hydroxy-6-methyl-4H-pyran-4-one |
| 2a | 3-[N-(2-aminoethyl)ethanimidoyl]-4-hydroxy-6-methyl-2H-pyran-2-one |
| 2b | 3-[N-(2-aminoethyl)ethanimidoyl]-6-methyl-2H-pyran-2,4(3H)-dione |
| 2c | 3-{1-[(2-aminoethyl)amino]ethylidene}-6-methyl-2H-pyran-2,4(3H)-dione |
| 2d | 3-[N-(2-aminoethyl)ethanimidoyl]-2-hydroxy-6-methyl-4H-pyran-4-one |
| 3a | 4-hydroxy-6-methyl-3-[N-phenylethanimidoyl]-2H-pyran-2-one |
| 3b | 6-methyl-3-[N-phenylethanimidoyl]-2H-pyran-2,4(3H)-dione |
| 3c | 3-(1-anilinoethylidene)-6-methyl-2H-pyran-2,4(3H)-dione |
| 3d | 2-hydroxy-6-methyl-3-[N-phenylethanimidoyl]-4H-pyran-4-one |
| 4a | 3-[ethanehydrazonoyl]-4-hydroxy-6-methyl-2H-pyran-2-one |
| 4b | 3-[ethanehydrazonoyl]-6-methyl-2H-pyran-2,4(3H)-dione |
| 4c | 3-[amino(hydrazino)methylene]-6-methyl-2H-pyran-2,4(3H)-dione |
| 4d | 3-[ethanehydrazonoyl]-2-hydroxy-6-methyl-4H-pyran-4-one |
| 5a | 4-hydroxy-3-[N-hydroxyethanimidoyl]-6-methyl-2H-pyran-2-one |
| 5b | 3-[N-hydroxyethanimidoyl]-6-methyl-2H-pyran-2,4(3H)-dione |
| 5c | 3-[1-(hydroxyamino)ethylidene]-6-methyl-2H-pyran-2,4(3H)-dione |
| 5d | 2-hydroxy-3-[N-hydroxyethanimidoyl]-6-methyl-4H-pyran-4-one |
2.1 Experimental results
The 1H and 13C NMR spectra were recorded on a Brucker AVANCE DPX 250 spectrometer at 250 and 26.9 MHz using CDCl3 as solvent and TMS as internal standard. The NMR data for series 2 (RCH2CH2NH2) show unambiguously the occurrence of both the enamine (c) and imine (a) form in CDCl3 [20]. In Table 2 are represented the forms (a) and (c) of the series 2.
Enamine (c) and imine (a) forms of the series 2.
3-{1-[(2-aminoethyl)amino]ethylidene}-6-methyl-2H-pyran-2,4(3H)-dione (2c). 1H NMR (250 MHz, CDCl3), 5,73 (s, 2H, CH2), 12.20 (s, 1H, NH), 2.15 (s, 3H, CH3), 3.15 (m, 2H, CH2), 3.66 (m, 2H, CH2), 2.50 (s, 2H, NH2), 2.65 (s, 3H, CH3); 13C NMR (62.9 MHz, CDCl3), 162 (C2), 96 (C3), 192 (C4), 107 (C5), 164 (C6), 176 (C8), 17.7 (C11), 45 (C12), 44 (C13), 19.6 (C15).
3-[N-(2-aminoethyl)ethanimidoyl]-4-hydroxy-6-methyl-2H-pyran-2-one (2a). 1H NMR (250 MHz, CDCl3), 5.60 (s, 2H, CH2), 13.3 (1H, OH), 2.00 (s, 3H, CH3), 2.41 (s, 3H, CH3); 13C NMR (62.9 MHz, CDCl3), 162 (C2), 96 (C3), 192 (C4), 107 (C5), 164 (C6), 176 (C8), 17.7 (C11), 45 (C12), 44 (C13), 19.6 (C15).
Indeed, the 1H NMR spectra display two broadened signals at 13.3 and 12.2 ppm due to the OH proton of imine and NH proton of enamine respectively. The signals of remaining protons and carbons of both the two series occur at very similar positions. Moreover, the experimental data show that the tautomeric equilibrium is shifted toward the enamine form in this series, the molar fractions being 63% for the enamine form and 37% for the imine one in CDCl3, as computed via the peak intensities of the NMR spectrum.
On the contrary, NMR spectroscopy in the same solvent indicates that only the imine form is observed for series 5 (ROH) [22] whereas in the case of series 1 (RH) [23] and series 3 (RC6H5) [23,24] the occurrence of a single tautomeric form, namely the enamine one is observed.
2.2 Computational details
The calculations were performed using the Gaussian 03 [25] program. Geometries of the tautomers were fully optimized at the B3LYP [26,27] level of theory using standard 6-311+G** and 6-311++G** basis sets. All the energy minima were checked by a vibrational frequency analysis at the same level of theory. A Natural Bond Orbital (NBO) [28] analysis was then carried out [29]. To estimate the influence of a polar medium on tautomeric equilibria, we applied the Polarizable Continuum Model (PCM) of Tomasi et al. [30,31]. PCM belongs to the category of solvation methods based on a continuum description of the solvent [31]. The physical system is represented by a charge distribution which describes the target molecule (or group of molecules) one has identified as solute. This charge occupies a given volume of space, called the molecular cavity defined through interlocking van der Waals spheres centred at atomic positions. The van der Waals surface is constructed from spheres located on heavy (that is, non-hydrogen) elements only (United Atom Approach). The molecular cavity is surrounded by an infinite dielectric continuum (the solvent) characterised by specific macroscopic properties (density, dielectric constant, refractive index, etc.). Two solvents of different dielectric constants CHCl3 (ɛ = 4.9), DMSO (ɛ = 46.7) which are currently used experimentally, were considered in the present work. Geometry optimisations of the tautomers in solution followed by a vibrational frequency analysis have been carried out at the same level of theory.
2.3 Theoretical results
Each series of heterocyclic compounds studied in this work could exist under four tautomeric forms, as shown on Scheme 1. To name a given tautomeric form, we have used the following labels: 1, 2, 3, 4 and 5 stand for a given series of heterocycles; a, b, c and d, stand for a given tautomeric form according to the position of the labile hydrogen atom, in the heterocyclic system. We remind that the substituents are H, CH2CH2NH2, C6H5, NH2 and OH respectively for series 1, 2, 3, 4 and 5. The calculated B3LYP/6-311+G** energies (sum of electronic and thermal free energies including the zero point vibration energy) of the different tautomers in gas phase and in solution (CHCl3, DMSO) are given respectively in Tables 3 and 4.
B3LYP/6-311+G** calculated energies (a.u.) of the different tautomers in gas phase.
| Tautomeric forms | Gas phase | ||||
| Series 1 | Series 2 | Series 3 | Series 4 | Series 5 | |
| Form (a) | −590.5849 | −724.4495 | −821.5337 | −645.8961 | −665.9166 |
| Form (b) | −590.5645 | −724.4338 | −821.5170 | −645.8781 | −665.7522 |
| Form (c) | −590.5991 | −724.4591 | −821.5404 | −645.8919 | −666.7716 |
| Form (d) | −590.5733 | −724.4354 | −821.5226 | −645.8798 | −665.7558 |
B3LYP/6-311+G** calculated energies (a.u.) of the imine and enamine tautomers in solution.
| Series | Tautomeric forms | Solvent | |
| CHCl3 (ɛ = 4.9) | DMSO (ɛ = 46.7) | ||
| Series 1 | 1a | −590.5967 | −590.6020 |
| 1c | −590.6166 | −590.6235 | |
| Series 2 | 2a | −724.4641 | −724.4712 |
| 2c | −724.4837 | −724.4908 | |
| Series 3 | 3a | −821.5471 | −821.5531 |
| 3c | −821.5616 | −821.568 | |
| Series 4 | 4a | −645.9106 | −645.9171 |
| 4c | −645.9103 | −645.9212 | |
| Series 5 | 5a | −665.7986 | −665.8056 |
| 5c | −665.7973 | −665.8074 |
B3LYP/6-311++G** computations that we carried out led us to almost the same results.
The results indicate that imine (a) and enamine (c) forms are the two predominating tautomers for the five series of compounds, in the gas phase as well as in solution. From Tables 3 and 4 (ɛ is the dielectric constant of the solvent) the most stable tautomer for series 1, 2 and 3 is the enamine form. For series 4 and 5, the imine form is preferred in gas phase and in CHCl3. On the contrary, in DMSO the enamine (c) form is more stabilized for series 5. Our results confirm experimental data [20,22–24].
In order to check the reliability of our calculations we also carried out another DFT computation but using the MPW1PW91 functional [32] and the 6-311++G** basis set. We used this latter functional which is a modified Perdew-Wang one because it is well suited for non bonded interactions and transition state studies and leads to results which are as reliable as B3LYP's regarding ground state properties [32]. The energy MPW1PW91 computations in solution (CHCl3) for series 2, indicate that the enamine form (−724.2925 a.u.) is more stable than the imine one (−724.2737 a.u.) the energy difference being equal to 0.0188 u.a. confirming the B3LYP result (0.0196 u.a.).
It is worth noting that for both form (a) and form (c), an intramolecular hydrogen bond exists between respectively N9 and H13 and between O10 and H21 (Scheme 1), which is partly responsible for the higher stability of these forms. It is also the case for form (d). According to the obtained results, it can be seen that for all series, form (b) which is not a fully conjugated system, is the less stable tautomer. Very recently, Dobosz and Zakrzewska [1] who studied substituted 2-acylmethylpyridine systems involving an imine–enamine equilibrium, have observed the predominance of enamine form above imine one in vacuum. They tentatively explained the stabilization of tautomers containing an intramolecular hydrogen bonds saying that the quasi-rings created with the share of these intramolecular H-bonds improve the aromaticity of such systems. After all, several kcal/mol energy stabilization should be gained by such H-bonds.
We found interesting to compare our theoretical optimized geometries to available experimental data. Table 5 lists the calculated B3LYP/6-311+G** and X-Ray [23,24] bond distances (Å) for the enamine form of series 3.
Calculated B3LYP/6-311+G** and experimental bond distances (Å) for enamine form of the series 3.
| Bond | Gas phase | CHCl3 | DMSO | Experimental distances | |
| [23] | [24] | ||||
| O1C2 | 1.407 | 1.403 | 1.401 | 1.398 | 1.396 |
| C2C3 | 1.461 | 1.447 | 1.444 | 1.449 | 1.437 |
| C3C4 | 1.474 | 1.458 | 1.457 | 1.421 | 1. 438 |
| C4C5 | 1.452 | 1.447 | 1.447 | 1.436 | 1.439 |
| C5C6 | 1.343 | 1.344 | 1.344 | 1.326 | 1.326 |
| O1C6 | 1.355 | 1.358 | 1.360 | 1.361 | 1.361 |
| C6C11 | 1.492 | 1.490 | 1.490 | 1.484 | – |
| C8C3 | 1.390 | 1.429 | 1.421 | 1.423 | 1.422 |
| N9C8 | 1.370 | 1.331 | 1.328 | 1.323 | 1.318 |
| O10C4 | 1.230 | 1.257 | 1.259 | 1.269 | 1.257 |
| C12C8 | 1.503 | 1.500 | 1.499 | 1.490 | – |
| C21N9 | 1.422 | 1.427 | 1.429 | 1.423 | – |
| C22C21 | 1.398 | 1.397 | 1.397 | 1.385 | – |
| C23C22 | 1.392 | 1.393 | 1.394 | 1.386 | – |
| C24C23 | 1.394 | 1.395 | 1.395 | 1.366 | – |
| C25C24 | 1.393 | 1.394 | 1.395 | 1.364 | – |
| C26C25 | 1.392 | 1.393 | 1.393 | 1.390 | – |
| C21C26 | 1.398 | 1.397 | 1.397 | 1.379 | – |
| O7C2 | 1.208 | 1.214 | 1.217 | 1.205 | 1.208 |
| N9H20 | 1.04 | 1.03 | 1.02 | 0.95 | 0.91 |
| H20O10 | 1.62 | 1.65 | 1.65 | 1.81 | 1.71 |
| N9O10 | 2.54 | 2.56 | 2.56 | 2.52 | 2.52 |
It is worth noting that the solvent has a non negligible effect on several bond lengths, i.e., C8–C3 and O10–C4 which increase from the gas phase values by ca. 0.03–0.04 Å and N9–N8 which diminishes by 0.04 Å. The calculated bond distances are in good agreement with those obtained experimentally, except a distance like N9–H20 since hydrogen atoms cannot be precisely X-Ray located. It is interesting to note that the computed bond lengths in solution are closer to crystallographic data than those obtained in gas phase. Indeed, the mean deviations are respectively equal to 0.020 Å in the gas phase, 0.014 Å in CHCl3 and 0.013 Å in DMSO. This result is not too surprising because environmental effects are also at work in the crystal. The agreement between computed angles and X-Ray data is excellent (Supplementary Information). The crystallography data [23] for form (3c) shows a short intramolecular contact 2.52 Å long between N9 and O10. Gilli et al. [24] have shown that series 3 and similar compounds adopt the enamine tautomeric form. In this form the intramolecular hydrogen dN--O bond length is between 2.52 Å and 2.56 Å, leading to a remarkable delocalization of the O=CC=CNH π-conjugated system.
In Table 6 are given the energy differences between the two most stable tautomers (a) and (c), in gas phase and in solution.
Calculated energy differences (kcal/mol) between the imine and enamine tautomers.
| Series | Gas phase | CHCl3 | DMSO |
| Series 1 | 8.9 | 12.5 | 13.4 |
| Series 2 | 6.0 | 12.3 | 12.3 |
| Series 3 | 4.2 | 9.1 | 9.3 |
| Series 4 | −2.6 | −0.2 | 2.6 |
| Series 5 | −4.7 | −0.8 | 1.1 |
The enamine form (c) is more stable than the imine one (a) by 8.9 kcal/mol, 6.0 kcal/mol and 4.2 kcal/mol respectively for series 1, 2 and 3, in the gas phase. According to these results, the largest difference is observed for series 1. For series 4 and 5, the imine form is preferred over the enamine form, the energy difference being respectively equal to 2.6 kcal/mol and 4.7 kcal/mol. Moreover, our results show that the enamine form is more stabilized than the imine one, in polar solvent for all species. The largest stabilization in a polar solvent of the enamine form is observed for series 1. The energy differences between imine and enamine tautomers increase going from gas phase to solution, and with the increase of solvent polarity, for series 1, 2 and 3. Obviously, in the case of series 4 and 5, the opposite tendency is observed. These equilibrium shifts can be understood considering the electrical properties of these species.
The polarizabilities for imine and enamine tautomers in gas phase and solution for all the studied series are given in Table 7.
B3LYP/6-311+G** calculated polarizability (Å3) of the imine and enamine tautomers in gas phase and solution.
| Series | Polarizability (Å3) | |||
| Tautomeric forms | Gas phase | CHCl3 | DMSO | |
| Series 1 | 1a | 116.8 | 144.0 | 157.1 |
| 1c | 117.4 | 144.9 | 158.0 | |
| Series 2 | 2a | 155.2 | 188.2 | 204.4 |
| 2c | 157.7 | 190.9 | 207.2 | |
| Series 3 | 3a | 197.7 | 244.6 | 267.2 |
| 3c | 198.2 | 245.0 | 267.2 | |
| Series 4 | 4a | 128.1 | 157.7 | 172.1 |
| 4c | 134.3 | 166.9 | 182.5 | |
| Series 5 | 5a | 124.3 | 153.5 | 167.6 |
| 5c | 124.7 | 154.2 | 168.2 |
As listed in Table 7, the polarizability of the two tautomers increases considerably going from gas phase to solution and with the solvent polarity. Moreover, the polarizability of the enamine form is higher than imine one. The largest difference of polarizability is observed in the case of series 4. The difference is 6.2 Å3, 9.2 Å3 and 10.4 Å3 in gas phase, CHCl3 and DMSO respectively. Considering the dipole moments (Supplementary Information), it can be seen the greater increase of this property for the enamine form relatively to the imine one, with the polarity of the solvent. For instance, in the case of series 5, the dipole moments (in Debye) of tautomer (5a) are equal to 3.4, 3.5 and 4.2 respectively in gas phase, and CHCl3 then DMSO solvated, whereas they are equal to 2.2, 3.6 and 4.9 for tautomer (5c). Thus, the dipole moment of form (5c) becomes greater than form (5a) one, in a polar solvent. The obtained results for all series confirm that enamine form should be more stabilized than imine one in polar solvents.
2.4 NBO analysis
To understand the electronic effects induced by the substituting groups on the stability of the imine and enamine forms, a NBO analysis using the B3LYP/6-311+G** results in gas phase has been carried out. In this analysis, a stabilization energy E(2) [33] related to the delocalization trend of electrons from donor to acceptor orbitals, is calculated via perturbation theory. If the stabilization energy E(2) between a donor bonding orbital and an acceptor orbital is large, there is a strong interaction between them. Table 8 lists the calculated second order interactions energies E(2) between donor–acceptor orbitals within the imine and enamine forms, for the five series of heterocycles. In this table, LP represents a lone pair orbital, σ* or π* (empty, antibonding) acceptor bond orbitals.
Stabilization energies associated with electron delocalization for imine and enamine tautomers, in gas phase.
| Tautomeric forms | Delocalization | Energies: E (2) (Kcal/mol) | ||||
| Series 1 | Series 2 | Series 3 | Series 4 | Series 5 | ||
| 32.5 | 36.3 | 32.2 | 31.3 | 30.2 | ||
| 29.1 | 32.4 | 29.2 | 28.2 | 28.4 | ||
| 23.4 | 22.3 | 23.5 | 23.5 | 23.9 | ||
| 32.2 | 31.7 | 31.7 | 32.4 | 32.3 | ||
| Enamine form | 33.1 | 33.3 | 33.3 | 33.1 | 33.1 | |
| 36.7 | 37.1 | 36.8 | 36.8 | 36.8 | ||
| 54.9 | 71.8 | 58.8 | 47.5 | 36.5 | ||
| 8.9 | 10.8 | 10.3 | 10.8 | 11.5 | ||
| 32.6 | 32.3 | 32.1 | 31.0 | 30.6 | ||
| 22.8 | 22.6 | 23.1 | 20.8 | 21.7 | ||
| 29.9 | 29.6 | 29.4 | 30.8 | 30.4 | ||
| Imine form | 37.1 | 36.9 | 37.2 | 35.6 | 36.2 | |
| 40.9 | 39.5 | 39.8 | 38.6 | 39.1 | ||
| 17.8 | 20.7 | 17.9 | 18.1 | 16.9 | ||
| 44.9 | 44.6 | 44.4 | 41.6 | 42.0 | ||
| / | / | / | 18.1 | / | ||
| / | / | / | / | 15.6 |
In the case of the enamine form, our data indicate that the lone pair of the nitrogen atom of the enamine function (N9) mixes strongly with the antibonding (C3–C8) bond orbital. The high value of this energy indicates that this interaction plays an important role in the stabilization of the enamine form. This interaction exhibits the highest E(2) value for all the studied series, and decreases in the order: series 2〉 3〉 1〉 4〉 5. It is the lowest for series 5. It varies remarkably with the nature of the substituents; it is higher for series 2, and lower for series 5 with a difference of 35.4 kcal/mol. The (C3–C8) bond orbital mixes with the antibonding (C4–O10) orbital. The energy of this interaction decrease in the order: series 2〉 3〉 1〉 4〉 5. It can also be seen the significant hydrogen bond type interaction between LP(O10) and σ*(N9–H21). All these results shows an intramolecular N—H---O bond associated with delocalization of the O=C and C=CNH, system which stabilise remarkably this tautomeric form and confirm a previous conclusion [24]. In the imine form, the heteroatom bearing the labile hydrogen is oxygen O10 and not nitrogen N9. In this form we note also the occurrence of a hydrogen bond interaction between LP(N9) and σ*(O10–H13). Note that in enamine LP(N9) is of π symmetry, and in the imine it is a σ one.
According to Table 8, the most important interaction for the imine form is LP(O10)→π*C3C4. This energy is in the range 41.6–44.9 kcal/mol for the five series. It is higher for series 1 and lower for series 4, with a difference of 3.2 kcal/mol. In the case of series 4 and 5, the substituting group located on N9, i.e. O11 or N11 bears a lone pair which undergoes an interaction with the adjacent π*C8=N9; obviously, such an interaction does not exist for the substituting groups of series 1,2 and 3. As it can be seen in Table 8, the lone pair on the electronegative atom (N or O) of the substituting group is delocalized to π*C8=N9 orbital of the imine function. This delocalization stabilizes the imine form by 18.1 kcal/mol and 15.6 kcal/mol, respectively for the series 4 and 5.
The most stable form is enamine unless a substituting group containing a heteroatom is attached to N9. In the latter case there is a weakening of the LP(N9) →π*C3–C8 interaction accompanied by new stabilizing interactions occurring in the imine form only, between the lone pair borne by the heteroatom LP(O11) or LP(N11) of the substituting group and π*C8=N9.
As it has been explained above LP(N9) carries a great importance as its interaction with π*C3=C8 drives mainly the relative stability of forms (a) and (c). The charge variation of the N9 nitrogen atom of the enamine function is the direct consequence of inductive and conjugation effects of substituents. N9 bears a higher negative natural charge for series 1, 2 and 3 than in series 4 and 5, and this for either form (a) or (c). For instance, natural charge on (N9) atom decreases from −0.553 (R=CH2−CH2−NH2) to −0.292 (R=OH) in form (c) and from −0.579 to −0.266 in form (a). The stabilizing LP(N9) − π*C3=C8 interaction energy is high when the natural negative charge on N9 is high.
The introduction of NH2 and OH as substituting groups leads to two effects; first, an inductive one which reduces the negative charge borne by N9 as seen before, but also to the occurrence of a new LP(O11) or LP(N11) → π*C8=N9 interaction. The latter one is more stabilizing in series 4 (R=NH2) than in series 5 (R=OH) for electronegativity reasons as it can be seen in Table 8.
Solvation has an important effect on the interaction energy as it can be seen in Table 9. The stabilization of the enamine form in a polar solvent comes partly from this interaction. We found that the other E (2) values do not vary significantly with solvation.
Stabilization energies in gas phase and in solution.
| (Enamine form) | Energies: E (2) (Kcal/mol) | ||||
| Series 1 | Series 2 | Series 3 | Series 4 | Series 5 | |
| Gas phase | 8.9 | 10.8 | 10.3 | 10.8 | 11.5 |
| CHCl3 | 12.54 | 15.66 | 15.48 | 18.08 | 18.65 |
| DMSO | 13.35 | 17.39 | 16.34 | 19.80 | 20.26 |
2.5 Tautomeric equilibrium
The tautomeric imine (a)–enamine (c) equilibrium is represented In Scheme 2 and the computed molar fractions for the two predominant forms in gas phase and solution are given respectively in Tables 10 and 11. No experimental data for the equilibrium constants of the studied heterocyclic compounds are available for comparison. The results given in Table 3 indicate that the (b) and (d) tautomeric forms are the less stable ones for all species; we checked that their molar fractions in the mixture of tautomers are negligible.
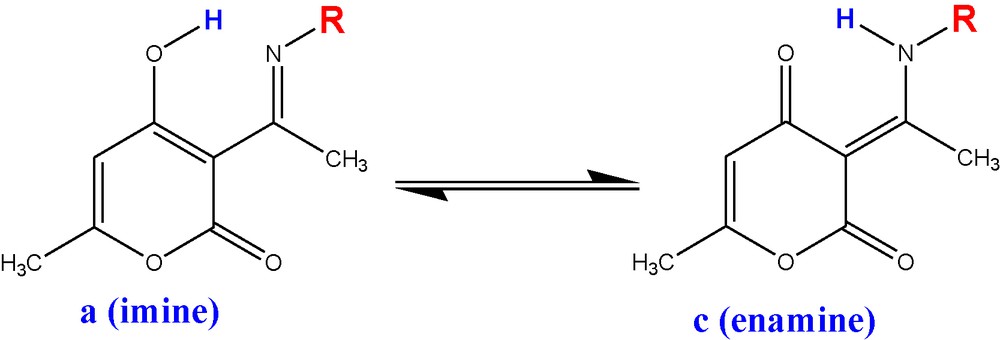
Imine–enamine equilibrium.
Calculated equilibrium constants for the imine–enamine equilibrium in gas phase and in solution.
| Series | Equilibrium | Gas phase | CHCl3 | DMSO |
| Series 1 | 1a/1c | 3.39.106 | 1.42.109 | 6.53.109 |
| Series 2 | 2a/2c | 2.58.104 | 1.03.109 | 1.02.109 |
| Series 3 | 3a/3c | 1.20.103 | 4.67.106 | 7.14.106 |
| Series 4 | 4a/4c | 1.16.10−2 | 7.27.10−1 | 0.76.102 |
| Series 5 | 5a/5c | 3.58.10−4 | 2.52.10−1 | 6.72 |
Calculated molar fractions for imine and enamine tautomers in gas phase and in solution.
| Series | Tautomeric forms | Gas phase | CHCl3 | DMSO |
| Series 1 | [1a] | 2.9.10−7 | 7.01.10−10 | 1.52.10−10 |
| [1c] | 0.9999 | 0.9999 | 0.9999 | |
| Series 2 | [2a] | 3.8.10−5 | 9.64.10−10 | 9.79.10−10 |
| [2c] | 0.9999 | 0.9999 | 0.9999 | |
| Series 3 | [3a] | 8.2.10−4 | 2.13.10−7 | 1.39.10−7 |
| [3c] | 0.9991 | 0.9999 | 0.9999 | |
| Series 4 | [4a] | 0.9884 | 0.5787 | 1.28.10−2 |
| [4c] | 1.15.10−2 | 0.4212 | 0.9871 | |
| Series 5 | [5a] | 0.9996 | 0.7984 | 0.21 |
| [5c] | 3.58.10−4 | 0.2015 | 0.87 |
Equilibrium constants Kt are calculated using the usual equation: where δΔGa,c is the difference of Gibbs free energies of tautomers (c) and (a): δΔGa,c = ΔGc − ΔGa.
The R value is equal to 1.987 cal K−1 mol−1 and T is 298.15 K. The molar fractions [a] and [c] of tautomers (a) and (c) were calculated using the following equations:
Calculated values of the equilibrium constants and molar fractions in gas phase and solution obviously confirm the predominance of the enamine form above the imine form, for series 1, 2 and 3. However, our method of calculation based on DFT overestimates [14] the stability of the enamine form, as it can be seen for series 2.
As expected, comparison of equilibrium constants shows that large changes occur from gas phase to solution. For series 4 and 5, the obtained results confirm the predominance of the imine above the enamine form in gas phase and in CHCl3. On the contrary, in the more polar solvent DMSO, the equilibrium is shifted in favor of the enamine form. This result is also in good agreement with the studies indicating that polar solvents favor the enamine form [34]. As it has been seen above in the text, the higher polarizability of the enamine forms leads to a greater stabilization of these forms in a polar solvent. Such a displacement of the tautomeric equilibrium in all series, favoring the enamine tautomer with the polarity of the solvent, is independent of the nature of the substituting group. The molar fraction of the enamine form increases by 0.96 and 0.86 mol/l respectively for series 4 and 5 when going from gas phase to DMSO.
3 Conclusions
In the light of the obtained results, several conclusions can be made: among four different possible tautomers, the substituted pyronic species under consideration come only in two predominant imine and enamine forms, both in gas phase and in solution. It was shown that the nature of the substituents borne by the N9 nitrogen atom has an important effect on the stability of the two tautomers. Our method of computation indicates the right predominating tautomer in the five series of studied compounds, although it overestimates the stability of the enamine form, as it has been seen for series 2. Alkyl or phenyl substituents favor the enamine forms, whereas the imine form is preferred in the case of NH2 or OH groups, in agreement with experiment, so that such substituting groups which bear lone pairs should be preferred for synthetic purposes.
It has also been shown that the imine–enamine equilibrium is solvent dependent, and that the enamine form is stabilized more than the imine one in polar solvent, in all cases. The higher polarizability of the former form is mainly responsible for that. In order to improve the production of compounds of pharmacological interest which needs a predominating imine form, it appears necessary to use also low-polarity solvents during the synthesis processes.
Acknowledgments
We thank the French and Algerian governments for the research grant CMEP/07 MDU 700.


