1 Introduction
The low coordinated compounds of main group elements have attracted recent interest. Similarly to carbenes [1] and silylenes [2], the low coordinated phosphorus compounds, the phosphinidenes (phosphanylidenes, P–R) are also of much importance in main group chemistry because of their continuously emerging potential as one-phosphorus building block offering convenient synthesis of a plethora of cyclic compounds and also because of possible catalytic applications [3].
Phosphinidenes – such as the well-known parent carbene, the methylene (CH2) – are extremely unstable compounds. The stability of phosphinidenes was the subject of recent studies [4]. The electronic ground state of the parent phosphinidene (P−H) (and most of its substituted derivatives [5]) is a triplet state. In order to stabilize the singlet state, thermodynamic stabilization is necessary, which can be achieved using an appropriate substituent. Complexation by transition metals acts stabilizing, and such complexes are useful synthons [6]. Stabilization of uncomplexed phosphinidenes is a more difficult task. In our previous work [7], we studied the substituent effect on the stability of phosphinidene and found that π-donor and σ-acceptor groups (like amino group [8]) stabilize remarkably the singlet state, and that methyleneamino (–N=CR2) group was most effective due to its donation–back donation effect. In particular (Me3Si)2C=N–P is expected to be thermodynamically stable against dimerisation/oligomerisation reactions. The synthesis of this compound, however, seems to be rather difficult because of the instability of the possible precursors, therefore search for new synthetic pathways is of importance.
For the in situ generation of complexed phosphinidenes, two main routes are more widely used (Scheme 1).
Marinetti et al. reported [9] the phosphanorborandiene complex offering access to transition metal complexes of phosphinidenes (reaction (1)). Afterwards, the phosphanorcaradiene was found to be a convenient phosphinidene precursor [10]. It is worth noting that in both reactions the formation of an aromatic ring is the driving force of the reactions.
Albeit free phosphinidenes are not easily accessible, (three membered ring) phosphiranes [11], azaphosphirenes [12], diphosphenes (R–P=P–R’) [13] and phosphanylidene-phosphoranes (R3P=P–R’, [14]) can be applied to generate free phosphinidenes and their complexes in situ.
Recently we reported [15] a set of possible precursor for generation of free phosphinidene (Scheme 2, E=N), which can be described as complexes of phosphinidenes with N-donor ligands. All these structures are modified analogues of the 1,3,2-diazaphospholene (1Na–d).

Since the stability of these complexes depends on: (i) the stability of the phosphinidene itself; and (ii) the type and number of annelations, the dissociation reaction (Scheme 3) of certain complexes can result in the formation of free phosphinidene. These complexes can be divided into two classes: the annelated haterocycles (type I, E=N) contain pyridoannelation(s) along the N–C bonds, while the cage compounds (type II, E=N) possess benzannelation(s) to the pyrazine ring. Note that complexes 6Na–d and 7Na–d can be regarded as phosphinidene complexes of the bipyridine and phenanthroline ligands, respectively, which are of high importance in coordination chemistry.

The similarity between nitrogen and phosphorus is well known and is reflected in the chemical behavior of their compounds, however, there are some differences between the two elements. A highly important difference is the pyramidality of the three-coordinate pnictogen atoms. While the bond angles in ammonia are nearly tetrahedral and the inversion barrier is about 5 kcal mol−1 [16], the bond angle in phosphine is quite acute (nearly 90°) and the inversion barrier is as large as 35 kcal mol−1 for PH3 [17]. Consequently, differences can also be expected between the stability (and thus the ability of phosphinidene liberation) of N-donor and P-donor ligands. Henceforth the terms ‘P complexes’ and ‘N complexes’ will be used for the phosphinidene complexes with P-donor and N-donor ligands, respectively. The aim of this study is to investigate systematically the possibility of phosphinidene generation from the complexes of phosphinidenes with P-donor ligands, focusing on the comparison between the N and P complexes.
2 Computations
All the computations have been carried out with the Gaussian 03 code [18]. The combination of the B3LYP functional [19] and the 6-311+G** basis set was proved to be appropriate for very similar complexes of phosphinidenes with N-donor ligands. For all the optimized structures vibrational analysis was performed to check whether the stationary point located is a minimum or a saddle point of the potential energy surface. For the calculation of nucleus independent chemical shift (NICS) [20] values the B3LYP/6-311+G** level was also applied. Visualization of the molecules was performed using the Molden program [21].
3 Results and discussion
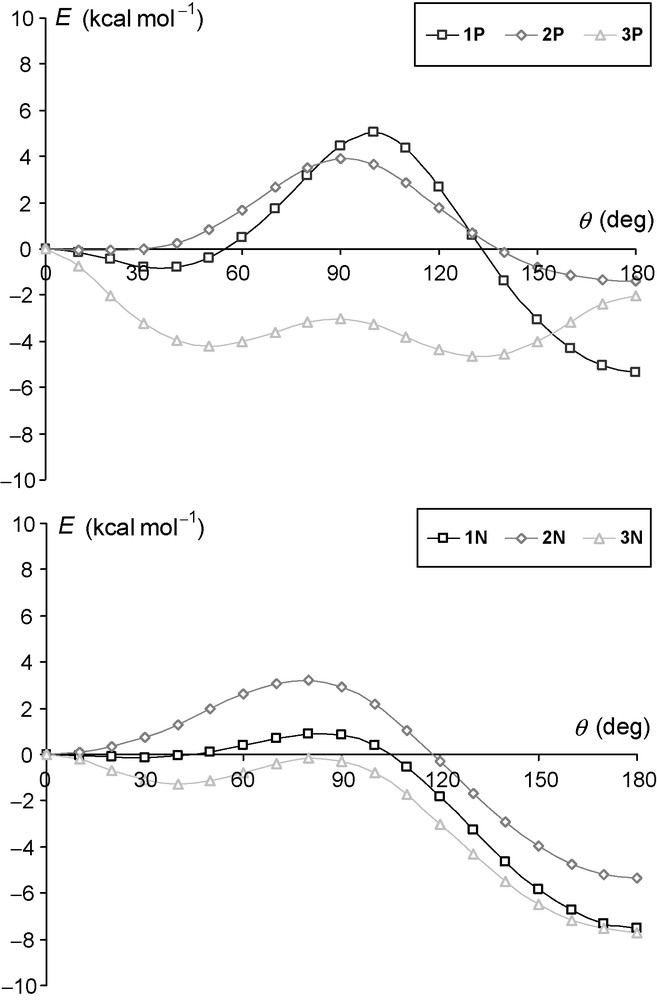
For compounds 1Pa–d … 7Pa–d the standard energies and Gibbs free energies of dissociation reactions (3)/(4) have been calculated at the B3LYP/6-311+G** level of theory. Besides the parent molecules (a: R: H), the complexes delivering the most stable phosphinidenes [7] have been studied [b: R: NH2, c: N=CH2, d: N=C(SiH3)2]. In contrast to N complexes, for some P complexes (mainly complexes of type I) two or more conformers have been found. In these cases, the lowest energy isomer was used to calculate the reaction energies; the optimized geometries and total energies of the other conformers are collected in the Supplementary material.
This structural difference between N and P complexes (Fig. 1) can be explained by the pronounced pyramidalization (as indicated by bond angle sums of 301–310°) of the bridgehead phosphorus centers, whereas the arrangement about the nitrogen atoms in 1Pa–d … 4Pa–d was nearly planar [15]. It is worth noting that the ring annelation can reduce the pyramidality (and the inversion barrier) of the tricoordinate phosphorus if the cyclic delocalization is extended to several rings [22]. In the present cases, however, no π-sextet can form in the five-membered ring, and accordingly the phosphorus remains pyramidal. Although the conformers of the cyclic “complexes” (type I) have remarkably different geometries, their energies are similar (Supporting information), so the dissociation properties are not expected to depend significantly on the actual conformer. For the complexes 5Pa–d and 7Pa–d, only one minimum was found (similarly to their N-analogues), whilst for 6Pa–d, two different conformers could be optimized, the endo- and exo-conformers having very similar energies.

The structural difference between N and P complexes.
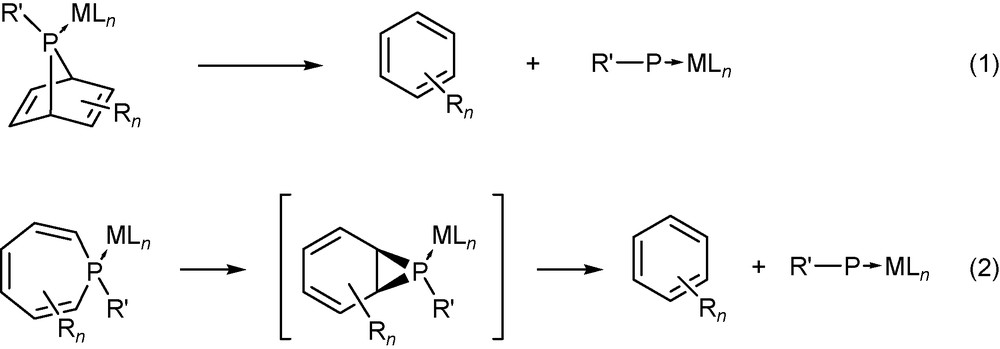
At this point it is worth mentioning that the P- and N-donor ligands formed after phosphinidene formation can also have different rotamers, and that the thermodynamics of the dissociation reaction are determined by the most stable form. The same ligands were used also to complex transition metals [23]. For the ligands depicted in Scheme 4, the energy profiles for rotation around the E−C−C−E torsion angle (θ, e.g. θ = 0° for the s-cis rotamer) were determined using relaxed optimization scans with the step size of 10° at the B3LYP/6–311+G** level of theory (Fig. 2).

Energy profile of rotation around the E−C−C−E dihedral angle for ligands 1E, 2E and 3E (E: P or N) at the B3LYP/6-311+G** level (in kcal mol−1).
Interestingly, the geometries at θ = 0° are rotational transition states for all ligands except 2N, whereas the geometries at θ = 180° were found to be minima of the potential energy surfaces; the only exception is ligand 3P. The s-cis conformers are not planar even for 2P, however, the energy surface is very flat in this case. The most remarkable difference between the P and N ligands is found for the bipyridine-like compounds: whereas bipyridine (3N) features an s-trans isomer with planar geometry, in the case of biphosphinine (3P) both the s-cis and s-trans isomers have tilted rings, and the energy profile for a 180° bond torsion exhibits therefore three rather than two transition states.
Analyzing the energy profiles in Fig. 2, the energy differences between different conformers are lower for the P ligands than for the N ligands, and since the activation barriers of rotation are reasonably low, it can be expected that the most stable rotamer of the ligand will be the final product in the dissociation reaction. For this reason, all energies of dissociation reactions have been calculated with the most stable conformers.
The standard dissociations reaction energies and Gibbs free energies at 298 K are shown in Table 1.
Standard dissociation energies (ΔEdiss) and Gibbs free energies (ΔGdiss) at 298 K for the reactions shown in Scheme 3 (in kcal mol−1) calculated at the B3LYP/6-311+G** level of theory.
| a R: H | b R: NH2 | c R: N=CH2 | d R: N=C(SiH3)2 | |||||
| ΔEdiss | ΔGdiss | ΔEdiss | ΔGdiss | ΔEdiss | ΔGdiss | ΔEdiss | ΔGdiss | |
| 1P | 103.3 | 89.8 | 64.4 | 50.8 | 47.1 | 32.7 | 33.0 | 18.9 |
| 2P | 76.7 | 62.7 | 40.4 | 26.3 | 21.6 | 6.7 | 6.5 | −8.2 |
| 3P | 53.2 | 40.6 | 20.3 | 8.8 | 0.4 | −13.1 | —a | —a |
| 4P | 53.0 | 40.2 | 21.3 | 8.5 | 1.4 | −11.9 | —a | —a |
| 5P | 65.8 | 53.7 | 33.0 | 20.8 | 13.0 | −0.2 | −0.5 | −13.3 |
| 6P | 79.1 | 65.9 | 45.3 | 31.8 | 25.5 | 11.3 | 11.8 | −2.0 |
| 7P | 95.9 | 82.6 | 60.5 | 46.8 | 41.3 | 27.0 | 27.3 | 13.4 |
a No geometry could be optimized for the complex (see in text).
Analyzing the data, it can be seen that the dissociation reaction energies are generally positive, however, for some complexes they are quite close to zero. Exceptionally, for 3Pd and 4Pd, no local minima could be found on the potential energy surface, but all optimization runs (even with the least step size) resulted in the dissociation of the complex. This is in good agreement with the fact that the (H3Si)2C=N–P is the most stable among the phosphinidenes investigated, and that the biphosphinine and 4,5-diphosphaphenantrene contain two and three aromatic rings, respectively, whilst the ligands arising from 1P and 2P complexes possess no or one aromatic ring. It is worth mentioning that the entropy contribution to the Gibbs free energy increases the propensity of the dissociation as expected. The extent of this effect is independent of either the ligand or the phosphinidene. The tendencies in the dissociation energies can be seen in Fig. 3.
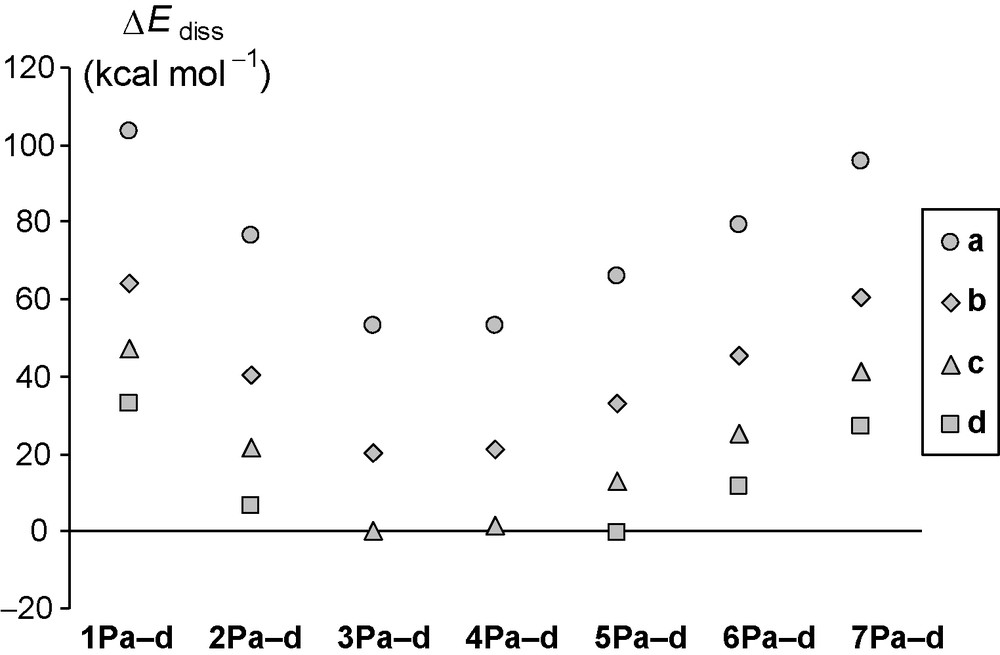
Standard dissociation reaction energies for the complexes 1Pa–d to 7Pa–d at the B3LYP/6-311+G** level of theory (in kcal mol−1). For further explanation see the text.
The trends in the dissociation energies are very similar to those observed for the phosphinidene complexes with N-donor ligands (1Na–d… 7Na–d). The dissociation energy not only correlates with the stability of phosphinidene (the more stable the phosphinidene, the less stable the complex), but the stability order of the complexes also looks similar, so the factors determining the stability of the complexes are presumed to be similar for the P- and N-donor ligands (Fig. 3). As the detailed explanation for the stability of the complexes with N-donor ligands have already been discussed elsewhere [15], here we highlight only the comparison between the P- and N-heterocyclic compounds.
As it can be seen in Fig. 4, the difference between type I and type II complexes is significant, however, the correlation is very good for the two separated sets of values (R2 = 0.982 for type I complexes, and R2 = 0.986 for type II complexes). This unexpected behavior emphasizes the different properties of the two subclasses of these compounds, which has already been observed for the N complexes.

Correlation between the dissociation energies of complexes 1Pa–d … 7Pa–d (ΔEdiss(P), in kcal mol−1) and 1Na–d… 7Na–d (ΔEdiss(N), in kcal mol−1 from Ref [15]) at the B3LYP/6-311+G** level of theory. The black and grey dots represent the cyclic (type I) and the cage (type II) complexes, respectively.
In particular, both the order of stability and the dissociation energies are very similar for the cyclic P and N complexes of type I, suggesting that the factors determining the dissociation properties (e.g. ring strain of the complexes, and the stability/aromaticity of the ligands) are very similar for both the P and N complexes of the different substituted phosphorus derivatives. Although, as discussed above, the structures of complexes 1Pa–d … 4Pa–d look more strained than the complexes 1Na–d… 4Na–d, this does not induce a remarkable destabilization of the P complexes when dissociation is concerned.
The largest difference between the dissociation energies of P and N complexes is the increased stability of the P complexes of type II. To understand this deviation (ca. 50 kcal mol−1), it is worth studying the structures of these complexes. The bridgehead pnictogens in norbornadiene-type structures are usually quite pyramidal, and this pyramidality can be assessed by the sum of bond angles (SBA) around the bridgehead atoms, which is usually small for such compounds (around 260°, cf. for a perfectly planar structure SBA = 360°). It is well known that nitrogen accommodates planar structures much more easily than phosphorus [24], thus the pyramidality in the equilibrium geometry is less pronounced for ammonia (SBA = 324°) than for phosphine (SBA = 280°). The energetic consequences of this effect can be seen in Fig. 5.

Relative energies (in kcal mol−1) of PH3 (grey) and NH3 (black) at different SBA values at the B3LYP/6-311+G** level.
Since the SBA is about 250–280° for most of the complexes of type II, it is clear from the curves, that the pyramidization of the nitrogen atom in these type of complexes is energetically more costly than that of the tricoordinate phosphorus. Furthermore, as the aromaticity of the resulting P and N heterocycles is similar according to the NICS values (Table 2), the difference in dissociation energies between the P and N complexes is principally attributable to the pyramidalization of the bridgehead atoms.
NICS(0) and NICS(1) values for 5E–7E calculated at the B3LYP/6–311+G** level (in ppm).
| 5P | 6P | 7P | |||
| A | B | A | B | ||
| NICS(0) | −5.9 | −5.6 | −8.8 | −7.7 | −7.6 |
| NICS(1) | −9.1 | −8.6 | −11.2 | −10.2 | −10.2 |
| 5N | 6N | 7N | |||
| A | B | A | B | ||
| NICS(0) | −5.3 | −6.1 | −8.8 | −9.2 | −7.2 |
| NICS(1) | −10.2 | −10.5 | −10.9 | −12.8 | −9.9 |
4 Conclusion
In this study we analyzed the dissociation properties of P-heterocyclic compounds that can be formally regarded as complexes of phosphinidenes with bidentate P-donor ligands. With respect to the standard dissociation energies and Gibbs free energies, the stabilities of the cyclic complexes (type I, 1Pa–d … 4Pa–d) are very similar to those of the analogous N-complexes (a remarkable correlation has been found), suggesting a similar strength of electronic effects in molecules with quite different geometries. Although there is also a good correlation between the P- and N-cage complexes (type II, 5Ea–d… 7Ea–d), the P complexes are in this case much more stable than the N analogues. The different behavior of both types of complexes can be explained by the different pyramidalization affinity of the tricoordinated phosphorus and nitrogen atoms. In addition, whereas the high dissociation liability of N complexes of type II might impede their synthesis, the P complexes should be more easily accessible because of their enhanced stability. Since both sets of compounds have remarkably different characteristics, a large variety of P complexes could also be applied as moderately unstable, easy-handle phosphinidene precursors, to select the best precursor for the selective synthesis of a given phosphinidene.
Acknowledgement
Financial support of the DFG–HAS travel grant and COST CM0802 action (PhoSciNet) is acknowledged.


