1 Introduction
Organic heterocyclic oligomers and polymers based on thiophene and pyrrole derivatives have attracted significant attention during the last decades due to their useful electrical and/or optical properties [1–6]. In particular, as well-defined thiophene oligomers and polymers with specific properties have become available, a wide range of semi-conductor devices has been fabricated, including thin-film field effect transistors [7], light-emitting diodes [8], and photovoltaic components [9] for technological applications such as flat television screens and solar cells. Organic-based semiconductor devices offer advantages over conventional silicon-based semiconductors in that they can be made small as well as having the necessary flexibility in larger systems.
The resulting organic electronic materials are generally fabricated by alternating layers of p-type and n-type materials. Thus, both p- and n-type compounds are needed. Depending on the nature of the semiconductors and electrodes used, the channel formed can be either n-type, where electrons are the charge carriers, or p-type where holes function as the carriers. In an n-channel material, the electrode injects electrons into the semiconductor and as a consequence, materials with a more stable lowest unoccupied molecular orbital (LUMO) (lower energy, higher electron affinity) in order to accommodate the extra electron. Electron withdrawing groups such as CN, F… can stabilize the LUMO, thereby improving the n-channel conductivity. For a p-channel material, a destabilized (higher energy, low ionization potential) highest occupied molecular orbital (HOMO) is desirable for ease of removal of electrons by the electrode. While organic compounds form a rich source for providing various p-type materials, they offer only rare and unstable materials for n-type counterparts. The deficiency and poor stability of n-type materials constitute a challenging issue in this field.
Some new potential n-type materials have been designed and synthesized. For example, tetradecafluorosexithiophene (denoted hereafter as pF-6T with pF standing for perfluoro and T for thiophene, Fig. 1) was the first perfluorinated oligothiophene synthesized in 2001 by Suzuki and co-workers [10]. Substitution of hydrogen by fluorine in the oligothiophenes has been demonstrated to be an effective way of converting p-type organic semiconductors to n-type materials. Subsequently, Marks and co-workers [11] reported in 2003 the first synthesis of a set of perfluoroarene-modified thiophene oligomers. Depending on the position of the electron-deficient perfluoroarenes within the building block, this new family of compounds can behave as either p-type or n-type semiconductors. These authors also found that an oligomer with perfluoroanenes in the inner positions of the chain (denoted as TFTTFT where T stands for thiophene and F for perfluoroarene Fig. 1) is a p-type semiconductor with similar behavior to that of the classical hexathiophene [12] (6T). In contrast, the oligomer containing perfluoroarene rings at the ends of the chain (FTTTTF) becomes an n-type semiconductor. A number of theoretical studies have also been devoted to different types of thiophene-based polymers [13].
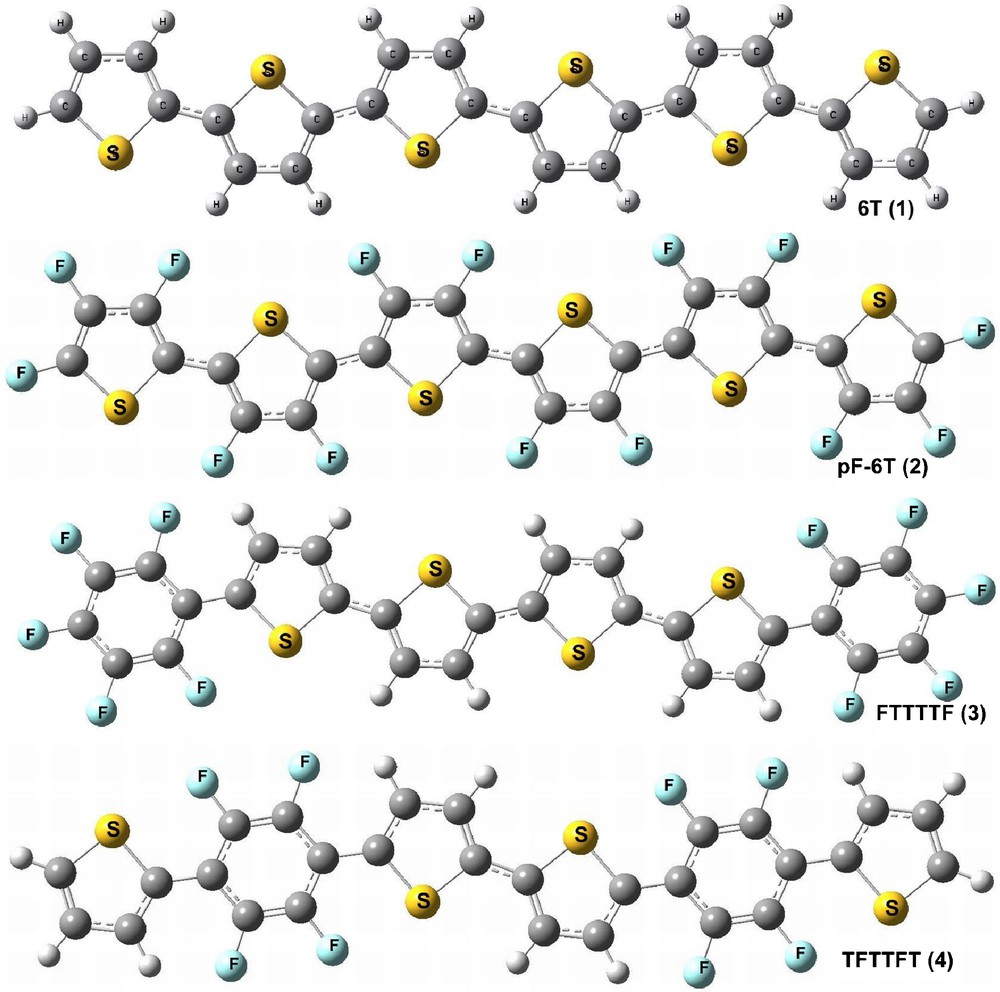
Optimized structure of α-sexithiophene (6T), perfluoro-α-sexithiophene (pF-6T), perfluoroarene-modified thiophene oligomers (FTTTTF) and (TFTTFT).
The remarkable experimental results [11,12] show that it is possible to convert a p-type to an n-type material by introducing electron-withdrawing groups into the p-type molecular core. In view of such an interesting perspective, we set out to use computational quantum chemical methods in order to: (1) investigate, as a calibration, the geometrical and electronic properties of oligomers based on thiophene monomers; and (2) search for potentially novel compounds with interesting properties. For the first goal, we considered the four known oligomers, namely α-sexithiophene (6T), perfluoro-α-sexithiophene (pF-6T), and two perfluoroarene modified thiophene oligomers (FTTTTF and TFTTFT). The latter two have been successfully synthesized and their crystal structures have been made available [10,11a], and can thus be used for purpose of comparison with theoretical results. For the second goal, we studied the molecular structures and electronic properties of the yet unknown 1H-phosphole analogues of the thiophene oligomers mentioned above.
The use of phospholes as building blocks for formation of polymers has been intensively explored, and recently reviewed by Reau and co-workers for polymers, and Matano and Imahori for porphyrins derivatives [14]. In earlier theoretical studies [15], we have found significant effects of fluorine substitution on the thermochemical parameters phosphole-based oligomers. For example, the frontier orbital energy gaps (Eg) (E(HOMO) – E(LUMO)) of the latter are reduced by up to 1 eV, following F-substitution at the phosphorous. A similar decrease is thus expected for the electron affinities (EA) of F-phospholes. Earlier theoretical studies [16] also showed that phospholes exhibit promising properties as building blocks for π-conjugated polymers. Thus, the P-systems examined consist of the non-substituted 1H-sexiphosphole oligomer (6-1H-P, 1H-P stands for 1H-phosphole), two fluoro-substituted sexiphosphole oligomers (6-1F-P and pF-6P), two oligomers based on the perfluoroarene modified non-substituted 1H-phosphole (1H-FPPPPF and 1H-PFPPFP), and two oligomers based on the perfluoroarene modified fluorinated substituted phosphole oligomers (1F-FPPPPF and 1F-PFPPFP). The geometric and electronic properties of these phosphole oligomers have been calculated for comparison with their thiophene counterparts (Fig. 1). We have studied the hexamers because of the availability of experimental results for the corresponding thiophenes.
2 Computational details
The 11 oligomers studied in this work are presented in Figs. 1–3. All of the geometries were first fully optimized with trans-oriented monomer units using density functional theory (DFT) method with the hybrid Becke, Yang and Parr functional (B3LYP) [17] and the split-valence plus d-polarization functions on S and P atom 3-21G(d) basis set and the 3-21G basis set on H. Harmonic vibrational frequencies were calculated at this level in order to establish the nature of the stationary points, as well as to determine Raman intensities to aid in the characterization of π-conjugated oligomers. Experimentally this characterization is based on the spectral region of the stretching modes of the CC and CC bonds along the backbone, following the effective conjugation coordinate (ECC) suggested by Zerbi et al. [18], and widely used to study the electronic structure of molecular materials [19–24]. Let us stress that there are several lower-lying conformers of the oligomers considered, including the cis or gauche conformers. However, they are not relevant to our purpose as they do not systematically lead to chain oligomers.
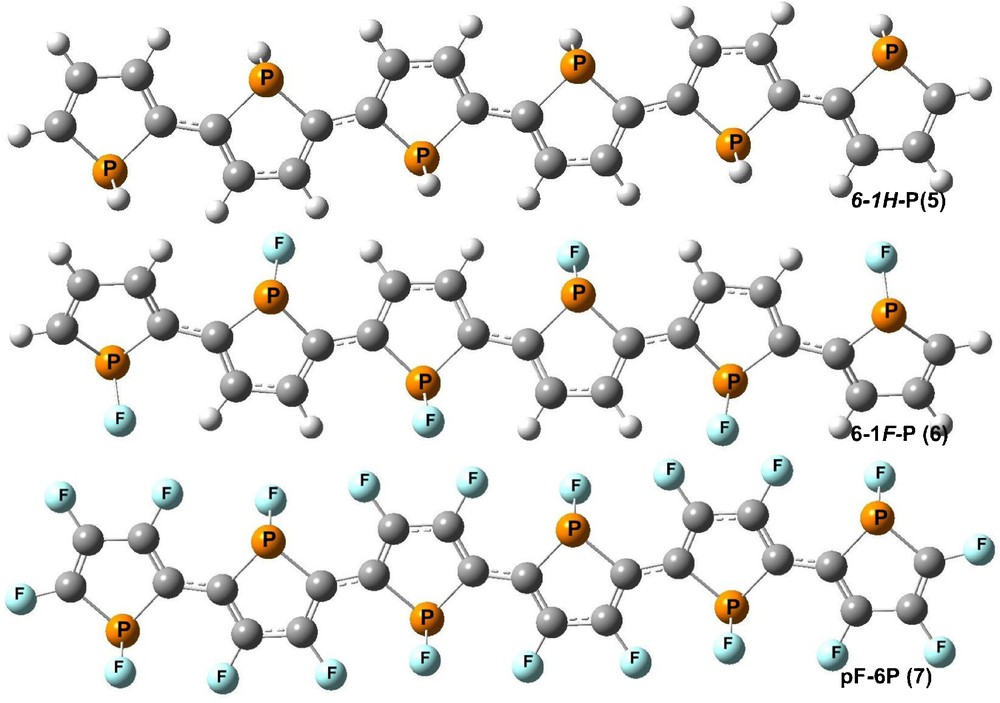
Optimized structure of 1H-sexiphosphole (6-1H-P), 1F-sexiphosphole (6-1F-P) and perfluoro-sexiphosphole (pF-6P) oligomers.
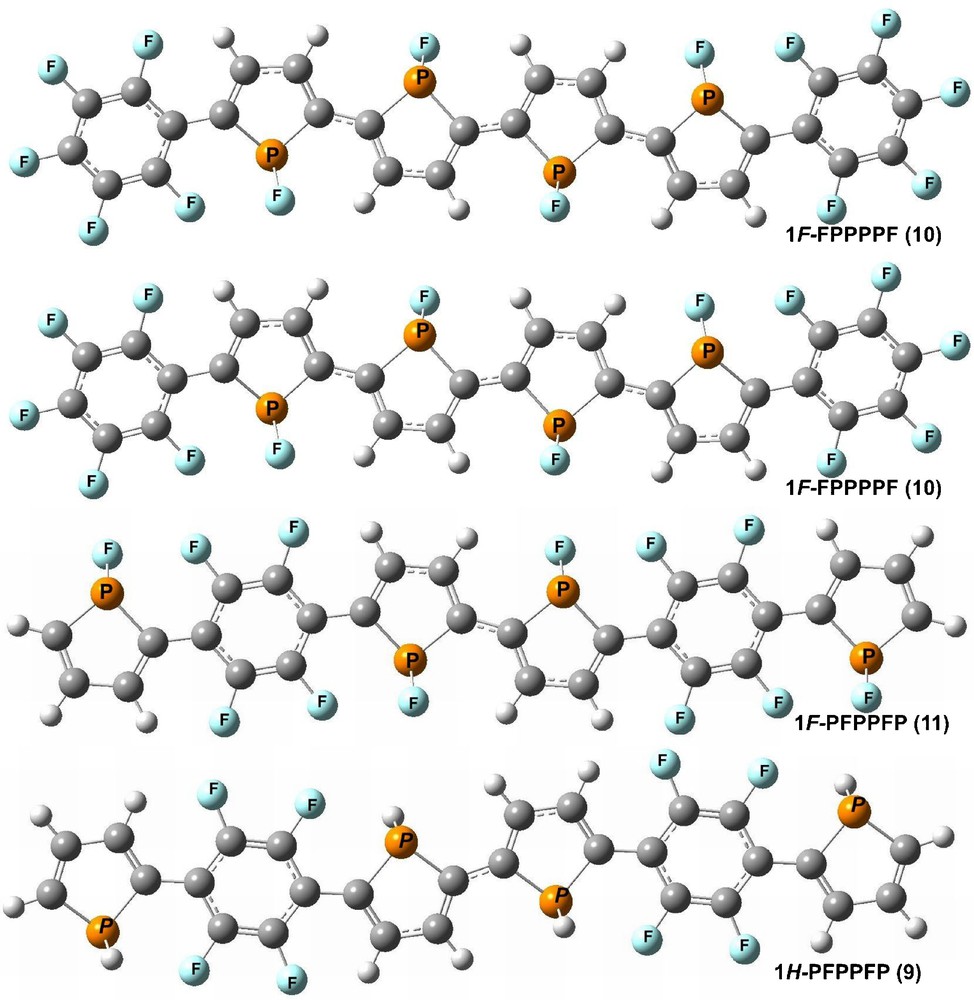
Optimized structure of perfluoroarene-modified 1H-phosphole (1H-FPPPPF) and (1H-PFPPFP), and perfluoroarene-modified 1F-phosphole oligomers (1F-FPPPPF) and (1F-PFPPFP).
Although the 3-21G(d) basis set employed is rather small, it provides when used in conjunction with the B3LYP functional, reasonably good geometrical and vibrational data as compared to experiment. To obtain somewhat better geometrical parameters and electronic properties, the oligomer geometries were reoptimized with a split valence plus polarization SV(P) basis set incorporating polarization functions on all atoms (B3LYP/SV(P)). There are, however, no significant changes in the geometrical parameters.
The energy gap can be calculated as the difference in both frontier orbital energies of the highest occupied molecular orbital and lowest unoccupied molecular orbital [25], or determined, as in the present work, by computing the electronic excitation energy using a time-dependent TD-DFT method [26,27]. For the π-conjugated systems such as the heterocyclic oligomers considered here, the lowest allowed excitations correspond to singlet π*(LUMO) ← π(HOMO) transitions. This approach is an efficient and reliable method for predicting energy gaps [28].
The inner-sphere reorganization energies of a hole, denoted by λ+, and an electron, λ−, corresponding to the cationic and anionic electronic states, were calculated for each oligomer. According to Marcus electron-transfer theory, the reorganization energy (λ) is an important parameter for predicting the self-exchange electron-transfer rate. The electron transfer rate correlates with λ such that a small value for λ corresponds to a fast rate [29–31]. Thus λ is a measure of the efficiency of charge carriers in materials. The value of λ can be obtained from both experiment and theory [13,32–43]. Following the original definition, λ for an electron-transfer process is associated with two geometry relaxation energies, λ1 and λ2, going from the neutral state to the charged-state and the reverse. A schematic definition of these parameters is given in Fig. 4. The λ+ and λ− terms can be estimated from the ionization energy (IE) and electron affinity (EA) of a neutral species as follows:
| (1) |
| (2) |
| (3) |
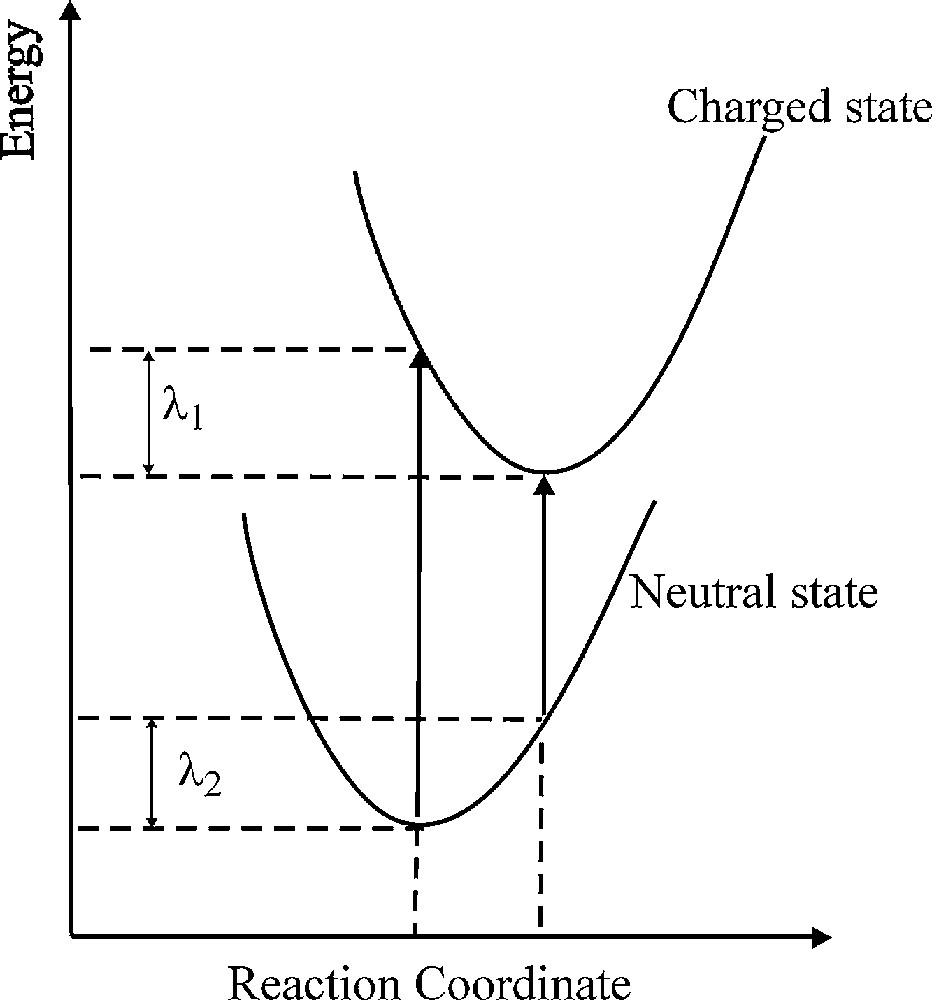
Potential energy surface of neutral and charged states that define λ1 and λ2.
The vertical and adiabatic ionization energies (IEv, IEa), and adiabatic electron affinities (EAa) were calculated because they are needed for the reorganization energies. We used two different methods to evaluate the vertical ionization energies (IEv). The first is the difference in total energies of both neutral and cation ground states obtained from the neutral geometry at the B3LYP/SV(P) level. The other simply corresponds to the negative value of the HOMO energy derived from HF/SV(P) wavefunction, within the framework of Koopmans’ theorem.
The geometries of the neutral, cation, and anion species of each oligomer were optimized at the (U)B3LYP/SV(P), using the Turbomole 5.7 program [44]. For the structures with terminal perfluoroarenes (FTTTTF, 1H-FPPPPF, and 1F-FPPPPF, Fig. 1), we employed the Gaussian 03 program [45]. The Turbomole program was further used for calculating frontier orbital properties such as ionization energies and energy gaps. Electronic density contours of 0.03 e/bohr3 were used for plotting the frontier orbitals of the neutral compounds with Gaussview 3.0 [46]. The vibrational spectra were calculated by using the Gaussian 03 program. The IR and Raman spectrum were produced by using the GaussSum 0.8 package [47]. The eigenvectors of Raman bands were displayed by the ChemCraft program [48] and the Mercury 1.3 software [49] was used for crystal structure visualization.
3 Results and discussion
The optimized geometries of the oligomers considered will be first presented, followed by their calculated Raman spectra. The different energetic parameters including the frontier orbital energy gaps, vertical ionization energies, and electron affinities, as well as the reorganization energies will be successively discussed. Cartesian coordinates of the optimized structures are given in the electronic supporting information (ESI).
3.1 Optimized geometries of neutral oligomers
We first analyze the geometrical parameters of the oligomers 6T, pF-6T, FTTTTF, and TFTTFT shown in Fig. 1, in order to understand the reason(s) why there are candidates for n-type and p-type semiconductors, and what could be changed in their structure by substituting fluorine atoms or perfluoroarene groups. The fully optimized geometrical parameters of these oligomers are summarized in Table 1, together with available crystal results for the purpose of comparison. The data focus on the maximum torsion angles between the adjacent outer rings (γ) and the distances (d) of the CC inter-ring bonds, CS, CC, and CC bonds in the thiophene rings.
Experimentala and Theoretical maximum torsional angles (degrees) and selected bond distances (Å) of 6T, pF-6T, FTTTTF and TFTTFT.
| Oligomer | γ | dCCb | dCCc | dCC | dCS |
| 6T | 5.6 | 1.445–1.450 | 1.415–1.424 | 1.373–1.387 | 1.730–1.754 |
| (4.1) | (1.439–1.444) | (1.400–1.416) | (1.342–1.388) | (1.709–1.738) | |
| pF-6T | 0.0 | 1.439–1.442 | 1.413–1.425 | 1.368–1.383 | 1.741–1.757 |
| (3.6) | (1.431–1.439) | (1.375–1.393) | (1.324–1.360) | (1.700–1.735) | |
| FTTTTF | 17.6 | 1.445–1.466 | 1.413–1.414 | 1.386–1.388 | 1.744–1.757 |
| (17.6) | (1.445–1.471) | (1.402–1.416) | (1.371–1.374) | (1.727–1.741) | |
| TFTTFT | 4.4 | 1.448–1.465 | 1.412–1.420 | 1.374–1.392 | 1.721–1.761 |
| (7.9) | (1.399–1.462) | (1.399–1.420) | (1.338–1.409) | (1.700–1.752) |
The γ bond angle values of 5.6, 0.0, 17.9, and 4.4° in 6T, pF-6T, FTTTTF, and in TFTTFT, respectively, show that pF-6T is planar, whereas the other compounds are quasi-planar. The largest γ value of 17.9° is found in FTTTTF, due to the torsion of two internal thiophene and terminal perfluoroarene rings. In earlier studies [11], it has been demonstrated that a limiting value of around 30° for this torsion angle is required to have a sufficient intermolecular π-overlap, and therefore an efficient conduction band. The maximum value of γ = 18° remains smaller than the limit. The γ value for FTTTTF agrees well with the experimental result [11a].
The CC inter-ring bond distances are consistently longer than the CC intra-ring lengths. In 6T and pF-6T, on the one hand, the bonds belonging to the outermost rings are actually shorter as compared with the corresponding bonds in the inner rings. In contrast, the bonds connecting with the perfluoroarene rings in both FTTTTF and TFTTFT are found to be longer. The CC inter-ring bond distances are dependent on the degree of conjugation of the π-system, the shorter the CC inter-ring bond distance, the more pronounced the linear π-conjugation between these building blocks. This shows that perfluorination of the non-substituted oligothiophene 6T giving pF-6T slightly reinforces the linear π-conjugation, as manifested by a decrease of CC inter-ring bond distances in going from 1.445 Å in 6T to 1.439 Å in pF-6T. In contrast, replacement of two thiophene rings in 6T by two perfluoroarene rings tends to increase the CC inter-ring bond distances to 1.455 Å in FTTTTF and 1.448 Å in TFTTFT. Thus, fluorination induces a linear π-conjugation in these oligomers, although the effect is not large. In general, the bond distances calculated at the B3LYP/SV(P) level are slightly longer than the crystal values, but they follow the same trend, except for the CS bonds in pF-6T and 6T.
The changes in the maximal torsional angles (γ) between adjacent outer-rings, as well as the changes in the CC inter-ring bond distances between the central moieties in pF-6T, FTTTTF, and TFTTFT, are not large as compared with the values of the original 6T oligomers. These results suggest that the substituted oligomers will not substantially reduce and could even improve the intermolecular π-overlap needed for an efficient charge transport in the relevant semiconductors.
The structures of the oligomers based on phosphole monomers are displayed in Figs. 2 and 3. Important geometrical parameters are summarized in Table 2. These results show that in most oligophospholes, the CC intra-ring distances are not shortened, as compared with the CC inter-ring bonds, especially for the bonds of the phosphole ends. This markedly differs from the case of oligothiophenes. The γ values in the fluoro-substituted phospholes increase from 10.7° in 6-1F-P and 9.0° in pF-6P, as compared to 7.3° in 6-1H-P, but the CC inter-ring bond distance between the central phosphole cores tends to decrease. The value of this bond distance is 1.435, 1.427, and 1.429 Å in 6-1H-P, 6-1F-P, and pF-6P, respectively. Thus, the presence of fluorine atoms does not reinforce a co-planarity but rather supports a linear π-conjugation in the phosphole oligomers. In the perfluoroarene-modified 1H-phosphole oligomers, the maximum deviation from co-planarity as given by the angle γ are 18.8° and 13.1° in 1H-FPPPPF and 1H-PFPPFP, respectively, versus a decrease to 10.5° and 10.0° in 1F-FPPPPF and 1F-PFPPFP for the perfluoroarene-modified 1F-phosphole oligomers. The CC inter-ring bond distances between the central phosphole cores in 1H-FPPPPF (1.437 Å) and 1H-PFPPFP (1.443 Å) are now longer than the inter-ring bond lengths in 1F-FPPPPF (1.429 Å) and 1F-PFPPFP (1.435 Å). In this case, the presence of fluorine at phosphorus, together with the terminal fluoroarene groups in the backbone significantly enhances the co-planarity (decreasing γ angle) and π-conjugation.
Comparison calculation maximum torsional angle (degrees) and CC inter-ring bond distances (Å) of neutral and charged states all compound.
| Oligomer | Max torsional angles | CC inter-ring | ||||
| Neutral | Cation | Anion | Neutral | Cation | Anion | |
| 6T | 5.6 | 1.9 | 2.0 | 1.445 | 1.418 | 1.418 |
| pF-6Ta | 0.0 | 0.0 | 0.0 | 1.439 | 1.414 | 1.414 |
| FTTTTF | 17.6 | 6.3 | 4.0 | 1.455 | 1.416 | 1.419 |
| TFTTFT | 4.4 | 2.0 | 2.1 | 1.448 | 1.420 | 1.421 |
| 6-1H-P | 7.3 | 7.3 | 7.0 | 1.435 | 1.405 | 1.406 |
| 6-1F-Pb | 10.7 | 11.8 | 9.2 | 1.427 | 1.394 | 1.396 |
| pF-6P | 9.0 | 8.4 | 6.5 | 1.429 | 1.399 | 1.403 |
| 1H-FPPPPF | 18.8 | 13.0 | 16.8 | 1.437 | 1.406 | 1.406 |
| 1F-FPPPPF | 10.5 | 11.1 | 13.2 | 1.429 | 1.396 | 1.397 |
| 1H-PFPPFP | 13.1 | 8.5 | 11.2 | 1.443 | 1.413 | 1.413 |
| 1F-PFPPFP | 10.0 | 11.8 | 8.2 | 1.435 | 1.404 | 1.406 |
a In pF-6T, the average CF bond distances are 1.332, 1.323, and 1.341 Å for the neutral, cation, and anion respectively.
b In 6-1F-P, the average PF bond distances are 1.641, 1.635, and 1.652 Å for the neutral, cation, and anion respectively.
Among the oligophospholes considered, pF-6P and 1F-FPPPPF are characterized by shorter CC interring bond distances and smaller γ values. This implies a more pronounced linear π-conjugation between the building blocks. In this context, they could be considered as candidates for both n-type and p-type semiconductors, comparable to their oligothiophene counterparts. In order to get more insight into this important property, we studied their vibrational spectra and electronic properties.
3.2 Predicted Raman spectra of neutral compounds
The Raman profiles in the 1700–800 cm−1 spectral region of 6T oligomers are displayed in Fig. 5, while the Raman profiles of the remaining oligomers are given in Fig. 1S in the ESI. The main peaks are summarized in Table 3. We are not going to discuss in detail every peak appearing in these Raman spectra. In order to gain some qualitative but meaningful structural information, we used the effective conjugation coordinate (ECC) approach [19], whose assumption is the existence of an effective π-electron delocalization (or conjugation) in the conjugated oligomer.

DFT//B3LYP/3-21G(d) Raman profiles (un-scaled, in cm−1) for 6T.
Some important Raman fingerprints of oligomers based on ECC analysis.
| Oligomer | Absorption bands (cm−1) | ||
| Line A (w) | Line B (s) | Line D (m) | |
| 6T | 1539 (1505)a | 1462 (1459)a | 1094 (1051)a |
| pF-6T | 1610 | 1468 | 1069 |
| FTTTTF | 1659 | 1461 | 1100 |
| TFTTFT | 1652 | 1459 | 1126 |
| 6-1H-P | 1470 | 1410 | 1065 |
| 6-1F-P | 1466 | 1413 | 1049 |
| pF-6P | 1613 | 1362 | 1052 |
| 1H-FPPPPF | 1657 | 1415 | 1073 |
| 1F-FPPPPF | 1651 | 1438 | 1062 |
| 1H-PFPPFP | 1658 | 1420 | 1061 |
| 1F-PFPPFP | 1652 | 1438 | 1072 |
a Observed value [50].
According to the ECC analysis, the Raman fingerprints for a class of oligomers and polymers can be recognized through four typical absorption bands and denoted as lines A, B, C, and D. In the case of 6T (Fig. 5), the lines A, B, and D have been identified and the relevant frequencies are calculated (observed value [50] in parentheses) at 1539 (1505), 1462 (1459), and 1094 (1051) cm−1, respectively. Line A is a band with weak intensity, and its normal mode is a collection of CC anti-symmetric vibrations. These modes, lying on the outer-most rings, are mixed to a large extent with stretching modes of the inner CC bonds. Line B is the strongest band and the normal mode motion corresponds to the regular CC symmetric vibrations and spreads over the whole molecular backbone. Line D is a sharp band of medium intensity and corresponds to the symmetric CCH bending mode in the inner thiophene ring. In addition, we notice low intensity peaks at 1410 (1368) and 1227 (1220) cm−1; these bands are also present in the corresponding IR spectrum, and arise from intra-ring and inter-ring CC stretching, respectively.
Similarly, the Raman spectra of other oligomers were also analysed and some important absorption bands are collected in the Table 3. From Table 3, the line B of 6-1H-P (1410 cm−1) or 6-1F-P (1413 cm−1) is red-shifted with respect to 6T (1462 cm−1), and thus corresponds to a certain decreasing π-conjugation, or a decrease of aromatic character in the structure of un-substituted oligophosphole. This is consistent with the non-aromatic character of the phosphole monomer [15,16]. Replacing hydrogen atoms by fluorine atoms on phosphorus atoms does not increase significantly the aromaticity of 6-1H-P.
Lines A and B in pF-6T or pF-6P are also red-shifted, but their normal modes involve different couplings of atomic motions as compared to the lines A and B in 6T or in 6-1H-P. These modes involve the sum of symmetrical stretching of inter-ring and intra-ring CC bonds along the whole chain, coupled with the in-plane bending of the CβF group. Such motion creates a π-conjugated system like a hetero-quinonoid, which induces a major intramolecular interaction, thus increasing the intramolecular charge transfer. This is similar to the changes occuring in the nuclear configuration of a π-conjugated system changing from a heteroaromatic-like shape to a heteroquinonoid-like pattern.
The Raman spectra (Fig. S1 of the ESI) for oligothiophenes and oligophospholes with terminal perfluoroarene ring in the backbone FTTTTF, 1H-FPPPPF and 1F-FPPPPF show weak peaks for the CC stretching vibrations of the perfluoroarene rings at 1659 cm−1 in FTTTTF, 1657 cm−1 in 1H-FPPPPF and 1658 cm−1 in 1F-FPPPPF. The same peaks appear with stronger intensities at 1652 cm−1 in TFTTFT, 1652 cm−1 in 1H-PFPPFP and 1652 cm−1 in 1F-PFPPFP. The peak positions characterizing this band for the perfluoroarene derivatives are red-shifted with significantly increased intensities for perfluoroarene rings substituted in the inner backbone. This is consistent with the lack of planarity of the terminal perfluoroarenes. Thus the vibrations do not involve the whole chain, but increasing π-electron density is transferred along the chain through an electron-acceptor perfluoroarene group into the inner backbone. The strongest bands corresponding to line B appear in FTTTTF at 1461 cm−1, in 1H-FPPPPF at 1415 cm−1 and in 1F-FPPPPF at 1420 cm−1, whereas they are present at 1459 cm−1 in TFTTFT, 1H-PFPPFP, and 1F-PFPPFP. The line B in oligophospholes is predicted to be at consistently lower wave numbers than those of oligothiophenes. Line D with sharp peak and medium intensities appears at 1100 cm−1 in FTTTTF, 1073 cm−1 in 1H-FPPPPF and 1061 cm−1 in 1F-FPPPPF. The line D in TFTTFT, 1H-PFPPFP, and 1F-PFPPFP appear as a doublet and of lower intensities. Overall, the calculated Raman spectra suggest a similarity in vibrations and degrees of conjugation between both series of thiophene and phosphole oligomers.
3.3 Frontier orbitals and energy gaps
Calculated frontier orbital energies and energy gaps for all oligomers considered are given in Table 4, along with the available experimental values. The experimental frontier orbital energies were determined from cyclic voltammetry as thin films on Au/glass versus SCE [11a]. These DFT orbital eigenvalues are in remarkably good agreement with the experimental values for both the HOMO and LUMO. In the HOMO, which can be regarded as π-bonding, the CC units exhibit an alternating phase with respect to their neighboring CC counterparts. In the π-anti bonding LUMO, the CC units have the same phase as their neighbors. Although each frontier orbital is expanded over the entire π-backbone, the largest components are centered on the central atoms.
| Compound | ɛHOMO | Experimentalc ɛHOMO | ɛLUMO | Experimentalc ɛLUMO | Eg | Experimental Eg | ff |
| 6T | −4.89 | −4.78 | −2.24 | −2.36 | 2.41 | 2.42d | 2.01 |
| pF-6T | −5.50 | −2.82 | 2.47 | 1.98 | |||
| FTTTTF | −5.30 | −5.27 | −2.54 | −2.69 | 2.50 | 2.58e | 1.99 |
| TFTTFT | −5.43 | −5.32 | −2.51 | −2.67 | 2.66 | 2.65e | 2.10 |
| 6-1H-P | −4.74 | −2.80 | 1.82 | 1.94 | |||
| 6-1F-P | −5.15 | −3.55 | 1.52 | 1.67 | |||
| pF-6P | −5.69 | −3.83 | 1.72 | 1.52 | |||
| 1H-FPPPPF | −5.16 | −3.02 | 1.98 | 1.83 | |||
| 1H-PFPPFP | −5.34 | −2.84 | 2.26 | 1.88 | |||
| 1F-FPPPPF | −5.44 | −3.62 | 1.67 | 1.50 | |||
| 1F-PFPPFP | −5.60 | −3.38 | 1.96 | 1.52 |
a The frontier orbital energies are calculated at B3LYP/SV(P)//B3LYP/SV(P) level.
b Eg is determined by using TD-DFT at B3LYP/SV(P)//B3LYP/SV(P) level.
c From cyclic voltammetry as thin films on Au/glass versus SCE [11a].
d The UV–VIS absorption measurement was carried out on sexithiophene single crystals [12].
e Film optical [11a] Eg
f Oscillator strength.
The results in Table 4 indicate that oligophospholes are characterized by lower energy gaps as compared to oligothiophenes. A perfluoro- or fluoroarene substitution on the parent oligothiophene 6T, or oligophosphole 6-1H-P leads to a reduction of the gap. Among oligothiophenes, pF-6T has the lowest values for both ɛHOMO and ɛLUMO; both energies are reduced by 0.6 eV, as compared to the corresponding energies in 6T. As a consequence, the energy gap in pF-6P of 2.47 eV is very similar to the value of 2.41 eV calculated for 6T. In FTTTTF and TFTTFT, the ɛHOMO (ɛLUMO) are reduced by 0.4 eV (0.3 eV) and 0.5 eV (0.3 eV), respectively, with respect to 6T. Since FTTTTF has a more stable LUMO, as compared to TFTTFT, it is expected that FTTTTF with two ending perfluoroarene moieties is more favored for electron injection into its LUMO, and thereby a better n-type material. Although the DFT LUMO is actually more appropriate for use in predicting Eg, the results listed in Table 4 show that for these molecules it also provides a reasonable estimate of the vertical electron affinity. A similar trend is found for oligophospholes. pF-6P has the largest frontier orbital stabilization of the entire series of oligomers considered, with a stabilization of both orbitals of ∼1.0 eV. As a consequence, only a small reduction of 0.1 eV is found for the energy gap.
When fluorine substitution occurs only at P-atoms, 6-1F-P, the energy gap becomes strongly reduced. This can be attributed to the stronger LUMO stabilization as compared to that of HOMO. Thus, 6-1F-P is characterized by an intrinsically small energy gap of 1.5 eV.
Replacement of two ends by two fluoroarenes in the backbone of non-substituted fluoro-substituted oligophosphole leads to a stabilization of both the HOMO and LUMO. In 1F-FPPPPF, the gap is decreased by ∼0.15 eV, as the LUMO is stabilized by 0.8 eV as compared to a stabilization of 0.65 eV for the HOMO.
The HOMO's for 1H-FPPPPF, 1H-PFPPFP, and 1F-PFPPFP are stabilized with smaller changes in the LUMO so that the gaps are increased by 0.16, 0.44, and 0.14 eV, respectively. Thus, it should be easier to create a hole in the HOMO's of these compounds. Overall, the calculated gaps show that substitution in the backbone of non-substituted oligophospholes by fluorine atoms or perfluoroarene can modify their optical properties. Among these, the 6-1F-P and 1F-FPPPPF can be regarded as potential candidates for n-type materials, whereas 1H-PFPPFP is better suited for a p-type material.
These results prompted us to further investigate the more doped derivatives for the sake of a comprehensive understanding of the factors influencing their charge carriers by evaluating the reorganization energies of both holes and electrons.
3.4 Ionization energies and electron affinities
The IEv and IEa and EAa were calculated to determine the reorganization energies and the carrier polarity of oligomers. The IE can be interpreted as a measure of the possibility of a polymer (or oligomer) to be useful for p-type doping, whereas the EA indicates the possibility of n-type doping. Thus the changes in IE's and EA's provide us with information on the injection barriers of electrons and holes. The calculated results are tabulated in Tables 5 and 6, and we now can summarize some conclusions:
- i) the differences in the IEv and IEa are 0.11–0.20 eV indicating a rather small geometry relaxation upon ionization;
- ii) most of the compounds studied have quite low IEv's, ranging from 5.73 to 6.69 eV as noted above. The unsubstituted oligophosphole 6-1H-P has the smallest IE, whereas the perfluorinated oligophosphole pF-6P has the largest IE. The energy difference between the lowest and highest IE is 0.9 to 1.0 eV. A larger IE implies that the corresponding cation has a higher energy as compared to its neutral parent and is less stable toward reduction. Thus, the corresponding compound is more likely to form a p-doped state;
- iii) all of the adiabatic EA's are positive so electron attachment invariably results in stable anions;
- iv) the calculated EA's vary in the range of 1.29–3.04 eV, with 6T having the smallest EA and pF-6P having the largest EA. The large effect of fluorine on EA's has been emphasized in previous studies [15,51]. A larger EA implies a low-energy anion and the material is thus more likely to form a n-doped state;
- v) a comparison of the properties of 6T and pF-6T allows us to examine the perfluorination effect. In the field of organic semiconductors, 6T is widely used as a material for p-doped state, owing to the high stability of its neutral form coupled with a lower stability of the anionic state. The calculated IE and EA of 6T are 5.82 and 1.29 eV, respectively. These values agree well with previous ab initio results [13b]. The IE and EA of pF-6T are predicted to be both 0.60 eV higher than those of 6T. Thus, the corresponding cation of pF-6T is less stable while its anion is more stable, with respect to the cation and anion of 6T. Thus, pF-6T can form an n-doped species as observed experimentally [52];
- vi) the IE of FTTTTF is 6.35 eV, a value similar to that of TFTTFT (6.38 eV). Its EA is 0.16 eV larger than that of TFTTFT, suggesting that FTTTTF would be more stablilized in the n-doped form than TFTTFT. Experimentally, FTTTTF has an electron mobility μ− = 0.08 cm2/Vs, whereas TFTTFT has a hole mobility of μ+ = 0.01 cm2/Vs;
- vii) for the unsubstituted oligophosphole 6-1H-P, the IE is predicted to be 0.24 eV smaller and its EA 0.67 eV larger than the corresponding values of 6T. Thus 6-1H-P could form either p- or n-doped materials. The smaller IE of 6-1H-P reflects a higher stability of its cationic form;
- viii) the IE's and EA's of the fluorinated oligophospholes 6-1F-P and pF-6P are also predicted to be larger than those of the non-substituted oligophosphole 6-1H-P. As a result, fluorine substitution tends to increase the stability of the n-doped forms. The ratio of the increments of IE and EA differs from each other. The IE and EA of 6-1F-P are 0.33 and 0.83 eV larger than those of 6-1H-P, respectively, whereas the IE and EA of pF-6P are 0.98 and 1.08 eV larger than those of 6-1H-P. The presence of extra CF bonds in pF-6P leads to a stronger effect on the IE than on the EA. In other words, CF bonds tend to enhance the stability of neutral form, whereas the PF bond creates a different effect in increasing the stability of anionic form;
- ix) as expected, the IE and EA of 1F-FPPPPF and 1F-PFPPFP are larger than those of 1H-FPPPPF and 1H-PFPPFP, due to the effect of the fluorine atoms. The IE and EA of 1F-FPPPPF are 0.23 and 0.65 eV larger than those of 1H-FPPPPF, so 1F-FPPPPF is more suitable for an n-doped material as compared to 1H-FPPPPF;
- x) the IE and EA of 1F-PFPPFP are 0.24 and 0.57 eV larger than those of 1H-PFPPFP. However, the IE and EA of the substituted oligophospholes with terminal perfluoroarene rings 1H-FPPPPF and 1F-FPPPPF are larger than those of 1H-PFPPFP and 1F-PFPPFP. These results show that the terminal fluoroarenes, substituted in the oligophospholes backbone, consistently increase the preference for n-doped forms.
B3LYP/SV(P) values for vertical, adiabatic ionization energies and adiabatic electron affinities (all values are in eV).
| Oligomer | Ionization energies | Adiabatic electron affinities | |
| Vertical (IEv) | Adiabatic (IEa) | EAa | |
| 6T | 5.95 | 5.82 | 1.29 |
| pF-6T | 6.56 | 6.42 | 1.89 |
| FTTTTF | 6.48 | 6.35 | 1. 74 |
| TFTTFT | 6.49 | 6.38 | 1.58 |
| 6-1H-P | 5.73 | 5.58 | 1.96 |
| 6-1F-P | 6.12 | 5.91 | 2.79 |
| pF-6P | 6.69 | 6.49 | 3.04 |
| 1H-FPPPPF | 6.28 | 6.14 | 2.25 |
| 1H-PFPPFP | 6.37 | 6.24 | 1.95 |
| 1F-FPPPPF | 6.55 | 6.37 | 2.90 |
| 1F-PFPPFP | 6.63 | 6.47 | 2.52 |
Relaxation energies and reorganization energies λ± (in eV) of hole and electron transport processes at the B3LYP/SV(P).
| Compounds | Hole-transport | Electron-transport | ||||
| λ+ | λ− | |||||
| 6T | 0.12 | 0.12 | 0.24 | 0.11 | 0.10 | 0.21 |
| pF-6T | 0.14 | 0.15 | 0.29 | 0.13 | 0.12 | 0.25 |
| FTTTTF | 0.13 | 0.13 | 0.26 | 0.14 | 0.14 | 0.28 |
| TFTTFT | 0.11 | 0.11 | 0.22 | 0.11 | 0.11 | 0.22 |
| 6-1H-P | 0.15 | 0.16 | 0.31 | 0.13 | 0.14 | 0.27 |
| 6-1F-P | 0.20 | 0.20 | 0.40 | 0.19 | 0.19 | 0.38 |
| pF-6P | 0.20 | 0.23 | 0.43 | 0.19 | 0.20 | 0.38 |
| 1H-FPPPPF | 0.15 | 0.15 | 0.30 | 0.15 | 0.16 | 0.31 |
| 1F-FPPPPF | 0.18 | 0.18 | 0.36 | 0.19 | 0.20 | 0.39 |
| 1H-PFPPFP | 0.13 | 0.14 | 0.27 | 0.12 | 0.13 | 0.25 |
| 1F-PFPPFP | 0.16 | 0.16 | 0.32 | 0.15 | 0.16 | 0.31 |
3.5 Reorganization energy
The reorganization energies (in eV) were calculated at the UB3LYP/SV(P) level. Table 6 lists the relaxation energies , and reorganization energies λ± of hole and electron transport processes. A selection of the maximal torsional angles and CC interring distances between the central moieties of these compounds in the neutral, cationic, and ionic states are presented in the Table 2.
The results in Table 6 show that in a hole-transport process involving the cationic state, the two reorganization energy components and are approximately equal. Similarly, the two components and for an electron-transport process involving the anionic species are also nearly equal.
Upon comparing the reorganization energies in the hole-transport (λ+) and electron-transport (λ−) processes of 6T and pF-6T, we notice that the values of λ+ = 0.25 eV and λ− = 0.21 eV for 6T are systematically smaller than the corresponding values λ+ = 0.30 eV and λ− = 0.25 eV for pF-6T. This difference can be explained by their respective geometric relaxations. When a charge-transport process occurs, both 6T and pF-6T increase the planarity in such a way that the main geometries parameters contributing to geometrical changes are the bond stretches. In 6T, the average CC bond shortening of 0.0270 Å in both the anion and the cation is significant. In pF-6T, a similar shortening of the CC of 0.025 Å in both the anion and the cation is found. The CF bonds lengthen slightly by 0.009 Å in the anion and decrease by the same amount in the cation. The reorganization energies in pF-6T are a bit larger than those in the 6T. Similarly, the increasing trend of λ+ and λ− for compounds with fluoro-substitution in the backbone is found in the order: pF-6P > 6-1F-P > 6-1H-P, 1F-FPPPPF > 1H-FPPPPF and 1F-PFPPFP > 1H-PFPPFP. The main factors governing this trend appear to be the changes in the CF bond and/or the PF bond lengths, which undergo expected geometric changes in the charged states.
Comparison of the reorganization energies λ+ and λ− for the compounds FTTTTF and TFTTFT shows that for the former bearing two terminal perfluoroarene rings, the energies λ+ = 0.26 eV and λ− = 0.27 eV are actually larger than the λ+ = 0.22 eV and λ− = 0.23 eV for the latter. This difference can again be explained by the geometrical variations (Table 2) that occur in the charged states. The CC bond stretches in FTTTTF are slightly shorter than those in TFTTFT, and the most significant change in FTTTTF is the torsional angle between both perfluoroarene and thiophene rings. This angle decreases from 17.6 to 6.3° and 4.0° in going from the neutral to the cationic and anionic states, respectively. Whereas in TFTTFT, the torsion angle changes only marginally (from 4.4 to 2.0° and 2.1°) for the cation or the anion, in FTTTTF, there is more relaxation in the charged states leading to an increase its reorganization energies. Similar trends are also found in the perfluoroarene-substituted oligophospholes, whose reorganization energies increase in the sequence: 1H-FPPPPF > 1H-PFPPFP and 1F-FPPPPF > 1F-PFPPFP.
In general, fluorine substitution in the oligomer backbone results in an increase of both the reorganization energies λ+ and λ− for hole- and electron-transport processes, due to the additional contributions of CF (for oligothiophenes) or PF (for oligophospholes) bond stretches. Replacement of a monomer unit (thiophene or phosphole) by the electron-withdrawing fluoroarene, for example, invariably leads to a marked variation of λ+ and λ−, due to changes in the ring torsions. Thus, the oligomers having two terminal perfluoroarene rings have a larger increase of λ+ and λ−, as compared with those having a perfluoroarene in the inner chain.
It is useful to compare the energy differences between λ+ and λ− in each compound to find out whether or not they are characteristic of n-type or p-type semiconductor materials. An n-type compound is expected when the magnitude of λ+ is larger than that of λ− and for a p-type compound, λ+ is smaller than λ−. The calculated λ+ values are larger than λ− for both unsubstituted oligomers 6T and 6-1H-P, and for the fluorinated oligomers pF-6T, 6-1F-P, and pF-6P so these compounds should be n-type materials. For oligomers with terminal perfluoroarene rings (FTTTTF, 1H-FPPPPF, 1F-FPPPPF), the values λ+ are smaller than the λ− ones so these should be p-type materials. Oligomers containing perfluoroarene rings within the backbone including TFTTFT, 1H-PFPPFP, and 1F-PFPPFP should be n-type materials, because their λ+ values are larger than their λ− counterparts.
Although variations in the magnitudes of λ+ and λ− for the series of compounds studied can be understood in terms of the geometrical changes occurred following ionization and electron attachment, other factors besides the energy difference between λ+ and λ− may play a role. Our prediction that pF-6T is an n-type semiconductor is in good agreement with previous theoretical [14a] and experimental [10,52] studies. The sequence of calculated reorganization energies, TFTTFT (λ+ = 0.22 eV) < 6T (λ+ = 0.25 eV) < FTTTTF (λ− = 0.27 eV), is consistent with the trend of experimental mobilities, (μ+ = 0.01 cm2/Vs) < 6T (μ+ = 0.03 cm2/Vs) < FTTTTF (μ− = 0.08 cm2/Vs). The type of transport predicted for these compounds based on λ+ and λ− is not well correlated with the reported results that 6T is better able to transport electrons than to transport holes [11,12]. In fact, 6T is well known to be a p-type semiconductor material. However, it should be stressed that the calculated λ+ = 0.25 eV is marginally larger than λ− = 0.21 eV. Although our calculated reorganization energies for 6T agree quite well with those previously reported [32], an oligomer having six units as used as our model may not be large enough to predict the properties of a much longer polymer. Similarly, FTTTTF is predicted to transport holes (λ+ = 0.26 eV is smaller than λ− = 0.28 eV), whereas TFTTFT can transport both holes and electrons with equal probability (λ+ = λ− = 0.22 eV). The hole motilities of FTTTTF and electron mobility of TFTTFT have been reported to be μ− = 0.08 cm2/Vs and μ+ = 0.01 cm2/Vs, respectively. In spite of the limited size of the oligomers considered, these results lend strong support for the view that although reorganization energy terms are important factors, they are not the only properties that determine the polarity of the charge carriers.
4 Concluding remarks
We have investigated the molecular structures and electronic properties of a series of thiophene and phosphole oligomers, substituted by either fluorine atoms or perfluoarence moieties. For the experimentally known oligothiophene derivatives (6T, pF-6T, FTTTTF, and TFTTFT), our calculations predict geometrical parameters in good agreement with the structures from X-ray diffraction studies. The electronic structure/thermochemical properties such as the HOMO and LUMO energies, the energy gap, ionization energies, and electron affinities are consistent with experimental results. Together, these show that pF-6T and FTTTTF are candidates for new n-type materials, whereas TFTTFT should be a p-type material. Fluorination of the oligothiophene (pF-6T) not only increases the chain planarity, thus enhancing its π-conjugation, but also reduces the LUMO energy, thus stabilizing the anion. The oligomers with terminal perfluoroarene rings are predicted to be p-type materials. For the unknown oligophospholes, the 6-1F-P and 1F-FPPPPF derivatives are found to exhibit interesting electronic properties such as small energy gaps, and a favorable LUMO stabilization, and can thus be regarded as potential candidates for n-type materials. In contrast, the 1H-PFPPFP oligomer has a larger HOMO stabilization and is predicted to be a p-type material. If these F-phosphole derivatives can be synthesized, they should have novel and interesting semiconductor properties.
Acknowledgements
MTN thanks the K.U.Leuven Research Council for continuing support (GOA and IDO programs), and the ICST supporting his stays in Vietnam. We are grateful to Dr. David Dixon, The University of Alabama, for his interest and valuable discussion.


