1 Introduction
The bonding of the beryllium diatomic molecule (Be2) in the ground state has attracted many researchers in the past. The spectroscopic study by Bondybey [1] reported the bond energy (De) of 790 ± 30 cm−1 and the bond length (Re) of 245 pm. Petersson and Shirley [2] have reported the vibrational constant (ωe) fitted on the observed data of 275.8 cm−1. Considering the compact closed-subshell structure of the ground atomic state (1s22s2), this bond can be regarded as astonishingly strong with relatively short equilibrium distance. The neighbour lithium atom which has an open-subshell (1s22s1) makes much stronger bond in the dimer Li2 with De = 8516.61 cm−1 according to the experimental data [3] while the best ab initio calculation gave 8353 cm−1 [4]. In this case, there exists an effective chemical bond made with both the covalent and resonant ionic contributions. In comparison, the magnesium dimer Mg2 has the bond energy less the zero-vibration energy (D0) of 404.1 ± 0.5 cm−1 and ωe = 51.12 cm−1 with Re = 389 pm according to the spectroscopic study of Li and Stwalley [5]. So, it appears that the Mg2 has the smallest metal-metal bond energy. The calcium dimer Ca2 has been observed and given De = 1102.08(9) cm−1 [6,7] and Re = 428 pm, ωe = 64.92 cm−1. The bond energy increase between Mg2 and Ca2 can be understood in terms of the increasing polarizability of the atoms. However, the singular data for Be2 cannot be explained in the same framework.
A recent paper by Røeggen and Almlöf [8] showed a long list of the experimental and theoretical studies on Be2 made in the past. To name only relatively recent quantum chemical studies, Evangelisti et al. [9] have made a full valence configuration interaction calculation with a basis set including f and g polarization functions and have shown the importance of high angular momentum functions in the basis. Stärck and Meyer [10] have made a multi-reference configuration interaction calculation including the core-valence interaction with an effective core potential, with f and g polariation functions, obtaining the bond energy (De) of 893 cm−1. The most recent theoretical study by Røeggen and Veseth [11] with an extended geminal model reported the bond energy (De) of 945 ± 15 cm−1. Those studies attempted to better understand the meaning of such strong bond between two compactly closed shell atoms.
In this paper, I report quantum chemical calculations on this state using different atomic basis sets and ab initio methods of different variational approximations. One might ask why another calculation would be necessary while there are already so many reported works, so it is necessary to explain the reason why. Indeed, past theoretical calculations were made in different times by different research groups using diverse methods. Although the essential conclusion drawn from those works should remain qualitatively valid, one may not easily compare the different compositions of the electron correlation quantitatively. Here, I tried to use a coherent set of bases and methods to study the interatomic interaction in a more systematic way than before to analyze quantitatively the different results obtained from them, so that one might clearly distinguish different levels of the electron correlation effect.
In experimental point of view, the highest lying vibrational energy levels are not reported yet, although a large number of levels were determined. The past experimental and theoretical data are also compared in this paper to estimate the most accurate spectroscopic data.
2 Method of calculation
Here, the atomic basis sets are generated in a systematic way to avoid unwanted basis set superposition errors and allow progressively higher angular momentum components. The molecular energy is calculated using the multi-reference single and double configuration interaction (MRCI) method, which is one of the mostly tested variational methods where the result is generally known to be reliable. The Gaussian type orbitals (GTO) are used for the atomic basis functions where the exponents of s- and p-type orbitals were determined from the Hartree-Fock (HF) calculation of the ground state beryllium atom using a program derived from ATOM [12]. At first, a set of 15 s-type GTOs were obtained to minimize the HF energies of the ground state (2s2, 1S) and the excited state 2s3s (3S), which thus includes diffuse functions. Then 8 p-type GTOs were obtained to minimize the 2s2p (3P° and 1P°) states. These 15s8p GTOs constitute the smallest basis set common to all other bases. To this, various numbers of the polarization and correlation functions (d, f, g, h) were added, including 5d GTOs for the (2s3d, 3D and 1D) states. Then molecular energy calculated in the MRCI was minimized with given polarization and correlation basis functions. The details about the choice of basis set will be explained in the result section. For the molecular calculations, the MOLCAS program suite [13] was used. The D2h point-group symmetry was used for the HF and CI calculations.
The largest basis set used was 15s8p5d3f2g1h, which makes in all 228 molecular orbitals, and where no orbital was discarded from the multi-reference HF and CI calculations. The CI involved the valence electron correlation by the MRSDCI scheme and the core-valence electron correlation by including as supplementary all single excitations from the core electrons. The largest CI calculation, which could be done with given computational conditions involved more than five million configuration state functions (CSF) for the ground state. Both the valence-only CI (VCI) and core-valence CI (CVCI) were performed. In the latter case, only all possible single excitations from the core electron (1s2) but not the core-core type double excitations were allowed in constructing the configuration state functions.
Similar ab initio calculation on the ground state of Li2, mentioned in above [4], gave 98.1% of the experimentally determined dissociation energy where the experimental value is considered as very accurate. It seems that the best experimental bond energy of Be2 known today [1], where the observed vibrational levels were extrapolated, has not the same degree of accuracy as in the Li2 case [3]. One might assume that the ab initio calculation presented in this work for Be2 would have the similar accuracy as in the Li2 case, with the error in the bond energy of about 2%.
3 Result and discussion
When only the 15 s and 8p GTOs are used in the VCI, a very weak long-range potential well of the van der Waals nature is obtained with Re = 503 pm and De = 26 cm−1 as can be seen in Table 1 and Fig. 1. The addition of the core-valence electron correlation effect through CVCI does not change the result. In the second calculation was added one d-type GTO for more polarization and correlation effects. The best exponent, i.e. which gives the lowest total energy, depends slowly upon the internuclear distance (R). It is 2.5 at R = 4.5 bohr (atomic unit) and 2.8 at infinity. When one d-type GTO with 2.5 was used for all R, the potential energy curve presented two minima, the lowest one at short distance and the higher one at large distance (spd in Fig. 1). In 1970s, this brought about a dispute about the origin of these double minima. When the exponent of the d-type GTO was varied as a function of R, the large-distance minimum disappeared leaving still a non-typical curve (spd′ in Fig. 1). The minimum around 255 pm gave somewhat larger bond energy, 240 cm−1 in VCI and 226 cm−1 in CVCI.
Bond energy (De, in cm−1) and bond distance (Re, in pm) of Be2 in the ground state calculated using different basis sets and valence configuration interaction (VCI) and core-valence configuration interactions (CVCI).
| Basis sets | Methods | De (cm−1) | Re (pm) |
| 15s8p | VCI | 26 | 503 |
| CVCI | 27 | 502 | |
| 15s8p1da | VCI | 240 | 256 |
| CVCI | 226 | 255 | |
| 15s8p5d | VCI | 392 | 255 |
| CVCI | 413 | 252 | |
| 15s8p5d1f | VCI | 690 | 250 |
| 15s8p5d3f | VCI | 716 | 250 |
| CVCI | 747 | 247 | |
| 15s8p5d3f2g | VCI | 789 | 248 |
| CVCI | 825 | 246 | |
| 15s8p3f2g1h | VCI | 784 | 248 |
| CVCI | 833 | 244 | |
| Experimentalb | 790 ± 30 | 245 |
a Inner well, see text.
b From Bondybey [1].
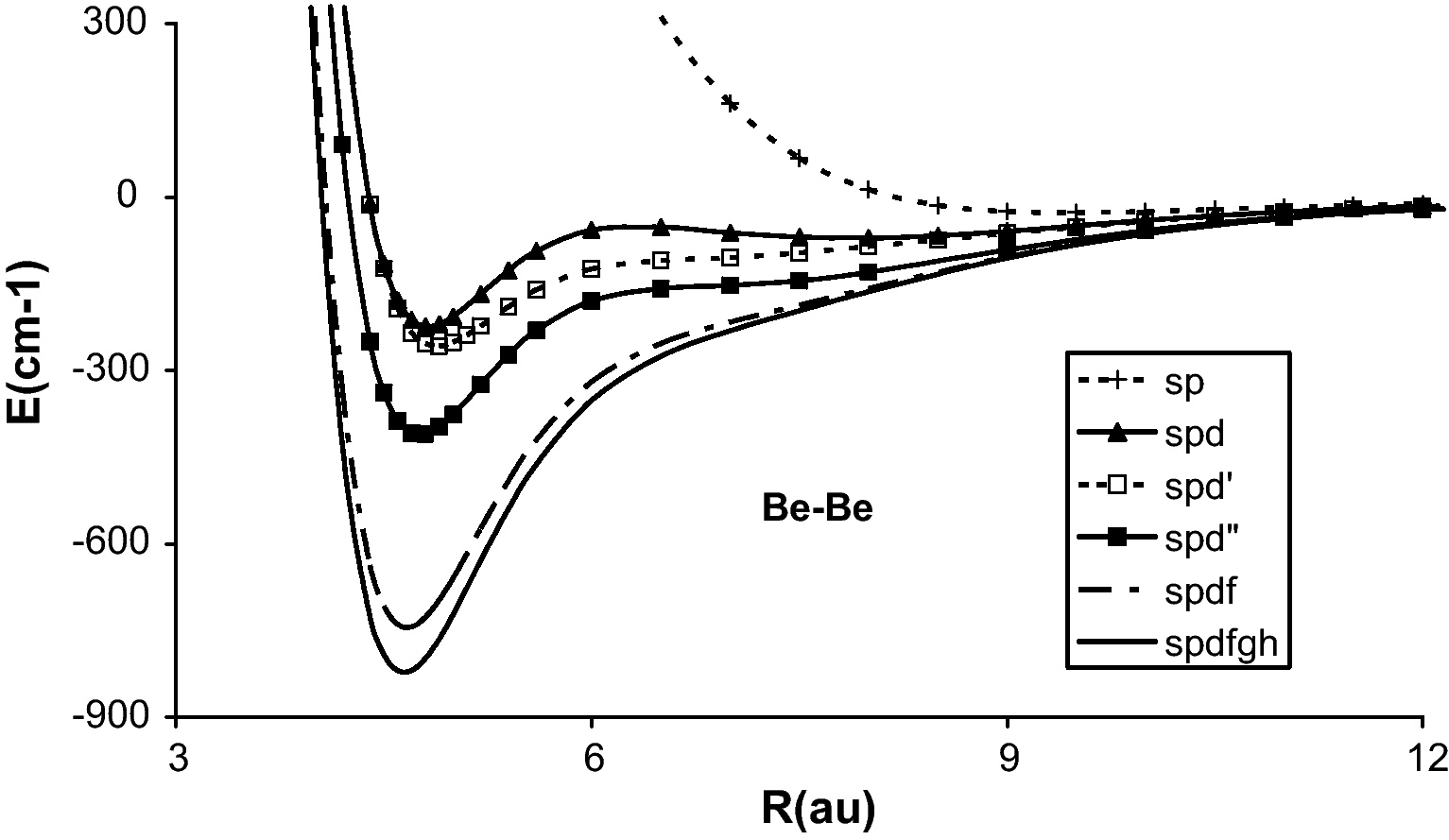
Potential energy curves of the ground state of Be2 calculated with the configuration interactions.
When five d-type GTOs were used (15s8p5d basis, spd″ in Fig. 1), the bond distance changed little but the bond energy increases significantly to 392 cm−1 (VCI) and 413 cm−1 (CVCI). It is interesting that the core-valence electron correlation effect increases in this case the bond energy, contrary to the 15s8p1d case.
One f-type GTO which minimizes the total energy at 4.5 bohr was found to have exponent 0.28. Addition of this atomic basis function furthermore increases the bond significantly to 690 cm−1 in VCI. This function was split into three functions according to the well-tempered way, that is, by multiplying and dividing by a given factor. The best factor appeared to be 1.8, so three f-type GTO with exponents of respectively 5.04, 2.8 and 1.556 were used, making the 15s8p5d3f basis. This basis gave the bond energy of 716 cm−1 (VCI) and 747 cm−1 (CVCI) at respectively 250 pm (VCI) and 247 pm (CVCI).
Analogously, one (with exponent 0.37) and two (exponents 0.37 × 1.4 and 0.37/1.4) g-type GTOs were added. This addition further increases the bond energy to 789 cm−1 (VCI) and 825 cm−1 (CVCI) and shortens the bond distance to 248 pm (VCI) and 246 pm (CVCI).
Finally, one h-type GTO with the best exponent of 0.45 at R = 4.5 bohr was added. The basis set superposition error, according to the counter-poise method of Boys and Bernardi, has been taken into account here. The total basis set superposition error about the bond distance (4.6 bohr) is less than 6 cm−1 which is much smaller than the interaction energy. This basis gave the largest bond energy 784 cm−1 (VCI) and 833 cm−1 (CVCI) with the bond length of 248 pm (VCI) and 244 pm (CVCI).
As can be seen in Table 1 and Fig. 1, the successive increase of the basis set size deepens the potential well and brings the bond distance to a shorter one, as is the case in general in metal-metal bonding. Except for the basis set too poor in the polarization and correlation functions, i.e. lacking higher angular momentum functions, the core-valence electron correlation also increases the bond energy and shortens the bond distance, as was studied before in the alkali dimers [14]. The potential energy curve obtained by employing the largest basis 15s8p5d3f2g1 h and subtracting the basis set superposition errors is reported in Table 2, which could be useful to the spectroscopists and others.
Potential energy curve of the ground state of Be2 calculated with the 15s8p3f2g1 h basis set (R in bohr i.e. atomic unit and E in cm−1).
| R (au) | E (cm−1) |
| 2.5 | 44562.3 |
| 2.6 | 38151.9 |
| 2.7 | 32060.7 |
| 2.8 | 26538.3 |
| 2.9 | 21519.0 |
| 3 | 17248.2 |
| 3.1 | 13659.6 |
| 3.2 | 10670.1 |
| 3.3 | 8198.5 |
| 3.4 | 6170.3 |
| 3.5 | 4519.5 |
| 3.6 | 3189.0 |
| 3.7 | 2128.0 |
| 3.8 | 1293.4 |
| 3.9 | 647.4 |
| 4 | 157.2 |
| 4.1 | –205.5 |
| 4.2 | –464.8 |
| 4.3 | –641.4 |
| 4.4 | –752.7 |
| 4.5 | –813.5 |
| 4.6 | –836.2 |
| 4.7 | –830.9 |
| 4.8 | –806.1 |
| 4.9 | –768.3 |
| 5 | –722.8 |
| 5.2 | –623.8 |
| 5.4 | –530.2 |
| 5.6 | –450.3 |
| 5.8 | –386.0 |
| 6 | –336.6 |
| 6.5 | –260.4 |
| 7 | –218.6 |
| 7.5 | –187.1 |
| 8 | –157.5 |
| 9 | –103.3 |
| 10 | –62.6 |
| 11 | –36.7 |
| 12 | –21.6 |
| 13 | –13.0 |
| 14 | –8.1 |
| 15 | –5.2 |
4 Conclusion
This work showed one extreme case of metal-metal bonding where the electron polarization and correlation effects play a crucial role in the bond energy. Another famous case is the chromium dimer (Cr2) where no quantum chemical method has succeeded in fully reproducing the observed bond properties. In particular, the long distance weak potential well was obtained and there was a historic debate on the possibility of the double potential wells, while no experimental evidence was reported to support such strangeness. In fact, it is not possible now to make a similar study in the case of Cr2 as was done in this work due to a larger number of electrons and the necessity of employing a much larger basis.
There was much interest to cool down the alkaline-earth atoms to ultracold temperature. The potential well and the long-range interatomic interaction of the dimers are so important to study that phenomenon [15]. One can find the most recent potential energy curves for the Mg2, Ca2, Sr2 and Ba2 diatomic molecules in the NIST website [16]. The quantum scattering calculation on the ground state Be atom has been reported before [17].


