1 Introduction
Heteropolyoxometalates are known to be very active in both acidic or redox reactions [1–3]. The most used compounds have the well-known Keggin structure [XM12O40]n− where one X heteroatom (typically phosphorus or silicon) is surrounded by 12 MO6 (M = W, Mo) octahedra which are assembled as four M3O13 triads [4]. Depending on the relative orientations of these triads, five different isomers, denoted as α, β, γ, δ and ɛ can be expected. Practically, only the α and β isomers, even if the structure of the γ isomer of [SiW12O40]4− has been reported recently [5], are known. The α isomer has the Td geometry and the 12 M atoms are equivalent. In contrast, the β isomer, obtained by rotation of 60° of one M3O13 triad, has the C3v geometry, leading to three different M atoms. These two isomers can interconvert and if the α isomer is usually the most stable for the fully oxidized heteropolyoxometalate, the β form can be more stable in some cases [6].
Unfortunately, these species are only stable in acidic media (pH < 2) and partially decompose when the pH increases. At pH around four, monolacunary complexes [XM11O39]p− are formed, corresponding to the loss of one M=O group. Four isomers can be formed (Fig. 1), depending on what M=O group has been lost: one isomer (α) when starting from α-XM12O40n− and three isomers (denoted as β1, β2 and β3) when starting from β-XM12O40n−. When X = Si and M = W the four isomers have been synthesized and some of their characteristics such as infrared spectra and 183W NMR data were reported [7,8]. These four isomers are also in equilibria, the transformations shown in Fig. 1 occurring, the most stable isomers being always the α ones.
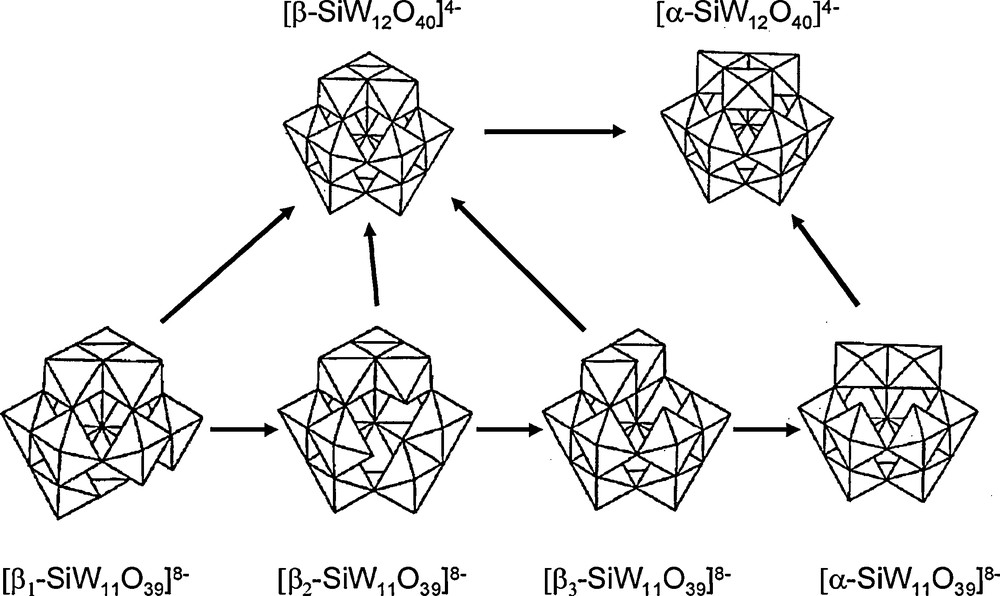
Isomers of the dodecatungstosilicate and undecatungstosilicate anions and their interconversions.
Experimentally, the stability order of these four isomers is then β1 → β2 → β3 → α [9]. To our knowledge, up to now, there is only one theoretical study of these monolacunary species: Laurencin et al. reported a theoretical study of the relative studies of the α and β3 isomers of [XW11O39]m− (X = P, Si) and used these results to interpret the structural differences in the metallic frameworks of the ruthenium derivatives of these compounds [10]. One reason of the lack of studies on these compounds is probably their lowest symmetry compared to the saturated [XM12O40]n−, for which many theoretical studies have been achieved this last decade (for a review, see [11–13]). For example, for the α isomer, the symmetry decreases from Td to Cs, leading to six different types of M atoms instead of one. This results in a drastic increase in the calculation time. Therefore, such calculations would have been unfeasible when the first quantum calculations on polyoxometalates were undertaken by M.M. Rohmer, M. Benard and co-workers [14–16]. As computation facilities now allow calculations on big systems, we have undertaken a theoretical study of these four polyoxometalates with the aim to determine if we were able to retrieve the experimental order of stability of the four isomers. The infrared spectra and 183W NMR chemical shifts of the four species were also calculated and compared to the experimental data, in order to check the validity of the calculations.
2 Computational details
2.1 Starting models
The four starting structures were created with the assumed geometries and symmetry operations and expressed as Z-matrices in order to keep the symmetry group unchanged during the optimizations. Some calculations were made with an alkaline atom in the lacuna of the polyoxometalate and solvent effects were also studied, as it had been reported that they could be of great importance [17].
2.2 Calculation details
DFT calculations were performed on the four isomers, using the ADF05/9 packages [18]. As is well known, the ADF uses Slater-type orbitals as basis functions. The frozen core approximation (small cores) has been retained for the geometry optimization of the complexes. This approximation assumes that molecular orbitals (MOs) describing inner shell electrons remain unperturbed in going from a free atom to a molecule. Thus, these inner electrons can be excluded from the variational procedure and, instead, be pre-calculated in an atomic calculation and kept frozen thereafter. The justification for this approximation is that the inner shell electrons of an atom are less sensitive to their environment than are the valence electrons. This approximation, widely used by ADF users, has been proved to (efficiently) lead to a structure extremely close to those obtained through all electron calculations. The geometries were optimized at the LDA level (VWN functional, [19]). It has been shown that for inorganic compounds, the geometries obtained at the LDA level are closer to experiment than those using GGA functionals or hybrids, which lead to larger bond lengths [20]. Furthermore, both of these approximations save a substantial computational time, in particular, for the calculation of the IR spectra. On the contrary, for the calculation of the shielding tensor (vide infra), it is necessary to take into account any change in all orbitals, including core orbitals which, being localised near the nuclei, are strongly interacting with the nuclear spin momentum. We have, therefore, calculated the shielding tensor with all electrons basis sets, and also performed calculations of relative total energies (namely relative bonding energies) with all electron basis sets, in order to evaluate the sensitivity of the calculation to the choice of the exchange-correlation functional. This can be done with the ADF keyword “metaGGA”. For the purpose, the orbitals were calculated at the GGA level with the PBE gradient-corrected exchange–correlation functional [21–23] and the TZP (Triple Zeta plus Polarisation) basis sets were retained for all these calculations, whereas DZP (Double Zeta plus Polarisation) basis sets were retained for all with small frozen cores at the LDA level. Finally, geometry optimizations were performed with the Scalar ZORA relativistic correction, whereas the 183W shielding tensor was calculated with the Spin-orbit ZORA relativistic correction [24]. All the structures were characterized by vibrational analysis in the harmonic approximation, with no imaginary frequency indicating that the molecular states are stable, and providing a full theoretical IR spectrum. The theoretical spectra are plotted through a convolution of the peaks with Gaussians (FWHM = 10 cm−1). No solvent modelling has been taken into account. It has been shown in many papers, e.g. dealing with [XM12O40]n−, that it may slightly affect the relative energies of isomers, reducing the energy differences by at most 8 kJ.mol−1 [13].
The functionals retained for the discussion were LDA (VWN) [19], VS98 [25], PBE [21–23], BmTau1 [26], TPSS [27,28], M06-L [29], TPSSh [27,28], B3LYP (VWN5) [30], PBE0 [31,32] and M06 [33].
The calculations with alkaline cations were performed with Gaussian 09 [34] on models consisting in small clusters composed of the five oxygen atoms of the lacuna and five hydrogen atoms placed along the W-O and Si-O bonds. The total charge of the cluster was chosen as −1 (as there are eight negative charges for the 39 oxygen atoms of the [SiW11O39]8− ion, the charge on five oxygen atoms should be ca. −1). The hydrogen positions were first optimized (at the B3LYP/6-31+G* level). That cluster is then kept frozen and the alkaline cation was then introduced and its position was optimized (at the B3LYP/6-31+G* level for Li, Na and K and with the LanL2DZ pseudopotential for Rb and Cs) in the frozen cluster.
3 Results and discussion
3.1 Comparison of the relative energies of the four isomers
The calculations were performed with a variety of exchange-correlation functionals implemented in ADF in order to determine the best choice for the descriptions of the four lacunary polyoxometalates and assess the reliability of the functional for this class of compounds. The criteria which was chosen was the experimental order of stability of the four isomers (β1 → β2 → β3 → α). Table 1 gives the compiled energies of the four isomers for some representative methods. A full table of energies obtained with a large panel of exchange-correlation functionals is given in Supplementary Materials. From the values one could calculate average energies. Interestingly is the rather small standard deviation (ca 6 kJ.mol−1) which may be disturbed by one or two functionals inappropriate for this kind of systems and which provides an estimation of the confidence of these energies. It shows in the same time that differences of functionals within their category (GGA, metaGGA, hybrids, with dispersion terms…) are rather small. Here, clearly only the LDA(VWN) method leads to results quite similar to the experimental ones, the β3 and α isomers having quite the same energy whereas the β1 and β2 ones are less stable. If the energy difference is relatively high from the β1 to β2 and from the β2 to β3 and α isomers (ca. 10 kJ.mol−1) and can reflect the experimental data, the energy difference between the β3 and α isomers is small and cannot reflect the complete transformation into the α isomer at room temperature which is observed experimentally. Such an observation has also been made by Laurencin et al. who performed calculations on the α and β3 isomers [10]. In order to better explain the experimental data, they made additional calculations with including an atom in the lacuna or in presence of a solvent but in all cases they were unable to reproduce the experimental features.
Compilation of the energies of the four isomers of [SiW11O39]8− as a function of the calculation method.
| β3 isomer | β2 isomer | β1 isomer | α isomer | |
| LDA(VWN) | 0 | 10.0 | 21.3 | 1.5 |
| GGA-metaGGA | ||||
| PBE | 0 | 14.9 | 25.3 | 9.6 |
| BmTau1 | 0 | 23.1 | 32.0 | 17.9 |
| TPSS | 0 | 12.9 | 22.9 | 7.9 |
| M06-L | 0 | 20.2 | 22.5 | 14.2 |
| VS98 | 0 | −9.5 | 4.7 | −12.7 |
| Hybrids | ||||
| TPSSh | 0 | 13.1 | 23.4 | 7.7 |
| B3LYP(VWN5) | 0 | 18.0 | 28.2 | 10.9 |
| PBE0 | 0 | 15.0 | 25.9 | 8.6 |
| M06 | 0 | 13.5 | 26.7 | 3.9 |
3.2 Description of the optimized structures
The four optimized structures are in full agreement with the proposed ones, the expected symmetries being kept whatever the calculation method used. However, as only the LDA(VWN) method leads to relative energies the closest to what is experimentally expected, we will mainly discuss the corresponding structures by this way. As far as the energies obtained with (meta) GGA and hybrid exchange-correlation functionals are concerned, quite similar trends are obtained with most functionals, VS98 excepted, which is known to perform only with organic systems. These trends are in agreement with experiment for the relative energies of the β1, β2 and β3 structures, but do not reproduce the greatest stability of α with respect to β3.
The domain range of the various W-O and Si-O bonds for the four isomers are listed in Table 2 (the list of coordinates of the four optimized structures are given in the supporting information) together with the corresponding experimental data for [SiW12O40]4− and [SiW11O39]8− derivatives. As there are no X-ray structures for undecatungstosilicates without transition metal in the lacuna, the comparisons can be relatively difficult. However, some conclusions can be drawn.
Theoretical and experimental distances (in Å) for the four isomers of [SiW11O39]8− and for some related compounds.
| Compound | Si-Oa | W-Oa | W-Ob | W-Oc | W-Od | W-Oe | Ref. |
| β1-[SiW11O39]8− | 1.699–1.742 | 2.268–2.458 | 1.816–2.152 | 1.849–2.117 | 1.771–1.783 | 1.757–1.766 | This work |
| β2−[SiW11O39]8− | 1.701–1.742 | 2.239–2.497 | 1.799–2.218 | 1.836–2.148 | 1.769–1.782 | 1.754–1.767 | This work |
| β3−[SiW11O39]8− | 1.713–1.738 | 2.255–2.677 | 1.812–2.190 | 1.828–2.132 | 1.773–1.782 | 1.756–1.771 | This work |
| α-[SiW11O39]8− | 1.700–1.735 | 2.259–2.495 | 1.817–2.156 | 1.841–2.124 | 1.774–1.786 | 1.762–1.763 | This work |
| [SiW12O40]4− | 1.594–1.627 | 2.320–2.387 | 1.885–1.908 | 1.925–1.953 | 1.694–1.697 | – | [35] |
| [SiW12O40]4− | 1.57–1.64 | 2.32–2.42 | 1.85–1.94 | 1.89–1.96 | 1.66–1.71 | – | [36] |
| [SiW12O40]4− (theory)a | 1.667 | 2.325 | 1.916 | 1.937 | 1.743 | – | [37] |
| [Ru(dmso)3(H2O)SiW11O39]6− | 1.59–1.64 | 2.25–2.50 | 1.78–2.12 | 1.87–2.06 | 1.68–1.75 | 1.74–1.82 | [38] |
| [Cu(H2O)SiW11O39]6− | 1.591–1.654 | 2.315–2.369 | 1.848–1.963 | 1.881–1.991 | 1.687–1.751 | – | [37] |
a Calculations method: B3LYP with the LANL2DZ pseudopotential for W and the 6-31G(d) basis set for all other atoms.
The calculated distances are quite similar to the experimental ones, with the exception of the Si-O ones which are slightly larger. When comparing the calculated values to those of the saturated Keggin ion [SiW12O40]4− there is a larger extend of variation of all W-O distances in the lacunary polyoxometalates, with, as expected, a more significant variation of the W-Ob distances which correspond to oxygen atoms between two triads. This shows clearly that the lacunary Keggin species are less constrained. These observations are also in agreement with the data reported for [Cu(H2O)SiW11O39]6− [37] and [Ru(dmso)3(H2O)SiW11O39]6− [38]. In the first case the copper atom is linked to the four oxygen atoms of the lacuna resulting in a structure quite similar to that of [SiW12O40]4− with only a small variation of the W-O distances. In the second case, the ruthenium atom is linked to two Od oxygen atoms, the oxygen atoms of the lacuna being free and so the structure is less strained. A comparison of the calculated values for the four isomers and for this compound shows that the distances ranges are quite comparable. When comparing the four isomers themselves, there is no clear difference from one to another, all distance ranges being quite the same. However, it is clear that in all cases the W-Oe bond is a double bond and it is always slightly shorter than the corresponding W-Od bonds. This result is also in agreement with the X-ray structure of the ruthenium derivatives. Note also that the calculated values are also in agreement with ref. [39]. The labelling of the different oxygen atoms is shown on Fig. 2.
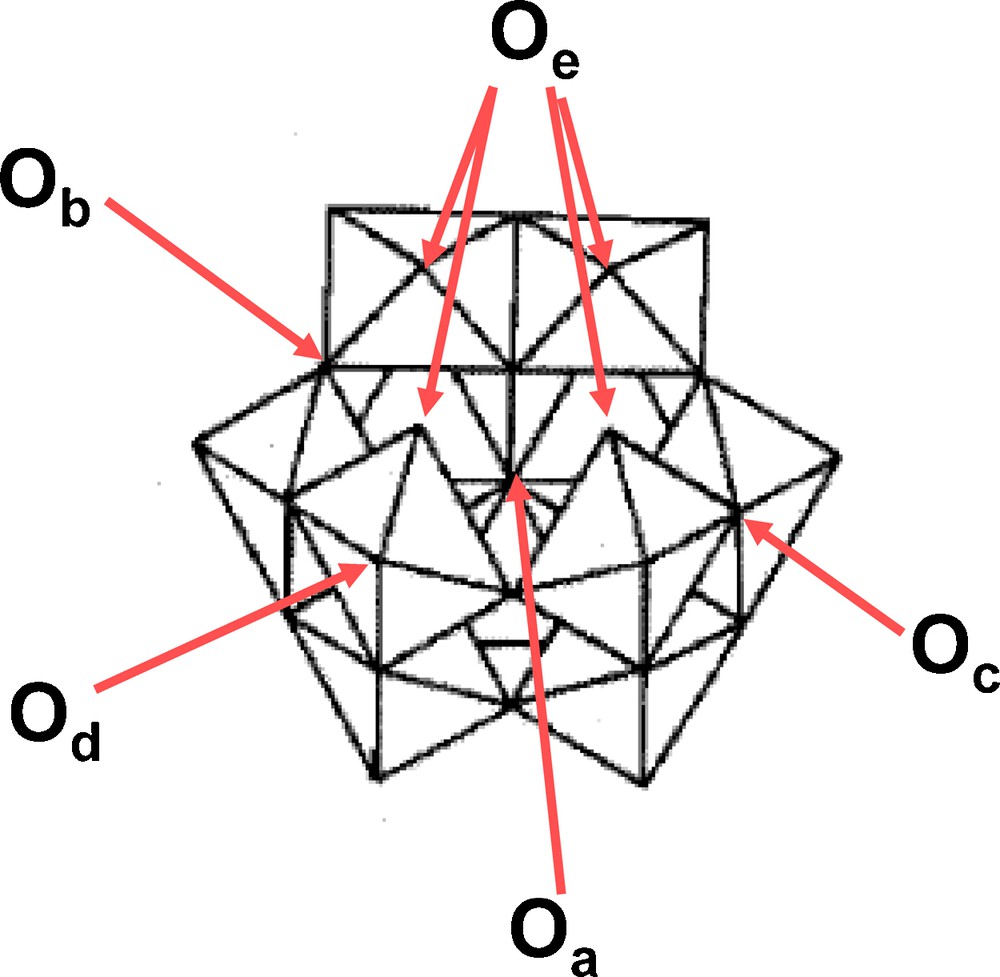
Labelling of the different oxygen atoms of [SiW11O39]8− depicted in the case of the α isomer.
A more detailed analysis of the four isomers can be made by studying the oxygen atoms of the lacuna. Fig. 3 displays the position of these four atoms together with that of the corresponding Oa oxygen atom with the corresponding distances. For the β1, β3 and α isomers the four oxygen atoms are in the same plane and lie at the corners of a rectangle. In the case of the β2 isomer, the four atoms are not in the same plane. There is also a noteworthy difference from one isomer to another, the diagonal of the rectangle varying from 4.88 Å for the β1 isomer to 5.20 Å for the β3 isomer. Clearly, the four isomers should serve as cryptates for different cations and this could be a method for their selective preparation (in the syntheses described in [7] only the potassium salt is used). In order to better quantify this assumption, some additional calculations were performed with a small cluster model composed of the five oxygen atoms of the lacuna and five hydrogen atoms along the M-O bonds (M = Si, W) and the alkaline cation. We choose to perform these calculations on this small cluster rather than on a system comprising all the polyoxometalate in order to model the first step of the interaction of the polyoxometalate with the alkaline cation and to avoid heavy computational resources. Indeed, the structure of the polyoxometalate will be strongly modified upon coordination of the cation (see, for example, the data for [Cu(H2O)SiW11O39]6− in Table 2) and so these calculations are only semiquantitative, if not qualitative. The positions of the hydrogen atoms were first optimized along the M-O bonds by assuming a global charge of −1 for the (HO)5 cluster (corresponding to the mean value deduced from the charge of the complete polyoxometalate, −8 for 39 oxygen atoms). This cluster was then kept frozen and the position of the cation optimized.
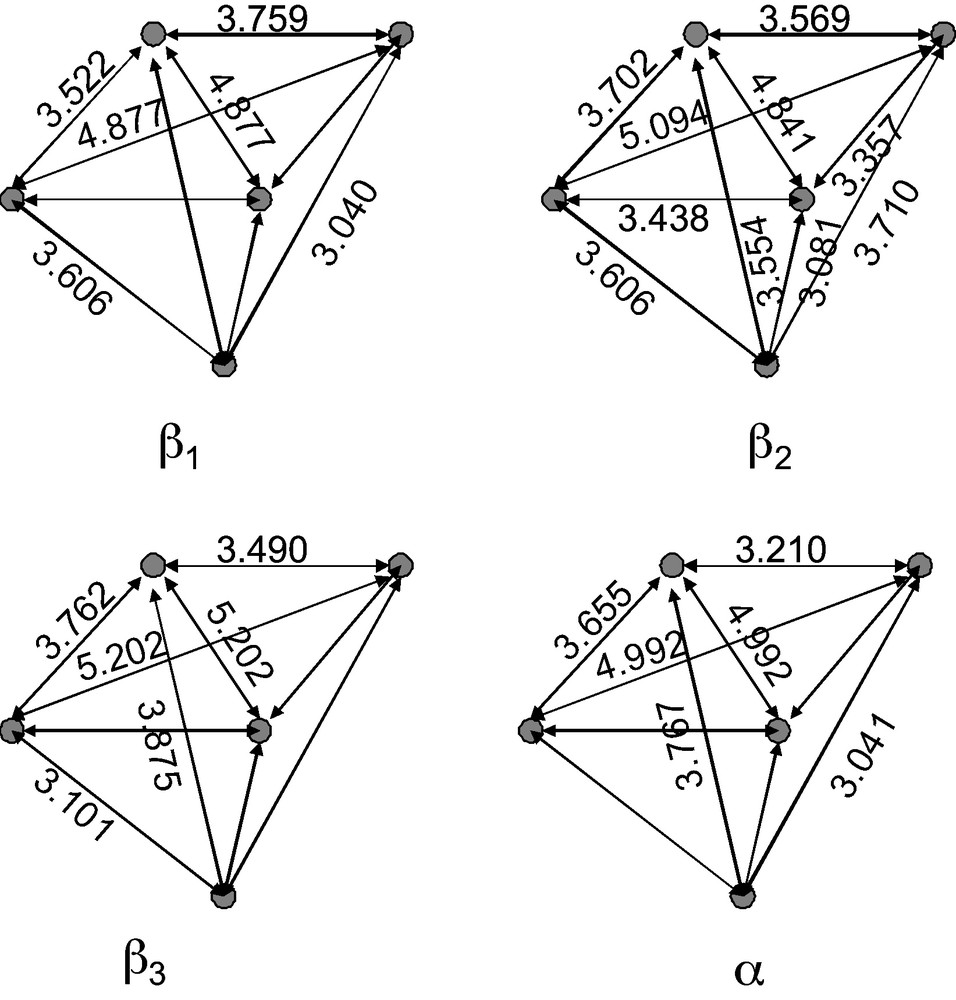
Relative positions of the five oxygen atoms of the lacuna for the four [SiW11O39]8− isomers. The oxygen atom below is the Oa one while the four atoms in quite the same plane are Oe.
In order to achieve reliable results, the energies of the (HO)5 cluster was then substracted from those of the corresponding [(HO)5-M] systems and finally all energies were given relative to that of the β3 polyoxometalate. The corresponding energies are listed on Table 3. All these energies are negative showing that the formation of the POM-cation complex is favored. This observation is in agreement with experimental data which show that in all cases the lacuna is filled by a cation which is difficult to remove. Clearly the lithium and sodium cations should favor the β1 structure while the caesium cation should strongly penalize the β3 structure. It is evident that these preliminary calculations can only give trends as they do not take into account the restructuration of the polyoxometalate which will occur after the insertion of the cation but they can be taken as a starting point for more sophisticated studies.
Energies (in kJ.mol−1) of the various (HO)5-M systems as a function of M and of the polyoxometalate.
| Lithium | Sodium | Potassium | Rubidium | Caesium | |
| Beta 1 | −51.6 | −45.1 | −25.7 | −27.0 | −65.9 |
| Beta 2 | −28.7 | −31.5 | −18.4 | −11.1 | −55.8 |
| Beta 3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Alpha | −28.6 | −26.6 | −12.2 | −15.5 | −55.3 |
3.3 Charges analysis and orbitals
The Mulliken and Hirshfeld charges of the different atoms are given in the supplementary material. There is no major difference between the four isomers. When looking at the Mulliken charges, the four oxygen atoms of the lacuna (without taking into account the atom linked to silicon) have the lowest negative charge, typically between −0.64 and −0.71 while both the terminal W=O and the bridging W-O-W oxygen atoms have a slightly more negative charge, between −0.78 and −0.95. The highest charges are localized on the oxygen atoms of the SiO4 tetrahedron, betwen −0.92 and −0.97. When looking at the Hirshfed charges, the situation is rather different with here also quite the same values for the four isomers. The oxygen atoms of the SiO4 tetrahedron and those bridging two triads have quite the same charge, ca. −0.31 while those of the lacuna and of bridging atoms of the same triad have a charge of ca −0.36 and the terminal ones a charge of ca. −0.48. Even if these values should be taken with care, as pointed out by Courcot et al. [40], it appears that the oxygen atoms of the lacuna are not those having the highest charge, in contrast with what could be expected. A consequence should be that the interaction with cations should not be, from an electrostatic point of view, with these atoms but with the terminal ones. Analysis of the frontier orbitals is also in agreement with that assumption. Indeed both the HOMO and LUMO are mainly localized on two terminal oxygen atoms of WO6 octahedra of the lacuna, showing that the reaction of the polyoxometalate will first take place on these oxygen atoms, as observed experimentally in [Ru(dmso)3(H2O)SiW11O39]6− [38]. Displacement into the lacuna should then occur in a second step and should correspond to a further stabilization by completing the Keggin structure.
3.4 Infrared spectra
The calculated infrared spectra of the four isomers of SiW11O398− are displayed on Fig. 4. As the experimental spectra were reported in [7], it is possible to compare these two sets of data. One of the main experimental differences between the four isomers is the shift of the high frequency band in the order α (1000 cm−1), β1 (990 cm−1), β2 (988 cm−1) and β3 (985 cm−1). The other main difference is the 850–900 cm−1 range where the number and/or the positions of the bands differ from one isomer to one another. If there is a qualitative good agreement between the experimental and theoretical numbers of bands, there is, however, a discrepancy in the positions, which are always at lower wavenumbers for the theoretical values as generally observed. The order of the high frequency band is also different, but this can be due to the fact that the calculations were made for a naked polyoxometalate while the experimental spectra correspond to salts. Indeed, it had been shown that the position of these bands were highly dependent on the nature of the countercation, the position of the bands being shifted by more than 10 cm−1 [41].
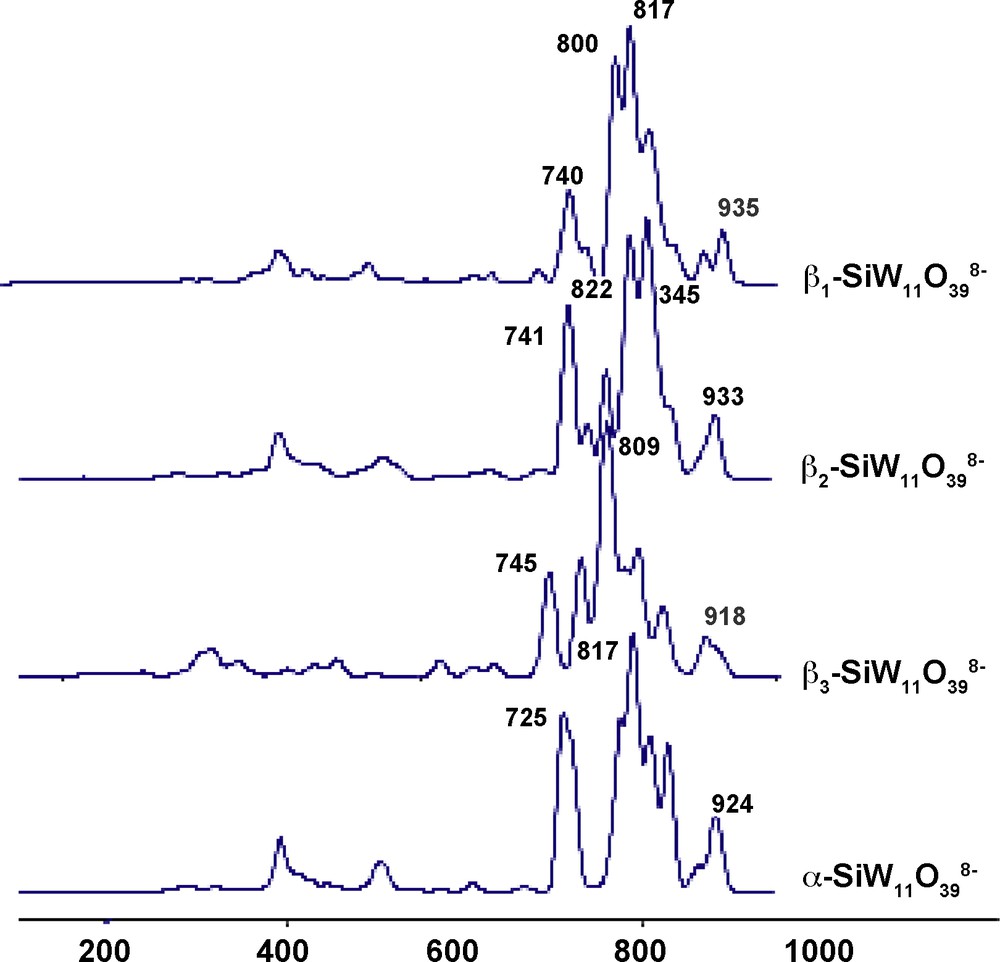
Calculated infrared spectra of the four isomers of [SiW11O39]8−.
3.5 NMR spectra
The 183W absolute chemical shifts of the tungsten atoms in the four isomers were calculated and compared to the experimental values depicted in ref [8]. The Uncoupled GIAO-DFT method together with ZORA relativistic corrections have led to an excellent description of the NMR spectra of complexes involving heavy metals such as 195Pt platinum complexes [42,43] or Hg complexes [44]. The implementation of the method into ADF code is described in refs [44–48]. Classically, in order to make easier the comparison, the calculated NMR shieldings are transformed into relative chemical shifts by using the relation δrel = δref − δabs, where δref is the NMR shielding of a reference (typically Na2WO4 in a 2 M aqueous solution for 183W NMR). However, such a method can lead to increased errors as the chemical shifts are calculated for two compounds and we preferred to compare the absolute theoretical chemical shifts to the experimental ones.
If there is a very good agreement between these two sets, a linear correlation is obtained between them, and the slope of this line of the plot should be −1. Table 4 shows, for the four isomers, the calculated NMR shieldings together with the experimental values and their attributions made on the basis of our results and of the experimental data. Fig. 5 shows the correlation between the experimental and theoretical chemical shifts based on the assignments proposed in Table 4. The attributions of the experimental data are made by assuming that the experimental NMR 183W chemical shifts increase when the theoretical ones decrease, without taking into account the assignments proposed by Smith et al. in their paper [8].
Theoretical (absolute) and experimental (relative to 1 M Na2WO4) 183W NMR chemical shifts of the four isomers of SiW11O398−.
| Atom | α-SiW11O398− | β1-SiW11O398− | β2-SiW11O398− | β3-SiW11O398− | ||||
| Th. | Exp. | Th. | Exp. | Th. | Exp. | Th. | Exp. | |
| W1 | – | 685.5 | −153 | 640.7 | −130 | – | ||
| W2 | 597.0 | −127 | 592.9 | −104 | 630.5 | −113 | 605.5 | −137 |
| W3 | 597.0 | −127 | 592.9 | −104 | 652.7 | −143 | 605.5 | −137 |
| W4 | 576.2 | −115 | 609.1 | −120 | 604.2 | −82 | 630.9 | −157 |
| W5 | 618.8 | −142 | 598.2 | −141 | 684.4 | −171 | 605.2 | −136 |
| W6 | 573.3 | −100 | 635.6 | −140 | 630.7 | −117 | 613.0 | −138 |
| W7 | 576.2 | −115 | 618.9 | −166 | – | 639.9 | −163 | |
| W8 | 618.8 | −142 | – | 621.1 | −106 | 640.6 | −52 | |
| W9 | 573.3 | −100 | 618.9 | −166 | 611.1 | −99 | 639.9 | −163 |
| W10 | 602.5 | −120 | 598.2 | −141 | 700.3 | −177 | 605.2 | −136 |
| W11 | 661.5 | −175 | 609.1 | −120 | 709.2 | −193 | 630.9 | −157 |
| W12 | 661.5 | −175 | 635.6 | −140 | 641.1 | −138 | 613.0 | −138 |
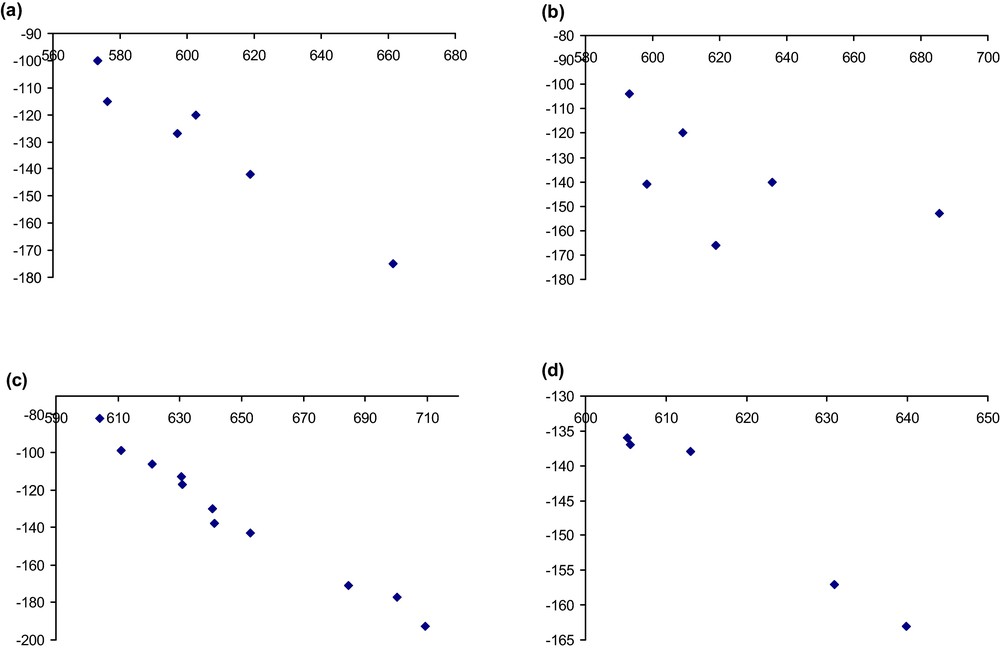
Correlation between theoretical and experimental chemical shifts for the α (a), β1 (b), β2 (c) and β3 (d) isomers of [SiW11O39]8−. In the case of the β3 isomer, the experimental peak at −52 ppm has been omitted.
The agreement with the experimental and theoretical values is relatively good, if one excepts the β3 isomer, for which there is some discrepancy and which will be discussed below. From a general point of view, the range of calculated chemical shifts is quite comparable to the experimental one: 88 ppm vs. 75 ppm for the α isomer, 93 ppm vs. 62 ppm for the β1 isomer and 105 ppm vs. 111 ppm for the β2 isomer. In the case of the β3 isomer the chemical shift ranges are 35 ppm theoretically and more than 110 ppm experimentally. When plotting the experimental vs. theoretical curves there is a good correlation between theory and experimental for the α and β2 isomers while for the β1 and β3 isomers there is some discrepancy due to one single experimental value which does not correlate with the theoretical data. From a general point of view, the slope of the line fitting experimental vs. theoretical values is always around −0.8 while a value of −1 was expected (quite the same slope is obtained for the β1 and β3 isomers after removing the data which does not fit the curve). This is mainly due to the fact that the calculations did not take into account the solvation of the polyoxometalates, as it has been pointed out by Poblet et al. [49,50] for similar systems, or Penka et al. for platinum complexes [43]. The quality of the basis set should also significantly, but to a lesser extent, affect the theoretical values, in particular through a slight modification of distances obtained from the geometry optimization [39,49,50] which strongly correlate with differences in the chemical shits for heavy atoms [43]. However, this has not a great importance in the present work, because the goal is to assign the spectra, as well as to compare the relative energies of the isomers. For the purpose one can trust the linear correlation between experimental and theoretical values, whereas the deviation of the slope with respect to one is understood and therefore unimportant.
Let us now discuss more precisely on the β1 and β3 isomers. Experimentally, only the attributions of the peaks at −153, −140 and −141 ppm for the β1 isomer and at −120 ppm for the α isomer were proposed on the basis of the 2JW-O-W couplings and of the intensity ratios calculated by Pope et al. [51]. Not only are these attributions not similar to those chosen by us for the β1 isomer, but there is also a large discrepancy for the W1 tungsten atom for which the chemical shift should be highly shielded and found at ca. −230 ppm. When looking at the spectrum of Smith et al. this peak, which corresponds to the tungsten atom with intensity one, is clearly seen at −153 ppm. The only possibility, as sometimes observed with all NMR spectrometers without digital acquisition is that the peak was outside the spectral window and appeared inside by a folding up of the spectrum. Such a phenomenon is possible due to its great difference with the other signals.
In the case of the β3 isomer, the main problem arises from the experimental signal at −52 ppm that Smith et al. found for the polyoxometalate. This signal cannot be due to the polyoxometalate on the basis of our studies. When looking at the 183W NMR spectrum of α-[NaSiW11O39]7− described by Smith [8] and by Brevard et al. [52], this compound has a peak near −54 ppm. Very probably, the peak at −52 ppm is due to a complex of the polyoxometalate with Na+. As this peak has a very low intensity, it is probable that the other signals of α-[NaSiW11O39]7− are masked by the other resonances.
4 Conclusion
We have studied by DFT methods the various isomers of the undecatungstosilicate [SiW11O39]8−. The stability order was well reproduced by use of the LDA(VWN) method with the exception of the α and β3 isomers which were found to have quite the same energy. The structural parameters correspond well to those determined by X-ray diffraction studies in various silicotungstic heteropolyoxometalates. The main conclusion was that the W-O distances of the oxygen atoms of the lacuna were very short and corresponded to W=O bonds rather than to W-O ones. The charge and frontier orbitals analyses show that the reactivity of these lacunary species does not occur via the lacuna oxygen atoms but via terminal oxygen atoms of the corresponding WO6 octahedra. The infrared and 183W NMR spectra of the four isomers were also calculated and compared to experimental values. In the case of 183W NMR the calculated data fit well with the experimental ones, with the exception of two experimental peaks, which have been re-assigned. Some preliminary studies were also made with an additional alkaline atom in the lacuna and show that some isomers could be stabilized by use of the proper cation. Further calculations with optimization of the complete structure are in progress and will be published elsewhere.
Acknowledgements
The authors gratefully acknowledge the GENCI/CINES for HPC resources/computer time (Project cpt2130).


