1 Introduction
Soon after the discovery of C60 in 1985, the detection of the first endohedral fullerene, La@C60, provided evidence that the interior space of fullerenes can host atoms or molecules [1]. In 1999, the synthesis of Sc3N@C80 was reported. This molecule was the prototype of a new family of nitride endohedral metallofullerenes (EMFs) and the third most abundant fullerene after C60 and C70 [2]. During the past decade, intense research developed by several worldwide groups allowed one to incarcerate a variety of atoms and small molecules inside carbon cages, such as metallic nitrides [3], carbides [4–7], sulfides [8,9] and oxides [10,11] as well as up to three individual metal atoms [12,13]. The new properties of EMFs as compared to those of hollow fullerenes make them suitable for potential applications in biomedicine and material sciences [14,15]. Unstable empty cages are stabilized by the encapsulation of individual metal ions or metal clusters since an electron transfer from the guest to the host occurs. The formal number of electrons transferred to the fullerene is a fundamental issue to determine which cage is selected. In 2005, our group showed that the carbon frameworks with the largest gaps between the third and fourth unoccupied orbitals are the most suitable hosts for clusters that formally transfer six electrons [16]. When there is a transfer of four electrons, as in some metal carbides (M2C2), metal oxides (Sc2O) or sulphides (Sc2S), the orbital gap between the second and third unoccupied orbitals has to be considered [17]. Popov and Dunsch have demonstrated that the most favourable hexaanionic fullerenes match with the most favourable nitride EMFs [18]. The analysis of the orbital gaps for all the IPR isomers between C80 and C100 leads to the conclusion that the isomers Ih(7)-C80 and C3v(8)-C82 are the cages with the most favourable electronic structure to encapsulate clusters when formal transfers of six and four electrons take place, respectively [17,19].
Since the three lowest unoccupied molecular orbitals in a carbon cage are rather similar, the simple inspection of their orbital shapes cannot explain the orbital rule. Therefore, a different approach is required. The inverse pentagon separation index (IPSI) revealed very efficient information for this purpose. IPSI is a scalar quantity that measures the separation among the twelve pentagons that are always present in a fullerene. Due to the highest pyramidalization of the carbon atoms that form pentagonal rings, the electron density transferred is preferentially localized on them. Therefore, the most suitable cages are those with the maximum pentagon separation, that is, the cages with lower IPSI values [20]. The maximum separation among pentagons minimizes the electrostatic repulsion induced by the six extra electrons on the carbon cage.
The relative energies of the hexaanions C2n6− also correlate with the number of pyracylene units present in the structure [20]. In the present paper, we show that there is a relationship between the energies of the cage orbitals that accept the electrons, the IPSI values and the number of pyracylene motifs of the cages. Moreover, these parameters are fundamental to answer questions as, for example, why Sc3N does not select the most stable empty D5d-C80 isomer, which can be seen as the iconic Ih-C60 with 20 additional carbon atoms in the equatorial zone, (Fig. 1a), instead of the Ih-C80 or D5h-C80 cages with few pyracylene motifs (Fig. 1b). Violations of the IPR rule have been observed for several metallofullerenes for small-medium cages (2n ≤ 84) since the isolation and characterization of Sc2@C66 and Sc3N@C68 [21,22]. We here will also show why it is so unlikely to find non-IPR fullerenes for large carbon cages (2n > 84).

Structures of IPR cages Ih-C60, D5h-C70, D5d-C80, Ih-C80 and D5h-C80. a: D5h-C70 and D5d-C80 cages can be formally obtained from the C60 one, by adding C atoms in the equatorial zone. The bonds where the new atoms are added are represented with broken lines. In black, new atoms and bonds formed; in white, the common part; b: comparison of three different isomers of C80. In black, the 12 pentagons; in red, the 6,6 bonds from pyracylene units.
2 Computational details
Semi-empirical calculations at the AM1 level for the hexaanions, tetraanions and neutral empty cages were performed with the Gaussian03 code [23]. DFT calculations were carried out for EMFs with the ADF2007 program [24,25] using exchange and correlation functionals of Becke [26] and Perdew [27]. Relativistic corrections were included by means of the zero-order regular approximation. Triple-ζ polarization basis sets were used to describe the valence electrons of the C, N and M atoms. Frozen cores that consisted of the 1 s shell were described by means of single Slater functions. IPR and non-IPR cages were identified by their symmetry and by the number assigned according to the spiral algorithm. The truncated numbering system that counts only IPR isomers is used for IPR cages [28].
3 Results and discussion
3.1 IPSI: a measure for the size and topology of the cages
The IPSI provides a measure for the separation among the twelve pentagons present in a fullerene cage. It has been shown that IPSI values correlate with the relative stability of charged cages for a given C2n family, especially for tetra- and hexaanions due to the larger ability of pentagons to attract the extra negative charge [20]. Thus, the larger the separation is, the smaller the Coulomb repulsion and the larger the stabilization are. Fig. 2 shows such correlations for the 24 IPR and 110 non-IPR cages with only one pair of adjacent pentagons (APP1) of the C84 family. It can be observed that the set of IPR cages group well separated from that of the APP1. The presence of one adjacent pentagon pair makes the IPSI larger for the APP1 set than for the IPR structures. Similarly, isomers with two pairs of adjacent pentagons (APP2) have their IPSI values well separated from those of the APP1 family. Therefore, the IPSI is able to classify the C2n isomers according to their number of adjacent pentagon pairs.

Relative stability (kcal·mol−1) for all the IPR (circles) and APP1 (triangles) isomers of the C84 cage, with respect to the IPSI value. In green, hexaanionic cages; in red, tetraanionic cages; in blue, neutral cages. The most stable cages are, for the IPR systems, isomers 23 (neutral and tetraanion) and 21 (hexaanion); for non-IPR cages, isomers 51545 (neutral), 51383 (tetraanion) and 51365 (hexaanion).
For each of the IPR and APP1 sets, the relative energies of hexaanions and tetraanions correlate with IPSI (Fig. 2). For neutral cages, a larger dispersion of the points is observed in both sets since minimization of the steric strain is more important than minimization of the Coulomb repulsion. It is interesting to point out that for each isomer within the IPR or APP1 sets, as the negative charge increases, the IPSI value decreases (compare red and green circles for IPR or red and green triangles for APP1 in Fig. 2). Such increase of charge, which resides preferentially on pentagons, induces a larger separation among them so as to minimize the repulsion and, consequently, a lower value for IPSI. Hence, an increase of the volume of the cage is also reflected in the IPSI parameter.
Such correlation between IPSI and the volume of the cage can also be observed in the M3N@Ih-C80 series (M = Sc, Y, Gd, La). An increase of the radius of the metal ion entails a larger deformation of the Ih-C80 cage, i.e. an increase of its volume, and consequently smaller values for IPSI as shown in Table 1. The empty cage shows the largest IPSI value. Only the case when M = Y, with very similar radius as Gd, does not fit so well into a linear correlation.
IPSI and rM3+ values for M3N@Ih-C80 (M = Sc, Lu, Y, Gd and La).
| rM3+ (Å) | IPSI (Å−1) | |
| Empty | 12.569 | |
| Sc3N | 0.75 | 12.491 |
| Lu3N | 0.85 | 12.462 |
| Y3N | 0.90 | 12.441 |
| Gd3N | 0.94 | 12.450 |
| La3N | 1.05 | 12.435 |
Interestingly, the relative stability of charged fullerenes was shown to be also correlated with the number of pyracylene units [20]. The pyracylene motif places two pentagons as close together as possible while avoiding direct pentagon-pentagon adjacencies. Hence, the pyracylene motif is not the best disposition to obtain maximal separation between two neighbouring pentagons. Thus, those cages with low number of pyracylene units are the most suitable ones to encapsulate metallic clusters. Since both the IPSI and the number of pyracylene units provide information about the separation among pentagons in a given C2n family, these two parameters must be correlated. Fig. 3 shows that for hexaanionic IPR C80 and C96 cages such a correlation exists. We have only taken into account hexaanionic cages because they are the most appropriate to be described by the maximum pentagon separation rule. Whereas a clear correlation is observed for the C80 family, larger dispersion is found for the large C96 set, especially for the highest-energy hexaanionic cages with a large number of pyracylene motifs. This result is in agreement with the fact that the predictive power of these two parameters decreases when the cage size increases.
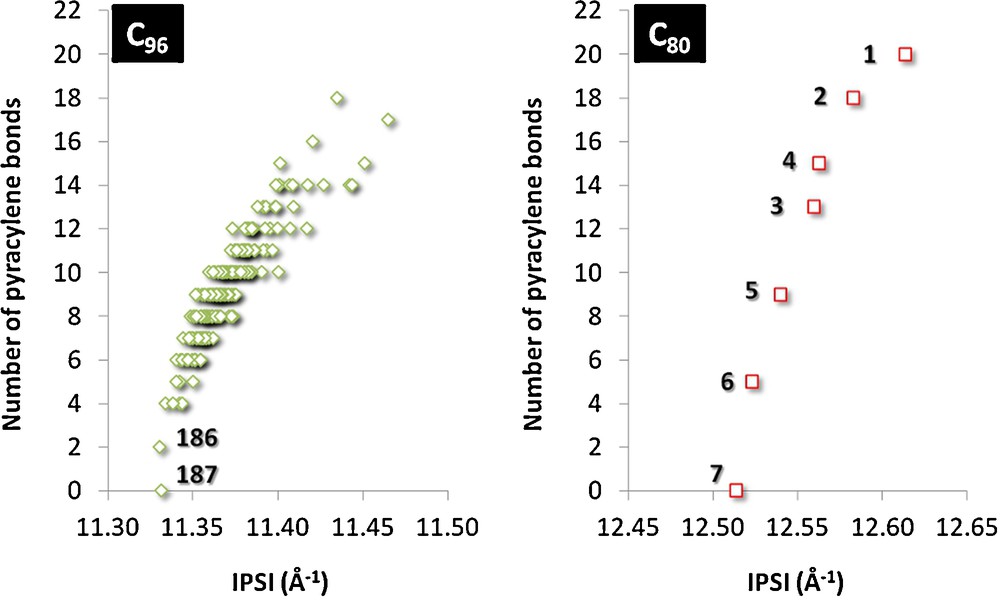
Correlation between IPSI and the number of pyracylene units for C96 (left) and C80 (right) IPR cages.
3.2 Orbital and topological rules: is there a connection?
In 2005, our group formulated the following orbital rule to predict the most suitable carbon cage to encapsulate metallic clusters provided that a formal transfer of six electrons takes place: “a suitable host must have three low-lying unoccupied molecular orbitals and sizeable energy gap between the LUMO-4 and LUMO-3”, where LUMO-n is the nth-lowest unoccupied molecular orbital. The orbital energy gap can also be referred as (LUMO+3) – LUMO+2) energy gap [16]. All the nitride EMFs whose structures have been characterized by single crystal X-ray diffraction satisfy this rule so far. Moreover, this rule has successfully predicted the cage isomers in La3N@C92, La3N@C96 and La2@C100, which have been recently characterized by electrochemical measurements [29] or X-ray crystallography for the latter case [30].
It has been observed that the energies of the LUMO orbitals hardly change for different endohedral metallofullerenes or negatively charged empty cages [31]. On the other hand, significant changes are detected on the three highest-occupied orbitals of the fullerene anions, which are occupied once the transfer of six electrons takes place. These results are in agreement with the changes found in the experimental reduction and oxidation potentials of nitride EMFs [31]. This evidence shows that the different HOMO-LUMO gaps in such systems are basically affected by the change of the HOMO energies. A plot of the relative energies of the hexaanionic cages for the IPR C80, C88 and C96 families with respect to the HOMO-LUMO gaps, which are equivalent to the gaps between the LUMO−3 and LUMO−4 in the neutral cages, is depicted in Fig. 4a. The plot clearly shows that the cages with the largest HOMO-LUMO gap are among the most stable isomers in all the three families, which is in agreement with the “(LUMO−4) − (LUMO−3) rule”. However, no clear correlation for cages with smaller HOMO-LUMO gaps exists (Fig. 4a). Since the orbital rule requires three low-lying unoccupied orbitals of the neutral cage, we have also plotted the relative stabilities of the hexaanions with respect to the average energy of their three highest-occupied orbitals, i.e. those that accept the six electrons. Interestingly, much better correlations are observed (Fig. 4b). Therefore, the lower the energies of the three HOMOs are, the higher the stabilization of the hexaanion. However, it also happens that the almost-linear trend observed for C80 is progressively lost for larger cages. Thus, in terms of thermodynamic stability, the energies of the three orbitals that are to be occupied after the electron transfer are more significant than the HOMO-LUMO gap. Large HOMO-LUMO gaps are consequence of low-energy HOMOs.

Correlation between the relative energies of hexaanions for the C80 (red), C88 (blue) and C96 (green) families and (a) the orbital HOMO-LUMO gaps; (b) the average of the energies of the three highest-occupied molecular orbitals. The most stable cages for each family are identified by their isomer number.
Finally, we would like to point out the correlation that exists between the IPSI and the average energy of the three HOMOs for the different C2n families analyzed throughout this work (Fig. 5). As for previous analysis, the correlation is gradually lost as the size of the cage increases. This last correlation links the orbital rule based on energy gaps and the topological rule, which explains the physics of the problem.
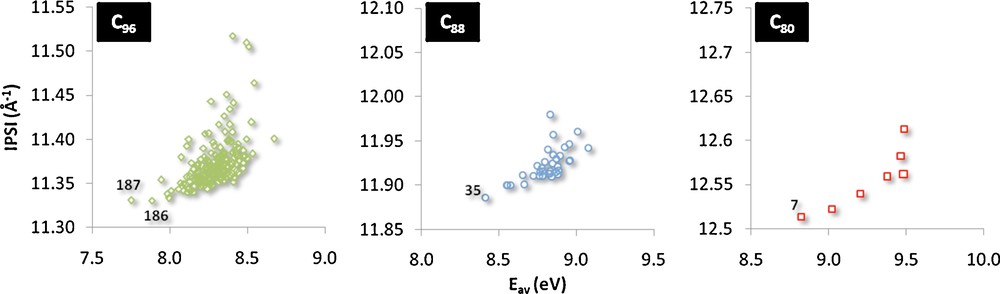
Correlation between the average energy of the three HOMOs with IPSI for the C80, C88 and C96 families. The most stable cages for each family are identified by their isomer number.
3.3 IPR versus non-IPR cages: the importance of the charge transfer
The isolated pentagon rule (IPR) and the intimately related pentagon adjacency penalty rule (PAPR) indicate that the presence of adjacent pentagon pairs destabilize the structure of the fullerene cages due to an increase of the steric strain [28]. In particular, a destabilization of 19–24 kcal mol−1 per APP was proposed [32]. All the neutral and non-functionalized C2n fullerenes (2n ≥ 60) characterized so far present IPR cages, in good agreement with the abovementioned rules. As first seen in 2000 and confirmed during the last decade, endohedral metallofullerenes may show non-IPR cages with a reduced number of APP (up to three) [33]. Moreover, some functionalized fullerenes have been found to present non-IPR cages, such as the chlorinated C72Cl4, which has a cage with one APP [34,35]. All of these non-IPR cages have been found for middle-sized fullerenes (66 ≤ 2n ≤ 84), where the number of IPR isomers is small or even null. The charge transfer from the internal metal cluster to the carbon cage is the main cause for such stabilization. Bonds at pentagon-pentagon junctions, called 5,5 bonds or pentalene bonds, which are specific for non-IPR cages, are more electrophilic than 5,6 and 6,6 bonds. Consequently, non-IPR cages localize more negative charge on pentagons than IPR structures do [20].
Fig. 6 (top) shows that most of the 24 neutral IPR structures of C84 present lower energies than the 110 non-IPR structures with a single APP, as predicted by the isolated pentagon rule. The difference between average values for the energies of the two sets is 45 kcal mol−1 at the semiempirical AM1 level for the neutral cages. For the hexaanions (Fig. 6, bottom), the energies of the two sets overlap and the difference between their average energies decreases to 19 kcal mol−1. Apart from this significant reduction on the energy difference, it is important to remark that there is one non-IPR isomer, Cs(51365)-C84, which is competitive with the lowest-energy IPR hexaanion, D2(21)-C84 (only 1 kcal mol−1 higher in energy). This non-IPR cage is ultimately selected due to the extra stabilization gained by the coordination of the M3N cluster to the pentalene bond. A similar type of analysis was also carried out for the C92 family. Most of the 86 IPR cages are found to be considerably more stable than the 840 non-IPR structures with one APP, with an energy difference between the average values around 31 kcal mol−1 for the neutral cages (Fig. 7, top). This value, which is somewhat smaller than that found for the C84 family, and the larger overlap observed for the two sets point to a slight reduction of the strain energy in APP1 cages as their sizes increase. For the hexaanions, the average energy difference is also reduced, but only by 6 kcal mol−1. Now, the points of the two sets do not overlap so much as for the C84 family and the IPR structures clearly show the lowest energies without any competitive non-IPR cage (Fig. 7, bottom). With such a sizable number of IPR isomers (86), it is more likely to have some structure with the appropriate topology, i.e. low IPSI and low number of pyracylene motifs, to accept the formal transfer of four or six electrons. Larger cages (2n > 92) show a similar behavior because the number of IPR isomers is large enough to have structures with low number or even zero pyracylene motifs (for example, 1 cage for C100 and three cages for C104). This is the reason why non-IPR cages have not been observed so far (and most likely will not be observed with the present synthetic procedures) for EMFs with large-size cages.

AM1 relative energies for IPR and non-IPR with one adjacent pentagon pair (APP1) C84 isomers. Neutral cages at the top and hexaanionic cages at the bottom.

AM1 relative energies for IPR and non-IPR with one adjacent pentagon pair (APP1) C92 isomers. Neutral cages at the top and hexaanionic cages at the bottom.
4 Conclusions
The IPSI, which is a measure of the separation among the twelve pentagons in a fullerene, is able to distinguish between IPR structures and those that show other topologies with one or more pairs of adjacent pentagons. Moreover, it provides an indirect measure of the change in the size or volume of the cage when comparing empty cages with different negative charges or endohedral metallofullerenes with different metal atoms in their interior. IPSI correlates with the number of pyracylene motifs, since the two parameters give information about the separation among pentagons in a fullerene. A connection between the orbital and topological rules is found: the more separated the pentagons in the fullerene cage are, the lower the energies of the cage orbitals that accept the electrons. Finally, an explanation for the absence of non-IPR cages in large-size EMFs is also provided. Among the large number of IPR structures in these families, the occurrence of a cage with the appropriate topology to encapsulate a metal cluster is highly probable.
Acknowledgements
This work was also supported by the Spanish Ministry of Science and Innovation (CTQ2008-06549-C02-01/BQU) and by the Generalitat de Catalunya (2009SGR462 and XRQTC). N.A. is indebted to Ministerio de Educación (Spain) for a FPU predoctoral fellowship. X.A.-A. is indebted to Ministerio de Ciencia e Innovación (Spain) for a FPI predoctoral fellowship.


