Plan
Comptes Rendus
no. 2-3

First principles investigation of the atomic structure and magnetic properties of copper hydroxide acetate
Fan Yang1  ; Mauro Boero2, 3  ; Pierre Rabu2  ; Carlo Massobrio2
1 School of Electronic and Electrical Engineering, Wuhan Textile University, Wuhan, 430073, China
2 Institut de physique et chimie des matériaux de Strasbourg (IPCMS), UMR 7504, CNRS and University of Strasbourg, 23, rue du Loess, BP43, 67034 Strasbourg cedex 2, France
3 Research Center for Integrated Science, Japan Advanced Institute of Science and Technology (JAIST), 1-1 Asahidai, Nomi-shi, Ishikawa 923-1292, Japan
Comptes Rendus. Chimie, Volume 15 (2012) no. 2-3, pp. 202-208.

Résumés

Within the density functional theory (DFT) framework, we study the structural properties and the spin density distribution of copper hydroxide acetate Cu2(OH)3(CH3COO)·H2O, a fundamental compound in the field of hybrid organic-inorganic materials. In particular, after a careful comparison of the computed structure with the experimentally obtained X-ray pattern, we provide an insight into the effect of two exchange-correlation functionals (BLYP and HCTH/120) on the description of the magnetic properties and on the related changes in the atomic structure. Since these compounds are known to possess a piezomagnetic character, for the total spin value S = 0 and S = 4, we inspect at different pressures, and for each one of the two exchange-correlation functionals, the changes in the geometry and in the spin density distribution. We notice that, at total spin density S = 0, and for both the external pressures of 3 and 5 GPa, most of the local spin densities are due to dyz orbitals with about 25% contribution from dz2 orbitals. Such a feature is insensitive to the exchange-correlation functional adopted. Overall, our results provide an important first step towards the comprehension of the effects of an external stress on the magnetic properties of this class of hybrid materials.

En utilisant la théorie de la fonctionnelle de la densité (DFT), nous étudions les propriétés structurales et magnétiques du matériau hybride Cu2(OH)3(CH3COO)·H2O. En particulier, après une comparaison avec la structure obtenue par diffraction de rayons X, nous avons étudié comment les propriétés magnétiques et structurales changent sous l’effet d’un changement dans la partie échange et corrélation de l’hamiltonien DFT. À cet effet, nous avons utilisé deux fonctionnelles d’échange et de corrélation (BLYP et HCTH/120). Comme ces matériaux hybrides sont bien connus pour avoir un caractère piézomagnétique, en fixant la valeur du spin totale à S = 0 et S = 4, nous avons procédé à l’analyse de la structure, ainsi que de la distribution de la densité de spin lorsqu’une pression est appliquée. Pour des valeurs de pression de 3 et 5 GPa, la distribution locale des spins est due en majeure partie aux orbitales dyz avec 25 % de contribution des orbitales dz2. Ce caractère général ne paraît pas dépendre du choix de la fonctionnelle d’échange-corrélation. Ce travail est un bon point de départ pour l’étude sous haute pression de cette famille de matériaux hybrides.

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crci.2011.09.007
Mots clés : Hybrid materials, Copper hydroxide, Density functional theory, Exchange-correlation, Functional, Car-Parrinello method
Fan Yang 1 ; Mauro Boero 2, 3 ; Pierre Rabu 2 ; Carlo Massobrio 2

1 School of Electronic and Electrical Engineering, Wuhan Textile University, Wuhan, 430073, China
2 Institut de physique et chimie des matériaux de Strasbourg (IPCMS), UMR 7504, CNRS and University of Strasbourg, 23, rue du Loess, BP43, 67034 Strasbourg cedex 2, France
3 Research Center for Integrated Science, Japan Advanced Institute of Science and Technology (JAIST), 1-1 Asahidai, Nomi-shi, Ishikawa 923-1292, Japan 
@article{CRCHIM_2012__15_2-3_202_0,
     author = {Fan Yang and Mauro Boero and Pierre Rabu and Carlo Massobrio},
     title = {First principles investigation of the atomic structure and magnetic properties of copper hydroxide acetate},
     journal = {Comptes Rendus. Chimie},
     pages = {202--208},
     publisher = {Elsevier},
     volume = {15},
     number = {2-3},
     year = {2012},
     doi = {10.1016/j.crci.2011.09.007},
     language = {en},
}
TY  - JOUR
AU  - Fan Yang
AU  - Mauro Boero
AU  - Pierre Rabu
AU  - Carlo Massobrio
TI  - First principles investigation of the atomic structure and magnetic properties of copper hydroxide acetate
JO  - Comptes Rendus. Chimie
PY  - 2012
SP  - 202
EP  - 208
VL  - 15
IS  - 2-3
PB  - Elsevier
DO  - 10.1016/j.crci.2011.09.007
LA  - en
ID  - CRCHIM_2012__15_2-3_202_0
ER  - 
%0 Journal Article
%A Fan Yang
%A Mauro Boero
%A Pierre Rabu
%A Carlo Massobrio
%T First principles investigation of the atomic structure and magnetic properties of copper hydroxide acetate
%J Comptes Rendus. Chimie
%D 2012
%P 202-208
%V 15
%N 2-3
%I Elsevier
%R 10.1016/j.crci.2011.09.007
%G en
%F CRCHIM_2012__15_2-3_202_0
Fan Yang; Mauro Boero; Pierre Rabu; Carlo Massobrio. First principles investigation of the atomic structure and magnetic properties of copper hydroxide acetate. Comptes Rendus. Chimie, Volume 15 (2012) no. 2-3, pp. 202-208. doi : 10.1016/j.crci.2011.09.007. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2011.09.007/

Version originale du texte intégral

1 Introduction

Copper hydroxide acetate Cu2(OH)3(CH3COO)·H2O is the prototype of a whole family of organic-inorganic transition metal layered compounds Cu2(OH)3X, (where X is an exchangeable anion), having interesting magnetic properties, appealing for applications in memory switches and data storage devices [1]. The structure of Cu2(OH)3(CH3COO)·H2O can be summarized as made of two-dimensional triangular arrays of CuII ions kept separated by CH3COO− spacers [2]. From the structural point of view, copper hydroxide acetate has close similarities with copper hydroxonitrate, Cu2(NO3)(OH)3, where NO3 groups are replaced by CH3COO− acetate anions. The interlayer distance is then tuned by the nature of the chemical species inserted between the inorganic layers and by the conformations they can assume according to their higher or lower flexibility [2]. In Cu2(OH)3X systems, the magnetic properties are strongly dependent on the nature of the interlayer organic spacers and, hence, on their local chemical properties. Application of an external pressure can induce modifications in the arrangement of the interlayer species and the interlayer distance, thereby modifying the magnetic properties of the material. A comparison of the magnetic behavior of Cu2(NO3)(OH)3 and Cu2(OH)3(CH3COO)·H2O has shown that they both exhibit antiferromagnetic (AF) interlayer interactions. However, replacement of the NO3− by the CH3COO− acetate ion units results in the appearance of weak ferromagnetic (F) intra-layer interactions, a behavior quite different from the persisting AF intra-layer character shown by Cu2(NO3)(OH)3 [2].

Density functional theory (DFT) is particularly useful to provide insight into the bonding properties and the magnetic behavior of Cu2(OH)3(CH3COO)·H2O [3]. Moreover, within the Cu2(OH)3X family, another convincing example has been reported for Cu2(NO3)(OH)3 [4]. For that specific system, electronic localization properties and spin topology could be efficiently described by gradient corrected exchange-correlation functionals. Subsequently, results were refined within a hybrid DFT/Hartree-Fock functional approach, which allowed for a precise estimation of the exchange coupling constants and for a complete characterization of the temperature behavior of the magnetic susceptibility [5]. We have to remark that such a protocol was not directly applicable in the case of copper hydroxide acetate, because a complete structural determination of comparable accuracy was not yet available. An X-ray powder diffraction study of Cu2(OH)3(CH3COO)·H2O has highlighted the role of water molecules in between the layers, prone to be easily and reversibly removed by moderate heating [6]. However, due to the lack of synthesized single crystal of suitable quality, the set of atomic coordinates was incomplete. For these reasons, our former study was aimed at complementing experiments and at recovering the missing piece of information [3].

In this article, instead, we focus on the effect of the DFT level adopted to characterize the material, with specific emphasis on the exchange-correlation interaction, an issue which is always crucial to assess the reliability of the computational protocol adopted. We provide a first insight into the effects of an external pressure on the structural and electronic properties of copper hydroxide acetate in two different spin configurations, AF and F, since such a system has been experimentally proven to possess a peculiar piezomagnetic character disclosing a wealth of promising technological applications [2].

2 Computational methods

We use a first-principle molecular dynamics approach as coded in the CPMD package [7,8]. Our calculations are performed within the DFT framework [9], including generalized gradient approximations after Becke [10] for the exchange energy and Lee et al. [11] for the correlation energy (BLYP) and after Hamprecht et al. (HCTH/120) [12]; the latter functional, comprehensive of both the exchange and the correlation parts, has already been shown to be particularly suited to describe geometry, energetics and hydrogen bonding of heterogeneous and organic materials [13]. Valence electrons, including semi-core 3d states in the case of Cu atom, are treated explicitly and represented in a plane-wave (PW) basis set with an energy cutoff set to 90 Ry and the Brillouin zone sampled at the Γ point only. The core-valence interaction is described by Trouiller and Martins norm-conserving pseudopotentials [14] and non-linear core corrections [15] have been included in the case of Cu.

Our calculations are performed on a system composed of 72 atoms (8 Cu, 24 O, 8 C and 32 H) in a periodically repeated simulation box. The lattice parameters are identical to the ones provided by Ref. [6], obtained by X-ray powder diffraction studies, namely a = 5.6025 Å, b = 6.1120 Å, c = 18.747 Å and β = 91° 012′. Let us just recall that the outcome of these measurements could not provide, in the acetate groups, the crystallographic positions of C and O atoms [6]. Moreover, as usual in X-ray crystallography, no information on the positions of the H atoms is available. Hence, this missing piece of information had to be provided by our simulations.

In order to generate a set of distinct electronic and structural ground states, differing in the local spin topology, we repeated our PW-based calculations by assigning different initial random values to the Fourier coefficients ci(g) of the expansion, g being the reciprocal lattice vectors of the periodic simulation cell and i the electronic state index. For each one of these choices, the electronic structure is relaxed to its ground state by minimization of the total energy with respect to the coefficients of the PW expansion. We have to recall that a standard PW approach does not allow any specific choice of a given spin topology, which is known only at the end of the electronic relaxation procedure.

Optimization of the structural geometries is carried out via first principles damped dynamics. This ensures a consistent and progressive quench of the ionic velocities and allows for an efficient search of the minimum energy configuration, assumed to be achieved when the residual forces on the atoms are smaller than 0.001 Hartree/au. The above procedure was repeated for different values of the external pressure Pext, starting from the formerly obtained Pext = 0 GPa case [3], then for Pext = 3 GPa and Pext = 5 GPa. In all of these calculations, both the BLYP and the HCTH/120 functional were used, the total spin multiplicity 2S + 1 was set equal to 1 (S = 0), this choice being consistent with the bulk antiferromagnetism of this compound [2]. In addition, the F case (total spin multiplicity equal to 9, S = 4) was also considered. In each case considered here and discussed below, the spin density distribution is given by the standard formula (1):

ρs(x)=ρα(x)−ρβ(x)=∑iψiα(x)2−∑iψiβ(x)2(1)
where α and β indicate the up- and down-spin components, respectively, and ψiα,β(x) are the Kohn-Sham orbitals of our systems.

3 Results and discussion

3.1 Diffraction pattern: an experimental and theoretical comparison at zero pressure

In this section we show that the optimized structure proposed and extensively discussed in a former work [3] can be substantiated by experiments. We recall here that the main motivation for the computational study of Ref. [3] was the incompleteness of the set of atomic coordinates made available experimentally in Ref. [6]. Our computational studies could provide a set of coordinates enriching and completing the structural determination by Masciocchi et al. obtained on the basis of powder X-ray diffraction analysis [6]. The DFT results of Ref. [3], besides providing the missing hydrogen atoms positions, were able to solve the ambiguity on the acetate anions between methyl residue and oxygen atom of the carboxylate. Actually, the P1 symmetry of the model prevents from constraining the atom positions to obey any crystal cell symmetry operation, except translational periodicity. To confirm that the model is consistent with structural data, we computed the powder X-ray diffraction pattern of the modeled structure in order to compare it to the experimental pattern. To this aim, we synthesized Cu2(OH)3(CH3COO)H2O by titration of copper acetate with NaOH in water at 60 °C as described in the literature [6,16]. The experimental powder diffraction pattern was recorded with a Bruker D8 diffractometer (CuKα1). A side loaded sample holder was used to try to minimize preferred orientation of the powder. We calculated the model pattern with the FullProf software package [17] starting from the full atomic positions set refined by DFT calculation in the P1 space group. All atom positions were fixed, but we adjusted the profile parameters and scale factors, taking into account some (001) preferential orientation, to minimize the weight of the 00l very intense diffraction lines in the least square refinement process. The result is given in Fig. 1. The calculated profile matches quite well the experimental intensities. The experimental data show few additional small peaks that are ascribed to impurity which is very common in this system.

Fig. 1

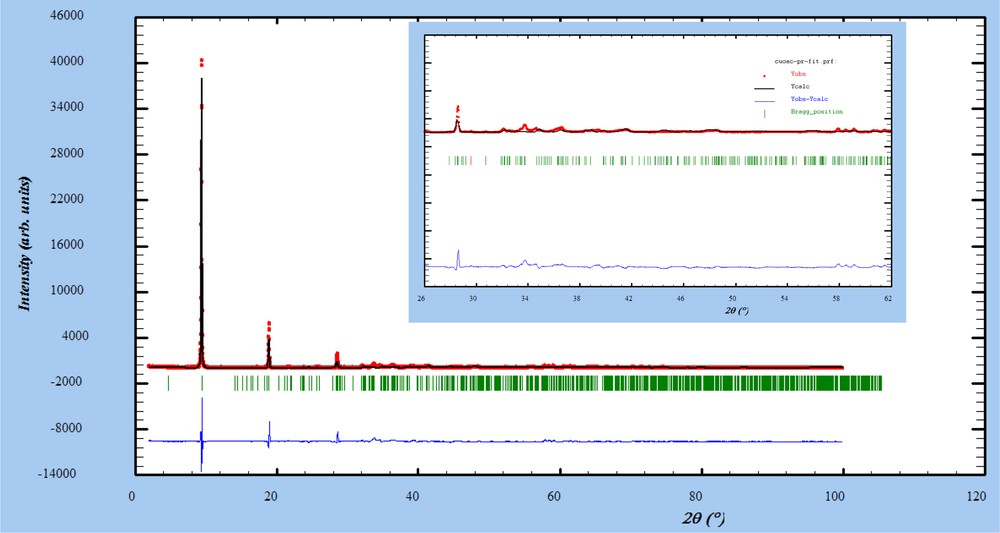
Powder X-ray diffraction pattern of Cu2(OH)3(CH3COO)H2O (CuKα1, red dots), calculated pattern of the model structure (black line) and difference between observed and calculated data (blue line). The vertical green bars indicate the position of the peaks in the P1 approximation.

In the present case, a clear-cut structural refinement is elusive, primarily because the symmetry of the crystal structure is clearly not P1 as fixed in our calculation. Moreover, as emphasized in Ref. [6], accurate structure refinement of this phase is far from being straightforward because experimental powder X-ray diffraction are biased by several effects, like presence of extra phase, preferential orientation, disorder and water instability. Nevertheless, the comparison of the model profile with the experimental data confirms that DFT calculations are a valuable mean to obtain a structure to be exploited in the search of a description of magneto-structural correlations.

3.2 Energetics and spin topology

We first analyzed the system in its AF state, i.e. in its singlet spin state S = 0 at a pressure of 3.0 GPa. Upon full relaxation of the electronic degrees of freedom and of the internal atomic coordinates, the spatial distribution of the spin density corresponds to the one shown in Fig. 2. For the selected value of the isosurface shown in the figure, i.e. 10−2 e/Å3, a predominant number of spin densities belonging to the same band (say, the majority one, α), are clearly visible on the Cu sites. In addition, α spin density contributions are visible on O atoms of the OH− groups directly coordinated by the Cu atoms. It appears that electron transfer from the O to the Cu atoms leaves the O atoms with the same spin polarization (α) of the neighboring O atoms, due to the involvement of minority spin levels (β), the only ones prone to be transferred to the partially unoccupied β band of the Cu atoms. The feature common to both the BLYP and the HCTH/120 functional is the zero value of the global spin of each layer, hereafter denoted as Σ = 0. A slight difference is represented by the fact that, inside each layer, the local topology, i.e. the spin-up (α) and the spin-down (β) distributions differ in terms of the Cu site where they are located. We recall that variations in the local spin topology for different S = 0 configuration have been found and described in detail in Ref. [3], where different spin configurations at S = 0 lay within 0.15 eV. As can be inferred from the shape of the spin densities on top of each Cu atom, the contribution to the spin arises almost exclusively from the d-orbitals of Cu, with a dominant dyz character plus a contribution, amounting to about 25%, from dz2 orbitals. In fact, even a simple visual inspection of just one layer (Fig. 2) shows that if three Cu sites carrying a dyz-shaped spin density, the fourth one presents a dz2-shaped feature. The same calculation, at the identical pressure of 3 GPa, was performed for the F case. By imposing a total spin S = 4, we find the spin distribution shown in Fig. 3. As in the former case, dyz and dz2 orbitals of Cu represent the major contribution to the spin density. Minor contributions come from the p-states, mainly lone pairs, of the O atoms belonging to the OH and CH3COO groups bound to Cu atoms. The total energy differences E(S = 4) − E(S = 0) separating the AF system from the F configuration at the pressure of 3 GPa are 0.715 eV and 0.215 eV according to the BLYP and to the HCTH/120 calculations, respectively (Table 1). While it appears legitimate to seek further confirmations to these trends by resorting to hybrid functionals [18–20], the AF state turns out to be always the ground state not only at ambient pressure [3] but also at higher ones at least up to 5 GPa. At 5 GPa, we find that the total energy E(S = 0) is lower than E(S = 4) by 0.368 eV in the case of the BLYP functional and 0.242 eV in the case of the HCTH/120 functional. Interestingly, for both functionals BLYP and HCTH/120 and with increasing pressures, (3 GPa and 5 GPa), the values of the energy of the F state approach those of the AF state, calling for a transition in the magnetic nature at higher pressure. This is exactly in line with the experimental predictions, the only notable difference being the value of the transition pressure, substantially lower in the experimental results (about 1.5 GPa) [21].

Fig. 2

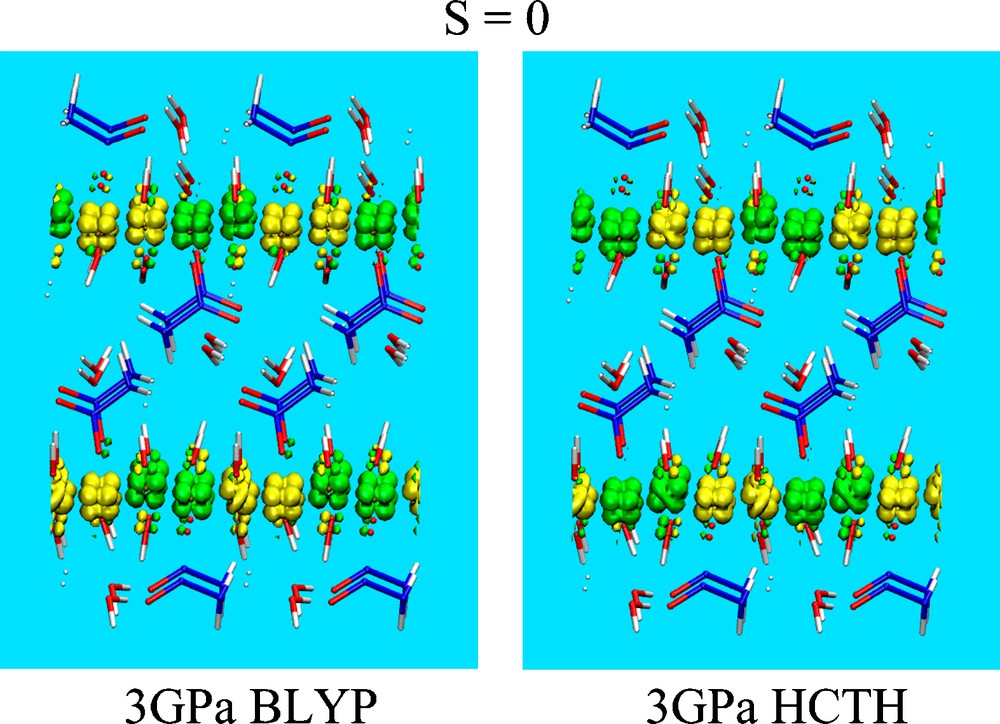
Spin density distribution for the optimized structures of Cu2(OH)3(CH3COO)·H2O seen along the [010] direction (xz plane) for a total spin S = 0 and for an external pressure of 3 GPa. Each configuration corresponds to a given spin topology for the in-plane Σ = 0 case. The spin density isosurfaces are green (α spin states) and yellow (β spin states), O atoms are red, C atoms are blue and H atoms are white. The ground state configuration is the one on the top of the left column. Isosurfaces of spin densities are shown at ± 10−2 e/Å3. The right panel refers to the BLYP calculation, the left panel to the HCTH/120 calculation.

Fig. 3

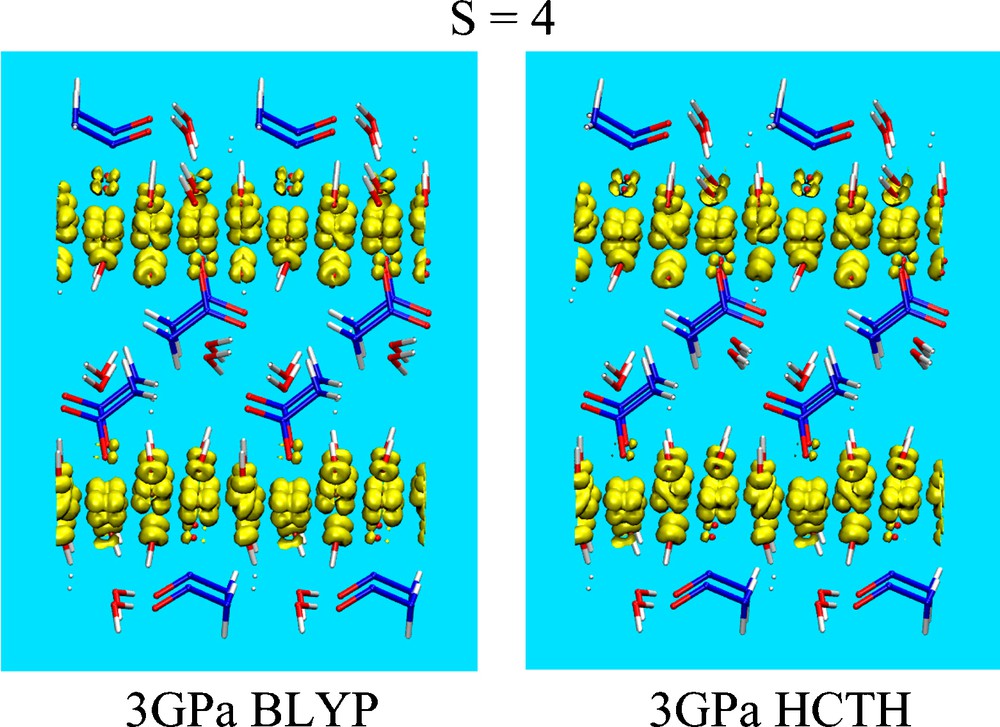
Spin density distribution for the optimized structures of Cu2(OH)3(CH3COO)·H2O seen along the [010] direction (xz plane) for a total spin S = 4 and for an external pressure of 3 GPa. The isosurface values of the spin density and the color code are identical to the former figures. Right and left panels show the results of BLYP and HCTH/120 calculations, respectively.

Table 1

Energy difference (ΔE = ES=4–ES=0) between the S = 0 and S = 4 structures at 0, 3 and 5 GPa for the BLYP and HCTH/120 choices of the exchange-correlations functionals within density functional theory (DFT).

(GPa)ΔEBLYP (eV)ΔEHCTH (eV)
01.40.388
30.7150.215
50.3680.242

A word of comment is in order to understand why the energy difference E(S = 4) − E(S = 0) reported in Table 1 for the HCTC case is lower at a pressure of 3 GPa (0.215 eV) than at a pressure of 5 GPa (0.242), in apparent contradiction with the idea that a transition in the magnetic nature (i.e. from AF to F) should set in with increasing pressure. We recall that Table 1 contains the results for a single spin configuration at S = 0. However, notable energy differences (up to 0.15/0.2 eV) are observed among different spin configurations obtained (Ref. [3]) for the same S = 0 value. Accordingly, error bars of at least 0.15 eV have to be assigned to the energies shown in Table 1, thereby undermining the significance of the differences between the HCTH/120 values at 3 and 5 GPa. Finally, only minimal changes in the topology of the local spin densities are encountered at the pressure 5 GPa. Therefore, the same considerations developed for the case of 3 GPa and exemplified by Figs. 2 and 3 apply to the 5 GPa case.

3.3 Structural properties

The main geometrical parameters of the optimized AF structure, with a total spin S = 0, are reported in Table 2, for both the BLYP and the HCTH/120 functionals and for both the pressures considered here (3 and 5 GPa). As in the case of 0 GPa discussed in a previous work [3], the general trend of the interatomic distances in the various groups (OH−, CH3COO− and H2O) tend to replicate rather regularly inside the cell. However, due to fact that an external stress is applied, a few of the longer and more flexible CH3COO− groups start approaching the Cu atoms, while other CH3COO− groups seem to be only slightly squeezed. In particular, we can notice that at 3 GPa, while the Cu(1)–O1, Cu(1)–O2, Cu(3)–O1, Cu(4)–O2, and Cu(8)–O1 distances are substantially unchanged with respect to the same system at 0 GPa, (at least at the BLYP level, see ref. [3]), other distances change. Specifically, Cu(2)–O1, Cu(1)–O2, and Cu(4)–O1 increased of about 0.02–0.03 Å, whereas Cu(3)–O1, Cu(3)–O2, Cu(5)–O1, Cu(6)–O1, and Cu(7)–O1 decrease by amounts ranging from 0.02 Å to 0.12 Å. Another feature worthy of note is again related to the specific choice of the exchange-correlation functional. Almost all the Cu–O distances computed within the HCTH/120 approach are systematically slightly larger than the corresponding ones obtained by BLYP calculations. On the other hand, at the same pressure (3 GPa) the spin state of the system seems to be less important in terms of structural modifications (Table 3). In fact, both approaches show Cu–O distances nearly unchanged in going from the S = 0 to the S = 4 state; even the flexible CH3COO− groups are displaced by less than ± 0.01–0.02 Å when going from the AF to the F state. This is consistent with the findings of the 0 GPa case, where the structures obtained for the AF and the F spin topologies were found to be very close [3,16].

Table 2

Representative interatomic distances for the system with total spin S = 0 at pressures of 3 and 5 GPa at the BLYP and a HCTH/120 level.

5 (GPa)3 (GPa)5 (GPa)3 (GPa)
BLYPHCTHBLYPHCTHBLYPHCTHBLYPHCTH
Cu(1)–O1(O∈CH3COO)2.132.172.152.18Cu(5)–O1(O∈CH3COO)2.512.582.672.68
Cu(1)–O2(O∈CH3COO)2.192.192.172.17Cu(5)–O2(O∈OH)1.901.921.931.94
Cu(1)–O3(O∈OH)1.931.951.941.97Cu(5)–O3(O∈OH)1.921.931.971.97
Cu(1)–O4(O∈OH)1.961.971.971.99Cu(5)–O4(O∈OH)1.971.992.002.03
Cu(1)–O5(O∈OH)2.012.032.102.10Cu(5)–O5(O∈OH)2.002.022.032.05
Cu(1)–O6(O∈OH)2.102.132.232.23Cu(5)–O6(O∈OH)2.222.212.232.23
Cu(2)–O1(O∈CH3COO)2.052.092.072.09Cu(6)–O1(O∈CH3COO)2.482.502.632.60
Cu(2)–O2(O∈CH3COO)2.102.192.092.11Cu(6)–O2(O∈OH)1.881.891.921.94
Cu(2)–O3(O∈OH)1.881.871.901.91Cu(6)–O3(O∈OH)1.891.911.931.95
Cu(2)–O4(O∈OH)1.891.901.921.94Cu(6)–O4(O∈OH)2.012.032.032.04
Cu(2)–O5(O∈OH)2.162.152.272.26Cu(6)–O5(O∈OH)2.062.062.072.09
Cu(2)–O6(O∈OH)2.963.023.033.05Cu(6)–O6(O∈OH)2.232.262.292.30
Cu(3)–O1(O∈CH3COO)1.982.002.012.03Cu(7)–O1(O∈CH3COO)2.572.612.662.67
Cu(3)–O2(O∈CH3COO)2.032.062.062.09Cu(7)–O2(O∈OH)1.881.891.941.95
Cu(3)–O3(O∈OH)1.901.921.931.95Cu(7)–O3(O∈OH)1.911.941.951.97
Cu(3)–O4(O∈OH)1.911.931.931.95Cu(7)–O4(O∈OH)1.971.981.982.00
Cu(3)–O5(O∈OH)2.252.262.282.29Cu(7)–O5(O∈OH)1.981.992.012.01
Cu(3)–O6(O∈OH)2.722.842.862.87Cu(7)–O6(O∈OH)2.722.792.762.80
Cu(4)–O1(O∈CH3COO)2.102.132.082.11Cu(8)–O1(O∈CH3COO)3.063.143.043.06
Cu(4)–O2(O∈CH3COO)2.152.252.092.12Cu(8)–O2(O∈OH)1.871.891.951.96
Cu(4)–O3(O∈OH)1.901.911.921.94Cu(8)–O3(O∈OH)1.931.941.971.98
Cu(4)–O4(O∈OH)1.931.951.941.96Cu(8)–O4(O∈OH)1.951.971.992.01
Cu(4)–O5(O∈OH)2.152.112.392.36Cu(8)–O5(O∈OH)2.002.002.002.02
Cu(4)–O6(O∈OH)2.232.232.422.41Cu(8)–O6(O∈OH)2.292.302.312.33
Table 3

Representative interatomic distances for the system with total spin S = 4 at pressures of 3 and 5 GPa at the BLYP and a HCTH/120 level.

5 (GPa)3 (GPa)5 (GPa)3 (GPa)
BLYPHCTHBLYPHCTHBLYPHCTHBLYPHCTH
Cu(1)–O1(O∈CH3COO)2.152.192.172.18Cu(5)–O1(O∈CH3COO)2.482.562.622.67
Cu(1)–O2(O∈CH3COO)2.202.192.202.19Cu(5)–O2(O∈OH)1.921.941.951.96
Cu(1)–O3(O∈OH)1.941.971.961.97Cu(5)–O3(O∈OH)1.941.952.001.99
Cu(1)–O4(O∈OH)1.971.992.002.00Cu(5)–O4(O∈OH)1.982.002.022.04
Cu(1)–O5(O∈OH)1.982.012.042.07Cu(5)–O5(O∈OH)2.012.032.042.06
Cu(1)–O6(O∈OH)2.052.082.122.21Cu(5)–O6(O∈OH)2.222.202.202.22
Cu(2)–O1(O∈CH3COO)2.102.142.102.10Cu(6)–O1(O∈CH3COO)2.452.442.582.59
Cu(2)–O2(O∈CH3COO)2.162.242.122.11Cu(6)–O2(O∈OH)1.891.891.931.94
Cu(2)–O3(O∈OH)1.881.881.901.93Cu(6)–O3(O∈OH)1.911.921.941.95
Cu(2)–O4(O∈OH)1.891.901.921.95Cu(6)–O4(O∈OH)2.022.042.042.05
Cu(2)–O5(O∈OH)2.132.122.212.24Cu(6)–O5(O∈OH)2.082.092.122.11
Cu(2)–O6(O∈OH)2.892.953.003.07Cu(6)–O6(O∈OH)2.212.222.232.29
Cu(3)–O1(O∈CH3COO)2.012.032.032.03Cu(7)–O1(O∈CH3COO)2.592.642.682.66
Cu(3)–O2(O∈CH3COO)2.052.082.092.10Cu(7)–O2(O∈OH)1.901.931.981.97
Cu(3)–O3(O∈OH)1.921.941.951.96Cu(7)–O3(O∈OH)1.941.971.991.98
Cu(3)–O4(O∈OH)1.921.941.951.96Cu(7)–O4(O∈OH)1.981.992.022.02
Cu(3)–O5(O∈OH)2.182.182.182.26Cu(7)–O5(O∈OH)1.992.002.022.04
Cu(3)–O6(O∈OH)2.303.143.082.84Cu(7)–O6(O∈OH)2.602.572.342.81
Cu(4)–O1(O∈CH3COO)2.122.142.072.11Cu(8)–O1(O∈CH3COO)3.093.183.093.06
Cu(4)–O2(O∈CH3COO)2.192.282.102.12Cu(8)–O2(O∈OH)1.881.891.931.97
Cu(4)–O3(O∈OH)1.911.921.931.94Cu(8)–O3(O∈OH)1.941.961.982.01
Cu(4)–O4(O∈OH)1.941.961.961.97Cu(8)–O4(O∈OH)1.971.982.012.01
Cu(4)–O5(O∈OH)2.102.082.362.34Cu(8)–O5(O∈OH)2.012.012.032.02
Cu(4)–O6(O∈OH)2.202.202.412.42Cu(8)–O6(O∈OH)2.302.312.272.32

By increasing the pressure to 5 GPa, the changes in the Cu–O distances become more evident and no one of the CH3COO− groups keeps its original separation from the corresponding Cu atom. Basically two distinct classes appear, the “compressed” CH3COO− groups, where the Cu–O distances are shortened, and the “elongated” CH3COO− groups, where the Cu–O distances result slightly enlarged (Table 2). To the first class belong Cu(1)–O1, Cu(2)–O1, Cu(3)–O1, Cu(3)–O2, Cu(5)–O1, Cu(6)–O1, and Cu(7)–O1, which shorten their distances to various amount from 0.02 Å to 0.15 Å. To the second (“elongated”) class belong Cu(1)–O2, Cu(2)–O2, Cu(4)–O1, Cu(4)–O2 and Cu(8)–O1 which farther apart from the Cu sites by amounts ranging from 0.01 Å up to about 0.1 Å. We can remark that also a few OH groups undergo slight modifications which can be classified into one of the two groups discussed above for the longer adducts. These modifications reflect the global rearranging of the structure when an external pressure is exerted and the most noticeable modifications, as expected, occur along the z crystallographic direction, where the material is more flexible. In a nutshell, the inorganic Cu planes approach each other and the organic groups and water molecules trapped in between the planes rearrange and reorient as a response to the mechanical stress. This, of course, influences also the hydrogen bond (H–bond) topology [22–24] of the water molecules trapped in the Cu2(OH)3(CH3COO)·H2O structure.

At the same pressure of 5 GPa, the F solution S = 4 shows geometrical features qualitatively (and almost quantitatively) very similar to the AF S = 0 case. As in the case of the 3 GPa pressure, also in this case a change in the total spin does not affect the structure apart from slight modifications of a few percent in the Cu–O distances. What is worthy of note, instead, is that also in this case HCTH/120 gives slightly larger distances with respect to the BLYP estimates. This seems to be consistent with the general feature of BLYP, which tend to bind more tightly O atoms to give slightly stronger H–bonds with respect to HCTH/120 [13,24,25]. Such a fact is also consistent with the larger AF–F energy differences (Table 1) found in the BLYP case and discussed in the previous section.

4 Conclusions

Ambiguities affecting the Cu2(OH)3(CH3COO)·H2O structure have been resolved by accurate first principles calculations, within the DFT approach. A stringent comparison of the theoretically refined structure with X-ray crystallography data has shown that indeed this is a viable way to complement experiments and to recover the missing pieces of information non accessible to experimental probes. Furthermore, this has provided a good starting structure to investigate the effects of an external pressure onto the atomic structure and the spin topology of such a material. One of the most remarkable features making this material appealing for practical applications is its unique piezomagnetic character. We have shown how a moderate pressure influences mostly the interlayer structure, where organic adducts are located, and how their larger/reduced flexibility allow for more/less remarkable geometrical modifications. Nonetheless, at least for the external pressures considered here (3–5 GPa), such modifications seem unable to affect the spin topology both in the anti-F and in the F states, opening a path to further investigation in a more extended range of pressure. Finally, the use of different prescriptions (BLYP, HCTH/120) for the exchange and correlation interaction has shown that an accurate description of these many-body effects are crucial in the calculation of the magnetic properties of this class of systems and provide a benchmark for future DFT approaches.

Acknowledgment

We acknowledge insightful discussions with E. Ruiz as well as Fabien Muller (ICPMS, service informatique) and Romaric David (University of Strasbourg, direction informatique). This work was granted access to the HPC resources of [CCRT/CINES/IDRIS] under the allocation 2009-x2009095071 made by Grand équipement national de calcul intensif (GENCI).

Bibliographie

[1] P. Rabu; M. Drillon; K. Agawa; W. Fujita; T. Sekine Magnetism: molecules to materials II (J.S. Miller; M. Drillon, eds.), Wiley-VCHa, Wenbheim, 2001, p. 357

[2] P. Rabu; S. Rouba; V. Laget; C. Hornick M Drillon, Chem. Commun. (1996), p. 1107

[3] Y. Fan; M. Boero; C. Massobrio J. Phys. Chem. C, 114 (2010), p. 20213

[4] C. Massobrio; P. Rabu; M. Drillon; C. Rovira J. Phys. Chem. B, 103 (1999), p. 9387

[5] E. Ruiz; M. Llunell; J. Cano; P. Rabu; M. Drillon; C. Massobrio J. Phys. Chem. B, 110 (2006), p. 115

[6] N. Masciocchi; E. Corradi; A. Sironi; G. Moretti; G. Minelli; P. Porta P. J. Solid State Chem., 131 (1997), p. 252

[7] R. Car; M. Parrinello Phys. Rev. Lett., 55 (1985), p. 2471

[8] CPMD, Copyright IBM Corp. 1990–2009, Copyright MPI für Festkörperforschung Stuttgart 1997–2001. http://www.cpmd.org.

[9] W. Kohn; L.J. Sham Phys. Rev., 140 (1965), p. A1133

[10] A.D. Becke Phys. Rev. A, 38 (1988), p. 3098

[11] C. Lee; W. Yang; R.G. Parr Phys. Rev. B, 37 (1988), p. 785

[12] F.A. Hamprecht; A.J. Cohen; D.J. Tozer; N.J. Handy J. Chem. Phys., 109 (1998), p. 6264

[13] M. Boero; M. Tateno; K. Terakura; A. Oshiyama J. Chem. Theory Comput., 1 (2005), p. 925

[14] N. Troullier; J.L. Martins Phys. Rev. B, 43 (1991), p. 1993

[15] S.G. Louie; S. Froyen; M.L. Cohen Phys. Rev. B, 26 (1982), p. 1738

[16] G. Rogez; C. Massobrio; P. Rabu; M. Drillon Chem. Soc. Rev., 40 (2011), p. 1031

[17] J. Rodriguez-Carvajal, FullProf Suite Windows, version June 2011, ILL. http://www.ill.eu/sites/fullprof/php/downloads.html.

[18] A.D. Becke A. D. J. Chem. Phys., 98 (1993), p. 5648

[19] P.J. Stephens; F.J. Devlin; C.F. Chabalowski; M.J. Frisch J. Phys. Chem., 98 (1994), p. 11623

[20] E. Ruiz; A. Rodriguez-Fortea; J. Tercero; T. Cauchy; C. Massobrio J. Chem. Phys., 123 (2005), p. 074102

[21] K. Sukuzi; J. Haines; P. Rabu; K. Inoue; M. Drillon J. Phys. Chem. C, 112 (2008), p. 19147

[22] A. Chialvo; P. Cummings P. J. Phys. Chem., 100 (1996), p. 1309

[23] M. Boero; K. Terakura; T. Ikeshoji; C.C. Liew; M. Parrinello Phys. Rev. Lett., 85 (2000), p. 3245

[24] M. Boero; T. Ikeshoji; K. Terakura K. Chem. Phys. Chem., 6 (2005), p. 1775

[25] M.E. Tuckerman; A. Chandra; D. Marx Acc. Chem. Res., 39 (2006), p. 151

Commentaires - Politique

Ces articles pourraient vous intéresser

Molecular structure, NMR analyses, density functional theory and ab initio Hartree–Fock calculations of 3-phenylpropylamine

Mustafa Senyel; Arslan Ünal; Özgür Alver

C. R. Chim (2009)

In-depth quantum chemical investigation of electro-optical and charge-transport properties of trans-3-(3,4-dimethoxyphenyl)-2-(4-nitrophenyl)prop-2-enenitrile

Ahmad Irfan; Abdullah G. Al-Sehemi; Shabbir Muhammad; ...

C. R. Chim (2015)