1 Introduction
Metal–metal (M–M) interactions between first-row transition metals are of fundamental significance in many areas of chemistry, from small molecules to nano-sized clusters to the active sites of various metalloenzymes [1–3]. However, M–M (multiple) bonding in first-row transition metal complexes is notably weaker than in their second- and third-row counterparts due to lower overlap of the 3d-orbitals. This weak bonding interaction tends to complicate computational analysis [4]. The chrominum–chromium bond is particularly challenging for density functional theory (DFT) and generally requires wavefunction-based methods that specifically treat static and dynamic electron correlation to achieve quantitative results, such as correctly predicting the Cr–Cr bond distance [4–6]. These methods remain, however, impractical for transition metal complexes due in part to their requirement for very large basis sets for accurate results [7]. Despite its shortcomings, DFT can still provide valuable insight into these complicated systems, e.g. Landis and Weinhold's utilization of natural bond orbital-based analysis on a “maximally bonded” dichromium complex [8]. Moreover, it has been shown that for metals other than chromium, standard DFT methods generally perform satisfactorily for M–M multiply-bonded compounds [6,9]. A series of homoleptic dimetal compounds exist [10], M2(form)4 (M = V–Ni, but M ≠ Mn; form = N,N’-diarylformamidinate, Scheme 1), which are being used in our group to test density functional methods applied to M–M bonded first-row transition metal species. These complexes tend to conform to rough D4 symmetry (Scheme 1, I). A notable exception is the fascinating and unusual compound Fe2(form)4 (1), which was first synthesized by Cotton and Murillo in 1994 [11], and displays D2 symmetry (Scheme 1, II) having each iron center in a distorted tetrahedral ligand environment. Despite having been synthesized more than 15 years ago, no investigation of the electronic structure of this compound has been reported, nor has a description of the bonding been proposed.
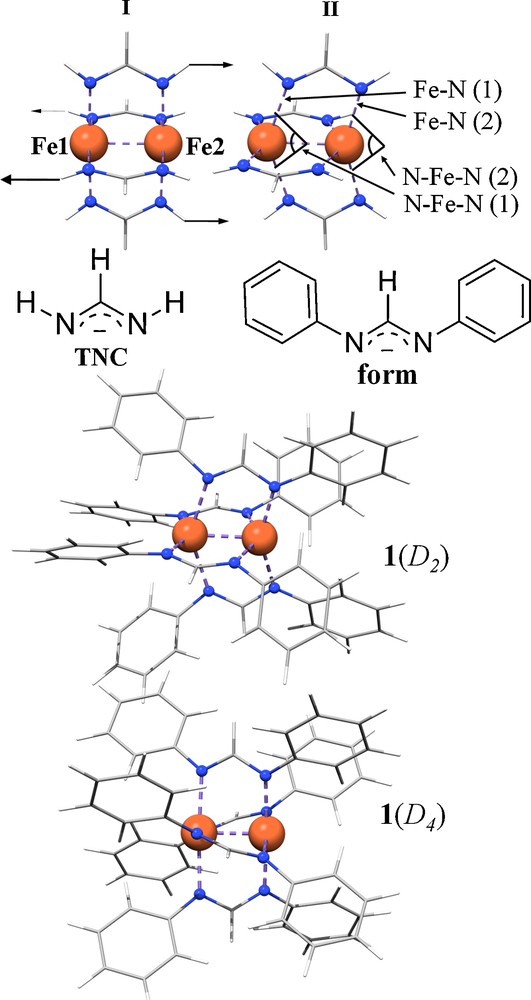
There are few non-organometallic compounds known that have been shown definitively to have an Fe–Fe bond. Examples are limited to Fe2(η2-(Mes)C = NtBu)2(μ-(Mes)C = NtBu)2, which was described by Floriani in 1994 [12] (Fe–Fe distance of 2.37 Å), Fe2(form)3, described by Cotton and Murillo in 1997 [13], with an Fe–Fe separation of 2.22 Å, and Fe2(tim)2 (tim = a macrocyclic ligand), recently reported by the Wieghardt group [14], which features an unsupported Fe–Fe σ bond with a distance of 2.69 Å. A computational investigation of Fe2(η2-(Mes)C = NtBu)2(μ-(Mes)C = NtBu)2 has been made suggesting an Fe–Fe bond made up of a half π and half δ component with the remaining electrons spin-aligned yielding a net S = 2 ground state [15]. The electronic structure of Fe2(form)3 has been investigated using SCF-Xα-SW calculations, which indicate an Fe–Fe bond order of 1.5 and seven unpaired electrons in orbitals of π* (2), σ*, δ (2), and δ* (2) symmetry [13]. An alternative valence-bond view of the electronic structure of this compound would be that the Fe(I) and Fe(II) ions are coupled via double exchange, with the three delocalized σ and π electrons of β spin causing alignment of the seven other spins in the system. This view is analogous to the description of double-exchange in mixed-valent iron-sulfur clusters, for which one may also consider Fe–Fe bonds to be present [16].
The Fe–Fe distance in 1 of 2.46 Å is close to that of metallic iron (2.52 Å) and fits in the range of Fe–Fe distances discussed above [17]. Classically, bonding invokes pairing of electrons in an in-phase molecular orbital. The bonding in 1 is unclear because of the reported room temperature magnetic moment of 8.8 μB (9.68 emu K mol−1) [18], consistent with eight unpaired electrons, which suggests strong ferromagnetic coupling between two high-spin Fe(II) centers and an S = 4 ground state. Because of these features, 1 poses significant challenges from a computational point of view centered around magnetism and bonding. It was not clear at the outset of our work that current DFT methods would be successful in describing the electronic structure of 1, prompting us to employ a number of density functionals (DFs) to address the problem. Five classes of approximate DFs, arranged in order of increasing complexity, are represented: local density approximation (LDA), generalized gradient approximation (GGA), hybrid-GGA (includes a percentage of Hartree-Fock [HF] exchange), meta-GGA (includes higher derivatives in the GGA DF) and hybrid-meta-GGA (includes percentage HF exchange to the meta-GGA DF).
The magnetic properties of the two interacting Fe ions in 1 in the present study are interpreted using the phenomenological Heisenberg-Dirac-van Vleck spin-Hamiltonian
| (1) |
| (2) |
Although one may question the applicability of the BS approach to strongly delocalized systems with metal–metal bonds, this approach has been found to provide a good description of weakly interacting electrons in metal–metal bonded systems [22].
The Mayer bond order (MBO) [23] used in the present study to interrogate the Fe–Fe bond is advantageous in that it has been shown to be a useful and robust tool in inorganic chemistry, from main group complexes, to transition metal complexes [24] as well as complexes with multiple M–M bonds [25].
In order to clarify the bonding in 1, the present work employs the above methods to answer the following three questions about this intriguing compound that have been unanswered for over 15 years:
- • Is there an electronic rationale for the D2 geometric distortion in 1?
- • Can we account for the S = 4 ground state?
- • What is the nature of the interaction between the iron centers in 1, i.e. is there an Fe–Fe bond?
1.1 Computational methods
Initial work on the truncated model 1m (Scheme 1, top) used the Amsterdam Density Functional (ADF) suite [26] to optimize geometries constrained to D2d and D4h symmetry. The input geometry was created from the coordinates from the crystal structure of 1 with the phenyl rings truncated to hydrogen atoms. Spin-unrestricted, S = 4 optimizations resulted in a D2d symmetric structure. Spin-restricted, S = 0 optimizations resulted in a D4h symmetric geometry, suitable for symmetry-constrained, S = 4 optimization that was necessary to obtain the D4h symmetric model. The optimizations were done with the VWN-5 LDA functional with Becke exchange and Perdew correlation for the GGA [27,28], using TZP basis sets with a frozen core through 1 s (C and N) or 2p (Fe) [29,30]. Subsequent frequency calculations returned zero imaginary frequencies for both D2 as well as D4 symmetric models.
The ORCA program package [31] was used for single point high-spin and BS calculations with BP86 [27,28], PBE [32–36], B3LYP [28,37–39], and PBE0 [32–36,40] functionals. The zeroth-order regular approximation for relativistic effects (ZORA) [41] following the model potential implementation of van Wüllen [42], and the scalar-relativistically recontracted [43] ‘def2’ basis sets from the Karlsruhe group [44] and corresponding auxiliary [45] basis sets were employed throughout. The def2-TZVP(-f) basis set was used for Fe atoms and def2-SV(P) was used on the remaining atoms. The auxiliary basis sets were used to expand the electron density in the resolution-of-the identity approximation (RI) together with BP86 and PBE. All calculations were performed with increased integration grids (‘Grid4’ in ORCA convention), along with tight SCF convergence criteria.
Computational analysis was then extended to the full ligand complex which follows the same set of methods discussed above for the truncated model: geometry optimizations were run using ADF to generate D2 and D4 symmetric models. The D4 model could again only be attained using symmetry-restricted optimization. Frequency calculations returned zero imaginary frequencies for both models. The high-spin and BS single point calculations were performed using the ORCA program [31] with BP86, B3LYP and modified B3LYP with HF exchange varying from 5, 10, 15, 25% and based on those results we also included 12, 13 and 14%. (The results of preliminary calculations on the truncated model using PBE0 with various amounts of HF exchange showed the same trend seen for the B3LYP calculations with the full ligand complex with smaller J values, Fig. S3). The full def2-TZVP basis set was used for all atoms running efficiently with the RIJCOSX ‘chain of spheres’ approximation to accelerate the computation of hybrid functionals [46]. In order to test the robustness of the results the DF dependence of the exchange coupling constant was tested by including two more GGA functionals BLYP [28,38] (0% HF) and PBE (0% HF), and one more hybrid-GGA PBE0 (the one parameter hybrid version of PBE with 25% HF), and the meta-GGA functional TPSS [47] (0% HF) along with its hybrid counterparts TPSSh [48] (10% HF) and the less-well-tested TPSS0 (25% HF). The basis set dependence was checked by including the basis sets def2-SV(P), def2-TZVPP for BLYP and B3LYP.
Finally, a series of geometry optimizations of Fe2(TNC)4 beginning from 1m(D2d) were carried out with ORCA with the def2-TZVP basis set and TPSS, BP86, BP86/broken symmetry (BS) surface, and B3LYP. These calculations were accelerated with the RI and RIJCOSX approximations as described above.
The corresponding orbital transformation (COT) [19b] was used to identify the magnetic orbitals produced by the BS calculations. Orbitals were plotted using the UCSF Chimera program package [49].
2 Results and discussion
2.1 Results with the truncated TNC ligand
To facilitate computations, our initial work has focused on model compounds in which the form ligand has been truncated to [HNCHNH]−(TNC in Scheme 1). This truncation provides qualitatively useful results demonstrated both in previous computational work on M–M bonded compounds [50], as well in the present study (vida infra). To distinguish the TNC results from those obtained using the full form ligand, the truncated model Fe2(TNC)4 will be denoted 1m. Two geometries for 1m were optimized: a D4h and a D2d structure, hereafter referred to as 1m(D4h) and 1m(D2d). The optimized structure of 1m(D2d) was obtained from a spin-unrestricted S = 4 optimization, whereas it was necessary to impose D4h symmetry on 1m to obtain an optimized structure for 1m(D4h) with S = 4. This result alone emphasizes that there is a geometric preference for the D2d geometry in the S = 4 state. The results of the optimized structures are given in Table 1 and Scheme 1, in which it can be seen that the calculated bond distances and angles in 1m(D2d) reflect those observed experimentally quite well. The Fe–Fe distance in 1m(D4h) is shorter than 1m(D2d) by 0.06 Å, the Fe–N ligand distances fall between the long (2.20 Å) and short (2.02 Å) distances of 1m(D2d) and the N–Fe–N angle becomes linear (∼176°).
Left: selected interatomic distances and angles (Å and deg) for Fe2(form)4, 1(exp), 1(D4)HS, 1(D2)HS, 1m(D4h)HS, 1m(D2d)HS. Specific distances and angles refer to those shown in Scheme 1. Right: The Fe–Fe distances for unrestricted S = 4 optimization of Fe2(TNC)4 using, A: BP; B: BP/broken-symmetry surface; C: B3LYP with def2-TZVP basis set.
| Compound | 1, expt. | 1m(D4h)HS | 1m(D2d)HS | 1(D4)HS | 1(D2)HS | A | B | C |
| Fe–Fe, Å | 2.462 (1) | 2.42 | 2.48 | 2.32 | 2.46 | 2.48 | 2.64 | 2.73 |
| Fe–N 1, Å | 2.002 (4) | 2.12 | 2.01 | 2.12 | 2.01 | 1.99 | 2.00 | 1.99 |
| Fe–N 2, Å | 2.171 (4) | 2.12 | 2.15 | 2.12 | 2.20 | 2.14 | 2.15 | 2.13 |
| N–Fe–N 1,° | 155.5 (2) | 177.3 | 150.3 | 176.8 | 150.1 | 150.5 | 157.8 | 150.5 |
| N–Fe–N 2,° | 149.2 (2) | 177.3 | 143.0 | 176.8 | 145.5 | 143.0 | 142.2 | 143.0 |
| N–Fe–Fe–N,° torsion | 0.0 | 0.0 | 0.0 | 20.7 | 3.8 | 0.0 | 1.0 | 0.0 |
The electronic structures of 1m(D4h) and 1m(D2d) were examined in the experimentally determined ground spin-state of S = 4. In order to gain more insight into the nature of this ferromagnetically coupled state, the corresponding antiferromagnetic singlet state, BS(4,4), has been investigated using the BS formalism.
To assess the electronic nature of the observed D2d geometric distortion, a comparison was made between 1m(D4h) and 1m(D2d), both in the S = 4 state. The molecular orbitals of 1m(D4h) and 1m(D2d) are compared in Fig. 1, organized in Walsh diagram fashion. The 10 Fe valence d orbitals (20 one-electron orbitals) for 1m(D4h) and 1m(D2d) are placed side by side, alpha to alpha, beta to beta. We have found it useful here to analyze the metal and ligand contribution to each orbital using pie charts that are color-coded for each of the four types of M–M bonding orbitals: σ from overlap of dz2 (green), π from dxz and dyz (red), δ from dxy (orange), and δ from dx2-y2 (light-blue). These pie charts allow simple assessment of the degree of metal-ligand orbital mixing. An advantage of using the truncated 1m model here is that metal-ligand mixing is not as extensive as in the case of the orbitals from the full molecule (vide infra).
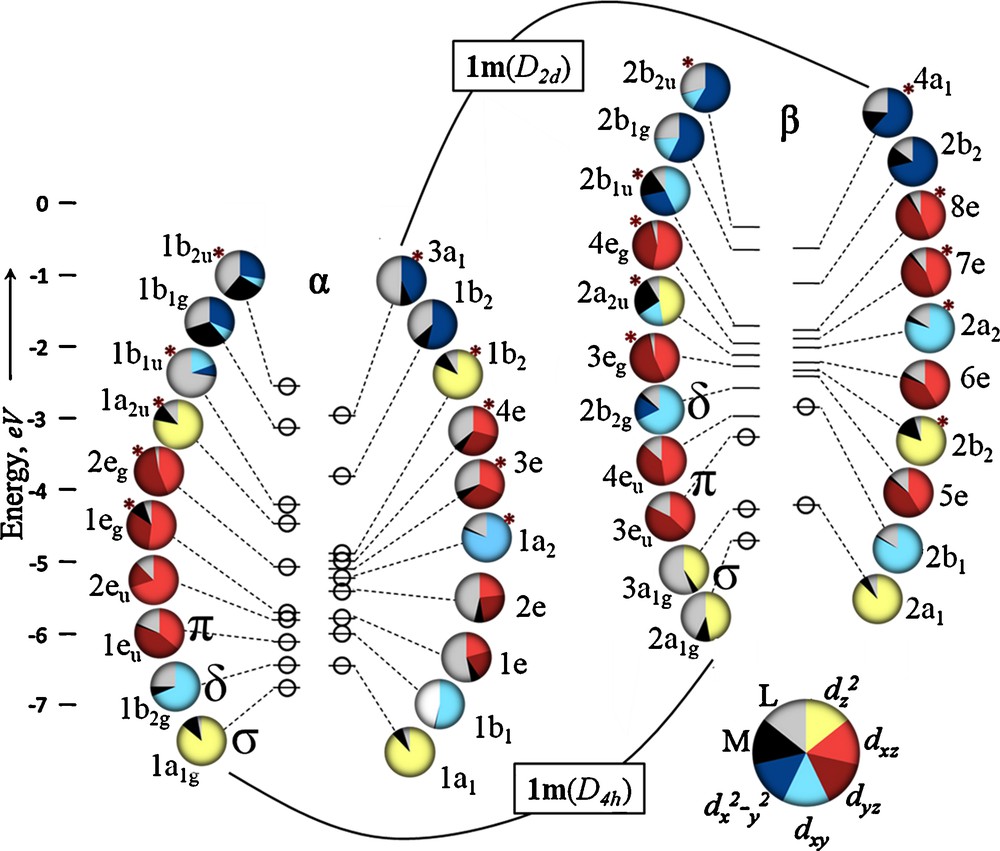
Molecular orbital energy level diagram for 1m(D4h), left, and 1m(D2d), right. Each circle represents a single electron with alpha spin grouped on the left and beta spin grouped on the right. The character of each orbital is indicated by a pie chart depicting the percent and type metal character of each orbital and its symmetry. The Fe dz2 orbitals in 1m(D4h) contribute equally to two beta spin sigma-bonding orbitals yielding 11 total M–M orbitals instead of the expected 10.
The valence Fe orbitals shown in Fig. 1 form the familiar and expected Fe–Fe σ (dz2), π (dxz, dyz), and δ (dxy, dx2-y2) combinations as well as the corresponding antibonding counterparts. In D4h symmetry, the ordering of these orbitals is generally as anticipated from other M–M multiply bonded compounds with the σ, π, and δ(dxy) bonding and antibonding orbitals significantly lower in energy than the δ(dx2-y2) orbitals. The latter are high in energy due to the fact that the dx2-y2 orbitals are pointed directly toward the bridging ligands and are thus strongly Fe–ligand antibonding in character, with the α-spin components showing less than 50% Fe character.
Upon moving from D4h to D2d symmetry, two major changes occur in the molecular orbital interactions in 1m. The dx2-y2 based orbitals (light-blue) decrease in energy and the π-orbitals (in red) move to higher energy and mix more heavily with the ligands. The former change is to be expected since the distortion breaks the direct approach of the ligand's bite into the dx2-y2 orbitals, which are required to be half-filled in the S = 4 state. The shift in the π orbitals is a result of more extensive metal-ligand orbital mixing in D2d symmetry than is possible for 1m(D4h) (Fig. 2). The extent of this mixing can be seen in the red pie charts in Fig. 1 for the α-spin π and π* orbitals, which decrease from ∼100% to 40–70% Fe character in 1m(D2d). These π-type MOs are Fe–ligand antibonding in character, hence they are destabilized as compared to 1m(D4h). Energetically the dx2−y2 and dxz, dyz interactions serve to offset each other, and so valence-orbital energies alone do not explain the stabilization of 1m(D2d) over 1m(D4h). Instead, what Fig. 1 makes clear with regard to geometric preference is that 1m(D4h) contains two α-spin π-bonding (1e and 2e) one β-spin π-bonding (5e) electron, giving an overall π3 electron configuration that is orbitally degenerate in D4h symmetry. The D2d geometric distortion lifts this orbital degeneracy. Thus, in addition to reducing unfavorable metal–ligand interactions, the D2d geometry can be attributed to a Jahn-Teller distortion. Additionally, the filled spin-up dx2−y2 orbital of b2u symmetry occurs at −2.62 eV, which is higher in energy than the lowest energy unoccupied spin-down orbital (4eu, −3.02 eV). Thus 1m(D4h) is actually an excited state and not a ground state species.
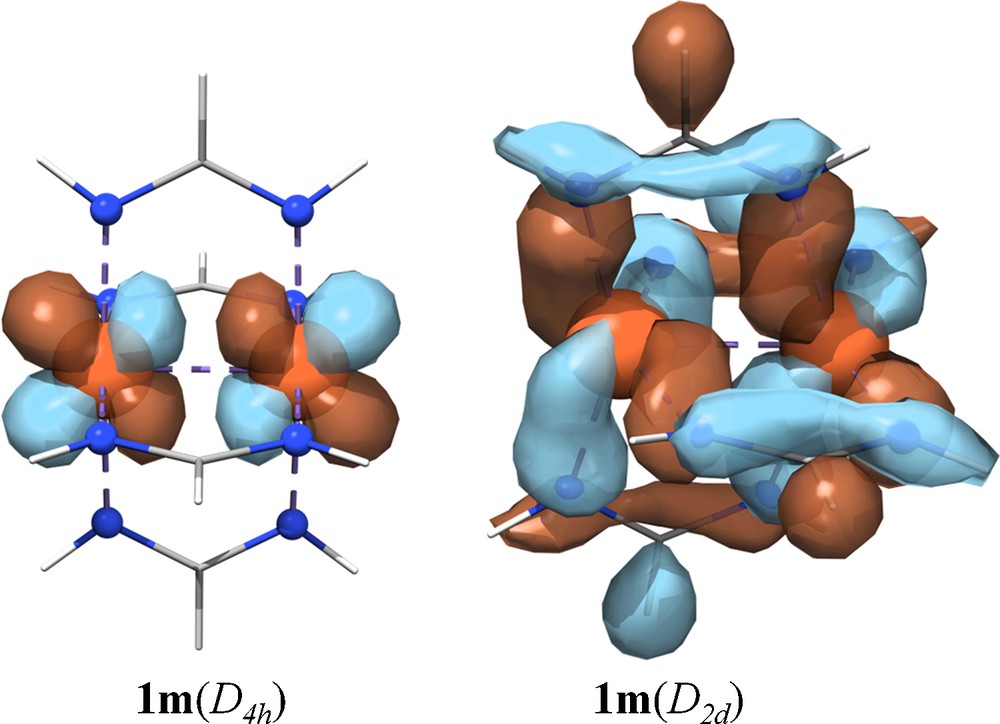
Representative metal–metal π* molecular orbitals that showcase the greater metal–ligand overlap facilitated by D2d molecular symmetry.
More results from the truncated model are presented in supporting information (Figs. S2 and S3), which will be mentioned with regard to the full ligand model results.
2.2 Results with the full form ligand
Symmetry- and spin-unrestricted, S = 4 geometry optimization with coordinates from the crystal structure of 1 led to a D2-symmetric structure which is in good agreement with crystallographic data (1(D2), Table 1). As with the model compound 1m, it was necessary to enforce D4 symmetry to optimize 1 in this geometry. The structure of 1(D2) matches the crystallographic data very well (Table 1). The same geometric shifts from 1m(D4h) to 1m(D2d) also occur for the full ligand, however, with reduced symmetry requirements from D4h to D4, the Fe–Fe distance shortens by ∼0.1 Å and a significant torsion angle (N–Fe–Fe–N) of 20.7° develops in 1(D4).
The computed energies of 1(D4)HS and 1(D2)HS fall close together (11–14 kJ/mol, depending on which functional is used, see Fig. 3), in agreement with the results from 1m, which suggest that the reason for distortion to D2 symmetry is to reduce the metal–ligand antibonding interactions of the half-filled Fe dx2−y2 orbitals, the lifting of a π3-orbitally degenerate state through Jahn-Teller distortion, and, like 1m(D4h), 1(D4) is an excited state, as evidenced by the non-aufbau electron configuration shown in Fig. 4. The valence molecular orbitals shown in Fig. 4 display a qualitative similarity to the 1m orbitals shown in Fig. 1. The main difference, as anticipated in the discussion above, is the greater degree of Fe–ligand mixing in 1 vs 1m, especially in the Fe–Fe orbitals of δ symmetry, which overlap better with the more electron-rich N–C–N π orbitals in the form ligand. There is a slight reordering of some of the orbitals in 1 vs 1m, such as the more conventional π < π < π* < π* ordering of the α orbitals in 1, as opposed to the π < π* < π < π* ordering seen in 1m. The features that do not change from 1m to 1 are the nature of the occupied orbitals in terms of their Fe–Fe character. Thus, in 1, as in 1m, the D4 symmetric state has formal orbital degeneracy, providing the impetus to distortion to D2 symmetry.
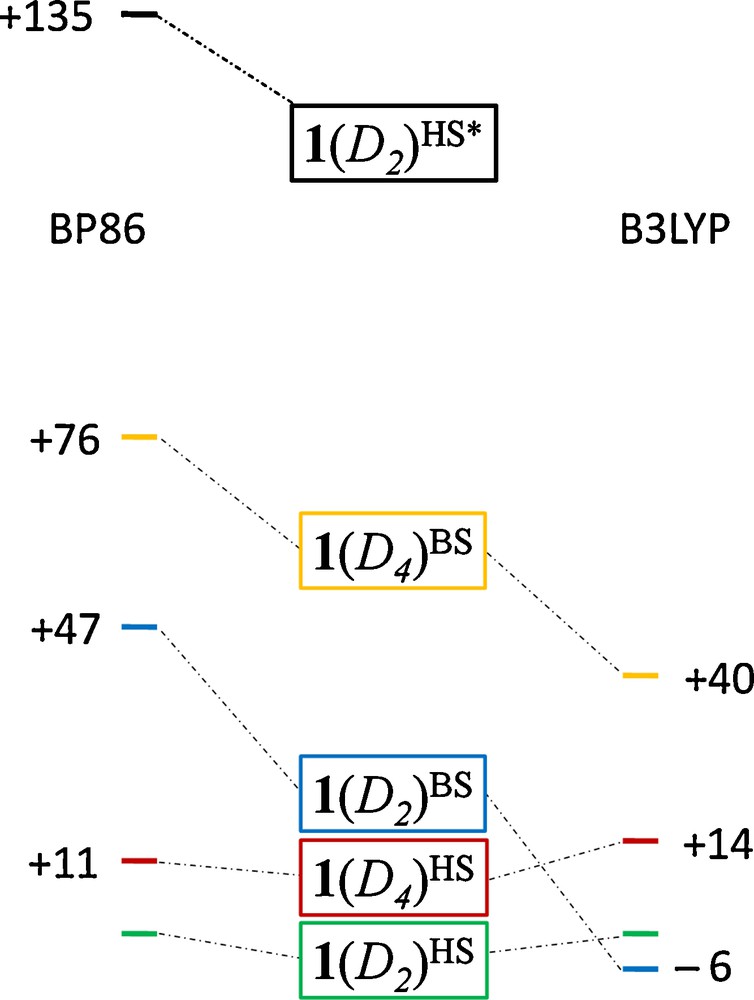
Relative energies in kJ mol-1 from BP86/def2-TZVP (left) and B3LYP/def2-TZVP (right) broken symmetry single point calculations with 1(D2)HS (the experimental ground state) set to 0 kJ mol-1. 1(D2)HS* denotes the predicted localized HDVV energy of 1(D2)HS.
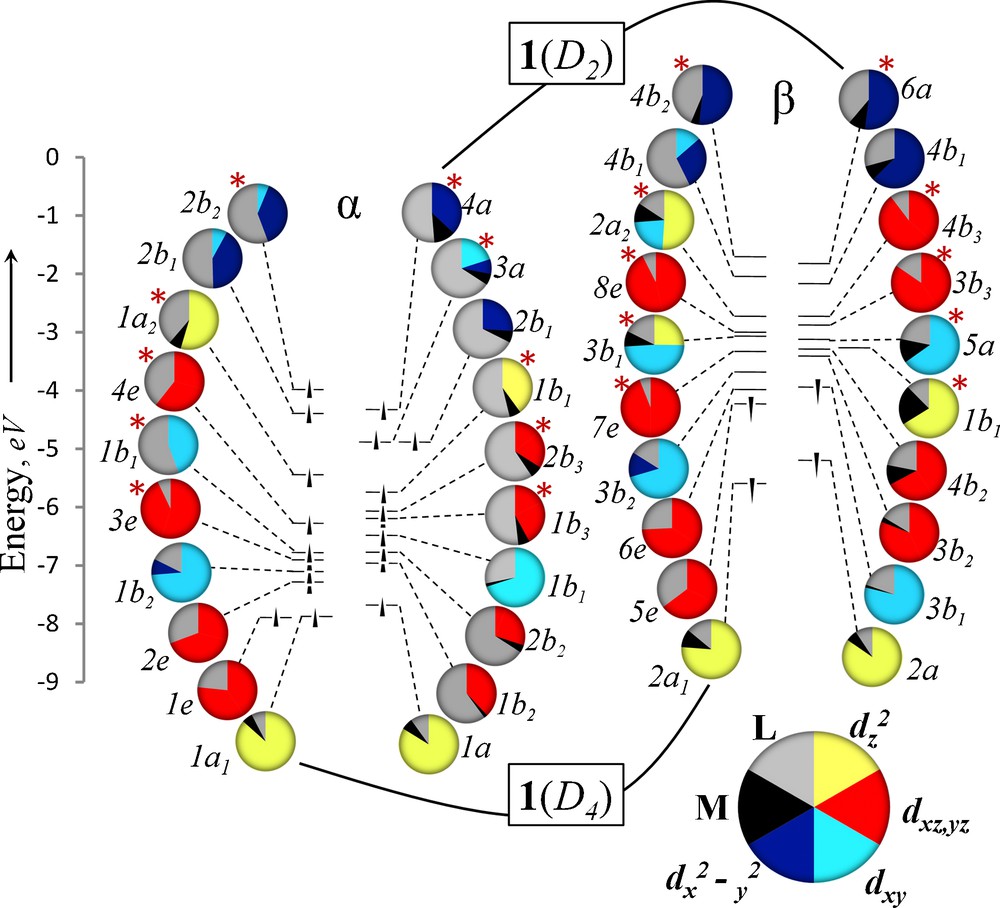
Molecular orbital energy level diagram for 1(D4), left, and 1(D2), right. The character of each orbital is indicated by a pie chart depicting the percent and type metal character of each orbital and its symmetry.
To gain insight into the origin of the experimentally observed high-spin ground state of 1, BS calculations were conducted on the open-shell (antiferromagnetically coupled) Ms = 0 states for 1(D4) and 1(D2) using both BP86 and B3LYP functionals (and the functionals in Table 2). The energies of the S = 4 HS and BS states for 1(D4) and 1(D2) are pictured in Fig. 3, relative to the energy of 1(D2)HS. As mentioned already, 1(D4)HS is elevated relative to 1(D2)HS by 11–14 kJ/mol, in agreement with the D2-symmetric crystal structure. The most notable feature of Fig. 3 is that the energies of the BS states for 1(D2) are remarkably different for the two functionals. The BP86 functional predicts a ferromagnetic ground state (J = +245 cm−1), while B3LYP favors an experimentally unobserved antiferromagnetic singlet (J = −30 cm−1). The experimental room temperature value of χ·T of 9.68 emu K mol−1 for 1 is consistent with eight unpaired electrons ( for S = 4). Here, χ is the measured molar magnetic susceptibility. Simulations of χ·T using the equation for the isotropic interaction within a symmetrical dinuclear complex with S1 = S2 = 2 indicate that J would need to be at least +125 cm−1 (Fig. S1) in order for a value of χ.T of 9.68 to be observable at room temperature [50]. Moreover, an antiferromagnetically coupled system would yield a much lower value of χ.T in the high temperature limit ( for S = 2). Thus, the BP86 functional yields an electronic structure more consistent with experimental data than does the B3LYP functional. The reasons for this discrepancy are investigated further below.
The results of the MBO for the BS calculations and the preceding HS calculations and the exchange coupling constant, J, associated with these calculations. Five types of functionals were used to insure the generality of the results: LDA (LSD), GGA (BLYP, BP86, PBE), hybrid-GGA (B3LYP, PBE0), meta-GGA (TPSS), and hybrid-meta-GGA (TPSSh, TPSS0).
| Functional | Type | MBO (HS) | MBO (BS) | J (cm-1) | ||
| LSD | LDA | 0.9511 | 0.4514 | +358 | ||
| BLYP | GGA | 0.9669 | 0.4494 | +243 | (+227)a | (+237)b |
| BP86 | GGA | 0.9406 | 0.4203 | +245 | (+239)b | |
| PBE | GGA | 0.9465 | 0.4280 | +255 | ||
| B3LYPHF = 5 | hybrid-GGAc | 0.9619 | 0.4147 | +168 | ||
| B3LYPHF = 10 | hybrid-GGAc | 0.9552 | 0.3887 | +56 | ||
| B3LYP*HF = 15 | hybrid-GGAc | 0.5520 | 0.3683 | −11 | ||
| B3LYPHF = 20 | hybrid-GGA | 0.4036 | 0.3515 | −30 | (−32)a | (−30)b |
| B3LYPHF = 25 | hybrid-GGAc | 0.3375 | 0.3367 | −33 | ||
| PBE0HF = 25 | hybrid-GGA | 0.3271 | 0.3220 | −34 | ||
| TPSS | meta-GGA | 0.9325 | 0.4030 | +168 | ||
| TPSShHF = 10 | hybrid-meta-GGA | 0.6046 | 0.3559 | −12 | ||
| TPSS0HF = 25 | hybrid-meta-GGA | 0.3004 | 0.3146 | −33 |
a def2-SV(P).
b def2-TZVPP.
c The amount of exact exchange was manually selected.
Analysis of the BP86 BS solution results indicate that the ferromagnetic ground state arises due to minimal overlap of the magnetic orbital pairs shown in Fig. 5, which were extracted from the wavefunction using the COT [19b]. The low overlap precludes the possibility of antiferromagnetic coupling in 1. However, surprisingly, the corresponding orbital overlap steadily diminishes with the addition of exact exchange. The sum of the S integral overlaps from the four magnetic orbital pairs for BP86 is 0.67 (Fig. 5), whereas this total for B3LYP is 0.32. And instead of near-zero overlap in B3LYP leading to greater ferromagnetic coupling than BP86, the low overlap produces unexpectedly weak antiferromagnetic coupling (−30 cm−1). The classical view of exchange coupling describes two main forces, spin polarization (SP) and spin delocalization (SD), which favor antiferromagnetic coupling and ferromagnetic coupling, respectively. The formamidinate ligand is isolobal to an acetate ligand, and therefore the same SP pathway that is operative in the antiferromagnetically coupled copper-acetate dimer [51,52] must be available in the case of 1. Indeed, SP is indicated by the large differences in energy between the α and β spin orbital pairs seen in Figs. 1 and 4. However, since the antiferromagnetic singlet state is higher in energy than the more delocalized HS state, SD is in 1 must be strong enough to outweigh the effects of SP. This analysis, in analogy to the case of ferromagnetic coupling via resonance delocalization in biologically important iron-sulfur clusters [16b], suggests substantial direct Fe–Fe interactions.
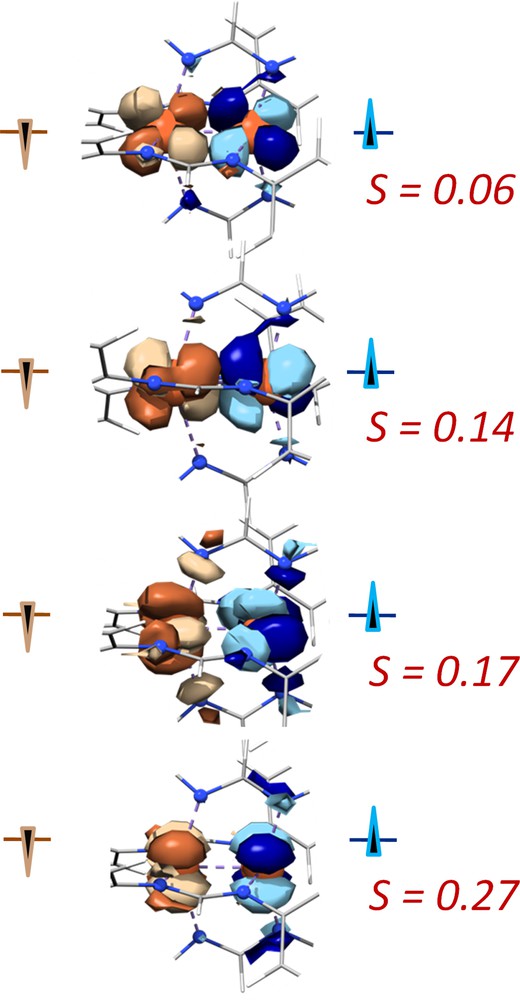
The corresponding orbitals from the broken symmetry solution of BP86/def2-TZVP for 1(D2). Two orbitals (one UCO pair) are pictured per structure. The beta electrons are brown and the alpha electrons are blue. The overlap integral, S, for each pair is in red.
With regard to direct Fe–Fe bonding in 1, inspection of the MO diagram for 1(D2)HS in Fig. 4 reveals that the 10 spin-up electrons constitute a complete set of filled bonding and antibonding M–M orbitals with no net Fe–Fe bond. The two beta spin orbitals, on the other hand, are Fe–Fe bonding orbitals, a σ-bonding orbital (2a) and a δ-bonding orbital (3b1) (Fig. 6). These filled one electron orbitals complete a σ2σ*1 half-bond and a δ2δ*1 half-bond, yielding a formal single Fe–Fe bond that is supported by the calculated MBO of 0.95. Interestingly, the calculated Fe–Fe MBO diminishes upon changing from 1(D2)HS to 1(D2)BS from 0.95 to 0.42. (Table 2), which points to the central role of an Fe–Fe bond in the SD that stabilizes the ferromagnetism of 1. (The results of systematic optimization of Fe2(TNC)4 show a clear connection between Fe–Fe bond distance and MBO (Fig. S2), and highlight the effect of exact exchange for this system).
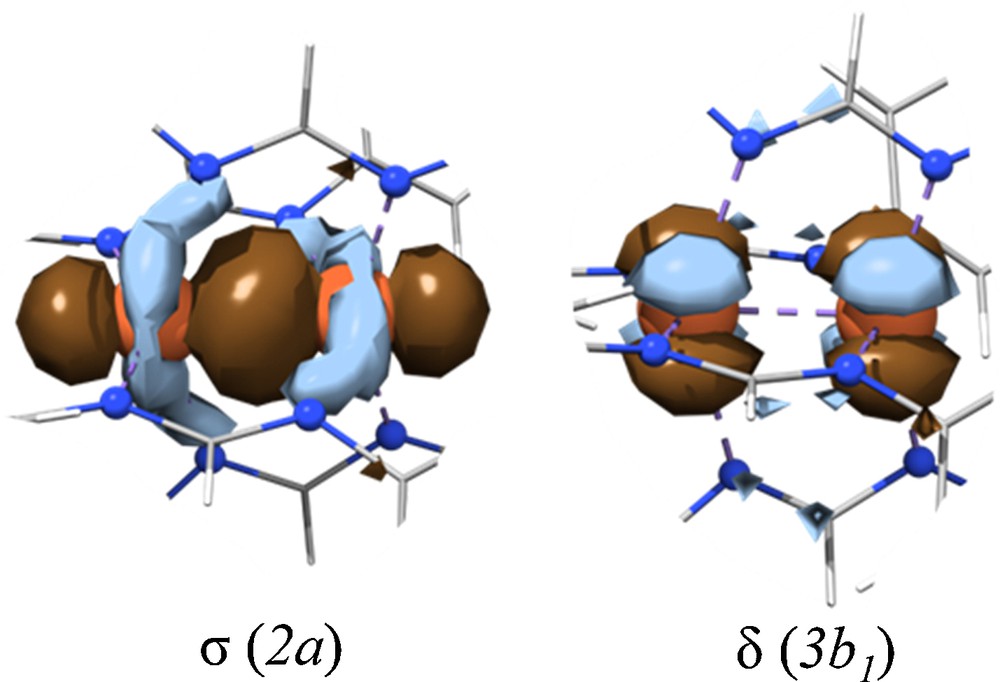
The two singly occupied, beta-spin bonding molecular orbitals responsible for the single bond calculated for 1(D2). Much of the form ligand was cropped out for clarity.
Another link between the Fe–Fe bond in 1 and its ferromagnetism is discernable upon further examination of the energetic discrepancy between BP86 and B3LYP highlighted in Fig. 3. As discussed above, BP86 provides a ground state that agrees with the experimental magnetic susceptibility measurement on 1, whereas B3LYP fails to do so. This observation is unusual since GGA functionals such as BP86 typically favor low spin states in iron complexes [53,54] and the addition of HF exchange to hybrid functionals such as B3LYP generally has a stabilizing effect on high spin states proportional to the amount of HF exchange added [53,55]. Curious about the influence of exact exchange on the bonding and magnetic properties of 1, a series of BS calculations were performed on 1(D2) with a range of HF exchange mixed into the functional. The results are shown in Fig. 7. Interestingly, for 1(D2), the amount of added HF exchange strongly affects both J as well as the Fe–Fe MBO. It is clear from this figure that as HF exchange is increased, J decreases. A result of these experiments that is more intuitive is the definite relationship between the ferromagnetism of the complex and the bond between the Fe centers. As HF exchange is added and J becomes smaller, the Fe–Fe single bond (MBO = ∼1) persists until the point when J becomes negative. As this occurs, the Fe–Fe MBO drops off steeply as J becomes more negative.
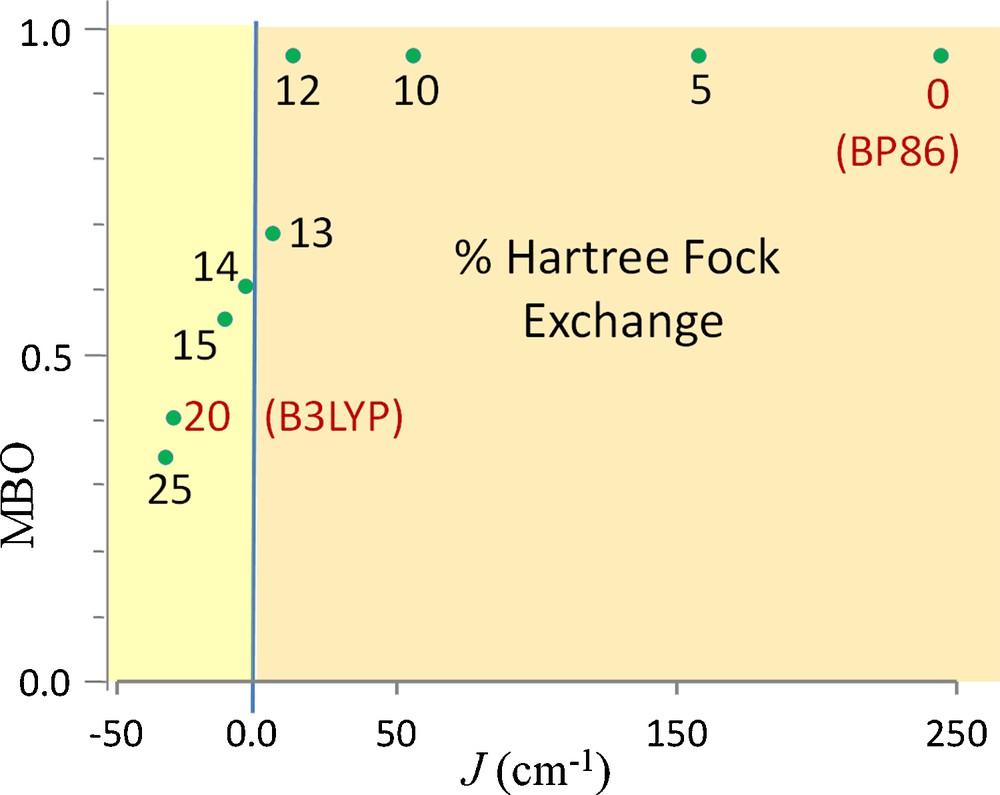
The correlation between Fe–Fe bonding (MBO) and the exchange coupling constant J. The numbers indicate the % HF exchange in the functional into the B3LYP functional. The red labels show the standard BP86 and B3LYP functional results. Ferromagnetic coupling (positive J) is predicated for the calculations for which the HS calculation preceding the BS calculation produced a Fe–Fe bond.
The largest effect of exact exchange on the Fe–Fe bonding orbitals for the HS calculations is to raise the beta δ bonding orbital while the σ* orbital energy drops. As the δ and σ* orbitals converge in energy, significant mixing is observed (Fig. S3). Once the σ* orbital moves below the δ orbital, the Fe–Fe bond is broken and the magnetic coupling becomes antiferromagnetic. This orbital effect is analogous to the observation made by Rong et al. based on a systematic investigation of LDA, GGA and hybrid-GGA functionals on the spin state of iron-containing complexes that “it is the outermost singly occupied molecular orbital that distinguishes the performance difference of different categories of approximate functional from each other,” with the conclusion that hybrid functionals are to be preferred [54a]. Here we report an exception to that rule due to the complicating factor of a weak M–M bonding interaction that is not described well by the addition of HF exchange and that GGA functionals provide a more useful model of the electronic structure in this particular case. We have shown that the electronic structure must facilitate electron delocalization between Fe centers by including partial σ and δ bonds in order to accord with both crystallographic and magnetic experiments to produce a ferromagnetically coupled, S = 4 ground state with an Fe–Fe bond of ∼2.46 Å presented by this remarkable complex.
The results of the magnetic coupling for all the functionals in Table 2 give credibility to the results and clearly show that the main influence over the magnetic coupling is the addition of HF exchange. The B3LYP functional has enjoyed great success in the chemical community, however, it has been shown to be unreliable in numerous cases [7]. Grimme reported a detailed comparison of wavefunction and DFT methods and found many errors for B3LYP that exceeded 20 kcal mol−1 that were not found for other functionals [56]. The PBE0 functional emerged from this study as the best performer (along with TPSS0). Since the magnetic coupling results of PBE0 (HF = 25%), TPSS0 (HF = 25%) and B3LYP (HF = 20%) are virtually identical, and basis set independent, the incorrect prediction of antiferromagnetic coupling by B3LYP is not just an accident, but a result of HF exchange. An interesting trend in the functional results of Table 2 is the progression from LSD to PBE to TPSS to TPSSh and TPSS0 (J (cm−1) = +358, +255, +168, −12 and −33, respectively) which are the first, second, third, and fourth rungs, respectively, of “Jacob's ladder” of DFs [47,48]. It is interesting that the coupling values of these functionals, which are said to be nested like Chinese boxes [47a], such that PBE contains LSD and TPSS contains PBE (and LSD), form a strong linear relationship (R2 = 0.9976, not presented), which decreases to R2 = 0.9711 upon inclusion of the hybrid values. Though the reasons for this behavior are not known, we point out here that strong ferromagnetic coupling is only predicted by the non-hybrid functionals which (for every case tested here) always indicate an Fe–Fe bond of order of ∼1 in the HS spin calculation that precedes the BS calculation. These observations are in line with the recent reports by Truhlar et al. that pure GGA functionals outperform their hybrid counterparts in describing metal–metal bonds [57,58].
Another noteworthy aspect of 1 that is brought up by the relationship between Fe–Fe bonding and ferromagnetic exchange is the similarity of 1 to compounds exhibiting double-exchange. Double exchange has been classically described for mixed valent iron-sulfer clusters in which the delocalization of a beta-spin electron gives rise to full spin alignment (ferromagnetic coupling) of the other Fe valence electrons [16a]. The electronic structure of 1 is similar except that there are two delocalized, beta-spin electrons instead of just one.
A double-exchange mechanism for Fe–Fe electron delocalization may be considered as a perturbation of the energies derived from the phenomenological Heisenberg-Dirac-van Vleck spin Hamiltonian. Since the HDvV model is based on a valence bond approach presupposing localized Fe valencies, a corrected HDvV energy for 1(D2)HS can be obtained, which we will call 1(D2)HS*, by removing energetic components due to Fe–Fe bonding, namely, half the energy difference between the β-spin σ and σ* orbitals, ΔE(σ), and ΔE(δ) for the β-spin δ and δ* orbitals. Thus, E(1(D2)HS*) may be defined as: E(1(D2)HS*) = E(1(D2)HS) + ½ ΔE(σ) + ½ ΔE(δ). Using the σ and δ orbital energies given in Fig. 4, the double-exchange stabilization energy amounts to ΔEDE = E(1(D2)HS*) − E(1(D2)HS) = 135 kJ/mol, which is quite substantial. In fact, as shown in Fig. 3, without the added double exchange stabilization, 1(D2) is predicted to be antiferromagnetic. We note that this analysis applies for the non-hybrid functionals such as BP86, since the hybrid functionals such as B3LYP lead to an electronic configuration having no delocalization stabilization as demonstrated by the β−σ, β−σ* electron configuration (Fig. S3). This analysis helps to explain the unusual observation that the high-spin state is preferred by the non-hybrid functionals in this system, since it is only in the non-hybrid case that the added stabilization due to electron delocalization of the Fe–Fe bond is seen.
3 Conclusions
The unusual D2 geometry of 1 is the result of a Jahn-Teller distortion, since in D4 symmetry, this compound would have an orbitally degenerate π3 ground state. The S = 4 ground state of this compound results from strong SD facilitated by an Fe–Fe single bond. The ferromagnetic coupling between the Fe(II) ions and the Fe–Fe bond are intimately linked, as is demonstrated by BS calculations with various amounts of HF exchange yielding exchange coupling constants that range from weakly antiferromagnetic to strongly ferromagnetic. This effect is reminiscent of the double-exchange, or resonance delocalization, observed in mixed-valent iron-sulfur clusters. It was heretofore thought that this effect requires mixed valency in the metal oxidation states, but the results described here suggest that this requirement is not absolute.
Acknowledgements
This work is dedicated in memory of Marie-Madeleine Rohmer. We thank the National Science Foundation for support of this work under CHE-0745500. The computational facilities were also supported by an NSF grant under CHE-0840494.


