Multifunction moonlighting and intrinsically disordered proteins: Information catalysis, non-rigid molecule symmetries and the ‘logic gate’ spectrum

Rodrick Wallace

doi:10.1016/j.crci.2011.10.003

Résumé

Intrinsically disordered proteins (IDP) appear far more likely to engage in functional moonlighting than well-structured proteins. The recent use of nonrigid molecule theory to address IDP structure and dynamics produces this result directly: mirror image subgroup or subgroupoid tiling matching of the molecular fuzzy lock-and-key can be much richer for IDP's since the number of possible group or groupoid symmetries can grow exponentially with molecule length, while tiling matching for 3D structured proteins is relatively limited. An ‘information catalysis’ model suggests how this mechanism can produce a vast spectrum of biological logic gates having subtle properties far beyond familiar AND, OR, XOR, etc. behaviors. Inferring the general from the particular, the analysis adds weight to arguments that a fundamental defining characteristic of the living state is the operation of chemical or other cognitive processes at virtually every scale and level of organization.

1 Introduction

Tompa et al. [1] have observed that intrinsically disordered proteins provide unprecedented examples of protein signal moonlighting – multiple, often unrelated, functions of the same molecule – by eliciting both inhibiting and activating action on different partners, or even on the same partner. Fig. 1, adapted from their paper, provides one schematic. The disordered protein can bind to more than one site on the partner molecule represented by a tilted square on the left of the figure. Binding to one site, as indicated by the shaded oval, creates an activated conformation, while binding to another site, the rectangle, results in an inhibited complex. Tompa et al. [1] indicate several different such possible mechanisms that are not mutually exclusive, but we will focus on this particular example. Generalization is direct.

Fig. 1
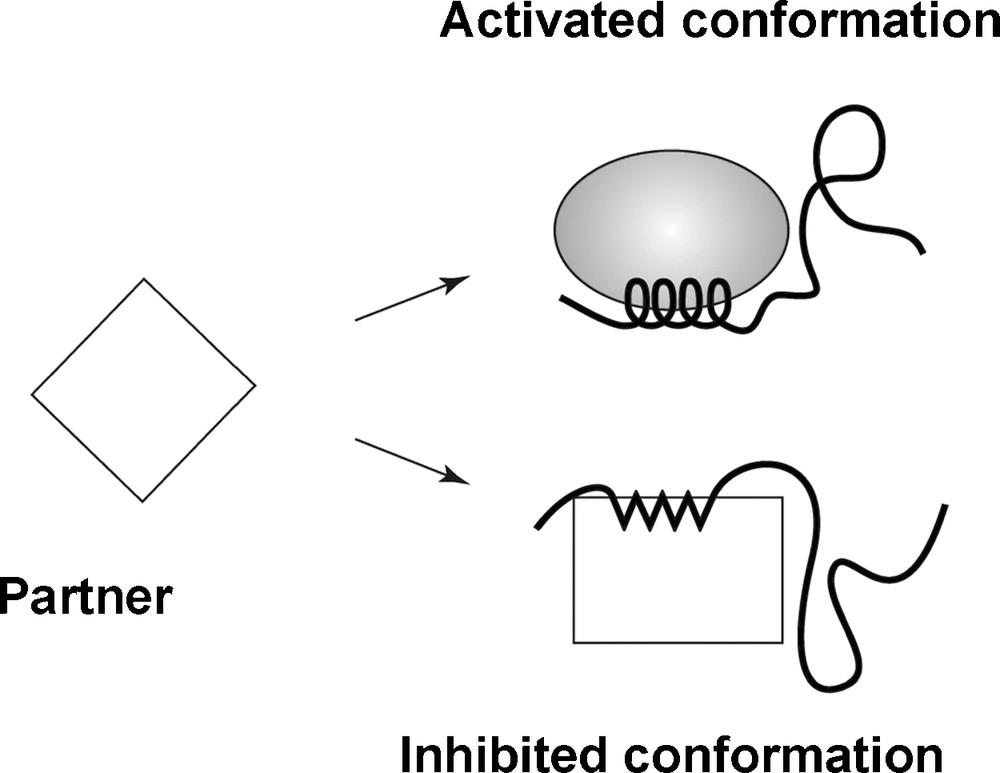
Adapted from Fig. 1 of [1]. The partner, represented by the tilted square, can bind in two ways with the incoming IDP. The shaded oval represents activated, and the rectangle, inhibited species. The ‘choice’ between them is, in this model, to be made by an information catalysis in which an incoming signal shifts the lowest energy state between the two otherwise thermodynamically competitive conformations. This is one example of a vast spectrum of similar chemical ‘logic gates’.

Wallace [2] has described IDP reaction dynamics via a statistical mechanics approach to a ‘symmetry spectrum’ derived from a groupoid generalization of the wreath product of groups [3] that characterizes ‘conventional’ nonrigid molecule theory [4,5]. The essential point is that the ‘fuzzy lock-and-key’ involves matching subgroups/subgroupoids between IDP and binding ligand via a set of mirror symmetries. The number of group/groupoid elements in a wreath product, related to the number of possible subgroups/subgroupoids, typically grows as the exponential power of the number of amino acids making up the IDP. That is, long IDP's have exponentially more possible linkages like that of Fig. 1 than do short.

More complete discussions of IDP from different perspectives can be found in [6,7].

For generalized switches and logic gates like Fig. 1, however, a comprehensive approach is necessary that reflects the operation of an elaborate regulatory system of chemical cognition analogous to what has been used to describe the immune system [8,9] or higher order neural and social function [10,11].

This idea has, in fact, been a subject of both speculation and research since the late 1930s, and is not restricted to intrinsically disordered proteins. We briefly reexamine some current and past examples, following the excellent review of James and Tawfik [12]. The essential point is that a single protein may equilibrate between thermodynamically equivalent preexisting conformations until one is ‘chosen’, in a sense, by some external signal.

Volkman et al. [13] show that the protein NtrC is allostatically regulated by phosphorylation: two conformations are present in unphosphorylated NtrC, with phosphorylation merely shifting the equilibrium toward the active conformation.

Cordes et al. [14] show that, with regard to the DNA-binding domain of the Arc repressor, the Arc-N11L mutant spontaneously interconverts between a two-stranded antiparallel β sheet and a two-3₁₀-helix structure. In the absense of a DNA ligand, the two conformations are in equilibrium at almost equal proportions. Addition of the DNA ligand shifts the equilibirum towards the β-sheet form.

According to Chien and Weissman [15], the prion protein PrP interconverts between an α-helix PrP^c and an all β-sheet conformation PrP^sc. The β-sheet is trapped by subsequent oligomerization, resulting in amyloid deposit and the onset of disease.

Very early on, Pauling [16] and Landsteinder [17] proposed that some proteins – antibodies – can exist as an ensemble of isomers with different structures but with similar free energy, so that, if each isomer was able to bind to a different ligand, functional diversity could go far beyond sequence diversity.

We begin with some formal development, based on the immune system example, leading to the idea of cognitive control in moonlighting pleiotropy, and by inference, for many other ‘logic gate’ structures as well.

From the perspective of Atlan and Cohen [8], who introduce a cognitive paradigm for the immune system, cognition involves comparison of a perceived signal with an internal, learned or inherited, picture of the world, and, upon that comparison, choice of a single response from a larger repertorie of possible responses. This inherently involves the transmission of information, since choice always necessitates a reduction in uncertainty ([18], p. 21). ‘Cognition’, in that sense, is quite routine, since even a thermostat would be cognitive from this perspective. The essential point is that sufficiently large biological structures can follow a great multiplicity of possible ‘reaction paths’, and focus must thereupon shift from the details of the chemical machinery itself to the details of its behavior in the context of signals, moving from what the system is in terms of its detailed molecular structure, to examining what it does. In computer terminology, this is analogous to focusing on the program the machine carries out rather than on a detailed study of the state of each logic gate at each clock cycle.

2 Symbolic dynamics of molecular switching

Symbolic dynamics is a ‘coarse-grained’ perspective on dynamic structures and processes that discretizes their time trajectories in terms of accessible regions so that it is possible to do statistical mechanics on symbol sequences ([19], Ch. 8) that can be said to constitute an ‘alphabet’. Within that ‘alphabet’, certain ‘statements’ are highly probable, and others far less so. The simple (ideal) oscillating reaction described by the equations dX/dt = ωY, dY/d t = −ωX has the solution X(t) = sin ωt, Y(t) = cos(ωt) so that $X {(t)}^{2} + Y {(t)}^{2} \equiv 1$ , and the system traces out an endless circular trajectory in time. Divide the X – Y plane into two components, the simplest possible coarse graining, calling the halfplane to the left of the vertical Y axis A and that to the right B. This system, over units of the period $1 / (2 π ω)$ , traces out a stream of A's and B's having a very precise grammar and syntax: ABABABAB…

Many other such statements might be conceivable, e.g.,

AAAAAA \dots, BBBBB \dots, AAABAAAB \dots, ABAABAAAB \dots,

and so on, but, of the infinite number of possibilities, only one is actually observed, is ‘grammatical’.

More complex dynamical reaction models, incorporating diffusional drift around deterministic solutions, or elaborate structures of complicated stochastic differential equations having various domains of attraction – different sets of ‘grammars’ – can be described by analogous means ([20], Ch. 3).

Rather than taking symbolic dynamics as a simplification of more exact analytic or stochastic approaches, it is possible to comprehensively generalize the technique itself. Complicated cellular processes may not have identifiable sets of stochastic differential equations like noisy, nonlinear mechanical clocks, but, under appropriate coarse-graining, they may still have recognizable sets of grammar and syntax over the long-term. Proper coarse-graining may, however, often be the hard scientific kernel of the problem.

The fundamental assumption for complicated biological reactions like the change in function between the upper and lower complexes of Fig. 1 is that reaction trajectories can be classified into two groups, a very large set that has essentially zero probability, and a much smaller ‘grammatical’ set. For the grammatical/syntactical set, the argument is that, given a set of elaborate trajectories of length n, the number of grammatical ones, N(n), follows a limit law of the form

H = \lim_{n \to \infty} \frac{\log [N (n)]}{n}

(1)

such that H both exists and is independent of path. If convergence occurs for some finite n_H, then the process is said to be of order n_H. This is a critical foundation of, and limitation on, the modeling strategy adopted here, and constrains its possible realm of applicability. It is, however, fairly general in that it is independent of the serial correlations along reaction pathways.

The basic argument is shown in Fig. 2, where an initial IDP/partner configuration, S₀, can either converge on an activated IDP complex S_act via the set of high probability reaction paths to the left of the filled triangle, or it can converge to a thermodynamically competitive inhibited state S_inhib to the right.

Fig. 2
An initial IDP/partner configuration S₀ can either converge on an active final configuration S_act via the set of high probability reaction paths to the left of the filled triangle, or it can converge to a thermodynamically competitive inhibited state S_inhib to the right.

The approach, via coarse-graining and symbolic dynamics, assigns classic information sources to the two sets of thermodynamically competitive ‘grammatical’ pathways. The essential question is how a regulatory catalysis can act in such a circumstance to change the probabilities of convergence on S_act or S_inhib.

3 The dual information source of a cognitive regulatory process

The first step in answering that question lies in describing the activity of a large class of regulatory activity in terms of another information source. To reiterate, Atlan and Cohen [8], in the context of a study of the immune system, argue that the essence of cognition is the comparison of a perceived signal with an internal, learned picture of the world, and then choice of a single response from a large repertoire of possible responses. Such choice inherently involves information and information transmission since it always generates a reduction in uncertainty. Structures that process information are constrained by the asymptotic limit theorems of information theory, in the same sense that sums of stochastic variables are constrained by the Central Limit Theorem, allowing the construction of powerful statistical tools useful for data analysis.

More formally, a pattern of incoming input S_i describing the status of the IDP/partner configuration – starting with the initial state S₀ – is mixed in a systematic algorithmic manner with a pattern of otherwise unspecified ‘ongoing activity’, including cellular, epigenetic and environmental signals, W_i, to create a path of combined signals x = (a₀, a₁,..., a_n,...). Each a_k thus represents some functional composition of internal and external factors, and is expressed in terms of the intermediate states as

S_{i + 1} = f ([S_{i}, W_{i}]) = f (a_{i})

(2)

for some unspecified function f. The a_i are seen to be very complicated composite objects, in this treatment, that we may choose to coarse-grain so as to obtain an appropriate ‘alphabet’.

In a simple spinglass-like model, S would be a vector, W a matrix, and f would be a function of their product at ‘time’ i.

The path x is fed into a highly nonlinear decision oscillator, h, a ‘sudden threshold machine’ pattern recognition structure, in a sense, that generates an output h(x) that is an element of one of two disjoint sets B₀ and B₁ of possible system responses. Let us define the sets B_k as

B_{0} = {b_{0}, ..., b_{k}},

B_{1} = {b_{k + 1}, ..., b_{m}} .

It is possible to assume an elaborate graded response, in precisely the sense studied by Pufall et al. [21], supposing that if $h (x) \in B_{0}$ , the pattern is not recognized, and if $h (x) \in B_{1}$ , the pattern has been recognized, and some action $b_{j}, k + 1 \leq j \leq m$ takes place. Typically, for the example of Fig. 2, the set B₁ would represent the final state of the IDP/final partner complex, either activated or inhibited, that is sent on in the sequence of biological processes.

The principal objects of formal interest are paths x triggering pattern recognition and response. That is, given a fixed initial state $a_{0} = [S_{0}, W_{0}]$ , examine all possible subsequent paths x beginning with a₀ and leading to the event $h (x) \in B_{1}$ . Thus $h (a_{0}, ..., a_{j}) \in B_{0}$ for all $0 < j < m$ , but $h (a_{0}, ..., a_{m}) \in B_{1}$ . B₁ is thus the set of final possible states, ${S_{a c t}} \cup {S_{i n h i b}}$ from Fig. 2 that includes both the active and inhibited complexes.

Again, for each positive integer n, let N(n) be the number of high probability grammatical and syntactical paths of length n which begin with some particular a₀ and lead to the condition $h (x) \in B_{1}$ . Call such paths ‘meaningful’, assuming, not unreasonably, that N(n) will be considerably less than the number of all possible paths of length n leading from a₀ to the condition $h (x) \in B_{1}$ .

While the combining algorithm, the form of the nonlinear oscillator, and the details of grammar and syntax, can all be unspecified in this model, the critical assumption that permits inference of the necessary conditions constrained by the asymptotic limit theorems of information theory is that, again, the finite limit

H = \lim_{n \to \infty} \frac{\log [N (n)]}{n}

both exists and is independent of the path x.

Call such a pattern recognition-and-response cognitive process ergodic. Not all cognitive processes are likely to be ergodic in this sense, implying that H, if it indeed exists at all, is path dependent, although extension to nearly ergodic processes seems possible [11].

Invoking the spirit of the Shannon-McMillan Theorem, as choice involves an inherent reduction in uncertainty, it is then possible to define an adiabatically, piecewise stationary, ergodic (APSE) information source X associated with stochastic variates X_j having joint and conditional probabilities $P (a_{0}, ..., a_{n})$ and $P (a_{n} | a_{0}, ..., a_{n - 1})$ such that appropriate conditional and joint Shannon uncertainties satisfy the classic information theory relations [22]

H = \lim_{n \to \infty} \frac{\log [N (n)]}{n} = \lim_{n \to \infty} H (X_{n} | X_{0}, ..., X_{n - 1}) = \lim_{n \to \infty} \frac{H (X_{0}, ..., X_{n})}{n + 1} .

(3)

This information source is defined as dual to the underlying ergodic cognitive process.

Adiabatic means that the information source has been parameterized according to some scheme, and that, over a certain range, along a particular piece of parameter trajectory, the source remains as close to stationary and ergodic as needed for information theory's central theorems to apply. Stationary means that the system's probabilities do not change in time, and ergodic, roughly, that the cross sectional means approximate long-time averages. Between pieces it is necessary to invoke various kinds of phase transition formalisms, as described more fully in [10].

4 Information catalysis

In the limit of large n, $H = \lim_{n \to \infty} \log [N (n)] / n$ becomes homologous to the free energy density of a physical system at the thermodynamic limit of infinite volume. More explicitly, the free energy density of a physical system having volume V and partition function Z (β) derived from the system's Hamiltonian – the energy function – at inverse temperature β is (e.g., [23])

F [K] = \lim_{V \to \infty} - \frac{1}{β} \frac{\log [Z (β, V)]}{V} \equiv \lim_{V \to \infty} \frac{\log [\hat{Z} (β, V)]}{V},

(4)

with

\hat{Z} = Z^{- 1 / β}

. The latter expression is formally similar to the first part of Eq. (3), a circumstance having deep implications: Feynman [24] describes in great detail how information and free energy have an inherent duality. Feynman, in fact, defines information precisely as the free energy needed to erase a message. The argument is surprisingly direct [25], and for very simple systems it is easy to design a small (idealized) machine that turns the information within a message directly into usable work – free energy. Information is a form of free energy and the construction and transmission of information within living things consumes metabolic free energy, with inevitable losses via the second law of thermodynamics.

Information catalysis, in the circumstance of Fig. 2, arises most simply via the ‘information theory chain rule’ (Cover and Thomas, 2006). Given X as the information source representing the reaction paths of Fig. 2, and Y, an information source dual to the sophisticated chemical cognition of the regulating system, one can define jointly typical paths z_i = (x_i,y_i) having the joint information source uncertainty H(X,Y) satisfying

H (X, Y) = H (X) + H (Y | X) \leq H (X) + H (Y) .

(5)

of necessity, then,

H (X, Y) < H (X) + H (Y)

(6)

H (Y | X) < H (Y) .

These relations imply that, by means of the identification of information as a form of free energy, at the expense of adding the considerable energy burden of the regulatory apparatus, represented by its dual information source Y, it becomes possible to canalize the reaction paths of Fig. 2, so as to make one set of pathways beginning with S₀ far more probable than another.

That is, by raising the entire reaction free energy landscape corresponding to H(X) by the amount H(Y) it becomes possible to deepen the energy channel leading from S₀ to the desired outcome, either S_act or S_inhib. Complicated internal reaction mechanisms have been subsumed by the Shannon-McMillan Theorem, in the same sense that the Central Limit Theorem subsumes the behavior of long sums of stochastic variates into the Normal distribution.

Within a cell, however, there will be an ensemble of possible reactions, driven by available metabolic free energy, so that, taking <..> as representing an average,

[< H (X, Y) >] < [< H (X) > + < H (Y) >] .

(7)

Typically, letting M represent the intensity of available metabolic free energy, one would expect

< H > = \frac{\int H \exp [- H / κ M] d H}{\int \exp [- H / κ M] d H} = κ M,

(8)

where κ, an inverse energy intensity scaling constant, may be quite small indeed, a consequence of entropic translation losses between metabolic free energy and the expression of information.

The resulting relation,

M_{X, Y} < M_{X} + M_{Y},

(9)

suggests an explicit free energy mechanism for reaction canalization.

If entropic translation losses are not linear with increase in information transmission rate H, one might replace $κ M$ in Eq. (8) with some function $Q (κ M)$ that ‘tops out’ with increasing M, for example $Q \propto \log [κ M]$ . This means that there are increasingly higher second law energy losses in the production of biological information from metabolic free energy.

The energy relation then becomes, after a little algebra,

M_{X, Y} < κ \times M_{X} \times M_{Y} ≪ M_{X} + M_{Y},

(10)

if either κ or one of the other M-terms is small, and a low energy information source regulator could thus be used to ‘leverage’ reaction canalization very efficiently.

Quite counterintuitively, then, entropic loss can be a powerful tool for triggering complex biological logic gates, in much the same sense that Tompa and Csermely [26] propose that entropy transfer can be used by generalized chaperones to trigger proper conformation in pathologically folded protein complexes.

It now seems possible to construct empirical statistical models of complex regulatory processes – via their observed grammar and syntax – that are much in the spirit of the regression models used to characterize other complicated phenomena.

5 Discussion and conclusions

Wallace [2], using a groupoid extension of conventional nonrigid molecule theory, introduced a literally astronomically large spectrum of possible symmetry classifications for IDP/partner complexes. The size of the appropriate symmetry group (or groupoid) must grow exponentially in the number of amino acid bases within the flexible IDP frond. For 30 to 100 amino acids, the nonrigid symmetry set is indeed astronomical, and can only be addressed by a statistical mechanics argument. The particular utility of IDP's for moonlighting, as inferred from [1], appears possible through the massive number of possible subgroup/tiling mirror image matchings that are available to the molecular fuzzy lock-and-key, as governed by a regulatory structure that is likely to be another example of sophisticated chemical cognition, akin to the immune system. Given these results, cognitive biochemical processes regulating IDP moonlighting are not likely to yield to exact ‘chemical’ description, not only from considerations of IDP symmetry group magnitude, but because their dynamics are particularly contingent on other signals that may arise from higher level, embedding, cognitive regulatory processes.

However, such behaviors, in terms of the dual information source, are nonetheless constrained by the asymptotic limit theorems of information theory, and this may allow construction of regression model-like statistical tools useful for scientific inference, focusing on the behaviors of the system rather than on a detailed description of its mechanical state under all circumstances and at all times. Again, the analogy is to describe the behavior of a computer in terms of its program, rather than attempting provide a full cross-sectional description of the state of each logic gate at each clock cycle.

It should be particularly emphasized that many of the composite IDP/partner/regulator ‘logic gates’ in Fig. 1 of [1] are likely to be quite different from ‘simple’ computer models, having extraordinarily subtle properties. There is no reason to believe evolution is restricted to binary mathematics (AND, OR, XOR, etc.).

Much of this is already common currency within protein science, although not, perhaps, systematized into a consistent mathematical formalism. Almost all the proposed mechanisms have been described using a different vocabulary, and, taking the suggestion of a reviewer, the text Table 1 attempts a translation of the model.

Model term	Protein science term
Subgroup/subgroupoid	Protein conformation
Cognition	Molecular recognition
Subgroup tiling	Conformation selection
Internal picture of the world	Preformed structural elements
Information catalysis	Cooperative structure transition

Finally, these considerations add considerable weight to an emerging perspective that sees a fundamental defining characteristic of the living state as the operation of chemical or other cognitive processes at virtually all scales and levels of organization [8–11,27].

Acknowledgments

The author thanks P. Tompa for useful discussions, and several reviewers for remarks and references useful in revision. A reviewer suggested the ‘Rosetta Stone’ translation table between the mathematical model and protein science terminology.