Plan
Comptes Rendus
no. 2-3

Electron transport through molecular wires based on a face-shared bioctahedral motif
Vitesh Mistry1  ; Vihar P. Georgiev1  ; John E. McGrady1
1 Inorganic Chemistry Laboratory, Department of Chemistry, University of Oxford, South Parks Road, Oxford OX1 3QR, United Kingdom
Comptes Rendus. Chimie, Volume 15 (2012) no. 2-3, pp. 176-183.

Résumé

Density functional theory in conjunction with non-equilibrium Green's functions is used to explore the electron transport properties of a series of molecules based on the face-shared bioctahedral (M2Cl9) motif. The metal-metal bond orders in the chosen molecules, [Rh2Cl9]3–, [Ru2Cl9]3– and [Mo2Cl9]3– vary from 0 (Rh) to 1 (Ru) and 3 (Mo), and the calculations indicate that there is a direct correlation between conductance and bond order. The [Mo2Cl9]3– case is particularly interesting as it is well known from crystallographic studies to be very flexible, the Mo–Mo bond length varying over a range of ∼0.35 Å depending on cation. The upper limit of this range marks the point where homolytic cleavage of the δπ components of the triple bond is complete, and this has a marked impact on electron transport. The localization of the metal-based orbitals means that those on the left (source) and right (drain) sides respond very differently to applied bias, giving rise to resonance effects at particular bias voltages, and hence to negative differential resistance effects.

Supplementary Materials:
Supplementary material for this article is supplied as a separate file:

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crci.2011.11.001
Mots clés : Density functional theory, Electron transport, Metal-metal bonds
Vitesh Mistry 1 ; Vihar P. Georgiev 1 ; John E. McGrady 1

1 Inorganic Chemistry Laboratory, Department of Chemistry, University of Oxford, South Parks Road, Oxford OX1 3QR, United Kingdom 
@article{CRCHIM_2012__15_2-3_176_0,
     author = {Vitesh Mistry and Vihar P. Georgiev and John E. McGrady},
     title = {Electron transport through molecular wires based on a face-shared bioctahedral motif},
     journal = {Comptes Rendus. Chimie},
     pages = {176--183},
     publisher = {Elsevier},
     volume = {15},
     number = {2-3},
     year = {2012},
     doi = {10.1016/j.crci.2011.11.001},
     language = {en},
}
TY  - JOUR
AU  - Vitesh Mistry
AU  - Vihar P. Georgiev
AU  - John E. McGrady
TI  - Electron transport through molecular wires based on a face-shared bioctahedral motif
JO  - Comptes Rendus. Chimie
PY  - 2012
SP  - 176
EP  - 183
VL  - 15
IS  - 2-3
PB  - Elsevier
DO  - 10.1016/j.crci.2011.11.001
LA  - en
ID  - CRCHIM_2012__15_2-3_176_0
ER  - 
%0 Journal Article
%A Vitesh Mistry
%A Vihar P. Georgiev
%A John E. McGrady
%T Electron transport through molecular wires based on a face-shared bioctahedral motif
%J Comptes Rendus. Chimie
%D 2012
%P 176-183
%V 15
%N 2-3
%I Elsevier
%R 10.1016/j.crci.2011.11.001
%G en
%F CRCHIM_2012__15_2-3_176_0
Vitesh Mistry; Vihar P. Georgiev; John E. McGrady. Electron transport through molecular wires based on a face-shared bioctahedral motif. Comptes Rendus. Chimie, Volume 15 (2012) no. 2-3, pp. 176-183. doi : 10.1016/j.crci.2011.11.001. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2011.11.001/

Version originale du texte intégral

1 Introduction

In the field of molecular electronics [1,2], nanoscale analogues of macroscopic wires, diodes and transistors are a central target. Conjugated organic systems [3], where the π framework provides a natural pathway for transfer of electrons, have been studied extensively but molecules featuring chains of transition metal atoms have received rather less attention. Nevertheless, their physical resemblance to macroscopic wires has encouraged a number of workers to explore their potential in electronics applications. For example, both da Silva [4] and Sanvito [5] have highlighted effective spin filtration by isolated cobalt centers and Baranger and Yang [6] have extended these ideas to show that a truly molecular cobaltocene unit can act similarly as an efficient spin filter. Genuine molecular ‘wires’ require rather more extended arrays [7], and in this context the sandwich complexes [ML]n, with L = cyclopentadienyl [8,9,10], benzene [11], borazine [12], borolyl [13] or cyclooctatetraenyl [14] have been extensively studied. The interactions between metal ions in such arrays offer a mechanism for controlling electron transport through switching between ferro- and antiferromagnetic states, and in dicobaltocene the former has been shown to be substantially more transparent than the latter [15]. ‘Magnetic superatoms’ such as VCs8 [16] also provide a basis for significant spin filtering [17], as do Single Molecule Magnets (SMMs). [18–23].

Molecules with direct covalent bonds between the metals represent a fundamentally different class of cluster, with more extensively delocalized molecular orbitals. Electron transport through ‘bare’ atomic wires has been discussed at length [24,25] but these offer limited potential for control at the synthetic level. Amongst the few truly molecular examples, Berber et al. have explored transport through octahedral Mo6 clusters [26], while Huang et al. have shown that isomeric forms of a quintuple Cr–Cr bond [27] can support large on/off current ratios [28]. The family of Extended Metal Atom Chains (EMACs), based on helical arrays of polypyridylamido ligands, provides a particularly striking resemblance to a macroscopic wire, and their electron transport properties prove to be highly dependent on the identity of the metal ion. Thus, the measured conductance G increases in the order Ni (0.006 μS) < Co (0.021 μS) < Cr (0.37 μS), the variation over two orders of magnitude suggesting that electronic configuration plays a critical role in controlling the flow of electrons. In recent papers [29], we have used density functional theory in conjunction with non-equilibrium Green's functions to establish a direct link between the electron transport properties and underlying electronic structure in both Co3(dpa)4(NCS)2 and Cr3(dpa)4(NCS)2.

There are only a very few complexes which bridge the divide between magnetically coupled and covalently-bonded regimes. One classic example is the chloride-bridged dimer, (Cp*RuCl)2(μ-Cl)2 which exhibits bond-stretch isomerism, crystallizing in two distinct forms, one with a direct Ru–Ru bond (Ru–Ru = 2.93 Å) the other where the metal centres are antiferromagnetically coupled (Ru–Ru = 3.75 Å) [30,31]. The metal-metal bonding in face-shared bioctahedral [Mo2Cl9]3–, where the Mo–Mo separations range from 2.53 Å to 2.78 Å depending on cation [32], is similarly versatile. The orbitals derived from the t2g sets of the individual octahedra split into a1′ and a2′′ (σ and σ*) and e′ and e′′ (δπ and δπ*) sets under the prevailing D3h symmetry, the latter having 2/3 δ and 1/3 π character in a perfect bioctahedron. A detailed analysis of the potential energy surface for the stretch along the trigonal axis suggested that the range of accessible distances corresponds to a transition from a triple covalent bond (∼2.4 Å) to a single σ bond (∼2.8 Å) where the remaining two electrons on each centre are only weakly coupled [33]. Given the obviously delicate balance between localization and delocalization of the electrons in these systems in the solid state, a natural question is whether a transition between the two could be induced by an electric field in a putative electronic device, and if so, what the consequences would be for electron transport. We address this question in this paper using a family of three compounds sharing the [M2Cl9]3– structural motif: [Rh2Cl9]3–, [Ru2Cl9]3–, [Mo2Cl9]3–. The first two (d6d6 and d5d5, respectively) are structurally and magnetically robust, and serve to establish the underlying transmission properties of the M2Cl9 unit and to provide a framework for understanding the more complex molybdenum analogue (Fig. 1).

Fig. 1

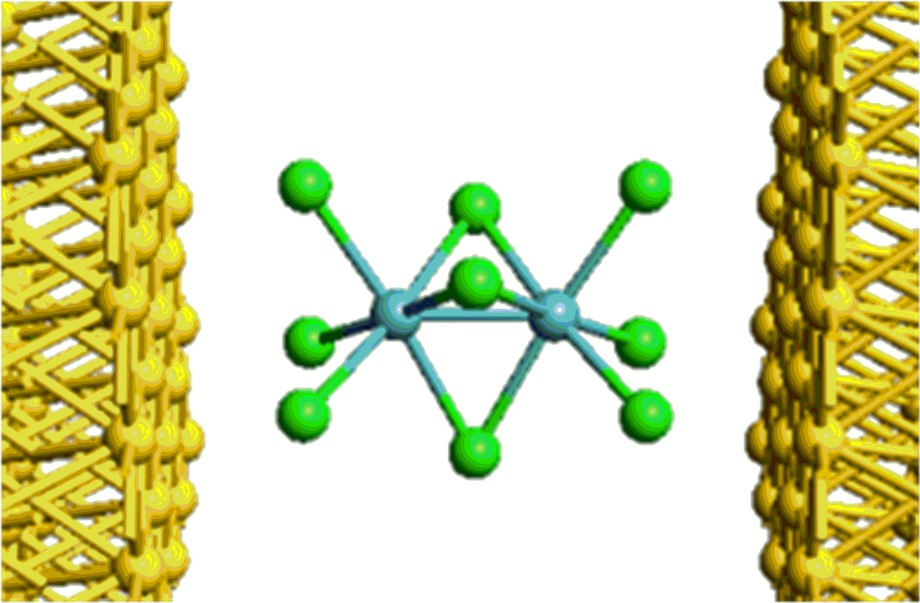
Face-shared bioctahedral structure of M2X9.

2 Computational methods

The spin-dependent electron transport properties of the [M2Cl9]3– species were computed using the AtomisticToolkit software package, ATK2010 [34,35]. The methodology combines a density functional theory treatment of the electronic structure with the Keldysh non-equilibrium Green's function approach to simulating coherent transport [36–38]. The scattering region, [Au125]-M2Cl9-[Au125], contains the bimetallic unit sandwiched between two blocks of five layers of 5 × 5 Au (111) (the buffering region). The electrodes are described by repeating units of three 5 × 5 Au (111) layers. The metal-metal axis was aligned such that it also passes through a gold atom on the surface layer of each electrode. The chlorine atoms were located in hollow sites with a distance of 2.39 Å between the atoms and the Au surface. The geometry of the [M2Cl9]3– unit in the scattering region was generated by optimizing the structure using ADF2009 [39] with the LDA VWN functional and a triple-zeta + polarisation quality basis of Slater-type functions (a full set of cartesian coordinates for the two-probe system is provided in the supporting information). In all cases the initial spin density was polarized in such a way that equal and opposite spins are placed on the two metal centres. Thus, a closed-shell singlet (i.e. zero spin density everywhere) is not imposed by the methodology, although such a situation can emerge as the result of the self-consistent procedure if it is more energetically favourable than the broken-symmetry alternative. In fact, a broken-symmetry solution emerges only for [Mo2Cl9]3– at long separations. In the transport calculations, the LDA functional with the self-interaction correction of Perdew and Zunger [40] was used throughout in conjunction with numerical basis sets of single-zeta (SZ) quality on Au and double-zeta + polarization (DZP) on Mo, Ru and Rh and Cl. Core electrons were described by norm-conserving pseudopotentials [41]. The initial spin density for the two-probe calculations was polarized to be consistent with the net spin densities arising from the electronic structure of the isolated molecules in the gas phase. A 1 × 1 × 91 Monkhorst-Pack grid was used for Brillouin zone sampling, and a 125 Rydberg mesh cut off, a finite temperature of 300 K at the electrodes and the real-space density constraint at the electrodes. At zero bias, the conduction, Gσ0, is given by the expression:

Gσ0=dldVv=0=e2hTσEf,0

3 Results and discussion

3.1 Optimised structures and gas-phase electronic structure

Optimised structures for the three complexes in their S = 0 ground states, along with Mulliken spin densities (ρα/β) are summarised in Table 1. There is a progressive decrease in metal-metal separation from Rh–Rh (3.17 Å) to Ru–Ru (2.73 Å) to Mo–Mo (2.38 Å), consistent with an increase in metal-metal bond order from 0 to 1 and then 3. The molecular orbital diagram in Fig. 2 for [Mo2Cl9]3– confirms the depopulation of both the Mo–Mo σ* and δπ* orbitals. We note that in all three cases the closed-shell singlet structure is not imposed by the computational methodology–the initial densities were spin polarised in all cases and the closed-shell solution emerges as the lowest energy alternative in the SCF procedure. The relationship between the electronic structure of [Mo2Cl9]3– and its structural and magnetic properties has been discussed at length in reference [33], specifically in the context of the comparison with its [Cr2Cl9]3– and [W2Cl9]3– congeners. As noted in the introduction, this triad forms a textbook comparison of the influence of position in the periodic table on metal–metal bond formation: in the W species direct covalent bonding gives a very short W–W bond while on-site exchange dominates in the Cr analogue, giving a very long Cr–Cr separation. The Mo species is midway between these extremes, with strong coupling in the σ orbital but only weak coupling in the δπ set. The result is a very flat potential energy surface that renders the structure very sensitive to the identity of the counteraction. The precise shape of the computed potential energy surface is very sensitive to computational methodology, and the inclusion of gradient corrections in the functional can lead to dramatic changes in equilibrium structure. To highlight the relative flatness of the surface, we have optimised the structure of the associated state with S = 2, where the δπ electrons are aligned ferromagnetically but the σ electrons remain spin paired. At the LDA level, this state lies only 0.24 eV above the closed-shell S = 0 equilibrium structure (2.38 Å), compared to a difference of 0.5 eV for the corresponding states of the tungsten analogue. The optimised Mo–Mo separation of 2.83 Å for this S = 2 state is consistent with a single bond. A single point broken-symmetry (MS = 0) calculation performed at this geometry gives an energy of +0.11 eV relative to the closed-shell singlet ground state. The net spin densities of ± 2.06 at the metal centres and the Kohn-Sham orbitals shown in Fig. 3 confirm complete cleavage of the δπ components but not the σ orbital. The significance of the spin density in broken-symmetry calculations has been extensively debated [42]: in a singlet state spin density is zero at all points in space, but the broken-symmetry ansatz allows for a non-physical separation of spin-α and spin-β density into separate regions of space. The electron density distribution in such a broken-symmetry does, however, reflect accurately the localisation of electron density on individual metal centres in an exchange coupled system. In summary, the elongation of the Mo–Mo separation by up to 0.45 Å from its equilibrium value of 2.38 Å incurs only a marginal energetic penalty, a fact that is clearly reflected in the Mo–Mo separations in the known crystal structures of [Mo2Cl9]3–, which span 2.53 Å–2.78 Å. In the subsequent sections we explore the potential impact of such a structural change on the ability of the system to support current flow (Table 1) (Fig. 2).

Table 1

Metal–metal separations, total energies and Mulliken spin densities, ρα/β, for [M2Cl9]3–.

r(M–M)/ÅEnergy/eVρα/βa
[Rh2Cl9]3–3.17–42.300.0
[Ru2Cl9]3–2.73–45.400.0
[Mo2Cl9]3–2.38–51.520.0
2.83–51.28± 2.06

a Note in cases where the spin densities are zero this is a result of the SCF procedure, and is not imposed by a spin-restricted protocol.

Fig. 2

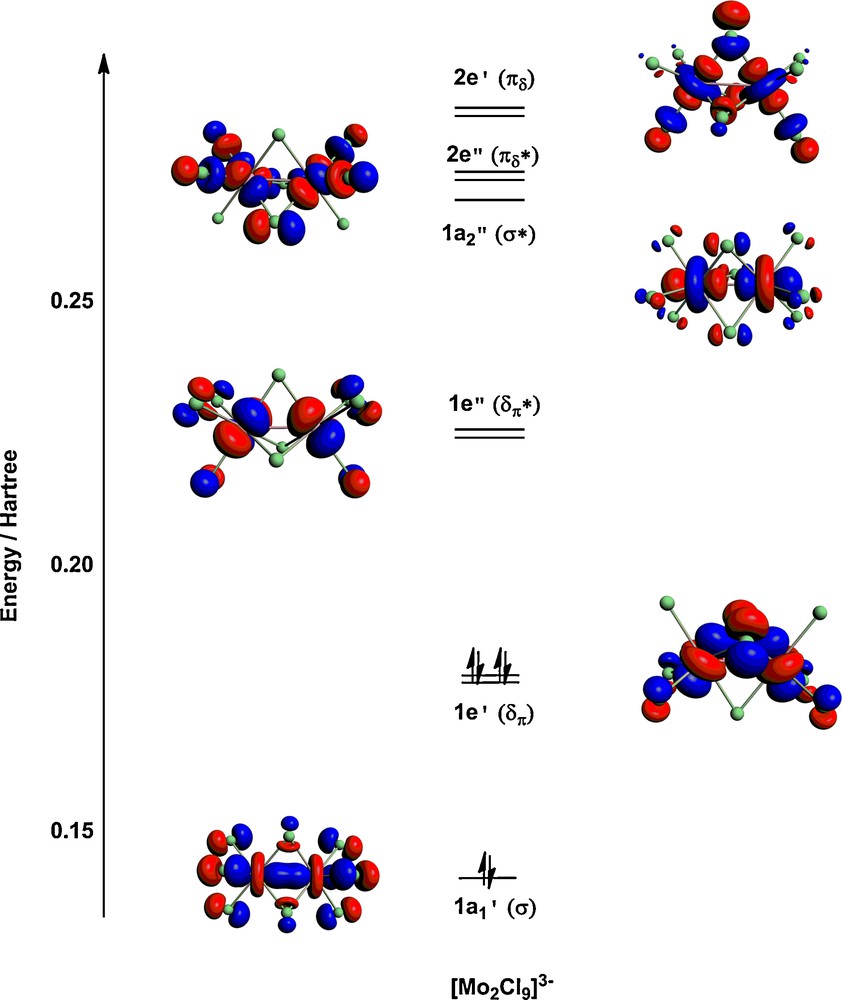
Frontier Kohn-Sham orbitals for [Mo2Cl9]3– at the equilibrium geometry. (Mo–Mo = 2.38 Å).

Fig. 3

Spin-α Kohn-Sham orbitals for [Mo2Cl9]3– at (a) Mo–Mo = 2.38 Å and (b) Mo-Mo = 2.83 Å. The spin-β counterparts are the mirror images.

3.2 Electron transport properties

The link between the equilibrium electronic structure of the isolated molecule and its zero-bias conductance, G, is established through the transmission function, T(E). The computed transmission spectra for each of [Rh2Cl9]3–, [Ru2Cl9]3– and [Mo2Cl9]3– (each at its equilibrium geometry shown in Table 1) are collected in Fig. 4, where the corresponding conduction channels (the eigenfunctions of the Molecular Projected Self-Consistent Hamiltonian) are also shown. In the case of [Mo2Cl9]3–, a comparison with the Kohn-Sham orbitals of the gas-phase species (Fig. 2) confirms a 1:1 correspondence between the peaks in the transmission spectrum and the electronic structure of the isolated molecule.

Fig. 4

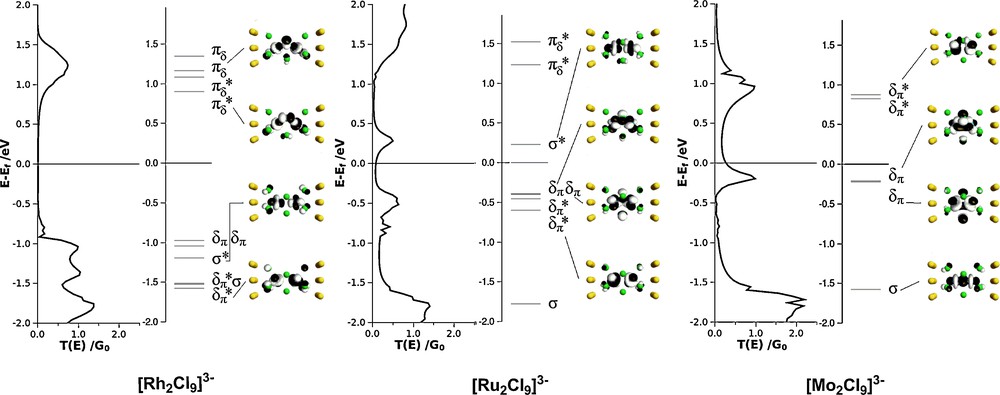
Transmission spectra, molecular energy spectra and eigenfunctions of the Molecular Projected Self Consistent Hamiltonian (MPSH) for [Rh2Cl9]3–, [Ru2Cl9]3– and [Mo2Cl9]3– (Mo-Mo = 2.38 Å). Only plots for the spin-α manifold are shown: those for the spin-β channels are identical.

In [Rh2Cl9]3– (Rh–Rh = 3.2 Å) the absence of any significant direct interaction between the metal-based orbitals leads to a narrow band of occupied σ, σ*, δπ and δπ* levels in a window between 1.0 and 1.5 eV below Ef. Similarly a band ∼1.2 eV above the Fermi level corresponds to the πδ and πδ* levels derived from the octahedral eg set. The complete absence of peaks in the region of the Fermi level leads to a rather small zero-bias conductance of 2.3 μS. For the ruthenium analogue [Ru2Cl9]3– (Ru–Ru = 2.75 Å) the increased interaction between the metals displaces the σ* level ∼0.3 eV above the Fermi level of the gold electrodes while its bonding counterpart is found at E–Ef ∼ 2.0 eV. Similar basic features in the gas-phase electronic structure have been noted previously [43]. The intermediate bond length is not, however, sufficiently small to allow significant overlap between the δπ and δπ* levels, which remain largely non-interacting and form a narrow band at E–Ef ∼ −0.5 eV. Note that the upward shift in these levels relative to [Rh2Cl9]3– is a direct result of the reduction in effective nuclear charge on moving to the left in the periodic table. The relatively close proximity of the σ* peak, which constitutes the dominant conduction pathway, to Ef leads to substantially increased zero-bias conductance (14.7 μS). Turning to the [Mo2Cl9]3– case (in its equilibrium geometry, Mo–Mo = 2.38 Å), the further decrease in metal–metal separation induces a substantial splitting of the σ/σ* levels and also now separates the δπ/δπ* manifold, such that the bonding and antibonding combinations straddle Ef, lying 0.2 eV and 0.8 eV below and above it, respectively. The relatively large amplitude at Ef caused by the tail of the δπ channel leads to a further substantial increase in zero-bias conductance (44.9 μS) relative to [Rh2Cl9]3– and [Ru2Cl9]3–. The computed current-voltage curves for these three systems shown in Fig. 5 confirm approximately ohmic behaviour, at least up to biases of ∼ ± 0.7 V and moreover that I(Mo) > I(Ru) > I(Rh). In their work on the Extended Metal Atom Chain molecules Peng, Jin et al. have proposed a direct correlation between metal–metal bond order and conductance [44], and such a correlation appears to be present in this face-shared motif.

Fig. 5

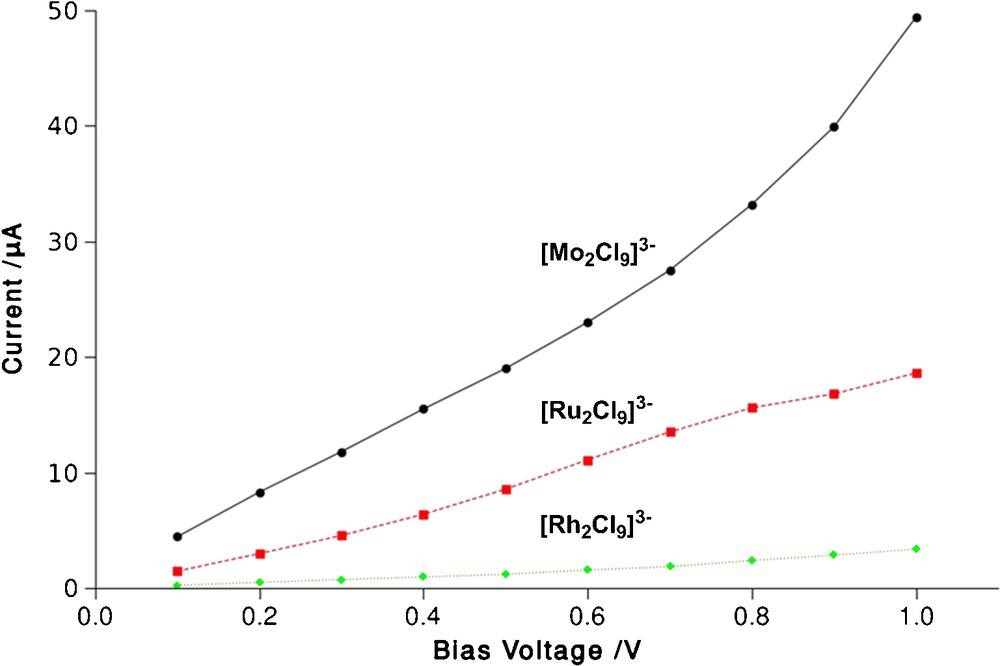
Computed current-voltage curves for [Rh2Cl9]3–, [Ru2Cl9]3– and [Mo2Cl9]3– (Mo–Mo = 2.38 Å).

3.3 Effect of structural distortions on the electron transport properties of [Mo2Cl9]3–

We showed earlier that stretching the Mo–Mo distance from its equilibrium value of 2.38 Å to 2.83 Å carries only a small energetic penalty, and moreover results in the collapse of the δπ/δπ* manifold such that these electrons are only weakly coupled. To explore the potential impact of such a transition on the behaviour under bias, we have repeated the two-probe calculation with the elongated [Mo2Cl9]3– unit (Mo–Mo = 2.83 Å) placed between the two gold electrodes with the same contact geometry. The calculation was initiated with a spin density polarisation consistent with antiferromagnetic coupling between the two metal centres, and the converged zero-bias spin densities on Mo of ± 1.600 are again indicative of homolytic cleavage of the δπ component of the Mo–Mo bond. For comparison, the self-consistent two-probe density for Mo–Mo = 2.38 Å showed no sign of spin polarisation, even when the initial guess was similarly polarised (Fig. 6).

Fig. 6

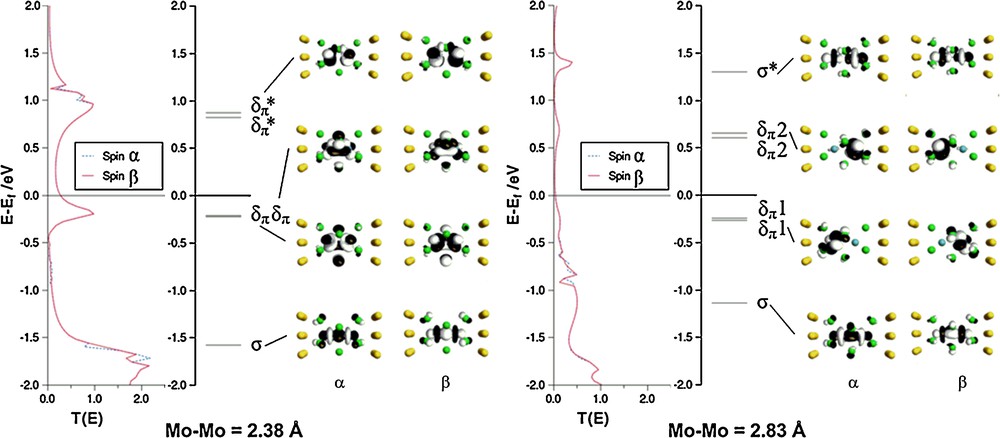
Transmission spectra, molecular energy spectra and eigenfunctions of the Molecular Projected Self Consistent Hamiltonian (MPSH) (spin-α and spin-β) for [Mo2Cl9]3– at equilibrium Mo-Mo separation (2.38 Å) and at Mo–Mo = 2.83 Å.

The orbitals also confirm that the distinct symmetry breaking in the δπ channels that was apparent in the gas-phase persists in the two-probe architecture: although the σ and σ* channels remain essentially delocalised, their δπ counterparts become almost completely localised on the source (spin-α) or drain (spin-β) side of the device. In the absence of significant overlap within the δπ set, we have adopted the δπ1/δπ2 nomenclature rather than δπ/δπ *. The elongation of the Mo–Mo separations compresses the σ/σ* gap somewhat (the orbitals lie at –1.1 and +1.4 eV, respectively) but these channels in the transmission spectrum remain otherwise unperturbed by the structural changes. In contrast, the localisation of the δπ levels results in a complete collapse of the corresponding peaks in the transmission spectrum because the channels no longer span both sides of the molecule. The zero-bias conductance is accordingly reduced to only 7.0 μS, a value even lower than that for [Ru2Cl9]3–. The reduced conductance relative to the structurally similar [Ru2Cl9]3–, where a metal–metal σ bond is also present, arises simply because the dominant σ* channel (along with all other metal-based orbitals) is relatively destabilised in the early transition metal element, and so displaced further above Ef.

At low biases, the current/voltage characteristics of [Mo2Cl9]3– in its short (Mo–Mo = 2.38 Å) and long (2.83 Å) geometries (Fig. 7(a)) can be readily extrapolated from the zero-bias transmission spectra: both show approximately ohmic behaviour with I(2.38 Å) > I(2.83 Å). However, whilst the current flow at Mo–Mo = 2.38 Å continues to increase approximately ohmically beyond 0.7 V, a distinct peak in the current at ∼0.9 V occurs for the elongated structure. Negative differential resistance (NDR, a decrease in current as bias is increased) effects such as this have been noted in a range of materials, and have been variously ascribed to strain effects [45], resonant tunnelling [46], charge redistribution [47], charging effects [48] and conformational changes [49]. We can understand the connection between the NDR and the spin polarisation in this case by considering the bias dependence of the transmission spectra and the corresponding eigenfunctions, also shown in Fig. 7 (note only the spin-α spectrum and eigenfunctions are shown). Each trace in Fig. 7(b) corresponds to a 0.3 V step in voltage, the weak 0 V peaks at E–Ef = –0.3 eV and +0.6 eV corresponding to the strongly localised δπ1 and δπ2 channels discussed in Fig. 6. As the bias is increased the lower (occupied) δπ1 channel enters the bias window and the electron density is therefore depleted to some extent. The loss of electron density from the molecular region is most pronounced in the spin-β manifold, simply because it is the spin-β component of δπ1 that is localised on the right-hand (drain) side of the device. The net result is that all orbitals on MoR, including the vacant δπ2, are stabilised relative to those on MoL. At 0.9 V the occupied δπ1 channel on MoL comes into resonance with the vacant δπ2 channel localised on MoR, giving a completely delocalised pathway very close to the Fermi level, and hence a spike in both T(E) (Fig. 7(b)) and I. The strong delocalisation of the δπ channel at 0.9 V is apparent in the orbital plots in Fig. 7(c).

Fig. 7

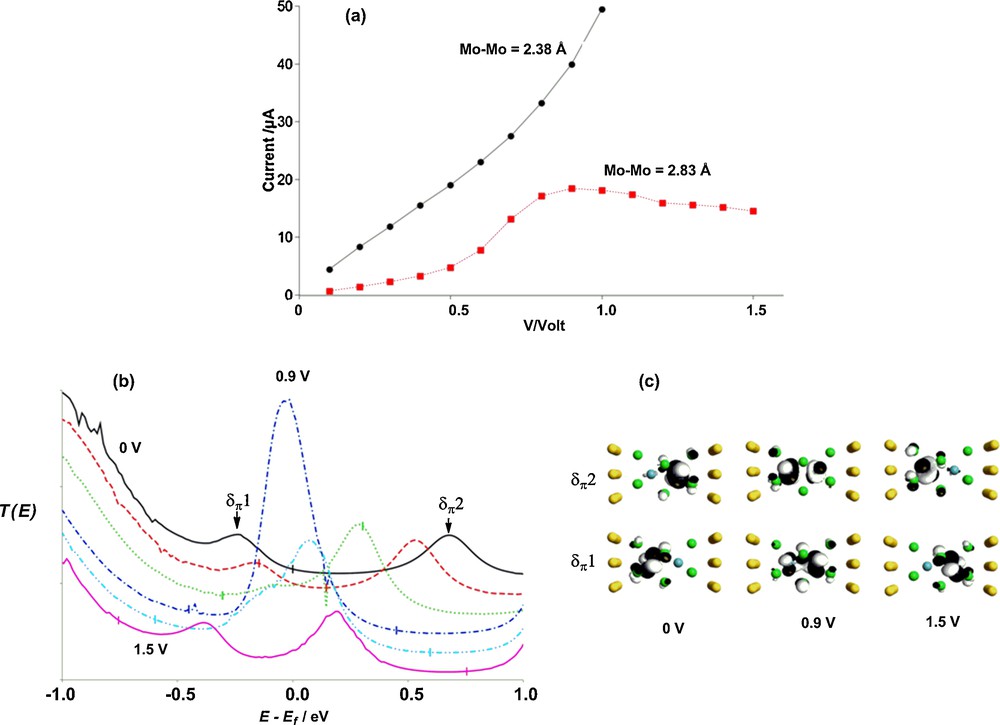
a: computed current-voltage curves for [Mo2Cl9]3− (Mo-Mo = 2.38 and 2.83 Å); b:voltage dependent transmission spectra (spin-α); c: spin-α eigenfunctions of the Molecular Projected Self Consistent Hamiltonian (MPSH). In Figure 7(b) successive transmission spectra (at 0.3 V intervals) are offset by 0.1 unit for clarity.

4 Conclusions

In this paper we have shown that the behaviour of well-defined bimetallic complexes in a putative molecular device can be related directly to their gas-phase electronic properties. The chosen complexes span a range of metal–metal bond types from no net bond ([Rh2Cl9]3–) through single ([Ru2Cl9]3–) and triple ([Mo2Cl9]3–) bonds. The increase in bond order leads to a higher density of states in the region around the Fermi level of the electrodes, and so there is a direct causal link between bond order and conductance. The [Mo2Cl9]3– case is unique in so much as the Mo–Mo bond is known to be very flexible: variations of ∼0.35 Å in the Mo–Mo bond length can occur depending on the identity of the cation. This variance maps out a flat region of the potential energy surface where the weaker δπ components of the bond are homolytically cleaved to generate diradical configurations at the two metal centres. In the context of electron transport, this localisation of the metal-based electrons has important implications. First, the loss of delocalisation reduces the conductance at zero bias. More interestingly, the spatial localisation of the orbitals means that the two metal centers respond differently to applied bias: those on the Mo centre close to the drain are stabilised relative to those attached to the source. The relative shifting of levels as a function of bias can lead to spikes in the transmission spectrum when orbitals on the left and right-hand side come into resonance, giving rise to negative differential resistance in the current/voltage plots. The applications of transition metal clusters in molecular electronics are only beginning to be explored, but this work suggests that the innate flexibility of metal–metal bonds may lead to unusual and potentially useful features.

Acknowledgements

We acknowledge the EPSRC (EP/F019327/1) for financial support and the Oxford Supercomputer Center (OSC) for computational resources.

Bibliographie

[1] A. Aviram; M.A. Ratner Chem. Phys. Lett., 29 (1974), p. 277

[2] G.E. Moore; M.A. Reed; J. Tour; A. Nitzan; M.A. Ratner Science, 38 (1965), p. 114

[3] W.Y. Kim; K.S. Kim; Y. Xue; M.A. Ratner; Y. Xue; M.A. Ratner; C. Gonzalez; Y. Simón-Manso; J. Batteas; M. Marquez; M.A. Ratner; V. Mujica; V. Mujica; A.E. Roitberg; M.A. Ratner; G.C. Liang; A.W. Ghosh; M. Paulsson; S. Datta Phys. Rev. B., 43 (2010), p. 111

[4] R.B. Pontes; E.Z. da Silva; A. Fazzio; A.J.R. da Silva J. Am. Chem. Soc., 130 (2008), p. 9897

[5] K. Tao; I. Rungger; S. Sanvito; V.S. Stepanyuk Phys. Rev. B., 82 (2010), p. 085412

[6] R. Liu; S.H. Ke; W. Yang; H.U. Baranger J. Chem. Phys., 127 (2007), p. 141104

[7] S. Sen; S. Chakrabarti J. Am. Chem. Soc., 132 (2010), p. 15334

[8] L. Wang; Z. Cai; J. Wang; J. Lu; G. Luo; L. Lai; J. Zhou; R. Qin; Z. Gao; D. Yu; G. Li; W.N. Mei; S. Sanvito; V. Garcia-Suarez; J. Ferrer; C.J. Lambert; Z. Yi; X. Shen; L. Sun; Z. Shen; S. Hou; S. Sanvito ACS Nano, 8 (2008), p. 3640

[9] J.C. Wu; X.F. Wang; L. Zhou; H.X. Da; K.H. Lim; S.W. Yang; Z.Y. Li; L. Zhou; S.Y. Yang; M.F. Ng; M.B. Sullivan; V.B.C. Tan; L. Shen J. Am. Chem. Soc., 113 (2009), p. 7913

[10] G. Zhang; Y. Qin; H. Zhang; Y. Shang; M. Sun; B. Liu; Z. Li J. Phys. Chem. C., 114 (2010), p. 9469

[11] V.V. Maslyuk; A. Bagrets; V. Meded; A. Arnold; F. Evers; M. Brandbyge; T. Bredow; I. Mertig; M. Koleini; M. Paulsson; M. Brandbyge; H. Xiang; J. Yang; J.G. Hou; Q. Zhu; S. Hou; Y. Chen; X. Shen; R. Li; J. Ning; Z. Qian; S. Sanvito Chem. Phys., 97 (2006), p. 097201

[12] S.S. Mallajosyula; P. Parida; S.K. Pati; L. Zhu; J. Wang J. Phys. Chem. C., 19 (2009), p. 1761

[13] H.S. Kang J. Phys. Chem., 114 (2010), p. 11266

[14] K. Xu; J. Huang; S. Lei; H. Su; F.Y.C. Boey; Q. Li; J. Yang; J. Huang; Q. Li; K. Xu; H. Su; J. Yang J. Phys. Chem. C., 131 (2009), p. 104704

[15] R. Liu; S.H. Ke; H.U. Baranger; W. Yang; N. Baadji; M. Piacenze; T. Tugsuz; F.D. Sala; G. Maruccio; S. Sanvito Nat. Mater., 5 (2005), p. 1959

[16] J. Ulises Reveles; P.A. Clayborne; A.C. Reber; S.N. Khanna; K. Pradhan; P. Sen; M.R. Pederson Nat. Chem., 1 (2009), p. 310

[17] H. He; R. Pandey; J. Ulises Reveles; S.N. Khanna; S.P. Karna Appl. Phys. Lett., 95 (2009), p. 192104

[18] H. Hao; X.H. Xheng; Z.X. Dai; Z. Zeng Appl. Phys. Lett., 96 (2010), p. 192112

[19] L. Zhu; K.L. Yao; Z.L. Liu Appl. Phys. Lett., 96 (2010), p. 082115

[20] H.B. Heersche; Z. de Groot; J.A. Folk; H.S. van der Zant; C. Romeike; M.R. Wegewijs; L. Zobbi; D. Barreca; E. Tondello; A. Cornia; M.H. Jo; J.E. Grose; K. Baheti; M.M. Deshmukh; J.J. Sokol; E.M. Rumberger; D.N. Hendrickson; J.R. Long; H. Park; D.C. Ralph Nano Lett., 96 (2006), p. 206801

[21] S. Barraza-Lopez; K. Park; V. Garcia-Suarez; J. Ferrer J. Appl. Phys., 105 (2009), p. E7E309

[22] D.D. Pemmeraju; I. Rungger; S. Sanvito Phys. Rev. B., 80 (2009), p. 104422

[23] L. Boani; W. Wernsdorfer Nat. Mater., 7 (2008), p. 179

[24] R.T. Senger; S. Tongay; E. Durgun; S. Ciraci; V.M. Garcia-Suarez; Z.D. Manrique; C.J. Lambert; J. Ferrer; V. Garcia-Suarez; A. Reily Rocha; S.W. Bailey; C.J. Lambert; S. Sanvito; J. Ferrer; A. Garcia-Fuente; A. Vega; V.M. Garcia-Suarez; Ferrer; Y. Xu; X. Shi; Z. Zeng; Z.Y. Zenf; B. Li J. Phys.; Cond. Matt., 72 (2005), p. 075419

[25] Y. Min; K.L. Yao; Z.L. Liu; G.Y. Gao; H.G. Cheng; S.C. Zhu; C.K. Yang; J. Zhao; J.P. Lu; C.L. Jo; C.L. Jo; J. Lee; Y.R. Jang; J. Lee; V.V. Ivanovskaya; C. Kohler; G. Seifert; C.L. Jo; J.I. Lee; Y.R. Jang; J.H. Park; J. Yu; G. Kim J. Chem. Phys., 20 (2009), p. 095201

[26] T. Yang; S. Berber; D. Tomanek Phys. Rev. B., 77 (2008), p. 165426

[27] T. Nguyen; A.D. Sutton; M. Brynda; J.C. Fettinger; G.J. Long; P.P. Power Science, 310 (2005), p. 844

[28] J. Huang; Q. Li; H. Ren; H. Su; J. Yang J. Chem. Phys., 125 (2006), p. 184713

[29] V.P. Georgiev; J.E. McGrady; V.P. Georgiev; J.E. McGrady J. Am. Chem. Soc., 49 (2010), p. 5591

[30] U. Kölle; J. Kossakowski; N. Klaff; L. Wesemann; U. Englert; G.E. Heberich Angew. Chem., Int. Ed., 30 (1991), p. 690

[31] J.E. McGrady Angew. Chem., Int. Ed., 29 (2000), p. 3077

[32] R. Stranger; I.E. Grey; I.C. Madsen; P.W. Smith; R. Saillant; R.B. Jackson; W. Streib; K. Folting; R.A.D. Wentworth; R. Stranger; P.W. Smith; I.E. Grey Inorg. Chem., 69 (1987), p. 162

[33] J.E. McGrady; R. Stranger; T. Lovell J. Phys. Chem. A., 101 (1997), p. 6265

[34] http://www.quantumwise.com/.

[35] M. Brandbyge; J.L. Mozos; P. Ordejon; P. Taylor; K. Stokbro; J.M. Soler; E. Artacho; J.D. Gale; A. Garcia; J. Unquera; P. Ordejon; D. Sanchez-Portal; J. Taylor; H. Guo J. Wang, Phys. Rev. B., 65 (2002), p. 165401

[36] W.Y. Kim; Y.C. Choi; S.K. Min; Y. Cho; K.S. Kim; M. Koentopp; C. Chang; K. Burke; R. Car J. Phys.: Condens. Mat., 38 (2009), p. 2319

[37] M. Paulsson, Non-equilibrium Green's Functions for Dummies, http://www.nanohub.org/resources/1932.

[38] S. Datta; S. Datta; J. Jortner; A. Nitzan; M.A. Ratner; S. Lindsay; R.H. Smit; Y. Noat; C. Untiedt; N.D. Lang; M.C. van Hemert; J.M. van Ruitenbeek; L.H. Yu; Z.K. Keane; J.W. Ciszek; L. Cheng; M.P. Stewart; J.M. Tour; D. Natelson Phys. Rev. Lett., Quantum transport: atom to transistorLecture notes in Physics, introducing molecular electronics, 131 (1997), p. 403 (14)

[39] E. J. Baerends, J. Autschbach, A. Bérces, F.M. Bickelhaupt, C. Bo, P.M. Boerrigter, L. Cavallo, D.P. Chong, L. Deng, R.M. Dickson, D.E. Ellis, M. van Faassen, L. Fan, T.H. Fischer, C. Fonseca Guerra, S.J.A. van Gisbergen, A.W. Götz, J.A. Groeneveld, O.V. Gritsenko, M. Grüning, F.E. Harris, P. van den Hoek, C.R. Jacob, H. Jacobsen, L. Jensen G. van Kessel, F. Kootstra, M.V. Krykunov, E. van Lenthe, D.A. McCormack, A. Michalak, J. Neugebauer, V.P. Nicu, V.P. Osinga, S. Patchkovskii, P.H.T. Philipsen, D. Post, C.C. Pye, W. Ravenek, J.I. Rodriguez, P. Ros, P.R.T. Schipper, G. Schreckenbach, J.G. Snijders, M. Solà, M. Swart, D. Swerhone, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T.A. Wesolowski, E.M. van Wezenbeek, G. Wiesenekker, S.K. Wolff, T.K. Woo, A.L. Yakovlev, T. Ziegler, ADF2008.01; SCM, Theoretical Chemistry, Vrije Universiteit: Amsterdam, The Netherlands, http://www.scm.com.

[40] J.P. Perdew; A. Zunger Phys. Rev. B., 23 (1981), p. 5048

[41] N. Troullier; J.L. Martins Phys. Rev. B., 43 (1991), p. 1993

[42] F. Neese Coord. Chem. Rev., 253 (2009), p. 526

[43] B.E. Bursten; F.A. Cotton; A. Fang; S.F. Gheller; G.A. Heath; D.C.R. Hockless; D.G. Humphrey; J.E. McGrady Inorg. Chem., 22 (1983), p. 2127

[44] L.Y. Hsu; Q.R. Huang; B.Y. Jin; T.W. Tsai; Q.R. Huang; S.M. Peng; B.Y. Jin J. Phys. Chem. C., 112 (2008), p. 10538

[45] H. Fang; R.Z. Wang; S.Y. Chen; M. Yan; X.M. Song; B. Wang; E.G. Emberley; G. Kirczenow Phys. Rev. B., 98 (2011), p. 082108

[46] S. Sen; S. Chakrabati; Y. Karzazi; J. Cornil; J.L. Bredas J. Am. Chem. Soc., 112 (2008), p. 1685

[47] Y. Min; K.L. Yao; H.H. Fu; Z.L. Liu; Q. Li J. Chem. Phys., 132 (2010), p. 214703

[48] J.M. Seminario; A.G. Zacarias; J.M. Tour J. Am. Chem. Soc., 122 (2000), p. 3015

[49] K. Stokbro; M. Brandbyge; J. Taylor; P. Ordejón Ann. N. Y. Acad. Sci., 1006 (2003), p. 212

☆ In memory of Marie-Madeleine Rohmer, whose work on metal–metal bonding was an inspiration.

Commentaires - Politique