Ferromagnetic coupling induced by spin-orbit coupling in dipyridylamide linear trinuclear Cu-Pd-Cu and Cu-Pt-Cu complexes

Daniel Maynau; Hélène Bolvin; Willem Van den Heuvel; Marc Bénard; Marie-Madeleine Rohmer; Nadia Ben Amor

doi:10.1016/j.crci.2011.10.004

Ferromagnetic coupling induced by spin-orbit coupling in dipyridylamide linear trinuclear Cu-Pd-Cu and Cu-Pt-Cu complexes

Daniel Maynau ^1,² ; Hélène Bolvin ^1,² ; Willem Van den Heuvel ³ ; Marc Bénard ⁴ ; Marie-Madeleine Rohmer ⁴ ; Nadia Ben Amor ^1,²

¹ Laboratoire de chimie et physique quantiques (LCPQ), université de Toulouse, UPS, IRSAMC, 118, route de Narbonne, 31062 Toulouse cedex, France
² Laboratoire de chimie et physique quantiques (LCPQ), CNRS, UPS, IRSAMC, 118, route de Narbonne, 31062 Toulouse cedex, France
³ Department of Chemistry, Katolieke Universiteit Leuven, Celestijnenlaan 200F, B-3001 Heverlee (Leuven), Belgium
⁴ Laboratoire de chimie quantique, institut de chimie, CNRS/université de Strasbourg, 4, rue Blaise-Pascal, 67000 Strasbourg, France

Comptes Rendus. Chimie, Volume 15 (2012) no. 2-3, pp. 170-175.

Résumés

Anglais
Français

The mechanism of the magnetic coupling in the [CuMCu(pda)₄Cl₂] complexes with M = Pd, Pt is analyzed. First principles calculations based on the wave function theory are performed (DDCI + SO-RASSI): it is shown that the interaction without spin-orbit coupling is antiferromagnetic while the contribution due to the spin-orbit is ferromagnetic. The agreement between calculations and experiment is very good for the CuPdCu complex but is lesser for the CuPtCu complex. A Hubbard model is used in order to rationalize these results: this shows that the two d frontier orbitals of the central atom play a key role in these two interactions. Although the model parameters extracted from CASCI calculations do not permit to recover the order of magnitude of the interactions, it allows understanding the main interactions that give physical insight.

Le mécanisme du couplage magnétique dans les complexes [CuMCu(pda)₄Cl₂] a été analysé dans le cas où M = Pd, Pt, à l’aide de calculs effectués à partir des premiers principes dans le cadre de la théorie de la fonction d’onde. Ces calculs DDCI + SO-RASSI ont montré que l’interaction sans couplage spin–orbite est antiferromagnétique, alors que la contribution due au spin-orbite est ferromagnétique. L’accord quantitatif entre les calculs et l’expérience est excellent pour CuPdCu, mais moins bon pour CuPtCu. Les résultats obtenus sont interprétés à partir d’un modèle de Hubbard : on montre que les deux orbitales frontières d de l’atome central jouent un rôle essentiel dans ces deux interactions. Bien que les paramètres modèles extraits des calculs CASCI ne permettent pas de retrouver l’ordre de grandeur des interactions, le modèle permet de comprendre leur nature et d’en interpréter le sens physique.

Métadonnées

Reçu le : 2011-09-06
Accepté le : 2011-10-14
Publié le : 2011-12-10

DOI : 10.1016/j.crci.2011.10.004

Keywords: Through-bond interactions, Magnetic properties, Quantum chemistry, Metal–metal interactions, Palladium, Platinium
Mots clés : Interactions à travers les liaisons, Propriétés magnétiques, Chimie quantique, Interactions métal–métal, Palladium, Platine

Affiliations des auteurs :

Daniel Maynau ^{1, 2} ; Hélène Bolvin ^{1, 2} ; Willem Van den Heuvel ³ ; Marc Bénard ⁴ ; Marie-Madeleine Rohmer ⁴ ; Nadia Ben Amor ^{1, 2}

¹ Laboratoire de chimie et physique quantiques (LCPQ), université de Toulouse, UPS, IRSAMC, 118, route de Narbonne, 31062 Toulouse cedex, France
² Laboratoire de chimie et physique quantiques (LCPQ), CNRS, UPS, IRSAMC, 118, route de Narbonne, 31062 Toulouse cedex, France
³ Department of Chemistry, Katolieke Universiteit Leuven, Celestijnenlaan 200F, B-3001 Heverlee (Leuven), Belgium
⁴ Laboratoire de chimie quantique, institut de chimie, CNRS/université de Strasbourg, 4, rue Blaise-Pascal, 67000 Strasbourg, France

@article{CRCHIM_2012__15_2-3_170_0,
     author = {Daniel Maynau and H\'el\`ene Bolvin and Willem Van den Heuvel and Marc B\'enard and Marie-Madeleine Rohmer and Nadia Ben Amor},
     title = {Ferromagnetic coupling induced by spin-orbit coupling in dipyridylamide linear trinuclear {Cu-Pd-Cu} and {Cu-Pt-Cu} complexes},
     journal = {Comptes Rendus. Chimie},
     pages = {170--175},
     publisher = {Elsevier},
     volume = {15},
     number = {2-3},
     year = {2012},
     doi = {10.1016/j.crci.2011.10.004},
     language = {en},
}

TY  - JOUR
AU  - Daniel Maynau
AU  - Hélène Bolvin
AU  - Willem Van den Heuvel
AU  - Marc Bénard
AU  - Marie-Madeleine Rohmer
AU  - Nadia Ben Amor
TI  - Ferromagnetic coupling induced by spin-orbit coupling in dipyridylamide linear trinuclear Cu-Pd-Cu and Cu-Pt-Cu complexes
JO  - Comptes Rendus. Chimie
PY  - 2012
SP  - 170
EP  - 175
VL  - 15
IS  - 2-3
PB  - Elsevier
DO  - 10.1016/j.crci.2011.10.004
LA  - en
ID  - CRCHIM_2012__15_2-3_170_0
ER  -

%0 Journal Article
%A Daniel Maynau
%A Hélène Bolvin
%A Willem Van den Heuvel
%A Marc Bénard
%A Marie-Madeleine Rohmer
%A Nadia Ben Amor
%T Ferromagnetic coupling induced by spin-orbit coupling in dipyridylamide linear trinuclear Cu-Pd-Cu and Cu-Pt-Cu complexes
%J Comptes Rendus. Chimie
%D 2012
%P 170-175
%V 15
%N 2-3
%I Elsevier
%R 10.1016/j.crci.2011.10.004
%G en
%F CRCHIM_2012__15_2-3_170_0

Daniel Maynau; Hélène Bolvin; Willem Van den Heuvel; Marc Bénard; Marie-Madeleine Rohmer; Nadia Ben Amor. Ferromagnetic coupling induced by spin-orbit coupling in dipyridylamide linear trinuclear Cu-Pd-Cu and Cu-Pt-Cu complexes. Comptes Rendus. Chimie, Volume 15 (2012) no. 2-3, pp. 170-175. doi : 10.1016/j.crci.2011.10.004. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2011.10.004/

Version originale du texte intégral

1 Introduction

Recently, the linear frameworks of polymetallic complexes have been studied as potential molecular wires. In order to be suitable for molecular electronics, one has to optimize the transmission of the information along the metallic wire; the key role is thus borne by the interaction between the metallic atoms. It is thus of primary importance to analyze the underlying mechanisms at work in these interactions. The family of trinuclear complexes with dipyridylamide (dpa) ligands has been extensively studied in previous works [1]. The Cu₂Pd(dpa)₄Cl₂ (denoted CuPdCu) and Cu₂Pt(dpa)₄Cl₂ (denoted CuPtCu) compounds have been characterized by magnetic spectroscopies and modelized by DFT calculations [2]. Weak antiferromagnetic interactions are found for CuPdCu and CuPtCu, −7.45 and −0.77 cm⁻¹ respectively, within the framework of Heisenberg Hamiltonian H = −J S_A.S_B. While the DFT calculations could reproduce the magnetic coupling in the CuPdCu complex, the vanishing of the magnetic interaction of CuPtCu could not be completely rationalized. This discrepancy was tentatively assigned to Spin-Orbit Coupling (SOC) of the heaviest central metal. Based on wave-function theory, the aim of this work is first to introduce SOC effects in the calculations. The highly accurate Difference Dedicated Configuration Interaction (DDCI) method has been applied in order to evaluate the Spin-Orbit Free (SOF) magnetic coupling while the SOC was calculated as the state interaction between the SOF states by the restricted active space state interaction approach (SO-RASSI) [3]. The second goal was to attempt to rationalize the results by the mean of a Hubbard-like model.

2 Methods and computational details

The geometries of the two Cu₂M(dpa)₄Cl₂ complexes (M = Pd, Pt) had been previously optimized [2] at the DFT level of theory using the B3LYP [4] exchange-correlation functional with the spin unrestricted option, in the D₄ symmetry group (Fig. 1).

Fig. 1
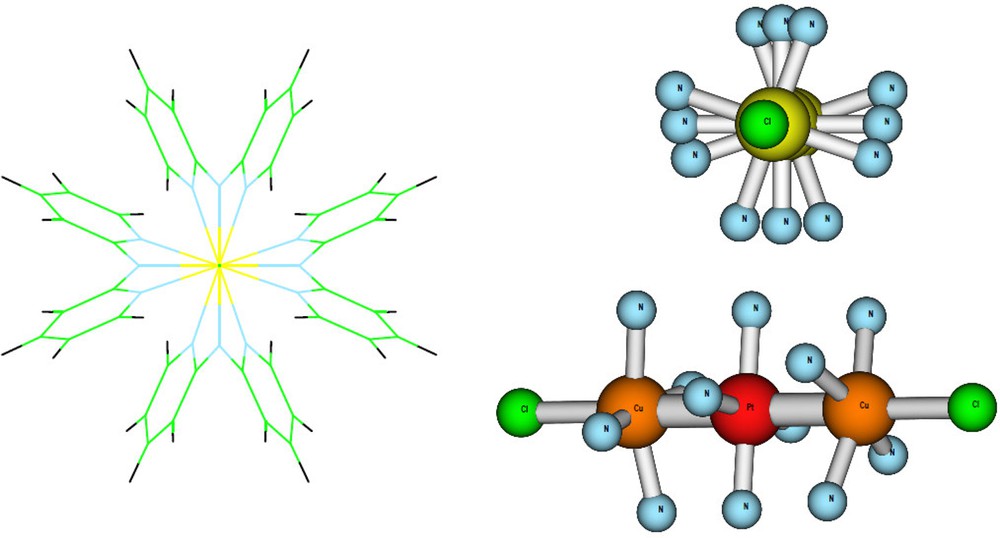
CuPdCu and CuPtCu linear complexes of dipyridylamide (dpa).

In the present work, the calculations have been done within the C₂ symmetry group, the C2 rotation axis being along the CuMCu axis; the three transition metal atoms were on the z-axis. The two low-lying states were the singlet and the triplet open shell states with the spin density localized on the copper atoms and a closed shell in configuration d⁸ on the central atom. These two states are the reference states in the magnetic interaction process.

In order to determine very precisely the magnetic coupling constant, the singlet and triplet states energies were determined with the Complete Active Space Self Consistent Field (CASSCF) method [5] and by including the dynamical correlation contributions using the DDCI method [6] implemented in the CASDI code [7]. This particular framework has shown to provide accurate results for magnetic multi-copper compounds [8]. The magnetic orbitals in CuPdCu and CuPtCu systems were similar, localized on the 3d_x²_−y² copper orbitals with a small contribution of the 3d_xy because of the helical deformation (Fig. 1), so that these magnetic orbitals always point at the nitrogen atoms of the ligands. The active space was defined by two electrons in two orbitals. Thanks to the localization procedure [9] of the orbitals, all the bonding and antibonding σ_C−H and σ_C−C orbitals were frozen in the DDCI calculations. The orbitals were provided by diagonalizing the average density matrix of the singlet and triplet states obtained at CAS + singles configuration interaction level. DDCI calculations were then performed to evaluate the singlet-triplet energy gap. These calculations were done with basis set and Core Ab Initio Model Potentials (AIMP) on Pd (11s8p7d/2s3p3d) [10], Pt (13s10p9d5f/2s3p3d1f) [11], Cu (9s6p6d/2s3p3d) [12], with Atomic Natural Orbitals (ANO) [13] for Cl (7s12p5d4f/4s3p), N (14s9p4d3f/3s2p) and with minimal contraction for more distant atoms: C (14s9p4d3f/2s1p) and H (8s4p3d/1 s).

The SOC was calculated as the state interaction between the SOF states by the restricted active space state interaction approach (SO-RASSI) [14] using MOLCAS 6.7 [15] quantum chemistry software. Scalar relativistic effects were included using the second order Douglas-Kroll-Hess transformation [16]. For this, Atomic Natural Orbitals-Relativistic Correlation Consistent (ANO-RCC) [17] basis sets were used with the following contraction scheme: for Pd [18] atom a [6s5p3d1f] set, for Pt [18] atom [7s6p4d2f], for Cl [19] [6s5p3d], for N [19] [3s2p], while for C [19] and for H [20] minimal basis sets were used. The SO-RASSI method was applied on the basis of CASSCF wave functions. There is no effect of the SOC when one just considers the interaction between the two magnetic states. Then, the state interaction has been enlarged. Since the magnetic coupling between the two copper atoms is supposed to transit through the central metallic atom (Pd or Pt), and since the low-lying excitations are localized on this atom, the active space was enlarged to include all the d orbitals of the central metal giving rise to a CAS(10,7). Around 70 SOF states are included in the state interation: singlet, triplet and quintet excited states of each symmetry, which correspond to all combinations for which the outer d shell of the central atom is populated with eight electrons. The SOF energies are the CASSCF energies except for the energy of the triplet reference state, which was modified in order to keep the DDCI gap.

3 Results and discussion

3.1 Magnetic parameters

The spin Hamiltonian underlying the magnetic properties of these complexes can be written as:

H = - J {\vec{S}}_{A} . {\vec{S}}_{B} + {\vec{S}}_{A} . D . {\vec{S}}_{B}

where S_A and S_B are the local spins on the copper atoms (S = 1/2), J is the exchange parameter and D is the Zero-Field Splitting (ZFS) tensor. Within this magnetic coupling scheme, one gets one singlet state $|0,0〉$ in terms of $|S, M_{S}〉$ and three triplet components $|1,1〉$ , $|1,0〉$ $|1, - 1〉$ . In the absence of SOC, the D tensor is zero, the three latter states are degenerate and

J = 〈0,0 |H| 0,0〉 - 〈1, M_{S} |H| 1, M_{S}〉

Once SOC is considered, since the effect is really tiny, one can still characterize the states by the previous denominations. The effect of SOC is double:

• it can bring a contribution to the isotropic exchange by shifting the value of J;
• an anisotropic coupling appears that leads to ZFS. In this latter case, the three triplet components are no more degenerate.

3.1.1 CuPdCu

At the DDCI level of calculation, the magnetic coupling is antiferromagnetic with a value of J = −11 cm⁻¹. The experimental value of J is −7.45 cm⁻¹. One may notice that the set of orbitals used in the CI calculation has a dramatic role. Indeed, when CASSCF orbitals of the singlet state (or of the triplet one) are used to calculate the singlet-triplet energy gap, the two magnetic states are found almost degenerate even at the DDCI level. To remove this degeneracy, an optimized averaged set of natural orbitals is necessary.

According to the double group symmetry rules, the ³A (and the ³B) states are split into A and B components. When the SOC is calculated on the basis of the two magnetic states, the A electronic ground state (coming mainly from the ¹A spin free state) is not modified while it is shifted down by 248 cm⁻¹ by enlarging the basis of CASSCF states to include all the excitations on the d-orbitals of the central metal (70 states). The three components of the a³A state are quasi degenerate, with a splitting of 0.03 cm⁻¹ between the |1, 0> component and the two others. This gap corresponds to a magnetic anisotropic parameter D of 0.03 cm⁻¹ which compares quite well to the experimental 0.06 cm⁻¹ value. However, there is a large contribution of the SOC to the isotropic exchange since the exchange parameter becomes −7 cm⁻¹: the SOC brings a ferromagnetic contribution of 4 cm⁻¹.

The antiferromagnetic behaviour as well as the quantitative values of the coupling constant (−7 cm⁻¹) and anisotropic parameter (0.03 cm⁻¹) are both in good agreement with experimental values for CuPdCu complex (−7.45 cm⁻¹ and 0.06 cm⁻¹ respectively).

3.1.2 CuPtCu

For this complex, the DDCI magnetic coupling constant J is −5.7 cm⁻¹ to be compared to the experimental −0.77 cm⁻¹ value. The SOC calculated on the basis of the two magnetic states does not change these results: the A electronic ground state (coming mainly from the ¹A spin free state) is shifted down by −0.06 cm⁻¹. But, when the state interaction includes 73 CASSCF wave-functions [13 ¹A, 17 ³A, 4 ⁵A, 12 ¹B, 18 ³B and 6 ⁵B], a ferromagnetic behaviour is obtained, with a J value of + 17 cm⁻¹. The |1,0> is the new ground state, stabilized by 1440 cm⁻¹ compared to the corresponding SOF states. The three components of the triplet are quasi degenerate, with a splitting of 0.83 cm⁻¹ between |1,0> and |1,±1> states. The splitting between the |1,1> and |1,−1> states is 0.002 cm⁻¹: one thus finds for the following anisotropic parameter D = 0.83 cm⁻¹ much larger than the experimental value of D = 0.003 cm⁻¹.

As in the CuPdCu complex, the SOC brings a ferromagnetic contribution to the isotropic exchange coupling. A more detailed analysis shows that the excited state interacting with the singlet magnetic state is the component |1,0> of the c³A state while the triplet magnetic state interacts mainly with the b¹A and the a⁵A states. All these states correspond to single excitation from the d_xy to the d_x²_–y² orbitals of the central atom. When an additional calculation is done, with only the first two singlet, three triplet and one quintet states of A symmetry, the J value is 15.5 cm⁻¹ while the triplet is lowered by 1440 cm⁻¹ and the splitting of the |1,0> component and the two others is already 0.83 cm⁻¹. So, we can conclude that the main contributions to the SOC state interaction are due to the local single excitation between the two frontier orbitals on the central atom, namely excitation from d_xy to d_x²_–y² orbitals.

3.2 Model Hamiltonian

In order to understand which interactions play a key role in each complex, we will analyze the different pathways of the magnetic coupling by means of a model Hamiltonian. According to the distance between the two metallic centres, the magnetic coupling between the two copper atoms is indirect. This antiferromagnetic coupling through closed shell atoms is due to a superexchange interaction. One can foresee two pathways for this interaction:

• a Cu–L–Cu interaction since the four bridging ligands are connected to the two copper atoms;
• a Cu–L–M–L–Cu pathway in which the coupling is relayed by the central metallic atom.

We have focused on the second mechanism since magnetic orbitals have a small contribution on the d_x²_–y² orbitals of the central atom and because SO-RASSI analysis shows that the SOC contribution to the isotropic exchange is mainly due to the states arising from a single excitation d_xy → d_x²_–y² on the central atom. The choice of the model Hamiltonian is based on these two considerations. The model is then built in a space with four electrons in the four following orbitals:

• a and b, the two magnetic orbitals localized on the copper atoms, i.e. the local d_x²_–y² as defined in a local framework of axis in which the x- and y-axis point at the nitrogen atoms of the ligands;
• c and d, the highest occupied d_xy and the lowest vacant d_x²_–y² respectively, localized on either Pd or Pt.

In order to build the model Hamiltonian, one takes into account the following features:

• the d_xy orbital of the central atom would not overlap with the d_x²_–y² orbitals of the copper atoms if there was no torsion along the z axis. The delta overlap between these two orbitals is thus due to the torsion angle. As delta overlaps are small and the torsion angle is not important (18°), we will neglect this direct interaction;
• the indirect interaction through the ligands is either through the sigma skeleton and connects two d_x²_–y² orbitals, or through the pi system and connects two d_xy orbitals. Based on these considerations, we have neglected in the model the interaction between d_xy and d_x²_–y² orbitals on Cu and M central atoms;
• by analyzing the SO-CASSCF results, it appears that the main contribution of the SOC to the exchange parameter is borne by the single excitation from d_xy to d_x²_–y² orbitals of the central atom.

We finally propose to take into account the following integrals in the model and to neglect all the other ones:

• one-electron integrals:
$\begin{array}{l} 〈a |H| d〉 = 〈b |H| d〉 = t \\ 〈d |H| d〉 - 〈a |H| a〉 = 〈d |H| d〉 - 〈b |H| b〉 = δ_{2} \\ 〈c |H| c〉 - 〈a |H| a〉 = 〈c |H| c〉 - 〈b |H| b〉 = δ_{1} \\ 〈c |H| d〉 = 〈\bar{d} |H| \bar{c}〉 = i ς \end{array}$
• and two-electron integrals:
$\begin{array}{l} 〈a \bar{a} |H| a \bar{a}〉 = 〈b \bar{b} |H| b \bar{b}〉 = U \\ 〈c \bar{c} |H| c \bar{c}〉 = 〈d \bar{d} |H| d \bar{d}〉 = W \end{array}$

the unbarred (barred) orbitals represent spin-orbitals with spin α (β).

The physical meaning of the previous parameters is:

• t is the effective coupling between a magnetic orbital (a or b) localized on one of the copper atoms and the d orbital localized on the central atom;
• δ1 (δ2) is the energy gap between the magnetic orbitals and the c (d) orbital of the central atom. A positive δ1 (δ2) value means that a and b orbitals are energetically below the c (d) one;
• ζ is the atomic SOC constant of the central atom;
• U and W are the one-centre electron-electron repulsion energies on the copper and the central atom respectively.

We will restrict the whole discussion to the M_S = 0 space. Within this scheme, the configuration a¹b¹c² gives rise to the two magnetic states at zeroth order:

\begin{array}{l} |S^{(0)}〉 = \frac{1}{\sqrt{2}} (|c \bar{c} a \bar{b}| - |c \bar{c} \bar{a} b|) \\ |T^{(0)}〉 = \frac{1}{\sqrt{2}} (|c \bar{c} a \bar{b}| + |c \bar{c} \bar{a} b|) \end{array}

These two states are degenerate at this level of calculation and their energy is taken as the reference. By configuration interaction within the model space, these two states interact with excited configurations and the difference of energy between the two ground states $|S〉$ and $|T〉$ corresponds to the magnetic coupling

J = 〈S |H| S〉 - 〈T |H| T〉

In the present case, the energy of the excited configurations is large compared to the magnitude of the coupling elements, and perturbation theory can be used. An effective Hamiltonian can be built in the zeroth order space generated by

|c \bar{c} a \bar{b}|

and

|c \bar{c} \bar{a} b|

. In other words, the effective coupling between these two determinants provides the splitting between the two magnetic states

J = - 2 〈|c \bar{c} a \bar{b}| |H^{e f f}| |c \bar{c} \bar{a} b|〉

The main mechanism of lowest order providing some exchange coupling is of fourth order. It corresponds to a superexchange mechanism [21,22] (Scheme 1):

Scheme 1
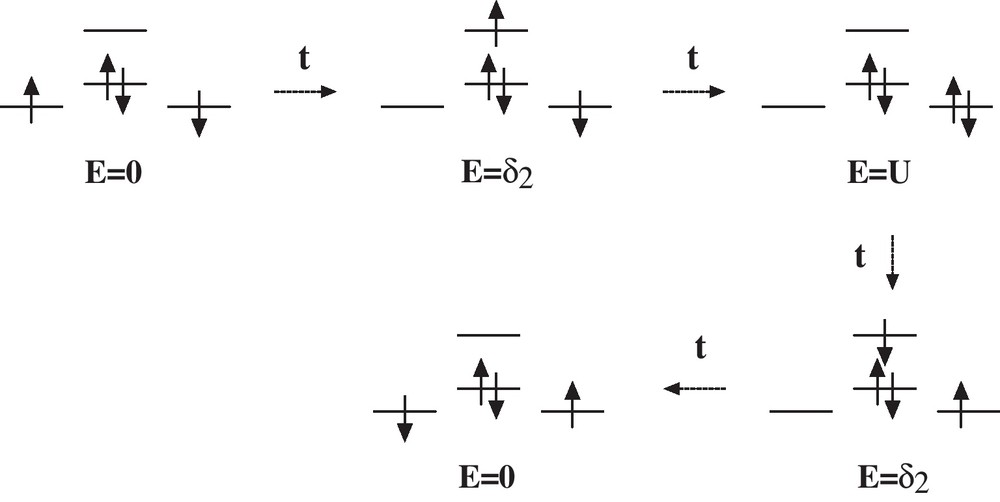
Coupling scheme of the superexchange.

This contribution can be evaluated as

J_{1} = - 4 \frac{t^{4}}{δ_{2}^{2} U}

t, δ₂, U and W have been evaluated from the fitting of the CASCI energies with three electrons in a, b and d orbitals while δ₁ has been calculated from a CASCI calculation with four electrons in a, b and c orbitals. The results for the CuPdCu and CuPtCu complexes are presented in Table 1.

(cm⁻¹)	t	δ₁	δ₂	U	W
CuPdCu	3000	73,700	153,900	211,200	61,500
CuPtCu	3300	87,500	161,200	211,900	45,900

These parameters show that the c orbital is above the a and b ones (δ₁ and δ₂ are positive); however, the c orbital is doubly occupied and the ground state corresponds to the a¹b¹c² configuration since the pairing energy is smaller in the Pd/Pt atom than in Cu one. Since Pd is more electronegative than Pt, δ₁ and δ₂ are smaller in the former and as the 4d orbitals are less diffuse than the 5d ones, W is larger and t smaller. With these parameters, one obtains a value of J₁ = −0.065 cm⁻¹ for CuPdCu and J₁ = −0.086 cm⁻¹ for CuPtCu.

When including the SOC, the coupling scheme of lowest order is the following one (Scheme 2).

Scheme 2
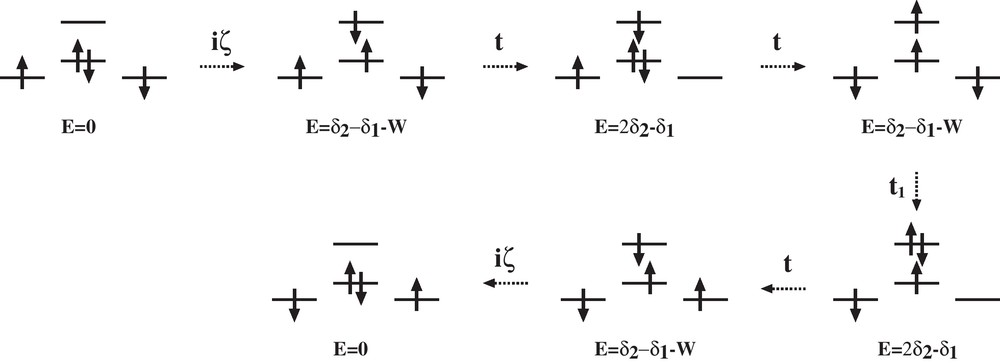
Coupling scheme of the SOC induced spin polarization.

This scheme corresponds to spin-polarization since in one of the intermediate states, there is a triplet state on the central atom: we denote this contribution as a SOC induced spin polarization one. This leads to a sixth order interaction and the SOC contribution to the isotropic exchange J₂ is expressed by:

J_{2} = 4 \frac{ζ^{2} t^{4}}{{(2 δ_{2} - δ_{1})}^{2} {(δ_{2} - δ_{1} - W)}^{3}}

Taking the value of SOC constants of the free ions, ζ = 1615 cm⁻¹ for the palladium atom, and ζ = 3370 cm⁻¹ for the platinum one, one finds J₂ = 0.002 cm⁻¹ for CuPdCu and J₂ = 0.004 cm⁻¹ for CuPtCu.

The parameters proposed above do not give the right order of magnitude of the interactions. Indeed, it has been shown [23,24] that the on-site repulsion parameters (U and W) are largely overestimated in a CASCI approach compared to a correlated one. However, this model proposes a mechanism that shows that the SOC on the central metallic atom can bring a ferromagnetic contribution to the exchange parameter.

4 Conclusion

In this article, a theoretical study of the two [CuPdCu(dpa)₄Cl₂] and [CuPtCu(pda)₄Cl₂] complexes is proposed. In these molecules, the two single electrons localized on the copper atoms are antiferromagnetically coupled. A previous DFT study had underlined the superexchange mechanism and had suggested that the SOC of the central atom could play a role. In order to elucidate this point, wave function theory calculations have been performed using highly accurate methods. It is shown that a high level of theory is necessary in order to obtain the right value of the exchange parameter and more precisely, an optimized set of orbitals is necessary. The SOF interaction brings an antiferromagnetic contribution while the SOC brings a ferromagnetic one to the exchange parameter. First principles results for CuPdCu are in very good agreement with the experimental values, even for the ZFS parameter. The agreement for the CuPdCu complex is not so accurate: there seems to be an overestimation of the SOC ferromagnetic contribution. In order to rationalize these results, a Hubbard model based on the two magnetic orbitals of the copper atoms and on the two frontier orbitals of the central metallic atom is proposed. Within the frame of this model, the SOF antiferromagnetic contribution corresponds to the superexchange through the non-occupied d orbital of the central atom. Once the SOC on the central atom is considered, there is a ferromagnetic contribution to the isotropic exchange that corresponds to SOC induced spin polarization mechanism. The anisotropic contribution is very small. Unfortunately, the numerical applications of these two contributions with model parameters issued from CASCI calculation do not permit to retrieve the correct order of magnitude: either the parameters are not adapted or the two proposed mechanisms are not sufficient.

Disclosure of interest

The authors declare that they have no conflicts of interest concerning this article.

Bibliographie

[1] J.K. Bera; K.R. Dunbar; S.M. Peng; C.C. Wang; Y.L. Jang; Y.H. Chen; F.Y. Li; C.Y. Mou; M.K. Leung J. Magn. Magn. Mater., 41 (2002), p. 4453

[2] I.P.C. Liu; G.H. Lee; S.M. Peng; M. Bénard; M.M. Rohmer Inorg. Chem., 46 (2007), p. 9602

[3] P.Å. Malmqvist; B.O. Björn; B. Schimmelpfennig Chem. Phys. Lett., 357 (2002), p. 230

[4] C. Lee; W. Yang; R.G. Parr; A.D. Becke; A.D. Becke J. Chem. Phys., 37 (1988), p. 785

[5] P.Å. Malmqvist; A. Rendell; B.O. Roos; B.O. Roos; P.R. Taylor; P.E.M. Siegbahn; B.O. Roos Chem. Phys. (K.P. Lawley, ed.), The complete active space self-consistent field method and its applications in electronic structure calculations, Advances in chemical physics; ab initio methods in quantum chemistry - II, 94, John Wiley & Sons Ltd, Chichester, England, 1990, p. 5477 (chapter 69)

[6] J. Miralles; O. Castell; R. Caballol; J.P. Malrieu Chem. Phys., 172 (1993), p. 33

[7] N. Ben Amor; D. Maynau Chem. Phys. Lett., 286 (1998), p. 211

[8] J. Cabrero; C. de Graaf; E. Bordas; R. Caballol; J.P. Malrieu Chem. Eur. J., 9 (2003), p. 2307

[9] D. Maynau; S. Evangelisti; N. Guihéry; C.J. Calzado; J.P. Malrieu J. Chem. Phys., 116 (2002), p. 10060

[10] Z. Barandiaran; L. Seijo; S. Huzinaga J. Chem. Phys., 93 (1990), p. 5843

[11] M. Casarrubios; L. Seijo J. Chem. Phys., 110 (1999), p. 784

[12] Z. Barandiaran; L. Seijo Can. J. Chem., 70 (1992), p. 409

[13] P.O. Widmark; B.J. Persson; B.O. Roos Theor. Chim. Acta, 79 (1991), p. 419

[14] P.Å. Malmqvist; B.O. Roos; B. Schimmelpfennig Chem. Phys. Lett., 357 (2002), p. 230

[15] MOLCAS software: K. Andersson, M. Barysz, A. Bernhardsson, M. R .A. Blomberg, Y. Carissan, D.L. Cooper, M.P. Fülscher, L. Gagliardi, C. de Graaf, B.A. Hess, D. Hagberg, G. Karlström, R. Lindh, P.Å. Malmqvist, T. Nakajima, P. Neogrády, J. Olsen, J. Raab, B.O. Roos, U. Ryde, B. Schimmelpfennig, M. Schütz, L. Seijo, L. Serrano-Andrés, P.E. M. Siegbahn, J. Stålring, T. Thorsteinsson, V. Veryazov, P.O. Widmark.

[16] B. Hess. Phys. Rev. A. (1986), p. 3742

[17] B.A. Hess, Phys. Rev. A., 33 (1986) 3742.

[18] B.O. Roos; R. Lindh; P.A. Malmqvist; V. Veryazov; P.O. Widmark J. Phys. Chem. A, 109 (2005), p. 6575

[19] B.O. Roos; R. Lindh; P.Å. Malmqvist; V. Veryazov; P.O. Widmark J. Phys. Chem. A, 108 (2005), p. 2851

[20] P.O. Widmark; P.A. Malmqvist; B.O. Roos Theor. Chim. Acta, 77 (1990), p. 291

[21] P. de Loth; P. Cassoux; J.P. Daudey; J.P. Malrieu J. Am. Chem. Soc., 103 (1981), p. 4007

[22] C.J. Calzado; J. Cabrero; J.P. Malrieu; R. Caballol J. Chem. Phys., 116 (2002), p. 2728

[23] C.J. Calzado; J. Cabrero; J.P. Malrieu; R. Caballol J. Chem. Phys., 116 (2002), p. 3985

[24] Z. Tabookht; X. López; M. Bénard; C. de Graaf J. Phys. Chem. A, 114 (2010), p. 12291

Commentaires - Politique