1 Introduction
There are two particular interesting properties of the acetylide ligand; the first one is its ability to coordinate to metal centers, in terminal and various bridging modes, which made them versatile ligands in the synthesis of polynuclearmetal complexes [1], whereas, the second is their mobility on the coordination sphere of the transition metal complexes [2]. Nevertheless, the fluxional behavior of this ligand, in transition metal complexes, was a key feature to the formation of the metal vinylidenes compounds [3]. In this respect, transition metal complexes containing bridging acetylide group have attracted enormous attention owing to their potential technological applications as precursors for non-linear optical materials, rigid-rod molecular wires, low dimensional, conducting, and liquid crystalline materials [4]. Moreover, structural studies of the transition metal-acetylide complexes yield valuable insights into the strength of the metal–acetylide interactions and into reaction mechanisms involving the acetylide moiety. In this regard, much effort has recently been devoted to the syntheses and characterizations of these complexes. Recently, Griffith et al. reported the synthesis of the trinuclear transition metal-acetylide complexes, [{Ru(CO)2(η5C5H5)}3(η1:η1:η2:-CC)]+, which have unique structural features and bonding interactions [5]. As shown in Fig. 1, the details of the structure of this complex, show some interesting feature. It contain a CC−2 unit bound to three of the metallic fragments Ru(CO)2(η5C5H5), [Ru]; two of these fragments, [Ru1] and [Ru3], are bound in η1 fashion with distance to the acetylide moiety of 2.065Å [Ru1-C1] and 2.043Å [Ru3-C2]. The third fragment, [Ru2], is bound in a η2 fashion to the acetylide carbon atoms in an unsymmetrical manner with Ru2-C1 and Ru2-C2 being 2.323 and 2.388 Å, respectively. The 1H NMR spectra at variable temperatures, suggest that CC−2 rotation moving is the kind of fluxional motion exhibited by these classes of complexes [5,6]. It consisted of a mechanism for exchanging the σ-π bound ruthenium atoms on the NMR timescale. One such mechanism for the exchange invokes the rotation of the CC−2 unit within a triangle defined by the three formally positive ruthenium atoms, which recently was described as “bearing-like” for the biacetylide between three metals [5]. On the basis of this mechanism, the complex (4a), G, would be fluctuating between two isomers. In the first one, G1, the clockwise rotation of CC−2 changes the Ru3 atom from terminal (σ bond) to bridging (π bonding mode), whereas, in the second, G2, the contraclockwise rotation of CC−2 causes the Ru1 atom to be a bridging one. The mechanism proposed is in Fig. 2. However, the rotation of the CC−2 moiety only changes the hapticity of the metals involved in this movement, accompanied by some rearrangement in the coordinate of [(CO)2(η5C5H5)] fragment to overcome this rotation.
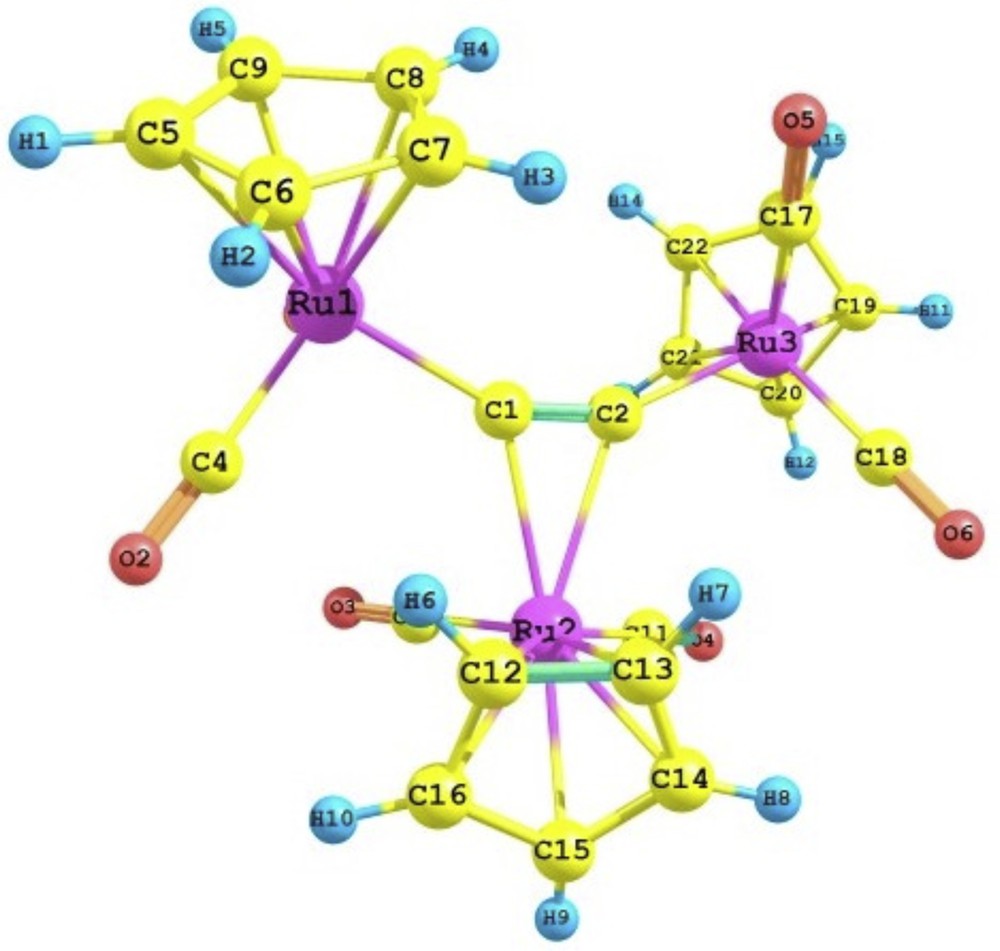
Molecular structure of the complex 4a (G).
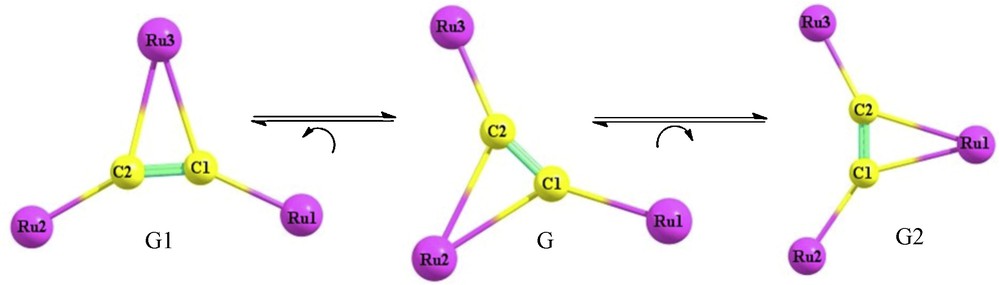
Clockwise/contraclockwise rotation of C2.
2 Computational details
The calculations have been performed at two levels of accuracy [7]. The density functional scheme has been employed to derive ground state energies and to perform the various geometry optimizations and transition state (TS) calculations. An extend Huckel calculation were subsequently performed on Cs symmetric constrain stationary points determined at the SCF level.
The calculations, of high levels of accuracy, were performed using the Amsterdam density functional (ADF) program developed by Baerends et al. [8]. To ensure high reliability of the results, three exchange-correlations functional were applied, LDA, PB86 and BLYP. This procedure allows drawing a conclusion which is not biased by the choice of a particular functional. The molecular orbitals (MO) were expanded in a double-ζ STO basis, with the core orbital (1s for C and O; 4p for Ru) kept frozen throughout. The geometries were fully optimized and normal mode analysis was carried out. Transition states were obtained by full transition state optimization of structures obtained from linear transit calculations, until the Hessian had only one imaginary eigenvalue. Saddle point determinations were initialized by a linear transit search from reactant (G) to product (G1) along an assumed reaction coordinate. In each step along the reaction coordinate, all other degrees of freedom were optimized. The equilibrium geometries were carried out with an integration accuracy of 5.0. The crystallographic coordinates were used as a starting geometry for complete geometry optimizations.
Throughout this paper, we will use qualitative molecular orbital methods, in particular extended Huckel theory. The EHMO calculations were conducted by using the program developed by Hoffmann and Lipscomb, [9] and modified by Mealli and Proserpio [14]. The atomic orbital (AO) parameters used were taken from the CACAO program [10].
2.1 Geometry optimization
The most important optimized geometry parameters are presented in S1-Table 1 (of the Supplementary information) along with the experimental data. The comparison with the gas phase experimental results shows that LDA levels of calculation yield excellent results. For the metal-carbon bond lengths, BLYP and PB86 calculations provide reasonably similar results, leads to values slightly higher than the experimental ones.
The maximum error is 0.097 Å for the Ru2-C1 and 0.025 Å for the Ru1-C1 bonds. On the other hand, LDA leads to metal-carbon bond lengths closer to the experimental ones. The maximum error is in the Ru1-C1 bond length, which is overestimated with respect to the experimental value by 0.029 Å.
The structural parameters optimized for the cationic compound reveals good agreement with experimental data, allowing some confidence in the reliability of calculation methods used. Nevertheless, for the bond length of the CC−2 moiety, the agreement between the LDA calculation and the experimental data is better than that of the other levels, this justifies our choice of this method for the rest of the work.
2.2 Qualitative analysis
EHMO computations were performed in order to qualitatively rationalize the electronic structure of the [{Ru(CO)2(η5C5H5)}3(η1:η1:η2:-CC)]+. The analysis is performed using the interactions between F1 = [Ru(CO)2(η5C5H5)]+ and F2 = [{Ru(CO)2(η5C5H5)}2(η1:η1:-CC)] fragments (Fig. 3). Ouddai et al. described the nature of the frontier orbitals of a second fragment, and showed that HOMO and HOMO-1 MOs are mainly the AO of CC π moiety [11].
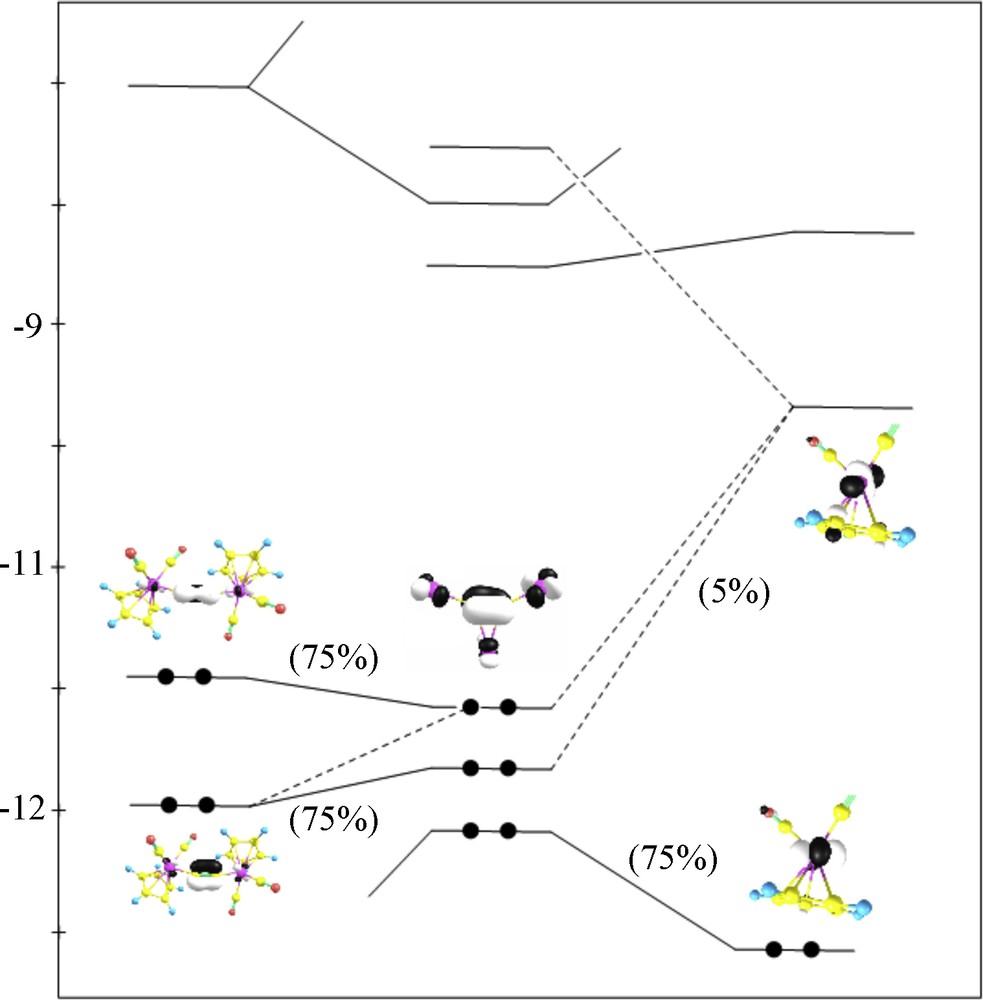
MO interaction between [Ru(CO)2(η5C5H5)]+ and [{Ru(CO)2(η5C5H5)}2(η1:η1:-CC)].
The calculations were performed in two steps. First, a Cs symmetry constraint optimization was performed using the LDA method. In the second step, the single point calculation was evaluated by Extend Huckel method. Table 1 compares the Cs structure with the geometry that was optimized without any symmetric constraint.
Comparison between geometry parameters in the constraint/no constraint structures.
| No constraint structure | Cs structure | |
| C1–C2(Å) | 1.268 | 1.267 |
| Ru1–C1(Å) | 2.036 | 2.027 |
| Ru2–C1(Å) | 2.319 | 2.351 |
| Ru2–C2(Å) | 2.369 | 2.351 |
| Ru3–C2(Å) | 2.033 | 2.072 |
| Ru1–C1–C2(°) | 153.6 | 156.5 |
| Ru3–C2–C1(°) | 157.4 | 156.5 |
| Ru2–C1–Ru1(°) | 129.9 | 129.1 |
| Ru2–C2–Ru3(°) | 129.6 | 129.1 |
The interaction diagram between the two fragments (Fig. 4) readily predicts that the main contribution to the lowest unoccupied molecular orbital (LUMO) comes from the AO of the F1 fragment, with a negligible (10%) contribution from AO of the F2 fragment. However, the HOMO originates from interactions between the HOMO of F2 (CC π) and the LUMO (5%) of F1 moiety. The negative overlap between the two fragments leads to antibonding interactions in this MO. The HOMO-1, which is built upon interactions between HOMO-1 of F2 (CC π) fragments and LUMO-1 (5%) of F1, features also an F1–F2 antibonding interaction.

Optimized structure of the complex G1.
2.2.1 Density functional theory (DFT) MO analysis
The fluxional behavior of our molecule, explained by the rotation movement of one part, CC−2, with respect to the other part, [Ru]. Hence, this movement would be controlled by the interactions that occur between the three Ruthenium atoms and the bridging acetylide ligand. Of practical interest, thus, are the orbitals that have large coefficients on CC−2, and are much localized in space likely to overlap with [Ru] orbitals.
From S2-Table 2 (of the Supplementary information), the greatly dominant CC−2 MO fragment is evident on the molecular orbital: HOMO-1 (82A), HOMO (83A), HOMO-1 (84A), HOMO-15 (68A), HOMO-16 (67A), and HOMO-17 (66A). The HOMO, is formed by an antibonding π interaction between the C2 (3A + 4A) orbitals and the metallic fragment orbital 78A, S1-Fig. 1 (of the Supplementary information). The composition and the character of HOMO-1 is slightly different from that of OM 83A. Another π bonding interaction is manifested very well on the molecular orbitals HOMO-15. This orbital is formed by the interaction of the MO fragment 3A with the metallic fragment orbitals 64A and 65A, Fig. 1. The other low-lying orbitals, HOMO-17 and HOMO-16, essentially describe the M-C σ bonding are formed mainly by the interaction of MOs fragments 3A, 4A and 5A of CC−2 with the metallic fragment orbital 81A and 64A, respectively.
The overall result is the weak attractive interaction between the two fragments, due to the small overlap population between [CC−2] and [Ru] fragments, 0.035, and due the antibonding character of the occupied orbitals, HOMO and HOMO-1. This bonding situation suggests that the union ([CC−2]-[Ru]) could be flexible, and therefore a good target for the fluxional process [12,13].
In order to gain a better quantitative understanding of the bonding situation in the title complex, we performed an energy decomposition analysis (EDA) [14].
In EDA, the interaction energy Δint was calculated and decomposed for the bonding between the F1 = [Ru(CO)2(η5C5H5)]+ and the F2 = [{Ru(CO)2(η5C5H5)}2(η1:η1:-CC)] fragments. The instantaneous interaction energy Δint can be divided into three components [Eq. (1)]:
| Δint = Δelstat + Δpauli+ Δorb | (1) |
The Δelstat is the “rigid” electrostatic interaction energy between the fragments, which is calculated from the wave functions of the fragments in separation. Δpauli is the Pauli repulsive and Δorb is the orbital interaction term resulting from the two-electron/two orbital bonding interactions. On the other hand, the bond decomposition energy (BDE) ΔE between the two fragments F1 and F2 divided into two main contributions Δprep and Δint where ΔE(BDE) = Δint + Δprep; Δprep is the energy necessary to promote the two fragments from their equilibrium geometry and electronic ground state to the geometry and electronic state that they have in the molecule. Our computed results are reported in Table 2.
EDA result; the value in parentheses gives the % contribution to the attractive interactions.
| Δint | Δpauli | Δelstat | Δorb | Δprep | BDE | |
| Term | −110.28 | 126.80 | −143.96 (60.72%) | −93.12 (39.76%) | −7.75 | 117.85 |
The energy terms of the EDA indicates that the orbital (covalent) contribution to interaction energy amounts to 39.76% of the attractive F1–F2 interactions while the electrostatic attraction contributes 60.72%, suggesting the predominate ionic character of the [Ru(CO)2(η5C5H5)]+ -Ru(CO)2(η5C5H5)}2(η1:η1:-CC)] interaction.
2.2.2 Transition states research
It is noteworthy that the rotation of CC−2, either in clockwise or in counterclockwise direction, would face the same factors that facilitate this movement, and hence, this promoted us to limited our transition states research in only one direction. This limitation is sufficient to give a better explanation of the fluxional behavior of this complex.
We have carried out a transition state research calculation on the first mechanism G→G1. First, the geometrical parameters of the isomer G1 were optimized at LDA/DZ level. The resulting molecule structure and parameters are given in Fig. 4.
Second, starting from the G (4a) complex, we model the fluxional process by a linear transit calculation, where we choose the bonds (Ru1-Ru2, Ru1-Ru3, Ru3-C1 and C1-C2), the bond angles (Ru3-Ru1-Ru2, C1-Ru3-Ru1 and C2-C1-Ru3) and the torsion angle (C1-Ru3-Ru1-C30 and C2-C1-Ru3-Ru1) as a reaction coordinates.
By linear transit, Fig. 5, and subsequent transition state optimization, we arrive at transition state TS (Fig. 6), which lies 6.88 kcal/mol above G.

Linear transit from G to G1.

Optimized structure of the TS; arrows represent important movements of atoms in imaginary frequency.
During the rotation process, Ru1–C1 and Ru3–C2 distances do not change very much upon going from G to TS, However, Ru2–C1 is considerably longer and Ru3–C1 moderately shorter in TS than in G. Furthermore, the changes of the percent compositions and the bonding character of HOMO, HOMO-1, HOMO-15-17, S2-Fig. 2 (of the Supplementary information), are considerably smaller, which can further facilitate the stabilization of the transition states, and lead to small energy barrier (6.88 kcal/mole). On the other hand, the energy required to cleave the [Ru(CO)2(η5C5H5)]+-[{Ru(CO)2(η5C5H5)}2(η1:η1:-CC)] bond, as estimated from BED above, is approximately 110.94 kcal/mol higher than that required to rotate the acetylide ligand.
3 Summary
The geometry, bonding nature, electronic structure, and fluxional behavior of [{Ru(CO)2(η5C5H5)}3(η1:η1:η2:-CC)]+ were theoretically investigated with the DFT, LDA/TZP, and extend Huckel calculation.
The present theoretical study shows that the filling of the occupied metal-acetylide antibonding orbitals, HOMO and HOMO-1, the small overlap population between the two fragments, and the non-directionality of this interaction due to its electrostatic nature, explain the height lability of the acetylide ligand. On the other hand, the fluxional behavior of the title compound easily occurs with a small energy barrier of 6.88 kcal/mol, and via a metal vinylidene-like transition state structure.


