A theoretical investigation on the densities and detonation properties of polynitrotetraazabenzimidazoles

Guozheng Zhao; Ming Lu

doi:10.1016/j.crci.2012.07.002

A theoretical investigation on the densities and detonation properties of polynitrotetraazabenzimidazoles

Guozheng Zhao ¹ ; Ming Lu ¹

¹ School of Chemical Engineering, Nanjing University of Science and Technology, Nanjing, 210094 Jiangsu, China

Comptes Rendus. Chimie, Volume 15 (2012) no. 9, pp. 808-814.

Résumé

The polynitrotetraazabenzimidazoles were optimized to obtain their molecular geometries and electronic structures at DFT–B3LYP/6-31 + G(d) level. The theoretical molecular density (ρ), heat of formation (HOF), detonation velocity (D) and detonation pressure (P), estimated using Kamlet–Jacobs equations, showed that the detonation properties of these compounds were excellent. It is found that there are good linear relationships between volume, density, detonation velocity, detonation pressure and the number of nitro group. The simulation results reveal that molecules F and L outperform HMX, which will be novel potential candidates for high energetic density compounds (HEDCs) when it is successfully synthesized. These results provide basic information for molecular design of novel HEDCs.

Métadonnées

Reçu le : 2011-12-13
Accepté le : 2012-07-05
Publié le : 2012-08-10

DOI : 10.1016/j.crci.2012.07.002

Mots clés : Polynitrotetraazabenzimidazoles, Density functional theory (DFT), Density, Detonation property, Thermal stability

Affiliations des auteurs :

Guozheng Zhao ¹ ; Ming Lu ¹

¹ School of Chemical Engineering, Nanjing University of Science and Technology, Nanjing, 210094 Jiangsu, China

@article{CRCHIM_2012__15_9_808_0,
     author = {Guozheng Zhao and Ming Lu},
     title = {A theoretical investigation on the densities and detonation properties of polynitrotetraazabenzimidazoles},
     journal = {Comptes Rendus. Chimie},
     pages = {808--814},
     publisher = {Elsevier},
     volume = {15},
     number = {9},
     year = {2012},
     doi = {10.1016/j.crci.2012.07.002},
     language = {en},
}

TY  - JOUR
AU  - Guozheng Zhao
AU  - Ming Lu
TI  - A theoretical investigation on the densities and detonation properties of polynitrotetraazabenzimidazoles
JO  - Comptes Rendus. Chimie
PY  - 2012
SP  - 808
EP  - 814
VL  - 15
IS  - 9
PB  - Elsevier
DO  - 10.1016/j.crci.2012.07.002
LA  - en
ID  - CRCHIM_2012__15_9_808_0
ER  -

%0 Journal Article
%A Guozheng Zhao
%A Ming Lu
%T A theoretical investigation on the densities and detonation properties of polynitrotetraazabenzimidazoles
%J Comptes Rendus. Chimie
%D 2012
%P 808-814
%V 15
%N 9
%I Elsevier
%R 10.1016/j.crci.2012.07.002
%G en
%F CRCHIM_2012__15_9_808_0

Guozheng Zhao; Ming Lu. A theoretical investigation on the densities and detonation properties of polynitrotetraazabenzimidazoles. Comptes Rendus. Chimie, Volume 15 (2012) no. 9, pp. 808-814. doi : 10.1016/j.crci.2012.07.002. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2012.07.002/

Version originale du texte intégral

1 Introduction

High material properties have been the prime importance in the development of new energetic materials for several applications, including advanced conventional weapons, rocket propellants, antiterroist work, demilitarization, as well as industrial applications [1–4]. The need for more energetic compounds with better stability and lower sensitivity is one of the main goals of energetic materials research [5–9]. The search for new potential high energy density materials (HEDMs) is on going [10–13]. Good thermal stability and low impact and shock sensitivities are of equal importance to detonation performance [14–16]. Unfortunately, high performance and low sensitivity seem to be mutually exclusive and very energetic compounds tend not to be stable, whereas stable materials are not energetic enough to replace commonly used compounds. Therefore, the foremost objective is to find the molecule with better detonation performance and thermal stability.

Nitramine compounds, as an important class of organic explosives, have received much recent attention in an energetic materials role due to a very advantageous combination of density, heat of formation and oxygen balance. These properties reveal a high performance of these energetic materials [17,18]. The two most prominent members of this class are RDX [19–22] and HMX [23–26]. CL-20 [2,4,6,8,10,12-hexanitrohexaazaisowurtzitane (HNIW)] is another new nitramine explosive, which has six N–NO₂ groups in its polycyclic structure, resulting in an increase in both density and detonation properties [27–31]. CL-20 is reported as an attractive high thermally stable explosive with decomposition temperature 228 °C. It can offer a higher velocity of detonation (9.38 km/s) and heat of formation (410 kJ/mol) [32].

The high energy of nitramine explosives is combined with the insensitive property of explosives containing benzene, and the concept of new nitramine explosives containing benzene is proposed, into which nitramine group with N–N bonds are introduced as much as possible. This study was motivated by, and based on, the concept of new nitramine explosives containing benzene. Reacting with formaldehyde, benzene-1,2,4,5-tetraamine yields a precursor with two imidazole rings, which provides more N–H and C–H sites for introducing nitro substituents, and thus generates a series of polynitrotetraazabenzimidazoles. The energy of the polynitrotetraazabenzimidazoles is derived from the combustion of the carbon backbone, the ring strain and the large number of inherently energetic C–N, C = N and N–N bonds. This shows that polynitrotetraazabenzimidazoles could ideally store a large amount of energy. On the other hand, the nitrogen content typically leads to high densities and thereby to good performance. Molecular structures with nitro group at varying positions in the basic skeleton considered are shown in Fig. 1.

Fig. 1
Structures and atom numbering of polynitrotetraazabenzimidazoles.

Theoretical studies make it not only possible to screen candidate compounds, but to provide comprehension of the relationship between molecular structure and property [33–36]. To date, information on the relationships between structure and property of polynitrotetraazabenzimidazoles was very sparse, and much few systematic survey were conducted to cover these compounds. In the present study, the molecular geometries and electronic structure were obtained with the density functional theory (DFT) method. Based on optimized geometries, molecular volume (V) and theoretical density (ρ) were calculated using a Monte–Carlo method. The most important detonation properties, such as detonation velocity (D) and detonation pressure (P) were estimated by using the K–J equation. Through calculations of bond dissociation energies (BDE), thermal stability was studied. These results provide theoretical support for molecular design of novel high energetic density compounds.

2 Computational methods

Computations were performed with Gaussian 03 package at B3LYP [37] method with 6-31 + G(d) basis set [38]. The geometric parameters were allowed to be optimized, and no constraints were imposed on molecular structure during the optimization process. Vibrational frequencies were calculated for the optimized structures to enable us to characterize the nature of stationary points, zero-point energy (ZPE) and thermal correction (H_T). All of optimized structures were characterized to be true local energy minima on potential energy surfaces without imaginary frequencies.

Detonation velocity and detonation pressure are the most important parameters to evaluate detonation characteristics of energetic materials. For the explosives with CHNO elements, the Kamlet and Jacob empirical equations were used to determine these parameters [39].

P = 1.558 N M^{1 / 2} Q^{1 / 2} ρ^{2}

(1)

D = 1.01 {(N M^{1 / 2} Q^{1 / 2})}^{1 / 2} (1 + 1.30 ρ)

(2)

where P is detonation pressure in GPa, D is detonation velocity in km/s, N is the number moles of gaseous detonation products per gram of explosive, M is the average molecular weight of the gaseous products, Q is the energy of explosion in J/g of explosive and ρ is the crystal density in g/cm. N, M and Q are decided according to the largest exothermic principle [40], i.e., for the explosives with CHNO elements, all the N atom converts into N₂, the O atom forms H₂O with H atom first and the remainder forms CO₂ with C atom. The remainder of C atom will exist in solid state if O atom does not satisfy full oxidation of C atom. The remainder of O atom will exist in O₂ if O atom is superfluous.

As for the known explosives, the Q and ρ can be measured experimentally; thus, their D and P can be calculated according to Eqs. (1) and (2). However, for those unsynthesized explosives and hypothetical compounds, their Q and ρ cannot be evaluated from experimental measures. The loading density of the explosives ρ can be replaced by the crystal theoretical density (ρ_cry), while the chemical energy of the detonation reaction Q can be calculated as the difference between the heats of formation (HOFs) of products and those of reactants (Q_cal). However, from K-J equations, it is found that Q has much less effect than ρ on D and P. Therefore, Q and HOF estimated by using semiempirical molecular orbital (MO) method (PM3) are precise enough to substitute the experimental data, which have been proven in previous studies [41–43]. A statistics average method was worked out to predict crystalline densities of energetic materials containing C, H, N and O elements. This method is found to be efficient and convenient [44–46]. The densities of nitramine compounds need the datum of molecular volumes. The molecular volume V was defined as inside a contour of 0.001 electrons/bohr³ density that was evaluated using Monte–Carlo integration. The molecular volumes obtained thus were random digits with normal distribution. We therefore performed 100 single-point calculations at B3LYP/6-31 + G(d) level from optimized structure to get an average volume. The theoretical molecular density ρ_theor (ρ_theor = M/V, where M is the molecular weight) is very close to the experimental crystal density ρ_cry.

To measure the strength of bonds and relative stabilities of polynitrotetraazabenzimidazoles, the bond dissociation energies of various bonds in molecules are calculated. BDE is the required energy in homolysis of a bond and is commonly denoted by difference between total energies of product and reactant after zero-point energy correction. The expressions for the homolysis of A—B bond (3) and for calculating its BDE (4) are shown as follows [47]:

A — B {(g)}^{} \to A (g) + B (g)

(3)

B D E {(A — B)}_{Z P E} = E {(A)}_{Z P E} + E {(B)}_{Z P E} - E {(A — B)}_{Z P E}

(4)

where A—B stands for neutral molecules and A• and B• for the corresponding product radicals after bond dissociation; BDE(A—B) is the BDE of bond A—B; E(A—B)_ZPE, E(A•)_ZPE and E(B•)_ZPE are zero-point energy corrected total energies of parent compound and corresponding radicals, respectively.

The oxygen balance (OB₁₀₀) is used in all predictive properties related to Q, D and P, detonation products and sensitivity [40]. It also represents the lack or excess of O₂ needed to produce the most stable products N₂, H₂O, CO and CO₂ in explosive compounds. D is a linear function of OB₁₀₀ and it is improved by taking into the consideration of the number of NO₂ groups. The ideal oxygen balance required for energetic compounds is zero and said to have negative oxygen balance if energetic compounds have less amount of oxygen than required for the complete oxidation.

3 Results and discussion

3.1 Density

In the present study, single–point molecular volume calculations at B3LYP/6-31 + G(d) were performed based on geometry optimized structures. The densities were calculated and listed in Table 2. All these data in Table 2 provide some clues about the explosive characters of these molecules. The largest value and the smallest one are 1.968 g/cm³ and 1.589 g/cm³, respectively. From A to F, it is clear that an increase in density is observed with an increase in the number of nitro groups. The same results were obtained for molecules G, H, I, J, K and L. Fig. 2 describes the linear relationship between V, ρ and the number of nitro groups (n). The correlation equations are as following:

A–F	V = 110.49 + 17.99n	R = 0.9996
	ρ = 1.54 + 0.07n	R = 0.9944
G–L	V = 109.03 + 18.48n	R = 0.9995
	ρ = 1.55 + 0.07n	R = 0.9807

Molecule	OB₁₀₀	V(cm³/mol)	ρ(g/cm³)	Q (J/g)	D(km/s)	P(Gpa)
A	−1.30	127.46	1.593	997.17	5.88	14.23
B	−0.90	147.08	1.686	1263.28	6.84	19.91
C	−0.63	164.35	1.783	1374.45	7.57	25.26
D	−0.43	184.07	1.836	1458.91	8.18	29.17
E	−0.27	200.28	1.912	1515.34	8.54	33.54
F	−0.15	217.53	1.968	1565.30	8.92	37.17

G	−1.30	127.78	1.589	996.04	5.87	14.14
H	−0.90	146.53	1.693	1263.98	6.86	20.07
I	−0.63	163.56	1.790	1373.84	7.59	25.45
J	−0.43	181.74	1.860	1457.14	8.13	29.91
K	−0.27	203.09	1.886	1505.46	8.44	32.51
L	−0.15	219.58	1.949	1557.75	8.85	36.38

Fig. 2
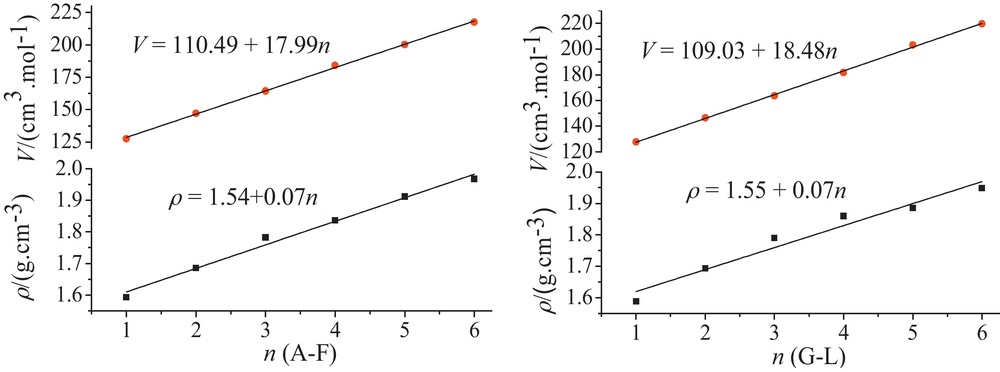
Correlations between V, ρ and the number of nitro group (n) for polynitrotetraazabenzimidazoles.

Introduction of a nitro group increases the density of molecules and therefore has a significant contribution to detonation velocity (D), and detonation pressure (P). Molecules E, F and L have a density above 1.90 g/cm³, and will be novel potential candidates for HEDC when it is successfully synthesized. Density (ρ) is the essential factor in determining detonation properties of energetic compounds. According to Kamlet and Jacob semi-empirical equations, for most of energetic compounds the D increases with the increasing of ρ. Also, P varies with the square of ρ, where ρ is greater than one.

3.2 Heats of formation and oxygen balance

Heat of formation reflects the energy content of a compound. High positive HOF is usually required for an effective energetic material. The zero-point energies (ZPE), thermal correction to enthalpy (H_T) and electronic energies calculated at B3LYP/6-31 + G(d) level for polynitrotetraazabenzimidazoles are listed in Table 1. It is evident from the data listed in Table 1 that all HOFs of nitramine compounds are quite large positive values, which shows that the introduction of nitro groups is the main energy origin of this series. It is also clear from the Table 1 that with the number of nitro groups (n) increasing, the HOFs of molecules increase, which may be attributed to the repulsion of nitro groups. For molecules A and B, G and H, each nitro group addition will increase HOF with 70.36 and 72.05 kJ/mol respectively. But for molecules C and D, I and J, each nitro group addition will increase HOF with 7.25 and 5.50 kJ/mol. It indicates that the value of HOF relates to the nature of C–NO₂ or N–NO₂. The space orientations of nitro groups also affect the HOFs of nitramine compounds. For the isomers with the same number of –NO₂ group (molecules F and L), the values of HOF are slightly different, indicating that HOF is a little influenced by the position of –NO₂ group. On the whole, according to n and the relative position of the nitro groups, the relative HOFs order of molecules can be distinguished, which is useful for evaluating the relative thermal stability of nitramine compounds.

Compound	E₀ (a.u.)	ZPE (a.u.)	H_T (a.u.)	HOF (kJ/mol)
A	−731.980246	0.137624	0.011365	363.29
B	−936.453445	0.139276	0.013921	433.65
C	−1140.933134	0.140917	0.016716	436.83
D	−1345.411235	0.142486	0.019566	444.08
E	−1549.889993	0.144088	0.022520	438.24
F	−1754.368230	0.145414	0.025516	442.04

G	−731.980186	0.137612	0.011356	362.33
H	−936.452996	0.139299	0.013912	434.38
I	−1140.932688	0.140928	0.016703	436.08
J	−1345.410921	0.142461	0.019560	441.58
K	−1549.885129	0.143516	0.022403	422.40
L	−1754.368128	0.145131	0.025549	428.53

Oxygen balance is another one of the most important criterion for selecting potential HEDC. It is found from Table 2 that in general, the higher oxygen balance is, the larger D and P values are, and the better performance of nitramine compounds is. The –NO₂ group is a good substituent for improving oxygen balance in designing potential HEDC.

3.3 Detonation properties

The detonation velocity (D) and detonation pressure (P) of molecules are computed by Kamlet–Jacobs empirical equations on the basis of their theoretical densities (ρ) and calculated gas phase heats of formation, which are the important parameters to evaluate performance of explosion of energetic materials. Table 2 shows the predicted detonation properties of polynitrotetraazabenzimidazoles. Because detonation pressures and detonation velocities are calculated by HOF of gas state, not of crystal, the calculated detonation properties of the nitramine compounds have some deviation. Although the error or limitation of calculation method leads to the predicted D and P somewhat deviate those from experiments, these results are still reliable and meaningful. It can be found from Table 2 that all polynitrotetraazabenzimidazoles have good detonation properties (Q = 996.04–1565.30 J/g, D = 5.87–8.92 km/s, P = 14.14–37.17 GPa). Meanwhile, with the number of nitro groups increasing from one to six, Q, D and P of the corresponding compounds increase. Molecule F is calculated to have the highest D and P values among polynitrotetraazabenzimidazoles. In terms of the predicted detonation parameters, the most powerful explosives among polynitrotetraazabenzimidazoles are molecules F and L.

As for the isomers with the same OB₁₀₀, no conspicuous discrepancy of their respective Q, D and P is found. As a whole, Q, D and P increase with the increasing number of –NO₂ groups. Fig. 3 presents the relationships between D, P and the number of nitro group (n). This may show good group additivity on detonation properties and support the claim that introducing more nitro substituents into a molecule usually helps to increase its detonation performance [40]. The correlation equations are as following:

A-F	D = 5.56 + 0.60n	R = 0.9817
	P = 10.60 + 4.56n	R = 0.9964
G-L	D = 5.61 + 0.58n	R = 0.9777
	P = 11.11 + 4.37n	R = 0.9909

Fig. 3
Correlations between D, P and the number of nitro group (n) for polynitrotetraazabenzimidazoles.

Comparing with famous nitramine explosive HMX (1,3,5-trinitro-1,3,5-triazinane) (ρ = 1.92 g/cm, D = 8.96 km/s, P = 35.96 GPa) [48], they have better detonation performance, which indicates that they are potential energetic compounds. Calculation results of detonation velocity and detonation pressure for polynitrotetraazabenzimidazoles indicate that molecules F and L outperform HMX. Therefore, for the design of a molecule, we could adjust detonation properties by changing the substituted group. Then the above prediction indicates that polynitrotetraazabenzimidazoles are appearing to be promising candidates comparable to the nitramine explosive HMX.

3.4 Thermal stability

The relationship between the impact sensitivity and electronic structures of polynitrotetraazabenzimidazoles can be established by the charge analysis of the nitro group [49]. Nitro compounds are very strong electron acceptors and have a strong ability to attract electrons. Such an ability can be represented by the net charges of the nitro group. The higher the negative charge on the nitro group, the lower the electron attraction ability and therefore the more stable the nitro compound. In the present study, the charge on the nitro group ( $- Q_{{NO}_{2}}$ ) is considered for its correlation to impact sensitivity:

Q_{N O_{2}} = Q_{N} + Q_{O_{1}} + Q_{O_{2}}

The charge on the nitro group ( $- Q_{{NO}_{2}}$ ) is calculated by the sum of atomic charges on the nitrogen (Q_N) and oxygen ( $Q_{O_{1}}$ and $Q_{O_{2}}$ ) atoms in the nitro group. The higher the $- Q_{{NO}_{2}}$ , the larger the impact insensitivity, and hence, $- Q_{{NO}_{2}}$ can be regarded as the criterion for estimating the impact sensitivities. Based on the highest $- Q_{{NO}_{2}}$ value, the probable decreasing order is as follows: molecule F (0.406) > HMX (0.400) > molecule L (0.131). This shows that molecule L is more insensitive than famous explosive HMX. Molecule F performs similarly to HMX.

Studies of bond dissociation energies (BDE) provide useful information for understanding stability of polynitrotetraazabenzimidazoles. The stability of compounds is affected by bond dissociation energies, so we select the weakest bonds (N–N bonds that are out of ring) as the breaking bond based on the bond overlap populations to calculate BDE at B3LYP/6-31 + G(d) level. The values of bond dissociation energies are listed in Table 3. The calculated BDE_ZPE values indicate relative stability of energetic materials. Variations of BDE_ZPE for N–NO₂ are in range of 62.13–117.92 kJ/mol. The initial step should be via N–NO₂ cleavage in thermal decomposition. The BDE_ZPE value of molecule B (117.92 kJ/mol) is the largest while the one of the molecule K is the smallest (62.13 kJ/mol) which is less stable than the former. When –NO₂ group is attached to the ring, BDE_ZPE value decreases for molecules B, D and F. The same results were obtained for molecules H, J and L. This shows that incorporating nitro group brings decreased stability. By analyzing structures of these compounds, it is easy to find that nitramine compounds have symmetric structures. Therefore, molecules B, D and F have higher BDE_ZPE than molecules A, C and E, respectively. This indicates that symmetric structure is very useful for improving thermal stability. The symmetry can delocalize π electron cloud density of system, but the five-membered rings of these compounds have larger tension, which make BDE_ZPE of nitramine compounds decrease. Repulsion is an important role in stability of nitramine compounds. Take molecule L as an example, the repulsion between neighboring nitro group rotate oxygen atoms from molecular plane and make value of BDE_ZPE decrease. This shows that structures of these compounds have a great influence on their thermal stability. The above investigations provide important theoretic information for molecular design of novel high energetic density polynitrotetraazabenzimidazoles.

Compound	A	B	C	D	E	F
Bond	N8–NO₂	N9–NO₂	N8–NO₂	N9–NO₂	N8–NO₂	N8–NO₂
BDE_ZPE (kJ·mol⁻¹)	107.37	117.92	73.71	76.37	63.71	64.01
Compound	G	H	I	J	K	L
Bond	N8–NO₂	N10–NO₂	N8–NO₂	N10–NO₂	N10–NO₂	N8–NO₂
BDE_ZPE (kJ·mol⁻¹)	107.34	116.71	72.52	75.64	62.13	64.47

4 Conclusion

The full geometrical optimizations of polynitrotetraazabenzimidazoles were performed using density functional theory at B3LYP/6-31 + G(d) level, without any symmetry restriction. The detailed structure–property studies were performed on these compounds to achieve energetic performance for the first time. Stability correlations are established for these molecules by analyzing bond dissociation energies. For the polynitrotetraazabenzimidazoles, with the increase in the number of nitro groups, volume, density, detonation velocity and detonation pressure linearly increase. Calculation results of detonation velocity and detonation pressure for nitramine compounds indicate that molecules F and L outperform HMX, which essentially satisfies the quantitative criteria for the energy as HEDCs. These results provide theoretical support for molecular design of novel high energetic density compounds and experimental synthesis.

Acknowledgements

This work was supported by the NSAF Foundation of National Natural Science Foundation of China and China Academy of Engineering Physics (Grant 11076017) and Nanjing University of Science and Technology Research Funding (NO. 2011YBXM03).

Bibliographie

[1] M. Rahm; S.V. Dvinskikh; I. Furo; T. Brinck Angew. Chem. Int. Ed, 50 (2011), p. 1145

[2] M.B. Talawar; R. Sivabalan; T. Mukundan; H. Muthurajan; A.K. Sikder; B.R. Gandhe; A.S. Rao J. Hazard. Mater., 161 (2009), p. 589

[3] M.M. Li; F.S. Li; R.Q. Shen; X.D. Guo J. Hazard. Mater., 186 (2011), p. 2031

[4] M. Smeu; F. Zahid; W. Ji; H. Guo; M. Jaidann; H. Abou-Rachid J. Phys. Chem. C, 115 (2011), p. 10985

[5] X.H. Li; R.Z. Zhang; X.Z. Zhang J. Hazard. Mater., 183 (2010), p. 622

[6] M.J. O’Connor; R.B. Yelle; T.M. Linz; M.M. Haley C. R. Chimie, 12 (2009), p. 385

[7] J.S. Li Propelllants. Explos. Pyrotech, 35 (2010), p. 182

[8] D.M. Badgujar; M.B. Talawar; S.N. Asthana; P.P. Mahulikar J. Hazard. Mater., 289 (2008), p. 289

[9] M. Rahm; T. Brinck Chem. Eur. J., 16 (2010), p. 6590

[10] T.L. Jackson; D.E. Hooks; J. Buckmaster Propellants. Explos. Pyrotech, 36 (2011), p. 252

[11] A. Bhattacharya; E.R. Bernstein J. Phys. Chem. A, 115 (2011), p. 4135

[12] A. Maiti; R.H. Gee Propelllants. Explos. Pyrotech., 36 (2011), p. 125

[13] X.L. Song; J.C. Li; H. Hou; B.S. Wang J. Comb. Chem., 30 (2009), p. 1816

[14] J.Y. Zhang; H.C. Du; F. Wang; X.D. Gong; Y.S. Huang J. Phys. Chem. A, 115 (2011), p. 6617

[15] T.M. Klapotke; D.G. Piercey; J. Stierstorfee Propelllants. Explos. Pyrotech., 36 (2011), p. 160

[16] G.X. Wang; X.D. Gong; Y. Liu; H.C. Du; X.J. Xu; H.M. Xiao J. Hazard. Mater., 177 (2010), p. 703

[17] M.H. Keshavarz J. Hazard. Mater., 190 (2011), p. 330

[18] M.H. Keshavarz; H. Sadeghi J. Hazard. Mater., 171 (2009), p. 140

[19] L.B. Munday; P.W. Chung; B.M. Rice; S.D. Solares J. Phys. Chem. B, 115 (2011), p. 4378

[20] H. Qiu; V. Stepanov; S.A.R. Di; T. Chou; W.Y. Lee J. Hazard. Mater., 185 (2011), p. 489

[21] M.D. Joseph; S.K. Jangid; R.S. Satpute; B.G. Polke; T. Nath; S.N. Asthana; A.S. Rao Propelllants. Explos. Pyrotech, 34 (2009), p. 326

[22] R. Podeszwa; B.M. Rice; K. Szalewicz Phys. Chem. Chem. Phys., 11 (2009), p. 5512

[23] T.T. Zhou; F.L. Huang J. Phys. Chem. B, 115 (2011), p. 278

[24] C.T. Konek; B.P. Mason; J.P. Hooper; C.A. Stoltz Chem. Phys. Lett., 489 (2010), p. 48

[25] L. Qiu; W.H. Zhu; J.J. Xiao; H.M. Xiao J. Phys. Chem. B, 112 (2008), p. 3882

[26] E.A. Glascoe; J.M. Zaug; A.K. Burnham J. Phys. Chem. A, 113 (2009), p. 13548

[27] P. Maksimowski; A. Fabijanska; J. Adamiak Propelllants. Explos. Pyrotech., 35 (2010), p. 353

[28] Y. Bayat; S.S. Hajimirsadeghi; S.M. Pourmortazavi Org. Process Res. Dev., 15 (2011), p. 810

[29] C.P. Lin; C.P. Chang; Y.C. Chou; Y.C. Chu; C.M. Shu J. Hazard. Mater., 176 (2010), p. 549

[30] D.C. Sorescu; B.M. Rice J. Phys. Chem. C, 114 (2010), p. 6734

[31] J.J. Haycraft J. Chem. Phys., 131 (2009), p. 214501

[32] A.K. Sikder; N. Sikder J. Hazard. Mater., 112 (2004), p. 1

[33] X.W. Zhang; W.H. Zhu; H.M. Xiao J. Phys. Chem. A, 114 (2010), p. 603

[34] L. Turker; T. Atalar; S. Gumus; Y. Camur J. Hazard. Mater., 167 (2009), p. 440

[35] G.H. Zhang; Y.F. Zhao; F.Y. Hao; P.X. Zhang; X.D. Song Int. J. Quantum. Chem., 109 (2009), p. 226

[36] X.W. Fan; X.H. Ju; H.M. Xiao J. Hazard. Mater., 156 (2008), p. 342

[37] C. Lee; W. Yang; R.G. Parr Phys. Rev. B, 37 (1988), p. 785

[38] M.J. Frisch; G.W. Trucks; H.B. Schlegel; G.E. Scuseria; M.A. Robb; J.R. Cheeseman; J.A. Montgomery; J.T. Vreven; K.N. Kudin; J.C. Burant; J.M. Millam; S.S. Iyengar; J. Tomasi; V. Barone; B. Mennucci; M. Cossi; G. Scalmani; N. Rega; G.A. Petersson; H. Nakatsuji; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; M. Klene; X. Li; J.E. Knox; H.P. Hratchian; J.B. Cross; C. Adamo; J. Jaramillo; R. Gomperts; R.E. Stratmann; O. Yazyev; A.J. Austin; R. Cammi; C. Pomelli; J.W. Ochterski; P.Y. Ayala; K. Morokuma; G.A. Voth; P. Salvador; J.J. Dannenberg; V.G. Zakrzewski; S. Dapprich; A.D. Daniels; M.C. Strain; O. Farkas; D.K. Malick; A.D. Rabuck; K. Raghavachari; J.B. Foresman; J.V. Ortiz; Q. Cui; A.G. Baboul; S. Clifford; J. Cioslowski; B.B. Stefanov; G. Liu; A. Liashenko; P. Piskorz; I. Komaromi; R.L. Martin; D.J. Fox; T. Keith; M.A. Al-Laham; C.Y. Peng; A. Nanayakkara; M. Challacombe; P.M.W. Gill; B. Johnson; W. Chen; M.W. Wong; C. Gonzalez; J.A. Pople Gaussian 03, Gaussian Inc., Pittsburgh PA, 2003

[39] M.J. Kamlet; S.J. Jacobs J. Chem. Phys., 48 (1968), p. 23

[40] X.H. Zhang; Z.H. Yun Explosive Chemistry, National Defence Industry Press, Beijing, 1989

[41] H.M. Xiao; J.F. Fan; X.D. Gong Propelllants. Explos. Pyrotech., 22 (1997), p. 360

[42] X. Ma; H.H. Schobert J. Phys. Chem. A, 104 (2000), p. 1064

[43] Y. Zhou; X.P. Long; Y.J. Shu J. Mol. Model, 16 (2010), p. 1021

[44] X.J. Xu; H.M. Xiao; X.D. Gong; X.H. Ju; Z.X. Chen J. Phys. Chem. A, 109 (2005), p. 11268

[45] X.J. Xu; H.M. Xiao; X.H. Ju; X.D. Gong; W.H. Zhu J. Phys. Chem. A, 110 (2006), p. 5929

[46] L. Qiu; H.M. Xiao; X.D. Gong; X.H. Ju; W.H. Zhu J. Phys. Chem. A, 110 (2006), p. 3797

[47] D.R. Lide CRC Handbook of Chemistry and Physics, CRC Press LLC, Boca Raton, Florida, 2002

[48] J.P. Agrawal; R.D. Hodgson Organic Chemistry of Explosives, John Wiley & Sons, 2007

[49] C.Y. Zhang J. Hazard. Mater., 161 (2009), p. 21

Commentaires - Politique

Ces articles pourraient vous intéresser

Computational studies on thermodynamic properties, detonation properties and bond dissociation energies for polydifluoroaminopurine compounds

Ting Yan; Guangdong Sun; Weijie Chi; ...

C. R. Chim (2013)

Molecular design of prismane-based potential energetic materials with high detonation performance and low impact sensitivity

Wei-Jie Chi; Ze-Sheng Li

C. R. Chim (2015)

Experimental study of the detonation of technical grade ammonium nitrate

Henri-Noël Presles; Pierre Vidal; Boris Khasainov

C. R. Méca (2009)