1 Introduction
Naturally occurring cyclodextrins (CDs) are α-1, 4-linked cyclic oligomers of d-glucopyranose which possess the remarkable property of forming inclusion complexes with a variety of small molecules of appropriate size through the influence of non-covalent interactions. The resultant inclusion complexes can induce modification of the physicochemical properties of the ‘guest’ molecules, particularly in terms of water solubility and solution stability [1–3]. Therefore, it is important to clarify the structures of the inclusion complexes from a viewpoint of enzyme-substrates within the hydrophobic cavities of CDs [4]. The most common CDs are α, β and γ-CDs, which consist of 6–8 glucopyranose units, respectively. Nevertheless, β-cyclodextrin (β-CD) (Fig. 1(a)) is by far the most widely used compound owing to the optimal size of its internal cavity (8 Å), the most accessibility, and the lowest price for the encapsulation of molecules [5].

Geometrical structures of β-CD (a) and paenol (b) optimized using the PM3 and B3LYP/6-31G* methods, respectively.
Paeonol (2′ hydroxy-4′ methoxyacetophenone, PAE), as shown on Fig. 1(b), is the main active compound of the Paeonia lactiflora Pallas, a traditional Chinese herb used commonly in Asia and Europe. PAE has antioxidant and anti-inflammatory activity as well as the ability to suppress tumor formation [6]. PAE can also inhibit melanin synthesis and down-regulate melanin transfer [7], whose effects can be exploited in cosmetic applications. Despite its many features that make it appropriate for potential medical uses, PAE is hydrophobic and has a low aqueous solubility, possibly limiting its range of applications. Tsai et al. [8] have synthesized and characterized the inclusion complex of PAE and β-CD in which PAE penetrated β-CD under the influence of the intermolecular hydrogen bond between PAE and β-CD. In continuation of the work of Tsai et al., the current study examines the detailed inclusion complexation of PAE and β-CD by means of PM3 semi-empirical method, density functional theory (DFT), Hartree–Fock (HF) and hybrid method (ONIOM2).
At present, there are a great number of theoretical methods used in molecular modeling for supermolecular systems such as the complexes of CDs or their derivatives with guest molecules. Among these theoretical methods, molecular mechanics (MM) [9,10], molecular dynamics (MD) [11–14], semi-empirical methods (such as AM1, PM3, among others) [15–21] and a hybrid Own N-layer Integrated Orbital Molecular Mechanics (our ONIOM) method [22–31] have been widely used in relatively larger size and numerous atoms of CDs and their derivatives. Among these frequently used methods, a hybrid ONIOM method, developed by Morokuma et al. [22–24], has captured many researchers’ interest because it can treat different parts of a system simultaneously with good accuracy and lower computational cost compared to ab initio and DFT, and it has been proved to be effective and reliable for investigating inclusion interaction of CDs or their derivatives with guests [28–31].
In this article, we first describe the formation of the Host-guest complexes between β-CD and PAE, using PM3 semi-empirical method to localize the minimum energy structures, which are used as starting structures for subsequent optimizations. After that, the structures are subjected to higher level calculations, such HF, DFT and ONIOM2 methods to approach the ideal geometry and provide further insight of the complexation process of PAE with β-CD. Furthermore, the natural bonding orbital (NBO) population analysis is employed to quantify the donor–acceptor interactions between host and guest.
2 Computational methodology
All theoretical calculations were performed using the GAUSSIAN 03 software package [32].
The initial structures of β-CD and PAE were constructed with the help of CS Chem3D Ultra (Version 10, Cambridge Soft. com) from the crystal structure and were fully optimized by PM3 and B3LYP/6-31G*, respectively, without any symmetry constraint. The solvent effects on the conformational equilibrium have been investigated using the PCM model for water (ɛ = 78.39) as a solvent with the PM3 method [33,34].
The inclusion model can be seen on Fig. 2. The glycosidic oxygen atoms of β-CD are placed in XY plane and their center is defined as the center of the whole system. PAE approaches and passes through the cavity of β-CD from +Z to −Z direction, and the distance between the labeled carbon atom C6 and β-CD ranges from −9 to +9 Å. The guest is initially located at a Z coordinate of 9 Å and is moved through the host cavity along the Z axis to −9 Å with a step of 1 Å. For each step, the geometry of the complex is fully optimized by PM3 without imposing any symmetrical restrictions. In order to find an even more stable structure of the complex, each guest molecule is calculated for all of the structures obtained by scanning θ, clock wisely circling around Z axis, at 20° intervals from 0° to 360°. Complexation energy upon complexes between PAE and the β-CD is calculated for the minimum energy structure according to Eq. (1) [35]:
| (1) |
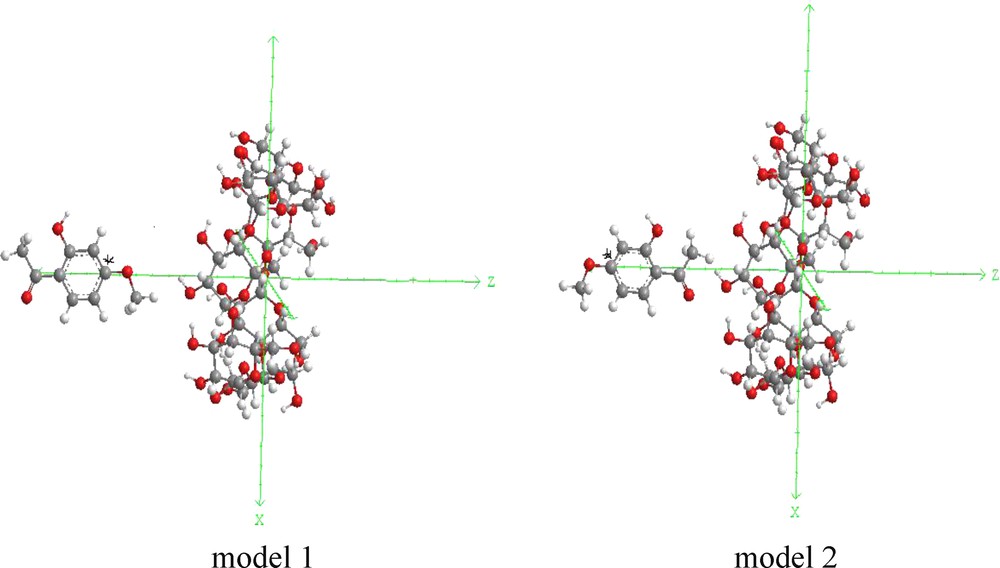
Coordinate systems used to define the process of complexation for: (a) model 1 and (b) model 2.
The deformation energy for each component (DEF) host and guest throughout the formation of the complex was defined as the difference in the energy of the totally optimized component compared to its energy in the complex (Eq. (2)) [36]:
| (2) |
Because of the computations at ab initio (HF) or DFT levels are prohibitively expensive in treating such large molecular systems; we just precede single point energy calculations to the PM3 optimized geometries using both HF method and DFT [37,38]. A medium basis set corresponding to 6-31G* was chosen.
To improve the precision of the theoretical results, the two most stable structures optimized by PM3 method for PAE/β-CD complexes were further optimized using a two-layered hybrid ONIOM method. The high-level layer, PAE, and low-level layer, β-CD, were treated by B3LYP/6-31G*, HF/6-31G* level of theory and PM3 method, respectively. The ONIOM energy is described as (Eq. (3)) [39]:
| (3) |
Finally, charge transfers between host and guest molecules have been studied using natural bond orbital NBO population analyses. Moreover, in the NBO approach [40], a stabilization energy E(2) related to the delocalization trend of electrons from donor to acceptor orbital is calculated via perturbation theory. A large stabilization energy E(2) between a lone pair LP(Y) of an atom Y, and an anti-bonding σ* (X-H) orbital, is generally indicative of an X-H···Y hydrogen bond.
3 Results and discussion
3.1 The passing process
All the optimized structures obtained by scanning the θ angle, from 0 to 360° at 20° intervals, and the coordinate Z, from −9 to +9 Å at 1 Å intervals, were used to find the most favorable approach of the PAE/β-CD. Two ΔE minima are found at Z = 0 Å, θ = 80° and Z = −1 Å, θ = 300° for model 1 (PAE entering into the cavity of β-CD from its wide side by OCH3 group) and model 2 (PAE entering into the cavity of β-CD from its wide side by COCH3 group).
The energy changes of PAE/β-CD model 1 and PAE/β- CD model 2 in the passing process are shown on Fig. 3a, b. As shown in Fig. 3a for the model 1, the energy decreases by −7.24 kcal/mol from the starting point A (ZA = −9 Å. ZA is the Z coordinate of point A) to point B (ZB = −6 Å; ΔE = −12.77 kcal/mol) and C (ZC = −4 Å; ΔE = −11.25 kcal/mol). Then, the energy increases sharply, and rapidly drops down to the point D (ZD = 0 Å; ΔE = −15.70 kcal/mol).
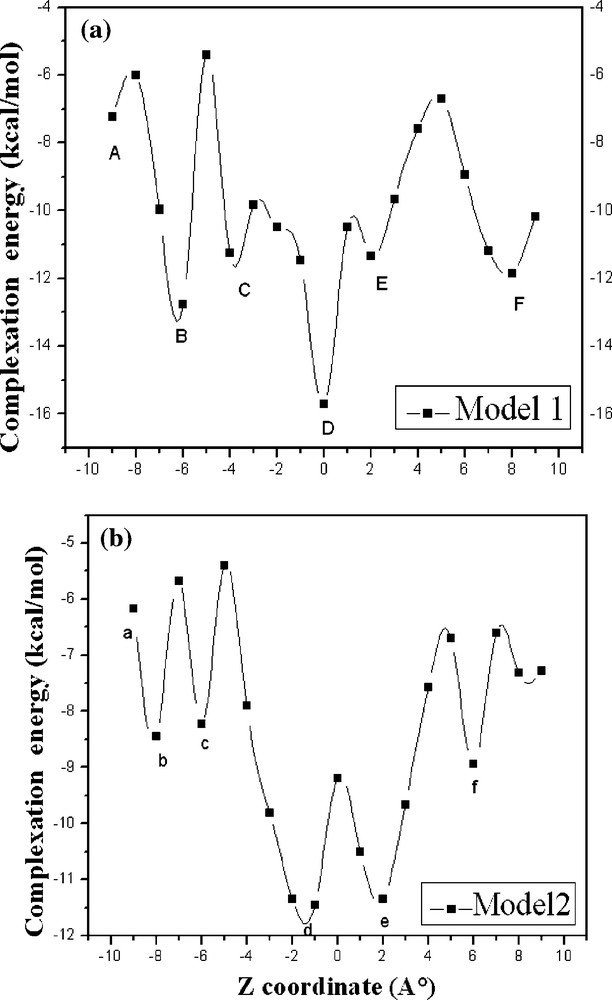
Stability energies of the inclusion complexation of PAE into β-CD at different positions (Z) and models: (a) model 1; (b) model 2. Points A, B, C, D, E, F represent ZA = −9 Å, ZB = −6 Å, ZC = −4 Å, ZD = 0 Å, ZE = 2 Å, ZF = 8 A, respectively. Points a, b, c, d, e, f represent Za = −9 Å, Zb = −8 Å, Zc = −6 Å, Zd = −1 Å, Ze = 2 Å, Zf = 6 Å, respectively.
Finally, the energy increases slowly, and drops down to the point F (ZF = 8 Å; ΔE = −11.86 kcal/mol). In the model 2 (Fig. 3b), the energy curve is somewhat similar to the process entering from the model 1. Points a, b, c, d, e, f appear at (Za = −9 Å; ΔE = −12.77 kcal/mol), (ZB = −8 Å; ΔE = −8.45 kcal/mol), (Zc = −6 Å; ΔE = −8.22 kcal/mol), (Zd = −1 Å; ΔE = −11.46 kcal/mol), (Ze = 2 Å; ΔE = −11.34 kcal/mol), (Zf = 6 Å; ΔE = −8.94 kcal/mol), respectively. Obviously, points D and d are the global minimum of the whole curve; the curves indicate that PAE and β-CD could form the most stable complexes. In these two positions (ZD = −1 Å and Zd = 0 Å), the methoxyphenyl of PAE just full access to the central of β-CD cavity.
3.2 Complexation energy of the β-CD/PAE complex
The energies, HOMO, LUMO, thermodynamic parameters (enthalpy, entropy, and free energy) and dipole moment (D) of the guest, host and inclusion complexes for the most stable structures are summarized in Table 1. PM3 calculated results in vacuum reveal that the energy of the complex is consistently lower than the energy sum of isolated host and guest and the complexation energy of model 1 is 4.51 kcal/mol lower than that of model 2, showing that the model 1 is more stable than the model 2. When the solvation effect is taken into consideration, the energy difference becomes 2.7 kcal/mol from the PM3 calculation in water. Although, the difference energy in solution becomes a little smaller compared with the calculated results in vacuum, it further confirms that the model 1 is much stabler than the model 2.
Thermodynamic parameters of the models 1 and 2 calculated by PM3 method and the single point energies by B3LYP/6-31G* and HF/6.31G*.
| PAE | β-CD | Model 1 | Model 2 | |
| PM3 | In vacuo | |||
| E (kcal/mol) | −98.26 | −1457.10 | −1571.05 | −1566.81 |
| ΔE (kcal/mol) | −15.96 | −11.45 | ||
| DEF (PAE) | 2.16 | 2.10 | ||
| DEF (β-CD) | 1.66 | 0.79 | ||
| EHOMO (eV) | −9.18 | −10.56 | −9.61 | −9.20 |
| ELUMO (eV) | −0.89 | 1.09 | −1.10 | −1.19 |
| EHOMO – ELUMO (eV) | −8.29 | −11.65 | −8.50 | −8.01 |
| μ (Debye) | 3.18 | 7.34 | 5.55 | 10.83 |
| H (kcal/mol) | 18.7 | −667.31 | −661.82 | −657.82 |
| ΔHa (kcal/mol) | −13.21 | −9.21 | ||
| G (kcal/mol) | −11.54 | −784.46 | −797.96 | −796.54 |
| ΔGa (kcal/mol) | −1.96 | −0.54 | ||
| ΔSb (cal/mol K) | −50.90 | −32.72 | ||
| In water | ||||
| E (kcal/mol) | −102.97 | −1480.67 | −1597.18 | −1595.48 |
| ΔE (kcal/mol) | −13.54 | −11.84 | ||
| EHOMO (eV) | −11.88 | −10.63 | −10.56 | −10.63 |
| ELUMO (eV) | −3.92 | 18.37 | −2.17 | −1.85 |
| EHOMO − ELUMO (eV) | −7.96 | 7.74 | −8.39 | −8.78 |
| μ (Debye) | 4.45 | 8.65 | 6.52 | 13.49 |
a ΔA = A complex – (A substrate + A β-CD); A = H, G.
b ΔS = (ΔH – ΔG) T.
The same result is also obtained with the B3LYP/6-31G* and HF/6-31G* single point calculation (Table 2) in which the energy difference becomes in vacuum and in water respectively −5.99 and −3.79 kcal/mol for B3LYP/6-31G*, −8.85 and −5.77 kcal/mol for HF/6-31G*.
Single point energies in kcal/mol of the models 1 and 2 calculated at B3LYP/6-31G* and HF/6-31G* in vacuum and in water.
| PAE | β-CD | Model 1 | Model 2 | |
| In vacuum | ||||
| B3LYP/6-31G* | ||||
| E (kcal/mol) | −360 623.19 | −26 811 832.20 | −27 172 507.57 | −27 172 501.58 |
| ΔE (kcal/mol) | −52.18 | −46.19 | ||
| RHF/6−31G* | ||||
| E (kcal/mol) | −358 292.53 | −2 666 495.63 | −3 024 748.09 | −3 024 788.16 |
| ΔE (kcal/mol) | −40.07 | −31.22 | ||
| In water | ||||
| B3LYP/6-31G* | ||||
| E (kcal/mol) | −360 633.14 | −26 811 850.01 | −27 172 425.15 | −27172428.94 |
| ΔE (kcal/mol) | −58.00 | −54.21 | ||
| RHF/6-31G* | ||||
| E (kcal/mol) | −358 300.01 | −2 666 499.21 | −3 024 760.10 | −3024765.77 |
| ΔE (kcal/mol) | −39.22 | −33.45 |
3.2.1 HOMO−LUMO parameters
The (EHOMO − ELUMO) gap is an important scale of stability [41] and chemicals with large (EHOMO − ELUMO) values tend to have higher stability. So, we investigated the electronic structure of these complexes using the PM3 method. The HOMO and LUMO energies of guest, host and their inclusion complexes in vacuum and in water are shown in Table 1. The gap (EHOMO − ELUMO) for the model 1 was more negative, which advocate that this complex is more stable in vacuum and in water than the model 2. This result was in good agreement with the complexation energy.
On the other hand, the results of the investigation of deformation energy reported in Table 1 demonstrate that the PAE molecule in the model 1 requires a slightly more energy for conformation adaptation inside the β-CD cavity than that of the model 2. The corresponding values are, respectively, 2.16 and 2.10 kcal/mol only. This can be supported by the fact that flexibility of the guest structure is one of the important structural requirements for β-CD upon complexation. At the same time, intermolecular hydrogen bonds also play pivotal role for this conformational exchange.
3.2.2 Dipole changes
All inclusion complex in vacuum and in water showed dipole moment values higher than the corresponding isolated guest molecule, where as compared to β-CD, the values were low or high. This indicates that the polarity of the β-CD cavity changed after the guest entered into the β-CD cavity. From these results, it can be concluded that the dipole moment values show a strong correlation with the complexation behavior of the molecules.
3.3 Geometrical structure
Based on the PM3 methods, it was found that there is one intermolecular hydrogen bonds between oxygen atom O (155) of methoxy group OCH3 of PAE and hydrogen atom H(132) of primary hydroxyl group of β-CD with a dH–O distance of 2.27 Å. H-bond lengths shorter than 3.0 Å, which just falls in the reported data [42]. The model 2 does not seem to be stabilized by such an interaction. The same result is also obtained with the B3LYP/6-31G* and HF/6-31G* single point calculations. The PM3, optimized structures of the models 1 and 2 in vacuum are shown on Fig. 4. From Fig. 4, it can also be seen that the PAE molecule is totally inserted in the hydrophobic cavity of the most favorable structures in model 1, so there is a stronger hydrophobic interaction between PAE and β-CD.
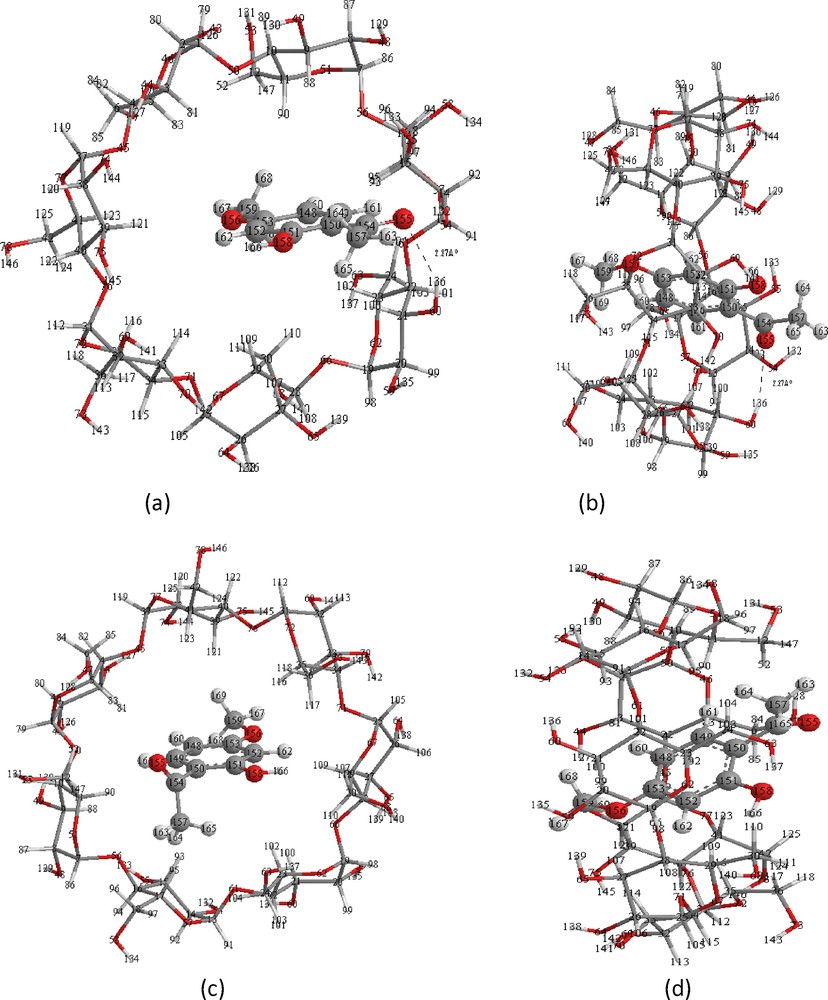
Energy-minimized structure obtained by PM3 calculations for the PAE/β-CD inclusion complexes. (a) and (c) seen from the secondary hydroxyl rim of the β-CD cavity corresponds respectively to the models 1 and 2; (b) and (d) seen from the side of the β-CD wall corresponds respectively to the models 1 and 2. Dotted lines are the hydrogen bonds.
In Table 3, we present the bond angle and the most characteristic dihedral angles of the guest molecule before and after complexation, obtained with PM3, B3LYP/6-31G* and HF/6-31G* methods. These results indicate that the guest in models 1 and 2 has completely changed its initial geometry. This change is clearly justified by the difference between the values of the dihedral angles of the guest molecule before and after the complexation. Thus, the molecule under consideration becomes deformed and adapts to a specific conformation inside the host cavity to form a more stable inclusion complex.
Comparisons of particular parameters of guest molecules in their free and complexed form (model 1 and model 2), respectively. θ1, θ 2 and θ 3 are defined by C4-C3-C7-C10, C3-C2-C1-H13 and C1-C6-O9-C12, respectively.
| Species | θ1 (°) PM3/RHF/DFT | θ2 (°) PM3/RHF/DFT | θ3 (°) PM3/RHF/DFT | Bond angle (°) PM3/RHF/DFT |
| C3-C7-O8 | ||||
| Free form | 0.0/0.0/0.0 | 180.0/0.0/180.0 | 0.0/0.0/0.2 | 118.6/119.1/120.1 |
| Model 1 form | −68.6/0.0/0.0 | 179.0/−180.0/−180.0 | −7.4/0.0/0.0 | 121.4/120.0/120.0 |
| Model 2 form | −73.0/0.0/0.0 | −179.0/−180.0/−180.0 | 8.5/0.0/0.0 | 121.8/120.0/120.0 |
3.4 Thermodynamic analysis for the complexation process of β-CD with PAE
The statistical thermodynamics calculations were performed using Harmonic frequency analysis in PM3 method for the most stable structures, characterizing them as true minima on the potential energy surface. The frequency analyses were then used for the evaluation of the thermodynamic parameters, such as enthalpy changes (ΔH°), entropy contribution (ΔS°) and Gibbs free energy (ΔG°), for the statistical thermodynamic parameters in complexation process of PAE with β-CD at 298.15 K at 1 atm were summarized in Table 1. It can be observed that the inclusion complexation of PAE with β-CD are exothermic judged from the negative enthalpy changes. The enthalpy change for the model 1 is more negative than that for the model 2. It means that both the inclusion processes are enthalpically favorable in nature due to the negative enthalpy changes. The ΔH° and ΔS° in the inclusion process of PAE with β-CD to form the most stable complexes are negative, suggesting that the formation of the inclusion complex is an enthalpy-driven process in vacuum. The Gibbs free energy change (ΔG) for the inclusion process is −1.96 kcal/mol and −0.54 kcal/mol for the models 1 and 2, respectively. The negative ΔG values suggest that the formation of β-CD/PAE inclusion complex is a spontaneous process.
3.5 ONIOM calculations
The two-hybrid ONIOM method [(B3LYP/6-31G*:PM3) and (RHF/6-31G*:PM3)] was adopted to fully optimize the geometries of the most stable complexes obtained by PM3 method, either reducing the computational cost or increasing the accuracy of the resulting structure. The system was divided into two parts: the most important part consisting of PAE molecule for the inner layer; and the minor part consisting of the remaining part β-CD for the outer layer. In Table 4, the total optimized energies (EONIOM) of the model 1 and model 2 calculated by ONIOM [(B3LYP/6-31G*:PM3) and (RHF/6-31G*:PM3)] method are −361 978.64, −361 972.36, −359 776.04 and −359 769.77 kcal/mol, respectively. The difference of the two complexation energy on ONIOM method is slightly larger than that on PM3 method, as the energy differences (ΔE) for ONIOM [(B3LYP/6-31G*:PM3), (RHF/6-31G*:PM3)] and PM3 methods are −6.28, −6.27 and −4.24 kcal/mol, respectively. These results follow the same trend as the PM3 optimizations, that the energy of the model 1 is more negative than that of the model 2. It can be seen that the model 1 is more stable than the model 2; that is to say, the interaction between PAE and β-CD in the model 1 is stronger than that in the model 2.
Relative potential energy for the optimized structures of complexes PAE/β-CD in both models as calculated by ONIOM2 method and intermolecular hydrogen bonds with O-H distance (Å) smaller than 3 Å.
| Computational methods | Model 1 | Model 2 | ΔE |
| E(PM3) | −1571.05 | −1566.81 | −4.24 |
| d (O8-H132) | 2.27 | ||
| EONIOM (RB3LYP/6-31G*:RPM3) | −361 978.64 | −361 972.36 | −6.28 |
| d (O8-H132) | 1.81 | ||
| EONIOM (RHF/6-31G*:RPM3) | −359 776.04 | −359 769.77 | −6.27 |
| d(O8-H132) | 1.82 |
The relative energy difference of the optimized complexes has the same order of magnitude than that obtained by PM3 method and according to Fig. 5. The PAE molecule is totally inserted in the hydrophobic cavity of the most favorable structures in model 1, with the OCH3 group positioned at the primary rim and the COCH3group closer to the secondary one and one hydrogen bonding is reported. These remarks are the same for the energy-minimized PM3 structure illustrated in Fig. 4.
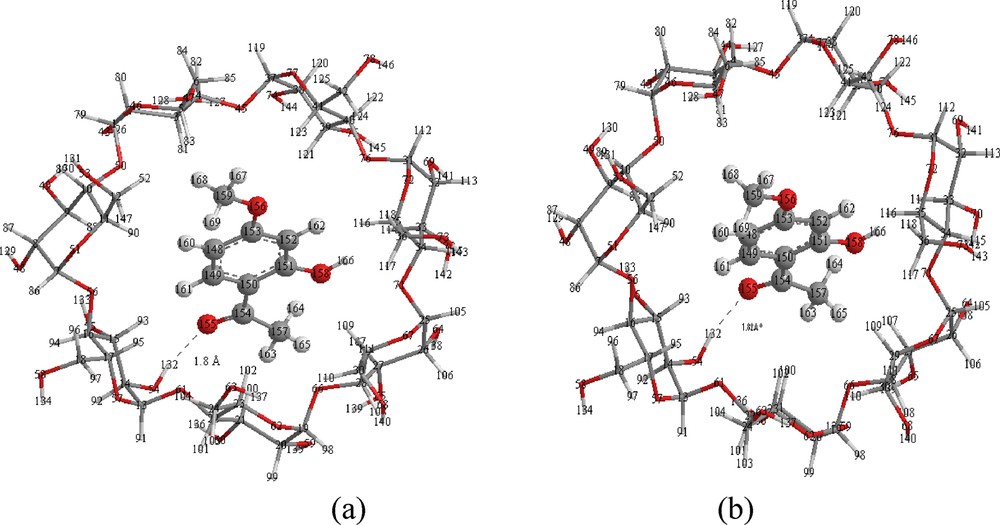
Structures of PAE/β-CD inclusion complexes for model 1 from ONIOM2 (RB3LYP/6-31G*: RPM3) (a) and ONIOM2 (RHF/6-31G*: RPM3) (b) calculations.
3.6 Hydrogen bonding and population analysis
In the NBO analysis of X-H···Y hydrogen bonded systems, the interaction between the lone pair (LP) (Y) of the proton acceptor and σ* (X-H) anti-bond of proton donor is characterized by a significant E(2) stabilization energy. The main contributions in the case where PAE is acting as a donor and in the case where β-CD is acting as a donor are both included in Table 5. We notice that when the PAE acts as a donor, the O155 atom in PAE is involved. The transfer occurs mainly from the LP of O155 atom to the anti-bonding acceptor σ*(O-H) orbital of β-CD. When the β-CD acts as a donor, the LP of O76 atom or the σ bond from the C-H group is mostly involved. In this case, the acceptors are the anti-bonding σ*(C-H) orbital, and the transfer occurs mainly from the LP of the O76 atom to the anti-bonding σ*(C-H) orbital. When PAE acts as a donor, the energy stabilization of inclusion complex is much larger than that when CD acts as donor. As an overall conclusion, we can confirm that intermolecular hydrogen bond is the leading factor in the charge transfer process, and is the main driving force of the formation of inclusion complex.
The electron donor orbital, electron acceptor orbital and the corresponding E(2) energies, distances and angles obtained with ONIOM2 (RB3LYP/6-31G*: RPM3)/(RHF/6-31G*: RPM3) calculations for model 1.
| PAE | β-cyclodextrin | d (Å) | Angle (°) | E (2) kcal/mol |
| PAE acts as donor | ||||
| LP (O 155) | σ*(O54—H132) | 1.8/1.8 | 170.02/167.27 | 12.45/12.76 |
| LP (O 158) | σ* (C27—H107) | 2.6/2.6 | 167.87/167.52 | 1.57/1.56 |
| LP (O 155) | σ* (C15—H93) | 2.6/2.6 | 127.14/127.30 | 2.32/2.31 |
| β-CD acts as donor | ||||
| LP (1) O76 | σ* (C15—H93) | 2.6/2.8 | 144.06/143.61 | 0.80/0.79 |
4 Conclusions
The stable structures and the inclusion process for PAE/β-CD inclusion complexes were studied by use of PM3, HF/6-31G*, B3LYP/6-31G* and ONIOM2 methods. The PAE guest molecule is embedded into the cavity of β-CD, and the inclusion complex in vacuum and in water formed by PAE entering into the cavity of β-CD, from its wide side by OCH3 group (model 1) is more stable than that formed by PAE entering into the cavity of β-CD from its wide side by COCH3 group (model 2). To form a stable inclusion complex, the conformation of PAE is significantly altered during complexation. In addition, the statistical thermodynamic calculations advocate that the formations of these inclusion complexes were enthalpy-driven process. The overall theoretical results suggest that hydrogen bonding effect play an important role in the complexation process.
Acknowledgments
This study was supported by Algerian Ministry of Higher Education and Scientific Research and General Direction of Scientific Research as a part of projects CNEPRU (No B01520090002) and PNR (8/u24/4814).


