1 Introduction
Cyclodextrins (CD) are cyclic oligosaccharides that present a hydrophilic external part and a relatively hydrophobic cavity in which guest molecules can be encapsulated by inclusion complex formation [1,2]. The most widely used (CDs) are α-, β- and γ (CDs). The ability of β-CD to form inclusion complexes with different products is well known. In particular, β-CD (Fig. 1a) has an internal cavity, shaped like a truncated cone of about 8 Å deep and 6.0–6.4 Å in diameter. This cavity possesses a relatively low polarity that can accommodate guest organic molecules inside. The formation of inclusion complexes of organic molecules with cyclodextrins is important for their pharmaceutical and technological applications [3–6].
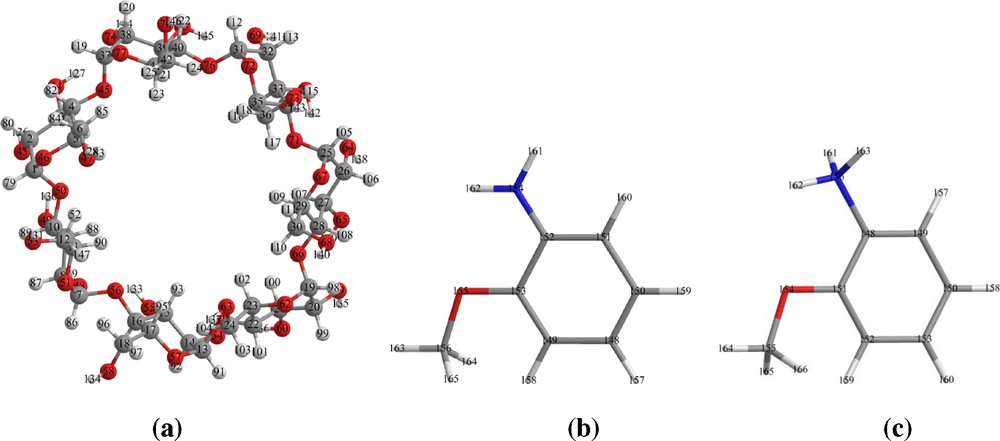
Geometrical structures of β-CD (a), neutral (b) and cationic (c) species of O-AN optimized at PM6 method.
The applications of O-AN (Fig. 1b) in various fields like catalysis and chemicals processing, chemical synthesis, colorants for paper, dyestuffs, pigments and optical brighteners. In electrochemical synthesis of polymer material using the O-AN [7] to form thin films and composite material. O-AN used as reducing agent in gold nano particle preparation in aqueous solution. Formulation and practical application of O-AN are often rendered difficult due to their adverse physicochemical properties such as poor solubility, instability, toxicity, and volatility [8]. The complexation between O-AN and cyclodextrins can result in products with superior performance (e.g., enhanced OAN solubility and stability, reduction of volatility).
Srinivasan et al. [9] prepared and characterized by XRD, SEM and FT-IR techniques, the solid complex of both species (neutral and cationic) of O-AN with β-CD. The results indicate that the O-AN molecule is entrapped in the β-CD cavity to form an inclusion complex. The thermodynamic parameters in this inclusion process show that the reaction of β-CD with both species of O-AN is exothermic and accompanied with a negative entropy (ΔS).
Recently, the new semi-empirical method PM6 (parameterized model 6) was introduced [10–14], which is superior to other semi-empirical QM methods in various aspects. As compared to the earlier semi-empirical methods AM1 and PM3, several modifications have been made to the neglect of diatomic differential overlap (NDDO) core–core interaction term and to the parameter optimization method.
In this study, the complexation and deformation energies of both β-CD and O-AN during the formation of inclusion complexes were studied, using PM6 semi-empirical method in order to localize the minimum energy structures, which are used as starting structures for subsequent optimizations. After that, the structures are subjected to higher-level calculations, such HF, DFT and ONIOM2 methods to approach the ideal geometry and provide further insight into the complexation process of O-AN with β -CD. Furthermore, the natural bonding orbital (NBO) analysis is employed to quantify the donor–acceptor interactions between host and guest.
2 Computational method
In this study, we have considered only the inclusion compounds in molar proportion 1:1 formed between one molecule of β-CD and one of O-AN, abbreviated O-AN1/β-CD (A), O-AN1/β-CD (B), O-AN2/β-CD (A) and O-AN2/β-CD (B), (1 and 2 represent neutral and cationic species of O-AN respectively).
The initial structures of the cationic and the neutral species of O-AN were constructed using Hyperchem 7.5 molecular modeling package [15]. The starting geometry of β-CD was taken from Chem-Office 3D ultra (version10, Cambridge software). The two structures O-AN and β-CD were then optimized by means of PM6 semi-empirical method prior to using Gaussian09 [16] for all relevant calculations.
The inclusion model is shown in Fig. 2. It contains one passing process and one circling process.
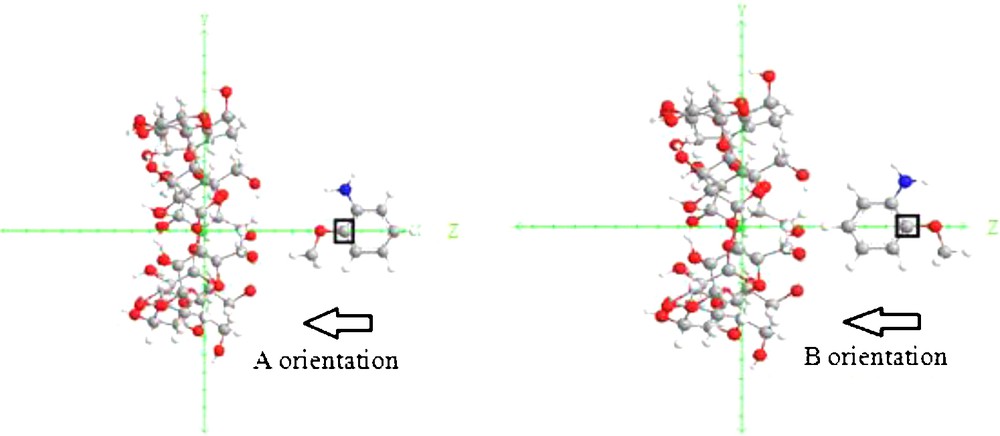
Coordinate systems to describe inclusion processes of O-AN with β-CD.
For the construction of O-AN/β-CD complex, the glycosidic oxygen atoms of the cyclodextrin molecule were placed on the XY plane and their center was defined as the center of the coordinate system. The secondary hydroxyl groups of the β-CD were placed pointing toward the positive Z axis. The hydroxyl group of the guest molecule was initially placed along the Z axis. Two possible orientations of the guest molecule in the complex were considered. The orientation in which the hydroxyl group of O-AN points toward the secondary hydroxyl of β-CD was called the “A orientation”, the other, in which the hydroxyl group of the guest points toward the primary hydroxyl of β-CD was called the “B orientation”, (Fig. 2).
The relative position between the host and the guest was measured by the Z-coordinate of the labeled carbon atom (C*) of the guest (Fig. 2). The inclusion process emulation was then achieved along the Z axis from 10 to –10 Å with a step of 1 Å. The generated structures at each step were optimized by PM6 methods without imposing any symmetrical restrictions.
In order to find an even more stable structure of the complex, each guest molecule is calculated for all of the structures obtained by scanning θ, clock wisely circling around Z-axis, at 30° intervals from 0° to 360°.
Complexation energy upon complexes between O-AN and the β-CD is calculated for the minimum energy structure according to Eq. (1).
| (1) |
The deformation energy for each component, the guest or the host molecule, throughout the formation of the complex, was defined as the difference in the energy of the totally optimized component compared to its energy in the complex as Eq. (2)
| (2) |
For the purpose of this work, the B3LYP [17–22] and B3PW91 [23–27] density functional were employed as they are the most widely used density functional and the most popular. In addition to the above-mentioned functional, we have also used the Minnesota density M05-2X functional, a member of the M05 families of density functionals developed by Zhao, Truhlar and Schultz, which gave good results [28,29] and is beginning to be increasingly used [30–32], and which gives us a good result in our study of the O-AN/β-CD complex.
3 Results and discussion
3.1 Passing and circling process
The graphical representation of the energy changes involved during the inclusion passing process of O-AN in β-CD at different Z positions for both orientations are illustrated in Fig. 3.

Binding energies of the inclusion complexation of O-AN1/β-CD (a) and O-AN2/β-CD (b) at different positions (Z) and for both orientations.
The first remark is that all complexation energies are negative, which show that the inclusion process of O-AN in β-CD is thermodynamically favorable. Second, the curves show several local minima, where the lowest minimum energy is precisely located at Z value of –6 Å and 0 Å respectively for neutral and cationic species of O-AN for the A orientation. The energy minimum for the B orientation is located at Z values of –3 Å and 1 Å respectively for neutral and cationic species of O-AN.
We can also notice that the lowest energy is obtained when θ is equal to 330° and 210° respectively for neutral and cationic species of O-AN for A orientation, but for the B orientation, it is located at 0° and 60° respectively for neutral and cationic species of O-AN. The energy changes of 1 and 2 complexes are exhibited in Fig. 4.
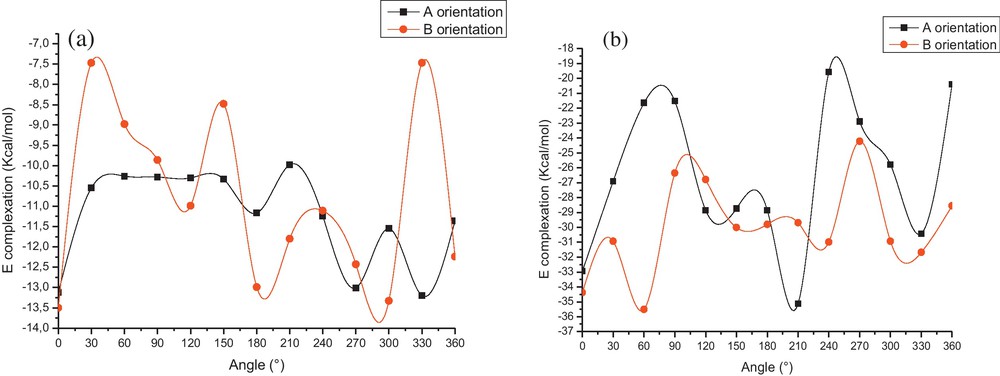
Stability energies of the inclusion complexation of O-AN1/β-CD (a) and O-AN2/β-CD (b) at different angles (θ), PM6 calculations.
3.2 The optimization
The calculated energies for the most stable structures obtained by PM6 study are summarized in Table 1. The values of the energy minimum for both A orientation and B orientation in anionic and cationic forms are respectively equal to –13.20, –13.50, –35.13 and –35.51 kcal/mol, which indicates that the complexation energy is slightly in favor of the B orientation in cationic form. This weak difference in the complexation obtained with PM6 does not allow determining the nature of the driving forces and their relative contributions. So, we did consider a higher level of calculation.
Thermodynamic parameters of the complexes A and B for neutral and cationic O-AN calculated by PM6 method.
| O-AN | O-AN+1 | β-CD | O-AN1/β-CD | O-AN2/β-CD | |||
| A | B | A | B | ||||
| PM6 | |||||||
| E (kcal/mol) | –14.05 | 127.38 | –1564.63 | –1591.88 | –1592.18 | –1472.38 | –1472.76 |
| ΔE (kcal/mol) | –13.20 | –13.50 | –35.13 | –35.51 | |||
| Edeformation (O-AN1) | – | – | – | 14.02 | 12.93 | – | – |
| Edeformation (O-AN2) | – | – | – | – | – | 11.63 | 11.28 |
| Edeformation (β-CD) | – | – | – | 8.79 | 11.73 | 11.29 | 13.91 |
| H° (kcal/mol) | 75.30 | 226.53 | –834.58 | –774.59 | –774.84 | –649.03 | –649.15 |
| ΔH° (kcal/mol) | –15.31 | –15.56 | –40.98 | –41.10 | |||
| G° (kcal/mol) | 50.20 | 199.92 | –941.26 | –913.34 | –914.59 | –786.89 | –787.58 |
| ΔG° (kcal/mol) | –22.28 | –23.53 | –45.55 | –46.24 | |||
| S° (kcal/mol) | 90.49 | 89.28 | 404.01 | 466.37 | 464.84 | 462.39 | 460.92 |
| ΔS° (kcal/mol) | –28.13 | –29.66 | –28.49 | –29.96 | |||
| B3LYP/6–31G* | |||||||
| E (kcal/mol) | –252334.19 | –252564.24 | –2682649.17 | –2934990.65 | –2934997.74 | –2935237.07 | –2935239.76 |
| ΔE (kcal/mol) | –7.29 | –14.38 | –23.66 | –26.35 | |||
| M05-2X/6-31G* | |||||||
| E (kcal/mol) | –252300.93 | –252528.66 | –2682441.34 | –2934744.22 | –2934755.02 | –2934987.57 | –2934990.77 |
| ΔE (kcal/mol) | –1.95 | –12.75 | –17.57 | –20.77 | |||
| MPW1PW91/6-31G* | |||||||
| E (Kcal/mol) | –252259.02 | –252503.05 | –2682040.49 | –2934312.50 | –2934315.52 | –2934558.29 | –2934560.86 |
| ΔE (kcal/mol) | –12.99 | –16.01 | –14.75 | –17.32 | |||
| B3PW91/6-31G* | |||||||
| E (kcal/mol) | –252215.09 | –252468.85 | –2681667.62 | –2933890.06 | –2933895.58 | –2934145.10 | –2934151.29 |
| ΔE (kcal/mol) | –7.35 | –13.87 | –8.63 | –14.82 | |||
| HF/6-31G* | |||||||
| E (kcal/mol) | –250721.62 | –250985.48 | –2667563.83 | –2918294.99 | –2918303.97 | –2918562.21 | –2918568.54 |
| ΔE (kcal/mol) | –9.54 | –18.52 | –12.90 | –19.23 |
The gap energetic between the two orientations for neutral and cationic species of O-AN obtained with PM6 is increased using single point calculations at B3LYP/6-31G*, M05-2X/6-31G*, B3PW91/6-31G*, MPW1PW91/6-31G* and HF/6-31G* levels and confirm the preference for the B orientation (O-AN2/β-CD) over the other three complexes (Table 1).
The results of the investigation of deformation energy reported in Table 1 show that the cationic form of O-AN molecule for orientation B requires slightly more energy than for orientation A (in neutral and cationic species) in order to adapt its structure to bind within the cavity of β-CD as indicated by the DEF [O-AN] of about 11.28 kcal/mol. This can be supported by the fact that flexibility of the guest structure is an important structural requirement for β-CD upon complexation.
3.3 Thermodynamics parameters
The statistical thermodynamic calculation was carried out at 1 atm pressure and 298.15 K temperature by PM6 method. The thermodynamic quantities the enthalpy changes (ΔH), Gibbs energy changes (ΔG) and entropy changes (ΔS) contributions are depicted in Table 1. As can be seen from Table 1, ΔG is negative which suggests that the inclusion process proceeded spontaneously at 298K. ΔH and ΔS are also negative, which indicates that the inclusion process is an exergonic and enthalpy-controlled process. The negative enthalpy change (ΔH) arose from the van der Waal's interaction, while the negative entropy change (ΔS) is the steric barrier caused by molecular geometrical shape and the limit of β-CD cavity to the freedom of shift and rotation of O-AN molecule. The same results are also given with the experimental observation [9].
3.4 Charge transfer
Liu and Guo suggest that charge–transfer interactions play a relevant role in the stabilization of their inclusion complexes [33]. The Mulliken charges of the heavy atoms of O-AN1 and O-AN2, charge transfer of complexes O-AN1/β-CD and O-AN2/β-CD are summarized in Table 2 by B3LYP/6-31G* and PM6 methods. The data show that the β-CD molecule accepts the electron from O-AN and the charge transfer of O-AN2/β-CD in B orientation (PM6: 1.079e, B3LYP/6-31G*: 1.018e) is the largest of all complexes.
Mulliken charges of the atoms of O-AN1 and O-AN2, charge transfer of the A and B orientations calculated by PM6//B3LYP/6-31G* method.
| O-AN | O-AN1/β-CD | O-AN+1 | O-AN2/β-CD | |||
| A | B | A | B | |||
| C148 | –0.040//–0.037 | 0.021//–0.035 | 0.058//–0.012 | –0.305//0.111 | –0.224//0.145 | –0.230//0.164 |
| C149 | –0.067//–0.075 | –0.091//–0.031 | –0.092//–0.038 | 0.146//0.028 | 0.144//0.001 | 0.143//0.018 |
| C150 | 0.047//–0.015 | –0.005//0.007 | –0.046//–0.025 | –0.032//0.052 | –0.060//0.014 | –0.060//–0.007 |
| C151 | –0.144//–0.088 | –0.027//–0.055 | –0.011//–0.035 | 0.377//0.420 | 0.348//0.409 | 0.350//0.360 |
| C152 | 0.201//0.323 | 0.064//0.227 | 0.032//0.220 | –0.135//0.005 | –0.148//–0.048 | –0.120//0.031 |
| C153 | 0.136//0.334 | 0.202//0.345 | 0.214//0.354 | 0.229//0.074 | 0.201//0.044 | 0.181//0.030 |
| N154 | 0.011//–0.162 | –0.012//–0.139 | –0.017//–0.147 | –0.405//–0.569 | –0.409//–0.566 | –0.400//–0.304 |
| O155 | –0.394//–0.550 | –0.404//–0.560 | –0.402//–0.559 | 0.330//0.356 | 0.317//0.319 | 0.320//0.295 |
| C156 | 0.250//0.272 | 0.269//0.263 | 0.281//0.287 | 0.793//0.520 | 0.765//0.420 | 0.775//0.448 |
| Somme | 0.000//0.000 | 0.016//0.022 | 0.017//0.045 | 1.000//1.000 | 0.934//0.738 | 1.079//1.018 |
For the O-AN1/β-CD complex, Mulliken charge distribution indicates that there is a small but non-trivial transferred charge. The amount of this charge is pretty similar in both A and B orientation. Hence, in spite of that charge–transfer interaction, is a non-trivial driving force in the complexation of O-AN1 and β-CD, the stability of the A orientation in relation to the B one is not necessary assessed by this interaction [34,35].
3.5 The structure parameters of inclusion complexes
Among the structures of the four inclusion complexes shown in Fig. 5, we could notice that O-AN2/β-CD in B orientation presents several intermolecular H-bonds in the structure. Here, the H-bond is defined as C–H-O or O–H-O and the N–H-O H bond lengths are less than 3 Å, which is in agreement with the reported data [36]. Obviously, the hydrogen bonds of O-AN2/β-CD are more than those of the other three. This explains why the complexation energy of the inclusion O-AN2/β-CD in B orientation is lower than the other three complexes.

ONIOM2 energy minimized structure of the O-AN1/β-CD A (a), O-AN1/β-CD B (b), O-AN2/β-CD A (a’) and O-AN2/β-CD B (b’). Top view. Hydrogen bonds are indicated by dotted lines.
Table 3 presents the most interesting bond distances, bond angles and dihedral angles of the O-AN before and after complexation in β-CD obtained from PM6 and B3LYP/6-31G* calculations for the most stable structure (Fig. 5). It was evident that after complexation, the conformation of O-AN was completely altered. The alterations were significant in dihedral angles, which indicated that the O-AN adopted a specific conformation to form a stable complex.
Geometrical parameters of O-AN1 and O-AN2 before and after inclusion in β-CD, bond distances (Å), angle (°) and dihedral angles (°) calculated by PM6//B3LYP/6-31G* methods.
| O-AN 1 | O-AN2 | O-AN1/β-CD | O-AN2/β-CD | |||
| A | B | A | B | |||
| PM6//B3LYP/6-31G* | PM6//B3LYP/6-31G* | PM6//B3LYP/6-31G* | ||||
| Bond lengths (A°) | ||||||
| C148–C149 | 1.408//1.408 | 1.0390//1.389 | 1.399//1.399 | 1.402//1.402 | 1.394//1.394 | 1.392//1.392 |
| C149–C153 | 1.384//1.384 | 1.405//1.405 | 1.393//1.393 | 1.392//1.392 | 1.401//1.401 | 1.402//1.402 |
| C149–H158 | 1.085//1.085 | 1.091//1.091 | 1.093//1.093 | 1.088//1.088 | 1.089//1.089 | 1.100//1.100 |
| C150–H159 | 1.088//1.088 | 1.094//1.094 | 1.091//1.091 | 1.089//1.089 | 1.102//1.102 | 1.091//1.091 |
| C152–C153 | 1.437//1.437 | 1.414//1.414 | 1.423//1.423 | 1.427//1.427 | 1.414//1.414 | 1.415//1.415 |
| C152–N154 | 1.392//1.392 | 1.478//1.478 | 1.432//1.432 | 1.427//1.427 | 1.474//1.474 | 1.475//1.475 |
| C153–O155 | 1.389//1.389 | 1.364//1.364 | 1.392//1.392 | 1.386//1.386 | 1.368//1.368 | 1.365//1.365 |
| N154–H161 | 0.997//0.997 | 1.034//1.034 | 1.033//1.033 | 1.025//1.025 | 1.051//1.051 | 1.044//1.044 |
| N154–H162 | 1.002//1.002 | 1.041//1.041 | 1.023//1.023 | 1.019//1.019 | 1.047//1.047 | 1.053//1.503 |
| Bond angles (°) | ||||||
| C149–C148–C150 | 120.305//120.302 | 120.894//120.897 | 120.520//120.520 | 120.355//120.355 | 120.763//120.761 | 120.991//120.991 |
| C149–C148–H157 | 119.171//119.172 | 119.813//119.814 | 119.525//119.525 | 119.447//119.447 | 119.814//119.813 | 119.536//119.532 |
| C150–C148–H157 | 120.526//120.526 | 119.292//120.288 | 119.977//119.977 | 120.197//120.197 | 119.416//119.419 | 119.473//119.477 |
| C148–C150–H159 | 120.151//120.151 | 119.331//119.332 | 120.765//120.765 | 120.160//120.160 | 119.784//119.781 | 119.622//119.619 |
| C150–C151–H160 | 119.684//119.684 | 120.243//120.241 | 120.361//120.361 | 119.806//119.806 | 120.342//120.345 | 120.265//120.265 |
| C152–C151–H160 | 120.234//120.234 | 120.446//120.441 | 119.289//119.289 | 119.727//119.727 | 120.471//120.465 | 120.189//120.185 |
| C151–C152–N15 | 121.991//121.991 | 120.499//120.501 | 119.601//119.601 | 120.391//120.391 | 120.519//120.519 | 121.375//121.375 |
| Dihedral angle (°) | ||||||
| C150–C148–C149–C15 | 0.000//0.000 | 0.000//0.000 | 0.827//0.827 | –0.304//–0.304 | 1.520//1.524 | 0.320//0.317 |
| C150–C148–C149–H158 | –180.000//–180.000 | 180.000//180.00 | –178.695//–178.695 | 178.998//178.998 | –179.142//–179.143 | –179.739//–179.739 |
| H157–C148–C149–C153 | 0.000//–180.000 | 0.000//–180.000 | –179.074//–179.074 | –179.917//–179.917 | –177.498//–177.496 | –179.831//–179.829 |
| C149–C148–C150–C151 | 0.000//0.000 | 0.000//0.000 | –0.937//–0.937 | 0.556//0.556 | –0.898//–0.899 | 0.031//0.032 |
| C149–C148–C150–H159 | –180.000//–180.000 | 180.00//180.000 | 179.732//179.732 | –179.512//–179.512 | 178.817//178.816 | –179.873//–179.873 |
| H157–C148–C150–C151 | 180.000//0.000 | 180.000//–180.000 | 178.964//178.964 | –179.833//–179.833 | 178.23//178.125 | –179.818//–179.823 |
| C148–C149–C153–C152 | 0.000//0.000 | 0.000//0.0000 | 1.046//1.046 | –0.641//–0.641 | –0.796//–0.800 | –0.355//–0.352 |
3.6 ONIOM calculations
In order to further understand molecular recognition between the guest and the host, we adopted ONIOM2 methods. In our hybrid model study, we submitted the host molecule β-CD to the low level of quantum calculations (PM6) since we assumed it provides only an environmental effect and contains the larger number of atoms, while the guest molecule O-AN (neutral and cationic species) is treated at a high level of calculation HF/6-31G*, B3LYP/6-31G*, M05-2X/6-31G* and MPW1PW91/6-31G*. Table 4 emphasizes the computational results of the ONIOM2 study. It is interesting to note that the results indicate that the complexation according to the B orientation in cationic species is significantly more favorable than the other three complexes. ONIOM2 calculations confirm PM6 results.
Relative energy for the optimized structures of complexes O-AN1/β-CD and O-AN2/β-CD in both orientations as calculated by ONIOM2 method.
| O-AN1/β-CD | O-AN2/β-CD | |||||
| A | B | ΔE | A | B | ΔE | |
| E (PM6) | –1591.88 | –1592.18 | –0.30 | –1472.38 | –1472.76 | –0.38 |
| EONIOM (B3LYP/6-31G*:PM6) | –253912.57 | –253913.17 | –0.60 | –254165.70 | –254165.96 | –0.26 |
| EONIOM (M05-2X/6-31G*:PM6) | –253879.69 | –253880.19 | –0.50 | –254130.88 | –254131.28 | –0.40 |
| EONIOM (MPW1PW91/6-31G*:PM6) | –253851.89 | –253852.26 | –0.37 | –254105.21 | –254105.40 | –0.19 |
| EONIOM (HF/6-31G*:PM6) | –252334.58 | –252335.07 | –0.49 | –252590.03 | –252590.53 | –0.50 |
Furthermore, it can be seen that the gap of the complexation energy between the two orientations in the four calculations vary considerably to –0.37 at –0.60 kcal/mol and –0.19 at –0.50 kcal/mol respectively in neutral and cationic species of O-AN. The more stable complex is obtained with [(B3LYP/6-31G*:PM6)] and [(HF/6-31G*:PM6)] level.
3.7 Natural Bond Orbital (NBO) analysis
NBO analysis provides an efficient method for studying intra- and intermolecular bonding and interaction between bonds, and also provides a convenient basis for investigating charge transfer or conjugative interaction in molecular systems. Some electron donor orbital, acceptor orbital and the interacting stabilization energy resulted from the second-order micro-disturbance theory are reported [37,38]. The second-order Fock matrix was carried out to evaluate the donor–acceptor interactions in the NBO analysis [39]. For each donor (i) and acceptor (j), the stabilization energy E(2) associated with the delocalization i → j is estimated as:
| (3) |
Donor–acceptor interactions and stabilization energies E(2) (kcal/mol).
| β-CD donor O-AN acceptor | E(2) B3LYP/6-31G* | E(2) M05-2X/6-31G* | E(2) MPW1PW91/6-31G* | E(2) HF/6-31G* | |
| B orientation for cationic O-AN | |||||
| δ (1) C 15 - H 93 | δ*(1) C 155 - H 165 | 3.01 | 3.10 | 3.04 | 2.87 |
| δ (1) O 53 - H 131 | δ*(1) C 155 - H 164 | 1.85 | 1.75 | 1.78 | 1.74 |
| LP (1) O 47 | δ*(1) N 156 - H 161 | 1.67 | 1.62 | 1.69 | 1.32 |
| LP (1) O 54 | δ*(1) C 152 - H 159 | 1.40 | 1.68 | 1.42 | 1.68 |
| LP (1) O 56 | δ*(1) C 155 - H 165 | 1.78 | 1.78 | 1.74 | 1.90 |
| LP (1) O 61 | δ*(1) C 155 - H 166 | 2.12 | 2.34 | 2.09 | 2.28 |
| LP (1) O 71 | δ*(1) N 156 - H 162 | 3.94 | 3.37 | 3.24 | 3.00 |
| O-AN donor β-CD acceptor | E(2) B3LYP/6-31G* | E(2) M05-2X/6-31G* | E(2) MPW1PW91/6-31G* | E(2) HF/6-31G* | |
| B orientation for cationic O-AN | |||||
| δ(1) C 151 - H 160 | δ*(1) C 41 - H 123 | 4.19 | 4.12 | 4.18 | 4.02 |
| δ(1) C 156 - H 165 | δ*(1) C 30 - H 110 | 1.78 | 1.90 | 1.90 | 1.48 |
| LP (1) N 154 | δ*(1) C 12 - H 52 | 1.39 | 1.44 | 1.39 | 1.39 |
| LP (1) N 154 | δ*(1) C 36 - H 118 | 2.45 | 2.51 | 2.45 | 2.44 |
From Table 5, it can be seen that a great number of donor σ C–H or σ N–H and acceptor σ*C–H interactions occur between the cavity and the guest molecule. The interactions energies of these contacts are in the range of 1.32–4.19 kcal/mol. The interactions are in detail:
- • when O-AN plays the role of acceptor, the important interaction is observed between LP (O 71) and σ* N 156 - H 162 (3.94 kcal/mol from B3LYP/6-31G* calculations);
- • vacant orbital σ *C–H of b-CD accepts donor σ C–H from guest molecule, where the greater interaction is formed between σ C 151 - H 160 and σ* C 41 - H 123 (4.19 kcal/mol from B3LYP/6-31G* calculations).
4 Conclusions
The stable structures and the inclusion process for neutral (O-AN1) and anionic (O-AN2) species of ortho-anisidine (O-AN)/β-cyclodextrin inclusion complexes were studied by use of PM6, DFT, HF methods and several combinations of ONIOM2 hybrid calculations.
The result suggests that the complexation energy of the O-AN2/β–CD in B orientation is significantly more favorable than the others. The statistical thermodynamic calculations suggest that the formation of the inclusion of β-CD with neutral and cationic species of O-AN was an exothermic reaction accompanied with negative ΔS. In addition, NBO analysis gives that mutual interactions between donor and acceptor orbital of each O-AN and β-CD plays an important role to the stabilization of such complex.
The solvent effect that is not considered in this study plays probably an important role of complexation between O-AN and cyclodextrins. Nevertheless, the present work represents a preliminary result, which gives an idea of the inclusion process of O-AN in CDs.
Acknowledgments
This study was supported by the Algerian Ministry of Higher Education and Scientific Research and the General Direction of Scientific Research as a part of projects CNEPRU (No. B01520090002) and PNR (8/u24/4814).



Vous devez vous connecter pour continuer.
S'authentifier