The nature of interactions between <i>N</i>-butylpyridinium tetrafluoroborate and thiophenic compounds: A theoretical investigation

Renqing Lü; Peng Gu; Dong Liu; Yukun Lu; Shutao Wang

doi:10.1016/j.crci.2013.05.015

The nature of interactions between N-butylpyridinium tetrafluoroborate and thiophenic compounds: A theoretical investigation

Renqing Lü ¹ ; Peng Gu ²; Dong Liu ²; Yukun Lu ¹; Shutao Wang ¹

¹ College of Science, China University of Petroleum (East China), Qingdao 266580, China
² College of Chemical Engineering, China University of Petroleum (East China), Qingdao 266580, China

Comptes Rendus. Chimie, Volume 16 (2013) no. 12, pp. 1118-1126.

Abstract

In an effort to understand the nature of the interactions between pyridinium-based ionic liquids and thiophenic compounds, the electronic and topological properties of the interactions between N-butylpyridinium tetrafluoroborate ([BPY]⁺[BF₄]⁻) and thiophene (TS), benzothiophene (BT), dibenzothiophene (DBT) have been investigated by density functional theory. The most stable structure of the [BPY]⁺[BF₄]⁻ ion-pair indicated that hydrogen bonding interactions between fluorine atoms on [BF₄]⁻ anions and C2–H2 on the pyridinium ring play an important role in the formation of the ion-pair. The NBO and AIM analyses indicate the occurrence of π–π stacking interactions. The electron density at bond critical points and Wiberg bond indices are correlated with the interacting distances of H···F interactions, so electron density and Wiberg bond index can demonstrate the interacting strength of H···F hydrogen bonds. The interaction energies suggest that DBT adsorbs prior to the other compounds on N-butylpyridinium tetrafluoroborate ionic liquid.

Supplementary Materials:
Supplementary material for this article is supplied as a separate file:

mmc1.doc

Metadata

Received: 2013-03-09
Accepted: 2013-05-27
Published online: 2013-07-09

DOI: 10.1016/j.crci.2013.05.015

Mots-clés : Ionic liquid, Density functional theory, Thiophene, Benzothiophene, Dibenzothiophene

Author's affiliations:

Renqing Lü ¹; Peng Gu ²; Dong Liu ²; Yukun Lu ¹; Shutao Wang ¹

¹ College of Science, China University of Petroleum (East China), Qingdao 266580, China
² College of Chemical Engineering, China University of Petroleum (East China), Qingdao 266580, China

@article{CRCHIM_2013__16_12_1118_0,
     author = {Renqing L\"u and Peng Gu and Dong Liu and Yukun Lu and Shutao Wang},
     title = {The nature of interactions between {\protect\emph{N}-butylpyridinium} tetrafluoroborate and thiophenic compounds: {A} theoretical investigation},
     journal = {Comptes Rendus. Chimie},
     pages = {1118--1126},
     publisher = {Elsevier},
     volume = {16},
     number = {12},
     year = {2013},
     doi = {10.1016/j.crci.2013.05.015},
     language = {en},
}

TY  - JOUR
AU  - Renqing Lü
AU  - Peng Gu
AU  - Dong Liu
AU  - Yukun Lu
AU  - Shutao Wang
TI  - The nature of interactions between N-butylpyridinium tetrafluoroborate and thiophenic compounds: A theoretical investigation
JO  - Comptes Rendus. Chimie
PY  - 2013
SP  - 1118
EP  - 1126
VL  - 16
IS  - 12
PB  - Elsevier
DO  - 10.1016/j.crci.2013.05.015
LA  - en
ID  - CRCHIM_2013__16_12_1118_0
ER  -

%0 Journal Article
%A Renqing Lü
%A Peng Gu
%A Dong Liu
%A Yukun Lu
%A Shutao Wang
%T The nature of interactions between N-butylpyridinium tetrafluoroborate and thiophenic compounds: A theoretical investigation
%J Comptes Rendus. Chimie
%D 2013
%P 1118-1126
%V 16
%N 12
%I Elsevier
%R 10.1016/j.crci.2013.05.015
%G en
%F CRCHIM_2013__16_12_1118_0

Renqing Lü; Peng Gu; Dong Liu; Yukun Lu; Shutao Wang. The nature of interactions between N-butylpyridinium tetrafluoroborate and thiophenic compounds: A theoretical investigation. Comptes Rendus. Chimie, Volume 16 (2013) no. 12, pp. 1118-1126. doi : 10.1016/j.crci.2013.05.015. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2013.05.015/

Version originale du texte intégral

1 Introduction

Fuel desulfurization has received worldwide attention because environmental regulation of the sulfur limit for fuels is becoming increasingly stringent. The EU legislation set the upper limit of the sulfur content in diesel fuels to 10 ppm in 2009 and the US Environmental Protection Agency (EPA) reduced the limit for the sulfur content in diesel fuels to 15 ppm in 2006–2010 [1,2]. Conventional hydrodesulfurization (HDS) is more effective for the removal of aliphatic sulfur compounds than for the removal of sulfur-containing aromatic compounds, such as thiophene, benzothiophene, and dibenzothiophene series. HDS requires high temperatures and high hydrogen pressures in order to eliminate the alicyclic sulfur compounds [3]. Alternative sulfur removal techniques should be explored. In the past years, ionic liquids have gained increasing interest due to their unique properties both as extractant and catalyst [4]. The first attempt of deep desulfurization using ionic liquids was made by Bosmann et al. in 2001 [5]. Lo et al. firstly investigated the removal of sulfur-containing compounds from light oils by a combination of both chemical oxidation and solvent extraction using imidazolium-based ionic liquids [6]. Following their reports, sulfur and nitrogen removals by extraction or oxidative desulfurization using ionic liquids have been extensively investigated.

Recently, pyridinium-based ionic liquids were employed to remove sulfur compounds from fuel [7–16]. The mechanism for the extraction of sulfur compounds with pyridinium-based ionic liquids was proposed as a possible π–π interaction between aromatic sulfur compounds and the pyridinium rings of ionic liquids.

In 2008, Gao et al. investigated the use of N-butylpyridinium tetrafluoroborate ([BPY]⁺[BF₄]⁻) as a solvent for deep desulfurization of fuels [7]. The high extraction of sulfur compounds with pyridinium-based ionic liquids was ascribed to a possible π–π interaction between ionic liquids and aromatics. However, the detailed structures and nature of the interactions between [BPY]⁺[BF₄]⁻ and thiophene (TS), benzothiophene (BT), dibenzothiophene (DBT) are still unknown. Therefore, this work reports an analysis of structures of [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, and [BPY]⁺[BF₄]⁻ − DBT complexes using quantum chemical calculations. The theoretical results here will confirm the formation of hydrogen bonding and π···π interactions between [BPY]⁺[BF₄]⁻ and TS, BT, DBT at the molecular level firstly.

2 Specification of initial structures

The structures of the N-butylpyridinium cation ([BPY]⁺), [BF₄]⁻, thiophene (TS), benzothiophene (BT), and dibenzothiophene (DBT) are shown in Fig. 1. The [BF₄]⁻ anion or/and TS, BT, DBT have been gradually placed in different regions around the [BPY]⁺ cation to form [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, and [BPY]⁺[BF₄]⁻ − DBT for optimization. The most stable structures were further employed for NBO and AIM analyses.

Fig. 1
Structures of (a) N-butylpyridinium([BPY]⁺) (b) [BF₄]⁻ (c) thiophene (TS) (d) benzothiophene (BT) and (e) dibenzothiophene (DBT).

3 Computational details

All geometric optimizations reported here were performed at the level of ω-B97XD/aug-cc-pVTZ with spherical-harmonic-type basis functions 5d and 7f. ω-B97XD was produced by Head-Gordon and Chai, whose work contains empirical dispersion and long-range corrections [17,18]. All the stationary structures have been fully optimized without geometrical constraints. A frequency analysis was performed on all structures to insure the absence of imaginary frequencies. To examine the nature of interactions, the electronic properties of stationary points are illustrated based on natural bond orbital (NBO) analysis [19]. These non-local donor–acceptor-orbital interactions are associated with the delocalization of electron density between states _i and _j in the NBO basis, as given by:

E (2) = △ E_{i j} = n_{i} \frac{{(F_{i j})}^{2}}{ε_{j} - ε_{i}}

where n_i is the donor orbital occupancy, ɛ_i and ɛ_j are the diagonal elements, and F_ij is the off-diagonal NBO Fork matrix element. Intermolecular interactions such as lone pair → anti-bonding orbital mixtures are representative of donor–acceptor bonding, whereas non-Lewis-type (highly delocalized) interactions such as anti-bond → anti-bond orbital mixtures represent effects like resonance stabilization. The AIM analysis was used to analyze the nature of interactions at the same level by AIM2000 package [20,21] with the wave function-generated results.

The interaction energies between [BPY]⁺[BF₄]⁻ and TS, BT, DBT were calculated using the following expression:

ΔE = –{E([BPY]⁺[BF₄]⁻ − TS/BT/DBT) − [E([BPY]⁺[BF₄]⁻) + E(TS/BT/DBT)]}

where E([BPY]⁺[BF₄]⁻ − TS/BT/DBT) represents the energies of [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, and [BPY]⁺[BF₄]⁻ − DBT, E([BPY]⁺[BF₄]⁻) and E([BPY]⁺[BF₄]⁻), E(TS/BT/DBT) the individual energies of [BPY]⁺[BF₄]⁻, TS, BT, DBT; ΔE is the interaction energies between [BPY]⁺[BF₄]⁻ and TS, BT, DBT. The basis set superposition error (BSSE) was also considered by the counterpoise method.

4 Results and discussion

4.1 Geometries of [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT and [BPY]+[BF₄]⁻ − DBT

In this section, we discussed the most stable geometries of [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT and [BPY]⁺[BF₄]⁻ − DBT. In order to give a visual understanding of [BPY]⁺[BF₄]⁻ pair interactions before the design of initial geometries for the ion-pair, the electrostatic potential for the most stable geometries of the isolated [BPY]⁺ cation and [BF₄]⁻ anion were calculated to gain the possible interaction modes between cation and anion shown in Fig. 2, respectively. The highly negative regions of the [BF₄]⁻anion are on the electronegative F atoms, while the highly positive regions in the [BPY]⁺ cation are around the pyridinium ring hydrogen atoms and the butyl hydrogen atoms. The possible interacting sites on the more positively charged regions of the [BPY]⁺ cation and the more negatively charged regions of the [BF₄]⁻ anion have been taken into consideration for the initial geometry design. The most stable structure of [BPY]⁺[BF₄]⁻ is shown in Fig. 3a. It can be found that [BPY]⁺[BF₄]⁻ has five F···H interactions. The interacting distances are 1.861 Å (F4···H2), 2.337 Å (F1···H2), 2.246 Å (F2···H71), 2.246 Å (F1···H71) and 2.506 Å (F4···H81), while the sum of Bondi's van der Waals radii of fluorine atom and hydrogen atom (1.47 Å and 1.20 Å) is 2.67 Å [22]. The short distances of H2 and H71-involved interactions may be ascribed to the highly positive H2 and H71 due to the withdrawing electron of the nitrogen atom. A single hydrogen atom may participate in two hydrogen bonds instead of one. This type of bonding is called bifurcated hydrogen bonding (three-center hydrogen bonding) [23]. The results show that H71 and H2 in [BPY]⁺[BF₄]⁻ are involved in the formation of bifurcated hydrogen bonding. The F···H contacts within the bifurcated hydrogen bonds are found to be unequivalent in terms of the different F···H distances. These deviations from linearity of the C–H···F angles are common for bifurcated hydrogen bonds.

Fig. 2
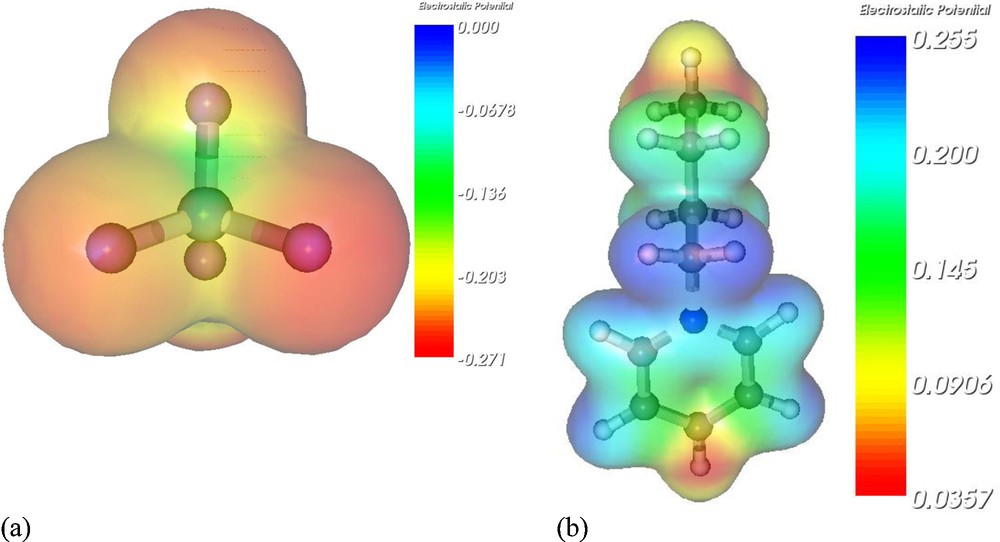
Electrostatic potentials (ESP) of (a) the [BF₄]⁻ anion and (b) the [BPY]⁺ cation.

Fig. 3
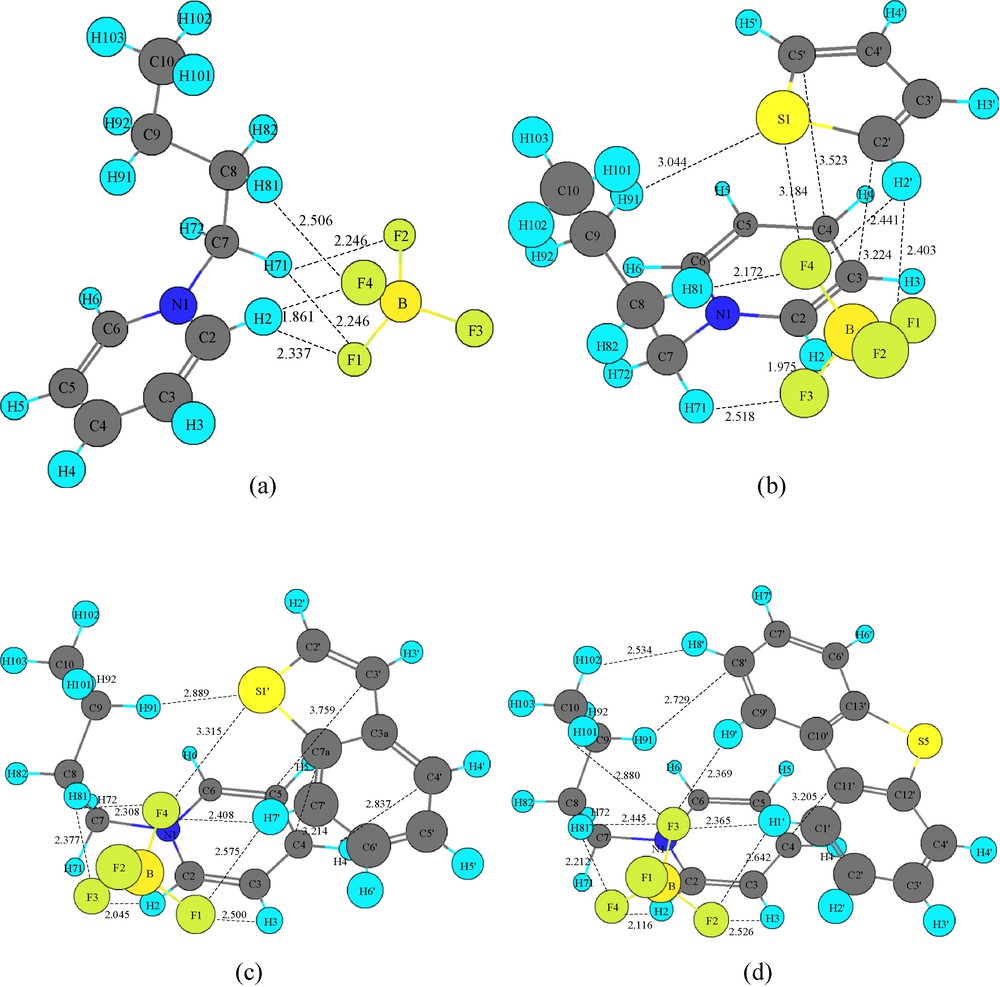
Optimized structures and some interacting distances (Å) of (a) [BPY]⁺[BF₄]⁻, (b) [BPY]⁺[BF₄]⁻ − TS, (c) [BPY]⁺[BF₄]⁻ − BT, and (d) [BPY]⁺[BF₄]⁻ − DBT. Color available on the web.

The most stable structures of [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT and [BPY]⁺[BF₄]⁻ − DBT are shown in Fig. 3b–3d. Similar results for the strongest hydrogen bonds between one fluorine atom on the [BF₄]⁻ anion and C2–H2 on the pyridinium ring were obtained for the above three structures. In the most stable [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT and [BPY]⁺[BF₄]⁻ − DBT structures, the ring planes of TS, BT, DBT and of the pyridinium ring are parallel to each other, implying that π–π interactions may occur. π–π Interaction (also called π–π stacking) refers to attractive non-covalent interactions between aromatic rings. Despite their frequent occurrence, there is no unifying picture of the factors that contribute to the interaction, which include electrostatic (quadrapole–quadrapole, quadrapole–dipole, and dipole–dipole), hydrophobic, and van der Waals interactions. This is complicated by the fact that aromatic rings interact in several different conformations, each of which is favored by a different combination of forces. The face-face stacked, edge-face stacked, and offset stacked geometries are three representative configurations of π–π interactions [24,25]. As shown in Fig. 3b–3d, the offset parallel stacking interactions between the pyridinium ring and TS, BT, DBT rings occur. The offset stacked interactions are dependent on the orientation of the rings; it seems that the interactions of S1···H91 (3.044 Å), F4···H2′ (2.441 Å), F1···H2′ (2.403 Å) in [BPY]⁺[BF₄]⁻ − TS, F1···H7′ (2.575 Å), F4···H7′(2.408 Å), S′···H91 (2.889 Å) in [BPY]⁺[BF₄]⁻ − BT, F3···H9′ (2.369 Å), F2···H1′ (2.642 Å), F3···H1′ (2.365 Å) in [BPY]⁺[BF₄]⁻ − DBT may pronouncedly influence the formation of π–π interactions [26]. The interactions of C5′···C4 (3.523 Å), C2′···C3 (3.224 Å) in [BPY]⁺[BF₄]⁻ − TS, C7a···C4 (3.214 Å) in [BPY]⁺[BF₄]⁻ − BT, C11′···C4 (3.205 Å) in [BPY]⁺[BF₄]⁻ − DBT demonstrate the occurrence of π–π interactions.

4.2 Interaction energies

The interaction energies between [BPY]⁺[BF₄]⁻ and TS, BT, DBT are important factors in reasonable explanations for the extraction of TS, BT and DBT by [BPY]⁺[BF₄]⁻ ionic liquids. So, we investigated the interaction energies between [BPY]⁺[BF₄]⁻ and TS, BT, DBT. Interaction energy (ΔE) is defined as the difference between the energy of the appointed complexes and the sum of the energies of its free fragments. The interaction energies between [BPY]⁺[BF₄]⁻ and TS, BT, DBT are 10.29 kcal/mol, 14.59 kcal/mol, and 18.30 kcal/mol, demonstrating that the magnitude of the interacting energies follows the trend [BPY]⁺[BF₄]⁻ − TS < [BPY]⁺[BF₄]⁻ − BT < [BPY]⁺[BF₄]⁻ − DBT.

4.3 NBO analysis

NBO analyses for TS, BT, DBT, [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, and [BPY]⁺[BF₄]⁻ − DBT were carried out to obtain the charge distribution and intrinsic properties of the interactions between [BPY]⁺[BF₄]⁻ and TS, BT, DBT. From NBO atomic charges, most of the positive charge is focused on the peripheral hydrogen atoms of the pyridinium ring and the butyl hydrogen atoms in the [BPY]⁺ cation, while the [BF₄]⁻ anion preferentially approaches the positively charged groups, indicating that the electrostatic interaction between the [BPY]⁺ cation and the [BF₄]⁻ anion is dominative for the formation of the ion-pair. The sums of the charges of [BF₄]⁻ in [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, and [BPY]⁺[BF₄]⁻ − DBT are −0.94337, −0.95082, −0.95787, −0.95663, suggesting that the negative charges migrate from [BF₄]⁻ to other parts. It is clear that TS, BT, DBT adsorptions on [BPY]⁺[BF₄]⁻ influence the charge distribution in [BPY]⁺[BF₄]⁻ and TS, BT, DBT. Compared with the NBO charges, the positive charge of H and the negative charge of F increase when they are involved in H···F interactions. The shorter the H···F contact, the larger the increase in the positive charges of hydrogen atoms and in the negative charges of fluorine atoms. The interactions between the F of [BF₄]⁻ and TS, BT, DBT increase the negative charges of F, resulting in the less negative charge migration of [BF₄]⁻ in [BPY]⁺[BF₄]⁻ − TS (−0.95082), [BPY]⁺[BF₄]⁻ − BT (−0.95787), and [BPY]⁺[BF₄]⁻ − DBT (−0.95663) in contrast with that of [BPY]⁺[BF₄]⁻ (−0.94337).

It seems quite well accepted that hydrogen bonding influences the structures of ionic liquids. The NBO method can provide information about the interactions in both filled and virtual orbital spaces that facilitates analysis of the intermolecular interactions. A second-order perturbation theory analysis of the Fock matrix was carried out to evaluate donor–acceptor interactions in the NBO basis. In this analysis, a stabilization energy E(2) related to the delocalization trend of the electrons from donor to acceptor orbitals was calculated via perturbation theory. If the stabilization energy E(2) between a donor bonding orbital and an acceptor-orbital is large, then there is a strong interaction between them. Table 1 lists the selected donor–acceptor interactions in [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, [BPY]⁺[BF₄]⁻ − DBT and their second-order perturbation stabilization energies. As indicated in Table 1, the C2–H2 involved hydrogen bonds are the strongest, in terms of the large E(2) of 16.67 kcal/mol (LP(F4)→σ*(C2–H2)) in [BPY]⁺[BF₄]⁻, 9.13 kcal/mol (LP(F3)→σ*(C2–H2)) in [BPY]⁺[BF₄]⁻ − TS, 7.01 kcal/mol (LP(F3)→σ*(C2–H2)) in [BPY]⁺[BF₄]⁻ − BT, 5.38 kcal/mol (LP(F4)→σ*(C2–H2)) in [BPY]⁺[BF₄]⁻ − DBT, in agreement with their short F···H contacts.

Donor	Acceptor	E(2) (kcal/mol)	Donor	Acceptor	E(2) (kcal/mol)
[BPY]⁺[BF₄]⁻
LP(F1)	π*(N1–C2)	1.47	LP(F1)	σ*(C7–H71)	1.46
LP(F1)	σ*(C2–H2)	0.31	LP(F1)	σ*(N1–C2)	0.06
LP(F1)	σ*(N1–C7)	0.06	LP(F1)	σ*(C2–C3)	0.08
LP(F3)	σ*(C2–H2)	0.12	LP(F3)	σ*(C7–H71)	0.18
LP(F4)	σ*(C2–H2)	16.67	LP(F4)	σ*(C8–H81)	1.27
LP(F2)	σ*(C7–H71)	2.43	LP(F2)	σ*(C8–C9)	0.18
LP(F2)	σ*(N1–C7)	0.10

[BPY]⁺[BF₄]⁻ − TS
LP(F1)	σ*(C2–H2)	1.18	LP(F1)	σ*(C2–N1)	0.43
LP(F1)	σ*(C4–C3)	0.11	LP(F1)	π*(C2′–C3′)	0.10
LP(F1)	π*(C2–N1)	0.19	LP(F1)	σ*(C2′H2′)	1.48
LP(F3)	σ*(C9–C8)	0.08	LP(F3)	σ*(C7–H71)	0.64
LP(F3)	σ*(C8–H81)	0.15	LP(F3)	σ*(C2–H2)	9.13
LP(F3)	σ*(C7–H72)	0.06	LP(F3)	σ*(C2–C3)	0.11
LP(F3)	σ*(C2′–H2′)	0.07	LP(F4)	σ*(C8–H81)	5.47
LP(F4)	π*(C2–N1)	0.12	LP(F4)	σ*(C2′–H2′)	0.66
LP(F4)	σ*(C2′–C3′)	0.24	LP(F4)	σ*(S1–C5′)	0.55
LP(F2)	σ*(C2–H2)	0.24	π(C4–C3)	π*(C2′–C3′)	0.06
LP(F2)	π*(C2–N1)	0.07	π(C5–C6)	π*(C4′–C5′)	0.11
σ(C9–H91)	σ*(S1–C2′)	0.07	π*(C4–C3)	π*(C2′–C3′)	1.51
π*(C2–N1)	π*(C2′–C3′)	0.12	π*(C5–C6)	π*(C4′–C5′)	0.46
π(C4′–C5′)	π*(C4–C3)	0.86	π(C2′–C3′)	π*(C4–C3)	0.54
π(C2′–C3′)	π*(C5–C6)	0.05	π(C4′–C5′)	π*(C5–C6)	0.14
LP(S1)	π*(C2–N1)	0.27	LP(S1)	σ*(C9–H91)	0.64

[BPY]⁺[BF₄]⁻ − BT
LP(F1)	σ*(C4–C3)	0.27	LP(F1)	σ*(C3–H3)	0.48
LP(F1)	π*(C4–C3)	0.22	LP(F1)	σ*(C2–N1)	0.22
LP(F1)	π*(C2–N1)	0.08	LP(F1)	σ*(C2–H2)	0.08
LP(F1)	σ*(C8–H81)	0.10	LP(F1)	σ*(C7′–H7′)	0.39
LP(F3)	σ*(C2–H2)	7.01	LP(F3)	σ*(C2–C3)	0.06
LP(F3)	π*(C2–N1)	0.20	LP(F3)	σ*(C8–H81)	1.75
LP(F4)	π*(C2–N1)	1.15	LP(F3)	σ*(C7′–H7′)	0.15
LP(F4)	σ*(C7′–H7′)	1.03	LP(F4)	σ*(C8–H81)	2.05
LP(F4)	σ*(C8–H82)	0.08	LP(F4)	σ*(C2′–S1′)	0.17
LP(F4)	π*(C6′–C7′)	0.06	LP(F4)	σ*(C6′–C7′)	0.05
LP(F2)	σ*(C8–H81)	0.06	LP(F2)	π*(C2–N1)	0.13
LP(F2)	σ*(C2–H2)	0.09	π(C6′–C7′)	π*(C2–N1)	0.05
π(C4–C3)	π*(C7a–C3a)	0.13	π(C4–C3)	π*(C6′–C7′)	0.27
π(C6′–C7′)	σ*(C3–H3)	0.05	π*(C4–C3)	π*(C6′–C7′)	0.16
π(C5′–C4′)	σ*(C4–H4)	0.84	π(C6′–C7′)	π*(C4–C3)	0.08
π(C3′–C2′)	π*(C5–C6)	0.14	π(C7a–C3a)	π*(C4–C3)	1.21
π(C7a–C3a)	π*(C5–C6)	0.09	π(C3’–C2’)	σ*(C5–H5)	0.06
LP(S1′)	σ*(C9–H91)	2.18

[BPY]⁺[BF₄]⁻ − DBT
LP(F1)	π*(C2–N1)	0.12	LP(F1)	σ*(C2–H2)	0.10
LP(F1)	σ*(C8–H81)	0.06	σ(C10–H101)	σ*(C8′–H8′)	0.11
LP(F3)	σ*(C9′–H9′)	1.67	LP(F3)	σ*(C1′–H1′)	1.63
LP(F3)	π*(C2–N1)	1.40	LP(F3)	σ*(C8–H81)	0.73
LP(F3)	σ*(C10–H101)	0.13	LP(F3)	σ*(C8–H82)	0.09
LP(F4)	σ*(C1′–H1′)	0.15	LP(F4)	σ*(C2–H2)	5.38
LP(F4)	σ*(C8–H81)	4.08	LP(F4)	π*(C2–N1)	0.15
LP(F4)	σ*(C2–C3)	0.05	LP(F2)	σ*(C2–H2)	0.13
LP(F2)	π*(C11′–C1′)	0.14	LP(F2)	σ*(C4–C3)	0.24
LP(F2)	σ*(C3–H3)	0.44	LP(F2)	π*(C4–C3)	0.19
LP(F2)	σ*(C2–N1)	0.18	LP(F2)	σ*(C8–H81)	0.09
LP(F2)	π*(C2–N1)	0.06	LP(F2)	σ*(C11′–C1′)	0.06
LP(F2)	σ*(C1′–H1′)	0.08	σ(C4–H4)	π*(C12′–C4′)	0.09
π*(C12′–C4′)	σ*(C4–H4)	0.13	π*(C4–C3)	σ*(C4′–H4′)	0.15
π(C13′–C10′)	π*(C4–C3)	0.47	π(C13′–C10′)	π*(C5–C6)	0.51
π(C6′–C7′)	σ*(C5–H5)	0.08	π(C11′–C1′)	π*(C5–C6)	0.06
π(C8′–C9′)	σ*(C9–H91)	1.19	π(C12′–C4′)	σ*(C4–H4)	0.39
π(C4–C3)	π*(C13′–C10′)	0.17	σ(C4–H4)	π*(C11′–C1′)	0.10
σ(C3–H3)	π*(C11′–C1′)	0.06	σ(C8′–H8′)	σ*(C9–H91)	0.07
π*(C4–C3)	π*(C11′–C1′)	2.83	π*(C5–C6)	π*(C8′–C9′)	0.06
σ(C8′–H8′)	σ*(C9–H91)	0.08	π(C11′–C1′)	π*(C2–N1)	0.06
σ(C12′–C4′)	σ*(C5–H5)	0.07	π(C12′–C4′)	σ*(C6–N1)	0.07
π(C2′–C3′)	σ*(C3–H3)	0.06	σ(C3′–C4′)	σ*(C5–H5)	0.06
σ(C4–H4)	σ*(C5–H5)	0.32	σ(C4–H4)	σ*(C6–N1)	0.17

The π–π interactions were studied based on the calculations of the natural bond orbital (NBO) method, which is now widely used for analyzing chemical bonds in non-covalent compounds. Table 1 shows that hydrogen bonding (LP(F)→ σ*(C–H)), and LP(F)···π occur between [BPY]⁺[BF₄]⁻ and TS, BT, DBT. The π(π*)→π* interactions between [BPY]⁺[BF₄]⁻ and TS, BT, DBT indicate the occurrence of π···π interactions. It is noted that the charges of sulfur of TS, BT, and DBT are +0.45934, +0.42368 and +0.41332, while the sulfur-involved interactions are LP(S1)→σ*(C9–H91) (0.64 kcal/mol), LP(S1)→π*(C2–N1) (0.27 kcal/mol) in [BPY]⁺[BF₄]⁻ − TS, LP(S1′)→σ*(C9–H91) (2.18 kcal/mol) in [BPY]⁺[BF₄]⁻ − BT, indicating that the trend of sulfur-involved interactions is BT > TS > DBT, which may be ascribed to steric hindrance.

In addition, the Wiberg bond index (WBI) [27] has been used to evaluate the number of covalent bonds, or evaluate the strength of covalent bonds. The Wiberg bond index is calculated as the sum of the quadratic non-diagonal elements of the density matrix between two atoms. In π–π stacking systems if the distance of a pair of atoms is within 3.7 Å, there may be a special π–π stacking bond for this pair of atoms and ring bond strength should be evaluated by the Wiberg bond index. So, we try to evaluate the ring bond strengths of the present π–π stacking system with the Wiberg bond index. Fig. 4 displays the Wiberg bond indices (WBI) of ring bonds. The significant changes of WBI of ring bonds may be ascribed to the π–π interactions. There exist bond critical points of C5′···C4, C2′···C3 in [BPY]⁺[BF₄]⁻, C3’···C5, C7a···C4 in [BPY]⁺[BF₄]⁻ − BT, and C4···C11′ in [BPY]⁺[BF₄]⁻ − DBT, their corresponding WBI are 0.0035, 0.0054, 0.0006, 0.0032 and 0.0028, indicating the occurrence of π–π interactions.

Fig. 4
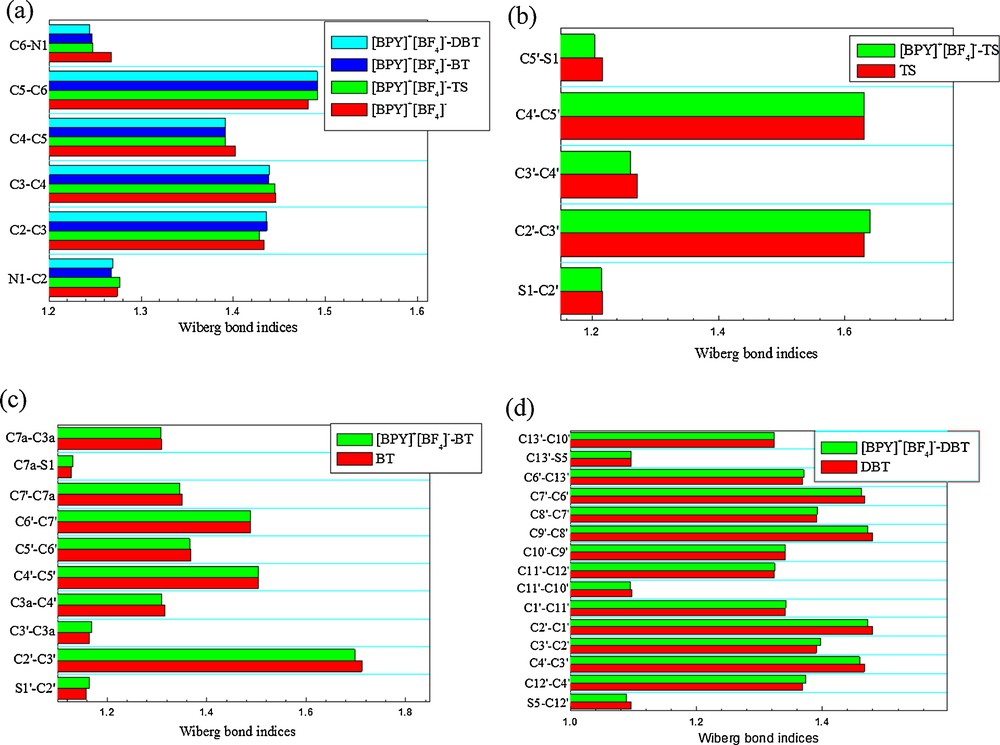
Wiberg bond indices of (a) pyridinium ring bonds of [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, and [BPY]⁺[BF₄]⁻ −vDBT, (b) thiophenic ring bonds of TS and [BPY]⁺[BF₄]⁻ − TS, (c) benzothiophenic ring bonds of BT and [BPY]⁺[BF₄]⁻ – BT, and (d) dibenzothiophenic ring bonds of DBT and [BPY]⁺[BF₄]⁻ − DBT. Color available on the web.

The WBI of the H···F interactions of [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ – BT, [BPY]⁺[BF₄]⁻ − DBT and their corresponding interacting distances are shown in Fig. 5. It can be seen that the WBI are correlated with their interacting distances. The higher the WBI, the longer the interacting distances.

Fig. 5
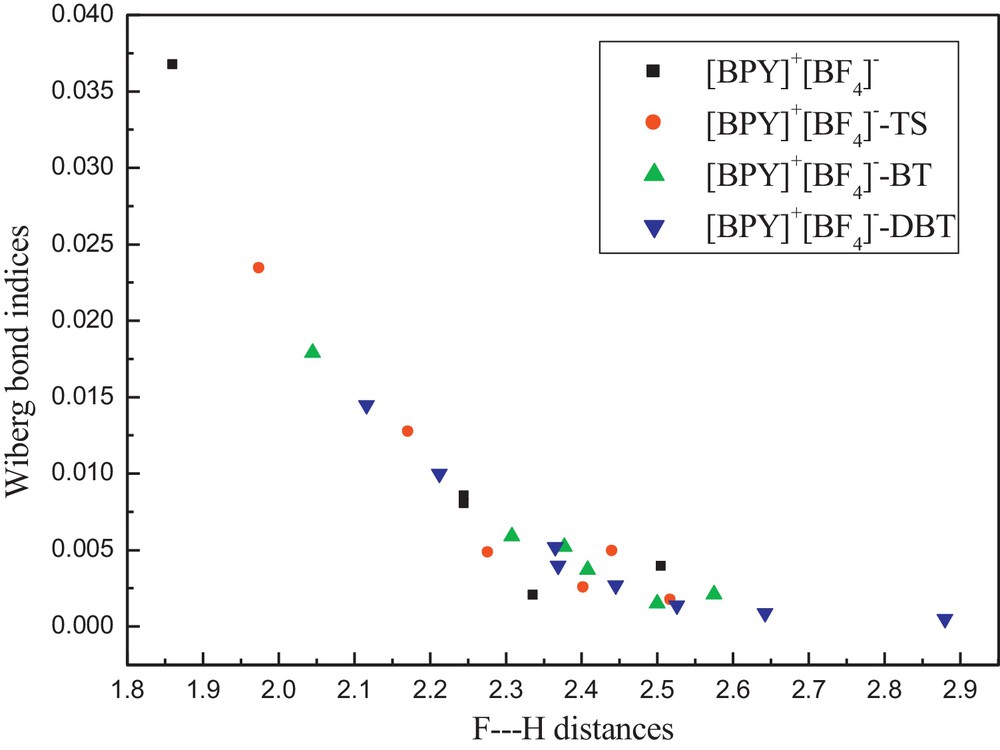
Relationship between F···H distances (Å) and their Wiberg bond indices. Color available on the web.

4.4 Topological properties analyses

The bond properties between each pair of atoms were systematically analyzed using quantum theory of atoms in molecules (AIM) [28], which is based on the topological analysis of electron density (ρ) and of its Laplacian (▿²ρ) at the bond critical points (BCPs). Covalent bonding is characterized by ▿²ρ < 0, while closed-shell bonding interaction is characterized by density depletion in the region of contact of the two atoms and ▿²ρ > 0. Electron density (ρ) is used to describe the strength of a bond, a stronger bond being associated with a larger value of ρ. The bond characteristics for the TS, BT, DBT, [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, [BPY]⁺[BF₄]⁻ − DBT were provided in Table 2. The evidence of interactions according to the AIM approach is the existence of a bond path between two atoms and the existence of a bond critical point (BCP) [29,30]. From the values of electron density listed in Table 2, it can be concluded that interactions between [BPY]⁺[BF₄]⁻ and TS, BT, DBT are all closed-shell systems in terms of positive values of ▿²ρ. A second AIM criterion to define hydrogen bond is that electron density (ρ) and the Laplacian of electron density (▿²ρ) at BCP must be within 0.002 ∼ 0.035 au and 0.024 ∼ 0.139 au ranges, respectively [29,30]. These values are within the commonly accepted values, indicating the occurrence of hydrogen bonding interactions in these systems. Bond critical points are F4···H2’, F4···S1, F1···H2’, S1···H91, C5’···C4, C2’···C3 in [BPY]⁺[BF₄]⁻ − TS, F1···H7’, F4···H7’, F4···S1’, H91···S1’, C3’···C5, C4’··H4, C7a··C4 in [BPY]⁺[BF₄]⁻ – BT, and F2···H1’, F3···H1’, F3···H9’, C8’···H91, C4···C11’ in [BPY]⁺[BF₄]⁻ − DBT, demonstrating that π···π interactions occur between [BPY]⁺[BF₄]⁻ and TS, BT, DBT. The tendency of sulfur-involved interactions between TS, BT, DBT and [BPY]⁺[BF₄]⁻ is BT > TS > DBT, in agreement with NBO analyses.

Species	X···Y	cp type	D/Å	ρ	▿²ρ	WBI
TS	TS ring	(3, +1)	···	0.03905	0.27129	···

BT	TS ring	(3, +1)	···	0.03701	0.25568	···
	BZ ring	(3, +1)	···	0.02053	0.16178	···

DBT	TS ring	(3, +1)	···	0.03517	0.24005	···
	BZ ring1	(3, +1)	···	0.02072	0.16270	···
	BZ ring2	(3, +1)	···	0.02072	0.16270	···

[BPY]⁺[BF₄]⁻	F1···H2	(3, −1)	2.337	0.01320	0.05963	0.0020
	F1···H71	(3, −1)	2.246	0.01387	0.05191	0.0085
	F4···H2	(3, −1)	1.861	0.02927	0.08921	0.0367
	F4···H81	(3, −1)	2.506	0.00804	0.03312	0.0039
	F2···H71	(3, −1)	2.246	0.01355	0.05211	0.0080
	PY ring	(3, +1)	···	0.02211	0.17729	···

[BPY]⁺[BF₄]⁻ − TS	F3···H71	(3, −1)	2.518	0.00797	0.03499	0.0017
	F3···H2	(3, −1)	1.975	0.02353	0.07393	0.0234
	F1···H2	(3, −1)	2.277	0.01303	0.05634	0.0048
	F4···H81	(3, −1)	2.172	0.01529	0.05125	0.0127
	F4···H2′	(3, −1)	2.441	0.00922	0.04051	0.0049
	F4···S1	(3, −1)	3.184	0.00651	0.03058	0.0029
	F1···H2′	(3, −1)	2.403	0.00911	0.03803	0.0025
	S1···H91	(3, −1)	3.044	0.00573	0.00470	0.0025
	C5′···C4	(3, −1)	3.523	0.00523	0.01397	0.0035
	C2′···C3	(3, −1)	3.224	0.00769	0.02143	0.0054
	PY ring	(3, +1)	···	0.02209	0.17742	···
	TS ring	(3, +1)	···	0.03901	0.27120	···

[BPY]⁺[BF₄]⁻ − BT	F3···H2	(3, −1)	2.045	0.02068	0.06820	0.0179
	F3···H81	(3, −1)	2.377	0.01027	0.04058	0.0052
	F1···H3	(3, −1)	2.500	0.00884	0.04017	0.0015
	F1···H7′	(3, −1)	2.575	0.00662	0.02990	0.0021
	F4···H81	(3, −1)	2.308	0.01194	0.04573	0.0059
	F4···H7′	(3, −1)	2.408	0.00957	0.03930	0.0037
	F4···S1′	(3, −1)	3.315	0.00502	0.02284	0.0019
	H91···S1′	(3, −1)	2.889	0.00771	0.02404	0.0062
	C3’···C5	(3, −1)	3.759	0.00347	0.01057	0.0006
	C4’··H4	(3, −1)	2.837	0.00646	0.02133	0.0016
	C7a··C4	(3, −1)	3.214	0.00764	0.02276	0.0032
	PY ring	(3, +1)	···	0.02211	0.17759	···
	TS ring	(3, +1)	···	0.03735	0.25561	···
	BZ ring	(3, +1)	···	0.02079	0.16179	···

[BPY]⁺[BF₄]⁻ − DBT	F4···H2	(3, −1)	2.116	0.01774	0.06064	0.0145
	F4···H81	(3, −1)	2.212	0.01445	0.05040	0.0100
	F2···H3	(3, −1)	2.526	0.00827	0.03784	0.0014
	F2···H1′	(3, −1)	2.642	0.00657	0.03002	0.0009
	F3···H1′	(3, −1)	2.365	0.01029	0.03987	0.0052
	F3···C2	(3, −1)	2.870	0.01000	0.03990	0.0072
	F3···H81	(3, −1)	2.445	0.00938	0.03995	0.0027
	F3···H101	(3, −1)	2.880	0.00364	0.01700	0.0005
	F3···H9′	(3, −1)	2.369	0.00935	0.03818	0.0040
	C8′····H91	(3, −1)	2.729	0.00741	0.02512	0.0021
	C4···C11′	(3, −1)	3.205	0.00754	0.02489	0.0028
	PY ring	(3, +1)	···	0.02210	0.17737	···
	TS ring	(3, +1)	···	0.03529	0.23886	···
	BZ ring1	(3, +1)	···	0.02094	0.16305	···
	BZ ring2	(3, +1)	···	0.02097	0.16353	···

As can be seen in Table 2, the values of electron density for hydrogen bonding interactions in all configurations decrease with increasing interacting distances. This decrease in electron density in BCPs can be ascribed to a decrease in interaction energy. For hydrogen bonds, there is a correlation between the interaction distances and topological parameters at the BCPs [31,32]. Here, the existence of such a correlation has been checked for configurations [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, and [BPY]⁺[BF₄]⁻ − DBT. Fig. 6 presents the linear correlation between F···H distances and their corresponding ln(ρ_b) values in [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, and [BPY]⁺[BF₄]⁻ − DBT, confirming the dependence of hydrogen bonding strength on their distances.

Fig. 6
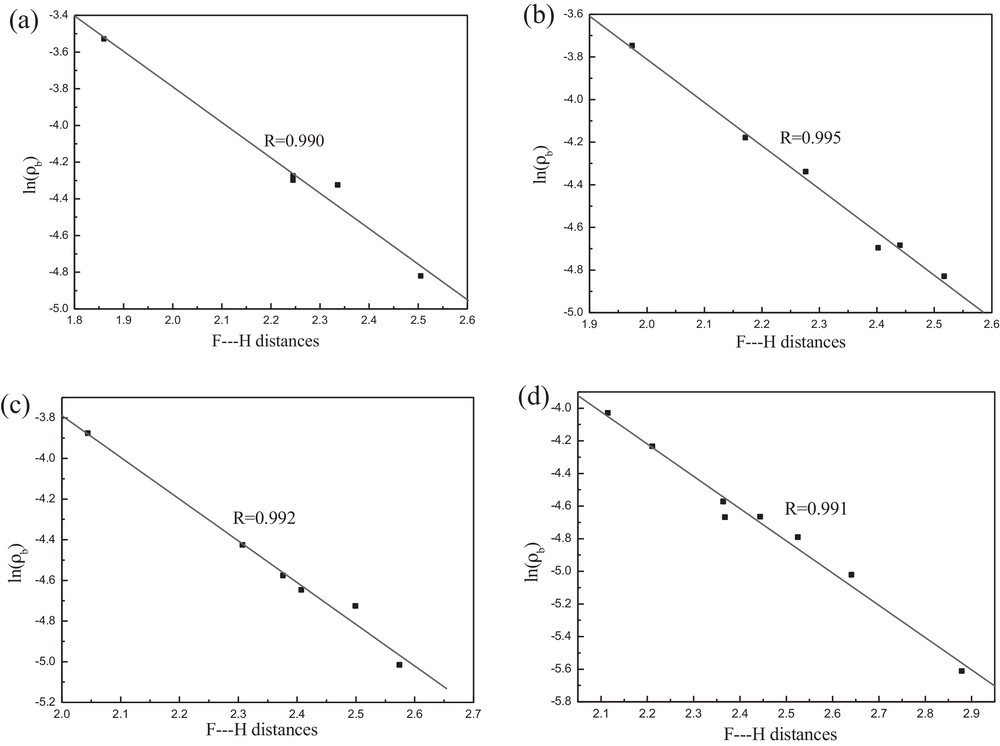
Regression plots between the F···H distances (Å) and the corresponding values of ln(ρ_b) of (a) [BPY]⁺[BF₄]⁻, (b) [BPY]⁺[BF₄]⁻ − TS, (c) [BPY]⁺[BF₄]⁻ − BT, and (d) [BPY]⁺[BF₄]⁻ − DBT.

5 Conclusions

In order to understand the nature of the interactions between N-butylpyridinium tetrafluoroborate ([BPY]⁺[BF₄]⁻) and thiophene (TS), benzothiophene (BT), dibenzothiophene (DBT), the structures of [BPY]⁺[BF₄]⁻, [BPY]⁺[BF₄]⁻ − TS, [BPY]⁺[BF₄]⁻ − BT, and [BPY]⁺[BF₄]⁻ − DBT were optimized using density functional theory, and the most stable geometries were discussed in terms of NBO and AIM analyses. The bond length, electron density at bond critical points and Wiberg bond index (WBI) were obtained. The results show that the multiple intermolecular hydrogen bonds play an important role in stabilizing the [BPY]⁺[BF₄]⁻ pair. NBO and AIM analyses proved that the π···π and hydrogen bonding interactions occur between [BPY]⁺[BF₄]⁻ and TS, BT, DBT. The order of the involved hydrogen interactions between [BPY]⁺[BF₄]⁻ and TS, BT, DBT is DBT > BT > TS in terms of WBI.

Acknowledgements

The authors gratefully acknowledge financial support from the Natural Science Foundation of China (21176259), awarded foundation for excellent young and middle-aged scientists of Shandong Province, China (BS2010NJ024) and the Natural Science Foundation of Shandong Province (ZR2011BQ004, ZR2011BQ020), China.

References

[1] http://www.epa.gov/otaq/fuels/dieselfuels/index.htm, accessed May 2013.

[2] http://www.dieselnet.com/standards/eu/fuel.php, accessed May 2013.

[3] A. Stanislaus; A. Marafi; M.S. Rana Catal. Today, 153 (2010), p. 1

[4] P.S. Kulkarni; C.A.M. Afonso Green Chem., 12 (2010), p. 1139

[5] A. Bosmann; L. Datsevich; A. Jess; A. Lauter; C. Schmitz; P. Wasseerscheid Chem. Commun. (2001), p. 2494

[6] W. Lo; H. Yang; G. Wei Green Chem., 5 (2003), p. 639

[7] H. Gao; M. Luo; J. Xing; Y. Wu; Y. Li; W. Li; Q. Liu; H. Liu Ind. Eng. Chem. Res., 47 (2008), p. 8384

[8] J. Wang; D. Zhao; E. Zhou; Z. Dong J. Fuel Chem. Technol., 35 (2007), p. 293

[9] D. Zhao; Y. Wang; E. Duan Molecules, 14 (2009), p. 4351

[10] H. Gao; Y. Li; Y. Wu; M. Luo; Q. Li; J. Xing; H. Liu Energy Fuels, 23 (2009), p. 2690

[11] D. Zhao; Y. Wang; E. Duan; J. Zhang Chem. J. Chin. Univ., 31 (2010), p. 488

[12] P. Verdía; E.J. González; B. Rodríguez-Cabo; E. Tojo Green Chem., 13 (2011), p. 2768

[13] R. Anantharaj; T. Banerjee J. Chem. Eng. Data, 56 (2011), p. 2770

[14] H. Gao; C. Guo; J. Xing; H. Liu Separation Sci. Technol., 47 (2012), p. 325

[15] C. Zhang; X. Pan; F. Wang; X. Liu Fuel, 102 (2012), p. 580

[16] B. Rodriguez-Cabo; M. Francisco; A. Soto; A. Arce Fluid Phase Equilib., 314 (2012), p. 107

[17] J.D. Chai; M. Head-Gordon J. Chem. Phys., 128 (2008), p. 084106

[18] J.D. Chai; M. Head-Gordon Phys. Chem. Chem. Phys., 10 (2008), p. 6615

[19] A.E. Reed; L.A. Curtiss; F. Weinhold Chem. Rev., 88 (1988), p. 899

[20] F. Biegler-König; J. Schönbohm J. Comput. Chem., 23 (2002), p. 14894

[21] F. Biegler-König; J. Schönbohm; D. Bayles J. Comput. Chem., 22 (2001), p. 545

[22] A. Bondi J. Phys. Chem., 68 (1964), p. 441

[23] I. Rozas; I. Alkorta; J. Elguero J. Phys. Chem. A, 102 (1998), p. 9925

[24] M.O. Sinnokrot; E.F. Valeev; C.D. Sherrill J. Am. Chem. Soc., 124 (2002), p. 10887

[25] C.A. Hunter; J.K.M. Sanders J. Am. Chem. Soc., 112 (1990), p. 5525

[26] M.J. Rashkin; M.L. Waters J. Am. Chem. Soc., 124 (2002), p. 1860

[27] K. Wiberg Tetrahedron, 24 (1968), p. 1083

[28] R.W.F. Bader Chem. Rev., 91 (1991), p. 893

[29] U. Koch; P.L.A. Popelier J. Phys. Chem., 99 (1995), p. 9747

[30] P.L.A. Popelier J. Phys. Chem. A, 102 (1998), p. 1873

[31] E. Espinosa; M. Souhassou; H. Lachekar; C. Lecomte Acta Cryst., B55 (1999), p. 563

[32] J. Netzel; S. van Smaalen Act Cryst., B65 (2009), p. 624

Comments - Policy